1.
Introduction
Mobile robot research includes navigation and positioning, motion control, path tracking and path planning. Path planning is one of the core contents of mobile robots. The so-called robot path planning technology refers to making feedback to the information collected by the environment through other sensors, and finding a collision-free motion path from the start point to the end point. Many scholars have proposed the path planning method of mobile robots, including path matching techniques such as module matching path planning, artificial potential field method, map construction path planning and artificial intelligence path planning [1]. The grid method in map construction path planning is widely used in global path planning of mobile robots, but it also has defects: the storage space is small and the search efficiency is reduced.
With the introduction of intelligent algorithms such as genetic algorithm, neural network, particle swarm optimization, immune algorithm, and ant colony optimization (ACO) [2,3,4], many scholars use artificial intelligence algorithms to perform path planning. Among them, ant colony optimization is widely used in path planning which is a heuristic search algorithm with strong robustness [5]. At the same time, the ant colony optimization also has many defects: the convergence speed is slow and it is easy to fall into the local optimal solution. Therefore, many scholars have made a lot of improvements to the ant colony optimization, including the improvement of the pheromone update method, the path selection strategy and combined with other algorithms as well as the multiple ant colony optimization [6]. For example, in [7], the generalized pheromone update rule is proposed to solve the deadlock phenomenon that ants face the concave obstacles to find the optimal solution. In [8], it is proposed to use different expected values. Adapting the volatilization coefficient to update the information hormone to find the optimal solution. In [9], a method to adjust the parameters of the ant colony optimization dynamically is proposed to achieve the pheromone update for finding the optimal solution. What was proposed in [10] is to discard the ants caught in the deadlock. When the number of iterations is greater than sixty generations, the pheromone intensity coefficient is reduced, so that the convergence speed of the algorithm is accelerated, and the optimization and obstacle avoidance capabilities are strengthened. In [11], a membrane evolutionary artificial potential field approach for solving the mobile robot path planning problem is proposed, which combines membrane computing with a genetic algorithm and the artificial potential field method to find the parameters to generate a feasible and safe path. In [12], the authors present a novel proposal to solve the path planning problem for mobile robots based on simple ant colony optimization meta-heuristic (SACO-MH). Based on the traditional ant colony optimization, node transition probability, node selection way and pheromone update method were respectively optimized and improved through introducing a new heuristic function factor, node random selection mechanism and update strategy of pheromone that includes the local updating and global updating of pheromone in [13]. An improved ant colony optimization is used in resolving this path planning problem, which can improve convergence rate by using this improved algorithm in [14]. A modified ant colony optimization for path planning of the mobile robot in a known static environment was proposed in [15]. A parallel elite ant colony optimization method is proposed to generate an initial collision-free path in a complex map in [16], and turning point optimization algorithm is used to optimize the initial path in terms of length, smoothness and safety. An efficient hybrid algorithm that takes profit of the advantages of both ACO and GA approaches for the sake of maximizing the chance to find the optimal path even under real-time constraints is designed in [17].
In view of the above problems and the solutions proposed by scholars, the improved algorithm still needs further optimization for robot path planning, especially in solving the problems of convergence speed and local optimal solution. The improved algorithm used in this paper is based on the traditional ant colony optimization. Firstly, the ant colony search ability at the initial moment is strengthened, the range is expanded, the local optimal solution is avoided, and the robustness is improved by adaptively changing the volatility coefficient. Secondly, the roulette operation is used in the state transition rule to effectively improve the quality of the solution and the convergence speed of the algorithm. Finally, the global search efficiency and convergence speed of the algorithm is effectively improved by the elite selection and the node crossover operation of the better path. The improved ant colony optimization has global control ability for pheromones at different moments, which provides a guarantee for improving the convergence speed and avoiding local optimal solutions. Finally, the improved ant colony optimization (IACO) is used to carry out the robot path planning. In the static obstacle environment, the optimal solution can be quickly obtained. In the complex static and dynamic obstacle environment, the corresponding strategies are proposed according to the motion state and motion law of static and dynamic obstacles to obtain the non-touch and sub-optimal paths to get relatively better results.
2.
Environmental modeling
Modeling methods for mobile robot working environment are mainly divided into the following types: Feature maps, grid maps. Among them, the grid method is widely used in robot working environment, because the grid method has the advantages of easy implementation and analysis, this paper will use the grid method to model the environment of mobile robots.
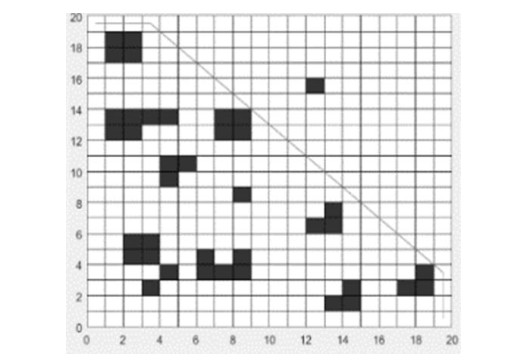
Firstly, a finite two-dimensional plane is defined as the moving area of the robot. Let's set the area to G. There are obstacles of the same size and position in the area. The white grid is the movable area of the robot which is recorded as 0. The black grid is a fixed obstacle which is marked as 1. The area marks the grid in order from left to right and top to bottom, and records it as 1, 2, 3, 4, ..., n, where each number represents a grid, as shown in Figure 1. In the lower left of the grid space, from left to right is defined as the positive X-axis direction, and from bottom to top is defined as the positive direction of the Y-axis. The length of the grid is defined as the unit length, thereby a two-dimensional coordinate plane XOY is established. The following is the correspondence between the grid number and coordinates:
In Eq (1), mod is the remainder operation; L is the serial number of the grid; N is the number of rows and columns of the grid; Ceil is the rounding function.
In order to avoid collision between the robot and the obstacle, the boundary of the obstacle is puffed, so the robot can be equivalent to a particle. The principle is to determine the position of the grid by judging the position of the obstacle point coordinates, and set the grid containing the obstacle as the obstacle grid.
3.
Obstacle problem analysis and its response strategy
3.1. U-shaped obstacles in static environment and their solutions
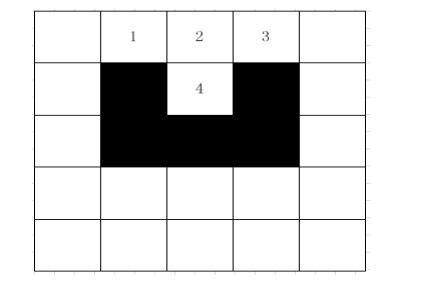
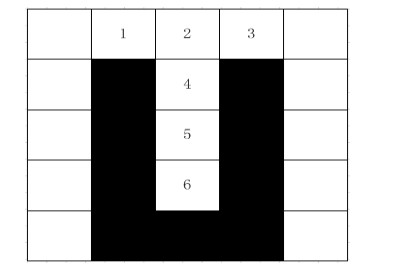
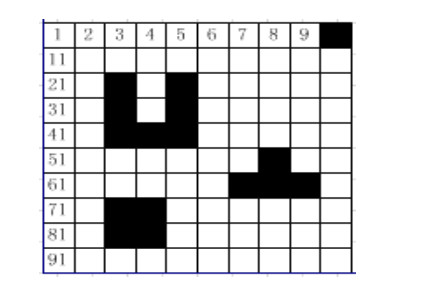
The ant colony optimization may fall into a local optimal solution when encountering a complex environment. In the running process of the algorithm, in order to prevent the ant from repeatedly accessing the same node, a taboo table is introduced, and the accessed node is stored as a node that the ant does not need to access in the next selection process. This causes the ants to fall into a deadlock when encountering a U-shaped obstacle. Figure 2 shows a U-shaped obstacle 1, it can be clearly seen that the ant can have the following route:1→2→3, 1→4→3, 1→2→4→3. The ants can pass smoothly when they encounter the U-shaped obstacle 1 without deadlock. Although there is no deadlock, it will affect the time it takes for the ant to find the path. Figure 3 shows the U-shaped obstacle 2 from which it can be clearly seen that the ant can have the following route: 1→2→3, 1→4→3, 1→2→4→3, 1→2→4→5 →6, 1→4→5→6. The ants will have a deadlock phenomenon when the route is 1→2→4→5→6, 1→4→5→6, which causes the loss of the overall energy of the ant group to reduce the convergence speed.
When U-shaped obstacle 1 and U-shaped obstacle 2 are encountered, the ants that have fallen into a deadlock are discarded. When the U-shaped obstacles are encountered, the improved ant colony optimization can effectively improve the ant colony search efficiency and the optimal path.
3.2. Motion problems and solutions in dynamic environments
3.2.1. Dynamic environment assumptions
Hypothesis 1: Considering the size of the mobile robot and the dynamic obstacle, they are considered as two circulars with diameters of Dr and Do respectively.
Hypothesis 2: Set the robot step length λ=dij (the distance between two adjacent grids), the robot is a uniform motion with a speed of VR, and the motion of the dynamic obstacle is a uniform motion with a speed of VDO.
Hypothesis 3: The set of points for global path planning of mobile robot is Rs; the set of points for dynamic obstacle path planning is DOS.
Hypothesis 4: The motion state of the mobile robot includes the following two types: A uniform motion state; a tentative state. The dynamic obstacle motion state is a uniform reciprocating motion state.
3.2.2. Dynamic environment collision problem and its strategy
The following collisions may occur with dynamic obstacles during the global path planning of mobile robots: (a) no collision; (b) side collision; (c) frontal collision.
In order to judge the motion state between the mobile robot and the dynamic obstacle, this paper firstly judges how the two will appear by not intersecting the motion trajectory, and then judges whether there is a collision between the two by the following methods aiming at different cases.
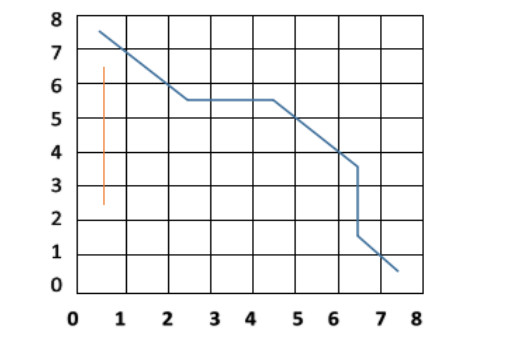
Case 1: The point set Rs of the global path planning of the mobile robot and the point set DOS of the dynamic obstacle for path planning have no intersection point, and then there will be no collision between the two. The blue line in Figure 4 shows the global path planning of the mobile robot, and the red line indicates the trajectory of the dynamic obstacle.
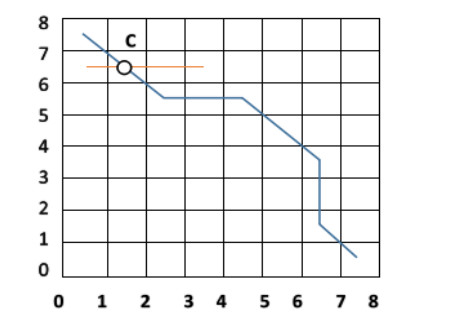
Case 2: The point set RS of the global path planning of the mobile robot has a point of intersection with the point set DOS of the dynamic obstacle for path planning, and there is only one intersection point, and there may be a side collision. It is estimated by the following case whether there is a side collision. It can be seen from Figure 5 that the mobile robot and the dynamic obstacle have an intersection point C, and the coordinates of this point are the intersection points of the point sets RS and DOS. Since the C point coordinates are known, the distance LRC from the starting point to the point C of the mobile robot can be obtained by the distance formula between the two points. Equations (2)-(4) are substituted according to the known conditions to solve the positional relationship between the mobile robot and the dynamic obstacle:
where, LDOC is the trajectory length of the moving obstacle and the dynamic obstacle moving at the same time. If LDOC is less than or equal to LDO (LDO is the dynamic obstacle one-way path length), the point where the dynamic obstacle is located and the intersection point C are directly obtained. The relative position of the relative position point coordinates to the intersection point C is set to CDOC, and if LDOC is greater than LDO, Eq (4) is used to determine the position of the dynamic obstacle when the TRC time is elapsed. Determine the size relationship between CDOC and (Dr+Do)/2:
When (Dr+Do)/2 is greater than or equal to CDOC, a side collision occurs.
When (Dr+Do)/2 is less than CDOC, no side collision occurs.
If the mobile robot and the dynamic obstacle have a side collision during the movement, the robot is in the standby mode, the waiting time is TRW. Then the robot continues to move according to the previous global planning path after the waiting time.
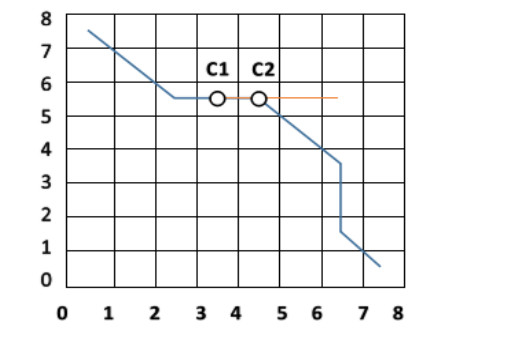
Case 3: The point set RS of the global path planning of the mobile robot has a point of intersection with the point set DOS of the dynamic obstacle path planning, and there are multiple intersection points, and there is a possibility of a frontal collision. It is estimated by the following case whether there is a frontal collision. As can be seen from Figure 6, the mobile robot and the dynamic obstacle have two intersection points C1 and C2, and the two-point coordinates are the intersection points of the point sets RS and DOS. The following method is used to determine whether a mobile robot and a moving obstacle has a frontal collision.
(a) When the mobile robot has passed the intersection point C2, the dynamic obstacle has not reached C2 points, and the distance between the two is greater than (Dr+Do)/2, and no collision occurs between the two.
(b) When the dynamic obstacle has returned to C2 points, the mobile robot has not reached C2 points, and the distance between the mobile robot and the dynamic obstacle is greater than (Dr+Do)/2, and no difference will occur between the two collision.
(c) When the mobile robot and the dynamic obstacle meet at the same from intersection points C1 to C2, the two directions of motion are opposite, and the distance between the two is less than or equal to (Dr+Do)/2 which will cause a frontal collision.
If the mobile robot and the dynamic obstacle have a frontal collision during the movement, the robot path is used to plan the local sub-goal mode. In the front collision intersection area, a new path is newly planned to replace the original path. When avoiding the front collision area, the initial global path planning scheme is still used to complete the task to the end point.
4.
Improved ant colony optimization
4.1. Adaptive adjustment of the volatilization coefficient
The ant colony optimization is affected by many factors in the running process. The dynamic adjustment parameter ρ mentioned in this paper solves the problem of the slow convergence and easily falling into the local optimal solution during the running process. When the volatilization coefficient ρ is large, the chance that the path that the ant has traveled before is re-selected will be increased. When it is too small, the global search ability will be improved and the convergence speed will be decreased. Thus, the parameter ρ is set to a maximum value in the initial time. Although the previous search path is more likely to be selected again, positive feedback of information plays a leading role.
In this paper, parameter ρmin is set to 0.1 and c is set to a random constant. The adaptive adjustment equation of ρ is as:
4.2. Fusion of multi-type state transition probabilities
The roulette algorithm is often used in genetic algorithms, so the roulette operation is applied to the urban transfer state rule. The greater the fitness, the greater the probability that the individual is selected, and the quality of the solution is greatly improved as well as the convergence speed of the algorithm.
where, q is the number of connecting lines between the i-th vertex and the i+1th vertex of the kth ant, called the number of ij sub-intervals; fij is called the i-th and j-th sub-interval solutions fitness; q∑i=1fij is the sum of all solutions for all q subintervals of ij.
4.3. Pheromone update
After all the ants have completed a path search, the ants are sorted according to the length of each ant's walking path (L1 ≤ L2 ≤ L3 ≤... ≤ Lm), and the contribution of each ant to the pheromone update is weighted according to the ant's order. The value is recorded as φ. Updating Eqs (8)-(10) are as follows:
In Eq (8), Δτij(t) is the pheromone increment from node i to node j; in Eq (9), Δτkij(t) is the pheromone left by the kth ant on path i to j. In Eq (10), Q is a constant, which refers to the total amount of pheromone released by the ant after a complete path search. φ = Lav−LφLav−Lk, Lav is the average length of the cycle. Lφ is the path length of the φ th better ant, and Lk is the path length of the kth ant searched in this cycle.
4.4. Better path node crossover operation
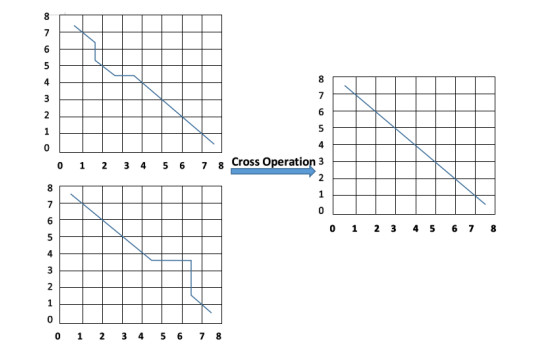
If the ant colony cannot obtain the optimal solution after each iteration, it is considered that the ant colony optimization may be in a stagnant state and fall into the local optimal solution. At this time, it is necessary to perform node crossover operation on some of the better paths. By correspondingly crossing the different sequence numbers of the better path, this operation is to compare the distance between the different sequence numbers by solving the distance between two points, and finally take the minimum value to perform the crossover operation to obtain the optimal solution. For example, serial group number A: 1→2→3→4→5→6→7→8 and serial group number B: 1→2→3→4→5→6→9→8 are two moving paths from starting point 1 to the end point 8, and the distance between the two points can also be obtained through the coordinate points. The distance between point 6 to point 7 and point 7 to point 8 in the sequence group number A can be obtained between the two points. As can be seen from the above, the distance between point 6 to point 9 and point 9 to point 8 in the sequence group number B can be obtained between the two points. Finally, the minimum distance can be obtained by comparing the values of LA67 and LB69. The minimum values of LA78 and LB98 can also be obtained by using this method, as a result, the shortest path can be obtained by using the node crossover operation. As shown in Figure 7, the global search efficiency of the improved algorithm has been significantly enhanced.
5.
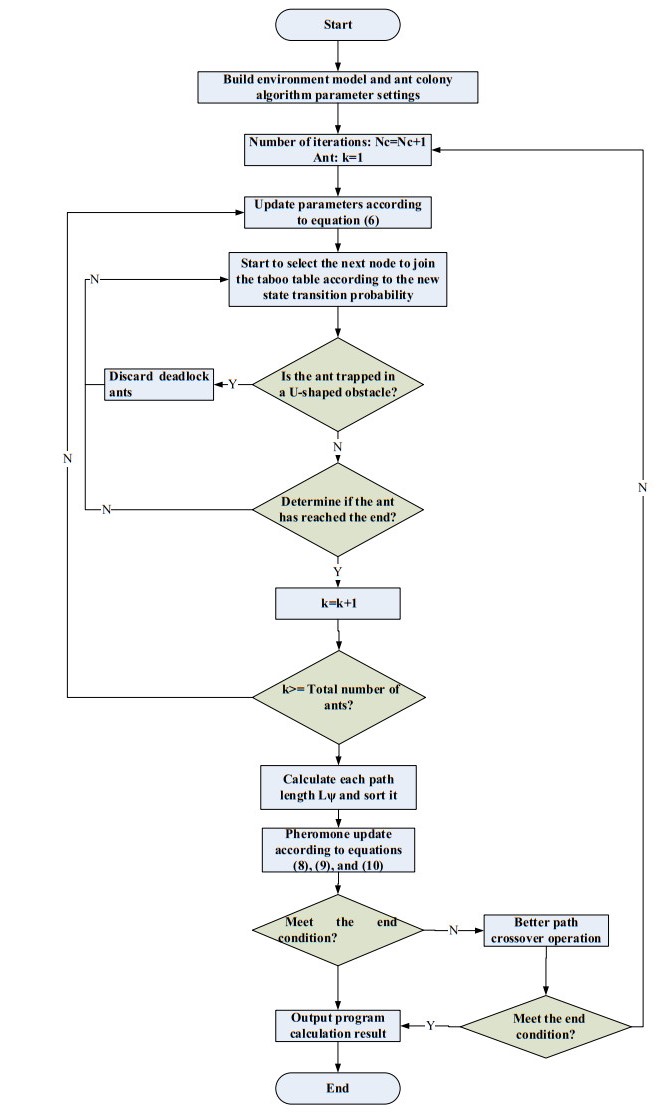
Steps and flow chart of IACO
Step 1: Build an environment model for mobile robot path planning, set the total number of ants to M = 50, initial value c = 0.9, parameters α = 1, β = 5, total pheromone Q = 1, maximum iteration number Nmax = 100. The initial tabuK is set to an empty set and the starting point is set to S. The target point is set to E.
Step 2: Set the initial value c and adjust the volatilization coefficient of ρ adaptively by using Eq (6).
Step 3: select the next node to join the taboo table according to the new state transition probability by using Eq (7).
Step 4: Determine whether the ant is trapped in a U-shaped obstacle. If yes, discard the deadlock ant and return to Step 3, otherwise proceeding to Step 5.
Step 5: Determine whether the ant reaches the end point. If it reaches the end point, the ant k = k+1, otherwise returning to Step 3.
Step 6: Determine whether the ant k is equal to M. If yes, proceed to the next step, otherwise returning to Step 2.
Step 7: Calculate the path length Lφ and sort it, then use Eqs (8)-(10) to update the pheromone.
Step 8: Determine whether the end condition (maximum number of iterations) is satisfied. If yes, end the output result. Otherwise, the optimal path node crossover operation is performed, and then it is judged whether the end condition is satisfied. If yes, the result is output. Otherwise, the process returns to Step 1 until the end of the loop.
The flow chart of IACO is shown in Figure 8.
6.
Mobile robot path planning in dynamic environment
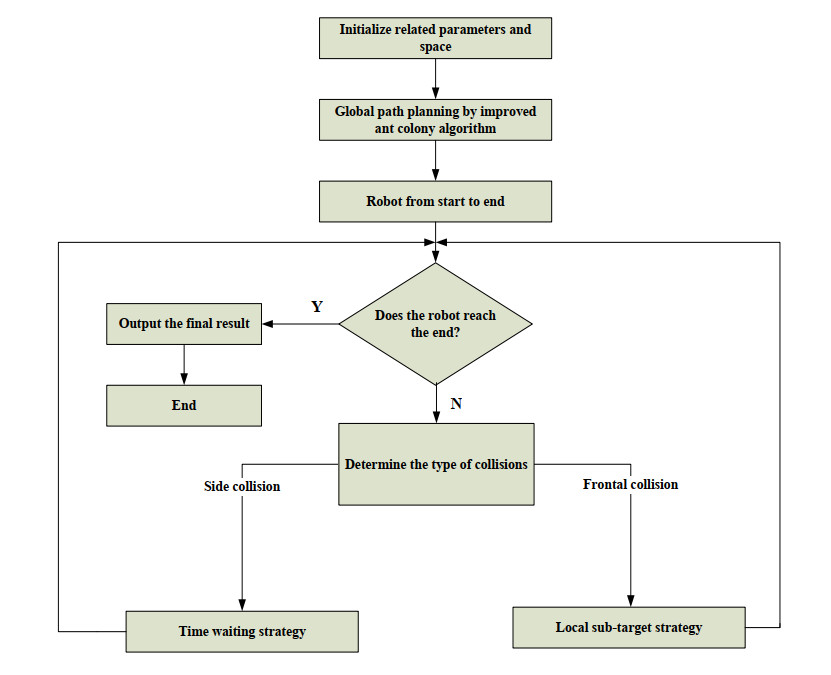
The robot dynamic path planning steps are as follows:
Step 1: Initialize algorithm related parameters and workspace.
Step 2: Solve a collision-free path by improving the ant colony algorithm without considering dynamic obstacles, so that the robot walks along the path to the end point.
Step 3: The mobile robot starts to go from the starting point S to the target point E. When the robot reaches the target point E, it outputs a global collision-free path and ends the task.
Step 4: First, determine whether there is an intersection point between the mobile robot and the set of dynamic obstacle points, and then determine whether there is a collision with the robot.
Step 5: If there is no intersection between the two, there will be no collision, and the robot will continue to go to the target point according to the global path plan.
Step 6: If there is an intersection between the two, collision may occur and the relevant collision strategy is executed.
Step 7: Determine whether the robot reaches the target point. If the target point is reached, the global collision-free path is output. Otherwise, return to step 3 until the end of the loop, and the result is output.
Figure 9 shows the flow chart for robot dynamic planning.
7.
Simulation experimental results and analysis
7.1. IACO experiment results and analysis
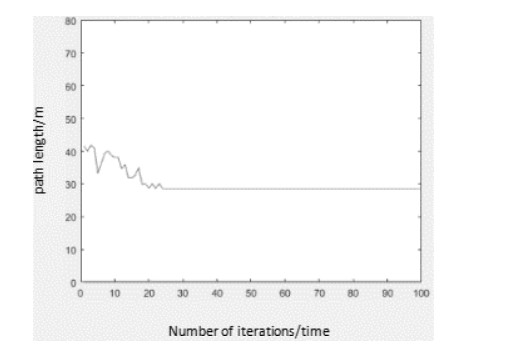
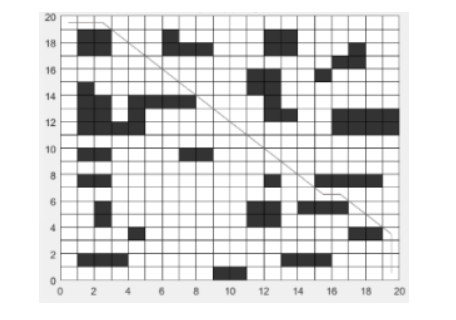
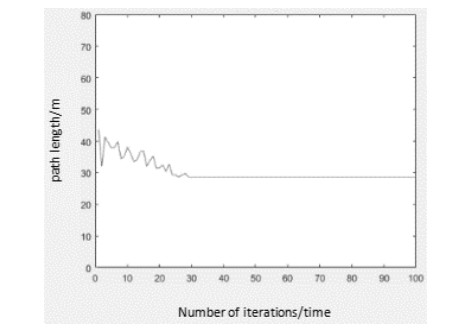
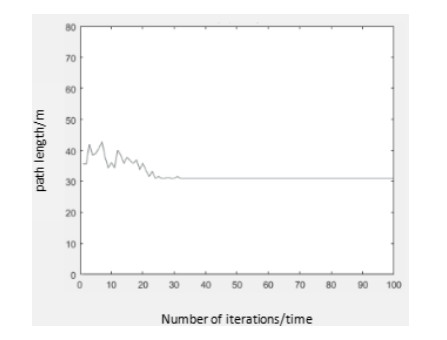
In order to verify the feasibility of the IACO in this paper, IACO is applied to the static mobile robot path planning. Table 1 shows the detail comparisons of the experimental results between the improved ant colony algorithm in literature [10] and our IACO. The improved algorithm in [10] can obtain the optimal path in the three environmental maps G1, G2 and G3. However, it takes a long time to reach the steady state after 46, 48 and 52 iterations respectively, and the experimental results (from Figures 10-15) of our IACO reach the steady state after 24, 30 and 32 iterations respectively under the premise for obtaining the optimal path.
Through the comparative analysis of the above three groups of experiments, IACO can effectively solve the slow convergence and local optimization existing in traditional ant colony optimization.
7.2. Experimental simulation and analysis in dynamic environment
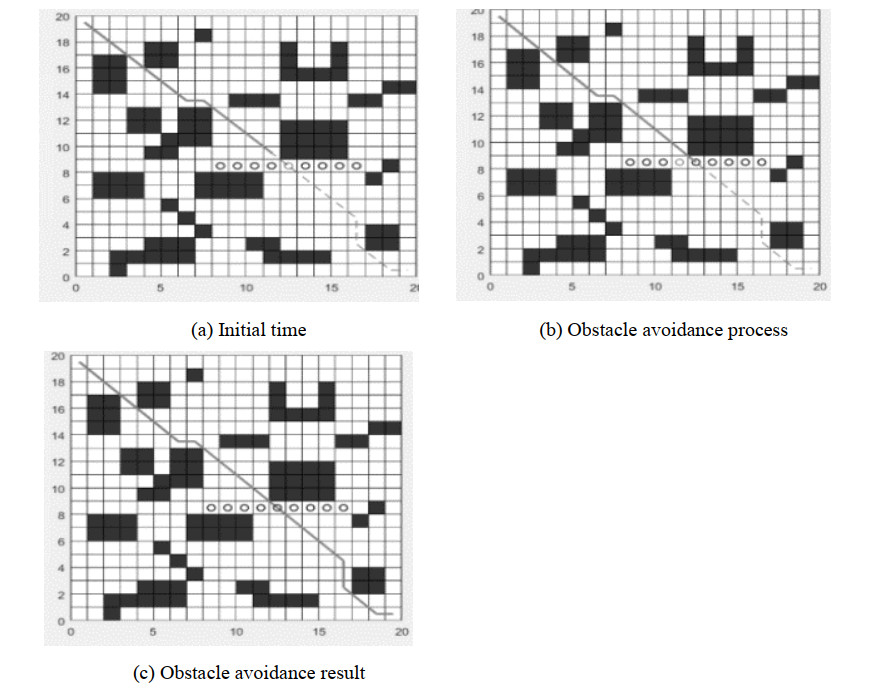
The relevant parameters of the robot in dynamic path planning are as follows: the diameter of mobile robot Dr is 1, the diameter of dynamic obstacle Do is1, robot uniform motion speed VR is 1, dynamic obstacle uniform motion speed VDO is 1. The motion trajectory of the dynamic obstacle DOS1 is a uniform reciprocating motion, and the motion path is P1 = [229 230 231 232 233 234 235 236 237...]. Firstly, the improved path algorithm is used for global path planning without considering dynamic obstacles, as shown in Figure 16.
After the global path is generated, the dynamic obstacle DOS1 is introduced into the environment, and the method of Case 2 is used to infer whether the two have a side collision. The point set RS of the mobile robot global path and the point set DOS of the dynamic obstacle path have an intersection. And there is only one intersection, the collision type is side collision. As shown in Figure 16, when the dynamic obstacle DOS1 is not detected, the mobile robot RS1 still avoids the obstacle according to the global path. When the mobile robot RS1 arrives at the serial number 212, and the mobile robot RS1 detects that the distance between the mobile robot RS1 and the dynamic obstacle DOS1 is equal to (Dr + Do)/2, the corresponding collision strategy is adopted at this time. As shown in Figure 17(a), when the mobile robot RS1 arrives at the position of the serial number 212, the mobile robot RS1 adopts a stand-alone waiting mode, and the waiting time is TRW. As shown in Figure 17(c), when the dynamic obstacle DOS1 arrives at the position point 232 from the intersection point 233, the mobile robot RS1 has arrives at the position point with the serial number 233 at this time. As shown in Figure 17(c), the mobile robot RS1 continues to complete the designated target according to the global path planning scheme and moves to the target point.
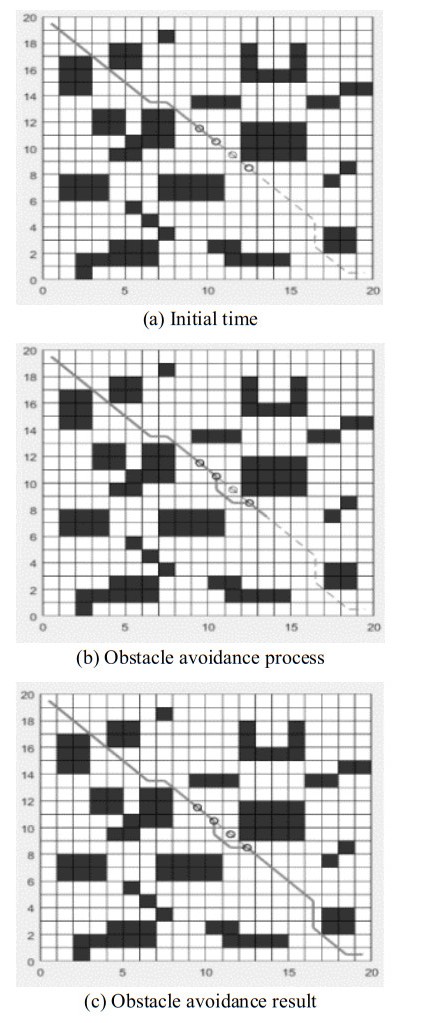
The dynamic obstacle DOS2 is introduced into the environment, and the motion path is P2 = [170 191 212 233 212 191...]. As shown in Figure 18, the mobile robot point set RS and the dynamic obstacle point set DOS have intersection points, and the number of intersection points are more than or equal to two. The mobile robot determines whether the two have a frontal collision according to the method for Case 3. The corresponding strategy for the frontal collision at the intersection point is to use the robot path planning local sub-goal method for avoiding the dynamic obstacle DOS2, and then the robot continues to complete the following tasks according to the original global path planning scheme.
8.
Conclusions
In order to solve the problem that the traditional ant colony algorithm is slow in convergence and easy to fall into the local optimal solution, this paper proposes an improved ant colony optimization (IACO), which firstly enhances the ant colony search ability at the initial moment by adaptively changing the volatilization coefficient. The scope is expanded to avoid falling into the local optimal solution. Secondly, the roulette operation is used in the state transition rule to improve the quality of the solution and the convergence speed of the algorithm effectively. Finally, through the elite selection and the node crossover operation of the better path, the global search efficiency and convergence speed of the algorithm are effectively improved. Simulation results indicate that our algorithm is superior and effective in static and dynamic path planning of mobile robots.
Acknowledgements
This paper was supported by Anhui Provincial Natural Science Foundation (Grant No. 1708085ME129) and the youth top-notch talent of Anhui Polytechnic University.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad: