Renewable energy integration and distributed generation in Kosovo: Challenges and solutions for enhanced energy quality

1.   Introduction

A common problem in cell biology research is the desire to differentiate cells into categorical populations based on some defining molecular characteristic. Some examples include the presence or absence of a particular gene transcript ^[1,2], cells presenting viral epitopes to indicate infection ^[3,4], or expression of particular membrane proteins ^[5,6]. Flow cytometry is an effective tool to count the number of cells exhibiting the identifying characteristic. The process involves suspending cells of interest in a sheath fluid that is pressurized and extruded single file past a laser beam ^[7,8,9]. Each cell will scatter the laser's light towards optical sensors positioned around the stream. Sensors directly in front of the laser measure the forward scattering about a single cell, and is used to quantify the cell's surface area, volume, and shape. Alternatively, side scattering sensors measure photons emitted by fluorescent markers and dyes excited by the laser. The fluorescent probes are designed a priori to bind specifically to cell surface proteins and structures that characterize the cell species. Thus, a sufficiently high fluorescence intensity is an indication the cell is of the desired type.

However, details of the protocol arise that can confound the final count of cells. If we focus on the example of a population of "mutant" cells, characterized by the expression of a particular membrane surface receptor, mixed in with a population of "wild-type" cells, we can design a fluorescing probe that binds specifically to the receptor. If we suspend all cells in a solution containing an excess of probes, we expect all probes to bind to free receptors. However, each probe-receptor binding event is a reversible process, allowing some expected proportion of receptors to remain unbound at equilibrium. Furthermore, variation may exist in the number of receptors expressed, increasing the ways in which a mutant may escape binding ^[4,5]. To combat this measurement of false negatives, one can increase the probe concentration in the suspension, increasing its excess and driving the equilibrium towards more bound receptors. Unfortunately, although the probes are designed to bind specifically to the receptors, they will have a relatively small, but non-zero binding affinity to the rest of the cell membrane and its other embedded structures ^[10]. Increasing the probe concentration will result in a higher nonspecific binding to wild-type cell membranes, allowing false positive counts of mutants. The equilibrium configuration of probe bindings to all cells, whether specifically or nonspecifically, will produce a distribution of fluorescence data over a range of intensities. Typically, cells that exhibit levels of fluorescence below a threshold intensity are ignored in a process known as "gating." Setting that gating threshold is often a heuristic procedure, though some methods for automatic gating based on data clustering have been developed ^[9,11]. However, these methods do not incorporate the underlying chemical kinetics of probe binding and largely ignore the effects of nonspecific binding.

We develop a kinetic model for both specific and nonspecific binding of probes to cells. We employ a variant on the Langmuir adsorption model ^[12] with two competing types of binding sites: receptors and a discretization of the cell membrane. Here, the concentration of initially added probes applies the "partial pressure" driving probe binding to the cell surfaces. We will show the isotherm of fractional binding site occupancy to exhibit two regimes in which the receptor and membrane binding sites become saturated at different rates. We discuss how the interface between the two regimes is the ideal concentration of probes to include in the assay and how the model can inform optimal experimental design. We then present a probabilistic model for the expected number density of cells over possible numbers of probe bindings. Employing this model, we develop a variant on the expectation-maximization (EM) mixture model ^[13] to estimate the total number of mutant cells without heuristic gating. Furthermore, we propose a method for inferring the probe binding affinity and the receptor number distribution using a serial dilution protocol. Finally, we discuss potential applications and problems of using our method for the fluorescence activated cell sorting (FACS) assay. It should be noted that throughout this paper we continue using the example of "mutant cells" expressing surface receptors, but our models and analyses extend to all physiological applications of flow cytometry with fluorescing surface markers.

2.   Materials and method

2.1.   Kinetic model

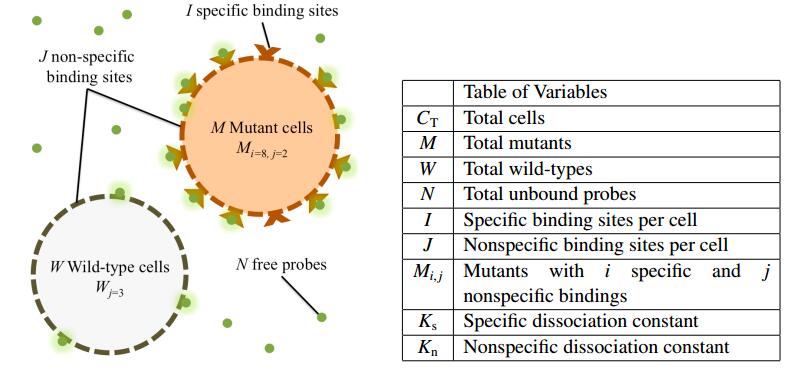
Let $C_{\mathrm{T}}$ be the total number of cells in a suspension also containing $N_{\mathrm{T}}$ probe molecules. We assume $C_{\mathrm{T}}$ is precisely counted by the forward scattering measurement to differentiate cells from free probes or debris. Let $M$ and $W = C_{\mathrm{T}} - M$ be the number of mutant cells and wild-type cells, respectively. By definition, mutants are the only cells that express the surface receptors. Let $N$ be the number of free, unbound fluorescing probes designed to specifically target the receptors with association and dissociation rates $p_{+}$ and $p_{-}$. Alternatively, for both mutants and wild-types, probes can bind and dissociate nonspecifically to the cell membrane itself with rates $q_+$ and $q_-$. Since, the on-rates $p_+$ and $q_+$ are likely to be comparable in magnitude, we expect probes bound nonspecifically to dissociate significantly more rapidly so that $q_- \gg p_-$.

The total number of receptors $I$ on a mutant cell varies across all cells with distribution $f(I)$ and mean $\langle I\rangle$. The exact distribution $f$ will depend on the details of the receptor and its expression and recycling pathways. A simple model for receptor expression is a production and degradation process with constant rates $\alpha$ and $\mu$, respectively. The steady-state receptor number of such an immigration-death model follows a Poisson distribution

where $\left < I\right > = \alpha/\mu$. We use this form of $f(I)$ in the simulations we perform in this paper; however, the full models we derive are independent of the choice for $f$. Thus, we denote the total number of mutant cells that carry exactly $I$ receptors as $M^I$.

Furthermore, we consider the the total surface area $A$ of the cell membrane and partition the binding region around a single receptor as $A_{\mathrm{s}}$. We define this region as that which a probe fated to adsorb to the cell surface is more likely to bind to the associated receptor than directly to the membrane. We can partition the remaining cell surface into $J = \frac{A}{A_{\mathrm{s}}} - I$ discrete effective binding sites for the membrane. We expect the binding region of a receptor to be relatively small compared to the total surface area, making $J\gg I$.

To accurately model the kinetic flows from one bound state of a mutant to another, it becomes necessary to track populations of cells indexed by both the number of probes bound specifically and nonspecifically. As shown in Figure 1, we define $M_{i, j}^I$ as the number of mutant cells with exactly $i$ probes bound to a maximum of $I$ specific binding sites and exactly $j$ probes adsorbed nonspecifically. For wild-type cells, probes can only attach nonspecifically, so we define $W_j$ as the number of wild-type cells with exactly $j$ adsorbed probes. We thus have the chemical rate equations

Figure 1.  Cartoon of probe molecules binding to wild-type $W$ and mutant $M$ cells used in a typical flow cytometry assay. Wild-type cells are assumed to bind probes only nonspecifically while each mutant cell expresses $I$ receptors to which probes specifically bind. The variables defining all quantities in the kinetic mass-action model analyzed in this paper are given in the table.

DownLoad: Full-Size Img PowerPoint

Let $v$ be the volume of the cell suspension containing all cells and probes. Normalizing the cell and probe counts by $v$, we have the relevant concentrations $[M_{i, j}^I]$, $[W_j]$, and $[N]$. We can now derive the mass-action equations as

At equilibrium, we expect detailed balance in each of Eq 2.2. For specific and nonspecific binding respectively, we can define the dissociation constants

One might interpret these constants as the probe concentration's resistance to binding and are parameters that will shape the entire dynamics of the model. Using inductive reasoning, we can characterize the mutant populations solely with the concentration of unbound cells:

By the conservation of total mutant cells with $I$ binding sites, we use the binomial expansion to derive

Using very similar arguments, we derive the concentration of unbound wild-types as

Next, we find the following result:

Using the conservation of the total concentration of initial probes $[N_{\mathrm{T}}]$ and $\left < I\right > = \sum_{I = 0} I f(I)$, we derive

It is possible to solve Eq 2.9 for $[N]$ analytically as the roots of a cubic polynomial with $[M]$, $[W]$, $[N_{\mathrm{T}}]$, $[K_{\mathrm{s}}]$, $[K_{\mathrm{n}}]$, $[J]$, and $\left < I\right >$ as parameters. However, in the next section, we will show how this kinetic model may be used to quantify the optimal total probe concentration $[N_{\mathrm{T}}]$ to use when performing the assay.

2.2.   Two species Langmuir adsorption model

If we define $\theta_{\mathrm{T}}$ as the fractional occupancy of total binding sites across all cells, using Eq 2.9 we have

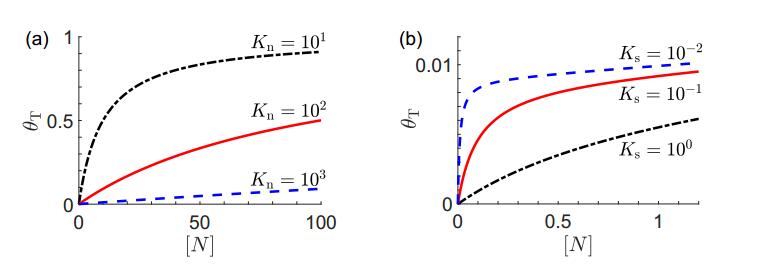
Each of the two terms resemble a Langmuir isotherm which measures the fractional occupancy of binding sites on a surface substrate ^[12]. Framed in the Langmuir adsorption picture, the concentration of free probes $[N]$ is directly analogous to the partial pressure of adsorbing gas. As shown in Figure 2(a), the fraction of occupied binding sites grows as you add more free probes, but eventually saturates.

Figure 2.  Fractional occupancy $\theta_{\mathrm{T}}$ of available binding sites as a function of the free probe concentration $[N]$. (a) The isotherms for large $[N]$ with $[C_{\mathrm{T}}] = 100$, $[M] = 10$, $K_{\mathrm{s}} = 10^{-1}$, $J = 10^3$, $\left < I\right > = 10$, and $K_{\mathrm{n}} = 10^1$, $10^2$, and $10^3$. The cell membrane reaches saturation of bound probes at a rate dictated by $K_{\mathrm{n}}$. (b) The isotherms for small $[N]$ values with $[C_{\mathrm{T}}] = 100$, $[M] = 10$, $K_{\mathrm{n}} = 10^{3}$, $J = 10^3$, $\left < I\right > = 10$, and $K_{\mathrm{s}} = 10^{-1}$, $10^{-2}$, and $10^{-3}$. Due to small $K_{\mathrm{s}}$, the occupancy reaches saturation for all available receptors quickly, then resumes the slower saturation of non-specific binding to membrane.

DownLoad: Full-Size Img PowerPoint

Note that the saturation is normalized according to the number of non-specific binding sites $J$ as we expect it to be much larger than $\left < I\right >$. Furthermore, the rate of adsorption is attenuated by the non-specific dissociation constant $K_{\mathrm{n}}$. For small $[N]$, when the cell membrane is far from saturation, we see the dynamics of the receptor binding site saturation in Figure 2(b). As $K_{\mathrm{s}} \gg K_{\mathrm{n}}$, the total occupancy increases rapidly to saturation relative to that of the more dominant non-specific isotherm. Thus, there is a critical free probe concentration $[N]^*$ such that when $[N]$ is below this threshold, each new probe introduced into the assay will contribute more to the occupancy of receptors than that of the nonspecific binding sites. This threshold can be obtained by differentiating the two terms in Eq 2.10 with respect to $[N]$ and setting them equal to each other. This results in the following critical free probe concentration:

Note that $[N]^*$ is a monotonically increasing function of the concentration of mutant cells $[M]$, which is typically unknown. Thus, a conservative recommended concentration $[N_{\mathrm{T}}]$ to use in the cell/probe suspension would involve setting $[M] = [C_{\mathrm{T}}]$ and evaluating Eq 2.10 with $[N]^*$. Furthermore, to ensure $[N]^*$ is strictly positive, the specific binding affinity of the probe is constrained by

In other words, for probes designed with weaker specific binding affinity than this threshold dictates, nonspecific binding sites are more likely to adsorb probes before any receptors for all values of $[N]$ and $[M]$. Though it is clear that the lowest $K_{\mathrm{s}}$ possible is ideal for an assay, one may use this upper bound to decide if an available probe will at all be effective for a specific experiment.

2.3.   Cell population mass density

In order to establish a connection between the equilibrium kinetic model and a typical output of a flow cytometry assay, we define the concentration of cells $[C_r]$ with exactly $r$ probes bound, regardless if they are bound specifically or nonspecifically, as

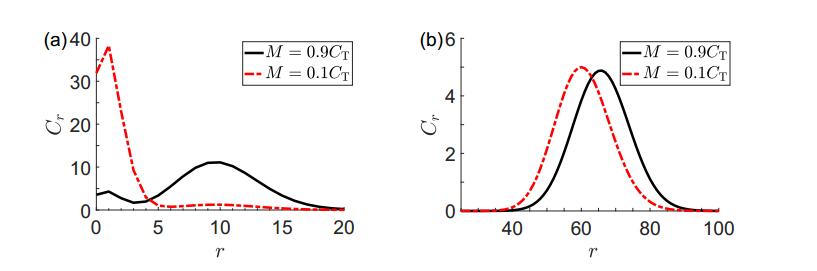
Equation 2.13 informs us of how the distribution of cell data will cluster, as illustrated in Figure 3(a). At relatively low concentrations of free probe $[N]$, the binding of receptors can saturate, but leave the wild-type cells with only nonspecific binding to have significantly lower probe bindings. This effectively makes the two clusters qualitatively separable and imposing a gating threshold is straightforward. However, at high levels of free probe, the clusterings overlap and are thus difficult to differentiate heuristically, as demonstrated in Figure 3(b). Furthermore, these distributions are taken over the probe binding number $r$ which is not directly measurable. We next show how $r$ and $[C_r]$ relate to the measured fluorescence intensity distribution.

Figure 3.  Expected population densities of cells $C_r$ with exactly $r$ probes bound. (a) Low concentrations of free probe $[N] = 1.2$ with $C_{\mathrm{T}} = 100$, $\left < I\right > = 10$, $J = 10^3$, $K_{\mathrm{s}} = 10^{-1}$, and $K_{\mathrm{n}} = 10^3$ for $M = 10$ and $90$ cells. The density will cause clustering of wild-type cells close to $r = 0$ and mutants close to $r = \left < I\right >$, though the non-specific binding allows some of the density associated with the mutants to contribute to the lower $r$ values of $C_r$. A clear boundary exists between the two densities and heuristic gating can partition the populations sufficiently. (b) Large concentrations of free probe $[N] = 60$ with $C_{\mathrm{T}} = 100$, $\left < I\right > = 10$, $J = 10^3$, $K_{\mathrm{s}} = 10^{-1}$, and $K_{\mathrm{n}} = 10^3$. The population densities of wild-types and mutants are now found in similar values of $r$ and overlap extensively, causing difficulty in differentiating the two clusters as probes saturate the membrane.

DownLoad: Full-Size Img PowerPoint

2.4.   Fluorescence intensity

As each cell passes through the cytometer, any bound probes will fluoresce with some strictly positive light intensity $F_{\mathrm{s}}$. However, some variation in the fluorescence signal arises from molecular variability and instrumentation noise. We also expect each cell to have some relatively small amount of auto-fluorescence with intensity $F_0$. Then if we define $x$ as the total fluorescence intensity of a given cell and $r$ as its corresponding number of bound probes, then we expect the probability density of $x$ to follow

In a typical flow cytometry assay, however, we do not know how many probes are bound to each cell. Furthermore, we do not know the species $b\in\{0, 1\}$ of the cell, where $0$ and $1$ denote wild-type and mutant respectively. Using Eqs 2.13 and 2.14, we derive the marginal density of fluorescence intensity as

Considering total number of probes $r$ bound to a cell regardless if they are bound specifically or nonspecifically is sufficient if each probe fluoresces with an intensity independent of binding. However, for some probes, the fluorescence may be a product of a conformation change when binding to the designed target. This means that for nonspecifically bound probes, their conformation change may be partial and can result in a lower mean fluorescence intensity $F_{\mathrm{n}}$. We must now consider how many probes are bound specifically and nonspecifically, making Eq 2.13 insufficient for computing the marginal density of $x$. Thus we derive the conditional densities

and

In the next section we will show how these mathematical results can be used to iteratively estimate the size of the mutant population $[M]$ from data and infer physical parameters such as $K_{\mathrm{s}}$ and $\langle I\rangle$.

3.   Results and Discussion

3.1.   EM mixture model estimation of mutant population

Using Eqs 2.16 and 2.17, we propose an iterative algorithm to automatically infer the concentration of mutant cells $[M]$ without heuristic gating. Let $x_k$ be a set of data, where $x_k$ is the fluorescence intensity measured for cell $k$ and let $b_k \in \{0, 1\}$ be its corresponding species assignment. Because this is an iterative method, we will index each numerical step with $t\in\{0, 1, 2, \cdots\}$. Using Bayes rule, we can compute the probability cell $k$ is a mutant as

where $[M]^{(t)}$ is the current mutant concentration estimate. The iterative procedure starts with an initial guess at the concentration of mutant cells $[M]^{(0)}$ which is used to calculate the probability in Eq 3.1. The next estimate $[M]^{(t+1)}$ is then given by

This process is repeated until $[M]^{(t)}$ converges. Note that, though calculating Eq 3.1 for a single $x_k$ can technically be a $\mathcal{O}(J^3)$ computational operation, some asymptotic arguments can be made to concatenate summations to terms that are sufficiently close to zero. More importantly, the only value that changes over all iterations is $[M]^{(t)}$. Thus, the more computationally heavy summations in Eqs 2.16 and 2.17 can be done once and stored in a matrix, making all subsequent iterations compute linearly with the number of cells $C_{\mathrm{T}}$.

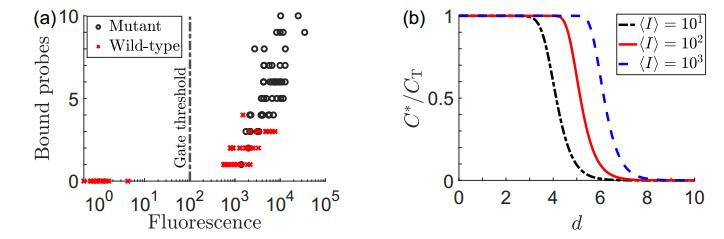
An example using our algorithm for estimating the mutant cell count from simulated data is shown in Figure 4(a) where $C_{\mathrm{T}} = 100$ and $M = W = 50$. Immediately evident is the wild-type cells' propensity to be clustered close to the mutants when as little as one probe is bound. When a reasonable gate threshold is drawn as demonstrated, the $87$ cells to the right are counted as mutants, resulting in $27$ false positives. Our algorithm accounts for the probability of wild-types having high fluorescence, resulting in the closer estimate of $M = 51$. Even for parameter regimes where probe binding to wild-types are rare, for large numbers of cells $C_{\mathrm{T}}$, the occasional nonspecific binding event will result in the gating process invariably over-counting mutants.

Figure 4.  (a) Simulated fluorescence data using parameters $C_{\mathrm{T}} = 100$, $[N] = 1.2$, $K_{\mathrm{s}} = 10^{-1}$, $K_{\mathrm{n}} = 10^{3}$, $J = 10^3$, $\left < I\right > = 5$, $F_0 = 1$, $F_{\mathrm{s}} = F_{\mathrm{n}} = 10^3$, and $\sigma_0 = 0.5$. We set $M = 0.5C_{\mathrm{T}}$ and assign each cell $k$ with a number of bound probes $r_k$ using Eq 2.13 and subsequent fluorescence intensity $x_k$ using Eq 2.14. At this particular parameter regime, $27$ of the $50$ wild-type cells managed to bind with at least one probe, increasing their relative fluorescence and clustering them with the mutants. A typical gating threshold, shown above, would separate the two clusters and count all $87$ cells on the right hand side as mutants; far larger than the true count of $50$. The iterative estimate using Eq 3.2 returns $M = 51$, relatively close to the actual count. (b) Probability that a given cell has one or more probes bound as a function of the dilution number $d$ as we vary the receptor distribution mean $\left < I\right >$. Here $[N] = 1$, $K_{\mathrm{n}} = 10^3$, $K_{\mathrm{s}} = 10^{-3}$, $J = 10^3$, and dilution factor $D = 10$.

DownLoad: Full-Size Img PowerPoint

3.2.   Parameter inference using serial dilution

In typical flow cytometry assays, probes designed to bind specifically to the receptors of interest are often prepared elsewhere. Thus it is not uncommon for an experimentalist to test the affinity of a probe prior to an assay in order to insure it is sufficiently effective for the planned experiment ^[5]. This is typically done by preparing a homogeneous suspension of mutant cells with the probes, so that $[M] = [C_{\mathrm{T}}]$. The experimentalist will then perform cytometry with a sufficiently high concentration of free probes $[N]$ and quantify the number of cells that contain any fluorescing probes. The solution of probes is subsequently diluted by some factor $D$ and the assay is repeated $d_{\mathrm{max}}$ number of times. This process, known as serial dilution, arises in many applications from testing antibacterial agents ^[15] to quantifying viral infectivity ^[16]. In this context, it is used to find the characteristic dilution number $d_c$ such that all cells are still bound to at least one probe. The experimentalist can then use the corresponding probe concentration for the flow cytometry assay. However, having provided a kinetic model, we can employ this process to infer physical parameters of interest. To do so, we start by using Eq 2.13 to derive the concentration of the number of cells $C^*$ with one or more probes attached as

where $d$ is the dilution number. If we normalize $[C^*]$ by the total concentration of cells $[C_{\mathrm{T}}]$, then we can treat the expression as a probability that a given cell will fluoresce as a function of $d$, as shown in Figure 4(b). The placement of the characteristic drop in probability is dictated by the parameters $K_{\mathrm{s}}$ and $\left < I\right >$. If we consider the data point $C_d^*$ as the number of cells that fluoresce at dilution $d$, then we expect its value to be binomial distributed and we can derive the likelihood function

For a given set of data $\{C_d^*\}$, the log of the likelihood is a function of the parameters and can be maximized to solve for maximum likelihood estimates (MLE) of these parameters. As the original intent of the serial dilution procedure is to quantify the affinity of specific probe binding, $K_{\mathrm{s}}$ would be the desired inferred parameter. However, depending on the underlying experiment, one can envision estimating the expression of surface receptors $\left < I\right >$ and its change under differing experimental environments.

3.3.   Applications in FACS

A very common use of flow cytometry is in fluorescence activated cell sorting (FACS) in which cells are physically sorted into bins based on their species type ^[8,17]. As each cell is sent past the laser, the intensity measurement informs the computer in real-time which category the cell falls into. The droplet containing the cell exits an electrically charged ring that induces an electric charge in the droplet. An electric field controlled by the computer is then used to propel the extruded cell into the appropriate bin based on the fluorescence measurement. However, the confounding factors previously discussed can cause incorrect sorting of cells due to non-specific binding and other background fluorescence. If all parameters are a priori known, then using Eq 3.1 can technically be used to determine the cell species as the expression quantifies the probability that a cell is a mutant over a wild-type cell given its fluorescence. A resulting probability larger than $0.5$ will indicate a mutant, making Eq 3.1 a decision function. However, there are two complications. One is that the evaluations of Eq 3.1 are relatively computationally intensive, especially if the expected number of receptors $\left < I\right >$ is large. The real-time nature of the physical process of FACS requires rapid evaluation, though increasing computational resources can alleviate the problem. The second, more pertinent issue is that, though we are assuming all parameters are known, it is unlikely that the concentration of mutants $[M]$ is a priori known. Biologists typically use cytometry assays after some experiment and the quantification of $[M]$ is often the primary desired quantity still undetermined. Furthermore, our method of estimating $[M]$ is a model-based clustering technique that leverages all data collectively, making real-time analysis problematic.

One potential solution for both problems is to use a two-pass cytometry method. One pass through the cytometer would be used to quantify the concentration of mutants $[M]$ while also storing the evaluations of Eq 3.1. All cells would be collected together and reintroduced to the sheath fluid for a second pass for the FACS step. Though it would be improbable to exactly match each cell with their stored evaluation in the first pass, this extra data will act as a prior for more informed statistical sorting of the cells. Though previously discussed applications of our model use protocols already practiced by biologists, the potential overhead of using a two-pass cytometry process would be subject to the specific requirements of each experiment employing the method.

4.   Conclusions

In this paper, we have created a full kinetic model of the specific and nonspecific binding dynamics of a cell/probe suspension at chemical equilibrium. Using a mass-action approach, we derived expressions for important equilibrium quantities as functions of physical and experimental parameters of the flow cytometry assay. The total number of afflicted cells, which we refer to as mutants, is often the primary desired quantity of the protocol as the probes are assumed to attach only to those cells. However, we show quantitatively how the nonspecific binding of probes to the membranes of both mutants and wild-type cells can confound the results. Furthermore, using the analogous Langmuir adsorption isotherm, we demonstrated how to choose probe concentration that will minimize these confounding effects. For the estimation of the total number of mutants in flow cytometry output, which is often subject to heuristic gating, we provided an iterative algorithm to obtain this number without input from the experimentalist. We claim that having a fundamental model for which the algorithm is based will increase the accuracy over other clustering attempts. Furthermore, we extract further utility from a serial dilution process often employed to measure the affinity of probes to infer true physical parameters of the cells. Lastly, we discuss the potential applications and issues with using our method for fluorescence activated cell sorting (FACS) while proposing a two-pass cytometry process to alleviate some of the problems.

Our model and analysis approach can be readily extended to include multiple probes, multiple specifically binding receptors, and more general distribution functions for receptor expression by the mutant cells. We expect that in such more complex, higher dimensional discrimination assays, our more systematic and quantitative analysis methods should provide more accurate results. Finally, we are developing a web based tool that fully implements our flow cytometry analysis procedure so that it can be applied to experimentally measured data. This will increase the accessibility of our model and enable quantitative comparisons with existing methods, including heuristic gating.

Acknowledgments

This research was supported by the National Science Foundation through grants DMS-1516675 and DMS-1814364 and the NIH through grant R01HL146552. We are especially grateful to Anupama Dimashkie and Dr. Saravanan Karumbayaram for insightful discussions.

Conflict of interest

The authors declare no conflict of interest in this manuscript.