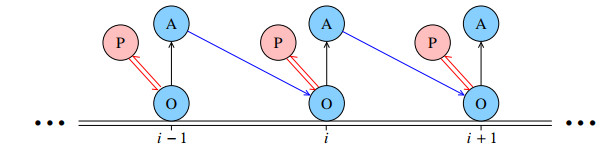
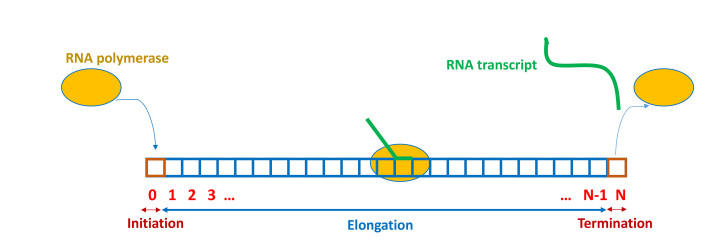
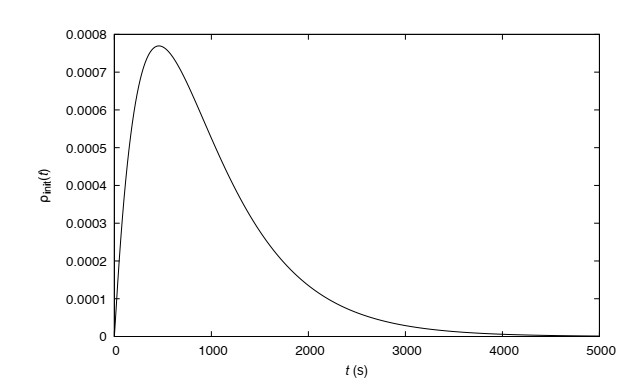
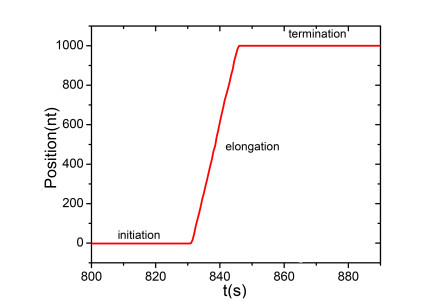
|
[1]
|
D. R. Larson, D. Zenklusen, B. Wu, J. A. Chao, R. H. Singer, Real-time observation of transcription initiation and elongation on an endogeneous yeast gene, Science, 332 (2011), 475–478. https://doi.org/10.1126/science.1202142 doi: 10.1126/science.1202142

|
|
[2]
|
S. Buratowski, S. Hahn, L. Guarente, P. A. Sharp, Five intermediate complexes in transcription initiation by RNA polymerase Ⅱ, Cell, 56 (1989), 549–561. https://doi.org/10.1016/0092-8674(89)90578-3 doi: 10.1016/0092-8674(89)90578-3

|
|
[3]
|
A. Dvir, J. W. Conaway, R. C. Conaway, Mechanism of transcription initiation and promoter escape by RNA polymerase Ⅱ, Curr. Opin. Genet. Dev., 11 (2001), 209–214. https://doi.org/10.1016/S0959-437X(00)00181-7 doi: 10.1016/S0959-437X(00)00181-7

|
|
[4]
|
X. Darzacq, Y. Shav-Tal, V. de Turris, Y. Brody, S. M. Shenoy, R. D. Phair, et al., In vivo dynamics of RNA polymerase Ⅱ transcription, Nat. Struct. Mol. Biol., 14 (2007), 796–806. https://doi.org/10.1038/nsmb1280 doi: 10.1038/nsmb1280

|
|
[5]
|
J. C. Venter, M. D. Adams, E. W. Myers, P. W. Li, R. J. Mural, G. G. Sutton, et al., The sequence of the human genome, Science, 291 (2001), 1304–1351.
|
|
[6]
|
C. N. Tennyson, H. J. Klamut, R. G. Worton, The human dystrophin gene requires 16 hours to be transcribed and is cotranscriptionally spliced, Nat. Genet., 9 (1995), 184–190. https://doi.org/10.1038/ng0295-184 doi: 10.1038/ng0295-184

|
|
[7]
|
J.-F. Lemay, F. Bachand, Fail-safe transcription termination: Because one is never enough, RNA Biol., 12 (2015), 927–932. https://doi.org/10.1080/15476286.2015.1073433 doi: 10.1080/15476286.2015.1073433

|
|
[8]
|
R. Ben-Yishay, Y. Shav-Tal, The dynamic lifecycle of mRNA in the nucleus, Curr. Opin. Cell Biol., 58 (2019), 69–75. https://doi.org/10.1016/j.ceb.2019.02.007 doi: 10.1016/j.ceb.2019.02.007

|
|
[9]
|
B. Daneholt, Assembly and transport of a premessenger RNP particle, Proc. Natl. Acad. Sci. U.S.A., 98 (2001), 7012–7017. https://doi.org/10.1073/pnas.111145498 doi: 10.1073/pnas.111145498

|
|
[10]
|
J. Sheinberger, Y. Shav-Tal, The dynamic pathway of nuclear RNA in eukaryotes, Nucleus, 4 (2013), 195–205. https://doi.org/10.4161/nucl.24434 doi: 10.4161/nucl.24434

|
|
[11]
|
A. Chaudhuri, S. Das, B. Das, Localization elements and zip codes in the intracellular transport and localization of messenger RNAs in Saccharomyces cerevisiae, WIREs RNA, 11 (2020), e1591.
|
|
[12]
|
U. Schmidt, E. Basyuk, M.-C. Robert, M. Yoshida, J.-P. Villemin, D. Auboeuf, et al., Real-time imaging of cotranscriptional splicing reveals a kinetic model that reduces noise: Implications for alternative splicing regulation, J. Cell Biol., 193 (2011), 819–829. https://doi.org/10.1083/jcb.201009012 doi: 10.1083/jcb.201009012

|
|
[13]
|
P. Cramer, A. Srebrow, S. Kadener, S. Werbajh, M. de la Mata, G. Melen, et al., Coordination between transcription and pre-mRNA processing, FEBS Lett., 498 (2001), 179–182. https://doi.org/10.1016/S0014-5793(01)02485-1 doi: 10.1016/S0014-5793(01)02485-1

|
|
[14]
|
A. Babour, C. Dargemont, F. Stutz, Ubiquitin and assembly of export competent mRNP, Biochim. Biophys. Acta, 1819 (2012), 521–530. https://doi.org/10.1016/j.bbagrm.2011.12.006 doi: 10.1016/j.bbagrm.2011.12.006

|
|
[15]
|
R. A. Coleman, B. F. Pugh, Slow dimer dissociation of the TATA binding protein dictates the kinetics of DNA binding, Proc. Natl. Acad. Sci. U.S.A., 94 (1997), 7221–7226. https://doi.org/10.1073/pnas.94.14.7221 doi: 10.1073/pnas.94.14.7221

|
|
[16]
|
J. F. Kugel, J. A. Goodrich, A kinetic model for the early steps of RNA synthesis by human RNA polymerase Ⅱ, J. Biol. Chem., 275 (2000), 40483–40491. https://doi.org/10.1074/jbc.M006401200 doi: 10.1074/jbc.M006401200

|
|
[17]
|
A. Kalo, I. Kanter, A. Shraga, J. Sheinberger, H. Tzemach, N. Kinor, et al., Cellular levels of signaling factors are sensed by β-actin alleles to modulate transcriptional pulse intensity, Cell Rep., 11 (2015), 419–432. https://doi.org/10.1016/j.celrep.2015.03.039 doi: 10.1016/j.celrep.2015.03.039

|
|
[18]
|
R. D. Bliss, P. R. Painter, A. G. Marr, Role of feedback inhibition in stabilizing the classical operon, J. Theor. Biol., 97 (1982), 177–193. https://doi.org/10.1016/0022-5193(82)90098-4 doi: 10.1016/0022-5193(82)90098-4

|
|
[19]
|
F. Buchholtz, F. W. Schneider, Computer simulation of T3/T7 phage infection using lag times, Biophys. Chem., 26 (1987), 171–179. https://doi.org/10.1016/0301-4622(87)80020-0 doi: 10.1016/0301-4622(87)80020-0

|
|
[20]
|
S. N. Busenberg, J. M. Mahaffy, The effects of dimension and size for a compartmental model of repression, SIAM J. Appl. Math., 48 (1988), 882–903. https://doi.org/10.1137/0148049 doi: 10.1137/0148049

|
|
[21]
|
J. Lewis, Autoinhibition with transcriptional delay: A simple mechanism for the zebrafish somitogenesis oscillator, Curr. Biol., 13 (2003), 1398–1408. https://doi.org/10.1016/S0960-9822(03)00534-7 doi: 10.1016/S0960-9822(03)00534-7

|
|
[22]
|
N. A. M. Monk, Oscillatory expression of Hes1, p53, and NF-κB driven by transcriptional time delays, Curr. Biol., 13 (2003), 1409–1413. https://doi.org/10.1016/S0960-9822(03)00494-9 doi: 10.1016/S0960-9822(03)00494-9

|
|
[23]
|
L.-J. Chiu, M.-Y. Ling, E.-H. Wu, C.-X. You, S.-T. Lin, C.-C. Shu, The distributed delay rearranges the bimodal distribution at protein level, J. Taiwan Inst. Chem. Eng., 137 (2022), 104436. https://doi.org/10.1016/j.jtice.2022.104436 doi: 10.1016/j.jtice.2022.104436

|
|
[24]
|
M. Jansen, P. Pfaffelhuber, Stochastic gene expression with delay, J. Theor. Biol., 364 (2015), 355–363. https://doi.org/10.1016/j.jtbi.2014.09.031 doi: 10.1016/j.jtbi.2014.09.031

|
|
[25]
|
K. Rateitschak, O. Wolkenhauer, Intracellular delay limits cyclic changes in gene expression, Math. Biosci., 205 (2007), 163–179. https://doi.org/10.1016/j.mbs.2006.08.010 doi: 10.1016/j.mbs.2006.08.010

|
|
[26]
|
M. R. Roussel, On the distribution of transcription times, BIOMATH, 2 (2013), 1307247. https://doi.org/10.11145/j.biomath.2013.07.247 doi: 10.11145/j.biomath.2013.07.247

|
|
[27]
|
M. R. Roussel, R. Zhu, Stochastic kinetics description of a simple transcription model, Bull. Math. Biol., 68 (2006), 1681–1713. https://doi.org/10.1007/s11538-005-9048-6 doi: 10.1007/s11538-005-9048-6

|
|
[28]
|
S. Vashishtha, Stochastic modeling of eukaryotic transcription at the single nucleotide level, M.Sc. thesis, University of Lethbridge, 2011, URL https://www.uleth.ca/dspace/handle/10133/3190.
|
|
[29]
|
V. Pelechano, S. Chávez, J. E. Pérez-Ortín, A complete set of nascent transcription rates for yeast genes, PLoS One, 5 (2010), e15442. https://doi.org/10.1371/journal.pone.0015442 doi: 10.1371/journal.pone.0015442

|
|
[30]
|
T. Muramoto, D. Cannon, M. Gierliński, A. Corrigan, G. J. Barton, J. R. Chubb, Live imaging of nascent RNA dynamics reveals distinct types of transcriptional pulse regulation, Proc. Natl. Acad. Sci. U.S.A., 109 (2012), 7350–7355. https://doi.org/10.1073/pnas.1117603109 doi: 10.1073/pnas.1117603109

|
|
[31]
|
A. Raj, C. S. Peskin, D. Tranchina, D. Y. Vargas, S. Tyagi, Stochastic mRNA synthesis in mammalian cells, PLoS Biol., 4 (2006), e309. https://doi.org/10.1371/journal.pbio.0040309 doi: 10.1371/journal.pbio.0040309

|
|
[32]
|
D. M. Suter, N. Molina, D. Gatfield, K. Schneider, U. Schibler, F. Naef, Mammalian genes are transcribed with widely different bursting kinetics, Science, 332 (2011), 472–474. https://doi.org/10.1126/science.1198817 doi: 10.1126/science.1198817

|
|
[33]
|
I. Jonkers, H. Kwak, J. T. Lis, Genome-wide dynamics of Pol Ⅱ elongation and its interplay with promoter proximal pausing, chromatin, and exons, eLife, 3 (2014), e02407. https://doi.org/10.7554/eLife.02407 doi: 10.7554/eLife.02407

|
|
[34]
|
P. K. Parua, G. T. Booth, M. Sansó, B. Benjamin, J. C. Tanny, J. T. Lis, et al., A Cdk9-PP1 switch regulates the elongation-termination transition of RNA polymerase Ⅱ, Nature, 558 (2018), 460–464. https://doi.org/10.1038/s41586-018-0214-z doi: 10.1038/s41586-018-0214-z

|
|
[35]
|
L. Bai, R. M. Fulbright, M. D. Wang, Mechanochemical kinetics of transcription elongation, Phys. Rev. Lett., 98 (2007), 068103. https://doi.org/10.1103/PhysRevLett.98.068103 doi: 10.1103/PhysRevLett.98.068103

|
|
[36]
|
L. Bai, A. Shundrovsky, M. D. Wang, Sequence-dependent kinetic model for transcription elongation by RNA polymerase, J. Mol. Biol., 344 (2004), 335–349. https://doi.org/10.1016/j.jmb.2004.08.107 doi: 10.1016/j.jmb.2004.08.107

|
|
[37]
|
F. Jülicher, R. Bruinsma, Motion of RNA polymerase along DNA: a stochastic model, Biophys. J., 74 (1998), 1169–1185. https://doi.org/10.1016/S0006-3495(98)77833-6 doi: 10.1016/S0006-3495(98)77833-6

|
|
[38]
|
H.-Y. Wang, T. Elston, A. Mogilner, G. Oster, Force generation in RNA polymerase, Biophys. J., 74 (1998), 1186–1202. https://doi.org/10.1016/S0006-3495(98)77834-8 doi: 10.1016/S0006-3495(98)77834-8

|
|
[39]
|
T. D. Yager, P. H. Von Hippel, A thermodynamic analysis of RNA transcript elongation and termination in Escherichia coli, Biochemistry, 30 (1991), 1097–1118. https://doi.org/10.1021/bi00218a032 doi: 10.1021/bi00218a032

|
|
[40]
|
S. J. Greive, J. P. Goodarzi, S. E. Weitzel, P. H. von Hippel, Development of a "modular" scheme to describe the kinetics of transcript elongation by RNA polymerase, Biophys. J., 101 (2011), 1155–1165. https://doi.org/10.1016/j.bpj.2011.07.042 doi: 10.1016/j.bpj.2011.07.042

|
|
[41]
|
T. Filatova, N. Popovic, R. Grima, Statistics of nascent and mature rna fluctuations in a stochastic model of transcriptional initiation, elongation, pausing, and termination, Bull. Math. Biol., 83 (2021), 3. https://doi.org/10.1007/s11538-020-00827-7 doi: 10.1007/s11538-020-00827-7

|
|
[42]
|
A. N. Boettiger, P. L. Ralph, S. N. Evans, Transcriptional regulation: Effects of promoter proximal pausing on speed, synchrony and reliability, PLoS Comput. Biol., 7 (2011), e1001136. https://doi.org/10.1371/journal.pcbi.1001136 doi: 10.1371/journal.pcbi.1001136

|
|
[43]
|
X. Xu, N. Kumar, A. Krishnan, R. V. Kulkarni, Stochastic modeling of dwell-time distributions during transcriptional pausing and initiation, in 52nd IEEE Conference on Decision and Control, 2013, 4068–4073.
|
|
[44]
|
M. Hamano, Stochastic transcription elongation via rule based modelling, Electron. Notes Theor. Comput. Sci., 326 (2016), 73–88. https://doi.org/10.1016/j.entcs.2016.09.019 doi: 10.1016/j.entcs.2016.09.019

|
|
[45]
|
S. Klumpp, T. Hwa, Stochasticity and traffic jams in the transcription of ribosomal RNA: Intriguing role of termination and antitermination, Proceedings of the National Academy of Sciences.
|
|
[46]
|
A. S. Ribeiro, O.-P. Smolander, T. Rajala, A. Häkkinen, O. Yli-Harja, Delayed stochastic model of transcription at the single nucleotide level, J. Computat. Biol., 16 (2009), 539–553. https://doi.org/10.1089/cmb.2008.0153 doi: 10.1089/cmb.2008.0153

|
|
[47]
|
M. J. Schilstra, C. L. Nehaniv, Stochastic model of template-directed elongation processes in biology, BioSystems, 102 (2010), 55–60. https://doi.org/10.1016/j.biosystems.2010.07.006 doi: 10.1016/j.biosystems.2010.07.006

|
|
[48]
|
A. Garai, D. Chowdhury, D. Chowdhury, T. V. Ramakrishnan, Stochastic kinetics of ribosomes: single motor properties and collective behavior, Phys. Rev. E, 80 (2009), 011908. https://doi.org/10.1103/PhysRevE.79.011916 doi: 10.1103/PhysRevE.79.011916

|
|
[49]
|
A. Garai, D. Chowdhury, T. V. Ramakrishnan, Fluctuations in protein synthesis from a single RNA template: Stochastic kinetics of ribosomes, Phys. Rev. E, 79 (2009), 011916. https://doi.org/10.1103/PhysRevE.79.011916 doi: 10.1103/PhysRevE.79.011916

|
|
[50]
|
L. Mier-y-Terán-Romero, M. Silber, V. Hatzimanikatis, The origins of time-delay in template biopolymerization processes, PLoS Comput. Biol., 6 (2010), e1000726. https://doi.org/10.1371/journal.pcbi.1000726 doi: 10.1371/journal.pcbi.1000726

|
|
[51]
|
L. S. Churchman, J. S. Weissman, Nascent transcript sequencing visualizes transcription at nucleotide resolution, Nature, 469 (2011), 368–373.
|
|
[52]
|
K. C. Neuman, E. A. Abbondanzieri, R. Landick, J. Gelles, S. M. Block, Ubiquitous transcriptional pausing is independent of RNA polymerase backtracking, Cell, 115 (2003), 437 – 447. https://doi.org/10.1016/S0092-8674(03)00845-6 doi: 10.1016/S0092-8674(03)00845-6

|
|
[53]
|
R. Landick, The regulatory roles and mechanism of transcriptional pausing, Biochem. Soc. Trans., 34 (2006), 1062–1066. https://doi.org/10.1042/BST0341062 doi: 10.1042/BST0341062

|
|
[54]
|
V. Epshtein, F. Toulmé, A. R. Rahmouni, S. Borukhov, E. Nudler, Transcription through the roadblocks: the role of RNA polymerase cooperation, EMBO J., 22 (2003), 4719–4727. https://doi.org/10.1093/emboj/cdg452 doi: 10.1093/emboj/cdg452

|
|
[55]
|
S. Klumpp, Pausing and backtracking in transcription under dense traffic conditions, J. Stat. Phys., 142 (2011), 1252–1267. https://doi.org/10.1007/s10955-011-0120-3 doi: 10.1007/s10955-011-0120-3

|
|
[56]
|
M. Voliotis, N. Cohen, C. Molina-París, T. B. Liverpool, Fluctuations, pauses, and backtracking in DNA transcription, Biophys. J., 94 (2008), 334–348.
|
|
[57]
|
J. Li, D. S. Gilmour, Promoter proximal pausing and the control of gene expression, Curr. Opin. Genet. Dev., 21 (2011), 231–235.
|
|
[58]
|
S. Nechaev, K. Adelman, Pol Ⅱ waiting in the starting gates: Regulating the transition from transcription initiation into productive elongation, Biochim. Biophys. Acta, 1809 (2011), 34 – 45.
|
|
[59]
|
P. B. Rahl, C. Y. Lin, A. C. Seila, R. A. Flynn, S. McCuine, C. B. Burge, et al., c-Myc regulates transcriptional pause release, Cell, 141 (2010), 432 – 445. https://doi.org/10.1016/j.cell.2010.03.030 doi: 10.1016/j.cell.2010.03.030

|
|
[60]
|
P. Feng, A. Xiao, M. Fang, F. Wan, S. Li, P. Lang, et al., A machine learning-based framework for modeling transcription elongation, Proc. Natl. Acad. Sci. U.S.A., 118 (2021), e2007450118. https://doi.org/10.1073/pnas.2007450118 doi: 10.1073/pnas.2007450118

|
|
[61]
|
B. Zamft, L. Bintu, T. Ishibashi, C. Bustamante, Nascent RNA structure modulates the transcriptional dynamics of RNA polymerases, Proc. Natl. Acad. Sci. U.S.A., 109 (2012), 8948–8953. https://doi.org/10.1073/pnas.1205063109 doi: 10.1073/pnas.1205063109

|
|
[62]
|
R. D. Alexander, S. A. Innocente, J. D. Barrass, J. D. Beggs, Splicing-dependent RNA polymerase pausing in yeast, Mol. Cell, 40 (2010), 582–593. https://doi.org/10.1016/j.molcel.2010.11.005 doi: 10.1016/j.molcel.2010.11.005

|
|
[63]
|
N. Gromak, S. West, N. J. Proudfoot, Pause sites promote transcriptional termination of mammalian RNA polymerase Ⅱ, Mol. Cell. Biol., 26 (2006), 3986–3996. https://doi.org/10.1128/MCB.26.10.3986-3996.2006 doi: 10.1128/MCB.26.10.3986-3996.2006

|
|
[64]
|
N. MacDonald, Time delay in prey-predator models, Math. Biosci., 28 (1976), 321–330. https://doi.org/10.1016/0025-5564(76)90130-9 doi: 10.1016/0025-5564(76)90130-9

|
|
[65]
|
N. MacDonald, Time lag in a model of a biochemical reaction sequence with end product inhibition, J. Theor. Biol., 67 (1977), 549–556. https://doi.org/10.1016/0022-5193(77)90056-X doi: 10.1016/0022-5193(77)90056-X

|
|
[66]
|
N. MacDonald, Biological Delay Systems: Linear Stability Theory, Cambridge, Cambridge, 1989.
|
|
[67]
|
M. Barrio, A. Leier, T. T. Marquez-Lago, Reduction of chemical reaction networks through delay distributions, J. Chem. Phys., 138 (2013), 104114. https://doi.org/10.1063/1.4793982 doi: 10.1063/1.4793982

|
|
[68]
|
A. Leier, M. Barrio, T. T. Marquez-Lago, Exact model reduction with delays: Closed-form distributions and extensions to fully bi-directional monomolecular reactions, J. R. Soc. Interface, 11 (2014), 20140108. https://doi.org/10.1098/rsif.2014.0108 doi: 10.1098/rsif.2014.0108

|
|
[69]
|
I. R. Epstein, Differential delay equations in chemical kinetics: Some simple linear model systems, J. Chem. Phys., 92 (1990), 1702–1712. https://doi.org/10.1063/1.458052 doi: 10.1063/1.458052

|
|
[70]
|
D. Bratsun, D. Volfson, L. S. Tsimring, J. Hasty, Delay-induced stochastic oscillations in gene regulation, Proc. Natl. Acad. Sci. U.S.A., 102 (2005), 14593–14598. https://doi.org/10.1073/pnas.0503858102 doi: 10.1073/pnas.0503858102

|
|
[71]
|
M. R. Roussel, R. Zhu, Validation of an algorithm for delay stochastic simulation of transcription and translation in prokaryotic gene expression, Phys. Biol., 3 (2006), 274. https://doi.org/10.1088/1478-3975/3/4/005 doi: 10.1088/1478-3975/3/4/005

|
|
[72]
|
B. H. Jennings, Pausing for thought: Disrupting the early transcription elongation checkpoint leads to developmental defects and tumourigenesis, BioEssays, 35 (2013), 553–560. https://doi.org/10.1002/bies.201200179 doi: 10.1002/bies.201200179

|
|
[73]
|
H. Kwak, N. J. Fuda, L. J. Core, J. T. Lis, Precise maps of RNA polymerase reveal how promoters direct initiation and pausing, Science, 339 (2013), 950–953. https://doi.org/10.1126/science.1229386 doi: 10.1126/science.1229386

|
|
[74]
|
A. R. Hieb, S. Baran, J. A. Goodrich, J. F. Kugel, An 8nt RNA triggers a rate-limiting shift of RNA polymerase Ⅱ complexes into elongation, EMBO J., 25 (2006), 3100–3109. https://doi.org/10.1038/sj.emboj.7601197 doi: 10.1038/sj.emboj.7601197

|
|
[75]
|
T. J. Stasevich, Y. Hayashi-Takanaka, Y. Sato, K. Maehara, Y. Ohkawa, K. Sakata-Sogawa, et al., Regulation of RNA polymerase Ⅱ activation by histone acetylation in single living cells, Nature, 516 (2014), 272–275. https://doi.org/10.1038/nature13714 doi: 10.1038/nature13714

|
|
[76]
|
B. Steurer, R. C. Janssens, B. Geverts, M. E. Geijer, F. Wienholz, A. F. Theil, et al., Live-cell analysis of endogeneous GFP-RPB1 uncovers rapid turnover of initiating and promoter-paused RNA polymerase Ⅱ, Proc. Natl. Acad. Sci. U.S.A., 115 (2018), E4368–E4376. https://doi.org/10.1073/pnas.1717920115 doi: 10.1073/pnas.1717920115

|
|
[77]
|
J. Liu, D. Hansen, E. Eck, Y. J. Kim, M. Turner, S. Alamos, et al., Real-time single-cell characterization of the eukaryotic transcription cycle reveals correlations between RNA initiation, elongation, and cleavage, PLoS Comput. Biol., 17 (2021), e1008999. https://doi.org/10.1371/journal.pcbi.1008999 doi: 10.1371/journal.pcbi.1008999

|
|
[78]
|
A. Kremling, Comment on mathematical models which describe transcription and calculate the relationship between mrna and protein expression ratio, Biotech. Bioeng., 96 (2007), 815–819. https://doi.org/10.1002/bit.21065 doi: 10.1002/bit.21065

|
|
[79]
|
N. Mitarai, S. Pedersen, Control of ribosome traffic by position-dependent choice of synonymous codons, Phys. Biol., 10 (2013), 056011. https://doi.org/10.1088/1478-3975/10/5/056011 doi: 10.1088/1478-3975/10/5/056011

|
|
[80]
|
M. R. Roussel, The use of delay differential equations in chemical kinetics, J. Phys. Chem., 100 (1996), 8323–8330. https://doi.org/10.1021/jp9600672 doi: 10.1021/jp9600672

|
|
[81]
|
R. A. Coleman, B. F. Pugh, Evidence for functional binding and stable sliding of the TATA binding protein on nonspecific DNA, J. Biol. Chem., 270 (1995), 13850–13859. https://doi.org/10.1074/jbc.270.23.13850 doi: 10.1074/jbc.270.23.13850

|
|
[82]
|
A. Dasgupta, S. A. Juedes, R. O. Sprouse, D. T. Auble, Mot1-mediated control of transcription complex assembly and activity, EMBO J., 24 (2005), 1717–1729. https://doi.org/10.1038/sj.emboj.7600646 doi: 10.1038/sj.emboj.7600646

|
|
[83]
|
R. O. Sprouse, T. S. Karpova, F. Mueller, A. Dasgupta, J. G. McNally, D. T. Auble, Regulation of TATA-binding protein dynamics in living yeast cells, Proc. Natl. Acad. Sci. U.S.A., 105 (2008), 13304–13308. https://doi.org/10.1073/pnas.0801901105 doi: 10.1073/pnas.0801901105

|
|
[84]
|
S. H. Hosseini, Analytic Solutions for Stochastic Models of Transcription, Master's thesis, University of Lethbridge, 2016, URL https://www.uleth.ca/dspace/handle/10133/4791.
|
|
[85]
|
H.-J. Woo, Analytical theory of the nonequilibrium spatial distribution of RNA polymerase translocations, Phys. Rev. E, 74 (2006), 011907. https://doi.org/10.1103/PhysRevE.74.011907 doi: 10.1103/PhysRevE.74.011907

|
|
[86]
|
M. H. Larson, J. Zhou, C. D. Kaplan, M. Palangat, R. D. Kornberg, R. Landick, et al., Trigger loop dynamics mediate the balance between the transcriptional fidelity and speed of RNA polymerase Ⅱ, Proc. Natl. Acad. Sci. U.S.A., 109 (2012), 6555–6560. https://doi.org/10.1073/pnas.1200939109 doi: 10.1073/pnas.1200939109

|
|
[87]
|
A. C. M. Cheung, P. Cramer, Structural basis of RNA polymerase Ⅱ backtracking, arrest and reactivation, Nature, 471 (2011), 249–253. https://doi.org/10.1038/nature09785 doi: 10.1038/nature09785

|
|
[88]
|
G. Brzyżek, S. Świeżewski, Mutual interdependence of splicing and transcription elongation, Transcription, 6 (2015), 37–39. https://doi.org/10.1080/21541264.2015.1040146 doi: 10.1080/21541264.2015.1040146

|
|
[89]
|
M. Imashimizu, M. L. Kireeva, L. Lubkowska, D. Gotte, A. R. Parks, J. N. Strathem, et al., Intrinsic translocation barrier as an initial step in pausing by RNA polymerase Ⅱ, J. Mol. Biol., 425 (2013), 697–712. https://doi.org/10.1016/j.jmb.2012.12.002 doi: 10.1016/j.jmb.2012.12.002

|
|
[90]
|
J. W. Roberts, Molecular basis of transcriptional pausing, Science, 344 (2014), 1226–1227. https://doi.org/10.1126/science.1255712 doi: 10.1126/science.1255712

|
|
[91]
|
J. Singh, R. A. Padgett, Rates of in situ transcription and splicing in large human genes, Nat. Struct. Mol. Biol., 16 (2009), 1128–1133. https://doi.org/10.1038/nsmb.1666 doi: 10.1038/nsmb.1666

|
|
[92]
|
E. Rosonina, S. Kaneko, J. L. Manley, Terminating the transcript: breaking up is hard to do, Genes Dev., 20 (2006), 1050–1056. https://doi.org/10.1101/gad.1431606 doi: 10.1101/gad.1431606

|
|
[93]
|
E. A. Abbondanzieri, W. J. Greenleaf, J. W. Shaevitz, R. Landick, S. M. Block, Direct observation of base-pair stepping by RNA polymerase, Nature, 438 (2005), 460–465. https://doi.org/10.1038/nature04268 doi: 10.1038/nature04268

|
|
[94]
|
L. M. Hsu, Promoter clearance and escape in prokaryotes, Biochim. Biophys. Acta, 1577 (2002), 191–207. https://doi.org/10.1016/S0167-4781(02)00452-9 doi: 10.1016/S0167-4781(02)00452-9

|
|
[95]
|
H. Kimura, K. Sugaya, P. R. Cook, The transcription cycle of RNA polymerase Ⅱ in living cells, J. Cell Biol., 159 (2002), 777–782. https://doi.org/10.1083/jcb.200206019 doi: 10.1083/jcb.200206019

|
|
[96]
|
H. A. Ferguson, J. F. Kugel, J. A. Goodrich, Kinetic and mechanistic analysis of the RNA polymerase Ⅱ transcription reaction at the human interleukin-2 promoter, J. Mol. Biol., 314 (2001), 993–1006. https://doi.org/10.1006/jmbi.2000.5215 doi: 10.1006/jmbi.2000.5215

|
|
[97]
|
D. A. Jackson, F. J. Iborra, E. M. M. Manders, P. R. Cook, Numbers and organization of RNA polymerases, nascent transcripts, and transcription units in HeLa nuclei, Mol. Biol. Cell, 9 (1998), 1523–1536. https://doi.org/10.1091/mbc.9.6.1523 doi: 10.1091/mbc.9.6.1523

|
|
[98]
|
P. J. Hurtado, A. S. Kirosingh, Generalizations of the 'linear chain trick': Incorporating more flexible dwell time distributions into mean field ODE models, J. Math. Biol., 79 (2019), 1831–1883. https://doi.org/10.1007/s00285-019-01412-w doi: 10.1007/s00285-019-01412-w

|
|
[99]
|
H. Golstein, Classical Mechanics, chapter 12, Addison-Wesley, Reading, Massachusetts, 1980.
|
|
[100]
|
H. G. Othmer, A continuum model for coupled cells, J. Math. Biol., 17 (1983), 351–369. https://doi.org/10.1007/BF00276521 doi: 10.1007/BF00276521

|
|
[101]
|
C. J. Roussel, M. R. Roussel, Reaction-diffusion models of development with state-dependent chemical diffusion coefficients, Prog. Biophys. Mol. Biol., 86 (2004), 113–160. https://doi.org/10.1016/j.pbiomolbio.2004.03.001 doi: 10.1016/j.pbiomolbio.2004.03.001

|
|
[102]
|
D. Sulsky, R. R. Vance, W. I. Newman, Time delays in age-structured populations, J. Theor. Biol., 141 (1989), 403–422. https://doi.org/10.1016/S0022-5193(89)80122-5 doi: 10.1016/S0022-5193(89)80122-5

|
|
[103]
|
G. Bel, B. Munsky, I. Nemenman, The simplicity of completion time distributions for common complex biochemical processes, Phys. Biol., 7 (2010), 016003. https://doi.org/10.1088/1478-3975/7/1/016003 doi: 10.1088/1478-3975/7/1/016003

|
|
[104]
|
P. Billingsley, Probability and Measure, Wiley, New York, 1995.
|
|
[105]
|
G. Bar-Nahum, V. Epshtein, A. E. Ruckenstein, R. Rafikov, A. Mustaev, E. Nudler, A ratchet mechanism of transcription elongation and its control, Cell, 120 (2005), 183–193. https://doi.org/10.1016/j.cell.2004.11.045 doi: 10.1016/j.cell.2004.11.045

|
|
[106]
|
J. W. Shaevitz, E. A. Abbondanzieri, R. Landick, S. M. Block, Backtracking by single RNA polymerase molecules observed at near-base-pair resolution, Nature, 426 (2003), 684–687. https://doi.org/10.1038/nature02191 doi: 10.1038/nature02191

|
|
[107]
|
M. A. Gibson, J. Bruck, Efficient exact stochastic simulation of chemical systems with many species and many channels, J. Phys. Chem. A, 104 (2000), 1876–1889. https://doi.org/10.1021/jp993732q doi: 10.1021/jp993732q

|
|
[108]
|
H. T. Banks, J. Catenacci, S. Hu, A comparison of stochastic systems with different types of delays, Stoch. Anal. Appl., 31 (2013), 913–955. https://doi.org/10.1080/07362994.2013.806217 doi: 10.1080/07362994.2013.806217

|
|
[109]
|
Y.-L. Feng, J.-M. Dong, X.-L. Tang, Non-Markovian effect on gene transcriptional systems, Chin. Phys. Lett., 33. https://doi.org/10.1088/0256-307X/33/10/108701
|
|
[110]
|
J. Lloyd-Price, A. Gupta, A. S. Ribeiro, Sgns2: A compartmental stochastic chemical kinetics simulator for dynamic cell populations, Bioinformatics, 28 (2012), 3004–3005. https://doi.org/10.1093/bioinformatics/bts556 doi: 10.1093/bioinformatics/bts556

|
|
[111]
|
T. Maarleveld, StochPy User Guide, Release 2.3.0, 2015, URL https://sourceforge.net/projects/stochpy/files/stochpy_userguide_2.3.pdf/download.
|
|
[112]
|
A. S. Ribeiro, J. Lloyd-Price, SGN Sim, a stochastic genetic networks simulator, Bioinformatics, 23 (2007), 777–779. https://doi.org/10.1093/bioinformatics/btm004 doi: 10.1093/bioinformatics/btm004

|
|
[113]
|
D. T. Gillespie, A general method for numerically simulating the stochastic time evolution of coupled chemical reactions, J. Comput. Phys., 22 (1976), 403–434. https://doi.org/10.1016/0021-9991(76)90041-3 doi: 10.1016/0021-9991(76)90041-3

|
|
[114]
|
R. J. Sims Ⅲ, R. Belotserkovskaya, D. Reinberg, Elongation by RNA polymerase Ⅱ: the short and long of it, Genes Dev., 18 (2004), 2437–2468. https://doi.org/10.1101/gad.1235904 doi: 10.1101/gad.1235904

|
|
[115]
|
E. A. M. Trofimenkoff, M. R. Roussel, Small binding-site clearance delays are not negligible in gene expression modeling, Math. Biosci., 325 (2020), 108376. https://doi.org/10.1016/j.mbs.2020.108376 doi: 10.1016/j.mbs.2020.108376

|
|
[116]
|
V. Epshtein, E. Nudler, Cooperation between RNA polymerase molecules in transcription elongation, Science, 300 (2003), 801–805. https://doi.org/10.1126/science.1083219 doi: 10.1126/science.1083219

|
|
[117]
|
C. Jia, L. Y. Wang, G. G. Yin, M. Q. Zhang, Single-cell stochastic gene expression kinetics with coupled positive-plus-negative feedback, Phys. Rev. E, 100. https://doi.org/10.1103/PhysRevE.100.052406
|
|
[118]
|
J. Szavits-Nossan, R. Grima, Uncovering the effect of RNA polymerase steric interactions on gene expression noise: Analytical distributions of nascent and mature RNA numbers, Phys. Rev. E, 108 (2023), 034405. https://doi.org/10.1103/PhysRevE.108.034405 doi: 10.1103/PhysRevE.108.034405

|
|
[119]
|
P. Bokes, J. R. King, A. T. A. Wood, M. Loose, Transcriptional bursting diversifies the behaviour of a toggle switch: Hybrid simulation of stochastic gene expression, Bull. Math. Biol., 75 (2013), 351–371. https://doi.org/10.1007/s11538-013-9811-z doi: 10.1007/s11538-013-9811-z

|
|
[120]
|
M. Dobrzyński, F. J. Bruggeman, Elongation dynamics shape bursty transcription and translation, Proc. Natl. Acad. Sci. U.S.A., 106 (2009), 2583–2588. https://doi.org/10.1073/pnas.0803507106 doi: 10.1073/pnas.0803507106

|
|
[121]
|
L. Cai, N. Friedman, X. S. Xie, Stochastic protein expression in individual cells at the single molecule level, Nature, 440 (2006), 358–362. https://doi.org/10.1038/nature04599 doi: 10.1038/nature04599

|
|
[122]
|
A. J. M. Larsson, P. Johnsson, M. Hagemann-Jensen, L. Hartmanis, O. R. Faridani, B. Reinius, et al., Genomic encoding of transcriptional burst kinetics, Nature, 565 (2019), 251–254. https://doi.org/10.1038/s41586-018-0836-1 doi: 10.1038/s41586-018-0836-1

|
|
[123]
|
Y. Wan, D. G. Anastasakis, J. Rodriguez, M. Palangat, P. Gudla, G. Zaki, et al., Dynamic imaging of nascent RNA reveals general principles of transcription dynamics and stochastic splice site selection, Cell, 184 (2021), 2878–2895. https://doi.org/10.1016/j.cell.2021.04.012 doi: 10.1016/j.cell.2021.04.012

|
|
[124]
|
C. Jia, Y. Li, Analytical time-dependent distributions for gene expression models with complex promoter switching mechanisms, SIAM J. Appl. Math., 83 (2023), 1572–1602. https://doi.org/10.1137/22M147219X doi: 10.1137/22M147219X

|
|
[125]
|
B. W. Lindgren, G. W. McElrath, D. A. Berry, Introduction to Probability and Statistics, 154–156, 4th edition, Macmillan, New York, 1978.
|
|
[126]
|
M. Janisch, Kolmogorov's strong law of large numbers holds for pairwise uncorrelated random variables, Theory Probab. Appl., 66 (2021), 263–275. https://doi.org/10.4213/tvp5459 doi: 10.4213/tvp5459

|
|
[127]
|
B. Li, J. A. Weber, Y. Chen, A. L. Greenleaf, D. S. Gilmour, Analyses of promoter-proximal pausing by RNA polymerase Ⅱ on the hsp70 heat shock gene promoter in a Drosophila nuclear extract, Mol. Cell. Biol., 16 (1996), 5433–5443. https://doi.org/10.1128/MCB.16.10.5433 doi: 10.1128/MCB.16.10.5433

|
|
[128]
|
R.-J. Murphy, Stochastic Modeling of the Torpedo Mechanism of Eukaryotic Transcription Termination, Master's thesis, University of Lethbridge, 2017, URL https://www.uleth.ca/dspace/handle/10133/4906.
|
|
[129]
|
B. Choi, Y.-Y. Cheng, S. Cinar, W. Ott, M. R. Bennett, K. Josić, et al., Bayesian inference of distributed time delay in transcriptional and translational regulation, Bioinformatics, 36 (2020), 586–593. https://doi.org/10.1093/bioinformatics/btz574 doi: 10.1093/bioinformatics/btz574

|
|
[130]
|
H. Hong, M. J. Cortez, Y.-Y. Cheng, H. J. Kim, B. Choi, K. Josić, et al., Inferring delays in partially observed gene regulation processes, Bioinformatics, 39 (2023), btad670. https://doi.org/10.1093/bioinformatics/btad670 doi: 10.1093/bioinformatics/btad670

|
|
[131]
|
D. Holcman, Z. Schuss, The narrow escape problem, SIAM Rev., 56 (2014), 213–257. https://doi.org/10.1137/120898395
|
|
[132]
|
M. R. Roussel, T. Tang, Simulation of mRNA diffusion in the nuclear environment, IET Syst. Biol., 6 (2012), 125–133. https://doi.org/10.1049/iet-syb.2011.0032 doi: 10.1049/iet-syb.2011.0032

|
|
[133]
|
S. Tang, Mathematical Modeling of Eukaryotic Gene Expression, PhD thesis, University of Lethbridge, 2010, URL https://www.uleth.ca/dspace/handle/10133/2567.
|









 DownLoad:
DownLoad: