Threshold dynamics of a switching diffusion SIR model with logistic growth and healthcare resources

1.   Introduction

For over 2 years, the coronavirus pandemic with its 6 million fatalities so far [1], has dominated global events, sometimes creating the impression that it is the only relevant infectious disease. However, in 2019 alone, there were also almost 5 million deaths related to antibiotic-resistant bacteria [2]. This emphasizes the importance of infectious diseases and that this threat will not disappear even if the current pandemic ends.

In addition to medications, vaccinations and personal protective equipment, disinfection measures are an important element in the fight against all infections. Irradiation with ultraviolet radiation in the UVC spectral range of 200–280 nm is one of the oldest and most effective disinfection techniques [3], which can quickly reduce pathogens by several orders of magnitude, even at very low irradiation doses [4],[5]. The effect is based on the destruction of DNA and RNA of bacteria, fungi and viruses [3]–[5] including coronaviruses like SARS-CoV-2 [4],[6]–[8]. Unfortunately, radiation of these wavelengths also cause harm to human DNA, which is why UVC radiation should not be applied in the presence of humans.

However, the development of LED technology in recent years, has made another almost unknown disinfection approach possible: irradiation with visible violet or blue light (instead of ultraviolet radiation). This visible light is absorbed by naturally present endogenous photosensitizers such as porphyrins or flavins, which have their absorption maxima in the violet and blue spectral range, respectively. During this absorption the photosensitizer molecule is transferred from its singlet ground state to an excited singlet state. This high energy state can decay be immediate emission of a fluorescence photon back to its ground state or it can reach a high energy triplet state. In the presence of oxygen two different types of chemical reactions that generate reactive oxygen species (ROS) are possible. Type I reactions lead to the formation of OH*, O₂^*− or H₂O₂ by electron transfer and type II reactions generate ¹O₂ by energy transfer. All of these radicals damage cell structures such as DNA, proteins or membranes [9]–[15] and can thus lead to cell death. If the irradiation dose is high enough, visible light appears to be effective against bacteria, fungi and even viruses [16]–[18] without endangering humans or human cells [19],[20].

White light also exhibits an antimicrobial activity, as it has blue emission components [21]–[24]. However, the effect is weak and a reduction of 90% takes at least many hours or even days. It is difficult to achieve a significant microbial reduction in a short time, with a white illumination. In the past we have already been able to demonstrate successful bacterial reduction with white illumination [24]. However the setup was performed in a laboratory environment with a very high illuminance of about 200,000 lux, which is way above typical indoor illumination levels. To reach more realistic use case scenarios, the antimicrobial effect of white illumination can be amplified by adding violet emissions [21],[24].

Therefore, this study will investigate to what extent bacterial reduction is possible under more realistic lighting conditions, by applying both white and violet radiation simultaneously, and how much this affects the color temperature of the illumination. The experiments will be conducted on Staphylococcus carnosus, as this non-pathogenic staphylococcal strain is similarly photosensitive as the pathogenic Staphylococcus aureus [25]. In addition, staphylococci also appear to be roughly similar to coronaviruses concerning light sensitivity [26]. Some manufacturers of white-violet LED lights already claim that their products can reduce coronaviruses by several orders of magnitude [27], which is why scientifically verifying this statement is of interest.

2.   Materials and methods

2.1.   Illumination device

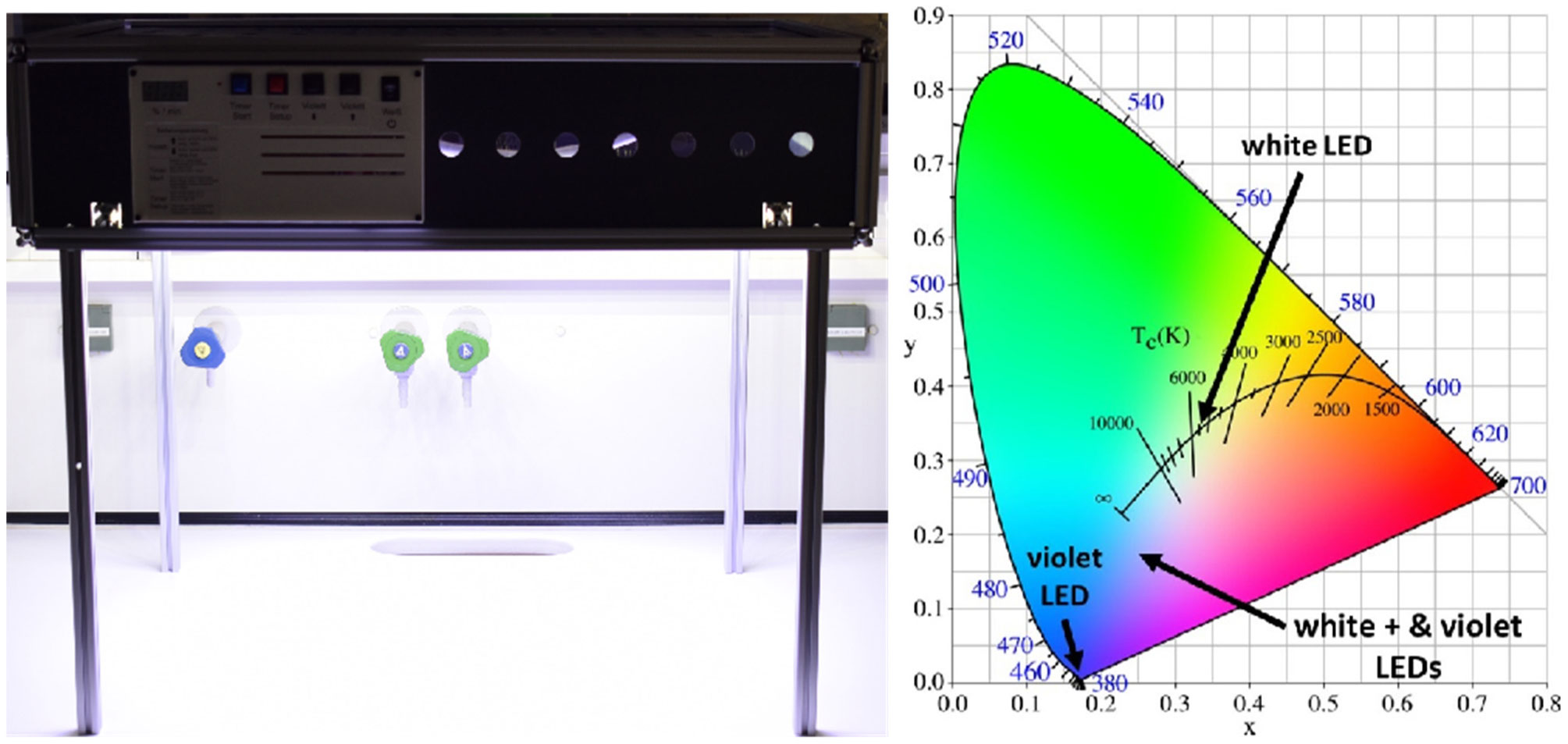
To illuminate an area of 60 × 40 cm², 6 × 4 white LEDs type PM2E-1LWE of Prolight Opto (Taoyuan City, Taiwan) and 6 × 4 violet 405 nm LEDs type PK2B-3JLE-GNVL of Prolight Opto were installed on a copper board at a height of approximately 50 cm above a work surface to be disinfected. The white and violet irradiation could be switched on independently. Dimming was also possible, but in all experiments presented here, both types of LED were operated at maximum or switched off. In the setting demonstrated on the left side of Figure 1, both LED types were operated at their maximum intensities.

The illuminance achieved with the white LEDs was 2,400 lux at a color temperature of 5600 K and a color rendering index of 74. The violet LEDs provided an irradiance of 2.5 mW/cm² @405 nm. The CIE (Commission Internationale de l'Éclairage) color coordinates of the combined white and violet lighting are illustrated in Figure 1 (right). Illuminance and irradiance below the luminaire were homogeneous with a deviation of +/− 10 % of the average values.

Figure 1.  Luminaire with white and violet LEDs for illuminating a work surface (left); Illustration of the color impression of the different illuminations in a CIE diagram (right). (Modified according to [28].).

DownLoad: Full-Size Img PowerPoint

2.2.   Microbiological experiments

The test organism in this study was Staphylococcus carnosus (DSM 20501), which was provided by Deutsche Sammlung von Mikroorganismen und Zellkulturen (Brauschweig, Germany). The application of this bacterium facilitated the investigation as it is non-pathogenic, but exhibits a photosensitivity comparable to that of S. aureus [25], which is one of the most important and deadliest bacterial pathogens [2]. S. carnosus was cultivated in M92 medium up to an optical density of about 0.2. This corresponded to a concentration of approximately 3 × 10⁷ colony forming units (cfu)/ml. The bacterial culture was then diluted 1 : 1000 in phosphate buffered saline (PBS).

Before applying this bacterial solution, the work surface, glazed stoneware of WALDNER Laboreinrichtungen (Wangen, Germany), was disinfected by a 70% ethanol solution and UVC irradiation. To obtain a homogenous distribution of bacteria on the work surface, the following procedure was performed: Two industrial paper towels of Glaeser, (Ulm, Germany) were placed side by side on the work surface and a Pasteur pipette was used to spread approximately 7 ml of bacterial solution evenly on each towel before the towels were manually flattened with sterile gloves. After about 1 hour the towel was dry and could be removed.

Bacterial concentration sampling was performed at predefined time intervals of 0 h, 12 h, 24 h, 36 h and 46 h and at predefined positions with caso contact agar plates of VWR (Darmstadt, Germany) under different illumination conditions (dark, white, white + violet). For each illumination situation 5 runs were performed, typically using 3 contact plates for each sampling, resulting in a total of about 250 analyzed contact agar plates.

The plates were cultivated at 37 °C in an incubator for about 24 h, before the number of staphylococcal colonies were counted. Colonies that seemed to be caused by other microorganisms, due to differences in shape, size or color, were ignored.

3.   Results

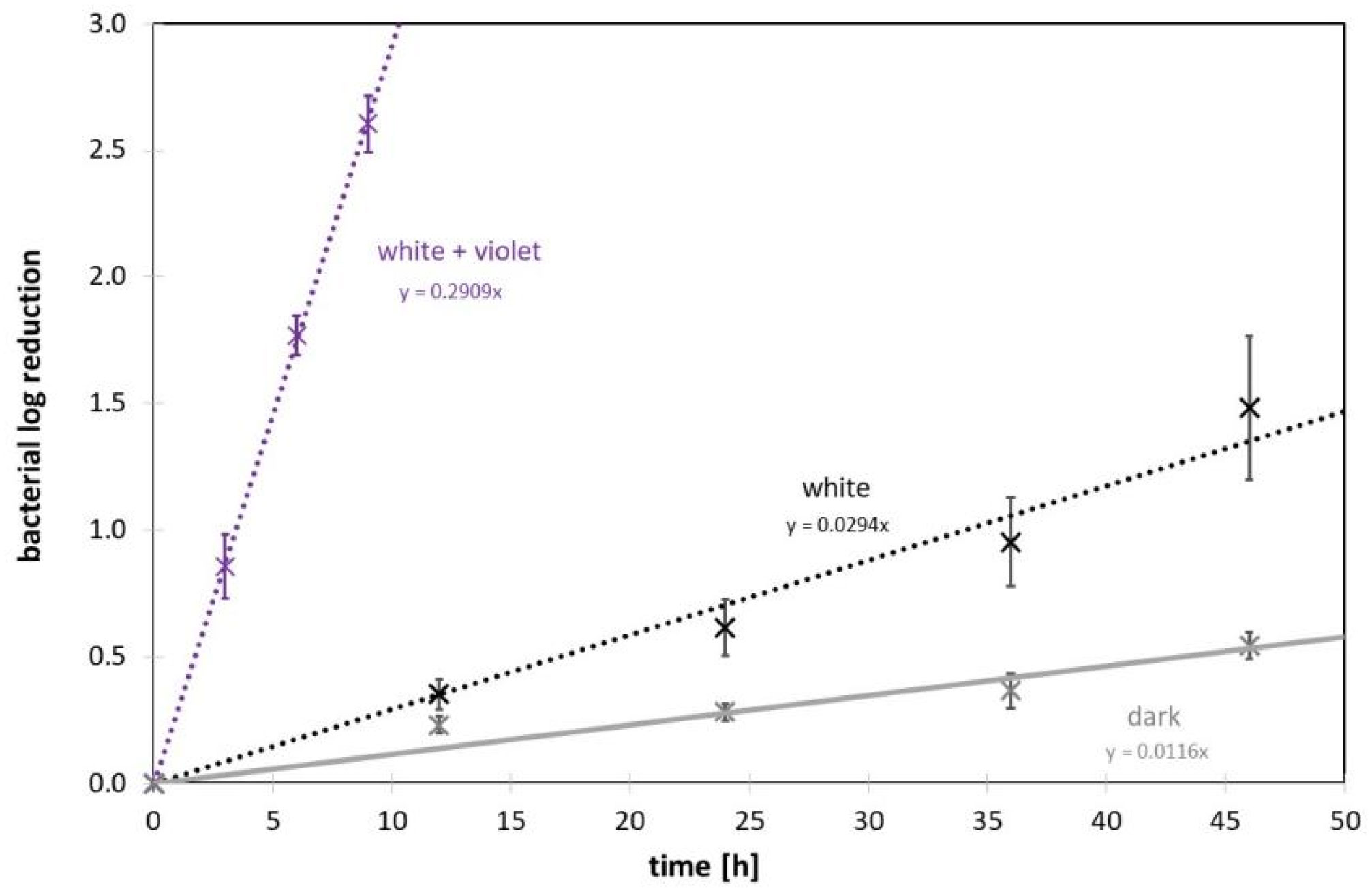
The time course of the bacterial reduction is given in Figure 2. Even without illumination, the staphylococcal concentration decreases. Extrapolation of the trend line leads to an expected decrease of 90% (1 log level) after 86 hours. For white illumination with 2,400 lux and a color temperature of 5600 K, the bacterial reduction progresses more quickly. After 34 hours, only 10% of the bacteria are still left. The combination of white and violet lighting is notably faster in reduction of bacterial load. A 90% staphylococcal reduction is achieved here after less than 3.5 hours. However, as can already be perceived in Figure 1, the illumination no longer appears properly white and the violet portion is recognizable.

Figure 2.  Relative changes in bacterial concentration on the test work surface with, white-violet, white and no illumination.

DownLoad: Full-Size Img PowerPoint

4.   Discussion

It turns out that even the (pure) white illumination causes a noticeable reduction of bacteria. Staphylococci are inactivated significantly faster than in the dark. However, the effect is rather small under the relatively bright lighting of 2,400 lux. Many workplaces are less brightly lit. The international standard EN 12464-1:2021 (“Light and lighting-Lighting of workplaces-Part 1: Indoor workplaces”) specifies an illuminance of only 500 lux for many office workplaces, but also for lecture halls and classrooms. Even for medical examination rooms the imposed illuminance is only 1,000 lux [29].

The situation is different for operating theatres. Illuminance levels of 10,000 to 100,000 lux are demanded here [29]. This is more than four times brighter than the test lighting studied. Therefore, a 90% bacterial reduction might be achieved within 1 to 10 hours of pure white lighting with illuminance levels between 100,000 and 10,000 lux, respectively.

In combination with the violet LEDs, the antimicrobial effect of the presented test illumination is about 10 times stronger than with pure white light (2,400 lux) alone, but 3.5 hours of irradiation are still required for a 90% bacterial reduction. This is still very long compared to typical UVC disinfection durations of minutes to seconds [5]–[8],[30]–[39]. However, for less time-critical applications, such as the disinfection of work areas or rooms overnight, such irradiation with white-violet light is conceivable and in contrast to UVC emitters, without any relevant risk to humans.

A question is whether the violet emission can be raised even further to increase the disinfection effect. This is possible in principle, but even with a tenfold increase in the violet radiation, a 90% reduction of bacteria would probably still take about 20 minutes. At the same time, the color impression of the illumination would move even further away from white, with the risk that this would be unpleasant for people. A potential blue light hazard would also have to be discussed.

In the introduction it was already mentioned that there exist white-violet luminaires, which are advertised by manufacturers with an antiviral effect [27]. In fact, scientific studies show that visible violet light even inactivates coronaviruses [18]. Many of the investigations appear to have been performed (unintentionally) with additional external photosensitizers, representing conditions differing from everyday settings, but not all of them [18]. In our own study without external photosensitizers, we achieved a 90% reduction of (bovine) coronaviruses with a 405 nm irradiation dose of 57.5 J/cm² [26]. This dose would be reached after 6.4 hours of violet irradiation with the illumination setup presented above. Thus, similar to bacteria, reduction by visible light is also possible for (corona-) viruses, but on a time scale of hours that depends strongly on the intensity of white and violet illumination.

5.   Conclusions

The light of white LEDs exhibits a weak antimicrobial effect due to its blue content. The brighter the blue emissions are, the stronger is the antimicrobial effect. Warm white LEDs emit a large proportion of green, yellow and red light, to which the human eye is very sensitive. However, this light is not absorbed by the relevant microbial photosensitizers and hardly contributes to photoinactivation of microorganisms. The weak blue emissions of warm-white LEDs therefore lead to only a modest antimicrobial effect. Cold-white LEDs have a strong blue component, but the eye is relatively insensitive in this spectral range, which is why cold-white LEDs appear darker than warm-white LEDs at the same total radiant power. Therefore, at the same brightness perception of a user, the blue component absorbable by microbial photosensitizers and thus the antimicrobial effect is much stronger with cold-white LEDs.

Combining white light with visible violet light can significantly increase the antimicrobial effect compared to a pure white illumination, but under realistic conditions it is impossible to achieve disinfection times equivalent to those of UVC irradiation.

The test organism investigated here was only a single staphylococcal strain, but firstly, staphylococcal strains such as S. aureus are among the most important bacterial pathogens and secondly, they have a rather average photosensitivity for violet light [16], so that similar results can be expected for other bacteria. Coronaviruses require similar or even higher doses for reduction [18]. Therefore, white or white-violet lighting should not be expected to work miracles in terms of very rapid reduction of bacteria or (corona-) viruses.