Analysis of peakon-like soliton solutions: (3+1)-dimensional Fractional Klein-Gordon equation

Waleed Hamali; Abdullah A. Zaagan; Hamad Zogan; Waleed Hamali; Abdullah A. Zaagan; Hamad Zogan

doi:10.3934/math.2024722

AIMS Mathematics

2024, Volume 9, Issue 6: 14913-14931. doi: 10.3934/math.2024722

Previous Article Next Article

Research article Special Issues

Analysis of peakon-like soliton solutions: (3+1)-dimensional Fractional Klein-Gordon equation

1.
Department of Mathematics, Faculty of Science, Jazan University, P.O. Box 2097, Jazan 45142, kingdom of Saudi Arabia
2.
Department of Computer Science, College of Engineering and Computer Science, Jazan University, Jazan, Kingdom of Saudi Arabia

In this study, we investigate the fundamental properties of ( $3+1$ )- $D$ Fractional Klein-Gordon equation using the sophisticated techniques of Riccatti-Bornoulli sub-ODE approach with Backlund transformation. Using a more stringent criterion, our study reveals new soliton solutions that have peakon-like properties and unique cusp features. This research provides significant understanding of the dynamic behaviours and odd events related to these solutions. This work is important because it helps to elucidate the complex dynamics that exist within physical systems, which will benefit many different scientific fields. Our method is used to examine the existence and stability of compactons and kinks in the context of actual physical systems. Under a double-well on-site potential, these structures are made up of a network of connected nonlinear pendulums. Both $2D$ and contour plots produced by parameter changes provide as clear examples of the efficiency, simplicity, and conciseness of the computational method used. The results highlight how flexible this approach is, and demonstrate how symbolic calculations broaden its application to more complex events. This work offers a useful framework and studying intricate physical systems, as well as a flexible computational tool that may be used in a variety of scientific fields.

Keywords:

Citation: Waleed Hamali, Abdullah A. Zaagan, Hamad Zogan. Analysis of peakon-like soliton solutions: (3+1)-dimensional Fractional Klein-Gordon equation[J]. AIMS Mathematics, 2024, 9(6): 14913-14931. doi: 10.3934/math.2024722

Related Papers:

[1]	Mustafa Inc, Hadi Rezazadeh, Javad Vahidi, Mostafa Eslami, Mehmet Ali Akinlar, Muhammad Nasir Ali, Yu-Ming Chu . New solitary wave solutions for the conformable Klein-Gordon equation with quantic nonlinearity. AIMS Mathematics, 2020, 5(6): 6972-6984. doi: 10.3934/math.2020447
[2]	Xiangmei Li, Kamran, Absar Ul Haq, Xiujun Zhang . Numerical solution of the linear time fractional Klein-Gordon equation using transform based localized RBF method and quadrature. AIMS Mathematics, 2020, 5(5): 5287-5308. doi: 10.3934/math.2020339
[3]	Khudhayr A. Rashedi, Musawa Yahya Almusawa, Hassan Almusawa, Tariq S. Alshammari, Adel Almarashi . Lump-type kink wave phenomena of the space-time fractional phi-four equation. AIMS Mathematics, 2024, 9(12): 34372-34386. doi: 10.3934/math.20241637
[4]	Sayed Saifullah, Amir Ali, Zareen A. Khan . Analysis of nonlinear time-fractional Klein-Gordon equation with power law kernel. AIMS Mathematics, 2022, 7(4): 5275-5290. doi: 10.3934/math.2022293
[5]	Canlin Gan, Weiwei Wang . Existence result for the critical Klein-Gordon-Maxwell system involving steep potential well. AIMS Mathematics, 2023, 8(11): 26665-26681. doi: 10.3934/math.20231364
[6]	Chun Huang, Zhao Li . New soliton solutions of the conformal time derivative generalized $ q $-deformed sinh-Gordon equation. AIMS Mathematics, 2024, 9(2): 4194-4204. doi: 10.3934/math.2024206
[7]	Qiuying Li, Xiaoxiao Zheng, Zhenguo Wang . Orbital stability of periodic standing waves of the coupled Klein-Gordon-Zakharov equations. AIMS Mathematics, 2023, 8(4): 8560-8579. doi: 10.3934/math.2023430
[8]	Yaojun Ye, Lanlan Li . Global existence and blow-up of solutions for logarithmic Klein-Gordon equation. AIMS Mathematics, 2021, 6(7): 6898-6914. doi: 10.3934/math.2021404
[9]	Yaya Wang, Md Nurul Raihen, Esin Ilhan, Haci Mehmet Baskonus . On the new sine-Gordon solitons of the generalized Korteweg-de Vries and modified Korteweg-de Vries models via beta operator. AIMS Mathematics, 2025, 10(3): 5456-5479. doi: 10.3934/math.2025252
[10]	Khalid Khan, Amir Ali, Muhammad Irfan, Zareen A. Khan . Solitary wave solutions in time-fractional Korteweg-de Vries equations with power law kernel. AIMS Mathematics, 2023, 8(1): 792-814. doi: 10.3934/math.2023039

Abstract

1. Introduction

Much focus in the last few years has been on the nonlinear phenomena, which appears in various fields of mathematical and physical sciences, such as physics, biology, and chemistry. In the mathematical and physical domains, nonlinear evolution equations are essential for modeling a wide range of physical processes, making the analytical solutions to related evolution equations important. Since nonlinear equations are used to describe many physical processes, it becomes vital to investigate analytical solutions, especially those in the form of solitons ^[1]. One characteristic that sets soliton solutions apart from other types of solutions is that they depend only on one set of variables. A soliton is defined as a self-reinforcing single wave or pulse in mathematics and physics that keeps its shape while moving at a steady speed. The inception of the soliton phenomena may be traced back to the groundbreaking observations made by John Scott Russell who at first noticed a single wave in the Union Canal in Scotland ^[2,3,4,5,6].

In fact, the framework designated as fractional partial differential equations (FPDEs) provides accurate representation for a wide range of technical and physical phenomena ^[7,8,9]. Applications of FPDEs in a variety of scientific and engineering fields demonstrate how versatile it is; these include financial modeling ^[10], wave modeling ^[11], signal control systems ^[12], earthquake modeling ^[13], and more. Because Fractional partial differential equations appear so frequently in various applications, they become more significant and has drawn the interest of scholars who understand how effective they are at handling a wide range of complex events. Because fractional partial differential equations have been used in so many different scientific and technical fields, mathematicians have created a variety of numerical and analytical methods to solve fractional-related problems ^[14,15]. It is noteworthy that fractional variational iteration method (FVIM) has been utilized by researchers to handle particular cases of fractional partial differential equations, as J. Song et al. in ^[16] illustrates. Furthermore, taking into account both beginning and boundary conditions, Duan et al. have effectively applied Adomian decomposition method (ADM) to obtain series-form solutions for various partial differential equations, including those involving fractional partial differential equations ^[17]. Furthermore, the Laplace ADM has been applied to solve problems with the Fractional partial differential equation ^[18]. Fractional k-dV-Burger equations were analytically derived using the homotopy perturbation method by Wang ^[19]. Meanwhile, the extend tanh-method has been employed by Raslan, et al. ^[20] to solve fractional equal width wave and modified equal wave equations and other different techniques ^{[21,22,23,24,25]}.

Also, embedded inside the framework of the presented methodology ^[26,27,28], which is known for its ability to successfully deal with intricate algebraic manipulations, is the ability to find answers to a wide range of events in biology, chemistry, physics, fluid mechanics, and optical fibers. It may improve optimization and prediction approaches, and provide adequate knowledge about the behavior of fluid flow when exploited in biological systems, commercial process functions, and environmental fluid dynamics processes. This further helps to elucidate the essential aspects embedded in the intricate dynamics associated with such systems. Meng et al. presented an observer design method tailored for nonlinear generalized systems with nonlinear algebraic constraints, offering practical applications in system control and optimization ^[29]. Meanwhile, Cai et al. explored the dynamic manipulation of terahertz wavefronts using cascaded metasurfaces, unveiling possibilities for advanced photonics applications ^[30]. Ali et al. introduced a new class of digital integrators based on trigonometric quadrature rules, contributing to the advancement of industrial electronics and digital signal processing techniques ^[31]. Guo and Hu proposed a time based generator-based approach for the practical predefined-time stabilization of high-order systems in the presence of unknown disturbances, offering robust solutions for circuit and system design challenges ^[32]. Additionally, Kai and Ji investigated the generalization of regularized long-wave equations ^[33], while Kai and Yin delved into the linear structure and soliton molecules of the Sharma-Tasso-Olver-Burgers equation, shedding light on fundamental aspects of nonlinear dynamics and mathematical physics ^[34].

Our goal in this work is to solve the fractional-order Klein-Gordon equation using the sub-ODE technique of Riccatti-Bornoulli. The overarching expression for the ( $3+1$ )- $D$ Fractional order Klein-Gordon equation is provided as follows ^[35]:

$\begin{equation} \begin{split} D_t^{2\alpha}F - \left(D_x^{2\beta}F + D_y^{2\gamma}F \right) + m^2 F + \lambda |F|^2F = 0, \quad 0 < \alpha, \beta, \gamma\leq 1. \end{split} \end{equation}$

(1.1)

Here, ( $m$ ) and ( $\lambda$ ) are constants. Conformable fractional derivatives are used in this analysis based on the following properties ^[36]. The operator representing derivatives of order ( $\alpha$ ) is defined as follows:

$\begin{equation} \begin{split} D_\theta^\alpha{q(\theta)} = \lim\limits_{m \to 0} \frac{q(m(\theta)^{1-\alpha}-q{(\theta)})}{m}, 0 < \alpha\leq1. \end{split} \end{equation}$

(1.2)

$\begin{equation} \left\{ \begin{aligned} &D_\theta^\alpha \theta^j = j \theta^{j-\alpha}, j\in R\\ &D_\theta^\alpha\left(j_1 \eta(\theta) \pm j_2 m(\theta)\right) = j_1 D_\theta^\alpha(\eta(\theta)) \pm j_2 D_\theta^\alpha(m(\theta)).\\ &D_\theta^\alpha \left[f o g \right] = \theta^{1-\alpha} g \left( \theta \right)D_\theta^\alpha f \left(g(\theta))\right. \end{aligned} \right. \end{equation}$

(1.3)

Quantum dynamics, the spatial distribution of physical plasma, and the propagation of different waves are some of the fascinating combinations of mathematics and physics that the Klein-Gordon equation presents. It is amazing how many methods have emerged lately to solve the Klein-Gordon models ^{[37,38,39,40,41,42,43,44,45]}. The recommended approach is different from the others in that it approaches problem-solving directly. Unlike other methods, this strategy navigates the complexity of the Klein-Gordon equation without resorting to discretization or linearization, hence avoiding illogical assumptions. The method's versatility and efficacy in resolving complex problems are enhanced by the broad range of families of solutions covered by the analytical solutions that are generated.

2. Methodology

Consider the following fractional partial differential equation (FPDE):

$\begin{equation} Q_1\left(f, D^\alpha_t (f), D^\beta_{x_1} (f), D^{\gamma}_{x_2}(f), fD^{\beta}_{x_1} (f), \ldots \right) = 0, \quad 0 < \alpha, \beta, \gamma\leq 1. \end{equation}$

(2.1)

Let $f$ stand for an unknown function in the given context that depends on ( $x_1, x_2, x_3 \ldots$ ) and ( $t$ ). $f$ and its fractional partial derivatives are involved in the polynomial equation ( $Q$ ). The fractional partial differential equation represented by equation (1.3) can be solved by the following steps in procedure:

(i) It is possible to define the variable ( $x$ ) in a variety of ways when using the variable transformation $f(t, x_1, x_2, x_3, \ldots x_n) = f(x)$ . In this particular case, a sophisticated form of transformation has been utilized:

$\begin{equation} \begin{aligned} & \psi = p \frac {x_1^\beta}{\beta}+q \frac {x_2^\gamma}{\gamma}+r \frac {t^\alpha}{\alpha} \ldots +\psi_o. \end{aligned} \end{equation}$

(2.2)

Here, $p, q, r, \ldots \psi_o$ are constants.

(ii) Equation (1.3) undergoes this transformation becoming a nonlinear ordinary differential equation (ODE) with the following structure:

$\begin{equation} Q_2\left(f, \frac {df}{d\psi} , \frac {d^2f}{d\psi^2}, f\frac {df}{d\psi}, \ldots \right) = 0. \end{equation}$

(2.3)

(iii) The following is an expression for the solution to equation (2.2) indicated by the Riccatti-Bornoulli sub-ODE approach. The constants $b_i$ must be found, subject to the restriction that $b_m \neq 0$ and $b_{-m} \neq 0$ occur simultaneously.

$\begin{equation} {f}(\psi) = \sum\limits_{i = -m}^{m} b_i{\varphi(\psi)}^i. \end{equation}$

(2.4)

(iv) Simultaneously, the function is acquired through the following transformation:

$\begin{equation} \varphi(\psi) = \frac{-\Gamma B + A \phi(\psi)}{A + B \phi(\psi)}. \end{equation}$

(2.5)

Let us consider the constants ( $\Gamma$ ), ( $A$ ), and ( $B$ ), given the constraint that $B\neq 0$ . Furthermore, let us assume that $\phi(\psi)$ is a function with the following definition:

$\begin{equation} \frac{d{\phi}}{d\psi} = \Gamma +{\phi(\psi)^2}. \end{equation}$

(2.6)

It is commonly acknowledged ^[46] that the following are the solutions to equation (2.5):

$\begin{align} (i) &\quad\text{If}\quad \Gamma < 0, \quad\text{then}\quad \phi(\psi) = -\sqrt{-\Gamma}\tanh(\sqrt{-\Gamma}\psi), \quad \text{or}\quad \phi(\psi) = -\sqrt{-\Gamma}coth(\sqrt{-\Gamma}\psi). \end{align}$

(2.7)

$\begin{align} (ii) &\quad\text{If}\quad \Gamma > 0, \quad\text{then}\quad \phi(\psi) = \sqrt{\Gamma}\tan(\sqrt{\Gamma}\psi), \quad\text{or}\quad \phi(\psi) = -\sqrt{\Gamma}cot(\sqrt{\Gamma}\psi). \end{align}$

(2.8)

$\begin{align} (iii) &\quad\text{If}\quad \Gamma = 0, \quad\text{then}\quad \phi(\psi) = \frac{-1}{\psi}. \end{align}$

(2.9)

(v) Achieving a homogenous balance between the highest-order derivative terms and the nonlinear factors in Eq (2.2) yields the equilibrium value. More specifically, the following formula ^[47] can be used to get the balance number:

$\begin{equation} D\left[\frac{d^k f}{d\psi^k}\right] = N + k, \quad D\left[f^J \frac{d^k f}{d\psi^k}\right]^s = NJ + s(k + N). \end{equation}$

(2.10)

(vi) We group the terms with the same power of $\varphi^{i}(\psi)$ , and substitute Eq (2.3) into Eq (2.2).

(vii) In the resulting polynomial, we set all of the coefficients of $\phi^{i}(\psi) = 0$ , resulting in a system of algebraic equations.

(viii) The software Maple is utilized to solve the resultant system in order to ascertain the unknown coefficients.

(ix) The answer $f(\psi)$ for Eq (1.3) is then obtained by substituting the derived values from step (viii) back into Eq (2.3).

3. Evaluation of the problem

By using the approach described in Section 2, we methodically solve the (3+1)-order fractional Klein-Gordon equation (1.1), concentrating on single wave solutions. By applying the following complex transformation, we consider the exact solution for the proposed fractional model:

$\begin{equation} \begin{aligned} & \psi = p \frac {x^\beta}{\beta}+\frac {y^\gamma}{\gamma}+a \frac {t^\alpha}{\alpha}.\\ & \eta = k \frac {x^\beta}{\beta}+\frac {y^\gamma}{\gamma}-\omega \frac {t^\alpha}{\alpha}.\\ & F(x, y, t) = e^{i\eta}f(\psi). \end{aligned} \end{equation}$

(3.1)

Here the function $\eta(x, y, t)$ describes the transformation of propagating waves. The dynamics of the traveling waves are given unique qualities by the presence of the non-zero parameter ( $\omega$ ).

$\begin{equation} D_t^{2\alpha}F = \omega^2 F -i\left(2\omega a \right)F' + a^2 F'' . \end{equation}$

(3.2)

$\begin{equation} D_x^{2\beta}F = -k^2 F + i \left(2 k p \right)F' +p^2 F'' . \end{equation}$

(3.3)

$\begin{equation} D_y^{2\gamma}F = -F + i2F' +F'' . \end{equation}$

(3.4)

Equation (1.1) is transformed into the following ordinary differential equation (ODE) by using the previously indicated complex transformation.

$\begin{equation} -(p^2+1)F''-2i \left(\omega a +kp+1 \right)F'+\left(\omega^2 +m^2 +k^2 +1 \right)F + \lambda F^3 = 0. \end{equation}$

(3.5)

We will now focus our efforts on solving the real part of the equation in order to arrive at the desired solution after removing the following constraint equation from the imaginary part of the equation:

$\begin{equation} \omega = \frac {-(kp + 1)}{a} \end{equation}$

(3.6)

We now address the real part of the equation, which is post-elimination of the constraint.

$\begin{equation} (p^2+1)F''- \left(\omega^2 +m^2 +k^2 +1 \right)F - \lambda F^3 = 0. \end{equation}$

(3.7)

Finding the point of homogeneous equilibrium ( $N = 1$ ) entails striking a harmonious balance between the nonlinear term and the highest order derivatives in the given equation. After equating the coefficients of $\phi^{i}(\psi) = 0$ and substituting Eq (2.2) and Eq (2.3) into Eq (3.7), we are left with an algebraic system of equations. The following results form the solutions to this system, which were found using the Maple software.

Case 1 :

$\begin{equation} \begin{split} b_{{0}} = 0, b_{{1}} = 0, b_{{-1}} = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) , k = k, \Gamma = 1/2\, {\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}, p = p, a = a. \end{split} \end{equation}$

(3.8)

Case 2:

$\begin{equation} \begin{split} b_{{0}} = 0, b_{{1}} = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}, b_{{-1}} = 0 , k = k, \Gamma = 1/2\, {\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}, p = p, a = a. \end{split} \end{equation}$

(3.9)

Case 3:

$\begin{equation} \begin{split} &b_{{0}} = 0, b_{{1}} = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}, b_{{-1}} = -1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) {\lambda}^{-1}{ \frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}}}, k = k, \\ &\Gamma = 1/8 \, {\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}, p = p, a = a. \end{split} \end{equation}$

(3.10)

The solution set corresponding to the given values of ( $\psi$ ) and ( $\eta$ ) is derived under the assumptions of Case 1.

$\begin{equation} \begin{aligned} \psi = {\frac {p{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}+{\frac { a{t}^{\alpha}}{\alpha}}, \\ \eta = {\frac {k{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}-{\frac { \omega\, {t}^{\alpha}}{\alpha}}. \end{aligned} \end{equation}$

(3.11)

Solution Set. 1: When $\Gamma < 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_1(x, y, t) = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k }^{2}+{m}^{2}+{\omega}^{2}+1 \right)\\ & \left( A-1/2\, B\sqrt {-{\frac {2 \, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}}\tanh \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \psi \right) \right)\\ & {e}^{i\eta} \left( -1/2\, {\frac { \left( {k}^{2} +{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A\sqrt {-{\frac {2 \, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}}\tanh \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.12)

$\begin{equation} \begin{split} &F_2(x, y, t) = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k }^{2}+{m}^{2}+{\omega}^{2}+1 \right)\\ & \left( A-1/2\, B\sqrt {-{\frac {2 \, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}}\coth \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \psi \right) \right)\\ & {e}^{i\eta} \left( -1/2\, {\frac { \left( {k}^{2} +{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A\sqrt {-{\frac {2 \, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}}\coth \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.13)

Solution Set. 2: When $\Gamma > 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_3(x, y, t) = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k }^{2}+{m}^{2}+{\omega}^{2}+1 \right)\\ & \left( A+1/2\, B\sqrt {2}\sqrt {{ \frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\tan \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \psi \right) \right)\\ & {e}^{i\eta} \left( -1/2\, {\frac { \left( {k}^{2} +{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}+1/2\, A\sqrt {2}\sqrt {{ \frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\tan \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.14)

$\begin{equation} \begin{split} &F_4( x, y, t) = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k }^{2}+{m}^{2}+{\omega}^{2}+1 \right)\\ & \left( A-1/2\, B\sqrt {2}\sqrt {{ \frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\cot \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \psi \right) \right)\\ & {e}^{i\eta} \left( -1/2\, {\frac { \left( {k}^{2} +{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A\sqrt {2}\sqrt {{ \frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\cot \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.15)

Solution Set. 3: When $\Gamma = 0$ , equation (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} F_5(x, y, t) = \sqrt { \left( 2\, \lambda\, {P}^{2}+2\, \lambda \right) ^{-1}} \left( {k }^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A-{\frac {B}{\psi}} \right) {e}^{i\eta} \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{ \omega}^{2}+1 \right) B}{{P}^{2}+1}}-{\frac {A}{\psi}} \right) ^{-1}. \end{split} \end{equation}$

(3.16)

The solution set corresponding to the given values of ( $\psi$ ) and ( $\eta$ ) is derived under the assumption of case 2.

$\begin{equation} \begin{aligned} \psi = {\frac {p{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}+{\frac { a{t}^{\alpha}}{\alpha}}.\\ \eta = {\frac {k{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}-{\frac { \omega\, {t}^{\alpha}}{\alpha}}. \end{aligned} \end{equation}$

(3.17)

Solution Set. 4: When $\Gamma < 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_6(x, y, t) = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}\times\\ & \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \tanh \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2 }+2}{{P}^{2}+1}}}\psi \right) \right)\\ & {e}^{i\eta} \left( A-1/2\, B \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \tanh \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2 }+2}{{P}^{2}+1}}}\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.18)

$\begin{equation} \begin{split} &F_7(x, y, t) = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}\times\\ & \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \coth \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2 }+2}{{P}^{2}+1}}}\psi \right) \right)\\ & {e}^{i\eta} \left( A-1/2\, B \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2}+2}{{P}^{2}+1}}} \coth \left( 1/2\, \sqrt {-{\frac {2\, {k}^{2}+2\, {m}^{2}+2\, {\omega}^{2 }+2}{{P}^{2}+1}}}\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.19)

Solution Set. 5: When $\Gamma > 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_8(x, y, t) = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}\times\\ & \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}+1/2\, A \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \tan \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+ 1}{{P}^{2}+1}}}\psi \right) \right)\\ & {e}^{i\eta} \left( A+1/2\, B\sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\tan \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{ P}^{2}+1}}}\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.20)

$\begin{equation} \begin{split} &F_9( x, y, t) = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}\times\\ & \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-1/2\, A \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}} \cot \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+ 1}{{P}^{2}+1}}}\psi \right) \right)\\ & {e}^{i\eta} \left( A-1/2\, B\sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}}\cot \left( 1/2\, \sqrt {2}\sqrt {{\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{ P}^{2}+1}}}\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.21)

Solution Set. 6: When $\Gamma = 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} F_{10}(x, y, t) = \sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}} \left( -1/2\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) B}{{P}^{2}+1}}-{\frac { A}{\psi}} \right) {e}^{i\eta} \left( A-{\frac {B}{\psi}} \right) ^{-1}. \end{split} \end{equation}$

(3.22)

The solution set corresponding to the given values of ( $\psi, \eta$ ) and ( $\Gamma$ ) is derived under the assumptions of Case 3.

$\begin{equation} \begin{aligned} &\psi = {\frac {p{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}+{\frac { a{t}^{\alpha}}{\alpha}}, \\ &\eta = {\frac {k{x}^{\beta}}{\beta}}+{\frac {{y}^{\gamma}}{\gamma}}-{\frac { \omega\, {t}^{\alpha}}{\alpha}}.\\ &\Gamma = 1/8\, {\frac {{k}^{2}+{m}^{2}+{\omega}^{2}+1}{{P}^{2}+1}}. \end{aligned} \end{equation}$

(3.23)

Solution Set. 7: When $\Gamma < 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_{11}(x, y, t) = -1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A-B\sqrt {-\Gamma }\tanh \left( \sqrt {-\Gamma }\psi \right) \right) {e}^{i \eta}{\lambda}^{-1}{\frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}} }}} \\ &\left( - \left( \Gamma \right) \, B-A\sqrt {-\Gamma }\tanh \left( \sqrt {-\Gamma }\psi \right) \right) ^{-1}+\sqrt {-{\frac {-2-2\, {P}^ {2}}{\lambda}}} \left( - \left( \Gamma \right) \, B-A\sqrt {-\Gamma } \tanh \left( \sqrt {-\Gamma }\psi \right) \right)\\ & {e}^{i\eta} \left( A-B\sqrt {-\Gamma }\tanh \left( \sqrt {-\Gamma }\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.24)

$\begin{equation} \begin{split} &F_{12}(x, y, t) = -1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A-B\sqrt {-\Gamma }\coth \left( \sqrt {-\Gamma }\psi \right) \right)\\ & {e}^{i \eta}{\lambda}^{-1}{\frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}} }}} \left( - \left( \Gamma \right) \, B-A\sqrt {-\Gamma }\coth \left( \sqrt {-\Gamma }\psi \right) \right) ^{-1}\\ &+\sqrt {-{\frac {-2-2\, {P}^ {2}}{\lambda}}} \left( - \left( \Gamma \right) \, B-A\sqrt {-\Gamma } \coth \left( \sqrt {-\Gamma }\psi \right) \right) {e}^{i\eta} \left( A-B\sqrt {-\Gamma }\coth \left( \sqrt {-\Gamma }\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.25)

Solution Set. 8: When $\Gamma > 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} F_{13}(x, y, t) = &-1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A+B\sqrt {\Gamma }\tan \left( \sqrt {\Gamma }\psi \right) \right) {e}^{i\eta}{ \lambda}^{-1}{\frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}}} \left( - \left( \Gamma \right) \, B+A\sqrt {\Gamma }\tan \left( \sqrt {\Gamma }\psi \right) \right) ^{-1}\\ &+\sqrt {-{\frac {-2-2\, {P}^{ 2}}{\lambda}}} \left( - \left( \Gamma \right) \, B+A\sqrt {\Gamma } \tan \left( \sqrt {\Gamma }\psi \right) \right) {e}^{i\eta} \left( A+ B\sqrt {\Gamma }\tan \left( \sqrt {\Gamma }\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.26)

$\begin{equation} \begin{split} F_{14}( x, y, t) = &-1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A-B\sqrt {\Gamma }\cot \left( \sqrt {\Gamma }\psi \right) \right) {e}^{i\eta}{ \lambda}^{-1}{\frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}}} \left( - \left( \Gamma \right) \, B-A\sqrt {\Gamma }\cot \left( \sqrt {\Gamma }\psi \right) \right) ^{-1}\\ &+\sqrt {-{\frac {-2-2\, {P}^{ 2}}{\lambda}}} \left( - \left( \Gamma \right) \, B-A\sqrt {\Gamma } \cot \left( \sqrt {\Gamma }\psi \right) \right) {e}^{i\eta} \left( A- B\sqrt {\Gamma }\cot \left( \sqrt {\Gamma }\psi \right) \right) ^{-1}. \end{split} \end{equation}$

(3.27)

Solution Set. 9: When $\Gamma = 0$ , Eq (1.1) yields the resultant single-wave solutions:

$\begin{equation} \begin{split} &F_{15}(x, y, t) = -1/4\, \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) \left( A-{\frac {B}{\psi}} \right)\\ & {e}^{i\eta}{\lambda}^{-1}{\frac {1}{\sqrt {-{\frac {-2-2\, {P}^{2}}{\lambda}}}}} \left( -1/8\, \left( {k}^{2}+{\frac {1}{ 64}}\, {\frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) ^{2}}{ \left( {P}^{2}+1 \right) ^{2}}}+{\omega}^{2}+1 \right) B \left( {P}^{ 2}+1 \right) ^{-1}-{\frac {A}{\psi}} \right) ^{-1}\\ &+\sqrt {-{\frac {-2- 2\, {P}^{2}}{\lambda}}} \left( -1/8\, \left( {k}^{2}+{\frac {1}{64}}\, { \frac { \left( {k}^{2}+{m}^{2}+{\omega}^{2}+1 \right) ^{2}}{ \left( {P }^{2}+1 \right) ^{2}}}+{\omega}^{2}+1 \right) B \left( {P}^{2}+1 \right) ^{-1}-{\frac {A}{\psi}} \right) {e}^{i\eta} \left( A-{\frac { B}{\psi}} \right) ^{-1}. \end{split} \end{equation}$

(3.28)

4. Results and discussion

Compared with traditional analytical methods, the Riccatti-Bornoulli sub-ODE approach shows remarkable analytical efficiency by producing a large number of periodic and single traveling wave solutions with parameterizable characteristics. The results of this novel approach reveal the fundamental principles of physical phenomena and provide exact answers for many nonlinear structures in science. In addition to its direct uses in physics, this method yields series-based answers that are useful as standards for numerical solvers, allowing them to assess the precision of their output and simplifying stability studies.

The development of solitons in our suggested methodology is a manifestation of the delicate equilibrium between linear and nonlinear effects. Solitons are defined as solitary waves that dissipate very little energy while propagating and continue to preserve their original form and velocity even after colliding with other similar waves. Our novel strategy produces three important and different families of solitary wave solutions, specifically for the fractional Klein-Gordon equation, which are hyperbolic, rational, and periodic solitary wave solutions. This wide range of solutions increases the generalizability of our approach in different circumstances and advances our understanding of soliton dynamics in those contexts. {To clarify what sets different periodic and single solutions apart from each other, we turn to the MATLAB, adjusting certain parameter values to the solutions themselves. As such, the images below represent the graphical representations that make it possible for one to understand such solutions features and behavior as a vivid example.

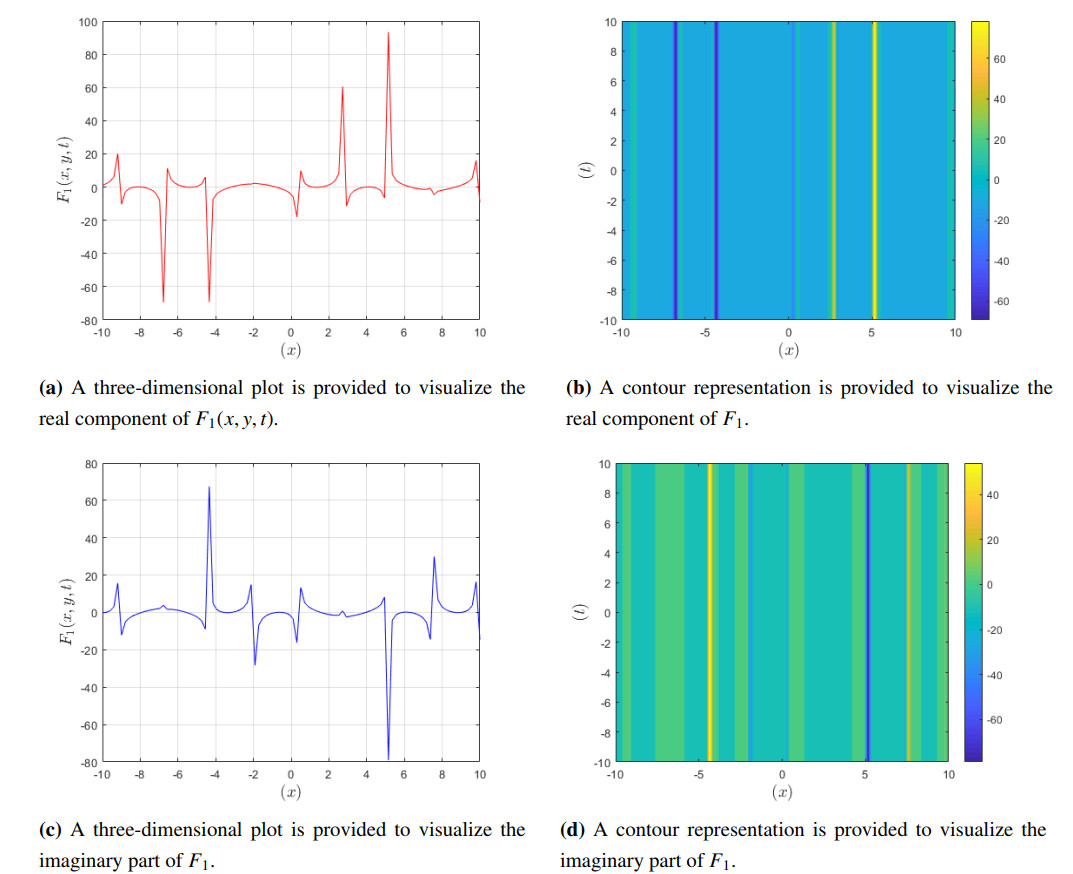
: Visualization of the detailed dynamics of the real and imaginary parts of the solution. In this figure, we observe the dromion structures which describe the dynamics and variations of the solution $F_1(x, y, t)$ at different scales in space and time. This visualization quantitatively elucidates the complexities and variations of the system.

Figure 1. These visual representations illustrate fluctuations in the complex dynamics of the solution

$F_{1}$ .

DownLoad: Full-Size Img PowerPoint

: Visualization of the lump-type kink soliton in the $F_8(x, y, t)$ . The evolution about the semi-axes types of kink soliton in the lump solution is documented in the figure.

Figure 2. These visual representation illustrate fluctuations in the complex dynamics of the solution

$F_{8}$ .

DownLoad: Full-Size Img PowerPoint

: Interplay of the real and imaginary parts of the solution $F_{10}(x, y, t)$ on several levels of detail. With the help of lump-type structures over a periodic background representation together, it is possible to convey the comprehensive picture of the underlying attributes and temporal behavior in the different type of phases and scales.

Figure 3. These visual representations illustrate fluctuations in the complex dynamics of the solution

$F_{10}$ .

DownLoad: Full-Size Img PowerPoint

: This figure shows the development of the cuspon kink soliton, in which the space and time differ somewhat between the complex parts of its solution, $F_{11}(x, y, t)$ . Neighborhoods of contrasting resolution with the feasible coefficients were actively resolved. The presented cuspon kink structures show the mixing spatial-temporal behavior of $F_{11}(x, y, t)$ , at different spatial and time scales.

Figure 4. These visual representations illustrate fluctuations in the complex dynamics of the solution

$F_{11}$ .

DownLoad: Full-Size Img PowerPoint

: Similar to , this figure illustrates the dynamics of the complex components of the lump-type kink soliton $F_{15}(x, y, t)$ .

Figure 5. These visual representations illustrate fluctuations in the complex dynamics of the solution

$F_{15}$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

The presented approach is used in this study to get analytical solutions for fractional Klein-Gordon equation, for which the fractional derivative is defined in a conformable context. To convert the provided fractional partial differential equations into ordinary differential equations, a complex transformation is used. Then, using unknown coefficients, the proposed approach is applied in series form. This system of equations has a solution that can be found using the Maple software, which makes it possible to identify the unknown coefficients. As a result, the the Riccatti-Bornoulli sub-ODE algorithm produces solutions for the given problems, which fall into the rational, hyperbolic, and trigonometric families. This methodology enables an extensive investigation of analytical solutions over various mathematical structures in the framework of Fractional Klein-Gordon equation. Compared to previous methods, the suggested method is an effective analytical technique since it may provide several periodic and single traveling wave solutions, each with tunable parameters. The outcomes of this approach are crucial in revealing the underlying principles that regulate physical events, providing unique solutions for many physical structures in the field of nonlinear research. In addition to its direct uses in the physical sciences, this method yields series-form solutions that are useful resources for numerical solvers. By facilitating stability analyses and allowing practitioners to assess the quality of their numerical results, these solutions help researchers gain a deeper understanding of the systems they are studying.

Acknowledgements

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number ISP-2024.

Conflict of interest

The authors declare no conflicts of interest.

Use of AI tools declaration

The authors declare they have not used AI tools in the creation of this article.

References

[1]	L. Debnath, A brief historical introduction to solitons and the inverse scattering transforma vision of Scott Russell, Int. J. Math. Educ. Sci. Technol., 38 (2007), 1003–1028. https://doi.org/10.1080/00207390600597849 doi: 10.1080/00207390600597849
[2]	H. Yasmin, N. H. Aljahdaly, A. M. Saeed, Probing families of optical soliton solutions in fractional perturbed RadhakrishnanKunduLakshmanan model with improved versions of extended direct algebraic method, Fractal Fract., 7 (2023), 512. https://doi.org/10.3390/fractalfract7070512 doi: 10.3390/fractalfract7070512
[3]	H. Yasmin, N. H. Aljahdaly, A. M. Saeed, Investigating families of soliton solutions for the complex structured coupled fractional biswasarshed model in birefringent fibers using a novel analytical technique, Fractal Fract., 7 (2023), 491. https://doi.org/10.3390/fractalfract7070491 doi: 10.3390/fractalfract7070491
[4]	A. Saad Alshehry, M. Imran, A. Khan, W. Weera, Fractional view analysis of KuramotoSivashinsky equations with non-singular kernel operators. Symmetry, 14 (2022), 1463. https://doi.org/10.3390/sym14071463
[5]	P. Sunthrayuth, A. M. Zidan, S. W. Yao, R. Shah, M. Inc, The comparative study for solving fractional-order FornbergWhitham equation via $\rho$ -Laplace transform, Symmetry, 13 (2021), 784. https://doi.org/10.3390/sym13050784 doi: 10.3390/sym13050784
[6]	H. M. Srivastava, H. Khan, M. Arif, Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions, Math. Meth. Appl. Sci., 43 (2020), 199–212. https://doi.org/10.1002/mma.5846 doi: 10.1002/mma.5846
[7]	R. Almeida, N. R. O. Bastos, M. Teresa, T. Monteiro, Modeling some real phenomena by fractional differential equations, Math. Methods Appl. Sci., 39 (2016), 4846–4855. https://doi.org/10.1002/mma.3818 doi: 10.1002/mma.3818
[8]	H. Sun, Y. Zhang, D. Baleanu, W. Chen, Y. Chen, A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul., 64 (2018), 213–231. https://doi.org/10.1016/j.cnsns.2018.04.019
[9]	V. Tarasov, Generalized memory: Fractional calculus approach, Fractals, 2 (2018), 23. https://doi.org/10.3390/fractalfract2040023 doi: 10.3390/fractalfract2040023
[10]	Y. Hu, B. Oksendal, Fractional white noise calculus and applications to finance, Inf. Dimens. Anal. Quantum Probab. Relat. Top., 6 (2003), 1–32. https://doi.org/10.1142/S0219025703001110 doi: 10.1142/S0219025703001110
[11]	W. Zhang, J. Li, Y. Yang, A fractional diffusion-wave equation with non-local regularization for image denoising, Signal Process, 103 (2014), 6–15. https://doi.org/10.1016/j.sigpro.2013.10.028 doi: 10.1016/j.sigpro.2013.10.028
[12]	J. Wu, A wavelet operational method for solving fractional partial differential equations numerically, Appl. Math. Comput., 214 (2009), 31–40. https://doi.org/10.1016/j.amc.2009.03.066 doi: 10.1016/j.amc.2009.03.066
[13]	S. Mukhtar, M. Sohaib, I. Ahmad, A numerical approach to solve volume-based batch crystallization model with fines dissolution unit, Processes, 7 (2019), 453. https://doi.org/10.3390/pr7070453 doi: 10.3390/pr7070453
[14]	R. Garrappa, Numerical solution of fractional differential equations: A survey and a software tutorial, Mathematics, 6 (2018), 16. https://doi.org/10.3390/math6020016 doi: 10.3390/math6020016
[15]	J. Jiang, Y. Feng, S. Li, Exact Solutions to the Fractional Differential Equations with Mixed Partial Derivatives, Axioms, 7 (2018), 10. https://doi.org/10.3390/axioms7010010 doi: 10.3390/axioms7010010
[16]	Y. Xie, I. Ahmad, T. I. Ikpe, E. F. Sofia, H. Seno, What Influence Could the Acceptance of Visitors Cause on the Epidemic Dynamics of a Reinfectious Disease?: A Mathematical Model, Acta Biotheor., 72 (2024), 3. https://doi.org/10.3390/axioms7010010 doi: 10.3390/axioms7010010
[17]	J. Duan, R. Rach, D. Baleanu, A. Wazwaz, A review of the Adomian decomposition method and its applications to fractional differential equations, Commun. Fract. Calc., 3 (2012), 73–99.
[18]	S. Mahmood, R. Shah, M. Arif, Laplace adomian decomposition method for multi dimensional time fractional model of Navier-Stokes equation, Symmetry, 11 (2019), 149. https://doi.org/10.3390/sym11020149 doi: 10.3390/sym11020149
[19]	Q. Wang, Homotopy perturbation method for fractional KdV-Burgers equation, Chaos Soliton. Fract., 35, (2008), 843–850. https://doi.org/10.1016/j.chaos.2006.05.074
[20]	K. R. Raslan, K. K. Ali, M. A. Shallal, The modified extended tanh method with the Riccati equation for solving the space-time fractional EW and MEW equations, Chaos Soliton. Fract., 103 (2017), 404–409. https://doi.org/10.1016/j.chaos.2017.06.029 doi: 10.1016/j.chaos.2017.06.029
[21]	H. Yasmin, N. H. Aljahdaly, A. M. Saeed, Investigating symmetric soliton solutions for the fractional coupled konnoonno system using improved versions of a novel analytical technique, Mathematics, 11 (2023), 2686. https://doi.org/10.3390/math11122686 doi: 10.3390/math11122686
[22]	M. M. Al-Sawalha, A. Khan, O. Y. Ababneh, T. Botmart, Fractional view analysis of Kersten-Krasilshchik coupled KdV-mKdV systems with non-singular kernel derivatives, AIMS Math., 7 (2022), 18334–18359. https://doi.org/10.3934/math.20221010 doi: 10.3934/math.20221010
[23]	H. Yasmin, A. S. Alshehry, A. H. Ganie, A. M. Mahnashi, Perturbed GerdjikovIvanov equation: Soliton solutions via Backlund transformation, Optik, 298 (2024), 171576. https://doi.org/10.1016/j.ijleo.2023.171576 doi: 10.1016/j.ijleo.2023.171576
[24]	I. Ahmad, H. Seno, An epidemic dynamics model with limited isolation capacity, Theor. Biosci., 142 (2023), 259–273. https://doi.org/10.1007/s12064-023-00399-9 doi: 10.1007/s12064-023-00399-9
[25]	W. Hamali, J. Manafian, M. Lakestani, A. M. Mahnashi, A. Bekir, Optical solitons of M-fractional nonlinear Schrdingers complex hyperbolic model by generalized Kudryashov method, Opt. Quant. Electron., 56 (2024), 7. https://doi.org/10.1007/s11082-023-05602-1 doi: 10.1007/s11082-023-05602-1
[26]	M. A. E. Abdelrahman, M. A. Sohaly, Solitary waves for the modified Korteweg-de Vries equation in deterministic case and random case, J. Phys. Math., 8 (2017). https://doi.org/10.4172/2090–0902.1000214.
[27]	M. A. E. Abdelrahman, M. A. Sohaly, Solitary waves for the nonlinear Schrdinger problem with the probability distribution function in the stochastic input case, Eur. Phys. J. Plus., 132 (2017), 339. https://doi.org/10.1140/epjp/i2017-11607-5 doi: 10.1140/epjp/i2017-11607-5
[28]	X. F. Yang, Z. C. Deng, Y. Wei, A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application, Adv. Diff. Equa., 1 (2015), 117–133. https://doi.org/10.1140/epjp/i2017-11607-5 doi: 10.1140/epjp/i2017-11607-5
[29]	S. Meng, F. Meng, F. Zhang, Q. Li, Y. Zhang, A. Zemouche, Observer design method for nonlinear generalized systems with nonlinear algebraic constraints with applications, Automatica, 162 (2024), 111512. https://doi.org/10.1016/j.automatica.2024.111512 doi: 10.1016/j.automatica.2024.111512
[30]	X. Cai, R. Tang, H. Zhou, Q. Li, S. Ma, D. Wang, et al., Dynamically controlling terahertz wavefronts with cascaded metasurfaces, Adv. Photonics, 3 (2021), 036003. https://doi.org/10.1117/1.AP.3.3.036003 doi: 10.1117/1.AP.3.3.036003
[31]	T. A. A. Ali, Z. Xiao, H. Jiang, B. Li, A class of digital integrators based on trigonometric quadrature rules, IEEE T. Ind. Electron., 71 (2024), 6128–6138. https://doi.org/10.1109/TIE.2023.3290247 doi: 10.1109/TIE.2023.3290247
[32]	C. Guo, J. Hu, Time base generator based practical predefined-time stabilization of high-order systems with unknown disturbance. IEEE Transactions on Circuits and Systems II: Express Briefs, (2023). https://doi.org/10.1109/TCSII.2023.3242856
[33]	Y. Kai, J. Ji, Z. Yin, Study of the generalization of regularized long-wave equation, Nonlinear Dynam., 107 (2022), 2745–2752. https://doi.org/10.1007/s11071-021-07115-6 doi: 10.1007/s11071-021-07115-6
[34]	Y. Kai, Z. Yin, Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation, Phys. Let. A, 452 (2022), 128430. https://doi.org/10.1016/j.physleta.2022.128430 doi: 10.1016/j.physleta.2022.128430
[35]	L. Debnath, Nonlinear partial differential equations for scientists and engineers, Boston: Birkhauser, (2005), 528–529. https://doi.org/10.1007/b138648
[36]	M. Z. Sarikaya, H. Budak, H. Usta, On generalized the conformable fractional calculus, TWMS J. Appl. Eng. Math., 9 (2019), 792–799.
[37]	M. A. Ramadan, M. S. Al-Luhaibi, Application of Sumudu decomposition method for solving linear and nonlinear Klein-Gordon equations, Int. J. Soft Comput. Eng., 3 (2016), 138–140.
[38]	M. Hussain, M. Khan, A variational iterative method for solving the linear and nonlinear Klein-Gordon equations, Appl. Math. Sci., 4 (2010), 1931–1940.
[39]	H. Hosseinzadeh, H. Jafari, M. Roohani, Application of laplace decomposition method for solving Klein-Gordon equation, World Appl. Sci. J., 8 (2010), 809–813.
[40]	S. Kulkarni, K. Takale, Application of Adomian decomposition method for solving linear and nonlinear Klein-Gordon equations, Int. J. Eng. Contemp. Math. Sci., 1 (2015), 21–27.
[41]	A. K. Adio, Natural decomposition method for solving the linear and nonlinear Klein Gordon equations, Int. J. Res. Appl., 4 (2016), 59–72.
[42]	D. Kumar, J. Singh, D. Baleanu, A hybrid computational approach for KleinGordon equations on Cantor sets, Nonlinear Dynam., 87 (2017), 511–517. https://doi.org/10.1007/s11071-016-3057-x doi: 10.1007/s11071-016-3057-x
[43]	B. Grebert, E. Paturel, KAM for the Klein Gordon equation on SdSd, Bollettino dellUnione Matematica Italiana, 9 (2016), 237–288. https://doi.org/10.1007/s40574-016-0072-2 doi: 10.1007/s40574-016-0072-2
[44]	D. A. Nugraha, A. Suparmi, C. Cari, B. N. Pratiwi, Asymptotic iteration method for solution of the Kratzer potential in D-dimensional Klein-Gordon equation, J. Phys. Conf. Ser., 820 (2017), 1–8. https://doi.org/10.1088/1742-6596/820/1/012014 doi: 10.1088/1742-6596/820/1/012014
[45]	Y. Luo, X. Li, C. Gu, Fourth-order compact and energy conservative scheme for solving nonlinear Klein-Gordon equation, Numer. Meth. Part. D. E., (2017), 1283–1304. https://doi.org/10.1002/num.22143
[46]	D. Lu, Q. Shi, New Jacobi elliptic functions solutions for the combined KdV-mKdV equation, Int. J. Nonlinear Sci., 10, 320–325.
[47]	Y. Zhang, Solving STO and KD equations with modified RiemannLiouville derivative using improved ( $G/G'$ )-expansion function method, Int. J. Appl. Math. 45 (2015), 16–22.

This article has been cited by:

1.	S Saravana Veni, M S Mani Rajan, Anjan Biswas, Ali Saleh Alshomrani, Exploring the dynamic interplay of intermodal and higher order dispersion in nonlinear negative index metamaterials, 2024, 99, 0031-8949, 085261, 10.1088/1402-4896/ad6352
2.	Yasir A. Madani, Khidir Shaib Mohamed, Sadia Yasin, Sehrish Ramzan, Khaled Aldwoah, Mohammed Hassan, Exploring novel solitary wave phenomena in Klein–Gordon equation using $$\phi ^{6}$$ model expansion method, 2025, 15, 2045-2322, 10.1038/s41598-025-85461-w

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1055) PDF downloads(50) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(5)

AIMS Mathematics

Analysis of peakon-like soliton solutions: (3+1)-dimensional Fractional Klein-Gordon equation

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Evaluation of the problem

4. Results and discussion

5. Conclusions

Acknowledgements

Conflict of interest

Use of AI tools declaration

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Analysis of peakon-like soliton solutions: (3+1)-dimensional Fractional Klein-Gordon equation

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Evaluation of the problem

4. Results and discussion

5. Conclusions

Acknowledgements

Conflict of interest

Use of AI tools declaration

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog