1. Introduction
In China, alpine meadow is mainly distributed on the Qinghai-Tibet Plateau and it covers an area of 6.372×107 ha [1]. Alpine meadow provides irreplaceable ecological services such as biodiversity conservation, carbon sequestration, soil and water protection, as well as maintaining cultural diversity and social stability [2,3,4]. In the meantime, the alpine meadow ecosystem is fragile and has degraded severely over the past few decades. It has been reported that about 33.4 of the total alpine meadow on the Qinghai-Tibet Plateau has degraded. The vegetation was damaged heavily, the soil quality declined, the grass productivity, economic potential and service function descended, the biodiversity was depressed, and the environment was deteriorated. As edificato and dominant species, the forage grass Kobresia was replaced by ruderals (such as Oxytropis, Ligularia, Aconitum szechenyianum) partly. On average, the coverage of vegetation is 46%, the proportion of forage grass is 25%, quite a few alpine meadows have become bare areas and the degradation trend is accelerating [5]. This brings a great threat to the survival of local pastoralists and livestock as well as to the sustainability of local ecosystem and has raised great concerns from scientists and local governments. Increasing efforts have been made to uncover the underlying causes of alpine meadow degradation and to restore degraded alpine meadows.
It has been proposed that possible causes of alpine meadow degradation are global warming, irrational utilization (such as blind reclamation of grassland, road construction, mining, gold and sand collection, gathering medicinal herbs), overgrazing, rodent damage and poaching [4,6,7,8,9]. However, there still lack of sufficient evidence to identify the underlying causes of leading alpine meadows to degrade [10].
From the restoration point of view, various strategies have been proposed and experimented [7,9,11,12,13]. These strategies include: (ⅰ) Meliorating the degraded alpine meadow through scarifying, reseeding, fertilizing, irrigating, ruderal controlling; (ⅱ) Adopting a new grazing system, such as graze prohibiting, seasonal grazing, determining amount of livestock according to grass yield; (ⅲ) Rodents control and protecting their natural enemies; (ⅳ) In winter, providing livestock with supplementary food and building plastic greenhouse shelters to protect livestock; and (ⅴ) Ecological migration. Restoration practices showed that most of these strategies are effective for a short time interval, while the long-term efficiency of any strategy has not been evaluated.
Mathematical modelling has been recognized to be an inexpensive and powerful tool in ecological and biological studies. However, only limited modeling exercises [14] have been conducted in studying the dynamics of an alpine meadow ecosystem. In [14], Chang et al. investigated the relations between grass, plateau pika (Ochotona curzoniae) and eagle through a mathematical model. In this work, we formulate a mathematical model based on the relations between forage grass, rodent, livestock and raptor. Model analysis helps us identify the causes of alpine meadow degradation and evaluate the efficiency of restoration strategies.
We organize the rest of this paper as follows. In Section 2, we present our model and carry out related mathematical analysis. We then analyze the causes of alpine meadow degradation in Section 3 and evaluate the efficiency of restoration strategies in Section 4. Our conclusion is provided in Section 5.
2. Model formulation and analysis
In brief, the vegetation of alpine meadow falls into two categories, one is forage grass on which livestock feeds, the other one is ruderal that livestock does not eat. On a healthy alpine meadow, forage grass occupies a large proportion. Along with alpine meadow degradation, the proportion of forage grass decreases and the proportion of ruderal increases. The amount of forage grass affects the development of animal husbandry directly and also is an index of alpine meadow degradation. So only the biomass of forage grass is considered in our modeling exercise.
Tibetan sheep, yak, horse are the main livestock on the alpine meadow and they all have similar feeding behavior. For simplicity, we use only one variable to stand for the livestock. Along with alpine meadow degradation, the amount of rodents including plateau pika and plateau zokor (Eospalax baileyi) increases rapidly. The abundant rodents compete with livestock for herbage, destroy soil structure and accelerate the degradation of alpine meadows.
The predators of rodents are mainly raptors (e.g. Buteo hemilasius, Falco cherrug) and carnivorous mammals (e.g. Mustela allaica, Vulpes ferrilatus). On a degraded alpine meadow, rodents are abundant and their predators are scarce. This phenomenon leads to a conjecture: the decrease of rodent's predators results in the increase of rodents and promotes further degradation of alpine meadows. So the predator of rodent is involved in the modelling and is referred to as raptors.
Livestock and rodent consume forage grass and without forage grass, livestock and rodent would die out. Raptor hunts rodent and without rodent, raptor would become extinct. Suppose that forage grass grows logistically. Let x(t),y(t),z(t),u(t) be the amount (or biomass) of rodents, forage grass, raptors and livestock at time t, respectively. Then our model is described by the following system
|
{x′=−d1x+αxy−μxzy′=ry(1−yK)−βxy−pyuz′=−d3z+ηxzu′=−d4u+qyu
|
(1)
|
where d1,d3,d4 are the mortality rates of rodents, raptors, livestock, respectively; r is the intrinsic growth rate of forage grass; K is the carrying capacity of forage grass, β is the rate at which rodents consume forage grass, α is the rate at which rodents increase through consuming forage grass, μ is the rate at which raptors consume rodents, η is the rate at which raptors increase through consuming rodents, p is the rate at which livestock consume forage grass, q is the rate at which livestock increase through consuming forage grass. For convenience, we denote
|
A≜d1α,B≜d3η,C≜d4qandθ≜1−βd3ηr=1−βBr<1
|
It is straightforward to obtain the following result concerning the existence of possible equilibria.
Theorem 2.1. For Model (1), there always exist the trivial equilibrium O:x=y=z=u=0 and a boundary equilibrium E1=(x,y,z,u) with x=z=u=0,y=K. If A<K, there exists another boundary equilibrium E2=(x,y,z,u) with x=rβ(1−AK),y=A,z=u=0. If C<K, there exists a boundary equilibrium E3=(x,y,z,u) with x=z=0,y=C,u=rp(1−CK). If A<θK there exists a boundary equilibrium E4=(x,y,z,u) with x=B,y=θK,z=α(θK−A)μ,u=0. If A<C<θK, there exists a positive equilibrium E5=(x,y,z,u) with x=B,y=C,z=α(C−A)μ,u=rp(θ−CK).
Theorem 2.2. The trivial equilibrium O is always unstable. If A>K and C>K, then E1 is locally asymptotically stable; If θK<A<K and A<C, then E2 is locally asymptotically stable; If C<K and C<A, then E3 is locally asymptotically stable; If A<θK, C>θK and θ>0, then E4 is locally asymptotically stable; If A<C<θK and θ>0, then E5 is locally asymptotically stable.
Proof. Here we only prove the locally stability of E5 as the stability of other equilibria can be proved similarly. At the equilibrium E5, the Jacobian matrix J5 of Model (1) reads as
|
[0αB−μB0−βC−rCK0−pCαη(C−A)μ0000qp(r−rCK−βB)00]
|
Its eigenvalues are determined by the equation
|
λ4+rCKλ3+[αηB(C−A)+αβBC+qC(r−rCK−βB)]λ2+αηBCr(C−A)Kλ+αηBCq(C−A)(r−rCK−βB)=0
|
To apply the Routh-Hurwitz criterion [15], we find that
|
Δ1=rCK>0,Δ2=rC2K(αβB+rq−rqCK−βqB)
|
|
Δ3=α2βηr2B2C3(C−A)K2,Δ4=αηqBC(C−A)(1−rCK−βB)Δ3
|
If A<C<θK and θ>0, then the Routh-Hurwitz criterion applies and all eigenvalues have negative real parts, and hence E5 is locally asymptotically stable.
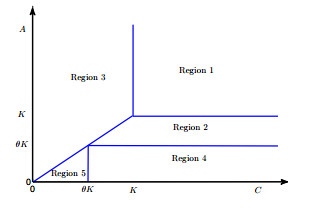
Remark 1. Based on Theorem 2.2, we can sketch stability regions in the C−A plane. If θ>0, the first quadrant of the C−A plane can be divided into 5 regions as shown in Figure 1. When the point (C,A) is located within Region i then the equilibrium Ei(i=1,2,3,4,5) is global asymptotically stable. If θ<0, then Regions 4 and 5 emerge into Region 2 and Regions 1 and 3 remain unchanged.
Theorem 2.3. If Ei(i=1,2,⋯,5) is locally asymptotically stable, then it is also global asymptotically stable in R+4∖{Ej,j≠i,j=1,2,⋯,5}.
Proof. Due to the similarity, we only prove that E5 is globally asymptotically stable here. Denote E5 by (x∗,y∗,z∗,u∗) and rewrite Model (1) as
|
{x′=αx(y−y∗)−μx(z−z∗)y′=−rKy(y−y∗)−βy(x−x∗)−py(u−u∗)z′=ηz(x−x∗)u′=qu(y−y∗)
|
(2)
|
Consider the Liapunov function defined by
|
V=(x−x∗−x∗lnxx∗)+αβ(y−y∗−y∗lnyy∗)+μη(z−z∗−z∗lnzz∗)+αpβq(u−u∗−u∗lnuu∗)
|
Then dVdt|(2)=−αrβK(y−y∗)2≤0. So E={dVdt|(2)=0}={y=y∗}. Thus Model (2) reduces to
|
{y=y∗x′=−μx(z−z∗)0=−β(x−x∗)−p(u−u∗)z′=ηz(x−x∗)u=constant
|
(3)
|
From the third and the fifth equations of system (3), one finds that x is a constant. Then the second equation gives z=z∗ or x=0. If z=z∗, then the fourth equation yields x=x∗. Furthermore, the third equation leads to u=u∗. If x=0, then the third equation implies u=rp(1−CK), and hence the fourth equation arrives z=γe−ηx∗t→0(t→+∞). Thus the largest invariant set in E is M={E5,E3} and all solutions of Model (2) approach E5 or E3 according to the LaSalle's invariance principle [15]. However, when A<C<θK, θ>0, E5 is locally asymptotically stable and E3 is unstable, so all solutions of Model (2) must approach E5 rather than E3. This proves that E5 is globally asymptotically stable.
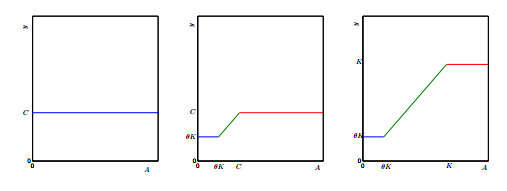
Remark 2. Theorems 2.2 and 2.3 indicate Model (2) always admits a unique stable equilibrium. As model parameters vary, there may be stability switches from one stable equilibrium to another. To illustrate this phenomenon, we present three bifurcation diagrams in the (A,y) plane for three cases: (ⅰ) C<θK; (ⅱ) θK<C<K; and (ⅲ) C>K below in Figure 2.
3. Causes of alpine meadow degradation
On both healthy alpine meadows and degraded alpine meadows, forage grass, rodents, livestock and raptors coexist, but there are much less forage grass and raptors, much more rodents and livestock on a degraded alpine meadow than on a healthy alpine meadow. Only at the equilibrium E5, these four components coexist. Thus it is reasonable to assume that a healthy alpine meadow in real world is approximately at the equilibrium state E5. When a degradation of the alpine meadow occurs, the values of parameters in Model (1) would change and hence the coordinates of E5 vary accordingly.
As a result of long-term evolution, the parameters in Model (1) are approximately constant, but some of them may vary significantly under special conditions. Alpine meadows are very sensitive to climate change. Global warming is an indisputable fact and would certainly affect the growth of forage grass, that is, global warming would vary the values of the parameters r and K of Model (1). Due to the complexity of climate change and the growing process of forage grass, it is still far from certain that global warming will have a positive or negative impact on the growth of forage grass. Irrational utilization of alpine meadows may destroy the vegetation or cut down the area of vegetation growing, as a whole, it reduces the value of r and K. Now, pastoralists take better care of their livestock, such as providing supplementary food and (or) building plastic greenhouse shelters in winter, providing effective medical treatment. All these would result in the decreasing of the mortality parameter d4. Given with the same amount of forage grass consumed, if supplementary food is supplied to livestock, then livestock would grow more and produce more offspring, that is, the parameter q would increase. When rodents were controlled with rodenticide, the mortality d1 would enlarge. As a result of poaching, many raptors would be killed and the mortality d3 then become enlarged.
Table 1 given below show how coordinates x∗,y∗,z∗,u∗ of E5 and values of A,θ vary when all parameters are fixed and one of d1,r,K,d3,d4,q increases.
Table 1. Variation of coordinates x∗,y∗,z∗,u∗ of E5 and values of A, θ when one of the parameters d1,r,K,d3,d4,q increases (all other parameters are fixed).
| Parameter |
d1 |
r |
K |
d3 |
d4 |
q |
| x∗ |
− |
− |
− |
↗ |
− |
− |
| y∗ |
− |
− |
− |
− |
↗ |
↘ |
| z∗ |
↘ |
− |
− |
− |
↗ |
↘ |
| u∗ |
− |
↗ |
↗ |
↘ |
↘ |
↗ |
| A |
↗ |
− |
− |
− |
− |
− |
| θ |
− |
↗ |
− |
↘ |
− |
− |
As seen from Table 1, despite the fact that global warming and irrational utilization of alpine meadow alter the values of r and K, they do not directly alter the amount of rodents and raptors at the equilibrium level. Thus here we seek other factors that cause alpine meadow degradation.
The results induced by the increasing of d3 and the decreasing of d4 (or the increasing of q) qualitatively match the reality: less forage grass, less raptors, more rodents (Table 1). The increasing of d3 results in the decreasing of livestock, the decreasing of d4 (or the increasing of q) results in the increasing of livestock. Their integrative effect determines whether the number of livestock increases or decreases. In this sense, the increasing of d3, together with the decreasing of d4 (or the increasing of q), is more likely the cause of alpine meadow degradation. Therefore, poaching raptors (increases d3) and providing supplementary food and (or) building plastic greenhouse shelters in winter (decreases d4), may indeed contribute to the degradation of alpine meadows.
Meanwhile, increasing d3 and decreasing d4 (or increasing q) may alter the stability of E5. When d3 increases, θ decreases (Table 1). If θ<0, then E5 disappears and E2 becomes stable. Thus rodents, forage grass coexist, while livestock and raptors die out. Consequently the alpine meadow ecosystem would be unsustainable. When d4 decreases (or q increases), C decreases (Table 1). If C<A, then E5 becomes unstable and E3 is stable. This implies that livestock and forage grass coexist while rodents and raptors would die out. The alpine meadow ecosystem is also unsustainable.
The decreasing of d4 (or the increasing of q) would lead to more livestock, yet forage grass cannot increase accordingly, and hence overgrazing would occur. The increasing of d3 leads to the decline of raptors and hence results in abundant rodents. Based on this, we think overgrazing and rodent damage are not the direct causes of alpine meadow degradation and they are only the phenomena presented by degraded alpine meadows.
4. Efficiency of restoration strategies
The restoration of a degraded alpine meadow helps it return to healthy status with more forage grass, more raptors, less rodents, less livestock and alpine meadow develops healthily by itself. Once the underlying causes of alpine meadow degradation are identified, one can conclude that an effective restoration strategy is to decrease d3, increase d4 and decrease q to their natural values. In practice, numerous restoration strategies are employed to restore degraded alpine meadows.
Some strategies aim to meliorate the vegetation, such as reseeding, fertilizing, irrigating, ruderal controlling and scarifying. This would enlarge parameters r and K in Model (1). It follows from Table 1 that this can enlarge the amount of livestock only, and cannot alter the amount of rodents, forge grass and raptors. That is, these strategies cannot totally restore a degraded alpine meadow. In addition, these measures cannot be implemented at a long-term scale and in a large area due to the limit of manpower, material and finance.
Graze prohibiting, seasonal grazing, determining amount of livestock according to grass yield, providing livestock with supplementary food, building plastic greenhouse shelters to protect livestock are common restoration strategies related to livestock. In practice, it is impossible to prohibit grazing for a long period of time in a huge area, otherwise, the alpine meadow would lose its function and the animal husbandry would be blocked. Graze prohibiting and seasonal grazing can only lighten grazing pressure during a short time interval in a small area and cannot alter parameters in Model (1). As a result, this cannot restore a degraded alpine meadow. Providing livestock with supplementary food and building plastic greenhouse shelters to protect livestock in winter are indeed the causes of alpine meadow degradation and will not help the restoration of degraded alpine meadows. Determining the amount of livestock according to grass yield is equivalent to increasing livestock mortality d4 to the natural value. This strategy turns out to be a good idea and is also practicable. To be effective, it needs scientifically evaluate grass production, cut down overfull livestock and implement the strategy at a long time scale. This also guarantees the remaining livestock enough food so that no supplementary food is needed and then value of q returns to its inherent measurement.
Rodent control may be achieved through rodenticide or through protecting its natural enemy. Protecting raptors can reduce the death rate of raptors such that the parameter d3 can return to its inherent measurement. Controlling rodent with rodenticide once can reduce rodent population temporarily, but cannot change the parameter values in Model (1). Thus has no help to restore a degraded alpine meadow. Controlling rodents with rodenticide for a long time is equivalent to increasing the rodent mortality d1. This may induce two outcomes according to whether A is larger or smaller than C. If A is larger than C, then the equilibrium E5 is unstable and E3 is stable. Thus rodents and raptors would die out, only forage grass and livestock coexist, the alpine meadow ecosystem is not healthy. If A is smaller than C, then equilibrium E5 is stable. This implies that the amount of rodents, forage grass and livestock will not change, while the amount of raptors decreases and hence the degraded alpine meadow cannot recover.
As a strategy of restoring degraded alpine meadows, ecological migration, has been implemented in several places. After a large number of pastoralists and livestock moved away, the remaining pastoralists may still care their livestock attentively. As pastoralists have enough livestock to meet their needs, the system becomes ecologically stable as parameters d4 and q return to their inherent measurements.
In summary, determining the amount of livestock according to grass yield, ecological migration and protecting raptors are effective integrated measures to restore a degraded alpine meadow.
Despite the fact that scarifying, reseeding, fertilizing, irrigating, ruderal controlling, graze prohibiting, seasonal grazing, rodents control with rodenticide cannot restore a degraded alpine meadow thoroughly, these strategies are conducive to its restoration. These strategies can help the alpine meadow ecosystem approach the positive equilibrium E5 to some extent. If effective restoration measures were implemented, then the alpine meadow ecosystem would approach E5 quickly.
5. Conclusions
Making use of a mathematical modelling exercise, in this work, we analyzed the underlying causes of alpine meadow degradation and evaluated the efficiency of restoration strategies. Our analysis suggests that the increasing of raptor mortality (d3), together with the decreasing of livestock mortality (d4) (or increasing of the rate (q) at which livestock increases), is the underlying causes of alpine meadow degradation. Further, to restore degraded alpine meadows, an effective strategy is controlling the amount of livestock according to the grass yield and/or ecological migration, together with protecting raptors; while meliorating vegetation and controlling rodent population with rodenticide are conducive to restoring degraded alpine meadows. Our analysis also suggests that providing supplementary food to livestock and building greenhouse shelters to protect livestock in winter contribute to alpine meadow degradation and have no help to its restoration.
Acknowledgments
The authors were very grateful to the anonymous reviewers' very helpful comments and suggestions. This work was supported by the National Natural Science Foundation of China [grant number 11371313,61573016], Qinghai Innovation Platform Construction Project [grant number 2017-ZJ-Y20], Shanxi 131 Talents Program and Shanxi 100 Talent Program.









 DownLoad:
DownLoad: