A new analytical algorithm for uncertain fractional differential equations in the fuzzy conformable sense

1.   Introduction

Fuzzy set theory plays a crucial role in exploring and analyzing a wide range of real-world problems, including quantum mechanics, astronomy, electronic mechanisms, quantum optics, artificial intelligence, population dynamics models, finance, technology, pattern recognition, economics, biology, and medicine ^[1,2,3,4,5]. Moreover, the application of fuzzy differential equations enables the modeling and solution of various mathematical problems in these fields, making them indispensable tools in applied mathematics ^[6,7,8,9,10].

Fuzzy set theory was initially established by Zadeh ^[1]. Subsequently, Dubois and Prade ^[11] introduced the concepts of fuzzy differential and differential integration for fuzzy valued functions. Furthermore, various researchers have made significant contributions to the field. Guo et al. ^[4] developed fuzzy population models, Agarwal et al. ^[12] introduced fuzzy fractional differential equations (FFDEs), and Fard and Salehi ^[13] along with Soolaki et al. ^[14] discussed fuzzy fractional variational problems using Caputo and combined Caputo differentiability, respectively. Zhang et al. ^[15] established generalized necessary and sufficient optimality conditions for fuzzy fractional problems based on the Atangana-Baleanu fractional derivative (FD) and generalized Hukuhara difference. Das and Roy ^[16] proposed a novel numerical method employing the Adomian decomposition method, specifically in the Riemann-Liouville sense, to solve FFDEs. Salahshour et al. ^[17] tackled FFDEs through fuzzy Laplace transform. Additionally, Bede and Gal ^[18] introduced the concept of strongly generalized differentiability for fuzzy valued functions. Hasan et al. ^[10] focused on the analytical and numerical solutions of fractional fuzzy hybrid systems in Hilbert space, with a specific emphasis on control using the Atangana-Baleanu Caputo FD. Finally, Behzadi et al. ^[19] applied the fuzzy Picard method to solve fuzzy quadratic Riccati and fuzzy Painlevé equations.

In 2014, the conformable FD was introduced by Khalil et al. ^[20]. This innovative definition of FD relies on the limit concept, similar to the classical derivative. The key advantage of the conformable FD is its ease of computation compared to previous fractional definitions like Caputo Fabrizio, Atangana-Baleanu, Riemann-Liouville, and the Caputo definitions ^{[21,22,23,24,25]}. Notably, the conformable FD satisfies all the fundamental concepts of the classical derivative, while other fractional derivative definitions may fall short in this aspect.

Moreover, the conformable FD offers the ability to compute for non-differentiable functions and provides efficient solutions for FFDEs and systems. It also brings modifications to significant transforms such as Laplace, Sumudu, and Nature transforms, making them effective tools for solving singular FFDEs ^[26]. Building upon the conformable FD, Abdeljawad ^[27] further developed the concept and introduced the conformable Laplace transform as a generalization of the Laplace transform in 2015.

In 2020, Abu Arqub and Al-Smadi ^[28] proposed the fuzzy conformable FD and integral. These concepts were employed to derive solutions for specific FFDEs involving strongly generalized differentiability. Recently, the fuzzy conformable Laplace (FCL) transform has been investigated as an analytic method for solving FFDEs by authors such as Harir et al. ^[29] and Sadabadi et al. ^[30].

In recent studies by Bataineh et al. ^[31], and Al-Zhour et al. ^[32], the residual power series method was utilized to obtain approximate solutions for FFDEs in the conformable sense. The method was applied under the assumption of strongly generalized differentiability. These equations have a general form as following initial value problem (IVP):

with the fuzzy initial condition (F-IC):

where $\mathfrak{P}^\beta$ represents the fuzzy conformable FD of order $\beta$, $\mathcal{Z}:\ [a, b]\times\Re_\mathcal{F}\rightarrow \Re_\mathcal{F}$ is a continuous analytical fuzzy valued function, $\psi$ is an analytical fuzzy valued function, $\tau\in\Re_\mathcal{F}$, where $\Re_\mathcal{F}$ is the set containing all fuzzy numbers.

There are three primary approaches for solving FFDEs in a conformable sense with fuzzy-initial conditions (F-ICs). The first approach involves dealing with the case where the initial value is a fuzzy number. In this scenario, the solution becomes a fuzzy function, necessitating the consideration of fuzzy derivatives. To address this problem, the use of strongly generalized differentiability is required. The second approach entails transforming the FFDEs into crisp equations, represented as a set of differential inclusions. However, a major drawback of using differential inclusions is the absence of a fuzzification of the differential operator. Consequently, the solution is not inherently a fuzzy-valued function. The last approach revolves around the crisp equation and the initial fuzzy values, which are in the solution. The weakness lies in the need to rewrite the solution in the fuzzy setting, which makes the solution techniques less user-friendly and more restricted, requiring numerous computational steps. To overcome this, we can substitute the crisp equation and the initial fuzzy values with real constants and arithmetic operations, treating them as operations on fuzzy numbers in the final solution. The latest approach, which focuses on exploring the fuzzy set of real-valued functions rather than fuzzy-valued functions, exemplifies the fulfillment of the aforementioned constraints.

In 2020, a new method called the Laplace-residual power series method (L-RPSM) was proposed and developed by Eriqat et al. ^[33]. This analytical numerical method aimed to enhance the simplicity and efficiency of the residual power series method for solving fractional differential equations (FDEs) in various fields of engineering and science. The L-RPSM demonstrated improved effectiveness in generating both exact and approximate solutions for different problems, including linear and nonlinear neutral pantograph FDEs ^[33], nonlinear bacteria growth model ^[34], nonlinear water wave FDEs ^[35], higher-order FDEs ^[36], a class of hyperbolic system of fractional FDEs ^[37], reaction-diffusion model ^[38], nonlinear time-dispersive FDEs ^[39], and nonlinear fisher FDEs ^[40]. Additionally, L-RPSM was employed by Oqielat et al. ^[41,42] for solving fuzzy quadratic Riccati equations and fuzzy fractional population dynamics model and others ^{[43,44,45,46,47,48,49,50,51]}.

The main goal of this paper is to find the exact solutions for FFDEs in the conformable sense under strongly generalized differentiability, as shown in (1.1) and (1.2). To achieve this objective, we have developed an efficient analytical algorithm based on the L-RPSM. Our algorithm involves applying the FCL transform to simplify the targeted equation. Then, we construct a new expansion using novel perspectives and theories to assume a series solution for the target equation in the FCL space. Subsequently, we utilize important facts related to the FCL residual functions to determine the coefficients of the assumed series solutions. Finally, we apply the inverse FCL transform to the series solutions in FCL space. This process allows us to obtain the exact solution in the form of a fuzzy convergent conformable fractional series, which represents the precise solution to the target equation in the original space.

The remaining sections of the paper are organized as follows: Firstly, we provide a brief retrieval of primary definitions and theorems related to fuzzy conformable fractional calculus in Section 2. Following that, in Section 3, we present a new expansion for constructing solutions to FFDEs in the conformable sense, along with an explanation of the definitions and theories associated with FCL transform theory. In Section 4, we extend the efficient analytic fractional conformable L-RPSM algorithm to effectively solve FFDEs in the conformable sense. In Section 5, we present specific numerical examples. Finally, in Section 6, we summarize the key findings and offer concluding remarks.

2.   Fuzzy conformable fractional calculus

In this section, we present the basic definitions and initial findings that are necessary for comprehending the theory of sufficient fuzzy analysis. This understanding will allow us to explore the solutions for specific categories of FFDEs. Throughout this article, we will utilize the notation $\Re_\mathcal{F}$ to represent the set encompassing all fuzzy numbers.

Definition 1. (^[20]) The operator $\mathfrak{P}^\beta$, which represents the $\beta$-th conformable FD of a function $\varphi: [\eta, \infty) \rightarrow \mathbb{R}$ starting from $\eta$, is expressed as follows:

and $\mathfrak{P}^\beta \varphi(\eta) = \underset{t\to\eta^{+}}{\lim}\mathfrak{P}^\beta \varphi(t)$ provided that $\underset{t\to\eta^{+}}{\lim}\mathfrak{P}^\beta \varphi(t)$ exists and $\varphi(t)$ is $(m-1)$-differentiable in some $(0, \eta)$.

Definition 2. (^[9]) A fuzzy set $\psi$ is a set that maps from the real numbers ($\Re$) to the range of [0, 1], and is defined as a fuzzy number if

● $\psi$ is normal, i.e., there is at least one point $\xi \in \Re$ such that $\psi(t) = 1$.

● $\psi$ is convex, i.e., for each $\xi, \ \eta \in \Re$, and $0 \leq \gamma \leq 1$, we have $\psi(\gamma\xi+(1-\gamma)\eta) \geq$ min $(\psi(\xi), \psi(\eta))$.

● $\psi$ is upper semi-continuous, i.e., $\underset{t\to\xi}{\lim} \ \psi(t) \geq \psi(\xi), \forall \xi \in \Re$.

● $[\psi]_0 = \overline{\{\xi \in \Re: \psi(\xi) > 0\}}$ is compact set.

Theorem 1. (^[5]) Assume $\underline{\psi}, \overline{\psi}: [0, 1]\rightarrow \Re$ hold the following conditions:

1) $\underline{\psi}$ is a bounded monotonic non-decreasing function.

2) $\overline{\psi}$ is a bounded monotonic non-increasing function.

3) $\underline{\psi} (1)\leq \overline{\psi}(1)$.

4) For each $i \in (0, 1], \ \underset{\wp\to i^{-}}{\lim}\underline{\psi}(\wp) = \underline{\psi}(i)$ and $\underset{\wp\to i^{-}}{\lim}\overline{\psi}(\wp) = \overline{\psi}(i)$.

5) $\underset{\wp\to 0^{+}}{\lim}\underline{\psi}(\wp) = \underline{\psi}(0)$ and $\underset{\wp\to 0^{+}}{\lim}\overline{\psi}(\wp) = \overline{\psi}(0)$.

Then, $\psi: [0, 1]\rightarrow \Re$ defined by $\psi(t) = \sup \{\wp|\underline{\psi}(\wp)\leq t \leq \overline{\psi}(\wp)\}$ is a fuzzy number with $\wp$-level set: $[\underline{\psi}_{\wp}, \overline{\psi}_{\wp}]$. Furthermore, if $\psi: [0, 1]\rightarrow \Re$ is a fuzzy number with $\wp$-level set $[\underline{\psi}_{\wp}, \overline{\psi}_{\wp}]$, then the functions $\underline{\psi}_{\wp}$ and $\overline{\psi}_{\wp}$ fulfill the conditions (i)–(v) mentioned above. Therefore, it is possible to represent the arbitrary fuzzy number $\psi$ as a pair of ordered functions $(\underline{\psi}_{\wp}, \overline{\psi}_{\wp})$.

Definition 3. (^[52]) For $\mathfrak{D}:\Re_\mathcal{F}\times \Re_\mathcal{F}\rightarrow \Re^{+}\cup \{0\}$, assume $\psi = (\underline{\psi}, \overline{\psi})$ and $\varphi = (\underline{\varphi}, \overline{\varphi})$ an arbitrary fuzzy numbers, then the mapping $\mathfrak{D}(\psi, \varphi)$ can be defined as $\mathfrak{D}(\psi, \varphi) = \underset{0\leq \wp \leq 1}{\sup}\mathfrak{D}_H\big\{[\psi]_\wp, [\varphi]_\wp\big\}$, where $\mathfrak{D}_H$ is the Hausdroff metric:

The Zadeh's Extension Principle is employed to define addition and scalar multiplication on $\mathfrak{D}$, resulting in a reduction of these operations to interval operations

We consider the differentiability of fuzzy-valued functions in the sense of H-difference, by using the following difference.

Definition 4. (^[52]) Let $\psi, \varphi\in\Re_\mathcal{F}$ and $\wp\in[0, 1]$, if the exists $\vartheta\in\Re_\mathcal{F}$ such that $\psi = \varphi+\vartheta$, then $\vartheta$ is called H-difference of $\psi$ and $\varphi$, denoted by $\psi\ominus\varphi$, and defined as follows:

Definition 5. (^[28]) The fuzzy conformable FD of order $\beta > 0$ for fuzzy function $\psi:\ (a, b)\rightarrow \Re_\mathcal{F}$ is denoted by $\mathfrak{P}^\beta$ and defined as:

Definition 6. (^[10,28]) For $t_0 \in [a, b], \ a > 0$, and $\beta > 0$, we say that $\psi:\ [a, b]\rightarrow \Re_\mathcal{F}$ is strongly-generalized $\beta$th-fuzzy conformable differentiable ($\beta$th-FCD) at $t_0$ if there exists an element $\mathfrak{P}^\beta \psi(\iota) \in \Re_\mathcal{F}$ such that either:

1) The H-differences

exist for each sufficiently small $\zeta > 0$, and

2) The H-differences

exist for each sufficiently small $\zeta > 0$, and

It is worth mentioning here that the limits are taken in the metric space $(\Re_\mathcal{F}, \mathfrak{D})$.

Remark 1. If $\psi$ satisfies the conditions of Definition 6-1), being fuzzy differentiable for any point $t \in (a, b)$, then $\psi$ can be considered a $(1;\beta)$-FCD on the interval $[a, b]$ with its derivative given by $\mathfrak{P}_1^\beta \psi(t)$. Similarly, if $\psi$ satisfies the conditions of Definition 6-2), being fuzzy differentiable for any point $t \in (a, b)$, then $\psi$ can be regarded as a $(2;\beta)$-FCD on the interval $[a, b]$, and its derivative is $\mathfrak{P}_2^\beta \psi(t)$.

Theorem 2. (^[10]) Assume that $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ is a fuzzy function satisfies the following conditions:

1) For each $t\in [a, b]$, there exists $\lambda > 0$ such that the H-differences: $\psi\big(t+\zeta t^{1-\beta}\big)\ominus\psi(t)$ and $\psi(t)\ominus\psi\big(t-\zeta t^{1-\beta}\big)$ exists for all $\zeta \in [0, \lambda)$.

2) For each $t\in [a, b]$ and $h > 0$ there exists a constant $l > 0$ such that $\mathfrak{D}_H\bigg(\frac{\psi\big(t+\zeta t^{1-\beta}\big)-\psi(t)}{\zeta, \mathfrak{P}^\beta \psi(t)}\bigg) < h$, and $\mathfrak{D}_H\bigg(\frac{\psi(t)-\psi\big(t-\zeta t^{1-\beta}\big)}{\zeta, \mathfrak{P}^\beta \psi(t)}\bigg) < h$, for all $\zeta\in[0, l)$. Then, the set of functions $[\psi(t)]_\wp$ is $\beta$th-FCD and its derivative is $[\mathfrak{P}^\beta \psi(t)]_\wp = \big[\mathfrak{P}^\beta \underline{\psi}_\wp(t), \mathfrak{P}^\beta \overline{\psi}_\wp(t)\big]$, where $[\psi(t)]_\wp = \big[ \underline{\psi}_\wp(t), \overline{\psi}_\wp(t)\big]$ for each $\wp \in [0, 1]$.

Theorem 3. (^[10,28]) Assume that $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ is a fuzzy function. Let $[\psi(t)]_\wp = \big[ \underline{\psi}_\wp(t), \overline{\psi}_\wp(t)\big]$ for each $\wp \in [0, 1]$. Then,

1) If $\psi$ is $(1;\beta)$-FCD, then $\underline{\psi}_\wp$ and $\overline{\psi}_\wp$ are $\beta$th-FCD functions on $[a, b]$ and $[\mathfrak{P}^\beta \psi(t)]_\wp = \big[\mathfrak{P}^\beta \underline{\psi}_\wp(t), \mathfrak{P}^\beta \overline{\psi}_\wp(t)\big]$.

2) If $\psi$ is $(2;\beta)$-FCD, then $\underline{\psi}_\wp$ and $\overline{\psi}_\wp$ are $\beta$th-FCD functions on $[a, b]$ and $[\mathfrak{P}^\beta \psi(t)]_\wp = \big[\mathfrak{P}^\beta \overline{\psi}_\wp(t), \mathfrak{P}^\beta \underline{\psi}_\wp(t)\big]$.

3.   Fuzzy conformable Laplace transform

In this section, we review and construct the definitions and theories related to FCL transform that will be used to construct our approach for solving FFDEs in the conformable sense.

Definition 7. (^[29,30]) Let $\beta\in (0, 1]$ and $[ \psi(t)]_\wp$ be a continuous fuzzy value function for $\wp\in[0, 1]$. If the function $e^{-s\frac{t^\beta}{\beta}} [ \psi(t)]_\wp t^{\beta-1}$ is integrable on $[0, \infty)$, then the FCL transform of order $\beta$ starting from zero of $[ \psi(t)]_\wp$ is defined as:

Moreover, we have

In parametric form, we get

where,

Theorem 4. (^[29]) Let $\beta\in(0, 1]$ and $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ be a continuous fuzzy function for $\wp\in [0, 1]$ such that $\mathfrak{L}_\beta\big[[ \psi(t)]_\wp\big] = \big[\Psi(s)\big]_\wp$ exists. Then, the following equation holds:

where $\mathfrak{L}\big[[g(t)]_\wp\big] = \int^{\infty}_{0}{e^{-st} [g(t)]_\wp dt}$.

Lemma 1. Let $\beta\in(0, 1]$, $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ and $\varphi: [a, b]\rightarrow \Re_\mathcal{F}$ be continuous fuzzy functions for $\wp\in [0, 1]$ and of exponential order $\jmath$ and $\phi$ respectively. Suppose $\mathfrak{L}_\beta\big[[ \psi(t)]_\wp\big] = \big[\Psi(s)\big]_\wp$ and $\mathfrak{L}_\beta\big[[ \varphi(t)]_\wp\big] = \big[\Phi(s)\big]_\wp$ are exist, where $s > 0$ and $\gamma$ and $\mu$ are constants. Then, the following properties hold:

1) $\begin{aligned}[t]\mathfrak{L}_\beta\big[\gamma[ \psi(t)]_\wp+\mu[ \varphi(t)]_\wp\big] = \gamma \big[\Psi(s)\big]_\wp+\mu\big[\Phi(s)\big]_\wp\end{aligned}$.

2) $\begin{aligned}[t]\mathfrak{L}_\beta\big[\gamma\big] = \frac{\gamma}{s}\end{aligned}$.

3) $\begin{aligned}[t]\mathfrak{L}_\beta\big[t^\gamma\big] = \beta^\frac{\gamma}{\beta}\frac{\Gamma\big(1+\frac{\gamma}{\beta}\big)}{s^{1+\frac{\gamma}{\beta}}}\end{aligned}$.

4) $\begin{aligned}[t]\mathfrak{L}_\beta\Big[ \sin{\Big(\gamma\frac{t^\beta}{\beta}}\Big)\Big] = \frac{\gamma}{\gamma^{2}+s^{2}}\end{aligned}$.

5) $\begin{aligned}[t]\mathfrak{L}_\beta\Big[ \cos{\Big(\gamma\frac{t^\beta}{\beta}}\Big)\Big] = \frac{s}{\gamma^{2}+s^{2}}\end{aligned}$.

6) $\begin{aligned}[t]\mathfrak{L}_\beta\big[t^{n\beta}[ \psi(t)]_\wp\big] = (-\beta)^{n}\frac{d^{n}}{ds^{n}}\big[\Psi(s)\big]_\wp\end{aligned}$.

Proof. Part (1)–(5) have been proven in ^[27,29]. Now, to prove part (6), consider the following identity

Therefore, we have:

Thus, we obtain:

The general result now follows by induction on $n$. Hence, if $\psi$ is $(1;\beta)$-FCD, the proof of the fact is concluded. Similarly, we can employ a similar approach to establish the result when $\psi$ is $(2;\beta)$-FCD. □

Theorem 5. (^[29,30]) Assume that $\beta\in (0, 1]$ and $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ is a fuzzy function. Let $[\psi(t)]_\wp = \big[ \underline{\psi}_\wp(t), \overline{\psi}_\wp(t)\big]$ for each $\wp \in [0, 1]$ and $\mathfrak{L}_\beta\big[[ \psi(t)]_\wp\big] = \big[\Psi(s)\big]_\wp = \big[\underline{\Psi}_\wp(s), \overline{\Psi}_\wp(s)\big]$ exists. Then,

1) If $\psi$ is $(1;\beta)$-FCD, then

In parametric form, we get

where

2) If $\psi$ is $(2;\beta)$-FCD, then

In parametric form, we get

where

Theorem 6. Let $\beta\in(0, 1]$ and $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ be a continuous fuzzy function for $\wp\in [0, 1]$ such that $\mathfrak{L}_\beta\big[[ \psi(t)]_\wp\big] = \big[\Psi(s)\big]_\wp$ exists. Then

1) If $\psi$ is $(1;\beta)$-FCD, then

In parametric form, we get

where

2) If $\psi$ is $(2;\beta)$-FCD, then

In parametric form, we get

where

where $\mathfrak{P}^{n\beta}$ means apply conformable FD, $\mathfrak{P}^{\beta}$, $n$-times.

Proof. Assume that $\psi(t)$ is $(1;\beta)$-FCD for $\wp \in [0, 1]$. In parametric form for $n = 2$, we get $\mathfrak{L}_\beta\big[[\mathfrak{P}^{2\beta} \psi(t)]_\wp\big] = \Big[\mathfrak{L}_\beta\big[\mathfrak{P}^{2\beta} \underline{\psi}_\wp(t)\big], \mathfrak{L}_\beta\big[\mathfrak{P}^{2\beta} \overline{\psi}_\wp(t)\big]\Big]$.

Using Theorem 5, we have:

Therefore, for $n = 1, 2$ the formula is true. Using the induction, suppose that the formula is true for $n = m$ as

To complete the proof, we have prove it true for $n = m+1$. In parametric form for $m+1$, we get $\mathfrak{L}_\beta\big[[\mathfrak{P}^{(m+1)\beta} \psi(t)]_\wp\big] = \Big[\mathfrak{L}_\beta\big[\mathfrak{P}^{(m+1)\beta} \underline{\psi}_\wp(t)\big], \mathfrak{L}_\beta\big[\mathfrak{P}^{(m+1)\beta} \overline{\psi}_\wp(t)\big]\Big]$. Hence,

Thus, the formula for $m+1$ as below is true

The part (2) of the theorem can be proved in the same manner. □

Theorem 7. Let $\beta\in(0, 1]$ and $\psi: [a, b]\rightarrow \Re_\mathcal{F}$ be a continuous fuzzy function for $\wp\in [0, 1]$. If $\mathfrak{L}_\beta\big[[ \psi(t)]_\wp\big] = \big[\Psi(s)\big]_\wp$ exists, and $s > 0$. Then, the initial value theorem for FCL transform is given by

Proof. We know that $\mathfrak{L}_\beta\big[[\mathfrak{P}^\beta \psi(t)]_\wp\big] = \Big[\mathfrak{L}_\beta\big[\mathfrak{P}^\beta \underline{\psi}_\wp(t)\big], \mathfrak{L}_\beta\big[\mathfrak{P}^\beta \overline{\psi}_\wp(t)\big]\Big]$. Now, from the definition of FCL transform, we have,

According to Theorem 5, we have

Now, taking limit as $s\to \infty$ for the expansions in Eq (3.1), we have,

After simplify Eq (3.2), we get

Therefore, we have

Therefore, the proof of the fact $\underset{s\to\infty}{\lim}s\big[\Psi(s)\big]_\wp = [ \psi(0)]_\wp$ is complete in case $\psi$ is $(1;\beta)$-FCD. We can use the same manner to prove it in case $\psi$ is $(2;\beta)$-FCD. □

Definition 8. (^[53]) We can define a fractional power series around $t_0$ as the series that can be represented by the following expression:

Theorem 8. (^[31]) For $\wp \in [0, 1]$, let $\underline{\psi}_{\wp}(t)$, and $\overline{\psi}_{\wp}(t)$ have the following fractional expantions about $t = 0$,

where $\beta\in (0, 1]$ and $t\in [0, R)$. If $\mathfrak{P}^{\beta}\underline{\psi}_{\wp}(t)$, and $\mathfrak{P}^{\beta}\overline{\psi}_{\wp}(t)$ are two continuous on $[0, R)$, then the value of the unknown coefficients $\Im_m$ and $\ell_m$ for $m = 0, 1, 2, \ldots$, are in the forms

where $\mathfrak{P}^{m\beta} = \mathfrak{P}^{\beta}.\mathfrak{P}^{\beta} \cdots \mathfrak{P}^{\beta}$ (repeated $m$ times).

Theorem 9. For $\wp\in [0, 1]$, assume that $\underline{\Psi}_{\wp}(s) = \mathfrak{L}_\beta[\underline{\psi}_{\wp}(t)]$ and $\overline{\Psi}_{\wp}(s) = \mathfrak{L}_\beta[\overline{\psi}_{\wp}(t)]$ exist and have the following expansions:

Then the values of unknown coefficients $\Im_m$ and $\ell_m$ are expressed as $\Im_m = \big(\mathfrak{P}^{m\beta} \underline{\psi}_{\wp}\big)(0)$ and $\ell_m = \big(\mathfrak{P}^{m\beta} \overline{\psi}_{\wp}\big)(0)$, where $\mathfrak{P}^{\beta}\underline{\psi}_{\wp}(t)$, and $\mathfrak{P}^{\beta}\overline{\psi}_{\wp}(t)$ are two continuous functions defined on the interval $[0, R)$, where $\beta\in (0, 1]$. The notation $\mathfrak{P}^{m\beta} = \mathfrak{P}^{\beta} \cdot \mathfrak{P}^{\beta} \cdots \mathfrak{P}^{\beta}$ denotes the composition of the conformable FD $\mathfrak{P}^{\beta}$ repeated $m$ times.

Proof. Let us consider that $\underline{\Psi}_{\wp}(s)$ and $\overline{\Psi}_{\wp}(s)$ can be expressed using the expansions given in Eq (3.7). It is important to note that if we multiply Eq (3.7) by $s$ and take the limit as $s$ approaches infinity, all terms in the expansions, except the first term, become negligible. Therefore, according to Theorem 7, we can deduce that $\Im_0 = \underset{s\to\infty}{\lim}s\underline{\Psi}_{\wp}(s) = \underline{\psi}_{\wp}(0)$ and $\ell_0 = \underset{s\to\infty}{\lim}s\overline{\Psi}_{\wp}(s) = \overline{\psi}_{\wp}(0)$. As a result, the expressions presented in Eq (3.7) can be simplified as follows:

Furthermore, considering other aspects, when we multiply Eq (3.8) by $s^2$, we obtain the following expansions for $\Im_1$ and $\ell_1$:

By taking the limit as $s$ approaches infinity for the expressions in Eq (3.9), we obtain:

When we multiply the expressions in Eq (3.8) by $s^3$ and take the limit as $s$ approaches infinity, we obtain:

By observing the patterns and continuing to multiply the expressions in Eq (3.8) by $s^{m+1}$, and computing the limit of the expansions of $\Im_m$ and $\ell_m$ as $s$ tends to infinity, we can derive the general formulas as follows: $\Im_m = \big(\mathfrak{P}^{m\beta} \underline{\psi}_{\wp}\big)(0)$ and $\ell_m = \big(\mathfrak{P}^{m\beta} \overline{\psi}_{\wp}\big)(0)$, where $m = 0, 1, 2, \ldots$. This establishes the proof of Theorem 9. □

Remark 2. The form of the inverse FCL transform for the expansions stated in Eq (3.7) as presented in Theorem 9 is given by:

which is corresponding to the fractional power series in Eq (3.5) stated in Theorem 8.

Theorem 10. Let us assume that $\underline{\Psi}_{\wp}(s) = \mathfrak{L}_\beta[\underline{\psi}_{\wp}(t)]$ and $\overline{\Psi}_{\wp}(s) = \mathfrak{L}_\beta[\overline{\psi}_{\wp}(t)]$ exist for $\wp\in [0, 1]$. If we have $\big|s\mathfrak{L}_{\beta}\big[\mathfrak{P}^{(m+1)\beta} \underline{\psi}_\wp(t)\big]\big|\leq \mathcal{M}$ and $\big|s\mathfrak{L}_{\beta}\big[\mathfrak{P}^{(m+1)\beta} \overline{\psi}_\wp(t)\big]\big|\leq \mathcal{N}$, where $s, \ \mathcal{M}$, and $\mathcal{N}$ are positive numbers, then the remaining terms $\underline{\mathfrak{R}_m}(s)$ and $\overline{\mathfrak{R}_m}(s)$ of the expansions in Eq (3.7) respectively satisfy the following inequalities:

Proof. Let's begin by assuming that $\mathfrak{P}^{j\beta} \underline{\psi}_\wp(t)$ and $\mathfrak{P}^{j\beta} \overline{\psi}_\wp(t)$ are defined as $s > 0$ for $j = 0, 1, 2, \cdots, m+1$. Additionally, given the conditions, let's assume that:

The expressions for the remainders $\underline{\mathfrak{R}_m}(s)$ and $\overline{\mathfrak{R}_m}(s)$ of the expansions in Eq (3.7) are given by:

By considering the definition of the remainders, we can derive the following:

From Eqs (3.13) and (3.15), we can observe that $|s^{m+2}\underline{\mathfrak{R}_m}(s)|\leq \mathcal{M}$ and $|s^{m+2}\overline{\mathfrak{R}_m}(s)|\leq \mathcal{N}$. Therefore, we have:

By rearranging Eq (3.16), we can deduce the following inequalities: $|\underline{\mathfrak{R}_m}(s)|\leq \frac{\mathcal{M}}{s^{m+2}}$ and $|\overline{\mathfrak{R}_m}(s)|\leq\frac{\mathcal{N}}{s^{m+2}}$. These inequalities provide the necessary bounds and conclude the proof. □

4.   The L-RPSM: construction and analysis

In this section, we utilize the L-RPSM to generate analytical fuzzy numerical solutions for the IVPs (1.1) and (1.2), where $\wp$ belongs to the interval $[0, 1]$. Our approach involves transforming the IVPs (1.1) and (1.2) into crisp systems of FFDEs. The nature of the crisp systems depends on the type of differentiability, characterized by $\psi(t)$ as either $(1;\beta)$-FCD or $(2;\beta)$-FCD.

To ensure clarity and without sacrificing generality, we focus solely on constructing the L-RPSM solution for $(1;\beta)$-FCD. However, using the same methodology, we can also construct the L-RPSM solution for $(2;\beta)$-FCD.

Now, let's assume that $\psi(t)$ represents $(1;\beta)$-FCD for $\wp\in [0, 1]$. Accordingly, the IVPs (1.1) and (1.2) can be reformulated as the following FFDEs:

with the F-ICs:

where $t\in [0, b]$ and $\beta\in (0, 1]$.

Utilize the L-RPSM, we first employ the FCL transform for the expansions in Eq (4.1) as follows:

Based on Theorem 5, we can express the expansions presented in Eq (4.3) in the following manner:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

The main idea of L-RPSM is to construct the solution for the target equation in FCL space as in Eq (4.4), and then employ inverse FCL transform for this solution to obtain the solution for the target equation in the original space. To achieve our goal, we assume that the solution for the expansions in Eq (4.4) has the following expression:

Furthermore, we can utilize the initial value theorem for the FCL transform, as stated in Theorem 7, to establish that $\Im_0 = \underset{s\to\infty}{\lim}s\underline{\Psi}_{\wp}(s) = \underline{\psi}_{\wp}(0) = \underline{\omega}_\wp$ and $\ell_0 = \underset{s\to\infty}{\lim}s\overline{\Psi}_{\wp}(s) = \overline{\psi}_{\wp}(0) = \overline{\omega}_\wp$. Consequently, we can express the L-RPSM solutions for the expansions in Eq (4.4) as follows:

In order to utilize the L-RPSM and determine the values of the unknown coefficients in the series presented in Eq (4.5), we define the Laplace residual function of the expansions in Eq (4.4) in the following manner:

Below are a few key facts regarding the FCL residual functions:

1) $\begin{aligned}[t]\underline{LRes}_\wp(s) = 0\end{aligned}$ and $\begin{aligned}[t]\overline{LRes}_\wp(s) = 0\end{aligned}$.

2) Since $\underline{\mathcal{Z}}_\wp$ and $\overline{\mathcal{Z}}_\wp$ are analytic functions, Eq (4.6) take the following expressions:

where $\underline{\mathfrak{Z}}^m_\wp$ and $\overline{\mathfrak{Z}}^m_\wp, \ m = 1, 2, \ldots$ are fuzzy operators.

1) Since $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0, \ s > 0$, we have $\Im_m-\underline{\mathfrak{Z}}^{m-1}_\wp(\Im_\imath, \ell_\imath) = 0$ and $\ell_m-\overline{\mathfrak{Z}}^{m-1}_\wp(\Im_\imath, \ell_\imath) = 0$, for $m = 1, 2, \ldots$, and $\imath\in\{0, 1, 2, \ldots, m-1\}$.

2) After a few straightforward collocation steps, we obtain the values of the coefficients $\Im_m$ and $\ell_m$ for $m = 1, 2, \ldots$ in the following form:

where $m = 1, 2, \ldots$, and $\imath\in\{0, 1, 2, \ldots, m-1\}$.

Hence, by substituting the calculated coefficients back into Eq (4.5), we can express the exact solutions for Eq (4.4) in the FCL space as an infinite series in the following manner:

The final stage of the L-RPSM involves transforming the solution presented in Eq (4.9) back to the original space by applying the inverse FCL transform to the expressions in Eq (4.9). Consequently, the exact solution for the IVPs (4.1) and (4.2) can be represented as an infinite series in the following manner:

To provide further clarity, we have outlined the following algorithm:

Algorithm 1. The procedure for obtaining the L-RPSM solutions for the IVPs (4.1) and (4.2) is as follows:

Step A. Apply the FCL transform to Eq (4.1), resulting in:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

Step B. Express the solutions $\underline{\Psi}_{\wp}(s)$ and $\overline{\Psi}_{\wp}(s)$ of the expressions in Step A as follows:

Step C. Define the FCL residual functions as follows:

Step D. Substitute the series solution in Step B into the FCL residual functions in Step C as:

Step E. Rearrange the terms of the expansions for the equations in Step D and collect it to the same power of $s$, resulting in:

where $\underline{\mathfrak{Z}}^m_\wp$ and $\overline{\mathfrak{Z}}^m_\wp, \ m = 1, 2, \ldots$ are fuzzy operators.

Step F. Utilize the facts $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$ to derive the expressions for the coefficient values as follows:

where $m = 1, 2, \ldots$, and $\imath\in\{0, 1, 2, \ldots, m-1\}$.

Step G. Substitute the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ into the series solutions in Step B.

Step H. Employ the inverse FCL transform on the $\underline{\Psi}_{\wp}(s)$ and $\overline{\Psi}_{\wp}(s)$ to obtain the L-RPSM solutions $\underline{\psi}_{\wp}(t)$ and $\overline{\psi}_{\wp}(t)$ of the IVPs (4.1) and (4.2). Then, stop.

Similarly, using the same methodology, we can construct series solutions for the crisp system of FFDEs when $\psi(t)$ represents $(2;\beta)$-FCD.

5.   Applications

In this section, we address three important and interesting applications. We discuss and analyze the numerical simulations of these applications and present graphical results for various parameters. Our computational and presentation processes involve the utilization of both MATHEMATICA 11 and MAPLE 2018.

Application 1. (^[31]) Consider the following fuzzy conformable fractional IVPs

subject to the following F-IC:

where $\wp\in[0, 1]$.

We will now examine two specific cases for dealing with the solutions for the applications, which are as follows:

Case 1: If $\psi(t)$ is $(1;\beta)$-FCD, then the crisp system of the fuzzy conformable fractional IVPs (5.1) and (5.2) can be written in the following form:

subject to the following F-ICs:

Utilizing the L-RPSM, the FCL transform of the crisp system in Eq (5.3) takes the form:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

In this orientation as well, the fuzzy series solutions of the expansions in Eq (5.5) can be written as:

and the FCL residual functions of the crisp system in Eq (5.5) is represented as:

Substitute the expansions of series solution in Eq (5.6) into the FCL residual functions in Eq (5.7), respectively, as:

Since $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$, the recurrence relation which determines the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ given by:

Compute and substitute the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ back into Eq (5.6) to have the solutions of Eq (5.5) in FCL space as following series form:

Employ the inverse FCL transform into the expansions in Eq (5.10) to have the exact solutions of IVPs (5.3) and (5.4) in the original space as follows:

For the standard case $\beta = 1$, Eq (5.11) have the following form:

which are equivalent to the exact solutions $[\psi(t)]_{\wp} = [\wp+1, 3-\wp](e^t-1)$ of the IVPs (5.3) and (5.4) in ordinary derivative.

Case 2: If $\psi(t)$ is $(2;\beta)$-FCD, then the crisp system of the fuzzy conformable fractional IVPs (5.1) and (5.2) can be written in the following form:

subject to the following F-ICs:

The form of the crisp system in Eq (5.13) in FCL space is obtained by utilizing the FCL transform, and it can be written as:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

Similarly, in this particular orientation, the expansions in Eq (5.15) can be expressed as fuzzy series solutions in the following manner:

The representation of the FCL residual functions for the crisp system in Eq (5.15) can be given as:

By substituting the series solution expansions from Eq (5.16) into the FCL residual functions stated in Eq (5.17), we obtain the following expression:

The recurrence relation that governs the values of the coefficients $\Im_m$ and $\ell_m$ is established based on the facts $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$. It can be expressed as follows:

To obtain the solutions of Eq (5.15) in FCL space, we compute and substitute the values of the coefficients $\Im_m$ and $\ell_m$, where $m = 1, 2, \ldots$, back into Eq (5.16). This results in the solutions taking the following series form:

By applying the inverse FCL transform to the expansions presented in Eq (5.20), we can obtain the exact solutions of IVPs (5.13) and (5.14) in the original space. The solutions are given as follows:

In the case where $\beta = 1$, Eq (5.21) takes on the following form:

which are equivalent to the exact solutions $[\psi(t)]_{\wp} = 2(e^t-1)+[1-\wp, \wp-1](1-e^{-t})$ of the target problems in ordinary derivative.

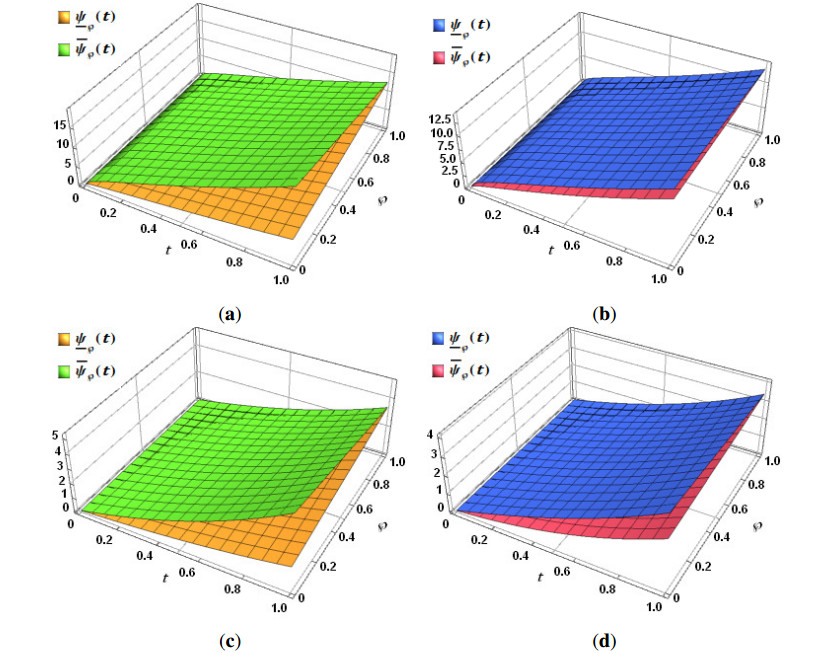
Figure 1 presents the surface graphs of the solutions of Application 1 for both cases at different values of $\beta$. Figure 2 provide the 2D graphs of the solutions of Application 1 at $\beta = 1$ for different values of $\wp$. Numerical simulation of the solutions is performed of Application 1 for both cases at different values of $\wp$ and $\beta$ with some selected grid points on the interval $[0, 1]$ as shown in Table 1.

Application 2. (^[32]) Consider an electrical $\mathcal{R}\mathcal{L}$ circuit with an $\mathcal{A}\mathcal{C}$ source

subject to the following F-IC:

Suppose that $\mathcal{R} = 1$ Ohm, $\mathcal{L} = 1$ Henry, $\Omega(t) = \sin{\big(t^\beta\big)}$, and $\omega(\kappa) = \begin{cases} 25\kappa-24, & 0.96\leq \kappa \leq 1; \\ 101-100\kappa, & 1\leq \kappa \leq 1.01;\\ 0, & \mathrm{other wise.} \end{cases}$ Then,

Case 1: When $\psi(t)$ is $(1;\beta)$-FCD, the crisp system of the fuzzy conformable IVPs (5.23) and (5.24) can be expressed in the following form:

subject to the following F-ICs:

By applying the L-RPSM, we can express the FCL transform of the crisp system described in Eq (5.25) as follows:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

In this particular arrangement, the expansions given in Eq (5.27) can also be represented by the fuzzy series solutions as:

And thus, the representation of the FCL residual functions for the crisp system in Eq (5.27) takes the form of fuzzy expressions as:

Let us substitute the series solution expansions from Eq (5.28) into the FCL residual functions presented in Eq (5.29), yielding the following representation:

As $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$, the values of the coefficients $\Im_m$ and $\ell_m, \ m = 0, 1, 2, \ldots$ are determined by the following recurrence relation:

and

To obtain the solutions of Eq (5.27) in FCL space, calculate and substitute the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ back into Eq (5.28). The resulting solutions can be expressed in the following series form:

By applying the inverse FCL transform to the expansions provided in Eq (5.33), and rearranging the resulting terms, we can obtain the exact solutions of IVPs (5.25) and (5.26) in the original space as follows:

When considering the standard case where $\beta = 1$, Eq (5.34) can be expressed in the following form:

Hence, these expressions above correspond to the exact solutions of the IVPs (5.25) and (5.26) in ordinary derivative:

where $[\omega]_{\wp} = \Big[\frac{24}{25}+\frac{1}{25}\wp, \frac{101}{100}+\frac{1}{100}\wp\Big]$.

Case 2: If $\psi(t)$ is an $(2;\beta)$-FCD function, we can represent the crisp system of fuzzy conformable IVPs (5.23) and (5.24) using the following form:

subject to the following F-ICs:

By employing the L-RPSM, the FCL transform of the crisp system described in Eq (5.36) can be expressed as:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

In a similar vein, we can depict the fuzzy series solutions of the expansions presented in Eq (5.38) in the following manner:

and the FCL residual functions of the crisp system in Eq (5.38) is represented as:

By performing the substitution of the series solution expansions from Eq (5.39) into the FCL residual functions described in Eq (5.40), we obtain the following representation:

Given that $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$, the recurrence relation that determines the values of the coefficients $\Im_m$ and $\ell_m, \ m = 0, 1, 2, \ldots$ can be expressed as:

and

Compute the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$, and then substitute them back into Eq (5.39). This process results in the solutions of Eq (5.38) in FCL space, expressed in the following series form:

Upon applying the inverse FCL transform to the expansions provided in Eq (5.44), and subsequently rearranging the terms, we can present the exact solutions of IVPs (5.36) and (5.37) in the original space as follows:

In the case of $\beta = 1$, Eq (5.45) can be expressed in the following form:

which are equivalent to the exact solutions of the IVPs (5.36) and (5.37) in ordinary derivative:

where $[\omega]_{\wp} = \Big[\frac{24}{25}+\frac{1}{25}\wp, \frac{101}{100}+\frac{1}{100}\wp\Big]$. Figure 3 presents the surface graphs of the solutions of Application 2 for both cases at different values of $\beta$. Numerical simulation of the solutions is performed of Application 2 for both cases at different values of $\wp$ and $\beta$ with some selected grid points on the interval $[0, 1]$ as shown in Table 2.

Application 3. (^[31,32]) Consider the following fuzzy conformable fractional IVPs

subject to the following F-IC:

where $\wp\in[0, 1]$.

Case 1: If $\psi(t)$ is $(1;\beta)$-FCD, then the crisp system of the fuzzy conformable fractional IVPs (5.47) and (5.48) can be written in the following form:

subject to the following F-ICs:

According to Algorithm 1, the initial step involves applying the FCL transform to the crisp system described in Eq (5.49). The resulting transformed form can be represented as:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

In this orientation as well, the fuzzy series solutions of the expansions in Eq (5.51) can be written as:

and the FCL residual functions of the crisp system in Eq (5.51) is represented as:

Substitute the expansions of series solution in Eq (5.52) into the FCL residual functions in Eq (5.53), respectively, as:

Since $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$, the recurrence relation which determines the values of the coefficients $\Im_m$ and $\ell_m, \ m = 0, 1, 2, \ldots$ given by:

and

Compute and substitute the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ back into Eq (5.52) to have the solutions of Eq (5.51) in FCL space as following series form:

Employ the inverse FCL transform into the expansions in Eq (5.57) to have the exact solutions of IVPs (5.49) and (5.50) in original space as follows:

For the standard case $\beta = 1$, Eq (5.58) have the following form:

which are equivalent to the exact solutions $[\psi(t)]_{\wp} = \frac{1}{2}[\wp-1, 1-\wp]\big(3e^{t^2}-1\big)$ of the IVPs (5.49) and (5.50) in ordinary derivative.

Case 2: If $\psi(t)$ is $(2;\beta)$-FCD, then the crisp system of the fuzzy conformable fractional IVPs (5.47) and (5.48) can be written in the following form:

subject to the following F-ICs:

The FCL transform of the crisp system in Eq (5.60) takes the form:

where $\underline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\underline{\psi}_\wp(t)\Big]$ and $\overline{\Psi}_\wp(s) = \mathfrak{L}_\beta\Big[\overline{\psi}_\wp(t)\Big]$.

Let us represent the fuzzy series solutions of the expansions in Eq (5.62) in the following arrangement:

and the FCL residual functions of the crisp system in Eq (5.62) is represented as:

Substitute the expansions of series solution in Eq (5.63) into the FCL residual functions in Eq (5.64), respectively, as:

Considering that $\underline{LRes}_\wp(s) = 0$ and $\overline{LRes}_\wp(s) = 0$, the coefficients $\Im_m$ and $\ell_m, \ m = 0, 1, 2, \ldots$ can be determined through the following recurrence relation:

and

By computing and substituting the values of the coefficients $\Im_m$ and $\ell_m, \ m = 1, 2, \ldots$ back into Eq (5.63), we can express the solutions of Eq (5.62) in FCL space as the following series form:

Employ the inverse FCL transform into the expansions in Eq (5.68) to have the exact solutions of IVPs (5.60) and (5.61) in original space as follows:

For the standard case $\beta = 1$, Eq (5.69) have the following form:

which are equivalent to the exact solutions $[\psi(t)]_{\wp} = \frac{1}{2}[\wp-1, 1-\wp]\big(3e^{-t^2}-1\big)$ of the IVPs (5.60) and (5.61) in ordinary derivative.

Figure 4 presents the surface graphs of the solutions of Application 3 for both cases at $\beta = 1$. Figure 5 provides the 2D graphs of the solutions of Application 3 at $\beta = 1$ for different values of $\wp$. The 2D graphs of the solutions at $\wp = 0.5$ and different values of $\beta$ is performed of Application 3 as shown in Figure 6.

6.   Conclusions

In this paper, we focused on using the fuzzy conformable derivative in fractional fuzzy equations instead of other conventional FDs, such as the Caputo derivative. The solutions obtained through this approach exhibited smoothness and closely resembled ordinary derivatives. Moreover, the mathematical calculations involved in finding these solutions were relatively simpler compared to equations employing other types of FDs. This is because the fuzzy conformable FD offers several advantages.

Furthermore, we used a new algorithm to find a series of solutions to initial problems on FFDEs in the sense of strongly generalized differentiability. We chose the L-RPSM method, which was successful in finding an exact solution in general. The results show that the power series analysis method is a powerful and easy-to-use analytic tool to solve IVPs on FFDEs in the conformable sense.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors sincerely thank the referees for carefully reading the manuscript and for valuable helpful suggestions. This research is funded fully by Zarqa University-Jordan.

Conflict of interest

No potential conflict of interest was reported by the authors.