Global analysis of a diffusive Cholera model with multiple transmission pathways, general incidence and incomplete immunity in a heterogeneous environment

1.   Introduction

Cholera is an emergency enteric epidemic induced by Vibrio cholerae (V. cholerae), and transmission of this disease is greatly compounded by interactions among host, pathogen, and environment. More specially, it can be transmitted by drinking or eating unpasteurized food or water infected with V. cholerae, by touching people with Cholera, hands and objects contaminated with the carrier's excreta, and by eating food contaminated with flies ^[1,2]. Symptoms such as vomiting, leg cramps, and diarrhea can occur within 12 hours to five days after infection. World Health Organization (WHO) assessed that between 1.3 and 4 million incidences of Cholera occur and between 21,000 and 143,000 die annually, with children in Africa and Southeast Asia being the most impacted ^[3]. Cholera can also break out commonly in countries with weak infrastructure and health systems, such as, Yemen, where 1,115,378 cases of suspected Cholera as well as 2310 deaths were reported between April 2017 and July 2018 ^[4]. The treatment methods for controlling Cholera include vaccines, rehydration therapy, and antibiotics. At present, vaccines are extensively used in certain areas; for example, Haiti successfully controlled the Cholera outbreak with the vaccine in 2020 ^[5].

Dynamical models have contributed to an essential role in gaining insight into the transmission mechanism, development process, and transmission pattern of Cholera, providing a contribution to the defense and management of strategic diseases. To date, a large number of scholars have devoted themselves to the study of Cholera (see, e.g., ^{[6,7,8,9,10,11]}), and the majority of models are characterized by ordinary/partial differential equations. The research contents include the nonnegative and boundedness of solutions, the persistence and extinction of this disease, bifurcation and chaotic phenomena, etc. In particular, Teytsa et al. ^[12] established the influence of phage bacterial invasion and optimal control on indirect transmission of Cholera disease by demonstrating that the release of lytic phages dramatically reduced the transmission of disease. Vaccines have always performed an active role in controlling and eradicating diseases, and this is also true for Cholera. For instance, Lin et al. ^[13] presented a Cholera model with high infectivity, low infectivity, and incomplete immunity, characterized the global dynamics of the equilibria, and simulated the Cholera epidemic in Haiti. In addition, there have also been numerous proposals for Cholera models with age structure ^[14], patch model ^[7], multiple disease stages ^[15], and so on. The relevant researches are still continuing.

As we all know, the propagation of Cholera is closely linked to numerous factors, for example, environmental sanitation, water and food resources, personal habits, and spatial heterogeneity. Lately, several reaction-diffusion models with environmental heterogeneity were developed to explore effective control strategies to eliminate this disease ^[16,17,18]. Specifically, Wang et al. ^[19] introduced a model in a closed environment and conducted a bifurcation analysis of the steady-state solution, which showed that spatial heterogeneity of model parameters can generate backward bifurcation. Avila-Vales et al. ^[20] proposed a $SIR$ model with saturation incidence and Holling type Ⅱ treatment, and theoretical results suggest that heterogeneity in transmission rates produces bifurcation, which leads to disease persistence. In ^[21,22,23], authors presented some reaction-diffusion models and attained $\mathcal{R}_{0}$, which examined the presence as well as global stability of steady states. Wang et al. ^[24] established a reaction-convection-diffusion model based on the high infectivity of bacteria, and revealed that ignoring high infectivity underestimates the risk of illness propagation. Wang et al. ^[25] also developed a Cholera transmission model with high bacterial infectivity and different diffusion rates, assuming different transmission rates for susceptible and infected individuals, which showed that by controlling the mobility of susceptible individuals, the illness would be eradicated to some extent.

Motivated by the previous works, in this article, a reaction-diffusion model of Cholera transmission with horizontal/environmental propagation as well as general incidence is proposed, where the incomplete immunity, Holling Ⅱ treatment rates, different diffusion rates, and environmental viruses are also introduced. The remaining sections of this article are structured below: In Sections 2 and 3, the model is established and the well-posedness of the model is analyzed. The basic reproduction number is presented and the global stability of disease-free steady state and the persistence of disease is analyzed in Section 4. The positive steady state of the model is investigated in Section 5 from the branching theory point of view. Some numerical simulations and a short summary are given in Sections 6 and 7, respectively.

2.   Mathematical model

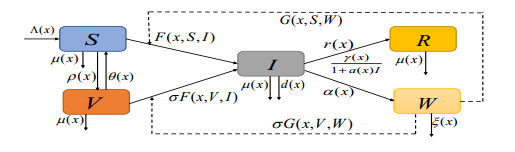
Following the pattern of Cholera transmission, the population of a given area is divided as: susceptible, vaccinated, infected, and recovered individuals are represented by $S(x, t)$, $V(x, t)$, $I(x, t)$, and $R(x, t)$, respectively. Further, the concentration of pathogen particles is represented by $W(x, t)$. The corresponding flow chart for Cholera propagation is shown in Figure 1. Based on the variability of Cholera spreading routes and the restricted diffusion of V. cholerae in the environment, the partially degenerate reaction-diffusion model is described by

and

subject to the boundary conditions

and initial conditions $S(0, x) = S_{0}(x)$, $V(0, x) = V_{0}(x)$, $I(0, x) = I_{0}(x)$, $V(0, x) = V_{0}(x)$, $R(0, x) = R_{0}(x)$, $W(0, x) = W_{0}(x)$, $x\in\mathbb{D}$, where $\mathbb{D}$ is a connected, bounded subset of $\mathbb{R}^{n}$ with smooth boundary $\partial\mathbb{D}$. The means of other model parameters are as: $d_{1}$, $d_{2}$, $d_{3}$, $d_{4} > 0$ stand for the diffusion rates measuring the movement for susceptible, vaccinated, infected, and recovered individuals, respectively; $\Lambda(x)$, $\mu(x)$, $d(x)$, $\rho(x)$, $\theta(x)$ stand for the population replenishment rate, the natural mortality rate, the disease-related mortality rate, the vaccination rate, and the rate of loss of immunization, respectively; $r(x)$ denotes the natural recovery rate; $\alpha(x)$ represents the bacterial shedding rate of infected individuals and $\xi(x)$ stands for the decay rate of bacteria; $\gamma(x)/(1+a(x))$ denotes the treatment function, where $\gamma(x)$ stands for the maximum treatment rate per individual per unit of time, and $a(x)$ represents the influence of delayed treatment in infected individuals; $\sigma$ denotes the reduction of vaccine efficacy; $F(x, S, I)$ and $G(x, S, W)$ indicate general incidence functions responding to direct transmission from infected individuals to susceptible individuals and indirect transmission from environmental viruses to susceptible individuals, respectively; $F(x, V, I)$ and $G(x, V, W)$ correspond to transmission between vaccinated individuals and infected individuals and between vaccinated individuals and environmental viruses, respectively.

As model (2.1) does not contain the variable $R$, one can overlook the $R$-equation and restrict attention to the kinetic behavior of model (2.1). In light of the model's biological context, all parameters are hypothesized to be positive, continuous, and bounded on $\overline{\mathbb{D}}$. Moreover, let us hypothesize that the functions $F$ and $G$ fulfill the under mentioned cases.

($\mathrm{H}_1$) For $x\in \overline{\mathbb{D}}$ and $S, \ V, \ I\geqslant0$, $F(x, S, 0) = F(x, 0, I) = 0$, $F(x, V, 0) = F(x, 0, I) = 0$ and $\partial F(x, S, I)/\partial I > 0$, $\partial F(x, V, I)/\partial I > 0$, $\partial^{2} F(x, S, I)/\partial I^{2}\leqslant0$, $\partial^{2} F(x, V, I)/\partial I^{2}\leqslant0$.

($\mathrm{H}_2$) For $x\in \overline{\mathbb{D}}$ and $S, \ V, \ W\geqslant0$, $G(x, S, 0) = G(x, 0, W) = 0$, $G(x, V, 0) = G(x, 0, W) = 0$; $\partial G(x, S, W)/\partial W > 0$, $\partial G(x, V, W)/\partial W > 0$, and $\partial^{2} G(x, S, W)/\partial W^{2}\leqslant0$, $\partial^{2} G(x, V, W)/\partial W^{2}\leqslant0$.

($\mathrm{H}_3$) There are Hölder continuous functions $\beta_{i}: \mathbb{D}\rightarrow \mathbb{R}_{+}$ that satisfy $F(x, y, I)\leqslant \beta_{1}(x)yI$, $G(x, y, W)\leqslant\beta_{2}(x)yW$, $y\in\{S, V\}$, for $x\in\mathbb{D}$, $S, \ I, \ V, \ W\geqslant0$.

Remark 2.1. Some frequently used incidences satisfy $(\mathrm{H}_{1})$ and $(\mathrm{H}_{2})$, such as the bilinear incidence rates $F(x, S, I) = \beta_{1}(x)SI$, $G(x, S, W) = \beta_{2}(x)SW$ (see ^[7,15]); the saturated incidence rates $F(x, S, I)$ $= {\beta_{1}(x)SI}/{(\kappa_{1}(x)+I)}$, $G(x, S, W) = {\beta_{2}(x)SP}/{(\kappa_{2}(x)+P)}$ (see ^[26]), where $\beta_{i}(x), \kappa_{i}(x) > 0$, $i = 1, 2$. The condition $(\mathrm{H}_{3})$ is given to better prove the fitness of solution. At the same time, we also find that the above common incidence also satisfies the condition $(\mathrm{H}_{3})$.

3.   Well-posedness

Let $\mathbb{X}: = C(\overline{\mathbb{D}}, \mathbb{R}^{4})$ be the Banach space, and define $\mathbb{X}^{+}: = C(\overline{\mathbb{D}}, \mathbb{R}_{+}^{4})$. Set $\psi^{+}: = \max_{x\in\overline{\mathbb{D}}}\{\psi(x)\}$, $\psi^{-}: = \min_{x\in\overline{\mathbb{D}}}\{\psi(x)\}$, where $\psi$ represents any of $\Lambda$, $\mu$, $\rho$, $\theta$, $r$, $\gamma$, $a$, $\alpha$, $\xi$.

To do so, denote $\pi_{1}(x) = \rho(x)+\mu(x)$, $\pi_{2}(x) = \theta(x)+\mu(x)$, $\pi_{3}(x) = d(x)+r(x)+\mu(x)$, and $\pi_{4}(x) = \xi(x)$, and let $\Gamma_{i}(t):C(\overline{\mathbb{D}}, \mathbb{R})\rightarrow C(\overline{\mathbb{D}}, \mathbb{R})$ $(i = 1, 2, 3)$ be the $C_{0}$ semigroup related to $d_{i}\Delta-\pi_{i}(x)$ satisfying the Neumann boundary condition. Hence,

where $T_{i}(x, t, y)$ denotes the Green function related to $d_{i}\Delta-\pi_{i}(x)$ satisfying (2.2). Further, let $(\Gamma_{4}(t)\phi)(x) = e^{-\pi_{4}(x)t}\phi(x)$. Thus, $\Gamma(t): = diag\{\Gamma_{1}(t), \Gamma_{2}(t), \Gamma_{3}(t)$, $\Gamma_{4}(t)\}:\mathbb{X}\rightarrow \mathbb{X}$, $t\geqslant0$, which formulates a strongly continuous semigroup ^[27].

For every $\phi = (\phi_{1}, \phi_{2}, \phi_{3}, \phi_{4})^{T}\in\mathbb{X}^{+}$, define $Z = (Z_{1}, Z_{2}, Z_{3}, Z_{4})^{T}:\mathbb{X}^{+}\rightarrow \mathbb{X}$ by

where $T$ denotes the transposition. Hence, model (2.1) can be reformulated as

In the results below, the local solutions of model (2.1) with (2.2) on $\mathbb{X}^{+}$ are involved.

Lemma 3.1. For $\phi\in\mathbb{X}^{+}$, model (2.1) possesses a unique solution $u(\cdot, t, \phi): = (S(\cdot, t), V(\cdot, t), I(\cdot, t)$, $W(\cdot, t))$ on $[0, \tau_{\max})$ with $u(\cdot, 0, \phi) = \phi$, where $\tau_{max}\leqslant\infty$. Moreover, $u(\cdot, t, \phi)\in\mathbb{X}^{+}$, $0\leqslant t < \tau_{\max}$.

Proof. For $h\geqslant0$, one obtains

which means for $\phi\in\mathbb{X}^{+}$, $\lim_{h\rightarrow0^{+}} \text{dist}(\phi+h\Gamma(\phi), \mathbb{X}^{+}) = 0$. Based on Ref. [28, Corollary 4], model $(2.1)$ is a unique mild solution ($S(x, t)$, $V(x, t)$, $I(x, t)$, $W(x, t)$) on $[0, \tau_{\max})$, where $\tau_{\max}\leqslant\infty$. □

Consider the model as below

where $d > 0$, $b(x) > 0$, and $c(x) > 0$ are continuous.

Lemma 3.2 (Lemma 1 in Ref. ^[29]). Model (3.2) possesses a globally asymptotically stable steady state $\hat{\omega}(x)$ in $C(\overline{\mathbb{D}}, \mathbb{R}_{+})$. Further, if $b(x)\equiv b$, $c(x)\equiv c$, $\forall x \in \overline{\mathbb{D}}$, then $\hat{\omega}(x) = b/c$.

Next, one proves that the local solution of model (2.1) can be expanded to the global solution, i.e., $\tau_{\max} = \infty$.

Lemma 3.3. For every $\phi\in\mathbb{X}^{+}$, model (2.1) has a unique solution $u(x, t)$ with $u(x, 0, \phi) = \phi$ for $[0, \infty)$. Moreover, the model generates a semiflow $\Phi(t)$ as ultimately bounded.

Proof. In terms of the first two equations of the model (2.1), one can readily derive that

Hence,

which implies $\|S(x, t)\|\leqslant \mathcal{M}_{1}, \ \|V(x, t)\|\leqslant \mathcal{M}_{2}$, for $\mathcal{M}_{1}, \mathcal{M}_{2} > 0$ and $0\leqslant t < \infty$. Hence, one gets that $S(x, t)$ and $V(x, t)$ are ultimately bounded. Adding the three previous equations of (2.1) and integrating with respect to $\mathbb{D}$ gives

where $|\mathbb{D}|$ denotes the measurement of region $\mathbb{D}$. It follows that

with $\mathcal{M}_{11} = \Lambda^{+}|\mathbb{D}|/\mu^{-}$. In a similar way, the $W$-equation satisfies

Thus, one gets

In short, there exists a number $\mathcal{M}_3 > 0$,

Next, let us verify the solution $(I, W)$ of model (2.1) as ultimately bounded. Motivated by [30, Lemma 2.4], for $T > 0$, one needs to justify

where $\mathcal{M}_{2^{k}} > 0$ is a constant.

It immediately follows that for $k = 0$, (3.4) holds. Assuming that (3.4) is valid for $k-1$, i.e.,

The $I$-equation of model (2.1) is multiplied by $I^{2^{k}-1}$ and integrated over $\mathbb{D}$ to derive

Recall that

Hence, inequality (3.6) becomes

where $L_{k} = (2^{k}-1)/(2^{2k-2})$. Due to $\limsup_{t\rightarrow \infty}\|S(x, t)\|\leqslant\mathcal{M}_{1}$, $\limsup_{t\rightarrow \infty}\|V(x, t)\|\leqslant\mathcal{M}_{2}$, there is $t_{0} > 0$ satisfying when $t\geqslant t_{0}$, and one has

By means of Young's inequality: $ab\leqslant\varepsilon a^{p}+\varepsilon^{-\frac{q}{p}}b^{q}$, where $a$, $b$, $\varepsilon > 0$, $1/p+1/q = 1$. By setting $\varepsilon_{1} = \xi^{-}/(4\beta_{2}^{+}(\mathcal{M}_{0}+1))$, $\mathcal{M}_{0} = \max\{\mathcal{M}_{1}, \mathcal{M}_{2}\}$, $p = 2^{k}$, and $q = 2^{k}/(2^{k}-1)$, we have

Thus, (3.7) is reorganized as:

where $C_{k} = \sigma\beta_{1}^{+}(\mathcal{M}_{2}+1)+\sigma\beta_{2}^{+}(\mathcal{M}_{2}+1) +\sigma\beta_{2}^{+}(\mathcal{M}_{2}+1)C_{\varepsilon_{1}}+\beta_{1}^{+}(\mathcal{M}_{1}+1)+\beta_{2}^{+}(\mathcal{M}_{2}+1)C_{\varepsilon_{1}}$.

Similarly, multiplying the $W$-equation with $W^{2^{k}-1}$, one yields

By choosing $p = 2^{k}/(2^{k}-1)$ and $q = 2^{k}$, we have

where $\varepsilon_{2} = \xi^{-}/4\alpha^{+}$, $C_{\varepsilon_{2}} = \varepsilon_{2}^{1-2^{k}}$. Hence, (3.11) becomes

Adding (3.10) and (3.13), one has

where $Q_{k} = \alpha^{+}C_{\varepsilon_{2}}+C_{k}$. Applying the interpolation inequality,

Let $\varepsilon_{3} = L_{k}/(2Q_{k})$, $\zeta = I^{2^{k-1}}$, then

Therefore, inequality (3.14) becomes

where $\varsigma_{*} = \min\{Q_{k}, {\xi^{-}}/{4}\}$. It follows from (3.5) that $\limsup_{t\rightarrow \infty}\int_{\mathbb{D}}I^{2^{k-1}}\mathrm{d}x\leqslant\mathcal{M}_{2^{k-1}}^{2^{k-1}}$, which means

Therefore, by the continuous embedding $L^{q}(\mathbb{D})\hookrightarrow L^{p}(\mathbb{D})$, one has

where $\mathcal{M}_{p} > 0$ is a constant. The fractional power space is represented by $Y_{a}\ (0\leqslant a\leqslant1)$. By Ref. [30, Lemma 2.4], one gets that $Y_{a}\subset C(\overline{\mathbb{D}})$ by choosing $p > n/2$ and $a\geqslant n/2p$. Thus, we can get

which demonstrates that Lemma 3.3 is valid. □ Let

then $\Phi(t)\phi\in{\bf D}$, $t\geqslant t_{1}$, for some $t_{1}\geqslant0$. In addition, in analogy to the approach in Ref. [31, Theorem 2.1], we learn for set $\mathcal{V}\subset\mathbb{X}^{+}$, $\Phi(t)\phi\in{\bf D}$, $t\geqslant t_{2}$, for $t_{2}\geqslant0$.

As the last equation of model (2.1) has no diffusion, the weak compactness of solution semiflow $\Phi(t)$ is hard to obtain, and we substitute the weak compactness with the asymptotic smoothness of the solution semiflow. At first, one defines the Kuratowski measure of noncompactness, $\tau(\cdot)$,

for set $\mathcal{V}\subset\mathbb{X}^{+}$. It's convenient to deduce that $\mathcal{V}$ is precompact if and only if $\kappa(\mathcal{V}) = 0$.

Denote ${\bf x}: = (S, V, I)$, ${\bf y}: = (W)$, and ${\bf g}(x, t, {\bf x}, {\bf y}) = -\alpha(x)I-\xi(x)W$. Taking the partial derivative of ${\bf g}(x, t, {\bf x}, {\bf y})$ relative to ${\bf y}$ yields

Lemma 3.4. In case there exists $q > 0$ satisfying

then $\Phi(t)$ is $\kappa$-contracting, i.e., $\lim_{t\rightarrow \infty}\kappa(\Phi(t)\mathcal{V}) = 0$ for set $\mathcal{V}\subset\mathbb{X}^{+}$.

Proof. In a similar way to [32, Lemma 4.1], we can demonstrate that $\Phi(t)$ is asymptotically compact on $\mathcal{V}$, i.e., for $t_{n}\rightarrow \infty$ and any sequence $\phi_{n}\in\mathcal{V}$, a subsequence $t_{n_{k}}\rightarrow \infty$ and $\phi_{n_{k}}$ satisfying $\Phi(t_{n_{k}})\phi_{n_{k}}$ converges to $k\rightarrow \infty$ in $\mathbb{X}$. Further, we define $\omega(\mathcal{V}) = \{\phi\in\mathbb{X}^{+}:\lim_{k\rightarrow \infty}\Phi(t_{n_{k}})\phi_{n_{k}} = \phi \ \text{for some sequences}\ \phi_{n_{k}}\in\mathcal{V}\}$ to be the omega limit set of $\mathcal{V}$. Based on [33, Lemma 23.1(2)], one learns that $\omega(\mathcal{V})$ is an invariant set, compact, nonempty in $\mathbb{X}^{+}$, and $\omega(\mathcal{V})$ attracts $\mathcal{V}$. Based on [34, Lemma 2.1(b)], one has

where $\text{dist}(\Phi(t)\mathcal{V}, \omega(\mathcal{V}))$ represents the distance from $\Phi(t)\mathcal{V}$ to $\omega(\mathcal{V})$. Therefore, $\Phi(t)$ is $\kappa$-contracting. It finishes the proof. □

Combining [35, Theorem 1.1.3(b)], Lemmas 3.3 and 3.4, the below result can be derived.

Theorem 3.1. The solution semiflow $\Phi(t):\mathbb{X}^{+}\rightarrow \mathbb{X}^{+}$ of model (2.1) has a global attractor.

4.   Threshold dynamics

4.1.   Basic reproduction number

It is now clear that model (2.1) has a disease-free steady state $\mathcal{E}_{0} = (S^{0}(x), V^{0}(x), 0, 0)$ satisfies

The linearized subsystem of (2.1) at $\mathcal{E}_{0}$ is

Under assumption $(\mathrm{H}_1)$ and $(\mathrm{H}_2)$, the linear system (4.1) is cooperative. Denote $\mathcal{T}(t)$ to be the solution semiflow of (4.1) on $C(\overline{\mathbb{D}}, \mathbb{R}^{2})$, where operators are

Allow us to denote $\tilde{\mathcal{T}}$ as the positive semigroup generated by $\mathcal{B}$. According to [37, Theorem 3.12], one gives the next generator operator

Define the spectral radius of $\mathcal{L}$ as the basic reproduction number $\mathcal{R}_{0}$, i.e.,

Similar to Refs. [36, Lemma 2.2] and ^[37], the below consequence is valid.

Lemma 4.. $\mathcal{R}_{0}-1$ has the identical sign to $s(\mathcal{A})$, where $s(\mathcal{A}) = \sup\{|\lambda|, \lambda\in\sigma(\mathcal{L})\}\}$ is the spectral bound of $\mathcal{A}$.

Lemma 4.2. Let $\tilde{\lambda}_0$ satisfy

with $\partial \phi/\partial n = 0$, $x\in\partial\mathbb{D}$, then $\mathcal{R}_{0} = 1/\tilde{\lambda}_{0}$.

Proof. $\mathcal{F}\mathcal{B}^{-1}$ is calculated to give

where

Due to

therefore, $\mathcal{R}_{0}$ is the principle eigenvalue of

In other words,

It finishes the proof. □

Remark 24.1. Following Lemma 4.2, $\mathcal{R}_{0}$ can be shown by the variational approach of the form

Remark 4.2. Assuming that all parameters of (2.1) are independent of $x$ yields

In particular, if

then

which will be used in our numerical simulation.

Lemma 4.3. If $\mathcal{R}_{0}\geqslant1$ $(s(\mathcal{A})\geqslant0)$, $s(\mathcal{A})$ is the principal eigenvalue of problem

associated with a strongly positive eigenfunction.

Proof. According to (4.1), it can be derived that

where $\mathcal{P}(x, I, W) = F(x, \phi_{1}, \phi_{3})+G(x, \phi_{1}, \phi_{4})+\sigma F(x, \phi_{2}, \phi_{3})+\sigma G(x, \phi_{2}, \phi_{4})-\gamma(x)\phi_{3}/(1+a(x)\phi_{3})$.

We rewrite $\tilde{\mathcal{T}}(t)$ as $\tilde{\mathcal{T}}(t) = \tilde{\mathcal{T}}_{3}(t)+\tilde{\mathcal{T}}_{4}(t)$, where $\phi = (\phi_{3}, \phi_{4})\in C(\overline{\mathbb{D}}, \mathbb{R}^{2})$,

Similar to Ref. [30, Lemma 2.5], $\bar{\mathcal{T}}_{4}(t)$ is tight. Therefore, it yields from (4.7) that

As a consequence, for every set $\mathcal{A}$ in $C(\overline{\mathbb{D}}, \mathbb{R}^{2})$, one has

From the above inequality, $\mathcal{T}$ is a $\tau$-contraction on $C(\overline{\mathbb{D}}, \mathbb{R}^{2})$ with contraction function $e^{-\xi^{-}t}$, i.e., the essential spectra radius, $\omega_{ess}(\mathcal{T}(t))\leqslant-\xi^{-}$. Because $\omega_{ess}(\mathcal{T}(t))$ is defined as $\omega_{ess}(\mathcal{T}(t)): = \lim_{t\rightarrow \infty}\vartheta(\mathcal{T}(t))/t$, $\vartheta$ is the measure of non-compactness.

As is well known (see Ref. ^[38]) $\omega = \max\{s(\mathcal{A}), \omega_{ess}(\mathcal{T}(t))\},$ where $\omega: = \lim_{t\rightarrow \infty}\ln\|\mathcal{T}(t)\|/t$ is the exponential growth bound of $\mathcal{T}(t)$ such that $\|\mathcal{T}(t)\|\leqslant\mathcal{M}e^{\omega t}$, for $\mathcal{M} > 0$. In addition, the spectral radius $r(\mathcal{T}(t))$ of $\mathcal{T}(t)$ fulfills

which means that $\omega(\mathcal{T}(t)) < r(\mathcal{T}(t))$, $t > 0$. Thanks to the generalized Krein-Rutman Theorem (see, Ref. [39, Lemma 2.2]), this concludes the proof. □

4.2.   Stability of steady states

Throughout this subsection, one concentrates on obtaining threshold results for model (2.1) in terms of $\mathcal{R}_{0}$. To begin with, one gives the stability $\mathcal{E}_{0}$ for $\mathcal{R}_{0} < 1$.

Theorem 4.1. If $\mathcal{R}_{0} < 1$ $($or $s(\mathcal{A}) < 0$$)$, the $\mathcal{E}_{0}$ is locally asymptotically stable. Further, if $\gamma(x) = 0$, then $\mathcal{E}_{0}$ is globally asymptotically stable for $\mathcal{R}_0 < 1$.

Proof. By analogy with Ref. [36, Theorem 3.1], it is clear that $\mathcal{E}_{0}$ is locally asymptotically stable for $\mathcal{R}_{0} < 1$, so we just need to prove the global attraction of $\mathcal{E}_{0}$ with $\gamma(x) = 0$ in this case. Fix $\epsilon_{0} > 0$. From (3.3), there exists $t_{1} > 0$ fulfilling that as $t\geqslant t_{1}$, $0\leqslant S(x, t)\leqslant S^{0}(x)+\epsilon_{0}$, $0\leqslant V(x, t)\leqslant V^{0}(x)+\epsilon_{0}$. With the help of the comparison principal yields $(I(x, t), W(x, t))\leqslant(\hat{I}(x, t), \hat{W}(x, t))$ on $\overline{\mathbb{D}}\times[t_{1}, \infty)$, where $(\hat{I}(x, t), \hat{W}(x, t))$ meets

with $\hat{I}(x, t_{1}) = I(x, t_{1})$, $\hat{W}(x, t_{1}) = W(x, t_{1})$, $x\in\mathbb{D}$. For adequately small $\epsilon_{0} > 0$, $s(\mathcal{A}_{\epsilon_{0}}) < 0$ as $s(\mathcal{A}) < 0$, as well as a corresponding eigenvector $(\psi_{3}^{\epsilon_{0}}, \psi_{4}^{\epsilon_{0}}) > (0, 0)$. Assume that for $\phi\in\mathbb{X}^{+}$, one obtains $(I(x, t_{1}, \phi), W(x, t_{1}, \phi))\leqslant\iota(\psi_{3}^{\epsilon_{0}}(x), \psi_{4}^{\epsilon_{0}}(x))$ for $x\in\overline{\mathbb{D}}$, $\iota > 0$. Further, we can arrive at

Thus, $\lim_{t\rightarrow \infty}I(x, t) = 0$, $\lim_{t\rightarrow \infty}W(x, t) = 0$ uniformly for $x\in\overline{\mathbb{D}}$. Furthermore, one can derive $\lim_{t\rightarrow \infty}S(x, t) = S^{0}(x)$, $\lim_{t\rightarrow \infty}V(x, t) = V^{0}(x)$ uniformly for $x\in\overline{\mathbb{D}}$. It finishes the proof. □

Theorem 4.2. Suppose that $\mathcal{R}_{0} > 1$ $($or $s(\mathcal{A}) > 0$$)$. There exists $\varepsilon > 0$ satisfying $u_{0} = (S_{0}(x), V_{0}(x)$, $I_{0}(x), W_{0}(x))\in\mathbb{X}^{+}$ with $I_{0}(x)\not\equiv0$ or $W_{0}(x)\not\equiv0$, then $u(x, t, u_0) = (S(x, t), V(x, t)$, $I(x, t), W(x, t))$ satisfies $\liminf_{t\rightarrow \infty}u(x, t; u_0)$ $\geqslant(\varepsilon, \varepsilon, \varepsilon, \varepsilon)$, uniformly for $x\in\overline{\mathbb{D}}$. Moreover, at least one endemic steady $\mathcal{E}^{*}$ is included in the model (2.1).

Proof. Let $\mathbb{X}_{0}: = \{\phi\in\mathbb{X}^{+}:\phi_{3}(x)\not\equiv0 \, \, \text{and} \, \, \phi_{4}(x)\not\equiv0\}$, $\partial \mathbb{X}_{0}: = \mathbb{X}^{+}\backslash\mathbb{X}_{0} = \{\phi\in\mathbb{X}^{+}: \phi_{3}(x)\equiv0\, \, \text{or}\, \, \phi_{4}(x)\equiv0\}$, $\mathcal{M}_{\partial}: = \{\phi\in\partial\mathbb{X}_{0}:\Phi(t)\phi\in\partial\mathbb{X}_{0}, \ t\geqslant0\}$, where $\Phi(t):\mathbb{X}^{+}\rightarrow \mathbb{X}^{+}$ is the semiflow generated by model (2.1). Clearly, $\mathbb{X}^{+} = \mathbb{X}\cup\partial \mathbb{X}_{0}$, where $\mathbb{X}_{0}$ is relatively open in $\mathbb{X}^{+}$. Next, we will finish the proof with three claims.

● Claim 1. For $t\geqslant 0$, $\Phi(t)\mathbb{X}_{0}\subseteq \mathbb{X}_{0}$.

Due to $u_{0} = (S_{0}(x), V_{0}(x), I_{0}(x), W_{0}(x))\in\mathbb{X}_{0}$, then $I_{0}(x)\not\equiv0$ and $W_{0}(x)\not\equiv0$. Let $\check{I}$ fulfill the following equation

with $\check{I}(x, 0) = I(x, 0) = I_{0}(x)$, $x\in\mathbb{D}$. From the maximum principal and $I_{0}(x)\not\equiv0$, one has $\check{I}(x, t) > 0$, for $x\in\overline{\mathbb{D}}$, $t > 0$. Further, it yields from $\partial I/\partial t\geqslant d_{3}\Delta I-(\mu(x)+d(x))I-\gamma(x)I/(1+a(x)I)$ and the comparison principal that $I(x, t)\geqslant\check{I}(x, t) > 0$ $x\in\overline{\mathbb{D}}$, $t > 0$. Further, by the $W$-equation of (2.1), one derives

This means that for $x\in\overline{\mathbb{D}}$, $t > 0$, $W(x, t) > 0$. Thus, $\Phi(t)u_{0}\in\mathbb{X}_{0}$, that is, the conclusion in Claim 1 is valid.

● Claim 2. For all $\phi\in\mathcal{M}_{\partial}$, $\omega(u_{0}) = \{(S^{0}(x), V^{0}(x), 0, 0)\}$, where $\omega(u_{0})$ denotes the omega limit set of the orbit $\gamma^{+}(u_{0}): = \{\Phi(t)u_{0}:t\geqslant0\}$.

If $\phi\in\mathcal{M}_{\partial}$, we have $\Phi(t)\phi\in\partial\mathbb{X}_{0}$, i.e., $I(x, t)\equiv0$ or $W(x, t)\equiv0$. For the former case, based on the $W$-equation in model (2.1), we still have $\lim_{t\rightarrow \infty}W(x, t) = 0$ uniformly for $x\in\overline{\mathbb{D}}$. Consequently, from the previous two equations of model (2.1), one derives that $\lim_{t\rightarrow \infty}S(x, t) = S^{0}(x)$, $\lim_{t\rightarrow \infty}V(x, t) = V^{0}(x)$ uniformly for $x\in\overline{\mathbb{D}}$. For the latter case, $I(x, t^{*})\not\equiv0$ and $W(x, t^{*})\equiv0$ for some $t^{*} > 0$, utilizing the parabolic maximum principal in the $I$-equation of model (2.1), then $I(x, t) > 0$ for $x\in\overline{\mathbb{D}}$ and $t > t^{*}$. However, it is possible to derive $I(x, t)\equiv0$ from the $W$-equation of the model (2.1), where $x\in\overline{\mathbb{D}}$ and $t > t^{*}$; this is a contradiction. Therefore, we can also conclude that $\lim_{t\rightarrow \infty}S(x, t) = S^{0}(x)$, $\lim_{t\rightarrow \infty}V(x, t) = V^{0}(x)$ uniformly for $x\in\overline{\mathbb{D}}$. Thus, $\partial\mathcal{M}_{0}$ is positively invariant relative to $\Phi(x)$.

● Claim 3. $\forall \phi\in\mathbb{X}_{0}$, $\limsup_{t\rightarrow \infty}\|\Phi(t)\phi-\mathcal{E}_{0}\|\geqslant\delta_{0}$.

Thanks to the continuity of the principal eigenvalues $\lambda$, there is a small enough number $\varepsilon_{0} > 0$ meeting $\lambda(\varepsilon_{0})+\varepsilon_{0} < 0$, where $\lambda(\varepsilon_{0})$ satisfies

and $\psi_{\varepsilon_{0}}$ is the positive eigenvector corresponding to $\lambda(\varepsilon_{0})$. Assume that Claim 3 is not valid, then for any $0 < \varepsilon_{1} < \varepsilon_{0}$, $\limsup_{t\rightarrow \infty}\|\Phi(t)\phi-\mathcal{E}_{0}\| < \varepsilon_{1}$. So, for $x\in\overline{\mathbb{D}}$ and $t > t_{1} > 0$,

Assumptions $(\mathrm{H}_1)$ and $(\mathrm{H}_2)$ yield

for all $x\in\overline{\mathbb{D}}$. Therefore, for $(S_{0}(x), V_{0}(x), I_{0}(x), W_{0}(x))\in\mathbb{X}_{0}$, there is $\eta > 0$ satisfying $I_{0}(x)\geqslant\eta\psi_{\varepsilon_{0}}(x)$. Combining (4.12) and the arbitrariness of $\varepsilon_{0}$, we derive that $I(x, t)$ is the upper solution of the below problem

Evidently, $\eta e^{-\lambda(\varepsilon_{0})}\psi_{\varepsilon_{0}}(x)$ is the only solution to system (4.13). Therefore,

This contradicts Lemma 3.3, which proves the claim.

Comparable to the approach in Ref. ^[27], define $p(x):\mathbb{X}^{+}\rightarrow [0, \infty)$ for the semiflow $\Phi(t)$ as

Similar to Refs. [27, Theorem 3] and [41, Theorem 3.4], there exists a constant $\delta_{1} > 0$ that meets $\min_{\psi\in\omega(\phi)}p(\psi) > \delta_{1}$, for all $\phi\in\mathbb{X}_{0}$, which means that $\liminf_{t\rightarrow \infty} I(x, t)\geqslant\delta_{1}$, $\liminf_{t\rightarrow \infty}W(x, t)\geqslant\delta_{1}$, for $\phi\in\mathbb{X}_{0}$. Hence, there exists $\delta_{2} > 0$ satisfying $\liminf_{t\rightarrow \infty} S(x, t)\geqslant\delta_{2}$, $\liminf_{t\rightarrow \infty}V(x, t)\geqslant\delta_{2}$ for all $x\in\overline{\mathbb{D}}$. Let $\delta = \min\{\delta_{1}, \delta_{2}\}$, then the model is uniformly persistent. By Ref. [34, Remark 3.10 and Theorem 3.7], $\Phi(t):\mathbb{X}_{0}\rightarrow \mathbb{X}_{0}$ has a global attract $\mathcal{E}_{0}$. According to Ref. [34, Theorem 4.7], model (2.1) has one steady state at least $\mathcal{E}^{*} = (S^{*}(x), V^{*}(x), I^{*}(x), W^{*}(x))$. It finishes the proof. □

5.   Bifurcation analysis

Next, using the divergence theory, we will derive a few qualities of positive steady state of model (2.1) by taking the death rate due to disease $d(x) = d$ as a bifurcation parameter. Assuming that $(S(x), V(x), I(x), W(x))$ is the steady state of model (2.1), then

and $W(x) = \alpha(x)I/\xi(x)$. Obviously, $(S^{0}(x), V^{0}(x), 0)$ fulfills the Eq (5.1). Denote $d^{*}$ to be the principal eigenvalue of the below equation

and the corresponding positive eigenfunction $\psi_{0}(x)$ meeting $\max_{x\in\overline{\mathbb{D}}}\psi_{0}(x) = 1$. Moreover, it also realizes that $d = d^{*}$ is equivalent to $\mathcal{R}_{0} = 1$ or $\tilde{\lambda} = 1$. Let

If $\mathcal{L}(x)\equiv \mathcal{L}$ is a constant, then $b^{*} = \mathcal{L}$. In the following, we investigate the scenario where $\mathcal{L}(x)\not\equiv$ is a constant and it may vary in sign in $\mathbb{D}$. Analyze the below problem

By Ref. [42, Theorem 4.2], (5.4) admits a nonzero principal eigenvalue $\Lambda_{0} = \Lambda(\mathcal{L})$ if and only if $\mathcal{L}$ can change the sign and $\int_{\mathbb{D}}\mathcal{L} (x)\mathrm{d}x\not = 0$.

Regarding the sign problem of the principal eigenvalue $d^{*}$, our results are as follows.

Lemma 5.1. The principal eigenvalue $d^{*}$ of (5.4) satisfies the following characteristics

(i) if $\int_{\mathbb{D}}\mathcal{L}(x)\mathrm{d}x\geqslant0$, then $d^{*} > 0$ for all $d_{3} > 0$;

(ii) if $\int_{\mathbb{D}}\mathcal{L}(x)\mathrm{d}x < 0$, then $d^{*} > 0$ for $d_{3} < 1/\Lambda(\mathcal{L})$; $d^{*} < 0$ for $d_{3} > 1/\Lambda(\mathcal{L})$.

Now, we process considering $d$ as the bifurcation parameter and studying the local branch of the positive solution of (5.1), which branches from the branch of $\{(S^{0}(x), V^{0}(x), 0,$ $d):d\geqslant0\}$. At first, from the transformation $u = S$, $\omega = V$, $\nu = I$, Eq (5.1) can rewritten as

For $p > n$, let $\mathcal{X} = \{u, \omega\in W^{2, p}(\mathbb{D}):\partial u(x)/\partial n = \partial \omega(x)/\partial n = 0\}$ and $\mathcal{Y} = L^{p}(\mathbb{D})$. Define

Theorem 5.1. Let $d^{*}$ be the principal eigenvalue of problem (5.1).

(i) There is a connected component $\mathbb{B}_{1}$ of $\overline{\mathbb{B}}$ including $(u, \omega, 0, d^{*})$, and the projection $proj_{d}\mathbb{B}_{1}$ of $\mathbb{B}_{1}$ into the $d$-axis meets $(0, d^{*}]\subset proj_{d}\mathbb{B}_{1}\subset(0, \mathcal{C}]$ for

Specifically, for $0 < d < d^{*}$, Eq (5.1) has a positive steady state solution at least.

(ii) Near $d = d^{*}$, $\mathbb{B}_{1}$ is a smooth curve $E_{1} = \{(u(s), \omega(s), \nu(s), d(s)):s\in(0, \varepsilon)\}$, where $u(s) = u_{1}^{*}+s\phi_{0}(s)+o(s)$, $\omega(s) = \omega_{1}^{*}+s\chi_{0}(s)+o(s)$, and $\nu(s) = s\psi_{0}(s)+o(s)$. Here, $\psi_{0}(x) > 0$ is the principal eigenvalue and satisfies (5.2), and $(\phi_{0}(x), \chi_{0}(x)) < (0, 0)$ fulfills

Further, $d'(0) = \mathcal{N}/(\int_{\mathbb{D}}\psi_{0}^{2}(x)\mathrm{d}x)$, where $'$ stands for derivative and

Proof. Similar to the approach in Ref. ^[43], denote $\mathcal{G}:\mathcal{X}\times\mathcal{X}\times\mathcal{X}\times\mathbb{R}\rightarrow \mathcal{Y}\times \mathcal{Y}\times\mathcal{Y}$ by

Taking partial derivative with respect to $(u, \omega, \nu)$, we can get

Moreover, calculating the second-order partial derivatives for $\mathcal{G}$ about $(u, \omega, \nu)$ leads to

Therefore, it's convenient to check that the core $\mathcal{G}_(u, \omega, \nu)(S^{0}, V^{0}, 0, b^{*}) = span\{\psi_{0}, \chi_{0}, \phi_{0}\}$, with $\phi_{0}$ as the positive eigenfunction of (5.2), $(\phi_{0}, \chi_{0})$ fulfills (5.7). Based on the Lemma 3.2, $(S^{0}(x), V^{0}(x))$ is globally asymptotically stable in $C(\overline{\mathbb{D}}, \mathbb{R})$. This indicates that inverse $[d_{2}\Delta-(\mu(x)+\theta(x))]^{-1}$ and $[d_{1}\Delta-(\mu(x)+\rho(x))]^{-1}$ exist and are positive operators. Hence, $\phi_{0}(x) < 0$ and $\chi_{0}(x) < 0$ for $x\in\mathbb{D}$.

We next consider the range

It is convenient to observe that $(z_{1}, z_{2}, z_{3})\in range \, \mathcal{G}_{(u, \omega, \nu)}(S^{0}, V^{0}, 0, b^{*})$ if and only if there has $(\phi, \chi, \psi)\in\mathcal{X}\times\mathcal{X}\times\mathcal{X}$ satisfying

Hence,

Combining the integration by parts and the boundary conditions, we can derive $\int_{\mathbb{D}}\Delta\psi(x)\psi_{0}(x)\mathrm{d}x = \int_{\mathbb{D}}\Delta\psi_{0}(x)\psi(x)\mathrm{d}x$. Further, from (5.2) and (5.11), we can obtain $\int_{\mathbb{D}}z_{3}(x)\psi_{0}(x)\mathrm{d}x = 0$, which in contrast implicates that (5.10) is valid. Since

and $\int_{\mathbb{D}}[-\psi_{0}(x)]\psi_{0}(x)\mathrm{d}x < 0$, then $\mathcal{G}_{(u, \omega, \nu), b}(S^{0}, V^{0}, 0, b^{*})[\phi_{0}, \chi_{0}, \psi_{0}]\not\in range\mathcal{G}_{(u, \omega, \nu)}(S^{0}, V^{0}, 0, b^{*})$. Using the bifurcation theorem for simple eigenvalues from Ref. ^[44], it is derived that the positive solution set of (5.7) in $(S^{0}, V^{0}, 0, b^{*})$ is a curve of $E_{1}$, where $(u'(0), \omega'(0), \nu'(0)) = (\phi_{0}, \chi_{0}, \psi_{0})$. According to Ref. ^[45], we launch $b'(0)$ in the following form

where $l$ is defined as $\langle l, [z_{1}, z_{2}, z_{3}]\rangle = \int_{\mathbb{D}}z_{3}\psi_{0}(x)\mathrm{d}x$. By direct computing, one can conclude that the second component of $\mathcal{G}_{(u, \omega, \nu), (u, \omega, \nu)}(S^{0}, V^{0}, 0, d^{*}) [\phi_{0}, \chi_{0}$, $\psi_{0}]^{2}$ takes the from

Hence,

where $\mathcal{N}$ is defined as in (5.8). Similar to the methods in Ref.[19, Theorem 3.1] and [18, Theorem 5.3], it's verified that all conditions of Ref. [43, Theorem 4.4] are fulfilled. Therefore, the branching is generated around $(S^{0}, V^{0}, 0)$ as $\mathcal{R}_{0} = 1$. □

6.   Numerical simulations

Throughout this subsection, one conducts fits to account for the impacts of spatially heterogeneous parameters and individuals diffusion on disease propagation. In the interest of simplicity, we take the domain to be $\mathbb{D} = [0, 20]$, and set $d_{1} = 0.02$, $d_{2} = 0.05$, and $d_{3} = 0.005$ to reflect that the individual's mobility is impacted as a result of the disease. Specifically, we consider the general incidence functions $F(x, S, I) = \beta_{1}(x)SI/(1+qI)$, $G(x, S, W) = \beta_{2}(x)SW/(1+pW)$, $F(x, V, I) = \beta_{1}(x)VI/(1+qI)$, $G(x, V, W) = \beta_{2}(x)V/(1+pW)$, where $\beta_{i}(x)\in C^{2}(\overline{\mathbb{D}})$. According to ^[26,48], let's select the parameters $\mu(x) = 4.7\times10^{-5}+2.35\times10^{-5}\sin2x$, $d(x) = 3\times10^{-4}+3\times10^{-5}\sin2x$, $\alpha(x) = 50+50\sin2x$, $\xi(x) = 0.02+0.02\sin2x$, $r(x) = 0.25+0.2\sin2x$. The other parameters will be selected depending on the model.

To begin, we select $\sigma = 0.01$, $q = 2\times10^{-6}$, $p = 1\times10^{-6}$, $\Lambda(x) = 15+7.5\sin2x$, $\rho(x) = 4\times10^{-3}+2\times10^{-3}\sin2x$, $\theta(x) = 1.4\times10^{-4}+7\times10^{-5}\sin2x$, $a(x) = 1.75\times10^{-3}+8.75\times10^{-4}\sin2x$, $\beta_{1}(x) = 1.5\times10^{-9}+7.5\times10^{-10}\sin2x$, $\beta_{2}(x) = 1.88\times10^{-9}+9.4\times10^{-10}\sin2x$, $\gamma(x) = 0$. Other parameters are shown above, and we select

We apply the numerical method mentioned in Ref.^[36] to calculate $\mathcal{R}_{0}\approx0.9901 < 1$, which means the disease will ultimately become extinct. As a matter of fact, one can verify in Figure 2(a) and (b) that as time $t$ evolves, $I(x, t)$ and $W(x, t)$ tends to zero, which is compatible with the result that Theorem 4.1.

If we alter the parameters $r(x) = 0.012+0.0096\sin2x$, $\gamma(x) = 0.03+0.0015\sin2x$, and $\xi(x) = 0.02+0.01\sin2x$, the rest of the values are the same as in Figure 2. In this scenario, we derive $\mathcal{R}_{0}\approx2.4875 > 1$. It follows that Theorem 4.2 shows the illness is persistently present. This is shown in Figure 3(a) and (b), where $I(x, t)$, $W(x, t)$ are periodic oscillations in the whole region. From Figure 3(c) and (d), it can also be found that because of the spatial heterogeneity, $I(x, t)$ and $W(x, t)$ vary geographically across time.

Next, we turn to the influence of spatially heterogeneous parameters on disease propagation. In Figure 4(a)–(c), one illustrates how the vaccination rate $\rho(x)$ affects the quantity of $S(x, t)$, $V(x, t)$, and $I(x, t)$ as time $t = 1500$. In this case, let's choose $\rho(x) = 4\times10^{-3}+4\times10^{-3}\rho_{1}\sin2x$, with $\rho_{1}$ gradually increasing from $0$, $0.2$, $0.3$, to $0.5$. With a growing heterogeneity in vaccination rates, $S(x, t)$ and $V(x, t)$ show large regional diversity. The number of infections in areas with high vaccination rates is known to be relatively low due to the high number of vaccinations. Nevertheless, Figure 4(c) also shows in the same region, e.g., $x\in[12, 14]$, the amount of infected individuals doesn't oscillate significantly as $\rho_{1}$ increases, possibly due to the fact that vaccinated individuals remain at high risk of infection. Consequently, along with large-scale immunization, we should also concentrate on the effectiveness of the vaccine. From Figure 4(d)–(f), it is not uncommon to notice that similar results can be obtained when the model parameters $\theta(x)$ spatial heterogeneity are enhanced. Additionally, from Figure 4(g)–(i), one can observe that when the spatial heterogeneity of the maximum treatment rate $\gamma(x) = 0.03+0.03\gamma_{1}\sin2x$ changes, i.e., $\gamma_{1}$ increases from $0$, $0.25$, $0.5$, to $0.75$, the regional variability of the regional variability of $S(x, 1500)$, $I(x, 1500)$, and $W(x, 1500)$ will be smaller. In Figure 4(h), one could notice that at the identical location, e.g., $x\in [6, 8]$, the peak of infected individuals decreases as $\gamma_{1}$ increases, which means that by changing the heterogeneous intensity of the maximum treatment rate, the peak of the disease outbreak can be reduced to some extent. Simultaneously, in Figure 4(j)–(i), it can be noticed that when the spatial heterogeneity intensity $\xi_{1}$ of $\xi(x) = 0.02+0.02\xi_{1}\sin2x$ gradually increases from $0$, $0.2$, $0.4$, to $0.6$, we can also derive similar results as in Figure 4(g)–(i). This also reinforces the fact that improving local water sanitation and personal hygiene practices are also vitally important for disease control.

Further, let's clarify the way in which the diffusion coefficient influences the propagation of the illness. In Figure 5(a) and (b), variation of distribution of $S(x, 1500)$ for diffusion rates of $d_1 = 0.2$ and $0.002$ is shown. This means that as $d_{1}$ increases, the $S(x, t)$ gets more uniform throughout the region. Figure 5(c) and (d) also display the two scenarios for $S(x, t)$ at $t = 1500$ with diffusion rates $d_{3} = 0.5$ and $d_{3} = 0.005$. By comparing Figure 5(c) and (d), it is apparent that as the diffusion coefficient $d_{3}$ increases, the infected individuals present a homogeneous distribution throughout the field. Mathematical simulation outcomes indicate that the propagation of individuals can alter the local spatial distribution of the illness to some extent, and limiting the cross-regional movement of infected individuals during an epidemic is among the least powerful methods of controlling the illness.

In addition, we pay attention to how spatial heterogeneity contributes to the basic reproduction number $\mathcal{R}_{0}$. Here, let's choose the parameters $\xi(x) = 0.048+0.048c\sin kx$, $\beta_1(x) = 1.5\times10^{-9}+1.5\times10^{-9}c\sin kx$, $\beta_{2}(x) = 1.88\times10^{-9}+ 1.88\times10^{-9}\sin kx$, where $0\leqslant c\leqslant 1$ and $k = 2, 4, 6$. Other parameters are the same as in the Figure $3$. As illustrated by the graphs in Figure 6(a)–(c), variations in the spatial heterogeneity parameters $\beta_{1}(x)$ and $\beta_{2}(x)$ increase or decrease the risk of illness propagation, and by comparing Figure 6(b) and (c), it can be observed that $\mathcal{R}_{0}$ has different monotonicity for $c$ as $k$ takes different values. The above simulation results also indicated that overlooking spatial heterogeneity may result in misclassification of illness propagation.

Lastly, let's look at the link between $\mathcal{R}_{0}$ and the main parameters in the model. Here, we pick the parameters $\Lambda(x) = \Lambda+1.5\sin2x$, $\rho(x) = \rho+2\times10^{-3}\sin2x$, $\theta(x) = \theta+7\times10^{-5}\sin2x$, $\mu(x) = \mu+2.25\times10^{-5}\sin2x$, $\beta_{1}(x) = \beta_{1}+1.5\times10^{-6}\sin2x$, $d(x) = d+0.08\sin2x$, $\beta_{2}(x) = \beta_{2}+3.135\times10^{-6}\sin2x$, $r(x) = r+0.0096\sin2x$, $\xi(x) = \xi+0.01\sin2x$, $\gamma(x) = \gamma+0.0015\sin2x$, $\alpha(x) = \alpha+50\sin2x$. Based on the methods in ^[49], we choose $\Lambda = 15$, $\rho = 4\times10^{-3}$, $\theta = 1.4\times10^{-4}$, $\mu = 4.5\times10^{-5}$, $d = 0.1$, $\beta_{1} = 3\times10^{-6}$, $\beta_{2} = 6.27\times10^{-6}$, $r = 0.012$, $\gamma = 0.03$, $\xi = 0.02$, $\alpha = 50$, and the sensitivity indices for each parameter can be calculated separately for $\mathcal{R}_{0}$. As shown in Figure 7, $\mathcal{R}_{0}$ has the largest sensitivity index in relation to $\xi(x)$ and $\Lambda(x)$, followed by $\beta_{2}(x)$, $\alpha(x)$, $\rho(x)$, $\mu(x)$, $d (x)$, $\theta(x)$, $\gamma(x)$, $r(x)$, $\beta_{1}(x)$. We also observe that $\mathcal{R}_{0}$ is positively associated with the variables $\theta(x)$, $\beta_{1}(x)$, $\beta_{2}(x)$, $\alpha(x)$, $\Lambda(x)$, and those with $r(x)$, $d(x)$, $\gamma(x)$, $\rho(x)$, $\xi(x)$, $\mu(x)$ are negatively correlated. The above results reveal that it is necessary to disinfect contaminated environments in outbreak areas in a timely manner, and to seal off and control areas with frequent outbreaks to reduce the movement of people. At the same time, we should raise the awareness of the local people on self-prevention, such as drinking healthy and hygienic drinking water and maintaining good hygienic habits.

7.   Conclusions

Within this paper, we presented and discussed a SVIR-W spatially heterogeneous model of Cholera that combines multiple transmission pathways, incomplete immunity, general incidence, and Holling Ⅱ treatment. It turns out the basic reproduction number $\mathcal{R}_{0}$, which is a criterion condition, decided the persistence or extinction of epidemics. In other words, the disease-free steady state $\mathcal{E}_{0}$ is globally asymptotically stable with zero maximum treatment rate in case $\mathcal{R}_{0} < 1$ (see Theorem 4.2); the illness will be persistent in case $\mathcal{R}_{0} > 1$ (see Theorem 4.2). Furthermore, we performed a branching analysis with constant mortality due to disease as a branching parameter (see Theorem 5.1). It can be inferred that the forward branching is always undergone at $\mathcal{R}_{0} = 1$, and the presence of positive steady state is entirely excluded as $\mathcal{R}_{0}$ is smaller than 1. This means that $\mathcal{R}_{0}$ completely determines the persistence and extinction of diseases, which also implies that we can eliminate the disease by controlling parameters such as recruitment rate, bacterial shedding rate, and the spread of environmental viruses to susceptible individuals.

Numerically, we simulated the influence of some crucial parameters on the spatio-temporal distribution of the disease, which is helpful to prevent and manage the disease. Specifically, spatially heterogeneous parameters can cause the disease distribution to show geographical variability (see Figure 4(a)–(l)). The evolution of the dispersal coefficients will affect the spatial distribution of the illness, e.g., as the diffusion coefficient $d_{3}$ increases, an infected individual's distribution will quickly become homogeneous (see Figure 5(c) and (d)). We also explored the relationship between the propagation rates $\beta_{1}(x)$, $\beta_{2}(x)$, and $\mathcal{R}_{0}$. We note that the monotonicity of the basic reproduction numbers $\mathcal{R}_{0}$ and $c$ changes for different values of $k$ (see Figure 6(b) and (c)), which also suggests that spatial heterogeneity dilutes or amplifies the spread of the illness.

It's unfortunate that we only proved the global asymptotic stability of disease-free steady state $\mathcal{E}_{0}$ at a maximum treatment rate of $\gamma(x) = 0$. While we have not derived the kinetic behavior of the disease at a maximum treatment rate of $\gamma(x)\not = 0$, we will study this issue in-depth in the future. As is well known, many environmentally spread diseases have incubation periods during which the host can move randomly ^[46,47]. That implies that the effect of infection not only relies on the correlation of the present time and location, but also on the correlation of the previous position, which can generally be characterized by a nonlocal morbidity with a core function. Therefore, it appears relevant and essential to introduce nonlocal effects into models with environmental propagation. This is the focus of our future research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The authors would like to thank the anonymous reviewers and the editors for their valuable suggestions for the improvement of the paper. This research is partially supported by the National Natural Science Foundation of Xinjing Uygur Autonomous Region (Grant Nos. 2021D01E12 and 2022TSYCCX0015), the National Natural Science Foundation of China (Grant No. 12361103), the Scientific Research and Innovation Project of Outstanding Doctoral Students in Xinjiang University (Grant No. XJU2022BS022).

Conflict of interest

The authors declare that they have no conflict of interest.