A mathematical model for fractal-fractional monkeypox disease and its application to real data

1.   Introduction

The Sasa-Satsuma equation

so-called high-order nonlinear Schrödinger equation ^[1], is relevant to several physical phenomena, for example, in optical fibers ^[2,3], in deep water waves ^[4] and generally in dispersive nonlinear media ^[5]. Because this equation describes these important nonlinear phenomena, it has received considerable attention and extensive research. The Sasa-Satsuma equation has been discussed by means of various approaches such as the inverse scattering transform ^[1], the Riemann-Hilbert method ^[6], the Hirota bilinear method ^[7], the Darboux transformation ^[8], and others ^[9,10,11]. The initial-boundary value problem for the Sasa-Satsuma equation on a finite interval was studied by the Fokas method ^[12], which is also effective for the initial-boundary value problems on the half-line ^[35,36,37]. In Ref. ^[13], finite genus solutions of the coupled Sasa-Satsuma hierarchy are obtained in the basis of the theory of trigonal curves, the Baker-Akhiezer function and the meromorphic functions ^[14,15,16]. In Ref. ^[17], the super Sasa-Satsuma hierarchy associated with the $3 \times 3$ matrix spectral problem was proposed, and its bi-Hamiltonian structures were derived with the aid of the super trace identity.

The nonlinear steepest descent method ^[18], also called Deift-Zhou method, for oscillatory Riemann-Hilbert problems is a powerful tool to study the long-time asymptotic behavior of the solution for the soliton equation, by which the long-time asymptotic behaviors for a number of integrable nonlinear evolution equations associated with $2 \times 2$ matrix spectral problems have been obtained, for example, the mKdV equation, the KdV equation, the sine-Gordon equation, the modified nonlinear Schrödinger equation, the Camassa-Holm equation, the derivative nonlinear Schrödinger equation and so on ^{[19,20,21,22,23,24,25,26,27,28,29,30]}. However, there is little literature on the long-time asymptotic behavior of solutions for integrable nonlinear evolution equations associated with $3 \times 3$ matrix spectral problems ^[31,32,33]. Usually, it is difficult and complicated for the $3 \times 3$ case. Recently, the nonlinear steepest descent method was successfully generalized to derive the long-time asymptotics of the initial value problems for the coupled nonlinear Schrödinger equation and the Sasa-Satsuma equation with the complex potentials ^[33,34]. The main differences between the $2 \times 2$ and $3 \times 3$ cases is that the former corresponds to a scalar Riemann-Hilbert problem, while the latter corresponds to a matrix Riemann-Hilbert problem. In general, the solution of the matrix Riemann-Hilbert problem can not be given in explicit form, but the scalar Riemann-Hilbert problem can be solved by the Plemelj formula.

The main aim of this paper is to study the long-time asymptotics of the Cauchy problem for the generalized Sasa-Satsuma equation ^[38] via nonlinear steepest decent method,

where $a$ is a real constant, $b$ is a complex constant that satisfies $a^2\neq|b|^2$, the asterisk $"\ast"$ denotes the complex conjugate. It is easy to see that the generalized Sasa-Satsuma equation (1.2) can be reduced to the Sasa-Satsuma equation (1.1) when $a = -1$ and $b = 0$. Suppose that the initial value $u_0(x)$ lies in Schwartz space $\mathscr{S}(\mathbb{R}) = \{f(x)\in C^\infty(\mathbb{R}):\sup_{x\in\mathbb{R}}|x^\alpha\partial^\beta f(x)| < \infty, \forall\alpha, \beta\in\mathbb{N}\}$. The vector function $\gamma(k)$ is determined by the initial data in (2.15) and (2.19), and $\gamma(k)$ satisfies the conditions ($P_1$) and ($P_2$), where

with

($P_2$): When $\det B_1 > 0$ and $a > 0$, $(2a-|B_1\gamma(k)|^2)$ and $(2a-\det B_1|\gamma(k)|^2)/(1-\gamma^\dagger(k)B_1\gamma(k))$ are positive and bounded; otherwise, $(|B_1\gamma(k)|^2-2a)$ and $(\det B_1|\gamma(k)|^2-2a)/(1-\gamma^\dagger(k)B_1\gamma(k))$ are positive and bounded.

The main result of this paper is as following:

Theorem 1.1. Let $u(x, t)$ be the solution of the Cauchy problem for the generalized Sasa-Satsuma equation (1.2) with the initial value $u_0\in\mathscr{S}(\mathbb{R})$. Suppose that the vector function $\gamma(k)$ is defined in (2.19), the hypotheses $(P_1)$ and $(P_2)$ hold. Then, for $x < 0$ and $\sqrt{-\frac{x}{t}} < C$,

where $C$ is a fixed constant, and

$c(\cdot)$ is rapidly decreasing, $\Gamma(\cdot)$ is the Gamma function, $\gamma_1$ and $\gamma_2$ are the first and the second row of $\gamma(k)$, respectively.

Remark 1.1. The two conditions $(P_1)$ and $(P_2)$ satisfied by $\gamma(k)$ are necessary. The condition $(P_1)$ guarantees the existence and the uniqueness of the solutions of the basic Riemann-Hilbert problem (2.16) and the Riemann-Hilbert problem (3.1). The boundedness of the function $\delta(k)$ defined in subsection 3.1 relies on the condition $(P_2)$.

Remark 1.2. In the case of $a = -1$ and $b = 0$, the generalized Sasa-Satsuma equation (1.2) can be reduced to the Sasa-Satsuma equation. Then it is obvious that the condition $(P_1)$ is true, and the condition $(P_2)$ is reduced to the case that $|\gamma(k)|$ is bounded. Therefore, the conditions $(P_1)$ and $(P_2)$ in this case are equivalent to the condition related to the reflection coefficient in ^[34], that is, $|\gamma(k)|$ is bounded for the Sasa-Satsuma equation.

The outline of this paper is as follows. In section 2, we derive a Riemann-Hilbert problem from the scattering relation. The solution of the generalized Sasa-Satsuma equation is changed into the solution of the Riemann-Hilbert problem. In section 3, we deal with the Riemann-Hilbert problem via nonlinear steepest decent method, from which the long-time asymptotics in Theorem 1.1 is obtained at the end.

2.   Basic Riemann-Hilbert problem

We begin with the $3 \times 3$ Lax pair of the generalized Sasa-Satsuma equation

where $\psi$ is a matrix function and $k$ is the spectral parameter, $\sigma = \mathrm{diag}(1, 1, -1)$,

We introduce a new eigenfunction $\mu$ through $\mu = \psi e^{-ik\sigma x-4ik^3\sigma t}$, where $e^\sigma = \mathrm{diag}(e, e, e^{-1})$. Then (2.1a) and (2.1b) become

where $[\cdot, \cdot]$ is the commutator, $[\sigma, \mu] = \sigma\mu-\mu\sigma$. From (2.4a), the matrix Jost solution $\mu_\pm$ satisfy the Volterra integral equations

Set $\mu_{\pm L}$ represent the first two columns of $\mu_\pm$, and $\mu_{\pm R}$ denote the third column, i.e., $\mu_\pm = (\mu_{\pm L}, \mu_{\pm R})$. Furthermore, we can infer that $\mu_{+R}$ and $\mu_{-L}$ are analytic in the lower complex $k$-plane $\mathbb{C}_-$, $\mu_{+L}$ and $\mu_{-R}$ are analytic in the the upper complex $k$-plane $\mathbb{C}_+$. Then we can introduce sectionally analytic function $P_1(k)$ and $P_2(k)$ by

One can find that $U$ is traceless from (2.2), so $\det\mu_\pm$ are independent of $x$. Besides, $\det\mu_\pm = 1$ according to the evolution of det$\mu_\pm$ at $x = \pm\infty$. Because all the $\mu_{\pm}e^{ik\sigma x+4ik^3\sigma t}$ satisfy the differential equations (2.1a) and (2.1b), they are linear related. So there exists a scattering matrix $s(k)$ that satisfies

In this paper, we denote a $3 \times 3$ matrix A by the block form

where $A_{11}$ is a $2 \times 2$ matrix and $A_{22}$ is scalar. Let $q = (u, u^\ast)^T$ and we can rewrite $U$ of (2.2) as

where $"\dagger"$ is the Hermitian conjugate. In addition, there are two symmetry properties for $U$,

where $B$ and $\tau$ are represented as block forms. Hence, the Jost solutions $\mu_\pm$ and the scattering matrix $s(k)$ also have the corresponding symmetry properties

We write $s(k)$ as block form $(s_{ij})_{2 \times 2}$ and from the symmetry properties (2.10) we have

where $\mathrm{adj}X$ denote the adjoint of matrix $X$. Then we can write $s(k)$ as

where

From the evaluation of (2.6) at $t = 0$, one infers

which implies that

Theorem 2.1. Let $M(k; x, t)$ be analytic for $k\in\mathbb{C}\backslash\mathbb{R}$ and satisfy the Riemann-Hilbert problem

where

$\gamma(k)$ lies in Schwartz space and satisfies

Then the solution of this Riemann-Hilbert problem exists and is unique, the function

and $u(x, t)$ is the solution of the generalized Sasa-Satsuma equation.

Proof. The matrix $(J(k; x, t)+J^\dagger(k; x, t))/2$ is positive definite because of the condition $(P_1)$ that $\gamma(k)$ satisfies, then the solution of the Riemann-Hilbert problem (2.16) is existent and unique according to the Vanishing Lemma ^[39]. We define $M(k; x, t)$ by

Considering the scattering relation (2.6) and the construction of $M(k; x, t)$, we can obtain the jump condition and the corresponding Riemann-Hilbert problem (2.16) after tedious but straightforward algebraic manipulations. Substituting the large $k$ asymptotic expansion of $M(k; x, t)$ into (2.4a) and compare the coefficients of $O(\frac{1}{k})$, we can get (2.21).

3.   Long-time asymptotic behavior

In this section, we compute the Riemann-Hilbert problem (2.16) by the nonlinear steepest decent method and study the long-time asymptotic behavior of the solution. We make the following basic notations. (i) For any matrix $M$ define $\vert M\vert = (\mathrm{tr}M^{\dagger}M)^{\frac{1}{2}}$ and for any matrix function $A(\cdot)$ define $\Vert A(\cdot)\Vert_{p} = \Vert\vert A(\cdot)\vert\Vert_{p}$. (ii) For two quantities $A$ and $B$ define $A\lesssim B$ if there exists a constant $C > 0$ such that $\vert A\vert\leqslant CB$. If $C$ depends on the parameter $\alpha$ we shall say that $A\lesssim_{\alpha}B$. (iii) For any oriented contour $\Sigma$, we say that the left side is $+$ and the right side is $-$.

3.1.   The first transformation: reorientation

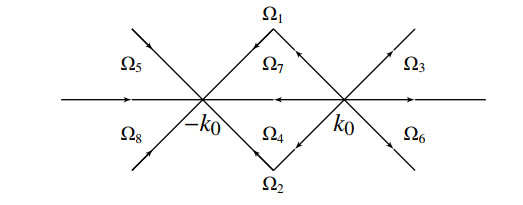
First of all, it is noteworthy that there are two stationary points $\pm k_0$, where $\pm k_0 = \pm \sqrt{-\frac{x}{12t}}$ satisfied $\frac{\mathrm{d}\theta}{\mathrm{d}k}\big\vert_{k = \pm k_0} = 0$. The jump matrix $J(k; x, t)$ have a lower-upper triangular factorization and a upper-lower triangular factorization. We can introduce an appropriate Rieman-Hilbert problem to unify these two forms of factorizations. In this process, we have to reorient the contour of the Riemann-Hilbert problem.

The two factorizations of the jump matrix $J$ are

We introduce a $2 \times 2$ matrix function $\delta(k)$ to make the two factorization unified, and $\delta(k)$ satisfies the following Riemann-Hilbert problem

which implies a scalar Riemann-Hilbert problem

The jump matrix $I-\gamma(k)\gamma^{\dagger}(k^{\ast})B_1$ of Riemann-Hilbert problem (3.1) is positive definite, so the solution $\delta(k)$ exists and is unique. The scalar Riemann-Hilbert problem (3.2) can be solved by the Plemelj formula,

where

Then we have by uniqueness that

Substituting (3.4) to (3.1), we have

which means that

Actually, the condition $(P_2)$ satisfied by $\gamma(k)$ guarantee the boundedness of $\delta_\pm(k)$ and we give a brief proof below. When $\det B_1 > 0$, we find that the Hermitian matrix $B_1$ can be decomposition. In other words, there exists a triangular matrix $S$ that satisfies $B_1 = a S^\dagger S$. So $\mathrm{tr}[\delta^\dagger_+B_1\delta_+] = a|S\delta_+|^2$. When $\det B_1 < 0$ and $|a| > 0$, the matrix $B_1$ has a decomposition $B_1 = S^\dagger DS$, where $S$ is a triangular matrix and $D$ is a diagonal matrix and the diagonal elements have opposite signs. In the case of $a > 0$, $B_1$ can be decomposed as below,

We denote $S\delta_+(k)$ by $(G_{ij})_{3 \times 3}$ and $c_1 = 2a-|B_1\gamma(k)|^2$ is negative, then

Noticing that $\det B_1 < 0$, we find a negative constant $c_2$ that satisfies $c_2\leqslant a\det B_1(c_3-1)/(1-\det B_1c_3)$, where $c_3$ is a constant and $0 < c_3 < 1$, which impies

The case that $a < 0$ is similar. In particular, when $a = 0$, then $|b| > 0$, it is easy to see that $B_1$ is not definite. For $|\mathrm{Re}b| > 0$, we have the decomposition

For $|\mathrm{Re}b| = 0$, we have

So we get the boundedness of $|\delta_+(k)|$. The others have the same analysis,

Hence, by the maximum principle, we have

for all $k\in\mathbb{C}$. We define the functions

We reverse the orientation for $k\in(-\infty, k_0)\cup(k_0, +\infty)$ as in Figure 1, and $M^\Delta(k; x, t) = M(k; x, t)\Delta^{-1}(k)$ satisfies the Riemann-Hilbert problem on the reoriented contour

where the jump matrix $J^\Delta(k; x, t)$ has a decomposition

3.2.   Extend to the augmented contour

For the convenience of discussion, we define

Theorem 3.1. The vector function $\rho(k)$ has a decomposition

where $R(k)$ is a piecewise-rational function and $h_2(k)$ has a analytic continuation to $L$. Besides, they admit the following estimates

for an arbitrary positive integer $l$. Considering the Schwartz conjugate

we can obtain the same estimate for $e^{2it\theta(k)}h^{\dagger}_{1}(k^{\ast})$, $e^{2it\theta(k)}h^{\dagger}_{2}(k^{\ast})$ and $e^{2it\theta(k)}R^{\dagger}(k^{\ast})$ on $\mathbb{R}\cup L^{\ast}$.

Proof. It follows from Proposition 4.2 in ^[18].

A direct calculation shows that $b_\pm$ of (3.20) can be decomposed further

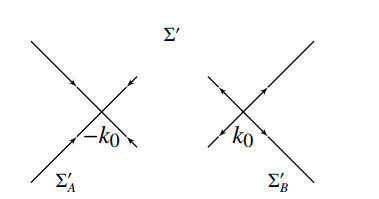
Define the oriented contour $\Sigma$ by $\Sigma = L\cup L^\ast$ as in Figure 2. Let

Lemma 3.1. $M^\sharp(k; x, t)$ is the solution of the Riemann-Hilbert problem

where the jump matrix $J^\sharp(k; x, t)$ satisfies

Proof. We can construct the Riemann-Hilbert problem (3.25) based on the Riemann-Hilbert problem (3.19) and the decomposition of $b_\pm$. In the meantime, the asymptotics of $M^\sharp(k; x, t)$ is derived from the convergence of $b_\pm$ as $k\to\infty$. For fixed $x$ and $t$, we pay attention to the domain $\Omega_{3}$. Noticing the boundedness of $\delta(k)$ and $\det\delta(k)$ in (3.16), we arrive at

Consider the definition of $R(k)$ in this domain,

where $m$ is a positive integer and $\mu_i$ is the coefficient of the Taylor series around $k_0$. Combining with the boundedness of $h_2(k)$ in Theorem 3.1, we obtain that $M^\sharp(k; x, t)\to I$ when $k\in\Omega_3$ and $k\to\infty$. The others are similar to this domain.

The above Riemann-Hilbert problem (3.25) can be solved as follows. Set

Let

denote the Cauchy operator, where $C_+f\ (C_-f)$ denotes the left (right) boundary value for the oriented contour $\Sigma$ in Figure 2. Define the operator $C_{\omega^\sharp}:\mathscr{L}^2(\Sigma)+\mathscr{L}^\infty(\Sigma)\to\mathscr{L}^2(\Sigma)$ by

for the $3 \times 3$ matrix function $f$.

Lemma 3.2 (Beals-Coifman). If $\mu^\sharp(k; x, t)\in \mathscr{L}^2(\Sigma)+\mathscr{L}^\infty(\Sigma)$ is the solution of the singular integral equation

Then

is the solution of the Riemann-Hilbert problem (3.25).

Proof. See ^[18], P. 322 and ^[40].

Theorem 3.2. The expression of the solution $q(x, t)$ can be written as

Proof. From (2.21), (3.24) and Lemma 2, the solution $q(x, t)$ of the generalized Sasa-Satsuma equation is expressed by

3.3.   Contour truncation

Set $\Sigma^\prime = \Sigma\backslash(\mathbb{R}\cup L_\epsilon\cup L_\epsilon^\ast)$ oriented as in Figure 3. We will convert the Riemann-Hilbert problem on the contour $\Sigma$ to a Riemann-Hilbert problem on the contour $\Sigma^\prime$ and estimate the errors between the two Riemann-Hilbert problems. Let $\omega^\sharp = \omega^e+\omega^\prime = \omega^a+\omega^b+\omega^c+\omega^\prime$, where $\omega^a = \omega^\sharp |_\mathbb{R}$ is supported on $\mathbb{R}$ and is composed of terms of type $h_1(k)$ and $h_1^\dagger(k^\ast)$; $\omega^b$ is supported on $L\cup L^\ast$ and is composed of contribution to $\omega^\sharp$ from terms of type $h_2(k)$ and $h_2^\dagger(k^\ast)$; $\omega^c$ is supported on $L_\epsilon\cup L_\epsilon^\ast$ and is composed of contribution to $\omega^\sharp$ from terms of type $R(k)$ and $R^\dagger(k^\ast)$.

Lemma 3.3. For arbitrary positive integer $l$, as $t\to\infty$,

Proof. The proof of estimates (3.30), (3.31), (3.32) follows from Theorem 3.1. Afterwards, we consider the definition of $R(k)$ on the contour $\{k = k_0+\alpha k_0e^{\frac{-3\pi i}{4}}\vert -\infty < \alpha < \epsilon\}$,

Resorting to $\mathrm{Re}(i\theta)\geqslant8\alpha^2 k_0^3$ and the boundedness of $\delta(k)$ and $\det\delta(k)$ in (3.16), we can obtain

Then we obtain (3.33) by simple computations.

Lemma 3.4. As $t\to\infty$, $(1-C_{\omega^\prime})^{-1}:\mathscr{L}^2(\Sigma)\to\mathscr{L}^2(\Sigma)$ exists and is uniformly bounded:

Furthermore, $\Vert(1-C_{\omega^\sharp})^{-1}\Vert_{\mathscr{L}^2(\Sigma)}\lesssim1$.

Proof. It follows from Proposition 2.23 and Corollary 2.25 in ^[18].

Lemma 3.5. As $t\to\infty$,

Proof. A simple computation shows that

After a series of tedious computations and utilizing the consequence of Lemma 4, we arrive at

Then the proof is accomplished as long as we substitute the estimates above into (3.35).

Notice that $\omega^\prime(k) = 0$ when $k\in\Sigma\backslash\Sigma^\prime$, let $C_{\omega^\prime}|_{\mathscr{L}^2(\Sigma^\prime)}$ denote the restriction of $C_{\omega^\prime}$ to $\mathscr{L}^2(\Sigma^\prime)$. For simplicity, we write $C_{\omega^\prime}|_{\mathscr{L}^2(\Sigma^\prime)}$ as $C_{\omega^\prime}$. Then

Lemma 3.6. As $t\to\infty$,

Proof. From (3.29) and (3.34), we can obtain the result directly.

Let $L^\prime = L\backslash L_\epsilon$ and $\mu^\prime = (1-C_{\omega^\prime})^{-1}I$. Then

solves the Riemann-Hilbert problem

where

3.4.   Noninteraction of disconnected contour components

Let the contour $\Sigma^{\prime} = \Sigma^{\prime}_{A}\cup\Sigma^{\prime}_{B}$ and $\omega^{\prime}_{\pm} = \omega^{\prime}_{A\pm}+\omega^{\prime}_{B\pm}$, where

Define the operators $C_{\omega^{\prime}_{A}}$ and $C_{\omega^{\prime}_{B}}$: $\mathscr{L}^{2}(\Sigma^{\prime})+\mathscr{L}^{\infty}(\Sigma^{\prime})\rightarrow\mathscr{L}^{2}(\Sigma^{\prime})$ as in definition (3.28).

Lemma 3.7.

Proof. See Lemma 3.5 in ^[18].

Lemma 3.8. As $t\rightarrow\infty$,

Proof. From identity

we have

Based on Lemma (3.7) and Lemma (3.4), we arrive at (3.38).

For the sake of convenience, we write the restriction $C_{\omega^{\prime}_{A}}\mid_{\mathscr{L}^{2}(\Sigma^{\prime}_{A})}$ as $C_{\omega^{\prime}_{A}}$, similar for $C_{\omega^{\prime}_{B}}$. From the consequences of Lemma 3.6 and Lemma 3.8, as $t\rightarrow\infty$, we have

3.5.   Rescaling and further reduction of the Riemann-Hilbert problems

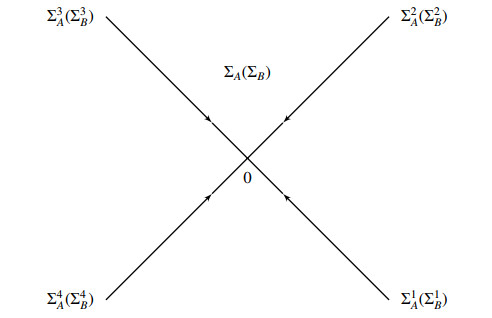
Extend the contours $\Sigma^{\prime}_{A}$ and $\Sigma^{\prime}_{B}$ to the contours

respectively. We introduce $\hat{\omega}^{\prime}_{A}$ and $\hat{\omega}^{\prime}_{B}$ on $\hat{\Sigma}^{\prime}_{A}$ and $\hat{\Sigma}^{\prime}_{B}$, respectively, by

Let $\Sigma_{A}$ and $\Sigma_{B}$ denote the contours $\{k = k_{0}\alpha e^{\pm\frac{\pi i}{4}}:\alpha\in\mathbb{R}\}$ oriented inward as in $\Sigma^{\prime}_{A}$, $\hat{\Sigma}^{\prime}_{A}$, and outward as in $\Sigma^{\prime}_{B}$, $\hat{\Sigma}^{\prime}_{B}$, respectively. Define the scaling operators

and set

A simple change-of-variable arguments shows that

where the operator $C_{\omega_{A}}\ (C_{\omega_{B}})$ is a bounded map from $\mathscr{L}^{2}(\Sigma_{A})\ (\mathscr{L}^{2}(\Sigma_{B}))$ into $\mathscr{L}^{2}(\Sigma_{A})\ (\mathscr{L}^{2}(\Sigma_{B}))$. On the part

of $\Sigma_{A}$, we have

on $L^{\ast}_{A}$ we have

where

Lemma 3.9. As $t\rightarrow\infty$, and $k\in L_{A}$, then

where $\tilde{\delta}(k) = e^{-2it\theta(k)}[\delta(k)R(k)-(\mathrm{det}\delta(k))R(k)]$.

Proof. It follows from (3.1) and (3.2) that $\tilde{\delta}$ satisfies the following Riemann-Hilbert problem:

where $f(k) = \delta_{-}(k)[\gamma^\dagger(k^\ast)B_1\gamma(k)I-\gamma(k)\gamma^\dagger(k^\ast)B_1]R(k)$. The solution for the above Riemann-Hilbert problem can be expressed by

Observing that

we obtain $f(k) = O((k^{2}-k^{2}_{0})^{l}).$ Similar to the Lemma 3.1, $f(k)$ can be decomposed into two parts: $f(k) = f_{1}(k)+f_{2}(k)$, and

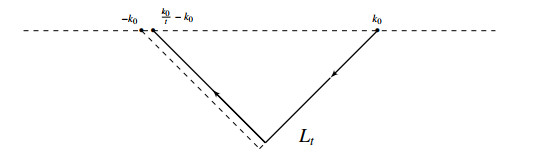
where $f_{2}(k)$ has an analytic continuation to $L_{t}$, $l$ is a positive integer and $l\geqslant2$,

(see Figure 5).

As $k\in L_{A}$, we obtain

As a consequence of Cauchy's Theorem, we can evaluate $I_{3}$ along the contour $L_{t}$ instead of the interval $(\frac{k_{0}}{t}-k_{0}, k_{0})$ and obtain $\left|I_{3}\right|\lesssim t^{-l+1}.$ Therefore, (3.45) holds.

Corollary 3.1. As $t\rightarrow\infty$, and $k\in L_{A}^\ast$, then

where $\hat{\delta}(k) = e^{2it\theta(k)}R^{\dagger}(k^{\ast})B_1[\delta^{-1}(k)-(\mathrm{det}\delta(k))^{-1}I]$.

Let $J^{A^0} = (I-\omega_{A^0-})^{-1}(I+\omega_{A^0+})$, where

It follows from (3.78) in ^[18] that

There are similar consequences for $k\in\Sigma_B$. Let $J^{B^0} = (I-\omega_{B^0-})^{-1}(I+\omega_{B^0+})$, where

Theorem 3.3. As $t\to\infty$,

Proof. Notice that

Utilizing the triangle inequality and the boundedness in (3.53), we have

According to (3.5) and a simple change-of-variable argument, we have

There are similar computations for the other case. Together with (3.39), one can obtain (3.57).

For $k\in\mathbb{C}\backslash\Sigma_A$, set

Then $M^{A^0}(k; x, t)$ is the solution of the Riemann-Hilbert problem

In particular

then

There is a analogous Riemann-Hilbert problem on $\Sigma_{B}$,

where $J^{B^0}(k; x, t)$ is defined in (3.54) and (3.56). In the meantime, we have

Next, we consider the relation between $M^{A^0}_1$ and $M^{B^0}_1$. From the expression (3.50), (3.52), (3.54) and (3.56), we have the symmetry relation

By the uniqueness of the Riemann-Hilbert problem,

Combining with the expansion (3.60) and (3.63), one can verify that

Therefore, from (3.57) and (3.61), we have

3.6.   Solving the model problem

In this subsection, we compute $(M_1^{A^0})_{12}$ explicitly. It is important to set

Then it follows from (3.59) that

The jump matrix is the constant one on the four rays $\Sigma_A^1$, $\Sigma_A^2$, $\Sigma_A^3$, $\Sigma_A^4$, so

Then it follows that $(\mathrm{d}\Psi/\mathrm{d}k+ik\sigma\Psi)\Psi^{-1}$ has no jump discontinuity along any of the four rays. Besides, from the relation between $\Psi(k)$ and $H(k)$, we have

It follows by the Liouville's Theorem that

where

Moreover,

Set

From (3.68) and its differential, we obtain

As is well known, the Weber's equation

has the solution

where $D_{\varrho}(\cdot)$ denotes the standard parabolic-cylinder function, and $c_1$, $c_2$ are constants. The parabolic-cylinder function satisfies ^[41]

As $\zeta\rightarrow\infty$, from ^[42], we have

where $\Gamma(\cdot)$ is the Gamma function. Set $\varrho = i\beta_{21}\beta_{12}$,

where $a_1, a_2, a_3, a_4$ are constants. As $\arg{k}\in(-\pi, -\frac{3\pi}{4})\cup(\frac{3\pi}{4}, \pi)$ and $k\rightarrow\infty$, we arrive at

then

Consequently,

For $\arg{k}\in(-\frac{3\pi}{4}, -\frac{\pi}{4})$ and $k\rightarrow\infty$, we have

then

Consequently,

Along the ray $\arg k = -\frac{3\pi}{4},$

Notice the $(2, 1)$ entry of the Riemann-Hilbert problem,

It follows from (3.71) that

Then we separate the coefficients of the two independent functions and obtain

Noting that $B^{-1}(J^{A^0}(k^\ast))^\dagger B = (J^{A^0}(k))^{-1}$, we have $\beta_{12} = -B_1^{-1}\beta_{21}^\dagger$, which means that

Finally, we can obtain (1.4) from (3.64), (3.69) and (3.77).

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11871440 and 11931017).

Conflict of interest

The authors declare no conflict of interest.