Ditch control and land reclamation promote vegetation recovery in Loess Plateau

1.   Introduction

The idea of "multi-attribute group decision making" (MAGDM) was put forward as a promising and important field of research at the beginning of the 1970s. Since then, a growing number of contributions have been made to theories and models that could be the basis for making decisions that are more methodical and logically sound, employing a variety of criteria. According to one viewpoint, decision-making is a process of problem-solving that ends with the choice of a solution that is thought to be either the best or, at the very least, a reasonable and acceptable alternative among a collection of plausible alternatives. The phrase "multi-criteria decision making" or "MAGDM" refers to a sub field of operations research that focuses on the process of selecting the best option for a given set of criteria by carefully and systematically examining all of the alternatives. By contrasting and comparing all of the options, this is achieved. MAGDM issues and related solutions are regularly encountered in a variety of disciplines, including the social sciences, economics, management, and medicine. Struggling to figure out how to incorporate ambiguous information pieces that have been offered by a broad range of sources in the process of arriving at a judgment or conclusion is one of the most challenging challenges one encounters when meeting complexity that requires MAGDM. When dealing with problems that call for MAGDM, this is one of the biggest difficulties one encounters. Numerous surveys, including those by Bana and Costa ^[1], demonstrate the field's vigour and the variety of methodologies that have been created. A few years later, Bellman, Zadeh, and Zimmermann introduced fuzzy sets into the field, paving the way for a new family of techniques to solve problems that had previously been inaccessible and unsolvable with conventional MAGDM techniques. There are various variations on the MAGDM theme, depending on the theoretical underpinnings used for the modeling. Since it protects against data theft and destruction, cybersecurity is essential. This includes sensitive data, personally identifiable information (PII), protected health information (PHI), personal data, information relating to intellectual property, and computer networks utilized by the government and industry. Without a cybersecurity programme, your business cannot defend itself against data breach operations, making it an inevitable target for cyber criminals.

Both inherent risk and residual risk are increasing as a result of improved worldwide connectivity and the use of cloud services like Amazon Web Services to store private and sensitive data. Due to widespread poor cloud service design, highly trained cybercriminals, and widespread inadequate cloud service setup, it is more likely that your company will be the victim of a successful cyberattack or data breach. Business executives cannot exclusively rely on standard cybersecurity tools like firewalls and antivirus software because hackers are growing more cunning and their strategies are becoming more resistant to traditional cyber defenses. To stay well-protected, it's crucial to cover all aspects of cybersecurity. Any level of your organisation has the potential to pose a cyber threat. To educate personnel about typical cyber threats, including social engineering scams, phishing, ransomware attacks (think WannaCry), and other programmes made to steal sensitive data, workplaces must offer cyber security awareness training. Due to the prevalence of data breaches, cybersecurity is essential across all industries, not just those with strict regulations like the health care sector. After a data breach, even small firms run the risk of having their reputations permanently damaged.

To help you understand the importance of cyber security, we've posted an essay describing the numerous components of cybercrime you might not be aware of. You should be concerned about cybersecurity risks if you aren't already. Cybersecurity is the practise of preventing and responding to attacks on computer systems, networks, hardware, and software. Your sensitive data is at risk from increasingly sophisticated and dynamic cyber attacks, which use cutting-edge methods that combine social engineering and artificial intelligence (AI) to bypass well-established data protection safeguards. The world is getting more and more dependent on technology, and as we create new technologies that will eventually connect to our linked devices via Bluetooth and Wi-Fi, this dependence will only grow. Intelligent cloud security solutions should be used in conjunction with stringent password rules such as multi-factor authentication to limit unauthorised access and protect customer data while adopting new technologies. Information theft is the most expensive and quickly spreading type of cybercrime. mostly as a result of cloud services' role in the growth of identity information vulnerability on the web. It's not the only one, though. Industrial controls, which are susceptible to disruption ordestruction, are used to regulate power grids and other infrastructure. In order to cause strife within a business or government, cyber attacks may also aim to threaten data integrity (destroy or change data), making identity theft their secondary goal. As they gain experience, cybercriminals change the targets they select, the methods by which they influence enterprises, and the manner in which they attack different security systems. Here, we go over numerous security measures and their difficulties.

A fuzzy set (FS) is a mathematical representation of a group of elements (objects) with fuzzy boundaries that allows for the potential of a progressive change in an element's belongings to a group, from full membership to non membership. This idea is presented in the fuzzy sets (FSs) theory as a way to mathematically express fuzzy concepts that people use to describe how they perceive real systems, their preferences, and goals, among other things. Applying the fuzzy decision theory, choose the best security system that will protect you from hackers. Many challenges exist in security systems that are only hazy when it comes to selecting the best option. When dealing with unstructured scenarios in decision-making situations, classic or crisp methods may not always be the most effective. Zadeh ^[2] developed FSs in 1965 as a technique to manage such inconsistency.

In FSs, Zadeh assigns membership grades in the range [0, 1] to a set of components. Since many of the set theoretic components of crisp conditions were given for FSs, Zadeh's work in this area is noteworthy. An improved version of the FS that contains membership and non-membership degrees was the intuitionistic fuzzy set (IFS), which was the subject of Atanassov's ^[3] research. IFSs have been shown to be useful and frequently used by academics to assess uncertainty and instability in data over the last few decades. To explain the hesitant fuzzy set (HFS) more forcefully than the preceding classical fuzzy set extensions, Torra ^[5] developed the HFS, which necessitates that the membership have a collection of potential values. In order to handle circumstances where experts are split between several possibilities for an indicator, alternative, element, etc. ^[6,7], a new model based on HFSs was recently put into place. HFSs are particularly effective at addressing the issues of group decision making when experts hesitate between several potential memberships for an element of a series of decisions ^[8]. Many extensions to HFS have been implemented to handle more complex environments ^[34], including the interval-valued hesitated fuzzy set ^[9,10], the hesitant-triangular fuzzy set ^[11,12], the hesitant-multiplicative set ^[13], the hesitant-fuzzy linguistic word set ^[14], the hesitant-fuzzy uncertain linguistic set ^[15], the dual HFS ^[16,17], and the generalized HFS ^[18]. Several scholars have used aggregation operators to apply the HFS notion to group decision-making settings ^{[19,20,21,22]}. The neutrosophic set (NS), a philosophical field and mathematical instrument for understanding the genesis, nature, and range of neutralities, was initially put forth by Smarandache ^[23]. It examines the origins, character, and scope of neutralities as well as how they interact with other ideational spectrums.

The NS generalizes the concepts of the classic set ^[27], fuzzy set, interval-valued fuzzy set, intuitionistic interval-valued fuzzy sets ^[28], dialetheist set, paradoxist set, and tautological set ^[29]. A NS is indicated by membership degree $\beta _{\Re }(\varkappa),$ indeterminacy $\alpha _{\Re }(\varkappa)$ and non membership degree $\gamma _{\Re }(\varkappa)$, where $\beta _{\Re}(\varkappa)$, $\alpha _{\Re }(\varkappa)$ and $\gamma _{\Re }(\varkappa)$ are elements from $\left] 0^{\bf{-, }}1^{+}\right[.$ Although NS philosophically generalises the notions of FS, IFS, and all the existing structures, it will be challenging to implement in real-world scientific and engineering situations. This concept is critical in many contexts, such as information fusion, where data from several sensors is integrated. Recently, neutrosophic sets have primarily been used in engineering and other sectors to make decisions. Wang et al. ^[30] proposed a single-valued neutrosophic set (SV-NS), which can handle inaccurate, indeterminate, and incompatible data challenges. Many other researchers have defined its extensions; for example, see ^[31]. On the one hand, an SV-NS is a NS that allows us to convey ambiguity, imprecision, incompleteness, and inconsistency in the real world. It would be more suitable to employ uncertain information and an inconsistent information matrix in decision-making ^[32,33,35]. SV-NSs, on the other hand, can be employed in scientific and technical applications since SV-NS theory is useful in modelling ambiguous, imprecise, and inconsistent data ^[36,37]. The SV-NS is suitable for collecting imprecise, unclear, and inconsistent information in multi criteria decision-making analysis due to its ability to easily capture the ambiguous character of subjective judgments. Many researchers work on the operators of the NSs, which can be seen as Domi operators ^[38], Einstein operators ^[39] and many others. Also, we can see the use of these operators in decision-making ^[40,41].

Motivation

The security categorization is used in the security controls selection process to choose the initial baseline of security controls (i.e., low or moderate) that will adequately safeguard the data and information systems that are housed within the cloud service environment. According to a risk assessment or a security requirement specific to an organization, a cloud service may call for the implementation of alternative or compensating security controls that were not part of the initial baseline, or it may call for the addition of additional security controls or enhancements to address specific organisational needs. In order to accomplish this, the Control Tailoring Workbook (CTW) gives the CSP a list of the FedRAMP security controls applicable to the cloud environment and helps identify the exception scenarios for the service offering. This allows the platform to be pre-qualified before resources are used to develop all of the other necessary FedRAMP documentation requirements. Your security systems and the procedures necessary for the GRC programme are regularly monitored by modern governance, risk, and compliance (GRC) solutions. These duties could include gathering evidence, risk assessment, risk management for vendors, staff training, and gap analysis. By actively protecting your data and assisting you in remaining compliant, you may earn the trust of your clients, business associates, suppliers, and investors. However, there are several GRC tools on the market, each claiming to be the best, making it easy to become perplexed if you are seeking GRC solutions. Therefore, in order to save you time and help you narrow down your search for the best GRC tools, we have chosen the top four. Using the SV-NHF environment, we choose the best option according to our system requirements.

In this research work, we administered the Einstein aggregation operators (AOs) to the SV-NHFS environment. i.e., the SV-NHFEWA, SV-NHFEOWA, SV-NHFEHWA, SV-NHFEWG, SV-NHFEOWG, and SV-NHFEHWG operators. Idempotency, boundness, and monotonicity are among the properties of the recommended operators that have been established. Such operators take the SV-NS AOs into consideration in hesitant scenarios, which is their main benefit. In the case of hesitant material, the lack of SV-NHFE AOs could lead to a scarcity of hesitant information.

This study's remaining sections are organised as follows: Briefly explained in Section 1 are some fundamental SV-FSs, HFSs, and SV-NHFS theory concepts. Section 2 provides an explanation of basic notations and ideas. In Sections 3 and 4, respectively, a unique idea of SV-neutrosophic hesitant fuzzy sets (SV-NHFSs) with Einstein aggregation operations is introduced. A collection of algebraic SV-NHF Einstein aggregation operators for aggregating uncertain data is provided in Section 5 for use in making decisions. Section 6 of the manuscript marks its conclusion.

2.   Preliminaries

Let's go over the basics of fuzzy sets, intuitionistic fuzzy sets, hesitant fuzzy sets, and neutrosophic sets in this part. Once they have been approved, these ideas will be implemented later.

Definition 1. ^[2] For a fixed set $\Xi$. A FS $\Re$ in $\Xi$ is presented as

for each $\delta _{\ell }\in \Xi,$ the membership degree (MD) $\Delta _{\Re}:\Xi \rightarrow \Delta$ specifies the degree to which the element $\delta_{\ell }\in \Re,$ where $\Delta \longrightarrow \left[0, 1\right]$ be the unit interval.

Definition 2. ^[3] For a fixed set $\Xi$. An IFS $\Re$ in $\Xi$ is presented as

$\Delta _{\Re }\left(\delta _{\ell }\right)$ is known as the MD and $\triangledown _{\Re }\left(\delta _{\ell }\right)$ is the non MD where $\left(\Delta _{\Re }\left(\delta _{\ell }\right), \triangledown _{\Re}\left(\delta _{\ell }\right) \right) \longrightarrow \left[0, 1\right].$ Moreover, it is required that $0\leq \Delta _{\Re }\left(\delta _{\ell}\right) +\triangledown _{\Re }\left(\delta _{\ell }\right) \leq 1,$ for each $\delta _{\ell }\in \Xi$.

Definition 3. ^[4] For a fixed set $\Xi$. A HFS $\Re$ in $\Xi$ is presented as

where $\Delta _{\Re _{h_{\varkappa }}}\left(\delta _{\ell }\right)$ is in the form of set, that's contained some possible values in unit interval, i.e., $\left[0, 1\right]$ which represent the MD of $\ \delta _{\ell }\in \Xi$ in $\Re$.

Definition 4. ^[23] Suppose $\Xi$ is a fixed set and $\Upsilon \in \Xi.$ A NS $\varkappa$ in $\Xi$ is denoted as MD $\Delta _{\varkappa }(\Upsilon),$ an indeterminacy $\Lambda_{\varkappa }(\Upsilon)$ and a non MD $\nabla_{\varkappa }(\Upsilon)$. $\Delta _{\varkappa }(\Upsilon),$ $\Lambda_{\varkappa }(\Upsilon)$ and $\nabla _{\varkappa }(\Upsilon)\ $are subset of $\ \left] 0^{\bf{-, }}1^{+}\right[$ and

The representation of NS $\varkappa$ is mathematically defined as:

where

Definition 5. ^[30] Let $\Xi$ be a fixed set and $\Upsilon \in \Xi.$ A SV-NS $A$ in $\Xi$ is defined as MD $\Delta _{A}(\Upsilon),$ an indeterminacy $\Lambda_{A}(\Upsilon)$ and a non MD $\nabla _{A}(\Upsilon)$. $\Delta_{A}(\Upsilon), \Lambda _{A}(\Upsilon)$ and $\nabla _{A}(\Upsilon)\ $are subsets of $\ \left[0, 1\right],$ and

The representation of SV-NS $A$ is mathematically defined as:

where

Definition 6. ^[24,25] Let $\Xi$ be a fixed set. The representation of SV-NHFS $\Re$ is mathematically defined as:

where $\Delta _{\ell _{\Xi }}(\Upsilon), \Lambda _{\ell _{\Xi }}(\Upsilon), \nabla _{\ell _{\Xi }}(\Upsilon)$ are set of some values in $[0, 1]$, indicate the hesitant grade of membership, indeterminacy and non membership of the element $\Upsilon \in \Re$ to the set $\Xi$.

Definition 7. ^[26] For a fixed set $\Xi,$ the $SV$-$NHFS$ $\Re$ is represented mathematically as follows:

where $\Delta _{\ell _{\Re }}(\Upsilon), \Lambda _{\ell _{\Re }}(\Upsilon)$ and $\nabla _{\ell _{\Re }}(\Upsilon)$ are sets of some values in $\left[ 0, 1\right]$ and denote the MD, indeterminacy and non MD sequentially. It satisfy the following properties:

and

and

For simplicity, we will use a pair $\Re =$ $(\Delta _{\ell _{\Re }}, \Lambda _{\ell _{\Re }}, \nabla _{\ell _{\Re }})$ to mean $SV$-$NHFS$.

Definition 8. Let

and

be two SV-NHFNs. Following are the fundamental set theoretic operations:

3.   Einstein operational laws based on SV-NHFEs

The application of t-norms in FS theory at the intersection of two FSs is widely recognized. T-conorms are being used to model disjunction or union. These are simple explanations of the conjunction and disjunction in mathematical fuzzy logic syntax, and they are used to combine criteria in MCDM. The Einstein sum ($\oplus _{\epsilon }$) and Einstein product ($\otimes_{\epsilon }$) are case studies of t-conorms and t-norms, respectively, and are stated in the SV-NHF environment as follows.

Based on the above Einstein operations, we give the following new operations on SV-NHF environment.

Definition 9. Let $\Re _{1} = \left(\upsilon _{h_{\ell _{1}}}, \tau _{h_{\ell_{1}}}, \Upsilon _{h_{\ell _{1}}}\right)$ and $\Re _{2} = \left(\upsilon_{h_{\ell _{2}}}, \tau _{h_{_{\ell _{2}}}}, \Upsilon _{h_{_{\ell_{2}}}}\right)$ be two SV-NHFEs and, then

4.   SV-NHF Einstein aggregation operators

Within this section, we explained several novel Einstein operators for SV-NHFNs, namely the SV-neutrosophic hesitant-fuzzy Einstein weighted averaging (SV-NHFEWA) operator, the SV-neutrosophic hesitant-fuzzy Einstein ordered weighted averaging (SV-NHFEOWA) operator, the SV-neutrosophic hesitant-fuzzy Einstein weighted geometric (SV-NHFEWG) operator, and the SV-neutrosophic hesitant-fuzzy Einstein ordered weighted geometric (SV-NHFEOWG) operator.

4.1.   SV-Neutrosophic hesitant fuzzy Einstein weighted averaging operators

Definition 10. Let $\Re _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath}}}}, \tau_{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\Re_{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1.$ Then $SV$-$NHFEWA$:$SV$-$HFN^{\tilde{\imath}}\longrightarrow$ $SV$-$NHFN$ such that

is called the SV-neutrosophic hesitant fuzzy Einstein weighted averaging operator.

Theorem 1. Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath}}}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs. Then the aggregation result using SV-NHFEWA, we can achieve the following

where $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}$ with $\Im _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1.$

Proof. We will demonstrate the theorem by mathematical induction. For $\tilde{\imath} = 2$

Since both $\Im _{1}._{\varepsilon }\delta _{1}$ and $\Im _{2}._{\varepsilon}\delta _{2}$ are SV-NHFNs, and also, $\Im _{1}._{\varepsilon }\delta_{1}\oplus _{\varepsilon }\Im _{2}._{\varepsilon }\delta _{2}$ is a SV-NHFN.

Then

Thus, the result holds for $\tilde{\imath} = 2$. Assume that the results holds for $\tilde{\imath} = \gimel$

Now we will prove for $\tilde{\imath} = \gimel +1$

Thus

There are some properties which are fulfilled by the SV-NHFEWA as follows:

Theorem 2. Suppose $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath} }}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath} }}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a group of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}$ with $\Im _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1;$ then we have the following:

${\bf{(1)}}$ Boundary:

where

${\bf{(2)}}$ Monotonicity: Let $\delta _{\hat{\jmath}}^{\ast } = \left(\dot{ \upsilon}_{h_{\ell _{\hat{\jmath}}}}, \dot{\tau}_{h_{\ell _{\hat{\jmath} }}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs. Then

Proof. (1) Let $f(x) = \frac{1-x}{1+x}, x\in \lbrack 0, 1],$ then $f^{\prime }(x) = \frac{ -2}{\left(1+x\right) ^{2}} < 0,$ so $f(x)$ is a decreasing function. Let max $\Xi _{\delta _{\hat{\jmath}}} = \max_{1\leq \hat{\jmath}\leq \tilde{\imath} }\max_{\Xi _{\delta _{\hat{\jmath}}}\in \upsilon _{h_{\ell _{\hat{\jmath} }}}}\Xi _{\delta _{\hat{\jmath}}},$ min $\Xi _{\delta _{\hat{\jmath} }} = \min_{1\leq \hat{\jmath}\leq \tilde{\imath}}\min_{\Xi _{\delta _{\hat{ \jmath}}\in \kappa _{h_{\ell _{\hat{\jmath}}}}}}\Xi _{\delta _{\hat{\jmath} }}$ and min $\Xi _{\delta _{\hat{\jmath}}} = \min_{1\leq \hat{\jmath}\leq \tilde{\imath}}\min_{\Xi _{\delta _{\hat{\jmath}}\in \Upsilon _{h_{\ell _{ \hat{\jmath}}}}}}\Xi _{\delta _{\hat{\jmath}}}$

Since $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}$ with $\Im _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1,$ we have

Thus,

Consider $g(y) = \frac{2-y}{y}, y\in (0, 1],$then $g^{\prime }(y) = -\frac{2}{y^{2} }, i.e., g(y)$ is a decreasing function on $(0, 1].$ Let max $\kappa _{\delta _{ \hat{\jmath}}} = \max_{1\leq \hat{\jmath}\leq \tilde{\imath}}\max_{\kappa _{\delta _{\hat{\jmath}}}\in \tau _{h_{\ell _{\hat{\jmath}}}}}\kappa _{\delta _{\hat{\jmath}}}$, min$\kappa _{\delta _{\hat{\jmath}}}$ = min$_{1\leq \hat{\jmath}\leq \tilde{\imath}}$min$_{\kappa _{\delta _{\hat{\jmath} }}\in \tau _{h_{\ell _{\hat{\jmath}}}}},$and min$\kappa _{\delta _{\hat{ \jmath}}}$ = min$_{1\leq \hat{\jmath}\leq \tilde{\imath}}$min$_{\kappa _{\delta _{\hat{\jmath}}}\in \Upsilon _{h_{\ell _{\hat{\jmath}}}}}.$

Let $SV-NHFEWA(\delta _{1}, \delta _{2}, ...., \delta _{\tilde{\imath}}) = \delta \left(\Xi _{\delta _{\hat{\jmath}}}\right),$ then $\leq \Xi _{\delta _{ \hat{\jmath}}}\leq.$

Definition 11. Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath}}}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{ \imath}}\Im _{\hat{\jmath}} = 1.$ Then $SV-NHFEWG:SV-NHFN^{\tilde{\imath} }\longrightarrow SV-NHFN$ such that

is called the SV-neutrosophic hesitant fuzzy Einstein weighted geometric operator.

Theorem 3. Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath}}}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs. Then the aggregation result using SV-NHFEWG, we can achieve the following

where $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}$ with $\Im _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1.$

There are some properties which are fulfilled by the SV-NHFEWG as follows:

Theorem 4. Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath}}}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}$ with $\Im _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1;$ then we have the following:

${\bf{(1)}}$ Boundary:

where

${\bf{(2)}}$ Monotonicity: Let $\delta _{\hat{\jmath}}^{\ast } = \left(\dot{ \upsilon}_{h_{\ell _{\hat{\jmath}}}}, \dot{\tau}_{h_{\ell _{\hat{\jmath} }}}, \Upsilon _{h_{\ell _{\hat{\jmath}}}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs. Then

We developed the following ordered weighted operators based on SV-NHFNs.

Definition 12. (1) Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath} }}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath} }}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1.$ Then $SV$-$NHFEOWA$: $SV$-$NHFN^{\tilde{ \imath}}\longrightarrow$ $SV$-$NHFN$ such that

where $\delta _{\rho (\hat{\jmath})}$ be the $\hat{\jmath}$th largest in them, is called the SV-neutrosophic hesitant fuzzy Einstein ordered weighted averaging operator.

(2) Let $\delta _{\hat{\jmath}} = \left(\upsilon _{h_{\ell _{\hat{\jmath} }}}, \tau _{h_{\ell _{\hat{\jmath}}}}, \Upsilon _{h_{\ell _{\hat{\jmath} }}}\right)$ $(\hat{\jmath} = 1, 2, ....., \tilde{\imath})$ be a collection of SV-NHFNs, $\Im = (\Im _{1}, \Im _{2}, ...., \Im _{\tilde{\imath}})^{T}$ are the weights of $\delta _{\hat{\jmath}}\in \lbrack 0, 1]$ with $\sum_{\hat{\jmath} = 1}^{\tilde{\imath}}\Im _{\hat{\jmath}} = 1.$ Then $SV-NHFEOWG:SV-NHFN^{\tilde{ \imath}}\longrightarrow SV-NHFN$ such that

where $\delta _{\rho (\hat{\jmath})}$ be the $\hat{\jmath}$th largest in them, is called the SV-neutrosophic hesitant fuzzy Einstein ordered weighted geometric operator.

5.   A method for decision making using suggested operators

Here, we designed a system for SV-NHF details information to be incorporated into MAGDM to represent uncertainty.

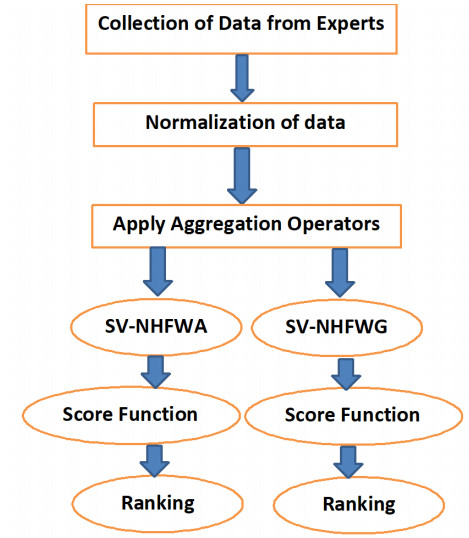
5.1.   Algorithm's steps

Step-1: The collection of data from experts.

Step-2: Normalize the experts data based on the benefit and cost.

Step-3: Apply the aggregation Operators as given below The SV-NHFWA operator

and the SV-NHFWG operator

Step-4: Find the score value based on the score function given below

Here ${M_{\delta }}, {N_{\delta }}$ and ${S_{\delta }}$ represent the number of the elements in each of the MD, an indeterminacy and non MD respectively.

Step-5: Rank the alternative based on score values and find the best option.

In the Figure 1, You can see the flow chart of the algorithm for decision-making.

5.2.   Numerical example

Cybersecurity is crucial since it guards against theft and destruction of many types of data. This covers delicate information, personally identifiable information (PII), protected health information (PHI), personal data, data pertaining to intellectual property, and information systems used by the government and business.

Case study: We provide a real-world example of cybersecurity types and challenges. Our aim is to choose the best type of security to handle and protect.

(1) $\mathring{C}_{1}:$ Internet of things security: In the context of the Internet of Things (IoT), where almost any physical or logical entity or object may be given a unique identifier and the capability to communicate autonomously over a network, "Internet of Things privacy" refers to the special considerations necessary to protect the information of individuals from exposure in the IoT environment. Insecure communications, security mechanisms that were originally developed for desktop computers but are difficult to implement on resource-constrained IoT devices, data leaks from IoT systems, malware risks, cyber attacks, secure networks, and secure data are the most frequent Internet of Things security issues.

(2) $\mathring{C}_{2}:$ Cloud security: Cloud computing's use of data privacy makes it possible to collect, store, move, and share data over the internet without endangering the privacy of individual users' personal information. Misconfiguration, which is a major contributor to cloud data breaches, unauthorised access, insecure interfaces and APIs, account hijacking, a lack of visibility, external data sharing, malicious insiders, and cyber attacks are a few obstacles.

(3) $\mathring{C}_{3}:$ Network security: By limiting the introduction or spread of a wide range of potential dangers within a network, network security is a set of technologies that safeguards the usefulness and integrity of a company's infrastructure. Among the challenges are numerous misconfigurations, lax oversight of privileged access, poor tool compatibility, a lack of visibility, and controls that are out of date with infrastructure changes.

Criteria: $\delta 1$ = Control of Hijacking data, $\delta 2$ = Lack of visibility, $\delta 3$ = Secure networks, and $\delta 4$ = Cyber attacks. The given weight vector is $\Im$ = (0.314, 0.355, 0.331)$^{T}$. Table 1 showing all the collective data of DM.

$\Im$ = (0.34, 0.35, 0.31)$^{T}$

Step 1. Because the attributes are uniform so there are no need to normalized.

Step 2. By exploiting the proposed SV-NHFWA operator, we achieve the overall preference values $\delta _{\tilde{\imath}}$ of the alternative $\delta _{\tilde{\imath}}(\tilde{\imath} = 1, 2, 3, 4).$ For instance

Similarly for other alternatives

Step 3. The score values are obtained as

Step 4.

Therefore

The best choice is $\delta _{2}.$

For SV-NHFWG operator

Here we start from all the collective data of the DM, which is shown in Table 2 as well,

Step 2. By exploiting the proposed SV-NHFWG operator, we achieve the overall preference values $\delta _{\tilde{\imath}}$ of the alternative $\delta _{\tilde{\imath}}(\tilde{\imath} = 1, 2, 3, 4).$

Step 3. The score values are obtained as

Step 4.

Therefore

The best choice is $\delta _{2}.$ The comparison analysis using $SV$-$NP$ $HFWA$ and $SV$-$NP$ $HFWG$ are shown in Table 3.

Therefore the best choice is $\delta _{1}.$ After applying test Step 1, we came up with the identical best alternative $\delta _{1}$ that we had in our suggested numerical case analysis. Test Steps 2 and 3, We are now testing the validity test Steps 2 and 3 to demonstrate that the proposed approach is reliable and relevant. To this end, we first transformed the MAGDM problem into three smaller sub-problems such as $\{\delta _{1}, \delta _{2}, \delta _{3}\}$ and $\{\delta _{2}, \delta_{3}, \delta _{4}\}$. We now apply our suggested decision-making approach to the smaller problems that have been transformed and have obtained the following ranking of alternatives: $\delta _{1} >$ $\delta _{3} > \delta _{4},$ $\delta _{1} >$ $\delta _{2} > \delta _{3}$ and $\delta _{2} > \delta _{3} > \delta_{4}$ respectively. We find that $\delta _{1} > \delta _{2} > \delta _{3} > \delta_{4}$ is the same as the standard decision-making approach results when assigning a detailed ranking.

6.   Conclusions

A strong fusion of a SV-NS and HFS called SV-NHFS was developed for situations where each object has a range of potential values that are dictated by MD, indeterminacy, and non MD. A SV-NHFEWA operator, SV-NHFEWG operator, SV-NHFEOWG operator and SV-NHFEOWA operators are all suggested in this article. Additionally, based on the SV-NHFEWA and SV-NHFEWG operators, we suggested novel MADM approach. More information on the advantages of these techniques is provided below.

(1) First, there are important characteristics of the SV-NHFEWG and SV-NHFEWA operators, including idempotency, commutativity, boundedness, and monotonicity.

(2) Second, the conversion of the SV-NHFEWA and SV-NHFEWG operators to the earlier AOs for SVNHFSs demonstrates the adaptability of the suggested AOs.

(3) Third, the results obtained by the SV-NHFEWA and SV-NHFEWG operators are accurate and dependable when compared to other existing techniques for MADM problems in an SV-NHF context, demonstrating their applicability in real-world situations.

(4) The methods for MAGDM that are suggested in this paper are able to further acknowledge more association between attributes and alternatives, demonstrating that they have a higher accuracy and a larger reference value than the methods currently in use, which are unable to take into account the inter-relationships of attributes in practical applications. This indicates that the methods for MAGDM that are suggested in this paper can recognize even more associations between attributes.

(5) The proposed aggregation operators are also put to use in practise to look at symmetrical analysis in the choice of a workable cybersecurity control selection technique.

(6) Future research on personalized individual consistency control consensus problems, consensus reaching with non-cooperative behavior management decision-making problems, and two-sided matching decision-making with multi-granular and incomplete criteria weight information could all benefit from the use of the proposed AOs. The degrees of membership, abstention, and non-membership have no bearing on this examination of the restrictions imposed by proposed AOs. On this side of the intended AOs, a new hybrid structure of interactive and prioritized AOs may be observed being implemented.

(7) We will examine the conceptual framework of SV-NHFSs for Einstein operations in future work using innovative decision-making approaches like as TOPSIS, VIKOR, TODAM, GRA, and EDAS. We'll also talk about how these techniques are used in domains including analytical thinking, intelligent systems, social sciences, finance, management of human resources, robotics, navigation, horticulture, soft computing, and many others.

Acknowledgements

The author (Muhammad Naeem) would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4310396DSR41.

Conflict of interest

The authors declare no conflict of interest.