1.
Introduction
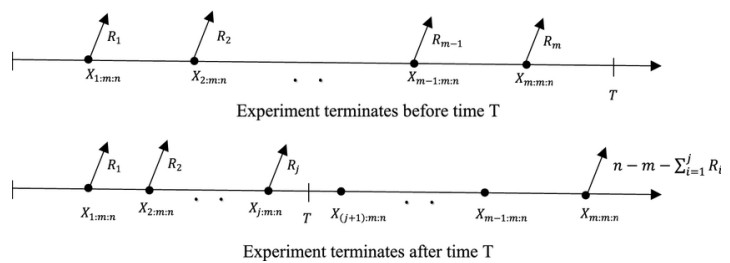
In the analysis of survival and reliability data, different engineering and medical applications arise. Due to the limitations of cost and time, life-testing experiments are frequently performed under censoring schemes. In the literature contexts, Type-I and Type-II censoring schemes are initially used. In Type-I censoring, the life testing experiment is terminated at a pre-determined time T and the total number of failures is considered a random variable, while in Type-II censoring, the total number of failures is pre-fixed and in this case, the termination time is considered a random variable. The weakness of the traditional Type–I and Type-II censoring schemes is that they do not have the flexibility to remove some of the surviving units at different stages of the life-testing experiment. Recently, a generalization of Type-II censoring scheme called progressive Type-II censoring is the most commonly used. Suppose that n units are put on the life test at time zero for failure and the experimenter initially specified the number m of units that will be failed during the life test with the proposed censored scheme: R=(R1,R2,...,Rm) of random removals. The mechanism to perform the life test under the progressive Type-II censoring scheme is carried out as follows: At the time of the first failure, x1:m:n, R1 of the remaining n−1 surviving units are randomly removed from the test. Continuing on, at the second failure time x2:m:n, R2 of the remaining n−R1−1 surviving units are randomly removed from the test and so on. This experiment is terminated at the time xm:m:n of the mth failure and at this time, the remaining n−m−∑ni=m+1Ri surviving units are all removed.
Balakrishnan [1] and Aggarwala and Balakrishnan [2] have introduced the concept of Type-II progressive censoring and an algorithm to simulate progressively Type-II censored samples from any continuous distribution. Recent statistical inferences for many lifetime distributions are also included in [3,4,5,6,7,8,9,10].
In many real practical settings, experimenters need to control the termination time of the life test and to change the number of removed units during the test. For these reasons, Ng et al. [11] have proposed the adaptive progressive Type-II censoring scheme (APT-II). In this scheme, the expected value of the ideal time T>θ for terminating the life test is initially determined. Now, if (xi:m:n,i=1,2,…,m) are the m completely observed failure times and(Ri,i=1,2,…,m) are the removed units at the times xi:m:n,i=1,2,…,m, respectively. APT-II censoring scheme is carried out as follows: if xm:m:n<T, the test is terminated at xm:m:n and we will have the standard progressive Type-II censoring, in this case: Rm=n−m−∑mi=1Ri, otherwise, if xj:m:n<T<xj+1:m:n, where j+1<m and xj:m:n is the jth failure before the ideal time T, then any surviving units will be removed from the test by placing Rj+1=Rj+2=…=Rm=0, and at the time xm:m:n all the remaining units are removed, in this case: Rm=n−m−∑ji=1Ri. This scheme provides a design in which the experimenter is assured of getting m observed failure times for efficiency of statistical inference and the total test time will be closest to the ideal time T. Figure 1 illustrates a schematic presentation of the life testing experiment based on the APT-II censoring scheme.
Many authors have considered classical and Bayesian estimations for the parameters of different distributions based on APT-II. Examples of many others, under the APT-II censoring scheme, are: Chen and Gui [12] discussed the estimation problem of a lifetime distribution with a bathtub-shaped failure rate function, Abu-Moussa et al. [13] discussed the maximum likelihood estimation for the Gompertz distribution. Mahmoud et al. [14] studied the Bayes estimation of the Pareto distribution. Asadi et al. [15] investigated the accelerated life test in Gompertz distribution for the evaluation of virus-containing micro-droplets data. AL Alotaibi et al. [16] considered the estimation of parameters of the XLindley distribution, Almalki et al. [17] have explored the partially constant-stress accelerated life tests model for estimation of the parameters of the Kumaraswamy distribution and Ahmad et al. [18] adopted both Bayesian and non-Bayesian inference for the exponentiated power Lindley distribution.
Using the power transformation method (see Shukala and Shanker [19]), Bhat and Ahmad [20] introduced a new form of Rayleigh distribution called the Power Rayleigh distribution (PRD) with probability density (PDF), cumulative distribution (CDF) and the reliability functions given, respectively, by:
The hazard rate function (HRF) of the PRD is given by
As a generalization of the standard Rayleigh distribution, which can be used in modeling the lifetimes of many pieces of equipment like resistors, transformers and capacitors (see Kundu and Raqab [21] and Ateeq et al. [22]), the hazard rate function of PRD is constant when β=0.5, increasing when β<0.5 and decreasing when β>0.5. For this flexibility, PRD can be utilized for more reliability and survival data analysis. Particularly, as shown by Bhat and Ahmad [20], this new distribution has superiority for modeling the stress and strength data. The PDF and the HRF of the PRD with different combinations of (θ,β) are presented in Figure 2.
Under the APT-II censoring scheme. Many authors have adopted statistical inference for the Rayleigh distribution and some of its generalizations. Recent studies were completed by Mahmoud and Ghazal [23] for the Exponentiated Rayleigh distribution, Almetwally et al. [24] for the Generalized Rayleigh distribution, Panahi and Moradi [25], Gao and Gao [26] and Fan and Gui [27] for the Inverted Exponentiated Rayleigh distribution. To the best of our knowledge, there exists no statistical inference about the parameters of the PRD based on any censoring scheme. The aim of this paper is to focus on classical and Bayesian point and interval estimation of the unknown parameters of the PRD using the APT-II censored data. This will extend the application of PRD as a life model to include more reliability and survival data.
The rest of this paper is organized as follows: Section 2 is devoted to point and interval estimation using the likelihood approach. Bayesian estimation under the squared error (SE) and the general entropy (GE) loss functions is explored in Section 3. In Section 4, both point and interval estimates are presented and the Bootstrap sampling method is also implemented. To evaluate the performance of the obtained point and interval estimates, a Monte Carlo simulation study is conducted in Section 5. Section 6 illustrates the application of the developed estimation procedure to a set of real-life data. Finally, a conclusion about this work is summarized in Section 7.
2.
Maximum likelihood estimation
Based on an APT-II observed censored sampled data from a continuous distribution with PDF f(x;φ) and CDF F(x;φ), Ng et al. [11] derived the likelihood function for a vector of parameter φ in the form:
where: xi=xi,m,n cj=n−m−∑ji=1Ri and C is a constant that is independent of the parameters φ. Substituting the corresponding formulas for f(xi;θ,β), F(xi;θ,β) of PRD from Eqs (1.1) and (1.2) in Eq (2.1). This implies that the corresponding likelihood function of the parameters θ and β using APT-II data is given by:
Therefore, the natural logarithmic function of the likelihood function is
Differentiating both sides of Eq (2.2) with respect to θ and β and equating the derived equations to zero, we get the likelihood equations:
When the shape parameter β is known, solving Eq (2.4) with respect to θ, the maximum likelihood estimate (MLE) of θ exists in an explicit form given by
When the two parameters are both unknown, numerical methods should be used to solve the system of the nonlinear equations in Eqs (2.4) and (2.5). In this paper, a multivariate Newton-Raphson numerical method is implemented to obtain the approximated values for the MLEs (ˆθ, ˆβ) of θ and β. Utilizing the invariance property of the MLEs, the MLE of the reliability function at a given time t is given by:
Under the APT-II censoring scheme, another desired statistical inference for the PRD is to find confidence interval estimates for the unknown parameters θ and β. It is mathematically difficult to construct exact confidence intervals because the distributions of the MLEs of θ and β are not in closed forms. The observed Fisher information matrix of (θ, β) can also be used to find approximated confidence intervals for the two unknown parameters (see Lawless [28]) which are defined as:
where:
Hence, the approximated variance-covariance matrix of (ˆθ, ˆβ) is simplified by
Consequently, based on the large sample theory of the MLEs, the asymptotic 100(1−α)% confidence intervals (ACIs) for θ and β are constructed respectively as:
where zα2 is the (1−α)% quantile of the standard Normal distribution, and ˆv11, ˆv22 are the diagonal elements of ˆv. Accordingly, the approximate 100(1−α)% confidence intervals for the reliability function at a given time t is
3.
Bayesian estimation
In statistical inference, the Bayesian estimation approach is a complement part to the conventional likelihood estimation approach. To apply the estimation procedures using the Bayesian approach, prior information of the parameters θ and β should be determined first. When no previous information is available about these parameters, it is convenient to specify their priors in such a way that their joint prior is proportional to their likelihood function. In this research, the joint prior distribution of the parameters θ and θ is proposed to take the form:
where π1(θ) is the Inverse Rayleigh distribution with scale parameter γ and π2(β|θ) is the Exponential distribution with scale parameter (λθ2) with prior densities given, respectively, by:
Substituting for π1(θ) and π2(β|θ) from Eqs (3.2) and (3.3) in Eq (3.1), the joint prior of θ and β has the form
Now, combining Eq (2.1) and (3.3), the posterior functions of θ and β is:
where: u=∑mi=1x2βi+∑ji=1Rix2βi+cjx2βm. Clearly, the joint prior given in Eq (3.4) is proportional to the posterior function of (θ,β) in Eq (3.5) and thus, it can be considered a conjugate prior. The conditional posteriors of θ and β can be obtained, respectively, as:
3.1. Bayesian estimation when the shape parameter is known
When the shape parameter β is known (As in the case of the standard Rayleigh distribution). The posterior function π∗(θ,β|x) given in Eq (3.4) becomes a function of θ only given by
Consequently, the Bayes point estimate of θ under the squared error loss function (SE) is obtained as the mean of the posterior, which is given by:
Similarly, the Bayes point estimate of θ under the general entropy loss function (GE) indexed with parameter α>0 is obtained as:
When the shape parameter is known, another common Bayesian inference is to find a credible interval in the form [ll,lu] for the parameters θ. The (1−α)% credible interval for the parameter θ can be obtained as
Substituting for π∗(θ|β,x) from Eq (3.5) in Eq (3.10) and simplifying the integral in the above equation, the lower and the upper bounds of the (1−α)% credible interval for θ can be obtained from the following equation:
where: z=(u2+γ2+λβ),andIg(x,y)=1Γ(y)∫x0ty−1e−t∂t is the incomplete Gamma function.
In addition to the constraint Eq (3.12), a (1−α)% highest posterior credible intervals (HPD) credible interval for θ can also be obtained by adding the constraint:
3.2. Bayesian estimation when both parameters are unknown
When the parameters θ and β are both unknown, it is difficult to obtain explicit forms of their Bayes point estimates under SE or GE loss functions because, in this case, the corresponding integrals:
cannot be found in closed forms for any number α∈R.
To overcome this problem, the Markov Chain Monte Carlo (MCMC) method can be used to approximate the above integrals. In this paper, we use the common type of MCMC, which is called the Metropolis-Hasting (M-H) developed by Metropolis et al. [29] and extended by Hasting [30] with Gibbs sampling to find Bayes point and interval estimates for the parameters θ and β. Assuming normal is the target distribution, the procedure of implementing the MCMC is performed through the following steps:
Step 1. Set the initial values of θ and β, (θ(0),β(0)).
Step 2. Put j = 1.
Step 3. Simulate θ∗, β∗ from the normal distributions N(θ(j−1),ˆv11), N(β(j−1),ˆv22) respectively, where ˆv11 and ˆv22 are the diagonal elements of the variance-covariance matrix computed given the values of θ(j−1),β(j−1).
Step 4. Compute the acceptance ratios:
Step 5. Generate u1, u2 from the uniform distribution U(0,1).
Step 6. If u1≤rθ∗, u2≤rβ∗, set: θ(j)=θ∗,β(j)=β∗, else: θ(j)=θ(j−1),β(j)=β(j−1).
Step 7. Use the generated sample to obtain an estimate of the reliability function: R(j)(t).
Step 8. Set j=j+1.
Step 9. Repeat Step 3- Step 8 N times to have (θ(1),θ(2),…,θ(N)),(β(1),β(2),…,β(N)) Then the Bayesian estimates of θ and β under SE are given, respectively, by
And under the GE, the Bayesian estimates of θ and β are given, respectively, by
where α is the parameter of the GE function and M is the number of iterations before the stationary distribution is achieved (the burn in-period) from N (the total number of iterations).
Based on the (M-H) algorithm, the Bayesian estimations of the reliability function under SE and GE at a given time t are:
Ascending order the values of θ(i), β(i) and R(i)(t), i=M+1,…,N generated by the M-H algorithm. The 100(1−α)% symmetric two-sided credible intervals of θ, β and the reliability function R(t) are given, respectively, by:
Using the method of Chen and Shao [31]. The symmetric 100(1−α)% two sided HPD credible intervals of θ, β and the reliability function R(t) are given, respectively, by:
where R∗(t) is the estimated R(t) by the (M-H) algorithm and i∗ is chosen such that:
where [y] denotes the greatest integer less than or equal y.
4.
Estimation using the Bootstrap technique
One common method to estimate the parameters of the underlying distribution is the Bootstrap resampling technique. This method gives better estimates of the parameters than the approximate Bayes and likelihood estimates when the effective sample m is small enough. Details about the Bootstrap estimation method are explored in Hall [32] and Efron and Tibshirani [33]. The procedure to obtain point and interval estimates for the parameters θ and β by this method is described in the following steps:
Step 1. Based on the specified values of n, m, T, R, ncompute ˆθmle and ˆβmle.
Step 2. Using ˆθmle and ˆβmle generate a Bootstrap resample.
Step 3. Calculate the Bootstrap estimates ˆθ1p and ˆβ1p.
Step 4. Repeat the steps 2 and 3 up to k times to have ˆθ1p,ˆθ2p,…,ˆθkp,ˆβ1p,ˆβ2p,…,ˆβkp.
Step 5. Use the generated sample to obtain an estimate of the reliability function: R(t)(1)p,R(t)(2)p,…, R(t)(k)p.
Step 6. Compute the Bootstrap point estimates
Step 7. Rearrange the Bootstrap estimates in ascending order to have 100(1−α)% percentile confidence intervals for θ, β and the reliability function R(t), respectively, as:
5.
Monte Carlo simulation study
We evaluate the performance of the point and interval estimates obtained in the previous sections. Thus, Monte Carlo simulations are performed by generating 1000 APT-II samples from the PRD with different settings of sample size, affective sample size, true parameter values and ideal termination time with the following censoring schemes:
SC.I presents left censoring at the beginning of the experiment, SC.II presents ordinary Type-II censoring and SC.III presents progressive APT-II at the expected mid-termination time of the experiment.
The simulation process is implemented through the following steps:
1) Determine the values of n, m, R, T and set the true parameter values (θ, β).
2) Generate a random sample of size n from the uniform distribution and apply the Balakrishnan and Sandho [34] algorithm to generate a random sample of size m from the PRD using the relation:
3) Determine the value of j and remove all observations greater than xj.
4) Generate (m − j − 1) Type-II censored sample from [f(xj)1 − F(xj+1)] where f(x) and F(x) are the PDF and the CDF of the PRD, and stop the experiment at xm.
5) Obtain point and interval estimates of the parameters θ, β and the reliability function at time t=1.5.
6) Repeat steps 2–5 and compute the average absolute biases (ABs), the mean squared errors (MSEs) of the point estimates, the average lengths (ALs) and the coverage probabilities (CPs) of the interval estimates.
For the case where the shape parameter β is assumed to be known, the true parameter values are taken to be (θ=1, β=0.8), the values of n and m are determined such that:
with the ideal terminations T=1 and T=2.
When both parameters are assumed to be unknown, the true parameter values are considered to be {(θ,β)=(2,0.4) and (2,0.8)} with ideal termination times (T=200 for (θ=2,β=0.4)) and (T=20 for (θ=2,β=0.8)), the sample sizes are proposed to be n=80, n = 50 and the effective sample size m is indicated such that the proportion of observed failures r=(mn) are: 0.80, 0.60 and 0.40.
In the Bayesian estimation, the values of the hyperparameters (γ, λ) are chosen in a way such that the prior mean is equal to the expected value of the unknown parameter; see Kundu [35]. The shape parameter of the GE loss is fixed to be equal to α=1.1. Bayesian point estimates and associated credible intervals are computed by generating 12000 samples using the M-H algorithm and discarding the first 2000 corresponding values of (θ, β) as burn-in periods. Simulation results are listed in Tables 1–7. Tables 1–7 manifest the following conclusions:
1) All the obtained (point and interval) estimates have satisfactory behavior and gave an efficient inference about the unknown parameters of the PRD and the reliability function.
2) All estimates perform better with an increase in sample size n, the proportion of effective sample size r and the ideal time T.
3) The point and interval estimates obtained by the Bootstrap sampling method are clearly better than their corresponding estimates obtained by the conventional likelihood method.
4) Under the same settings, the Bayes estimates obtained by the MCMC method are better than estimates obtained by the Likelihood and Bootstrap classical approaches.
5) We notice that the obtained estimates become better with a decrease in the value of the shape parameter.
6) It is noted that the CPs of the obtained interval estimates are almost close at a 95% confidence level, but when the lengths of (Asymptotic, Bootstrap or Credible) interval estimates become relatively small enough, the CPs of the interval estimates are strictly less than their nominal 95% confidence level.
7) In comparing schemes 1–3, we conclude that:
(i) Point estimates obtained under the progressive SC.II scheme are better than point estimates obtained under progressive (SC.I and SC.III) censoring schemes.
(ii) Interval estimates obtained under SC.III have smaller lengths than interval estimates obtained under progressive (SC.I and SC.II) schemes.
6.
Application to real data
We illustrate the application of the developed estimation methods. The inferential procedure is investigated in a real data set from Al-Aqtash et al. [36] This data set consists of 66 observations representing the breaking stress of carbon fibers of 50 mm length (GPa). Bhat and Ahmad [20] have analyzed this data to confirm the priority fit of the PRD in real-life data as compared to other generalizations of Rayleigh and Weibull distributions. Assuming the PRD modeling for this data, the MLEs of the parameters θ and β using the complete data set (see Bhat and Ahmad [20]) are ˆθcom=4.850, ˆβcom=1.721, the asymptotic 95% confidence intervals for θ and β are (2.818,6.883) and (1.396,2.045). The Kolmogorov-Smirnov (K-S), the Akaike's information and the negative log-likelihood goodness of fit test statistics are 0.08, 172.14 and 176.33, respectively, with a p-value = 0.768. Figures 3–6 present the empirical and the theoretical CDF, the histogram plot, the empirical survival function and the empirical cumulative hazard function of these data.
To confirm the validity of the PRD for the APT-II censored data, we generate APT-II censored data from the original data with m=40 and T=3.5 using two different censoring schemes as presented in Table 8. Based on the APT-II censored data, the performance of point estimates ˆθ and ˆβ of θ and β, respectively, are measured in terms of their relative efficiencies defined as:
The relative efficiencies of the point estimates and the ABLs of the interval estimates are listed in Table 9. Based on (2,0∗20,2,0∗20) and (8,0∗25,8,0∗15) APT-II censoring schemes, Figures 7 and 8 present the trace and the histogram plots for point estimates of (θ, β) using 12000 samples generated by the MCMC method and assuming M=2000 is the burn-in period. As clearly observed from Table 9, all point estimates have high relative efficiency and The Bayes point estimates under GE are the best among others as they have the highest relative efficiency. All estimates became better with a decrease in the sum of random removals and the interval estimates are also very close to the approximate intervals for (θ, β) obtained by the asymptotic distributions using the complete data set. It is clearly observed from Figures 7 and 8 that Bayesian estimates obtained by the MCMC converge to their means and thus the MCMC is recommended.
7.
Conclusions
In this paper, based on the Type-II censoring, we have considered point and interval estimation for the parameters and the reliability function of PRD via likelihood, Bayesian and Bootstrap estimation methods. The Bayesian estimation approach is carried out under the SE and GE loss functions. When the shape parameter is known, the ML and Bayesian point estimates of the scale parameter, as well as the corresponding asymptotic confidence, credible and HPD credible intervals, are obtained in explicit forms. When both parameters are unknown, the MLEs and the asymptotic confidence intervals of the unknown parameters are obtained using the Newton-Raphson numerical method, while Bayesian point estimators and associated credible and HPD credible intervals are obtained based on the MCMC method.
To evaluate the performance of the obtained point and interval estimates, a simulation study is conducted in different combinations of the life testing experiment, and the estimation procedure is also applied to a real-life data set. Concluding results indicated that both point and interval estimates are efficient and have good characteristics for estimating the model parameters with a specific preference for the Bayesian point and interval estimates obtained under the GE loss function.
As a generalization of the standard Rayleigh distribution, the main conclusions conducted from this work confirmed that the PRD is an appropriate lifetime model and can be effectively used with Type-II censored data. Future researchers may extend this work by employing PRD with other censoring schemes.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: