Simultaneous segmentation and classification of colon cancer polyp images using a dual branch multi-task learning network

1.   Introduction

The goal of this paper is to develop a simple model for understanding the effectiveness of two control measures for an infectious disease: the isolation of symptomatic individuals and contact tracing (and the subsequent quarantine). Our secondary goal is to develop a model that can be easily and reliably solved. Our starting point is the work of Fraser et al. ^[1], which studies the effectiveness of the same two control measures. The question is, for a given disease with its set of disease parameters, how successful the two measures need to be in order for the epidemic outbreak to be controllable. The main result of that work was elaborated and applied to COVID-19 ^[2].

The technique in ^[1] is to define and keep track of the sizes of different subsets of the infected population as they change over time. In particular, it defines the quantity $Y(t, \tau, \tau')$, where $Y(t, \tau, \tau') d \tau d \tau'$ is the number of individuals at time $t$ who were infected on the time interval $(t-\tau, t-\tau+d\tau)$ by individuals who were in turn infected on the time interval $(t-\tau', t-\tau'+d\tau')$. $Y(t, \tau, \tau')$ is translation-invariant in the sense that $Y(t+\delta, \tau+\delta, \tau'+\delta)$ = $Y(t, \tau, \tau')$ for any $\delta$, and therefore, satisfies a special partial differential equation – the (generalized) Von Foerster equation with no death (see Section 1.7 of ^[3], and also the supplemental material accompanying ^[2]). Additionally, it satisfies a boundary condition in the form of an integral equation and the control measures are encoded in this boundary condition. The rest of the technique is about solving the partial differential equation, and translation-invariance is key in helping to guess the form of the solution.

The technique is good at highlighting the exponential growth or decay of the solution, depending on the parameters of the disease and of the control measures. However, it has some limitations. First, the population-level model using differential equations is a result of averaging out random factors and individual-level details in the actual infection process. It becomes difficult to add back the probabilistic arguments and the individual-level details (such as timing) needed to evaluate the control measures under more complicated situations. For instance, the model cannot be easily extended to the two-class scenario such as in COVID-19, where some infected individuals remain asymptomatic throughout, and their infectiousness is substantially different from the symptomatic individuals ^[4]. The second limitation is theoretical, which has implications on whether and how the model can be solved. The solution to the model is said to correspond to the largest eigenvalue of an integral operator. However, the theoretical underpinning about why this is the case has not been explained. Furthermore, an iterative algorithm is used to obtain numerical solutions, but it is unclear why or when the algorithm would work (see the supplemental material of ^[2]).

In this paper, we present a probabilistic model at the individual level rather than the population level, and we provide theoretical results about obtaining solutions for the model. The probabilistic reasoning and theoretical results can address the above-mentioned limitations. The new model is probabilistic, and there is no deterministic dynamics to keep track of. It has the advantage of being simple, intuitive and more easily extensible to the aforementioned two-class situation. Additionally, it accounts for the probabilistic nature of the dynamic more fully and allows different probability distributions that describe different diseases. The following is a summary of our contributions.

● By considering a chain of transmissions, we derive a model in terms of an integral equation and we give a precise expression for the integral kernel. We show theoretically (Theorem 2.1) why the solution is associated with the largest eigenvalue of the underlying integral operator. The same theoretical result also shows why an iterative algorithm works for virtually all initial conditions. We also show that the eigenvalue and eigenfunction of the integral operator correspond to the reproduction number and the generation-time distribution, respectively, under the two control measures.

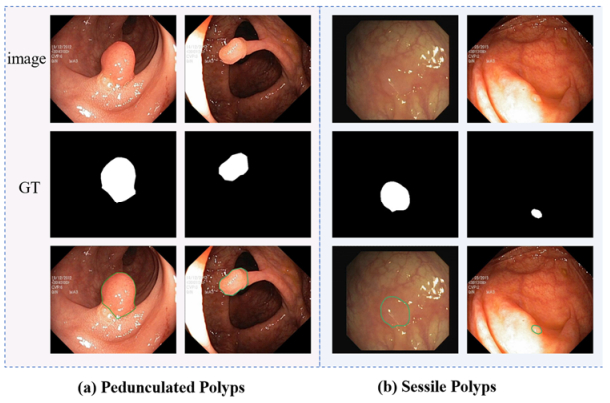
● We extend the model from the one-class case to the two-class case, where the infected population contain individuals who will remain asymptomatic throughout (the class $C_a$) and individuals who will eventually become symptomatic (the class $C_s$). The two-class case was not covered by the model in ^[1].

● We find that the model and its implications enhance our understanding about the impact of asymptomatic individuals. We show that when the infectiousness of the $C_a$ class is proportional to that of the $C_s$ class, we can transform the two-class scenario to an equivalent one-class ($C_s$-class-only) scenario with only symptomatic individuals. From this transformation, one can derive insights or confirm intuitions. For instance, when the individuals from both classes are equally infectious, the effect of having an individual from the $C_a$ class is exactly like pretending the individual is from the $C_s$ class, who then fails to isolate. As another example, although the individuals from the $C_a$ class cannot be isolated, sometimes having them is better than not having them with respect to slowing down the spread of infection. However, when the $C_a$-class individuals are sufficiently infectious, they cause a faster spread of infection than what happens without them.

● As an example, we apply an iterative algorithm to obtain numerical solutions for COVID-19 using the disease parameters compiled in ^[2]. We find that the isolation measure plays a much more important role for infection control than contact tracing.

One of the limitations of our model is that it only captures forward contact tracing. Forward contact tracing means discovering an infectee as a contact of the infector. In contrast, the discovery of the infector as a contact of an infectee is backward tracing, which is not modeled. The same assumption is implicitly made in ^[1] and ^[2]. It appears difficult to include backward tracing in the model.

Next, we briefly discuss additional related work. Aldis and Roberts introduced an integral equation model for the control of a smallpox outbreak ^[5]. They considered control measures such as isolation, tracing, and the vaccination of household members and work contacts, and a public education campaign. Their model shares similarity with the model in ^[1], in the sense that both track the time dynamics of different populations, supplemented with probabilistic arguments. Klinkenberg et al. adapted the results of ^[1] to evaluate the effectiveness of several variants of contact tracing, including single-step tracing with delay and iterative (multi-step) tracing ^[6]. Hellewell et al. evaluated the effectiveness of isolation and contact tracing for controlling COVID-19 outbreaks by simulating the infection spread as a branching process ^[7]. They found that the success rate of contact tracing must be very high in order to bring the outbreaks under control. The finding corroborates our numerical results. Peak et al. also used simulation to evaluate the effectiveness of contact tracing for several infectious diseases ^[8]. They distinguished two variants of contact tracing depending on what came after it: symptom monitoring versus quarantine.

Among the individual-level probabilistic models, our model and some of the analysis are closer to a sequence of work by Müller and his collaborators, e.g., ^[9,10]. The details of our model are sufficiently different, thereby leading to different types of equations to solve, different tools to use, and different end results. For instance, our model gives rise to repeated integrations with an integral operator. The issues about the eigenvalues and the spectral radius of the integral operator become prominent. We rely on the theory of positive integral operators to arrive at our main theoretical conclusion. Another one of our main contributions is to model and solve the two-class case. Those elements are not present in ^[9] or ^[10]. Müller and his collaborators built their models within the framework of branching processes ^[11], and this allowed them to cover more types of contact tracing, including backward tracing. Their models have the set of assumptions of a general branching process, they are sophisticated, and the results are very technical. Our model is much more straightforward because we only need to know when the first infectee is infected by a focal infector, i.e., the generation time. We do not need to know all the other infectees of the same infector. The reason is that we only model forward contact tracing but not backward tracing. The results of our model are easier to interpret because they are mostly about generation-time distributions under the control measures. We will have further discussion in the conclusion section.

Kretzschmar et al. developed a model primarily for evaluating the impact of delays when applying control measures for COVID-19 ^[12]. The model has the strength of incorporating details such as the distinction between close contacts and casual contacts, physical distancing, and various delays in the diagnosis, isolation, and contact tracing. Their calculation is based on isolating a single infector-infectee pair; there is no iteration and no equation to solve. Ball et al. modeled contact tracing with a modified birth-death process and analyzed the model via an embedded branching process ^[13]. Ripoll and Font formulated a discrete-time Markov chain model that incorporated the infectious asymptomatic phase of the disease progression ^[14]. With the model, they were able to study both asymptomatic and symptomatic transmissions. In particular, they evaluated the expected secondary asymptomatic cases produced by an asymptomatic primary case.

Another category of models for contact tracing and/or isolation is SEIR-type models and their generalizations ^{[15,16,17,18,19,20,21,22,23,24,25]}. In these population-level, differential-equation-based models, contact tracing (or isolation) is modeled as the removal of a portion of people per unit of time from each relevant sub-population. Our probabilistic model can complement the SEIR models, for instance, by capturing more timing details or matching the specific probability distributions of the underlying disease characteristics. Our model is unlike the SEIR-related models that try to model the infection dynamics over the entire life cycle of an epidemic, which requires taking into account how the susceptible population and the recovered population change over time. Our primary objective is to understand whether the spread of disease can be controlled before a substantial portion of the population is infected. Similar to ^[1], one of the underlying model assumptions is that the changes in the susceptible population and the recovered population are not significant enough to affect the infection dynamics that we model. Therefore, our model is appropriate for understanding the infection spread at the early stage of an epidemic. It is also appropriate for short-timescale snapshots of later stages, provided that, over the time interval for each such snapshot, the susceptible population and recovered population have not changed substantially. As they keep track of population changes over time, the SEIR models typically lead to renewal equations (see ^[26] and the supplemental material of ^[2]). In contrast, our model follows an infection chain from individual to individual, and our main Eqs (2.6) and (2.7) are not of the renewal type. For more discussions on various modeling methods, interested readers can refer to textbooks on mathematical epidemiology such as ^[27].

The remaining of the paper is organized as follows. In Section 2, we present the probabilistic model and the associated integral kernel for the one-class scenario, and we describe the main theoretical result, namely Theorem 2.1. In Section 3, we extend the model to the two-class scenario and give the integral kernel. In Section 4, we outline the numerical algorithm for finding the eigenvalue and eigenfunction of the integral operator, which is provably correct by our theoretical result, and we present sample solutions using the COVID-19 parameters given in ^[2]. We draw conclusions and discuss relevant issues in Section 5. The proof of Theorem 2.1 is left in Appendix A.

2.   One-class scenario - symptomatic individuals only

In this section, we consider a situation where every infected individual will eventually become symptomatic. We may still make statements such as 'an individual is asymptomatic before time $t$'. In that case, he/she is really pre-symptomatic before $t$.

We will show that the reproduction number under the two control measures is equal to the largest eigenvalue of the an integral operator (see Theorem 2.1), and we will give the expression of the integral kernel (see (2.3)). The corresponding eigenfunction is the generation-time distribution. Our method starts by following the individuals along a chain of infections.

Let $\beta(t)$ be the rate at which an individual infects others at a time $t$ after being infected at time $0$ in the absence of any control measures. It is a rate in the sense that the total number of people that the individual will infect by time $t$ is equal to $\int_{0}^t \beta(\tau) d\tau$, in the absence of control measures. $\beta(t)$ is also known as the infectiousness of the individual, as a function of time. Interestingly, after normalization, it is the density function for the generation time distribution for this individual. We assume $\beta(t)$ is the same for all the individuals and is a deterministic function. In practice, $\beta(t)$ or the regeneration time distribution is measured based on many infection cases that involve numerous individuals (see ^[2] as an example).

Remark. The time index $t$ can be understood as the age of the focal individual since infection.

We assume that $\beta(t)$ can take positive values only on $[a, b]$ for some constants $a$ and $b$, where $0 \leq a < b < \infty$.

We will consider two control measures: isolation and contact tracing (and the subsequent quarantine). We assume they take the following form:

● When an infected individual starts to develop symptoms, he/she will be isolated with probability $\epsilon_I$, where $0 \leq \epsilon_I \leq 1$.

● If an individual, say $A$, develops symptoms and is isolated, then contact tracing starts. Each of the individuals infected by $A$ will be discovered by tracing (and put into quarantine) with probability $\epsilon_T$, where $0 \leq \epsilon_T \leq 1$.

● There is no additional delay in either isolation or contact tracing.

Under the above assumptions, an individual who becomes symptomatic but fails to isolate may still be discoverable later by contact tracing and put into quarantine; if an asymptomatic individual, say $A$, is discovered through contact tracing, additional tracing of $A$'s contacts will only be initiated after $A$ develops symptoms. Note that only forward contact tracing is modeled.

The constants $\epsilon_I$ and $\epsilon_T$ are called the efficacy of isolation and the efficacy of tracing, respectively. When $0 < \epsilon_I \leq 1$, $\epsilon_T$ may take any value on $[0, 1]$. When $\epsilon_I = 0$, there will be no contact tracing; the only value that makes sense for $\epsilon_T$ is $\epsilon_T = 0$.

Consider a scenario where an individual $A$ infected an individual $B$. The time when $B$ was infected is taken as time $0$. The time interval from when $A$ was infected to when $B$ was infected is known as a generation time or generation interval ^[28,29,30]. Suppose it has a length $T_{AB}$, which is a random variable taking values on $[a, b]$. We are interested in the infectiousness of $B$ as a function of time under isolation and contact tracing, which is denoted by $\mu_B(t)$.

Note that $\mu_B(t) = \beta(t)$ until a control measure interrupts – either due to the isolation of $B$ or the quarantine of $B$ after the tracing of $A$'s contacts. Let $Y_{AB}$ be the time when $B$ is interrupted. If $B$ is never interrupted, we let $Y_{AB} = \infty$, which is an event that may have a positive probability. Note that $Y_{AB}$ depends on the random variable $T_{AB}$.

Specifically, $\mu_B(t)$ is defined as $\mu_B(t) = \mathbb{E}[\beta(t) {\bf 1}_{\{ Y_{AB} > t \}}]$, where ${\bf 1}$ denotes an indicator function. Then,

Note that, when computing the probability $P(Y_{AB} > t)$, we will need to take the expectation with respect to the distribution of $T_{AB}$.

We can express $\mu_A(t)$ similarly, i.e., $\mu_A(t) = \beta(t) P(Y_{A'A} > t)$, where $A'$ is the individual who infected $A$. Also, $Y_{A'A}$ depends on the random variable $T_{A'A}$, which represents the length of the generation interval between $A'$ and $A$. In general, $T_{A'A}$ and $T_{AB}$ do not have the same distribution, and hence, $\mu_A(t)$ and $\mu_B(t)$ are not the same. We will see that their distributions are related as in (2.5).

Remark. In the infection chain $A' \to A \to B$, it is not possible to discover $A$ when $B$ is found to be infected, because that would involve backward tracing, which is not modeled in this paper. Therefore, even if $B$ is discovered, the ability of $A$ to infect others will not change because of $B$. In short, $\mu_A(t)$ has no dependency on $B$.

Let $r_B = \int_{a}^b \mu_B(t) dt$, which is the total number of individuals directly infected by $B$ under the two control measures. Let $\nu_B(t) = \mu_B(t)/r_B$; $\nu_B(t)$ is the generation time distribution (in fact, a probability density function) of individual $B$. Similarly, let $r_A = \int_{a}^b \mu_A(t) dt$; then $\nu_A(t) = \mu_A(t)/r_A$ is the generation time distribution of individual $A$. Then, $\nu_A$ is the probability density function for the random variable $T_{AB}$.

We will focus on $B$. When there is no confusion, we use $Y$ for $Y_{AB}$ and $T$ for $T_{AB}$. For $t > 0$, we are interested in computing the probability of the event $\{Y > t\}$, conditional on $B$ being infected at time $0$ and $T = \tau$. In other words, the conditioning is on the event that $B$ is infected when the age of $A$ is $\tau$.

Remark. In the scenario of $A$ infecting $B$, the time $t$ is the age of $B$ and $\tau$ is the age of $A$.

Let $S(t)$ be the probability that an infected individual has not shown symptoms by time $t$ after being infected at time $0$. In other words, it is the complementary CDF of the incubation period.

For $\{Y > t\}$ to happen, $B$ can neither be isolated nor discovered through contact tracing before time $t$. $B$ is not isolated before time $t$ if either $B$ is asymptomatic before time $t$ or $B$ is symptomatic before $t$ but fails to isolate. The probability of this event is equal to

Next, consider how $B$ can be successfully discovered by contact tracing before time $t$. That happens if and only if $A$ develops symptoms on $(0, t]$, is isolated, and the tracing successfully discovers $B$. The probability is equal to $\epsilon_I \epsilon_T (S(\tau)-S(\tau+t))$. Note that in any outcome where $B$ is infected by $A$ at time $0$ and $T = \tau$, $A$ could not have developed symptoms before time $0$. For, otherwise, either $A$ was isolated and $A$ couldn't have infected $B$ at time $0$, or $A$ was not isolated and contact tracing couldn't have happened. Next, since $B$ is infected at time $0$, we must exclude from consideration the event that $A$ becomes symptomatic before time $0$ and is successfully isolated. The probability of that event is equal to $\epsilon_I(1-S(\tau))$. To compute any conditional probability, we need to normalize the probability by $1-\epsilon_I(1-S(\tau))$. Therefore, the conditional probability that $B$ is NOT discovered by contact tracing before time $t$ is

Therefore, the conditional probability of the event $\{Y > t\}$ is equal to

Let $k(t, \tau)$ be

Now, since $T$ has $\nu_A$ as its density function, we have

which leads to

Now, suppose the virus transmissions have gone on for more than a few generations along a chain of transmissions so that what is experienced by $A$ is statistically the same as what is experienced by $B$. If that is the case, we have $\nu_A(t) = \nu_B(t) = \nu$, and therefore, $r_A = r_B = \lambda$, for some probability density function $\nu$ and some scalar $\lambda$. Then, (2.5) implies

Let $\mathcal{K}$ be the integral operator with the integral kernel $k(t, \tau)$, which is defined on $[a, b] \times [a, b]$. In other words, the operator $\mathcal{K}$ is as follows:

We see that $\nu$ is an eigenfunction of the operator $\mathcal{K}$ and $\lambda$ is an eigenvalue.

In the following, we will provide a result to justify the above reasoning and conclusion, and make them more rigorous. Consider a chain of transmissions from individuals $0$ to $1$, $1$ to $2$, and so on. Let $\nu_0$ be the density function of $T_{0, 1}$. For $n \geq 1$, we can define $\mu_n$, $r_n$ and $\nu_n$ iteratively by $\mu_n = \mathcal{K} \nu_{n-1}$, $r_n = {\int}_a^b \mu_n(t) dt$, and $\nu_n = \mu_n/r_n$. Then, $\nu_n$ is the density function of $T_{n, n+1}$ for $n = 0, 1, 2, \ldots$. We then have the following iteration for $\nu_n$, where $n \geq 1$:

For our main result (Theorem 2.1) to hold, we need the following assumptions.

Assumption 1. $0 \leq \epsilon_I < 1$ and $0 \leq \epsilon_T \leq 1$.

Assumption 2. (i) There are some $a$ and $b$ with $0 \leq a < b < \infty$ such that $\beta(t)$ is continuous on $[a, b]$, positive on $(a, b)$, and equal to zero outside $[a, b]$; (ii) $S(t)$ is continuous on $[0, 2b]$.

Note that $\beta(t)$ may take the value $0$ at the end points $a$ and $b$. One of the main reasons that these assumptions are needed is so that the integral kernel $k(t, \tau)$ is continuous on $[a, b] \times [a, b]$ and positive on $(a, b) \times (a, b)$. The continuity part is clear. We will verify the positivity part. Consider $g(t, \tau)$ given in (2.2). When $\epsilon_I < 1$, $1 - \epsilon_I (1-S(t)) > 0$ for $t \in [a, b]$. Also, when $\epsilon_I < 1$,

for any $t \in [a, b]$ and $\tau \in [a, b]$, and therefore,

We see that $g(t, \tau) > 0$ on $[a, b] \times [a, b]$, and hence, $k(t, \tau) > 0$ on $(a, b) \times [a, b]$.

The following theorem is the one of our main results.

Theorem 2.1. Suppose $\nu_0$ is a continuous, nonnegative function on $[a, b]$ and it is not identically equal to $0$. As $n \to \infty$, $r_n \to \lambda$, where $\lambda > 0$ is the largest eigenvalue of $\mathcal{K}$. Additionally, $\nu_{n} \to \nu$, where $\nu$ is the unique eigenfunction of $\mathcal{K}$ corresponding to $\lambda$ that satisfies ${\int}_a^b \nu(t) dt = 1$. Furthermore, $\nu$ is continuous on $[a, b]$ and positive on $(a, b)$.

Remark. For $\nu_0$, the normalization ${\int}_a^b \nu_0(t) dt = 1$ is not needed. For any $n \geq 1$, because of the definition of $r_n$, each $\nu_n$ satisfies ${\int}_a^b \nu_n(t) dt = 1$.

Remark. The convergence is in the $L^2$ norm and the $L^1$ norm, and since the functions are continuous, the convergence is also pointwise.

Theorem 2.1 implies that the initial density function $\nu_0$ does not matter. As the virus is transmitted along a chain of individuals, the infectiousness $\mu_n(t)$ will converge to some $\mu(t)$, which is independent of $\nu_0$. Such $\mu(t)$ gives rise to the $\nu$ and $\lambda$ in the statement of the theorem through $\lambda = {\int}_a^b \mu(t) dt$ and $\nu(t) = \mu(t)/\lambda$. The quantity $\lambda$ can be understood as the reproduction number when the two control measures are present. It is not the same as the basic reproduction number $R_0$, which is the expected number of secondary cases produced by a primary case in the absence of any control measures. In the context of our model, $R_0 = {\int}_{a}^b \beta(t) dt$, and therefore, $R_0$ is given if $\beta(t)$ is known. Also note that both $\lambda$ and $R_0$ are reproduction numbers defined for the beginning of the epidemic outbreak. See ^[26,31] for general discussions about the basic reproduction number and how it is related to the largest eigenvalue of the next generation operator.

The theorem also suggests a straightforward iterative algorithm to compute $\mu$ and $\lambda$. In Section 4, we will use that algorithm to generate numerical results for some sample scenarios.

The proof for Theorem 2.1 relies on some results on positive integral operators. It is provided in Appendix A.

When $\epsilon_I = 1$, Theorem 2.1 can still hold if other conditions are met so that the kernel $k(t, \tau)$ is positive on $(a, b) \times (a, b)$. For instance, if $S(t)$ is continuous and positive on $[0, 2b]$, then $k(t, \tau) > 0$ on $(a, b) \times [a, b]$. Such a condition can occur when some infected individuals never develop symptoms. In that case, we have $S(t) \to s$ as $t \to \infty$, where $s$ is some positive constant. Technically, this is a two-class scenario, which is the subject of Section 3. However, we will see later that when the two classes of individuals have the same infectiousness function, it is an effectively a one-class scenario.

For consistency, we also need to make the additional restriction that $S(t)$ is constant for $t \geq b$. Otherwise, there would be individuals who only start to show symptoms after time $b$, and in all likelihood, are infectious for some period of time after $b$. That would contradict our assumption that $\beta(t)$, i.e., the infectiousness, is only positive on $[a, b]$. In applying the model to real-world situations, one can tolerate a small level of contradiction by choosing $b$ to be sufficiently large so that the distribution $S(t)$ may have a positive but exceedingly small probability mass beyond $b$ (while having $S(t) > 0$ for $t \leq 2b$). In that case, even if some individuals may start to show symptoms at a time beyond $b$, their numbers are so small that they have no practical impact, thus allowing us to make the simplifying assumption that $\beta(t) = 0$ for $t \geq b$.

3.   Two-class scenario - symptomatic and asymptomatic individuals

3.1.   General case

Let us distinguish two classes of infected individuals: the class of individuals who become symptomatic eventually, which will be called class $C_s$; and the class of individuals who remain asymptomatic throughout, which will be called class $C_a$. One of the reasons to make this distinction is that the two classes likely have different infectiousness. Let $\beta_s(t)$ denote the infectiousness of an individual in the $C_s$ class, and let $\beta_a(t)$ denote the infectiousness of an individual in the $C_a$ class. If both classes have the same infectiousness function, we will see later that, effectively, we are back to the one-class situation.

The main effort here is to derive the expression of the integral kernel, which is given in (3.7). We will see that Theorem 2.1 still holds, but with the new integral operator.

Note that when an individual is asymptomatic by some time $t$, it does not necessarily mean the individual is in the class $C_a$. It may happen that the individual will become symptomatic after $t$, and in that case, he/she belongs to $C_s$. On the other hand, if an individual becomes symptomatic by time $t$, then he/she definitely belongs to $C_s$.

For an individual in $C_s$, let $S(t)$ be the probability that an infected individual has not shown symptoms by time $t$ after being infected at time $0$. For an individual in $C_a$, such a probability is always equal to $1$ for all $t \geq 0$.

Suppose that once an individual is infected, whether he/she will eventually become symptomatic or remain asymptomatic throughout is a random event independent of everything else. Let $p_a$ be the probability that the infected individual remains asymptomatic throughout, i.e., belongs to $C_a$. Then, $1-p_a$ is the probability that the infected individual belongs to $C_s$. For notational convenience, when $p_a = 0$, we set $\beta_a(t) \equiv 0$; when $p_a = 1$, we set $\beta_s(t) \equiv 0$.

Consider a transmission chain of individuals $0 \to 1 \to 2 \to \cdots$. For each $n \geq 0$, let $T_{n, n+1}$ be the generation interval associated individual $n$ and individual $n+1$. Let $\nu_0$ be the density function for $T_{01}$.

We still need Assumption 1, in particular, $0 \leq \epsilon_I < 1$. We replace Assumption 2 by the following Assumption 3.

Assumption 3. (i) There are some $a$ and $b$ with $0 \leq a < b < \infty$ such that $\beta_a(t) + \beta_s(t)$ is continuous on $[a, b]$, positive on $(a, b)$, and equal to zero outside $[a, b]$; (ii) $S(t)$ is continuous on $[0, 2b]$.

Note that $\beta_a(t)+\beta_s(t)$ may take the value $0$ at the end points $a$ and $b$.

For the special case of $p_a = 1$, Assumption 3(i) says that $\beta_a(t)$ is continuous on the interval $[a, b]$ and positive on $(a, b)$. When $p_a = 0$, Assumption 3(i) says that $\beta_s(t)$ is continuous on the interval $[a, b]$ and positive on $(a, b)$.

The conditions in Assumption 3 are needed for technical reasons, but they are also realistic. The only major scenarios that are ruled out by Assumption 3 are when the supports of $\beta_a(t)$ and $\beta_s(t)$ do not overlap or only overlap at isolated points. It is difficult to come up with practical examples where such scenarios may occur.

Now, consider individual $1$, and assume he/she gets infected at time $0$. If individual $1$ is in $C_a$, then the probability that he/she is not isolated on $[0, t]$ is equal to $1$. If individual $1$ is in $C_s$, then he/she is not isolated before time $t$ if either he/she is asymptomatic before time $t$ or symptomatic before $t$ but fails to isolate; the probability of the event is equal to $1 - \epsilon_I (1-S(t))$.

The probability that individual $1$ is not contact-traced by time $t$ does not depend on individual $1$'s type. Let $q_{0, a}(\tau)$ be the conditional probability that individual $0$ is in $C_a$ given that individual $0$ infects $1$ $\tau$ time ago, i.e., $T_{01} = \tau$ (that is, the age of individual $0$ at time $t = 0$ is $\tau$). When individual $0$ is in $C_a$, there will be no contact tracing. The probability that individual $1$ is not discovered by contact tracing by time $t$ is equal to 1. When individual $0$ is in $C_s$, the probability that individual $1$ is not discovered by contact tracing by time $t$ is again given by (2.1).

Putting the two cases together, regardless of individual $1$'s type, the probability that individual $1$ is not discovered by contact tracing by time $t$ is equal to

For convenience, let us define

The physical meaning of $l(t)$ is that it is the infectiousness of individual $1$ if there is only one control measure – isolation – but no contact tracing. Let

$k_0(t, \tau)$ can be viewed as the infectiousness of individual $1$ when both control measures are present, given that individual $0$ infects $1$ $\tau$ time ago. We then have

Furthermore, define

Remark. Under Assumption 1, $1-\epsilon_I (1-S(t) > 0$ for $t \in [a, b]$. Then, under the additional Assumption 3(i), $l(t) > 0$ on $(a, b)$. Because of (2.8), we have $y_0(t, \tau) > 0$ on $[a, b] \times [a, b]$. Then, by Assumption 3(i), $k_0(t, \tau) > 0$ on $(a, b) \times [a, b]$.

Remark. Note that $k_0$ is used to derive $\mu_1$ and $\nu_1$. We will see that it is not needed during the remaining iterations. The only condition that we need $k_0$ to satisfy is: For any $\nu_0$ that is continuous on $[a, b]$, non-negative, and not identically equal to $0$, the resulting $\mu_1$ is also continuous on $[a, b]$, non-negative, and not identically equal to $0$. Since $k_0(t, \tau) > 0$ on $(a, b) \times [a, b]$, we see that $\mu_1(t) > 0$ for all $t \in (a, b)$, which is more than needed. Therefore, the precise form of $k_0$, which depends on the precise form of $q_{0, a}$, is not needed for our analysis and results. Similarly, regardless of what $q_{0, a}$ looks like, we always have $y_0(t, \tau) > 0$) on $[a, b] \times [a, b]$. We then have $\mu_{1, a}(t) > 0$ and $\mu_{1, s}(t) > 0$ for all $t \in [a, b]$, which is more than needed.

For $n \geq 1$, if $\mu_n(t)$, $\mu_{n, a}(t)$ and $\mu_{n, s}(t)$ are given, we define

and

Let $q_{n, a}(\tau)$ be the conditional probability that individual $n$ is in $C_a$ given that individual $n$ infects $n+1$ $\tau$ time ago, i.e., $T_{n, n+1} = \tau$. We will show how $q_{n, a}(\tau)$, $\mu_n(t)$, $\mu_{n, a}(t)$ and $\mu_{n, s}(t)$ can be derived iteratively.

After having considered what happens between individuals $0$ and $1$, we next consider the infector-infectee pair, individuals $1$ and $2$.

From $\mu_1(t) = p_a \mu_{1, a}(t) + (1-p_a) \mu_{1, s}(t)$, we have

The conditional probability $q_{1, a}(\tau)$ can be computed as follows.

Remark. For the conditional probability $q_{1, a}(\tau)$, the conditioning is on two events: the event that $2$ is infected by $1$ and the event that $T_{1, 2} = \tau$. The latter event implies the former. Hence, when applying the Bayes' formula, $\nu_1(\tau)$ shows up in the denominator in (3.2). In the numerator, $p_a r_{1, a}/r_1$ is the probability that individual $1$ belongs to $C_a$ conditional on the event that $2$ is infected by $1$. The key is that this probability is not equal to $p_a$, but equal to

The reason is that there is nothing special about $2$ among all the individuals infected by $1$. It is as if $2$ is chosen uniformly at random from the individuals infected by $1$. Therefore, the chance of picking up an individual $2$ whose infector – individual $1$ – is in $C_a$ is proportional to both $p_a$ and $r_{1, a}$. In the numerator of (3.2), we also need the probability of $T_{1, 2} = \tau$ conditional on that individual $1$ belongs to $C_a$ and that $2$ is infected by $1$. Since the event that $2$ is infected by $1$ contributes no new information, it can be dropped from the conditioning. Hence, the wanted probability is equal to $\nu_{1, a}(\tau)$. Alternatively, one can start the computation directly from (3.3). Note that $(p_a \mu_{1, a}(\tau) + (1-p_a) \mu_{1, s}(\tau)) \Delta \tau$ is the average number of individuals infected by $1$ on the time interval $[\tau, \tau+\Delta \tau]$. Out of that number, $p_a \mu_{1, a}(\tau) \Delta \tau$ is the part due to $1$ in $C_a$. The ratio in (3.3) gives the conditional probability that $1$ is in $C_a$, where the conditioning is on an observation that $1$ infects some individual $2$ at time $\tau$.

Regarding the isolation probability, the situation of individual $2$ is the same as that of individual $1$ discussed earlier: If individual $2$ is in $C_a$, the probability that $2$ is not isolated on $[0, t]$ is equal to $1$; if $2$ is in $C_s$, the probability is equal to $1-\epsilon_I (1-S(t))$.

Regarding the contact tracing probability, the situation faced by individual $2$ is similar to that faced by individual $1$. The only difference is that we need to replace $q_{0, a}$ by $q_{1, a}$. Then, the probability that individual $2$ is not discovered by contact tracing by time $t$, which will be denoted by $y(t, \tau)$, is equal to

Remark. For the same reasons discussed in an earlier remark, we have $y(t, \tau) > 0$ on $[a, b] \times [a, b]$ and $k(t, \tau) > 0$ on $(a, b) \times [a, b]$.

Let

Then, we have

Subsequently, we will show that $k(t, \tau)$ is the integral kernel for the remaining iterations, and therefore, it is the kernel that matters in the end.

For $n \geq 2$, if $\nu_{n-1}$ is given, we define

We see that for $n = 2$, we have $\mu_2(t) = p_a \mu_{2, a}(t) + (1-p_a) \mu_{2, s}(t)$; hence,

Going through the same procedure, one can show inductively that, for $n \geq 1$,

Note that the expression for $q_{n, a}(\tau)$ is the same for all $n \geq 1$. Therefore, the integral kernel used to go from individual $n-1$ to $n$ is the same for all $n \geq 2$.

To summarize, we have the following set of relations for all $n \geq 2$.

Furthermore, $\mu_{n, a}$ and $\mu_{n, s}$ are computed using the iterations in (3.7) and (3.8), respectively. We then have

The expressions for $\mu_{n, a}$ and $\mu_{n, s}$, together with (3.12), ensure that $q_{n, a}(\tau)$ has the same expression as $q_{n-1, a}(\tau)$, which is given by (3.9). We conclude that $k(t, \tau)$ given by (3.6) is the integral kernel for all the iterations except the first one.

In the two-class case, Theorem 2.1 still holds. The proof requires only minor changes. First, note that the kernel used for the first iteration to derive $\mu_1$ and $\nu_1$ is $k_0(t, \tau)$, which is different from the kernel used for the rest iterations, namely $k(t, \tau)$ (see (3.10)). This is not a problem since we can have $\nu_1$ as the initial density function, taking the role of $\nu_0$ in Theorem 2.1. As remarked earlier, $\mu_1(t) > 0$ and hence $\nu_1(t) > 0$ for $t \in (a, b)$. Therefore, $\nu_1$ satisfies the condition required by Theorem 2.1 for an initial density function.

We can then repeat the proof of Theorem 2.1, except that we need to replace the last part of the proof with the following:

Under Assumption 3, the integral kernel $k(t, \tau)$ is positive on $(a, b) \times [a, b]$ (see the earlier remarks). We will need to apply Theorem B.2 with $u(t) = l(t)$. By the same remark, $l(t)$ is continuous on $[a, b]$ and positive on $(a, b)$, and $y(t, \tau) = k(t, \tau)/l(t)$ is positive on $[a, b] \times [a, b]$. The conditions of Theorem A.2 are satisfied.

3.2.   Special case of $\beta_a=\beta_s$

In this case, the two classes of infected individuals have the same infectiousness function. Let $\beta(t) = \beta_a(t) = \beta_s(t)$ for $t \in [a, b]$.

Recall that $S(t)$ is the probability that an infected individual from $C_s$ has not shown symptoms by time $t$ after being infected at time $0$. For an individual in $C_a$, such a probability is always equal to $1$ for all $t \geq 0$. If we pick an infected individual uniformly at random, the probability that he/she has not shown symptoms by time $t$ is equal to $\hat{S}(t) \triangleq p_a + (1-p_a) S(t)$.

Suppose we pretend there is only a single class of infected individuals, and $\beta(t)$ and $\hat{S}(t)$ are the underlying parameters for everyone. We then have the single-class integral kernel $k(t, \tau) = \beta(t) \hat{g}(t, \tau)$, where $\hat{g}(t, \tau)$ is as defined in (2.2) with $S$ replaced by $\hat{S}$. We will show this reasoning is indeed correct. Note that $l(t)$ as given by (3.1) can be written as

Also, $y(t, \tau)$ as given in (3.5) can be written as

Then, $k(t, \tau) = l(t) y(t, \tau)$ has the same expression as $\beta(t) \hat{g}(t, \tau)$.

We conclude that, if the infectiousness functions for $C_a$ and $C_s$ are identical, then the two-class scenario is equivalent to the one-class scenario with the incubation period distribution being appropriately modified.

Next, we consider the role of $\epsilon_I$ in this special case. We have

We see an easy way to understand the effect of the asymptomatic individuals on the transmission and control of infectious diseases, when their infectiousness is comparable to that of the symptomatic individuals. Having a fraction $p_a$ of the individuals to be in the $C_a$ class is equivalent to a reduction of the efficacy of isolation from $\epsilon_I$ to $\epsilon_I (1-p_a)$. This confirms what one may have guessed based on intuition. The asymptomatic individuals are not isolated, but they can be contact-traced the same way as the symptomatic individuals. It is as if (in the one-class case) a fraction $p_a$ of the individuals completely fail to isolate and the rest of the individuals isolate at an efficacy level $\epsilon_I$.

3.3.   Special case of $\beta_a=x_a\beta_s$

The above result can be extended to the situation where the shapes of the infectious functions of the two classes are the same, except that one is stronger than the other in magnitude. Specifically, suppose $\beta_a = x_a \beta_s$ where $x_a > 0$ is some constant. For instance, if $x_a < 1$, then the individuals in $C_a$ are less infectious than those in $C_s$. Then,

We see that such a two-class scenario is equivalent to a one-class scenario with the same $S(t)$ and with the effective infectiousness function $\hat{\beta}(t)$ and the effective efficacy of isolation $\hat{\epsilon}_I$, where $\hat{\beta}(t) = (p_a x_a + 1-p_a) \beta_s(t)$ and $\hat{\epsilon}_I = \frac{(1-p_a) \epsilon_I}{p_a x_a + 1-p_a}$.

Remark. The one-class equivalent is not the result of averaging the infectiousness functions and averaging the incubation time distributions. The latter (and incorrect) approach would yield an integral kernel equal to

The difference is in the effective efficacy of isolation, which is $(1-p_a) \epsilon_I$ in the above versus $\frac{(1-p_a) \epsilon_I}{p_a x_a + 1-p_a}$ in the true equivalent. The two coincide only when $x_a = 1$. For a fixed $p_a$, the value of $\frac{(1-p_a) \epsilon_I}{p_a x_a + 1-p_a}$ ranges from $0$ to $\epsilon_I$ depending on $x_a$.

We have the following observations. When $x_a > 1$, the effective infectiousness is increasing in $p_a$ and is always greater than the baseline $\beta_s(t)$; when $x_a < 1$, the effective infectiousness is decreasing in $p_a$ and is smaller than the baseline. In either case, the effective efficacy of isolation is decreasing in $p_a$ and is smaller than the baseline $\epsilon_I$. We can conclude that when $x_a > 1$, a larger $p_a$ corresponds to faster infection spread. For the case of $x_a < 1$, as $p_a$ increases, there is competition between the decreasing infectiousness and the worsening isolation efficacy. Precise numerical solutions are needed to see how exactly the speed of the infection spread depends on $p_a$.

While holding $p_a$ constant, increasing $x_a$ has two effects. It increases the effective infectiousness and reduces the effective efficacy of isolation. Both make the infection spreads faster.

Earlier, we showed that when $x_a = 1$ (so that $\beta_a = \beta_s$), for any $p_a \in (0, 1)$, the two-class scenario is worse than the one-class ($C_s$-only) scenario with respect to the spread of infection. However, having asymptomatic individuals can sometimes be a better situation with respect to controlling the spread of infection. Note that when $x_a = 0$, $\hat{\beta}(t) = (1-p_a) \beta_s(t)$ and $\hat{\epsilon}_I = \epsilon_I$. Compared with the $C_s$-only scenario, the effective infectiousness is reduced while the effective efficacy of isolation is unchanged. By continuity, when $x_a$ is sufficiently small, having some asymptomatic individuals will lead to a slower spread of infection than not having them. More precisely, under each fixed $p_a \in (0, 1)$, there exists $x^* < 1$, which depends on $p_a$, such that for any $x_a < x^*$, the two-class scenario is better than the $C_s$-only scenario, whereas for any $x_a > x^*$, the two-class scenario is worse than the $C_s$-only scenario.

The special case where $\beta_a$ is proportional to $\beta_s$ not only has easy interpretations, but can also have practical relevance for some infectious diseases. In the case of COVID-19, there is preliminary evidence that supports a model where $\beta_a(t) = x_a \beta_s(t)$ and $x_a < 1$. Since it is clearly difficult to directly measure $\beta_a(t)$, we will look at indirect evidence coming from longitudinal viral load measurements using reverse transcriptase polymerase chain reaction (RT-PCR) tests. Together, the review articles ^[32] and ^[33] summarize the results of ten studies. Six out of the ten studies found similar initial viral loads between asymptomatic and symptomatic individuals, and three found lower viral loads from asymptomatic individuals. Five studies found faster viral clearance in asymptomatic individuals, and two found longer viral shedding duration in asymptomatic cases. As a notable example of these studies, ^[34] reported that 303 patients were monitored during their 20-day stay in an isolation facility. RT-PCR tests were performed on multiple days from day 8 through day 19. The viral loads were found to be similar in the asymptomatic and symptomatic patients. These studies suggest that $\beta_a(t)$ and $\beta_s(t)$ may not differ much in their general shape; that is, approximately $\beta_a(t) = x_a \beta_s(t)$ for all $t$, where $x_a$ is some positive constant.

The constant $x_a$ is not necessarily equal to 1 because the viral loads measured in RT-PCR tests cannot fully capture infectiousness (see ^[33] for a discussion). There is a large number of studies showing that the overall transmissibility of asymptomatic individuals is weaker than symptomatic ones, as measured by the secondary attack rate. The estimated difference in the attack rate varies over a wide range. Meta-analysis shows that the ratio (relative risk, RR) of the attack rate from asymptomatic individuals versus that of symptomatic individuals is as low as $0.04$ and as high as $0.78$ ^[35,36,37].

4.   Numerical experiments

Theorem 2.1 suggests the following procedure to compute the eigenvalue and eigenfunction of $\mathcal{K}$.

● Initialize $\nu_0$ to be any continuous, nonnegative function on $[a, b]$ that is not identically equal to $0$.

● For each $n \geq 1$, compute $\mu_n = \mathcal{K} \nu_{n-1}$, $r_n = {\int}_a^b \mu_n(t) dt$, and $\nu_n = \mu_n/r_n$.

● Stop at $n = N$ when $r_n$ stabilizes to within a desired error margin.

As an illustration, we will apply the algorithm to COVID-19 using the infection-related parameters compiled in ^[2] (see Table 1 there), which were obtained in the early stage of the pandemic. Using this early-stage data is appropriate because our primary interest is to study whether the two control measures can stop or curtail the spread of infection before a substantial portion of the population is infected. In the later stages, as the virus evolves, the infection parameters have clearly changed. Although it is tempting to obtain new parameters and conduct evaluations for later variants of the virus, there are some subtleties due to the fact that the population have acquired substantial immunity through vaccines or infections. It becomes difficult to judge whether any measured parameter is valid only for the immunity level at the time of measurement or it is valid without such population immunity.

We now describe the details of the parameters given in ^[2].

● $S(t)$: log-normal distribution with mean-log equal to $1.644$ and standard deviation of the log equal to $0.363$.

● $R_0$: the basic reproduction number, equal to $2.0$.

● $\beta_s(t)$: $\beta_s(t) = R_0 w(t)$, where $w(t)$ is the Weibull distribution with the shape parameter equal to $2.826$ and the scale parameter equal to $5.665$.

● $\beta_a(t)$: $\beta_a(t) = x_a \beta_s(t)$ where $x_a = 0.1$. This is a two-class scenario. As discussed at the end of Section 3, since $\beta_a$ is proportional to $\beta_s$, this two-class scenario has an one-class equivalent.

● $p_a$: equal to $0.4$

Our experiences have shown that the computed $r_n$ converges rapidly. For all our experiments, it takes no more than $10$ iterations – usually only a few – for $r_n$ to stabilize to within an error margin of $10^{-6}$. A practical implication is that the asymptotic results in this paper are relevant even during early stages of an outbreak, after a few generations of viral transmissions.

Figure 1 shows the results for different $(\epsilon_I, \epsilon_T)$ pairs that can achieve outbreak control, i.e., when the reproduction number under the control measures, $\lambda$, becomes equal to $1$. We see that, at least for this set of disease parameters, isolation is the key to outbreak control. For $\epsilon_I < 0.59$, the spread of the infection cannot be stopped even with $100\%$ success of contact tracing. For $\epsilon_I$ above that threshold, it is possible to control the spread with the help of contact tracing. Even in that regime, a drop in $\epsilon_T$ by a certain amount can be compensated by a smaller amount of improvement in $\epsilon_I$, again showing that the disease control is more sensitive to the efficacy of isolation.

5.   Conclusions and discussion

In this paper, we have demonstrated the usefulness of our individual-level probabilistic model, which can complement the population-level model in ^[1]. With our model, we get rid of some of the clutter in the population-level model caused by having to keep track of the dynamics of the population-level state variables, i.e., the sizes of different subsets of the infected population. Our approach is to keep track of each infected individual and his/her infector along a chain of infections. It gives us more freedom to incorporate individual-level time-varying details, as well as a better ability to make probabilistic arguments. The model and analysis of the two-class scenario are a result of that extra power of our approach. The main theorem of this paper is also related to following a chain of the infections till reaching equilibrium.

We have derived an explicit expression for the integral kernel for the two-class scenario, which can then be used by the iterative numerical algorithm to calculate the equilibrium generation time distribution and the reproduction number under the two control measures. The main theorem confirms that the iterative algorithm always works. A close examination of the expression yields important insights about the role of the asymptomatic individuals, at least for the important special case where the infectiousness of the two classes is proportional to each other. The insights are obtained by thinking about the two-class scenario in terms of its one-class equivalence, which has only symptomatic individuals. The effects of the asymptomatic individuals can be understood by supposing that all individuals will be symptomatic but with modified infectiousness and modified efficacy of the isolation measure.

When looking at the numerical results that we obtained for COVID-19 in the early stage of the pandemic, we see that the isolation measure plays a much more important role for infection control than contact tracing. The observation is surprising, considering how much emphasis contact tracing has received throughout the pandemic. Next, we discuss more about this point. First, recall that only forward contact tracing is modeled in this paper. Suppose $A$ infects $B$ and $B$ infects $C$. When we say $B$ is discovered by contact tracing, we mean that $B$ is discovered as one of $A$'s contacts. In practice, it may happen that $C$ is discovered before $B$ through medical diagnosis and $B$ is discovered as a result of tracing $C$'s contacts backwards. That is backward tracing, which is not modeled.

By the time an individual is discovered by backward tracing, it is likely that enough time has passed and the individual has ceased to be infectious or nearly so. Thus, omitting backward tracing is not expected to have much impact on the accuracy of the model with respect to modeling the traditional contact tracing. What could make a significant difference is more comprehensive tracing, i.e., tracing over multiple steps forward and backward. Suppose in the earlier example $B$ also infected $D$ and $E$. Then, when the backward tracing from $C$ leads to the discovery of $B$, more tracing can be initiated to find $B$'s contacts, which include $A$, $C$, $D$, and $E$. Although $B$ may no longer be infectious by the time he/she is discovered, $D$ and $E$ are likely to be infectious or will become infectious. Discovering and quarantining $D$ and $E$ will make a difference in infection control. In principle, the tracing process can go on to uncover the contacts of $A$, $D$ and $E$, and eventually, a cluster of infection may be discovered. Such clustered approach of comprehensive contact tracing may substantially elevate the importance of contact tracing and substantially improve our ability for infection control. It is not within the scope of this paper to model any comprehensive contact tracing scheme.

The scenario studied in this paper may also be modeled by a branching process (see ^[11,38]). For instance, Müller and co-authors have used general branching processes to model and analyze contact tracing ^[9,10]. The fundamental question answered by such a model is similar to ours, which is how many individuals are infected by a single infected person with or without control measures. A branching-process model captures the randomness in the number of offsprings of an individual. In particular, a general branching process specifies a random lifespan of an individual and a point process that represents the birth events of the offsprings of that individual. The point process is usually a Poisson process with an intensity (rate) function $\beta(t)$. Each offspring is a statistical copy of the parent. Our model can be compared with a general branching process. In our model, each individual's 'lifespan' (period of infectiousness) is a fixed interval $[a, b]$, where the time origin is the time of infection of the individual. We only model the random time till the first birth event, i.e., the time till the first infection by the focal individual. This is captured by the generation-time distribution. When there are no control measures, the generation-time distribution is simply the normalized infectiousness function $\beta(t)$. One of our main goals is to derive the steady-state generation-time distribution when the control measures are present. Looking back, the reason we don't need to model all the birth events from an individual is that we only consider forward contact tracing, i.e., the tracing of the infectee from the infector. A key fact is that each infectee has only one infector. In contrast, with branching processes, one can model backward tracing from any of the infectees to the infector, as was done in ^[9] and ^[10]. Overall, branching-process models are more powerful, and the analytical framework is more systematic. Our model is simpler but can address some questions more directly or address different kinds of questions.

Use of AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Data statements

Data sets generated during the current study are available from the corresponding author on reasonable request.

Acknowledgments

No funding was received for conducting this study.

Conflict of interest

The author declares there is no conflict of interest. The author has no relevant financial or non-financial interests to disclose.

Appendix

A.   Proof of Theorem 2.1

The proof relies on some spectral properties of continuous, positive integral kernels (see ^[39]), which can be viewed as the counterparts of similar properties for positive matrices stated in Perron's Theorem. Consider a compact subset $Z$ of some Euclidean space and a continuous kernel $k(t, \tau)$ defined on $Z \times Z$. The operator associated with the kernel is denoted by $\mathcal{K}$.

Here, the space of functions that the operator operates on are $L^2(Z)$, i.e., the square-integrable complex-valued functions on $Z$. The underlying scalar field is $\mathbb{C}$, the set of complex numbers.

Let $\lambda$ denote the spectral radius of the operator $\mathcal{K}$. The following theorem is from ^[39] (see Theorem 2 there).

Theorem A.1 (Theorem 2 in ^[39]). Suppose $k(t, \tau)$ is positive on $Z \times Z^o$, where $Z^o$ is the interior of $Z$. Then,

(i) $\lambda > 0$ and $\lambda$ is the largest eigenvalue of $\mathcal{K}$.

(ii) The eigenspace (the subspace spanned by the eigenfunctions) corresponding to $\lambda$, denoted by $N_\lambda$, is one-dimensional and it contains a positive eigenfunction $\phi_o(t)$.

(iii) If $\lambda'$ is another eigenvalue of $\mathcal{K}$, then $|\lambda'| < \lambda$.

(iv) $(\mathcal{K}/\lambda)^n$ converges to the one-dimensional projection operator on the eigenspace corresponding to $\lambda$.

In our case, $Z = [a, b]$. Under Assumption 2, the kernel $k(t, \tau)$ is positive on $(a, b) \times (a, b)$, but not necessarily on $[a, b] \times (a, b)$ (e.g., consider $\beta(a) = 0$ or $\beta(b) = 0$). There is an extension to the above theorem, which is labeled as Theorem $2'$ in ^[39]. It states the following.

Theorem A.2 (Theorem $2'$ in ^[39]). Suppose $k(t, \tau)$ is positive on $Z^o \times Z^o$. Suppose there exists a continuous function $u(t)$, positive on $Z^o$ such that $k(t, \tau)/u(t)$ is continuous on $Z \times Z$ and positive on $Z \times Z^o$. Then, the statements (i)-(iv) in Theorem B.1 still hold except that in part (ii) $\phi_o(t)/u(t)$ is asserted to be positive on $[a, b]$ instead of $\phi_o(t)$.

We next prove our main theorem.

Proof. (of Theorem 2.1) Under the theorem assumption, $\nu_0$ may not be positive on the entire interval $(a, b)$. Since $\nu_0$ is not identically equal to $0$ on $[a, b]$ and since it is continuous, there is a subinterval on $[a, b]$ on which $\nu_0$ is positive. Since the kernel $k(t, \tau)$ is positive on $(a, b) \times [a, b]$, $\nu_1$ must be positive on $(a, b)$. Therefore, without loss of generality, we will assume $\nu_0$ is positive on $(a, b)$. Then, for each $n \geq 1$, $\nu_n(t) > 0$ for $t \in (a, b)$ and continuous on $[a, b]$, $r_n > 0$, and ${\int}_a^b \nu_n(t) dt = 1$.

The proof relies on Theorems B.1 and B.2. In this case, the compact set $Z$ is $[a, b]$. Let us tentatively assume $k(t, \tau)$ is positive on $[a, b] \times (a, b)$.

Statement (ⅳ) of Theorem B.1 says that $(\mathcal{K}/\lambda)^n$ converges to some operator $\mathcal{L}$ and for any $f \in L^2(Z)$, $\mathcal{L} f = \alpha \phi_o$, where $\phi_o$ is a positive eigenfunction in $N_\lambda$ and $\alpha \in \mathbb{C}$ is a scalar depending on $f$.

We will show the eigenfunctions are continuous. Note that $\mathcal{K} \phi_o = \lambda \phi_o$. We will first show that $h \triangleq \mathcal{K} \phi_o$ is continuous on $Z$ for any compact set $Z$. For any $t, s \in Z$,

where $M$ is a constant given by $M = {\int}_Z \phi_o(\tau) d \tau$, and $0 < M < \infty$. Since $k(t, \tau)$ is continuous on a compact set, it is uniformly continuous on the set. Therefore, for any $\epsilon > 0$, one can find $\delta > 0$ such that for any $(t, \tau), (s, \tau) \in Z \times Z$ with $||t-s|| < \delta$, $\left| k(t, \tau) - k(s, \tau) \right| < \epsilon$, and hence, $\max_{\tau \in Z} \left| k(t, \tau) - k(s, \tau) \right| < \epsilon$. We see that $h(t)$ is (uniformly) continuous.

We return to our current case of $Z = [a, b]$. From (2.7), we have

By (iv), $\frac{\mathcal{K}^n}{\lambda^n}$ converges to some projection operator $\mathcal{L}$ in the sense of uniform convergence (see ^[40,41]). Since $\mathcal{L}$ is a projection operator, it is not $0$ (as an operator). We claim that $\mathcal{L} \nu_0 \geq 0$, it is not identically zero, and in fact, ${\int}_a^b (\mathcal{L} \nu_0)(t) dt > 0$.

First, it is easy to show that $\mathcal{L} f \geq 0$ for any nonnegative $f \in L^2(Z)$. Suppose otherwise. Then, $\mathcal{L} f = \alpha \phi_o$ for some $\alpha < 0$. Since, for each $n$, $\mathcal{K}^n$ is a positive integral kernel, we have $\frac{\mathcal{K}^n}{\lambda^n} f \geq 0.$ Then,

This contradicts the fact that $\frac{\mathcal{K}^n}{\lambda^n}$ converges to $\mathcal{L}$. A corollary is that, if $f \geq g \geq 0$, then,

and hence

It is well known that a linear operator whose range is finite dimensional is a compact operator, and that a compact operator is continuous. Hence, $\mathcal{L}$ is a continuous operator. Let us define a set of functions indexed by $\epsilon$, where $0 < \epsilon < b-a$.

Then, $\phi_\epsilon \to \psi$ in the $L^2$ norm as $\epsilon \to 0$, where $\psi$ is the function with $\psi(t) = \phi_o(t)$ for $t \in (a, b)$ and $\psi(a) = \psi(b) = 0$. With respect to the Lebesgue measure, $\left\|\psi-\phi_o \right\|_2 = 0$. Since $\mathcal{L}$ is continuous (equivalently, bounded), we have $\left\|\mathcal{L} \psi - \mathcal{L} \phi_o \right\|_2 = 0$. Then,

Again since $\mathcal{L}$ is continuous, we have $\left\| \mathcal{L} \phi_\epsilon - \mathcal{L} \psi \right\|_2 \to 0$ as $\epsilon \to 0$. Therefore, $\mathcal{L} \phi_\epsilon$ converges to $\mathcal{L} \phi_o$ in the $L^2$ norm. Since the domain of the functions is a finite interval, by Hölder's inequality, the convergence also holds in the $L^1$ norm. Since

and $\left\| \mathcal{L} \phi_\epsilon - \mathcal{L} \psi \right\|_1 \to 0$ as $\epsilon \to 0$, we see that ${\int}_a^b (\mathcal{L} \phi_\epsilon) (t) dt \to {\int}_a^b (\mathcal{L} \phi_o(t)) dt$ as $\epsilon \to 0$. Note that ${\int}_a^b (\mathcal{L} \phi_o) (t) dt = {\int}_a^b \lambda \phi_o(t) dt > 0$. Then, there exists a sufficient small $\xi > 0$ such that ${\int}_a^b (\mathcal{L} \phi_\xi) (t) dt > 0$.

Let us define

Each $\nu_\epsilon$ is a continuous and positive on $[a+\epsilon, b-\epsilon]$; so is each $\phi_\epsilon$. Then, there exists a constant $\eta(\epsilon) > 0$ such that $\eta(\epsilon) \nu_\epsilon(t) > \phi_\epsilon(t)$ for each $t \in [a+\epsilon, b-\epsilon]$.

Since $\nu_0 \geq \nu_\epsilon \geq 0$ for each $\epsilon$, by (A.2),

Then, for the aforementioned $\xi$, we have

Therefore, $\mathcal{L} \nu_0$ cannot be identically equal to $0$.

We have shown that $\mathcal{L} \nu_0$ is nonnegative, not identically zero, continuous, and ${\int}_a^b (\mathcal{L} \nu_0)(t) dt > 0$. We also know that ${\int}_a^b \nu_n(t) dt = 1$ for every $n$. By considering integrating the terms in (A.1), we see that

It follows that $\limsup_{n \to \infty} r_n \leq \lambda$ and $\liminf_{n \to \infty} r_n \geq \lambda$. Therefore, $r_n \to \lambda$ as $n \to \infty$.

Furthermore, we must have

Otherwise, there would exist sufficiently large $m$ and $n$ such that ${\int}_a^b \nu_m(t) dt \neq {\int}_a^b \nu_n(t) dt$, which is impossible.

We denote the limit in (A.3) by $c$, where $0 < c < \infty$. Note that the value of $c$ depends on $\nu_0$. We see that $\nu_n$ converges to $\nu \triangleq c \mathcal{L} \nu_0$ in $L^2$ and in $L^1$. Since $\nu \in N_\lambda$, we can write $\nu = \alpha \phi_o$ for some $\alpha \in \mathbb{C}$. Since ${\int}_a^b \nu(t) dt = 1$ (due to the $L^1$ convergence of $\nu_n$), we have $\alpha = 1/ {\int}_a^b \phi_o(t) dt$. Therefore, $\nu$ is positive and continuous on $[a, b]$, and $\nu$ is independent of the initial $\nu_0$.

Under Assumption 2, the kernel $k(t, \tau)$ is positive on $(a, b) \times (a, b)$, but not necessarily on $[a, b] \times (a, b)$ (e.g., consider $\beta(a) = 0$ or $\beta(b) = 0$). We will apply Theorem B.2 with $u(t) = \beta(t)$. Note that $\beta(t)$ is continuous on $[a, b]$ and positive on $(a, b)$, which is required by Theorem B.2. Before stating Theorem 2.1, we commented that $g(t, \tau) = k(t, \tau)/\beta(t)$ is positive on $[a, b] \times (a, b)$ (in fact, it is positive on $[a, b] \times [a, b]$). The conditions of Theorem B.2 are satisfied.

Then, $\phi_o(t)$ is still positive on $(a, b)$ (it is possible that $\phi_o(a) = 0$, $\phi_o(b) = 0$ or both). The argument for its continuity is unaffected, since it relies on $k(t, \tau)$ being continuous on its (compact) domain and $\phi_o$ being integrable. The rest of the arguments and conclusions also remain unchanged except that the limiting $\nu$, which is equal to $\alpha \phi_o$ for some constant $\alpha$, is continuous on $[a, b]$ and positive on $(a, b)$. □