A hybrid ensemble forecasting model of passenger flow based on improved variational mode decomposition and boosting

1.   Introduction

The prediction of passenger flow has a direct bearing on smart cities and intelligent transportation. Precise forecasting of passenger volume can aid in the logical design of public transportation routes, enhancing both the effectiveness of urban transportation and the well-being of individuals ^[1,2]. The province of Jilin considers tourism to be the main driver of economic growth. The Jilin International Rime Ice and Snow Festival, Changchun Ice and Snow Tourism Festival, and other annual events organized in Jilin Province in recent years have boosted the number of tourists visiting the province's tourist attractions. As a result, the creation of a tourist traffic forecast model aids in the formulation of scientific traffic management policies by tourism departments, therefore advancing the growth of smart cities in Jilin.

Numerous forecasting models have been developed and proposed by researchers on the subject of passenger flow forecasting. These methods may be broadly classified into three categories: statistical model, machine learning and AI, and decomposition hybrid approaches. The autoregressive moving average (ARMA) model ^[3], autoregressive integrated moving average (ARIMA) model ^[4], and seasonal autoregressive integrated moving average (SARIMA) model ^[5] are some of the fundamental statistical models now in use. The statistical model, it is thought, falls short in explaining the nonlinear aspects of the passenger flow time sequence.

As information technology advances, scientists are focusing more on AI and machine learning models as a solution to the issue that complex data shouldn't be analyzed using statistical approaches. For example, Chen et al. ^[6] referred to the theories of the support vector machine (SVM) and genetic algorithm (GA), and put forward a traffic flow forecasting model based on the least squares support vector machine (LS-SVM). Li et al. ^[7] constructed a new dynamic radial basis function (RBF) network to forecast the outward passenger flow. Gao et al. ^[8] constructed a scenic spot passenger flow forecasting method based on a convolutional neural network (CNN) and long-term and short-term memory (LSTM). This method considers various traffic flows around the scenic spot and has high accuracy and robustness. Lu et al. ^[9] constructed a forecasting method (GA-CNN-LSTM), which combined CNN and LSTM optimized by GA. Compared to other intelligent algorithms this method is more accurate at predicting the daily tourist flow of the Huangshan Scenic Area. Zou et al. ^[10] proposed a method to predict the passenger flow of bus lines by extreme gradient boosting (XGBoost). In comparison to the deep learning model LSTM and their benchmark models, XGBoost can obtain higher accuracy. Tan et al. ^[11] proposed a new two-stage heuristic algorithm based on an ant colony algorithm and established a mixed integer linear programming model. Liu et al. ^[12] combined deep learning with professional knowledge in the field of transportation to predict subway passenger flow. Liu et al. ^[13] proposed an optimization method for a driver's delivery route based on a language model.

Following the development of prediction technology, the usage of data preparation in AI and machine learning models has been developing. The model based on data preprocessing uses empirical mode decomposition (EMD) ^[14], empirical wavelet transform (EWT) ^[15], ensemble empirical mode decomposition (EEMD) ^[16] and variational mode decomposition (VMD) ^[17] to decompose or the original data. A lot of research has proved the effectiveness of these algorithms. For example, Wei and Chen ^[18] combined EMD and a back propagation neural network (BPN) to propose a hybrid EMD-BPN forecasting method. Liu et al. ^[19] put forward a mixed forecasting model, which combines wavelet transform and kernel extreme learning machine (KELM), and the model has been validated on Beijing subway data. Cao et al. ^[20] combined EEMD with LSTM to build a subway passenger flow forecasting model. The outcomes demonstrate that the EEMD-LSTM model has superior accuracy in projecting short-term subway passenger flow. The forecasting findings demonstrate that Cui et al.'s ^[21] model for forecasting tourist flow, based on EMD and gated recurrent unit (GRU), is more accurate than recurrent neural network (RNN) and LSTM at predicting the volume of visitors to the Black Valley picturesque area. According to the aforementioned studies, breaking down the series before making a prediction can significantly increase its accuracy. In addition, as a newly developed method, VMD is very efficient in processing nonlinear signals and has good forecasting ability in wind speed forecasting ^[22], crude oil price forecasting ^[23,24], carbon price forecasting ^[25] and so on.

Enlightened by the successful application of the models, this study builds a hybrid passenger flow forecasting model based on an improved variational mode decomposition and boosting algorithm. This model is used to study the tourist flow to well-known scenic locations in Jilin Province. Specifically, the original passenger flow sequence is preprocessed into various subsequences. The modified golden jackal optimization algorithm is applied to optimize the variational mode decomposition to prevent the improbability of arbitrarily specified parameters. Second, the subsequence is reconstructed and its complexity is estimated using sample entropy (SE). To dynamically decide the prediction submodels of the decomposition sequence and realize accurate point prediction, a prediction module with five submodels is then creatively built. The study's conclusions are an invaluable resource for anybody carrying out development planning, upkeep of attractive regions and provision of intelligent tourism services.

The following is an introduction to this paper's significant contributions.

(1) To predict tourist flow in picturesque areas, an original ensemble forecasting technique is developed. This study integrates the improved optimization algorithm, data pretreatment, subsequence reconstruction and reconstruction sequence prediction model to achieve accurate passenger flow prediction.

(2) Aiming at the problem of artificially selecting the parameters of variational mode decomposition, the improved variational modal decomposition is constructed to realize the automatic selection of modal number and penalty factor.

(3) Create the submodel prediction module and choose the proper predictor for the sub-sequence that has been broken down and rebuilt. Five benchmark predictors are used to predict the reconstructed subsequence. The best predictor is automatically selected based on the submodel selection module to improve the prediction performance of the integrated system.

The following is the structure of the remaining portions of this study: Section 2 provides a detailed description of the main research approaches and theories. Section 3 describes the hybrid passenger flow forecasting model's framework. Through empirical investigation, Section 4 confirms the hybrid model's performance. The main conclusions of this study are outlined in Section 5.

2.   Data decomposition method

2.1.   Data decomposition method

2.1.1.   VMD

VMD is a brand new non-recursive signal decomposition technique that is based on understandable mathematical concepts like frequency mixing, Wiener filtering, and the Hilbert transform. The baseband smooth eigenmode function is generated using this method after estimating the center pulsation frequency of each subsequence. The independence of each mode is guaranteed by this method of solution. VMD decomposes the original sequence $f$ into $k$ intrinsic mode functions (IMF). In the iterative solution process, VMD will continuously solve the optimal center frequency and power spectrum center of each eigenmode function. Its objective function and constraint conditions are as follows:

where ${u_k}$ denotes the $k - th$ mode, $\{ {\omega _k}\} = \{ {\omega _1}, {\omega _2}, \cdots, {\omega _k}\}$is the central frequency of the set of intrinsic mode functions and $(\delta (t) + j/\pi t)*{u_k}(t)$ is the unilateral spectrum of the mode function after the Hilbert transform. By including a Lagrange multiplier and a quadratic penalty term, the VMD approach converts the optimization problem in the aforementioned formula into an unconstrained issue that can be solved:

where $\alpha$ represents the quadratic penalty term and $\lambda$ is the Lagrange multiplier. The optimal solution to Eq (2) is solved using the alternating direction method of multipliers (ADMM) ^[26]. To constantly update ${u_k}$ and ${\omega _k}$, the subproblem is converted into the problem of finding the minimum value in Eq (3) and the optimal solution of ${u_k}$ and ${\omega _k}$ is expressed as follows:

where $n$ denotes the number of iterations and $\hat f(\omega)$, ${\hat u_i}(\omega)$, $\hat \lambda (\omega)$ and $\hat u_k^{n + 1}(\omega)$, respectively, represent the Fourier transforms of$f(t)$, $u(t)$, $\lambda (t)$ and $u_k^{n + 1}(t)$.

2.1.2.   Golden jackal optimization based on the Sobol sequence

A new swarm intelligence method called the golden jackal optimization (GJO) algorithm was presented in 2022. It was created by the cooperative hunting behavior of golden jackals ^[27]. The hunting process of jackals is mainly divided into three basic stages: (1) searching for prey and approaching it; (2) surrounding the prey and stimulating the prey until they stop moving; (3) attacking prey.

The initial solution of GJO is uniformly and randomly distributed in the solution space, then:

where ${Y_{n, d}}$ is the position coordinate of the $d$ dimension of the $n$ prey, $n$ is the number of prey, $d$ is the dimension, ${u_d}$ and ${l_d}$ are the upper and lower bounds of each dimension coordinate, respectively and $rand$ is a random variable between $(0, 1)$.

The hunting process of golden jackals is dominated by the male jackals, and the female jackals follow the actions of the male jackals. Their mathematical models are as follows ($\left| {E \geqslant 1} \right|$):

where $t$ is the current iteration number, ${Y_1}(t)$ and ${Y_2}(t)$ are the updated positions of male and female golden jackals, ${Y_M}(t)$ and ${Y_{FM}}(t)$ are the positions of male and female golden jackals, $Prey(t)$ is the prey position and $E$ is the escape energy of prey.

The formula for calculating the escape energy of prey is:

where ${E_0}$ represents the initial energy of prey, $r$ is a random variable between $(0, 1)$, $T$ represents the maximum number of iterations, ${c_1}$ is the default constant set to 1.5 and ${E_1}$ means decreasing prey energy.

In Eqs (6) and (7), $\left| {{Y_M}(t) - rl \cdot Prey(t)} \right|$ and $\left| {{Y_{FM}}(t) - rl \cdot Prey(t)} \right|$, respectively, calculate the distance between the male jackal and the female jackal and the prey. $rl$ is the random number vector calculated by Levy's flight function, mainly to avoid falling into local optimum during the solution.

where $u$ and $v$ are both random numbers between $(0, 1)$, $\beta$ is the default constant set to 1.5 and $\Gamma (·)$ is the gamma function.

Finally, the position of each prey is updated by the average value of Eqs (6) and (7); that is,

When prey is disturbed, its escape energy decreases and the mathematical model of golden jackals surrounding and devouring prey is as follows ($\left| {E < 1} \right|$):

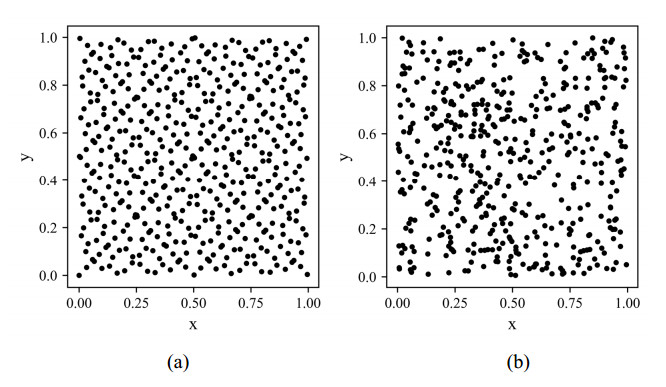
The initial population in the search space is produced by random number generation in the GJO process. The algorithm's performance will be impeded by the low ergodicity and erratic population distribution of this initialization strategy. The initial population of golden jackals is mapped using the Sobol sequence to enhance the capability of the global search. To compare the spatial distribution of the Sobol sequence with that of the random distribution generating the initial population, a plot of the random number distribution of the population with a population size of 500 was generated for the ranges $x \in [0, 1]$ and $y \in [0, 1]$.

The Sobol sequence is more effective in processing high-dimensional sequences because it has fewer calculations and faster sample rates. The range of setting the optimal solution is $[{l_d}, {u_d}]$ and random number ${K_n} \in [0, 1]$ produced by the Sobol sequence. The starting position of the golden jackal population can be defined as:

The pseudo-code of the above GJO based on the Sobol sequence is shown in Algorithm 1.

2.1.3.   Improved variational modal decomposition (IVMD)

According to the principle of the VMD algorithm, the penalty factor $\alpha$ and modal number $k$ for decomposition need to be determined manually before signal decomposition. The incorrect values $k$ and $\alpha$ will lead to under-decomposition or over-decomposition of the original signal. This study applies the GJO based on the Sobol sequence to the automatic optimization of parameter combinations $[k, \alpha]$ of VMD to prevent undesirable outcomes produced by artificially setting parameters. Among them, the construction of fitness functions is a key step in the optimization process. Gao et al. ^[28] constructed the fitness function by combining SE, aggregation algebra, and the Pearson correlation coefficient.

SE is independent of the length of the data and it measures the complexity of the time series by calculating the probability of new pattern generation. The smaller the SE value, the lower the complexity of the series. For a given original signal, the sample entropy is calculated as follows:

In the formula, $SampEn$ is the sample entropy function, $f$ is the original time series, $q$ is the embedding dimension, $r$ is the similarity tolerance and $B$ is the proportion of the number of state vectors similar to the original signal.

Aggregation algebra is the length of the best central frequency signal. The aggregation speed increases with decreasing value and the IMF frequency features become more pronounced. Aggregation algebra's calculation formula is as follows:

where $Omega$ represents the aggregation algebra of the optimal central frequency, and $length({\omega _k})$ is the length of extracting the optimal ${\omega _k}$.

The Pearson correlation coefficient can be used to measure the difference between the original signal and the reconstructed signal. The deviation is less the higher the value. Assuming that $x$ and$y$ are two-time series of length $N$, the Pearson correlation coefficient is calculated as follows:

where ${P^ * }$ is the Pearson correlation coefficient of $x$ and $y$; $\bar x$ and $\bar y$ are the average values of $x$ and $y$. The fitness function is calculated as Eq (20):

Based on the foregoing, this work proposes the improved GJO algorithm to improve the VMD algorithm's parameter $[k, \alpha]$. The initial parameters are as follows: the initial population is set to 20, maximum iterations are set to 20, the value range for $k$ is set to [2,10] and the value range for $\alpha$ is set to [100,3000]. The procedure is depicted in Figure 2.

2.2.   Data prediction model

2.2.1.   Boosting algorithm

The main goals of the boosting method, an integrated learning strategy, are to speed up the model's convergence and, therefore, raise the overall model's stability and accuracy. The most widely spread algorithms of the boosting algorithm are AdaBoost algorithm and BoostingTree.

● AdaBoost is an integrated algorithm for generating base learners in series ^[29]. By combining multiple base learners, the generalization performance is often better than that of a single learner, and it is not easily affected by over-fitting.

● Gradient boosting decision tree (GBDT) is a branch of the iterative decision tree model ^[30]. Its main idea is to reduce residuals through continuous iteration and form many regression decision trees through gradient direction optimization. Finally, it accumulates the conclusions of all regression trees to get the final model.

● Light gradient boosting machine (LightGBM) is an algorithm based on a gradient lifting decision tree, which is based on the unilateral sampling of the gradient when searching for the optimal segmentation point of the loss function ^[31]. For the sample, the smaller the gradient, the closer it is, so the weight can be lowered when searching for the segmentation point.

● XGBoost is a boosting ensemble learning algorithm that improves GBDT ^[32]. Its traits include low computational complexity, great precision and quick processing speed. It quickly gained the support of competitors in important modeling competitions and produced excellent results.

● CatBoost is a more effective gradient-lifting decision tree-based ensemble learning technique ^[33]. In the training process, a group of decision trees is established continuously. Compared with the previous trees, each continuous tree reduces the loss.

2.2.2.   Evaluation metrics

To boost the effectiveness of tourist flow forecasts, comprehensive evaluation metrics (CEM) are proposed to determine the reconstructed subsequence forecast model ^[34]. The specific steps are as follows:

(1) Calculate the mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) of five boosting models of each reconstructed subsequence. Table 1 displays the evaluation metrics.

Here, ${y_i}$ and ${\hat y_i}$ represent the actual value and the predicted value respectively, and $n$ is the number of samples.

(2) Normalize the four evaluation indexes according to Eq (21):

where $M_i^ *$ is the normalized value of MSE, RMSE, MAE and MAPE of the $i$ submodel; $M$ is the abbreviation of evaluation metrics.

(3) Calculate the comprehensive evaluation index of the $i$ submodel according to Eq (22):

(4) According to the CEM value of each boosting algorithm, the prediction model of the reconstructed subsequence is determined.

Finally, four metrics are employed to measure the prediction error to assess the performance of the suggested prediction model: RMSE, MAE, MAPE, and coefficient of determination (Rsquare). ${\text{Rsquare}} = \frac{{\sum\limits_{i = 1}^n {{{\left({{{\hat y}_i} - \bar y} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left({{y_i} - \bar y} \right)}^2}} }}$, $\bar y$ represents the average value of the actual value.

3.   The proposed hybrid passenger flow forecasting model

This section provides a mixed passenger flow forecasting model based on the mixed passenger flow forecasting model to accurately predict the tourist flow in Jilin Province. The model includes four steps, as shown in Figure 3.

Step 1: Expand data features. Collect the original passenger flow data and expand the features of the original time series data according to the historical time. Add four discrete variables such as "Weekday", "Week", "Weekend" and "Holiday". See Section 4.2 for details.

Step 2: Data decomposition. The parameters in the VMD algorithm are optimized using the GJO based on the Sobol sequence that was proposed in this study, and the original passenger flow time data is decomposed into IMF.

Step 3: IMF reconstruction. According to the sample entropy of each IMF, IMF with similar complexity is merged into a new subsequence.

Step 4: Ensemble prediction. Four discrete variables are introduced, and the prediction model determination method including five submodels AdaBoost, GBDT, XGBoost, LightGBM, and CatBoost are adopted, and the optimal model of each reconstruction subsequence is determined according to the values. The final passenger flow prediction result is then obtained by integrating the reconstructed subsequence prediction.

4.   Empirical analysis

4.1.   Data description

The daily passenger flow data of Changbai Mountain, World Sculpture Park and Changchun Zoological and Botanical Park in Jilin Province are chosen as the source data to assess the validity of the hybrid passenger flow forecasting model presented in this work. Each data set has 865 samples and covers all daily passenger flow data between August 2017 and December 2019. All data is provided by the Jilin Tourism Information Center. Data for this study is split into two sets: Training set and test set, which make up 90% and 10% of the total data, respectively. The overall trend of passenger flow data of the three scenic spots is shown in Figure 4.

4.2.   Extended data features

This study adds four discrete variables—"weekday", "week", "weekend" and "holiday"—to the original daily visitor data of scenic spots because the original data are time series and provide less information. Where "Weekday" stands for the weekday and its value is 1~5, "Week" denotes the week of the current month. If the day is a Weekend, the field "Weekended" is filled with one, otherwise, it is filled with zero. The word "Holiday" designates whether or not the day is a holiday. Fill in one if it's a holiday; otherwise, enter zero.

4.3.   Decomposition and reconstruction of passenger flow data

The original passenger flow data is nonlinear and non-stationary, as seen in Figure 4. To reduce the sequence complexity, three passenger flow datasets are decomposed using IVMD. The decomposition outcomes, using Changbai Mountain, Changchun Zoological and Botanical Park data as an illustration, are displayed in Figure 5. The passenger flow data from Changbai Mountain, Changchun Zoological and Botanical Park is decomposed by IVMD into seven IMF, which are arranged from low to high frequency. The trends and laws of the decomposed series are more obvious than those of the original series, which enables us to predict future trends and changes more accurately. IVMD divides the World Sculpture Park into 10 IMF, as shown in Figure 6.

In this study, the IMF is reconstructed according to the SE, and the SE of IMF is calculated as shown in Table 2 and Figure 7. To cut the cost of the calculation, reconstruct IMF with similar SE into a new subsequence.

For Changbai Mountain, because the SE of IMF1 is small, it is divided into Sub1. The difference in the SE of other IMF is big enough for the division to be reconstructed using a difference of 0.07 between the two IMF. For Sculpture Park, because the SE of IMF1 is small, it is divided into Sub1. The difference in the SE of other IMF is big enough for the division to be reconstructed using a difference of 0.08 between the two IMFs. For Zoological and Botanical Park, because the SE of IMF1 is small, it is divided into Sub1. The difference in the SE of other IMF is small enough for the division to be reconstructed using a difference of 0.04 between the two IMF. The reconstruction results are shown in Table 3.

4.4.   Prediction model

The extended data characteristics of the original passenger flow are introduced, and the optimal prediction model of each reconstructed subsequence is determined according to the minimum CEM value. Table 4 shows the optimal model determined by each reconstruction subsequence of three scenic spots. The reconstructed subsequence prediction values are integrated and, finally, the passenger flow prediction results of three scenic spots are obtained.

4.5.   Empirical analysis

Three comparative tests were conducted on three different datasets in this study to demonstrate how well the suggested hybrid passenger flow forecasting model performed. RMSE, MAE, MAPE, and Rsquare are the major metrics used to assess each prediction model's accuracy and error distribution. The closer the value of Rsquare is to one, and the smaller the values of RMSE, MAE, and MAPE, the better the model effect. The best evaluation index in each datasets is expressed in bold font.

4.5.1.   Experiment Ⅰ

In this experiment, the proposed hybrid passenger flow forecasting model is compared with five single models: AdaBoost, GBDT, LightGBM, XGBoost and CatBoost. Figure 8 and Table 5 display the experimental results, and the following inferences can be made:

(1) For Changbai Mountain, RMSE = 1255.2646, MAE = 840.9776, MAPE = 0.0973 and Rsquare = 0.9533 of the hybrid forecasting model are all better than the single boosting model. Compared with these five single models, the RMSE, Mae and MAPE of the hybrid forecasting model average decrease by 895.5644,374.0677 and 0.0247, respectively. The average increase of Rsquare is 0.1526, which shows that the proposed prediction model has high accuracy.

(2) For Sculpture Park, the hybrid forecasting model has a better forecasting effect than the single model, RMSE = 248.0198, MAE = 166.1583, MAPE = 0.0469 and Rsquare = 0.9563. It can be found that for AdaBoost, GBDT, LightGBM, XGBoost and CatBoost models, the Rsquare of the model is increased by 0.1434, 0.1547, 0.1495, 0.2169 and 0.2066, respectively. The prediction accuracy of the hybrid prediction model is greatly improved.

(3) For Zoological and Botanical Park, the hybrid model's prediction performance is also superior to that of the single AdaBoost, GBDT, LightGBM, XGBoost and CatBoost models, RMSE = 419.6541, MAE = 272.2626, MAPE = 0.0674 and Rsquare = 0.9597.

The suggested model outperforms the single model in terms of prediction effect and accuracy when the passenger flow data from three scenic locations are compared. It can not only avoid the shortcomings of a single model but also play a more comprehensive and effective prediction performance.

4.5.2.   Experiment Ⅱ

In this experiment, the same IVMD decomposition method and different boosting algorithms are used as comparison models to verify the validity of the determination rules of the subsequence prediction model. Figure 9 and Table 6 display the experimental results, and the following inferences can be made:

(1) For Changbai Mountain, among all the models, the proposed hybrid forecasting model has the best effect, with the smallest values of RMSE, MAE, and MAPE and the largest value of Rsquare. The MAPE is 0.0973, which is 0.0562, 0.0123, 0.0159, 0.0010 and 0.0191 lower than IVMD-AdaBoost, IVMD-GBDT, IVMD-LightGBM, IVMD-XGBBoost and IVMD-CatBoost, respectively.

(2) For Sculpture Park, among the six forecasting models based on IVMD, RMSE = 248.0198, MAE = 166.1583, MAPE = 0.0469 and Rsquare = 0.9563 of the hybrid forecasting model are superior to other comparison models.

(3) For Zoological and Botanical Park, the hybrid model proposed in this paper performs best, and its RMSE = 419.6541, MAE = 272.2626, and MAPE = 0.0674 are smaller than other comparative models. Rsquare = 0.9597 is higher than IVMD-AdaBoost, IVMD-GBDT, IVMD-LightGBM, IVMD-XGBoost and IVMD-CatBoost.

The subsequence prediction model determination rule chooses the best prediction model for each reconstructed subsequence in order to obtain the final passenger flow forecast value. By effectively exploiting the advantages of each prediction model, the hybrid prediction model raises the overall forecast accuracy.

4.5.3.   Experiment Ⅲ

This experiment will compare the proposed IVMD with EMD, VMD and complete ensemble extreme-point symmetric mode decomposition (CEESMDAN) and analyze the decomposition effect of IVMD. Among them, the subsequent prediction model of the comparison algorithm is the same as the proposed hybrid prediction model. C-EMD, C-VMD and C-CEESMDAN represent compositive models based on EMD technology, VMD technology and CEESMDAN technology. Figure 10 and Table 7 display the experimental outcomes. The inferences that can be made are as follows:

(1) For Changbai Mountain, the RMSE = 1255.2646, MAE = 840.9776, MAPE = 0.0973 and Rsquare = 0.9533 of the hybrid forecasting model have a better forecasting effect on passenger flow. The prediction and evaluation indexes based on EMD are RMSE = 1379.8929, MAE = 851.9099, MAPE = 0.0998 and Rsquare = 0.9286. The prediction and evaluation indexes based on VMD are RMSE = 1426.2054, MAE = 1034.4371, MAPE = 0.1077 and Rsquare = 0.9386. The prediction and evaluation indexes based on CEESMDAN are RMSE = 1608.8527, MAE = 920.4725, MAPE = 0.1005 and Rsquare = 0.8941. It can be found that IVMD is superior to other decomposition methods.

(2) For Sculpture Park, the MAPE of the hybrid forecasting model and the forecasting model based on EMD, VMD and CEESMDAN are 0.0469, 0.0566, 0.0713 and 0.0664, respectively. Compared with the forecasting model based on EMD, VMD and CEESMDAN, Rsquare = 0.9563 is increased by 0.0084, 0.0403 and 0.0122, respectively.

(3) For Zoological and Botanical Park, the accuracy of the hybrid forecasting model based on IVMD is still higher than the other three decomposition methods. Compared with other models, the RMSE, Mae and MAPE of the hybrid forecasting model are average reduced by 279.9724,168.2926 and 0.0462, respectively. The average increase of Rsquare is 0.0660, which shows the effectiveness of IVMD in passenger flow forecasts.

IVMD not only avoids mode aliasing but also decomposes the original passenger flow data into multiple IMF. Compared with VMD, IVMD also realizes the selection of optimal parameters, which helps improve the performance of the hybrid forecasting model. The forecasting error of the suggested hybrid forecasting model is also noticeably lower than that of the forecasting models based on EMD, VMD and CEESMDAN. As a result, IVMD is a useful decomposition technique to increase the model's prediction accuracy.

5.   Conclusions

Accurate prediction of tourist flow in scenic spots is of great significance to the development of intelligent transportation and smart cities. It can not only enhance the tourist experience but also promote the intelligent development of the city. This study established a hybrid passenger flow prediction model using the advantages of improved variational mode decomposition, sample entropy, and the boosting algorithm to enhance the prediction performance of the conventional passenger flow model. The original passenger flow data was divided into numerous IMF by IVMD and reconstructed into subsequences by sample entropy based on the properties of the original time series data. Each reconstructed subsequence's best prediction model was identified and forecasted based on the CEM minimum value. The final forecast result of the visitor flow to scenic spots was generated by combining the prediction results from each rebuilt subsequence.

The passenger flow data of Changbai Mountain, Sculpture Park, and Zoological and Botanical Park in Jilin Province were empirically studied to assess the reliability and applicability of the hybrid ensemble forecasting model. (1) The hybrid forecasting model outperformed the single model according to the findings. The RMSE of the model, using Changbai Mountain data as an example, is 1255.2646, MAE is 840.9776, MAPE is 0.0973 and Rsquare is 0.9533. The study's use of passenger flow data increases by tens of thousands every day, so the results of RMSE are hundreds or even thousands. (2) According to Experiment Ⅱ, the RMSE, MAE and MAPE of the hybrid prediction model based on the subsequence prediction model are lower than those of the contrast model on three datasets. The benefits of each prediction model can be efficiently incorporated into the hybrid model. (3) The passenger flow series is divided using the IVMD, which significantly raises forecast accuracy. In three datasets and four evaluation indexes, the hybrid prediction model was superior to the prediction models based on another decomposition algorithm.

In summary, the proposed hybrid forecasting model was an effective, reliable and accurate prediction model, which shows great advantages in accurate prediction results. The hybrid forecasting model has a wide range of potential applications and can promote the intelligent and sustainable development of the city. The influencing elements taken into account in this article are not all-inclusive, and unknown reasons such as financial crises, unexpected events and natural disasters were not considered. Future studies will take these characteristics into account, thus improving the prediction performance of the model.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Science and Technology Department Project of Jilin Province (Grant No. 20200403182SF), the Science and Technology Department Project of Jilin Province (Grant No. 20210101149JC) and the National Natural Science Foundation of China (Grant No. 12026430). The authors thank the editors for their comments and suggestions.

Conflict of interest

The authors declare there is no conflict of interest.