Counting rational points of two classes of algebraic varieties over finite fields

1.   Introduction

Plasma physics simply refers to the study of a state of matter consisting of charged particles. Plasmas are usually created by heating a gas until the electrons become detached from their parent atom or molecule. In addition, plasma can be generated artificially when a neutral gas is heated or subjected to a strong electromagnetic field. The presence of free charged particles makes plasma electrically conductive with the dynamics of individual particles and macroscopic plasma motion governed by collective electromagnetic fields ^[1].

Nonlinear partial differential equations (NPDE) in the fields of mathematics and physics play numerous important roles in theoretical sciences. They are the most fundamental models essential in studying nonlinear phenomena. Such phenomena occur in plasma physics, oceanography, aerospace industry, meteorology, nonlinear mechanics, biology, population ecology, fluid mechanics to mention a few. We have seen in ^[2] that the authors studied a generalized advection-diffusion equation which is a NPDE in fluid mechanics, characterizing the motion of buoyancy propelled plume in a bent-on absorptive medium. Moreover, in ^[3], a generalized Korteweg-de Vries-Zakharov-Kuznetsov equation was studied. This equation delineates mixtures of warm adiabatic fluid, hot isothermal as well as cold immobile background species applicable in fluid dynamics. Furthermore, the authors in ^[4] considered a NPDE where they explored important inclined magneto-hydrodynamic flow of an upper-convected Maxwell liquid through a leaky stretched plate. In addition, heat transfer phenomenon was studied with heat generation and absorption effect. The reader can access more examples of NPDEs in ^{[5,6,7,8,9,10,11,12,13,14,15,16]}.

In order to really understand these physical phenomena it is of immense importance to solve NPDEs which govern these aforementioned phenomena. However, there is no general systematic theory that can be applied to NPDEs so that their analytic solutions can be obtained. Nevertheless, in recent times scientists have developed effective techniques to obtain viable analytical solutions to NPDEs, such as inverse scattering transform ^[16], simple equation method ^[17], Bäcklund transformation ^[18], F-expansion technique ^[19], extended simplest equation method^[20], Hirota technique ^[21], Lie symmetry analysis ^{[22,23,24,25,26,27]}, bifurcation technique ^[28,29], the $(G'/G)$-expansion method ^[30], Darboux transformation ^[31], sine-Gordon equation expansion technique ^[32], Kudryashov's method ^[33], and so on.

The (2+1)-dimensional Bogoyavlensky-Konopelchenko (BK) equation given as

where parameters $\alpha$ and $\beta$ are constants, is a special case of the KdV equation in ^[34] which was introduced as a (2+1)-dimensional version of the KdV and it is described as an interaction of a long wave propagation along $x$-axis and a Riemann wave propagation along the $y$-axis ^[35]. In addition to that, few particular properties of the equation have been explored. The authors in ^[36] provided a Darboux transformation for the BK equation and the obtained transformation was used to construct a family of solutions of this equation. In ^[37], with $3\beta$ replaced by $4\beta$ and $u_y = v_x$ in (1.1), the authors integrated the result once to get

Further, they utilized Lie group theoretic approach to obtain solutions of the system of Eq (1.2). They also engaged the concept of nonlinear self-adjointness of differential equations in conjunction with formal Lagrangian of (1.2) for constructing nonlocal conservation laws of the system. In addition, various applications of BK equation (1.1) were highlighted in ^[37]. Further investigations on certain particular cases of (1.1) were also carried out in ^[38,39].

In ^[40], the 2D generalized BK equation that reads

was studied and lump-type and lump solutions were constructed by invoking the Hirota bilinear method. Liu et al. ^[41] applied the Lie group analysis together with $(G'/G)$-expansion and power series methods and obtained some analytic solutions of (1.3).

Yang et al. ^[42] recently examined a generalized combined fourth-order soliton equation expressed as

with constant parameters $\alpha, \; \beta$ and $\gamma$ which are not all zero, whereas all constant coefficients $\delta_i, \; 1 \leq i \leq 6$, are arbitrary. It was observed that Eq (1.4) comprises three fourth-order terms and second-order terms that consequently generalizes the standard Kadomtsev-Petviashvili equation. Soliton equations are known to have applications in plasma physics and other nonlinear sciences such as fluid mechanics, atomic physics, biophysics, nonlinear optics, classical and quantum fields theories.

Assuming $\alpha = 0$, $\beta = 1$, $\gamma = 0$ and $\delta_1 = \delta_2 = 1$, $\delta_3 = \delta_4 = \delta_5 = \delta_6 = 0$, the authors gain an integrable (1+2)-dimensional extension of the Hirota-Satsuma equation commonly referred to as the Hirota-Satsuma-Ito equation in two dimensions^[43] given as

that satisfies the Hirota three-soliton condition and also admits a Hirota bilinear structure under logarithmic transformation presented in the form

whose lump solutions have been calculated in ^[44]. On taking parameters $\alpha = 1$, $\beta = 0$, $\gamma = 0$ along with $\delta_1 = \delta_4 = \delta_6 = 0$ whereas $\delta_2 = \delta_3 = \delta_5 = 1$, they eventually came up with a two dimensional equation^[42]:

which is called a two-dimensional generalized Bogoyavlensky-Konopelchenko (2D-gBK) equation. We notice that if one takes $\alpha = \beta = 1$ in Eq (1.1) with the introduction of two new terms $u_{xx}$ and $u_{yy}$, the new generalized version (1.7) is achieved.

In consequence, we investigate explicit solutions of the new two-dimensional generalized Bogoyavlensky-Konopelchenko equation (1.7) of plasma physics in this study. In order to achieve that, we present the paper in the subsequent format. In Section 2, we employ Lie symmetry analysis to carry out the symmetry reductions of the equation. In addition, direct integration method will be employed in order to gain some analytic solutions of the equation by solving the resulting ordinary differential equations (ODEs) from the reduction process. We achieve more analytic solutions of (1.7) via the conventional $\left(G'/G\right)$-expansion method as well as Kudryashov's technique. In addition, by choosing suitable parametric values, we depict the dynamics of the solutions via 3-D, 2-D as well as contour plots. Section 3 presents the conservation laws for 2D-gBK equation (1.7) through the multiplier method and in Section 4, we give the concluding remarks.

2.   Symmetry analysis and analytic solutions of (1.7)

In this section we in the first place compute the Lie point symmetries of Eq (1.7) and thereafter engage them to generate analytic solutions.

2.1.   Lie point symmetries of (1.7)

A one-parameter Lie group of symmetry transformations associated with the infinitesimal generators related to (\real{gbk}) can be presented as

We calculate symmetry group of 2D-gBK equation (1.7) using the vector field

where $\xi^i, i = 1, 2, 3$ and $\phi$ are functions depending on $t$, $x$, $y$ and $u$. We recall that (2.2) is a Lie point symmetry of Eq (1.7) if

where $Q = u_{tx}+6u_xu_{xx}+u_{xxxx}+u_{xxxy}+3\left(u_{x}u_y\right)_{x} + u_{xx}+ u_{yy}$. Here, $R^{[4]}$ denotes the fourth prolongation of $R$ defined by

where coefficient functions $\eta^{t}$, $\eta^{x}$, $\eta^{y}$, $\eta^{xt}$, $\eta^{xx}$, $\eta^{xy}$, $\eta^{yy}$, $\eta^{xxxx}$ and $\eta^{xxxy}$ can be calculated from ^[22,23,24].

Writing out the expanded form of the determining equation (2.3), splitting over various derivatives of $u$ and with the help of Mathematica, we achieve the system of linear partial differential equations (PDEs):

The solution of the above system of PDEs is

where $A_1$–$A_3$ are arbitrary constants and $F(t)$, $G(t)$ are arbitrary functions of $t$. Consequently, we secure the Lie point symmetries of (1.7) given as

2.2.   Lie group transformations associated to (2.5)

We contemplate the exponentiation of the vector fields (2.5) by computing the flow or one parameter group generated by (2.5) via the Lie equations ^[22,23]:

Therefore, by taking $F(t) = G(t) = t$ in (2.5), one computes a one parameter transformation group of 2D-gBK (1.7). Thus, we present the result in the subsequent theorem.

Theorem 2.1. Let $T_{\epsilon}^i(t, x, y, u), i = 1, 2, 3, \dots, 6$ be transformations group of one parameter generated by vectors $R_1, R_2, R_3\dots, R_6$ in (2.5), then, for each of the vectors, we have accordingly

where $\epsilon \in \mathbb{R}$ is regarded as the group parameter.

Theorem 2.2. Hence, suppose $u(t, x, y) = \varTheta(t, x, y)$ satisfies the 2D-gBK (1.7), in the same vein, the functions given in the structure

will do, where $u^i(t, x, y) = T_i^{\epsilon} \cdot \varTheta(t, x, y), i = 1, 2, 3, \dots, 6$ with $\epsilon < < 1$ regarded as any positive real number.

2.3.   Symmetry reduction of 2D-gBK equation (1.7)

In this subsection, we utilize symmetries (2.5) with a view to reduce Eq (1.7) to ordinary differential equations and thereafter obtain the analytic solutions of Eq (1.7) by solving the respective ODEs.

Case 1. Invariant solutions via $R_1$–$R_3$

Taking $F(t) = 1/3$, we linearly combine translational symmetries $R_{1}$–$R_{3}$ as $R = b R_{1}+c R_{2}+a R_{3}$ with nonzero constant parameters $a$, $b$ and $c$. Subsequently utilizing the combination reduces 2D-gBK equation (1.7) to a PDE with two independent variables. Thus, solution to the characteristic equation associated with the symmetry $R$ leaves us with invariants

Now treating $\theta$ above as the new dependent variable as well as $r$, $s$ as new independent variables, (1.7) then transforms into the PDE:

We now utilize the Lie point symmetries of (2.7) in a bid to transform it to an ODE. From (2.7), we achieve three translation symmetries:

The linear combination $Q = Q_1+ \omega Q_2$ ($\omega \neq 0$ being an arbitrary constant) leads to two invariants:

that secures group-invariant solution $\Theta = \Theta (z)$. Thus, on using these invariants, (2.7) is transformed into the fourth-order nonlinear ODE:

which we rewrite in a simple structure as

where $A = c ^{2}- \omega c ^{2} + a ^2 \omega ^2-2 b a \omega + b ^2$, $B = 6(b c ^{2}- c ^{2} a \omega - c ^{3})$, $C = c ^{3} a \omega + c ^{4}- b c ^{3}$ and $z = c x+(a \omega - b)y - c \omega t$.

2.4.   Some analytic solutions of 2D-gBK equation (1.7)

In this section, we seek travelling wave solutions of the 2D-gBK equation (1.7).

A. Elliptic function solution of (1.7)

On integrating equation (2.9) once, we accomplish a third-order ODE:

where $C_1$ is a constant of integration. Multiplying Eq (2.10) by $\Theta '' (z)$, integrating once and simplifying the resulting equation, we have the second-order nonlinear ODE:

where $C_2$ is a constant of integration. The above equation can be rewritten as

Letting $U (z) = \Theta ' (z)$, Eq (2.11) becomes

Suppose that the cubic equation

has real roots $c_1$–$c_3$ such that $c_1 > c_2 > c_3$, then Eq (2.12) can be written as

whose solution with regards to Jacobi elliptic function ^[45,46] is

with (cn) being the elliptic cosine function. Integration of (2.15) and reverting to the original variables secures a solution of 2D-gBK equation (1.7) as

with $z = c x+(a \omega - b)y - c \omega t$ and $C_3$ a constant of integration. We note that (2.16) is a general solution of (1.7), where ${\rm{EllipticE}}[p; q]$ is the incomplete elliptic integral ^[46,47] expressed as

We present wave profile of periodic solution (2.16) in Figure 1 with 3D, contour and 2D plots with parametric values $a = -4$, $b = 0.2$, $c = -0.1$, $\omega = 0.1$, $c_1 = 100$, $c_2 = 50.05$, $c_3 = -60$, $B = 10$, $C = 70$, where $t = 1$ and $-10 \leq x, y\leq 10$.

However, contemplating a special case of (2.9) with $B = 0$, we integrate the equation twice and so we have

where $K_1$ and $K_2$ are integration constants. Solving the second-order linear ODE (2.17) and reverting to the basic variables, we achieve the trigonometric solution of 2D-gBK equation (1.7) as

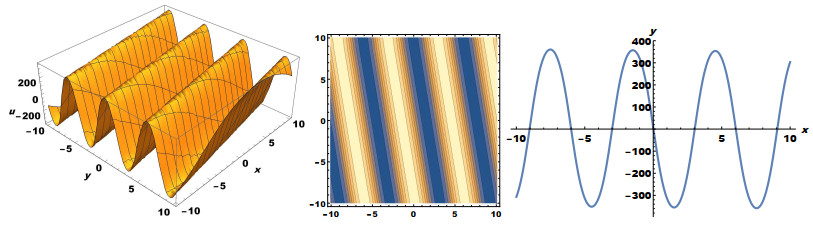
with $A_1$ and $A_2$ as the integration constants as well as $z = c x+(a \omega - b)y - c \omega t$. We depict the wave dynamics of periodic solution (2.18) in Figure 2 via 3D, contour and 2D plots with dissimilar parametric values $a = 1$, $b = 0.2$, $c = -0.1$, $\omega = 0.1$, $A_1 = 20$, $A_2 = -2$, $K_1 = 1$, $K_2 = 10$, where $t = 2$ and $-10 \leq x, y\leq 10$.

B. Weierstrass elliptic solution of 2D-gBK equation (1.7)

We further explore Weierstrass elliptic function solution of (1.7), which is a technique often involved in getting general exact solutions to NPDEs ^[47,48]. In order to accomplish this, we use the transformation

and transform the nonlinear ordinary differential equation (NODE) (2.12) to

with the invariants $g_2$ and $g_3$ given by

Thus, we have the solution of NODE (2.12) as

where $\wp$ denotes the Weierstrass elliptic function ^[46]. In consequence, integration of (2.21) and reverting to the basic variables gives the solution of 2D-gBK equation (1.7) as

with arbitrary constant $z_0$, $z = c x+(a \omega - b)y - c \omega t$ and $\zeta$ being the Weierstrass zeta function ^[46]. We give wave profile of Weierstrass function solution (2.22) in Figure 3 with 3D, contour and 2D plots using parameter values $a = 1$, $b = 0.2$, $c = -0.1$, $\omega = 0.1$, $A = 10$, $B = -2$, $z_0 = 0$, $C = 1$, $C_1 = 1$, $C_2 = 10$, where $t = 2$ and $-10 \leq x, y\leq 10$.

2.4.1.   Solution of (1.7) by Kudrayshov's approach

This part of the study furnishes the solution of 2D-gBK equation (1.7) through the use of Kudryashov's approach ^[33]. This technique is one of the most prominent way to obtain closed-form solutions of NPDEs. Having reduced Eq (1.7) to the NODE (2.9), we assume the solution of (2.9) as

with $Q (z)$ satisfying the first-order NODE

We observe that the solution of (2.24) is

The balancing procedure for NODE (2.9) produces $N = 1$. Hence, from (2.23), we have

Now substituting (2.26) into (2.9) and using (2.24), we gain a long determining equation and splitting on powers of $Q(z)$, we get algebraic equations for the coefficients $B_0$ and $B_1$ as

The solution of the above system gives

Hence, the solution of 2D-gBK equation (1.7) associated with (2.28) is given as

The wave profile of solution (2.29) is shown in Figure 4 with 3D, contour and 2D plots using parameter values $a = 1$, $b = -0.2$, $c = 20$, $\omega = 0.05$, $B_0 = 0$ with $t = 7$ and $-6 \leq x, y\leq 6$.

2.4.2.   Solution of (1.7) through $(G'/G)$-expansion technique

We reckon the $(G'/G)$-expansion technique ^[30] in the construction of analytic solutions of 2D-gBK equation (1.7) and so we contemplate a solution structured as

where $Q(z)$ satisfies

with $\lambda$ and $\mu$ taken as constants. Here, $B_0, \dots, B_M$ are parameters to be determined. Utilization of balancing procedure for (2.9) produces $M = 1$ and as a result, the solution of (1.7) assumes the form

Substituting the value of $\Theta(z)$ from (2.32) into (2.9) and using (2.31) and following the steps earlier adopted, leads to an algebraic equation in $B_0$ and $B_1$, which splits over various powers of $Q(z)$ to give the system of algebraic equations whose solution is secured as

where $\Omega_0 = B_1^6 \lambda ^4 \omega ^2-8 B_1^6 \lambda ^2 \mu \omega ^2-16 B_1^4 \lambda ^2 \omega ^2+16 B_1^6 \mu ^2 \omega ^2+64 B_1^4 \mu \omega ^2$. Thus, we have three types of solutions of the 2D-gBK equation (1.7) given as follows:

When $\lambda^2-4\mu > 0$, we gain the hyperbolic function solution

with $z = c x+(a \omega - b)y - c \omega t$, $\Delta_{1} = \frac{1}{2}\sqrt{\lambda^2-4\mu}$ together with $A_1$, $A_2$ being arbitrary constants. The wave profile of solution (2.33) is shown in Figure 5 with 3D, contour and 2D plots using parameter values $a = 3$, $b = 0.5$, $c = 10$, $\omega = -0.1$, $B_0 = 0$, $\lambda = -0.971$, $\mu = 10$, $A_1 = 5$, $A_2 = 1$, where $t = 10$ and $-10 \leq x, y\leq 10$.

When $\lambda^2-4\mu < 0$, we achieve the trigonometric function solution

with $z = c x+(a \omega - b)y - c \omega t$, $\Delta_{2} = \frac{1}{2}\sqrt{4\mu - \lambda^2}$ together with $A_1$ and $A_2$ are arbitrary constants. The wave profile of solution (2.34) is shown in Figure 6 with 3D, contour and 2D plots using parameter values $a = 1$, $b = 0.5$, $c = 0.3$, $\omega = 0.3$, $B_0 = 0$, $\lambda = -0.971$, $\mu = 2$, $A_1 = 5$, $A_2 = 1$ with $t = 10$ and $-10 \leq x, y\leq 10$.

When $\lambda^2-4\mu = 0$, we gain the rational function solution

with $z = c x+(a \omega - b)y - c \omega t$ and $A_1$, $A_2$ being arbitrary constants. We plot the graph of solution (2.35) in Figure 7 via 3D, contour and 2D plots using parametric values $a = 1$, $b = 1.01$, $c = 100$, $\omega = 0.1$, $B_0 = 10$, $\lambda = 10$, $A_1 = 3$, $A_2 = 10$, where $t = 2.4$ and $-5 \leq x, y\leq 5$.

Case 2. Group-invariant solutions via $R_4$

Lagrange system associated with the symmetry $R_4 = 3 t \partial/\partial y + (x - 2 y)\partial/\partial u$ is

which leads to the three invariants $T = t, \, \, X = x, \, \, Q = u + (y^2/3t) - (xy/3t)$. Using these three invariants, the 2D-gBK equation (1.7) is reduced to

Case 3. Group-invariant solutions via $R_1, \; R_2 \, {\rm{and}} \, R_5$

We take $G(t) = 1$ and by combining the generators $R_1, \; R_2$ as well as $R_5$, we solve the characteristic equations corresponding to the combination and get the invariants $X = x$, $Y = y - t$ with group-invariant $u = Q(X, Y) + t$. With these invariants, the 2D-gBK equation (1.7) transforms to the NPDE

whose solution is given by

with arbitrary constants $A_1$–$A_3$. Thus, we achieve the hyperbolic solution of (1.7) as

The wave profile of solution (2.40) is shown in Figure 8 with 3D, contour and 2D plots using parameter values $A_1 = 70.1$, $A_2 = -30$, $A_3 = 0$, where $t = 0.5$ and $-10 \leq x, y\leq 10$.

Besides, symmetries of (2.38) are found as

Now, the symmetry $P_1$ furnishes the solution $Q(X, Y) = f(z)$, $z = Y$. So, Eq (2.38) gives the ODE $f''(z) = 0$. Hence, we have a solution of (1.7) as

with $A_0$, $A_1$ as constants. Further, the symmetry $P_2$ yields $Q(X, Y) = f(z)$, $z = X$ and so Eq (2.38) reduces to

Integration of the above equation three times with respect to $z$ gives

and taking constants $A_0 = A_1 = 0$ and then integrating it results in the solution of (1.7) as

The wave profile of solution (2.44) is shown in Figure 9 with 3D, contour and 2D plots using parameter values $A_1 = 40$, $t = 3.5$ and $-10 \leq x \leq 10$.

On combining $P_1$–$P_3$ as $P = c_0 P_1 + c_1 P_2 + c_2 P_3$, we accomplish

Using the newly acquired invariants (2.45), Eq (2.38) transforms to the NODE:

Engaging the Lie point symmetry $P_4$, we obtain

and Eq (2.38) reduces to the NODE

Case 4. Group-invariant solutions via $R_6$

Lie point symmetry $R_6$ dissociates to the Lagrange system

which gives

Substituting the expression of $u$ in (1.7), we obtain the NPDE

which has two symmetries:

The symmetry $P_2$ gives $Q(X, Y) = f(z) + (1/15) T X$, $z = T$ and hence (2.50) reduces to

Solving the above ODE and reverting to the basic variables gives the solution of (1.7) as

where $A_1$ and $A_2$ are integration constants. The wave profile of solution (2.51) is shown in Figure 10 with 3D, contour and 2D plots using parameter values $A_1 = -0.3$, $A_2 = -50$ with $t = 1.1$ and $-10 \leq x, y\leq 10$.

Next, we invoke the symmetry $P_1+P_2$. This yields $Q(X, Y) = f(z) + X + (1/15) T X$$, \; z = T$. Consequently, we have the transformed version of (2.50) as

Solving the above ODE and reverting to basic variables gives the solution of (1.7) as

The wave profile of solution (2.52) is shown in Figure 11 with 3D, contour and 2D plots using parameter values $A_1 = -3.6$, $A_2 = 50$ with $t = 1.1$ and $-10 \leq x, y\leq 10$.

3.   Conservation laws of (1.7)

In this section, we construct the conservation laws for 2D-gBK equation (1.7) by making use of the multiplier approach ^[22,49,50], but first we give some basic background of the method that we are adopting.

3.1.   Fundamental operators and their relationship

Consider the $n$ independent variables $x = (x^1, x^2, \ldots, x^n)$ and $m$ dependent variables $u = (u^1, u^2, \ldots, u^m)$. The derivatives of $u$ with respect to $x$ are defined as

where

is the operator of total differentiation. The collection of all first derivatives $u_i ^{\alpha}$ is denoted by $u_{(1)}$, i.e., $u_{(1)} = \{u_{i}^{\alpha}\}, \, \, \alpha = 1, ..., m, \, \, i = 1, ..., n$. In the same vein $u_{(2)} = \{u_{ij}^{\alpha}\}, \, \, \alpha = 1, ..., m, \, \, i, j = 1, ..., n$ and $u_{(3)} = \{u_{ijk} ^{\alpha}\}$ and likewise $u_{(4)}$ etc. Since $u_{ij}^{\alpha} = u_{ji}^{\alpha}$, $u_{(2)}$ contains only $u_{ij}^{\alpha}$ for $i\leq j$.

Now consider a $k$th-order system of PDEs:

The {Euler-Lagrange operator}, for every $\alpha$, is presented as

An $n$-tuple $T = (T ^1, T ^2, \ldots, T ^n)$, such that

holds for all solutions of (3.3) is known as the conserved vector of system (3.3).

The multiplier $\Omega _{\alpha} (x, u, u_{(1)}, \ldots)$ of system (3.3) has the property that

holds identically ^[22]. The determining equations for multipliers are obtained by taking the variational derivative of (3.6), namely

The moment multipliers are generated from (3.7), the conserved vectors can be derived systematically using (3.6) as the determining equation.

3.2.   Construction of conservation laws for (1.7)

Conservation laws of 2D-gBK equation (1.7) are derived by utilizing second-order multiplier $\Omega (t, x, y, u, u_t, u_x, u_y, u_{xx}, u_{xy})$, in Eq (3.7), where $G$ is given as

and the Euler operator $\delta/\delta u$ is expressed in this case as\newpage

Expansion of Eq (3.7) and splitting on diverse derivatives of dependent variable $u$ gives

Solution to the above system of equations gives $\Omega (t, x, y, u, u_t, u_x, u_y, u_{xx}, u_{xy})$ as

with $C_1$ being an arbitrary constant and $f_{1}(t)$, $f_2(t)$ being arbitrary functions of $t$. Using Eq (3.6), one obtains the following three conserved vectors of Eq (1.7) that correspond to the three multipliers $u_x, \; f_{1}(t)$ and $f_2(t)$:

Case 1. For the first multiplier $Q_1 = u_x$, the corresponding conserved vector $(T_1^t, T_1^x, T_1^y)$ is given by

Case 2. For the second multiplier $Q_2 = f_1(t)$, we obtain the corresponding conserved vector $(T_2^t, T_2^x, T_2^y)$ as

Case 3. Finally, for the third multiplier $Q_3 = f_2(t)$, the corresponding conserved vector $(T_3^t, T_3^x, T_3^y)$ is

Remark 3.1. We notice that this method assists in the construction of conservation laws of (1.7) despite the fact that it possesses no variational principle ^[51]. Moreover, the presence of arbitrary functions in the multiplier indicates that 2D-gBK (1.7) has infinite number of conserved vectors.

4.   Conclusions

In this paper, we carried out a study on two-dimensional generalized Bogoyavlensky-Konopelchenko equation (1.7). We obtained solutions for Eq (1.7) with the use of Lie symmetry reductions, direct integration, Kudryashov's and $(G'/G)$-expansion techniques. We obtained solutions of (1.7) in the form of algebraic, rational, periodic, hyperbolic as well as trigonometric functions. Furthermore, we derived conservation laws of (1.7) by engaging the multiplier method were we obtained three local conserved vectors. We note here that the presence of the arbitrary functions $f_{1}(t)$ and $f_{2}(t)$ in the multipliers, tells us that one can generate unlimited number of conservation laws for the underlying equation.

Conflict of interest

The authors state no conflicts of interest.