Stochastic tumor-immune interaction model with external treatments and time delays: An optimal control problem

1.   Introduction and motivation

The Fox-Wright function, denoted by ${}_p\Psi_q$, which is a generalization of hypergeometric functions, and it defined as follows ^[1] (see also [2, p. 4, Eq (2.4)]):

where $A_j \geq 0\; \; (j = 1, \cdots, p)$ and $B_l\geq 0\; \; (l = 1, \cdots, q)$. The convergence conditions and convergence radius of the series on the right-hand side of (1.1) immediately follow from the known asymptote of the Euler gamma function. The defining series in (1.1) converges in the complex $z$-plane when

If $\Delta = 0,$ then the series in (1.1) converges for $|z| < \rho$ and $|z| = \rho$ under the condition $\Re(\mu) > \frac{1}{2},$ where

The Fox-Wright function extends the generalized hypergeometric function ${}_p F_q[z]$ the power series form of which is as follows [3, p. 404, Eq (16.2.1)]:

where, as usual, we make use of the Pochhammer symbol (or rising factorial) given below:

In the special case that $A_p = B_q = 1$ the Fox-Wright function ${}_p\Psi_q[z]$ reduces (up to the multiplicative constant) to the following generalized hypergeometric function:

For $p = q = a_1 = A_1 = 1, b_1 = \beta,$ and $B_1 = \alpha,$ we recover from (1.1) the two-parameter Mittag-Leffler function $E_{\alpha, \beta}(z)$ (also known as the Wiman function ^[4]) defined as follows (see, for example, [5, Chapter 4]):

To provide the exposition of the results in the present investigation, we need the so-called incomplete Fox-Wright functions ${}_p\Psi_q^{(\gamma)}[z]$ and ${}_p\Psi_q^{(\gamma)}[z]$ that were introduced by Srivastava et al. in [6, Eqs (6.1) & (6.6)]:

and

where $\gamma(a, x)$ and $\Gamma(a, x)$ denote the lower and upper incomplete gamma functions, the integral expression of which is as follows [3, p. 174, Eq (8.2.1-2)]):

and

These two functions satisfy the following decomposition formula [3, p. 136, Eq (5.2.1)]:

The positivity constraint of parameters $M, A_j, B_j > 0$ should satisfy the following constraint:

where the convergence conditions and characteristics coincide with the ones around the 'complete' Fox-Wright function ${}_p\Psi_q[z].$

The properties of some functions related to the incomplete special functions including their functional inequalities, have been the subject of several investigations ^{[7,8,9,10,11,12,13]}. A certain class of incomplete special functions are widely used in some areas of applied sciences due to the relations with well-known and less-known special functions, such as the Nuttall $Q$-function ^[14], the generalized Marcum $Q$-function (see e.g., [14, p. 39]), the McKay $I_\nu$ Bessel distribution (see e.g., [15, Theorem 1]), the McKay $K_\nu(a, b)$ distribution ^[16], and the non-central chi-squared distribution [17, Section 5]. The incomplete Fox-Wright functions have important applications in communication theory, probability theory, and groundwater pumping modeling; see [6, Section 6] for details. See also ^[18]. To date, there have been many studies on a some class of functions related to the lower incomplete Fox-Wright functions; see, for instance ^[19,20,21]. Also, Mehrez et al. ^[22] considered a new class of functions related to the upper incomplete Fox-Wright function, defined in the following form:

In ^[22], several properties of the function defined by (1.6), including its differentiation formulas, fractional integration formulas that can be obtained via fractional calculus and new summation formulas that comprise the incomplete gamma function, as well as some other special functions (such as the complementary error function) are investigated. In this paper, we apply another point of view to the following upper incomplete Fox-Wright function:

By using certain properties of the two parameters of the Mittag-Leffler and incomplete gamma functions, we derive new functional inequalities based on the aforementioned function defined in (1.7). Furthermore, two classes of completely monotonic functions are presented.

2.   Some useful lemmas

Before proving our main results, we need the following useful lemmas. One of the main tools is the following result, i.e., which entails applying the Mellin transform on $[b, \infty)$ of the function $e^{-\frac{t^2}{2}} E_{\alpha, \beta}(t):$

Lemma 2.1. ^[22] The following integral representation holds true:

Remark 2.2. If we set $b = 0$ in Lemma 2.1, we obtain

Lemma 2.3. ^[23] Let $(a_k)_{k\geq0}$ and $(b_k)_{k\geq0}$ be two sequences of real numbers, and let the power series $f(t) = \sum\limits_{k = 0}^\infty a_k t^k$ and $g(t) = \sum\limits_{k = 0}^\infty b_k t^k$ be convergent for $|t| < r.$ If $b_k > 0$ for $k\geq0$ and if the sequence $(a_k/b_k)_{k\geq0}$ is increasing (decreasing) for all $k,$ then the function $t\mapsto f(t)/g(t)$ is also increasing (decreasing) on $(0, r).$

The following lemma, is one of the crucial facts in the proof of some of our main results.

Lemma 2.4. If $\min(\alpha, \beta) > 1,$ then the function $t\mapsto e^{-t} E_{\alpha, \beta}(t)$ is decreasing on $(0, \infty).$

Proof. From the power-series representations of the functions $t\mapsto E_{\alpha, \beta}(t)$ and $t\mapsto e^{t},$ we get

Given lemma 2.3, to prove that the function $t\mapsto e^{-t} E_{\alpha, \beta}(t)$ is decreasing, it is sufficient to prove that the sequence $(c_k)_{k\geq0} = (a_k/b_k)_{k\geq0}$ is decreasing. A simple computation gives

Moreover, since the digamma function $\psi(t) = \Gamma^\prime(t)/\Gamma(t)$ is increasing on $(0, \infty)$, we get that the function

is increasing on $(0, \infty).$ This implies that the inequality

holds true for all $\lambda, \delta > 0.$ Now, we set $t = k+1, \lambda = 1$ and $\delta = (\alpha-1)k+\beta-1$ in (2.4), we get

Using the fact that $\Gamma(\alpha k+\alpha+\beta) > \Gamma(\alpha k+\beta+1)$ for all $\min(\alpha, \beta) > 1,$ and in consideration of (2.5), we obtain

Bearing in mind (2.3) and the inequality (2.6), we can show that the sequence $(c_k)_{k\geq0}$ is decreasing. This, in turn, implies that the function $t\mapsto e^{-t} E_{\alpha, \beta}(t)$ is decreasing on $(0, \infty)$ for all $\min(\alpha, \beta) > 1.$ □

Lemma 2.5. Let $\alpha > 0$ and $\beta > 0.$ If

then

where

Proof. The proof follows by applying [24, Theorem 3]. □

Remark 2.6. We see that the set $\mathbb{J}$ is nonempty; for example, we see that $(1, \beta)\in \mathbb{J}$ such that $\beta > 1.$ For instance, $(1, 2)\in \mathbb{J}.$

The result in the next lemma has been given in [25, Theorem 4]. We present an alternative proof.

Lemma 2.7. For $\min(z, \mu) > 0,$ the following holds:

Moreover, for $\min(z, \mu) > 0,$ we have

Proof. Let us denote

Given (1.3), we can obtain

We denote

We have that $F_\mu(0) = G(0) = 0.$ Since the function $z\mapsto \gamma^*(\mu, z)$ is log-convex on $(0, \infty)$ (see, for instance, the proof of Theorem 3.1 in ^[25]), we deduce that the function $z\mapsto F_\mu(z)$ is convex on $(0, \infty)$. This, in turn, implies that the function

is also increasing on $(0, \infty).$ Therefore, the function

is also increasing on $(0, \infty)$ according to L'Hospital's rule for monotonicity ^[26]. Therefore, we have

Then, through straightforward calculations, we can complete the proof of inequality (2.10). Finally, by combining (2.10) and (1.5), we obtain (2.11). □

3.   Main results

The first set of main results read as follows.

Theorem 3.1. Let $b > 0, z\geq0, \; \min(\alpha, \beta) > 1, \; b+2\nu > 1$ and $0 < 2\nu\leq1.$ Then, the following inequalities are valid:

where the equality holds true if $z = 0:$ also, here, ${\rm {erfc}}$ is the complementary error function, defined as follows (see, e.g., [3, Eq (7.2.1)]):

Proof. According to Lemma 2.4, the function $t\mapsto e^{-at}E_{\alpha, \beta}(at)$ is decreasing on $(0, \infty)$ for all $\min(\alpha, \beta) > 1$ and $a > 0.$ It follows that the function $t\mapsto t^{2\nu-1} e^{-at}E_{\alpha, \beta}(at)$ is decreasing on $(0, \infty)$ for each $\min(\alpha, \beta) > 1$ and $\nu\in(0, \frac{1}{2}].$ Then, for all $t\geq b,$ we have

Therefore

which readily implies that the upper bound in (3.1) holds true. Now, let us focus on the lower bound of the inequalities corresponding to (3.1). We observe that the function $t\mapsto t^{2\nu-1} e^{t}$ is increasing on $[b, \infty)$ if $b+2\nu-1 > 0$ and, consequently the function $t\mapsto t^{2\nu-1} e^{t} E_{\alpha, \beta}(t)$ is increasing on $[b, \infty)$ under the given conditions. Hence,

Then, we obtain

which completes the proof of the right-hand side of the inequalities defined in (3.1). This completes the proof. □

Setting $\nu = \frac{1}{3}$ in Theorem 3.1, we can deduce the following results.

Corollary 3.2. For all $b > \frac{1}{3}, z\geq0,$ and $\min(\alpha, \beta) > 1,$ the following inequality holds:

where $c(b) = \sqrt[6]{2\pi^3b^2}.$

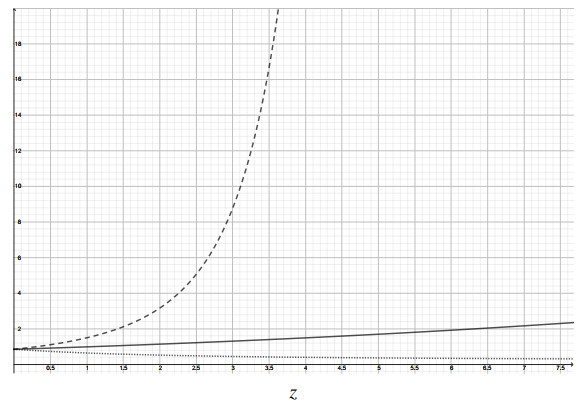
Example 3.3. Taking $(\alpha, \beta) = 2$ and $b = \frac{1}{\sqrt{2}}$ in Corollary 3.2 gives the following statement (see Figure 1):

Theorem 3.4. Let $\nu > 0, \; \min(z, b)\geq0,$ and $\min(\alpha, \beta) > 1.$ Then,

where $\phi_{\nu}(a, b)$ is defined by

Proof. By applying part (a) of Lemma 2.4, we get

Moreover, by using the monotonicity of the function $t\mapsto e^{at}E_{\alpha, \beta}(at)$, we have

Obviously, by repeating the same calculations as in Theorem 3.1, with the help of (3.8) and (3.9), we obtain (3.6). □

By applying $\nu = \frac{1}{2}$ in (3.6), we immediately obtain the following inequalities.

Corollary 3.5. Assume that $\min(z, b)\geq0$ and $\min(\alpha, \beta) > 1$. Then, the following holds:

where the equality holds only if $z = 0.$

Remark 3.6. It is worth mentioning that, if we set $\nu = \frac{1}{2}$ in Theorem 3.1, we obtain the inequalities defined in (3.10), but under the condition $b > 0.$

Corollary 3.7. Under the assumptions of Corollary 3.5, the following inequalities hold:

Proof. Taking $\nu = 1$ in (3.6) and keeping in mind the relation given by

we readily establish (3.11) as well. □

Now, by making use of Corollary 3.5 and Corollary 3.7 with $b = 0$, we obtain the following specified result.

Corollary 3.8. For $z\geq0$ and $\min(\alpha, \beta) > 1,$ we have

By making use of Corollary 3.7 with $b = 0$, we obtain the following specified result.

Corollary 3.9. For $z\geq0$ and $\min(\alpha, \beta) > 1,$ we have

Example 3.10. If we set $\alpha = \beta = 2$ in (3.13), we obtain the following inequalities (see Figure 2):

Example 3.11. If we set $\alpha = \beta = 2$ in (3.14), we obtain the following inequalities (see Figure 3):

Theorem 3.12. Let $\nu > 0, \min(z, b)\geq0,$ and $(\alpha, \beta)\in \mathbb{J}$ such that $\alpha\geq\frac{1}{2}.$ Then, the following inequalities hold:

Proof. By considering the left-hand side of the inequalities defined in (2.8), i.e., where we applied the substitution $u = t-c(\alpha, \beta),$ we have

which implies the right-hand side of (3.17). It remains for us to prove the left-hand side of the inequalities defined in (3.17). By applying the right-hand side of (2.8), we get

Then, we can readily establish (3.17) as well. □

Corollary 3.13. For $\min(z, b)\geq0$ and $(\alpha, \beta)\in \mathbb{J}$ such that $\alpha\geq\frac{1}{2},$ the following holds:

and the corresponding equalities hold for $z = 0.$

Proof. By applying $\nu = \frac{1}{2}$ in (3.17) and performing some elementary simplifications, the asserted result described by (3.19) follows. □

As a result of $b = 0$ in (3.19), we get the following result:

Corollary 3.14. For $\nu > 0$ and $(\alpha, \beta)\in \mathbb{J}$ such that $\alpha\geq\frac{1}{2},$ the inequalities

hold for all $z\geq0.$ Moreover, the corresponding equalities hold for $z = 0.$

Example 3.15. If we set $\nu = \frac{1}{2}, \alpha = 1,$ and $\beta = 2$ in (3.20), we obtain the following inequalities (see Figure 4):

where $z\geq0.$

Theorem 3.16. For $\min(\nu, z) > 0$ and $b\geq0$, the following holds:

Furthermore, if $\nu\geq 1, b\geq0$ and $z > 0,$ the following holds:

Proof. By applying (2.11) we obtain

which is equivalent to the inequality (3.22). Now, let us focus on the inequalities (3.23). By applying the following inequality [3, Eq (8.10.1)]

Then, we get

The proof is complete. □

We recall that a real valued function $f,$ defined on an interval $I,$ is called completely monotonic on $I$ if $f$ has derivatives of all orders and satisfies

These functions play an important role in numerical analysis and probability theory. For the main properties of the completely monotonic functions, we refer the reader to [27, Chapter IV].

Theorem 3.17. Let $\nu > 0$ and $b\geq0.$ If $0 < \alpha \leq1$ and $\beta\geq \alpha$, then the function

is completely monotonic on $(0, \infty).$ Furthermore, for $0 < \alpha \leq1$ and $\beta\geq \alpha,$ the inequality

holds for all $z > 0$ and $b\geq0.$

Proof. In ^[28], Schneider proved that the function $z\mapsto E_{\alpha, \beta}(-z)$ is completely monotonic on $(0, \infty)$ under the parametric restrictions $\alpha\in(0, 1]$ and $\beta\geq\alpha$ (see also ^[29]). Then, by considering (2.1), we conclude that

Finally, for inequality (3.27), we can observe that the function

is log-convex on $(0, \infty)$ since every completely monotonic function is log-convex; see [27, p. 167]. Now, for convenience, let us denote

Hence, the function $z\mapsto\mathcal{F}(z)$ is convex on $(0, \infty)$ such that $\mathcal{F}(0) = 0.$ Therefore, the function $z\mapsto\frac{\mathcal{F}^\prime(z)}{\mathcal{G}^\prime(z)}$ is increasing on $(0, \infty).$ Again, according to L'Hospital's rule of monotonicity ^[26], we conclude that the function

is increasing on $(0, \infty).$ Consequently,

On the other hand, by (2.1), we have

By combining (3.28) and (3.29) via some obvious calculations, we can obtain the asserted bound (3.27). □

By setting $b = 0$ in Theorem 3.17, we can obtain the following results:

Corollary 3.18. Let $\nu > 0$. If $0 < \alpha \leq1$ and $\beta\geq \alpha$, then the function

is completely monotonic on $(0, \infty).$ Furthermore, for $0 < \alpha \leq1$ and $\beta\geq \alpha,$ the inequality

holds for all $z\geq0.$

Example 3.19. Letting $\nu = \frac{1}{2}, \alpha = 1,$ and $\beta = 2$ in (3.27), we obtain the following inequality (see Figure 5):

Remark 3.20. As in Section 3, we may derive new upper and/or lower bounds for the lower incomplete Fox-Wright function ${}_2\Psi_1^{(\gamma)}[z]$, by simple replacing the relation (2.1) with the following relation:

4.   Applications

In [6, Section 6], Srivastava et al. presented several applications for the incomplete Fox-Wright functions in communication theory and probability theory. It is believed that certain forms of the incomplete Fox-Wright functions, which we have studied here, have the potential for application in fields similar to those mentioned above, including probability theory.

5.   Conclusions

In our present investigation, we have established new functional bounds for a class of functions that are related to the lower incomplete Fox-Wright functions; see (1.7). We have also presented a class of completely monotonic functions related to the aforementioned type of function. In particular, we have reported on bilateral functional bounds for the Fox-Wright function ${}_2\Psi_1[.].$ Moreover, we have presented some conditions to be imposed on the parameters of the Fox-Wright function ${}_2\Psi_1[.]$, and these conditions have allowed us to conclude that the function is completely monotonic. Some applications of this type of incomplete special function have been discussed for probability theory.

The mathematical tools that have been applied in the proofs of the main results in this paper will inspire and encourage the researchers to study new research directions that involve the formulation of some other special functions related to the incomplete Fox-Wright functions, such as the Nuttall $Q$-function ^[14], the generalized Marcum $Q$-function, and Marcum $Q$-function. Yet another novel direction of research can be pursued for other special functions when we replace the two-parameter Mittag-Leffler function with other special functions such as the three-parameter Mittag-Leffler function (or Prabhakar's function ^[30]), the two-parameter Wright function ^[2], and the four parameter Wright function; see [31, Eq (21)].

Author contributions

Khaled Mehrez and Abdulaziz Alenazi: Writing–original draft; Writing–review & editing. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number "NBU-FPEJ-2024-220-01".

Conflict of interest

The authors declare that they have no conflicts of interest.