Soil moisture routing modeling of targeted biochar amendment in undulating topographies: an analysis of biochar's effects on streamflow

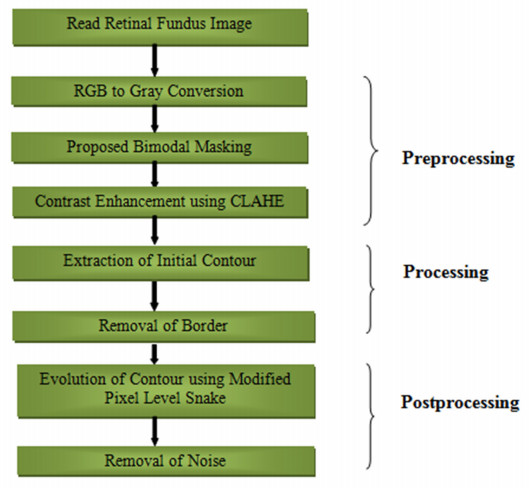
1.   Introduction

Retinal vascular network is a tree-like structure that includes arteries, arterioles, capillaries, veins and venules. It is useful to find the other normal features of retina such as macula or fovea or optic disk or for the automatic identification of pathological elements like hemorrhage, micro aneurysms, exudates or lesions ^[1]. As vascular diseases present a challenging health problem for society, so an efficient vascular segmentation algorithm is needed for understanding and analysis of vascular diseases in a better way. Segmentation of blood vessels using manual method and semi-automatic method is tedious and time consuming task because high skills and training is required in both these methods. Moreover, these segmentation techniques are susceptible to errors. With the use of fully automatic segmentation techniques, problems of manual segmentation and semi-automatic segmentation can be overcome. These automatic techniques are helpful in the advancement of computer-aided diagnostic systems which are used for identification of various ophthalmic disorders. Segmentation of vessels in an accurate manner is a tedious job because of the less variations in the contrast between vasculature and surrounding tissue, presence of noise in the retina image; variation in the vessel width, shape, branching angle and brightness of image and presence of lesions, exudates, hemorrhage and other pathologies.

Although various segmentation techniques have been used ^[2,3,4] for segmentation of different diseases and anatomical structures of the body but the main goal of this paper is to present the methodology used for extraction of vessels from fundus image. Modified Pixel level snake (PLS) technique has been used for extraction of vessels. PLS is an iterative technique, in which internal and external forces are used for evolution of pixels of contour. Various segmentation approaches can be used for extraction of blood vessels, which includes unsupervised approach ^[5,6,7,8], supervised approach ^{[9,10,11,12,13,14,15,16]}, tracking approach ^[17,18,19], deformable models approach ^{[20,21,22,23,24,25,26]}, filtering approach ^[27] and morphological approach ^[28,31].

Stall et al. ^[29] proposed a method for extraction of ridges of image from the color retinal fundus image. Soares et al. ^[30] presented a technique in which enhancement of retinal fundus image is performed using gabor filter and classification is performed using Bayesian classifier. Martinez et al. ^[32] proposed a method based on multiscale feature extraction approach for segmentation of vasculature map from red-free and fluorescein retinal fundus images. You et al. ^[33] presented a scheme based on the radial projection and semi-supervised method, for the extraction of retinal vasculature map. Alonso-Montes et al. ^[40] proposed a method based on PLS. In this, PLS has been used and tested in single instruction multiple data (SIMD) parallel processor array, for segmentation of retinal vasculature map. Time of execution and accuracy has also been analyzed. Perfetti et al. ^[41] proposed Cellular neural network (CNN) technique for extraction of vessels. Normally, in PLS, external potential is computed using edge based techniques. In our proposed methodology, BTH transformation is used for the computation of external potential, which results in improved accuracy of the extracted vasculature map.

Contribution of the proposed approach is as follows:

● Bimodal masking is applied for the extraction of the mask of the fundus image.

● Global thresholding is used for segmentation of vasculature map of fundus image.

● MPLS based on BTH transformation has been proposed for evolution of map in four cardinal directions.

The remaining paper is structured as follows. Section 2 described the materials used for proposed work. Section 3 described the methodology used for extraction of the vasculature map of the fundus image. Section 4 represented the results and discussions and section 5 represented the conclusion of the work.

2.   Materials

2.1.   Database used

For analysis purpose, the color fundus image of the retina has been taken from the DRIVE (Digital Retinal Images for Vessels Extraction) database ^[42]. This database contains 40 images, out of which 20 are test images and 20 are training images. Out of 40 images, 7 images are pathological images and 33 are normal images. Images are produced at 45° field of view (FOV), using Canon CR5 nonmydriatic 3CCd camera. Size of each image in this database is 565 × 584 pixels.

After implementation of the algorithm on the DRIVE dataset, simulation is also performed on 20 images (700 × 605 pixels each) of the STARE (Structured Analysis of Retina) database ^[43].

2.2.   Performance metrics

Pixel based classification is used for extraction of vasculature map from the fundus image. Pixel classification is done on the basis of whether the pixel belongs to the vessel or surrounding tissue. So, four different possible events are possible which include pixel classifications and pixel misclassifications. True positive (TP) and true negative (TN) are the two pixel classifications and false positive (FP), and false negative (FN) are the two pixel misclassifications which are used for evaluation of various performance metrics. An event is classified as TP if a vessel pixel is correctly identified as vessel and TN if the non-vessel pixel or pixel in the surrounding tissue is correctly identified as a non-vessel pixel. An event is said to be FN if the predicted pixel represents a non-vessel pixel but actually it was a vessel pixel. An event is said to be FP if the predicted pixel represents vessel pixel but actually it was a non-vessel pixel. The important performance metrics which can be derived from the above events are sensitivity, specificity, and accuracy.

2.2.1.   Sensitivity (SN)

SN metrics represents the ability of a segmentation method to detect the vessel pixels. SN is defined as the ratio of TP to the sum of TP and FN. Range of sensitivity is between 0 and 1. More SN means the algorithm is able to identify vessel pixels correctly. SN measure is expressed by Eq (1).

2.2.2.   Specificity (SP)

SP metrics represents the ability of a segmentation algorithm to detect background or non-vessel pixels. SP is also defined as the ratio of TN to the sum of TN and FP. Range of specificity is also between 0 and 1. More SP means the algorithm is able to identify non-vessel pixels correctly. SP measure is expressed by Eq (2).

2.2.3.   Accuracy (Acc)

Acc is evaluated by taking the ratio of total number of true events which is the sum of TP and TN, to the total population which is the total number of pixels actually present in the image. The formula for accuracy is expressed by Eq (3).

3.   Methods

Proposed methodology for automated extraction of vasculature map of fundus image is presented in Figure 1. The main components of the pre-processing are: RGB to gray conversion, generation of mask using bimodal masking and contrast enhancement using CLAHE (Contrast Limited Adaptive Histogram Equalization).

3.1.   RGB to gray conversion

Initially RGB fundus image (1_test of DRIVE database) is read and converted to gray scale image for segmentation of vessels. Conversion of RGB to gray image also reduces the time required for processing of the image. Different weights for R, G & B components are selected for conversion purpose. RGB to gray conversion is performed using the formula represented by Eq (4) ^[44].

Where r, g and b symbolize the red, green, and blue channels of the fundus image respectively and G is the gray image produced after conversion. The green channel is the channel which gives the maximum information of the fundus image, so the weight of the green channel is chosen larger as compared to other channels. RGB image and its corresponding gray-scale image is represented by Figure 2(a), (b) respectively.

3.2.   Proposed bimodal masking

Vasculature map of retinal fundus image is used for detection of diseases and monitoring of diseases. After applying certain image processing techniques on fundus images, the speed of analyzing these images can be increased. Since analyses require more time and computational effort, operations should be focused only on the object pixels. For getting the object pixels, first the binary mask is generated and then multiplied with the original image so as to get the accurate image required for segmentation.Flow chart for the generation of mask using bimodal masking is shown in Figure 2(c). Mask is generated from the gray image, obtained after RGB to gray conversion. Initially histogram of image is generated as shown in Figure 2(d) and then dominant peaks and valleys are identified according to the histogram ^[45]. Then the second valley is selected as threshold level for the conversion of gray image into binary image. Binary image is produced after thresholding is termed as final mask, shown in Figure 2(e). Figure 2(f) represents the mask of image, produced after simple thresholding techniques. So, it can be easily analyzed that the mask produced after bimodal masking is accurate as compared to simple thresholding technique.

3.3.   Contrast enhancement using CLAHE

CLAHE operation is performed for enhancement of contrast of an image. CLAHE works on small areas in the image rather than the entire image. These small regions are termed as 'tiles'. Enhancement of contrast has been performed tile wise. After that all neighboring tiles are combined using bilinear interpolation method. In this paper, two level enhancements have been done using CLAHE technique. It means CLAHE has been applied two times for getting the proper enhanced image. Size of tiles used for CLAHE is [8 8] and the number of bins is 128. Enhanced image produced after applying CLAHE technique is shown in Figure 3(a).

3.4.   Processing or segmentation

The main component of the pre-processing is global thresholding used for extraction of initial contour.

3.4.1.   Extraction of initial contour

Enhanced image produced using CLAHE is further used to produce the segmented image. For generation of segmented image, initially adaptive segmentation is required because gray values along vessels in retina vasculature are non-uniform. Input of adaptive segmentation is preprocessed image (enhanced image) and output is segmented image. Figure 3(b) represents the block diagram of adaptive segmentation. Average filter having size 9 is applied on preprocessed image to produce averaged image as shown in Figure 3(c). After that, a subtracted image is produced by taking the difference between the averaged image and the preprocessed image. Then a global thresholding technique is applied on the subtracted image for computation of threshold level of image. Global thresholding technique (Algorithm 1) is stated as follows:

Using this threshold, the subtracted image is converted to the binary image, which is called as the segmented image as represented by Figure 3(d). This segmented image will be used to find the initial contour which is defined implicitly as the region boundary. After that morphological operation, closing is applied on the segmented image by taking disk shaped structuring element (SE) having size 1. Then small areas having pixel size less than 35 are removed from the closed image. The image produced is called the initial contour of the image shown in Figure 3(e).

3.4.2.   Removal of border

Next task is to remove the border from the contour image because the retinal vasculature map does not include the outer border as shown in the initial contour image represented by Figure 3(e). So, the border is removed from the initial contour image using the mask produced using bimodal masking. To perform this operation, the initial contour image is subtracted from the complement of the mask. If after subtraction, some pixels contain values greater than 0, then value 1 is assigned to those pixels and if some pixels contain values less than zero, then 0 is assigned to those pixels. So after subtraction and assigning values to the subtracted image, a contour image without border is produced. After that morphological operation (dilation) using disk shape SE having size 1 is applied on the image. The image shown in Figure 3(f) is further used for evolution using MPLS.

3.5.   Post processing

The main components of the post processing are evolution of contour using modified PLS and removal of noise.

3.5.1.   Evolution of contour using modified pixel level snake

In a PLS algorithm the evolution of contour is performed by pixel-by-pixel shifting of the contour, towards a position where the potential is minimum. Figure 4 shows the flowchart of PLS algorithm. In this algorithm, contour pixels evolve iteratively according to the potential field. This potential field comprises of three potentials named as internal, external and balloon potential and the weights of these potentials are adjusted according to the application. The main components of a PLS algorithm is contour evolution. Topological Transformations module is also used to handle merging and splitting of contours. This module is basically used to avoid collisions between contours.

(1) External potential computation

In existing methods, external potential is calculated using edge based techniques like sobel and canny edge detection. But in this paper, MPLS is proposed in which external potential of image is calculated by using BTH transformation method because the external potential produced using BTH method contains more information about the vasculature map resulting in higher accuracy. Using this external potential, the total potential of the image is computed which evolves the contour in an efficient way as compared to previous existing methods. Flow chart for computation of external potential for modified PLS is shown in Figure 5(a). Here, BTH transformation is applied on the green channel of the retinal fundus image (as shown by Figure 5(b)) by taking three different structuring elements.

The BTH transform is the transformation which is evaluated by subtracting the input image from the closing of the input image. The BTH transform of image (f) is given by Eq (5).

Here, I is the input image; b represents the SE and $\odot$ represents the closing operation.

Output ${T}_{b}\left(I\right)$ represents the BTH transformed image.

Three different disk shaped structuring elements having size 2, 7, 11 are used for closing operation in computation of external potential. Then the sum of all three BTH transformed images is taken to produce the external potential image as represented by Figure 5(c). For evolution of contour towards minimum potential, complement of external potential is taken. Complement of external potential image (P_e) is represented by Figure 5(d).

This is the potential which guides the contour of the image towards edges of the vasculature map. If the image is static, then external potential is computed once. Applications like real time computer vision, in which moving images are there, external potential is computed for each frame of the image. Evolution of PLS will be done by external potential which is stronger in areas close to the edges.

(2) Internal potential computation

This potential is useful in maintaining the smooth shape of the contour. During the evolution of PLS, all vessel discontinuities are avoided using internal potential. Internal potential is computed from the initial contour. Flow chart for computation of internal potential of the image is shown in Figure 6(a). In this, initially a binary contour edge image is produced from the initial contour image shown in Figure 5(e) using the expression: C = I_C and not (I_CN and I_CS and I_CW and I_CE). Here I_C represents the initial contour of the image, I_CN represents I_C(x, y - 1), i.e., active region pixels in NORTH direction from the current pixel I_C(x, y).Similarly I_CE, I_CW and I_CS represents I_C(x, y+1), I_C(x -1, y), I_C(x+1, y), i.e., active region pixels in East, West and South directions from the current pixel I_C(x, y) respectively. Figure 6(b) represents the edge image produced from the initial contour image. Diffusion of image has been performed on edge image of initial contour by anisotropic diffusion method taking lambda = 0.25; and no. of iterations = 20. Anisotropic diffusion of contour image is performed to obtain an internal potential field. Anisotropic diffusion, also called Perona-Malik diffusion, is a technique used to reduce noise present in the image without removing important parts of the image content.

Anisotropic diffusion is defined by Eq (6).

Where $Δ$ denotes the laplacian, $\nabla$ denotes the gradient, div is the divergence operator and c(x, y, t) is the diffusion coefficient. Two functions for diffusion coefficient are proposed by Perona and Malik which are representedby Eqs 7(a) and 7(b).

And

Constant K is used to control the sensitivity to edges. Here the value of K is chosen as 40. The diffused image as shown in Figure 6(c) is multiplied with weight having value 0.1 to get an internal potential image. After that, the complement of the internal potential image (Pi) has been taken for contour evolution in the proper direction. Figure 6(d), (e) represent the weighted internal potential image and complemented image respectively.

(3) Balloon potential computation

When external potential is too weak, then it's not possible for external potential to guide the contour in all directions. In that case, there is one potential which produces forces, to guide the contour towards object pixels. Initially PLS is controlled by balloon potential because initially contour is far from vessel edges. To get balloon potential image, initial contour is multiplied with weight having value 0.1. Flowchart for computation of balloon potential is shown in Figure 7(a). Figure 7(b), (c) represents weighted balloon potential and complement of balloon potential image (P_b) respectively.

(4) Guiding force extraction module

Potential field is computed as the weighted sum of external, internal and balloon potential as represented by equation 8. All internal and external forces are produced through the potential field that guides the evolution of contour towards minimum energy level.

Here P_T represents the total potential field of an image, P_e represents the external potential of image, P_i represents the internal potential image and P_b represents the balloon potential of image. Figure 7(d) represents the potential field image produced after the addition of all potential images.

(5) Directional contour evolution with topological transformation and collision detection module

Evolution of directional contour is the most important part of PLS technique. It is performed in four prime directions: NORTH, EAST, WEST and SOUTH (NEWS). After iteration each pixel of contour is moved towards a position, where it can acquire minimum potential.

The expansion of contour may result in merging and splitting of contours. But in segmentation of retinal vasculature, it's required to prevent the collision between the contours. For preventing the collision, a collision detection module has been used. When contour expands in each direction, the two vessels may combine with each other. So, this expansion of contour is done in such a way that there should be no danger of collision. Figure 8(a) represents the different cases for dangers of collisions. Considering the danger of collision point in mind, expression for expansion in NORTH, SOUTH, EAST and WEST direction is computed below.

Expansion in north direction:

Pixel wise expansion of initial contour has been performed in the north direction based on potential of image. Expression for expansion in NORTH direction is given by Condition 1.

If (not D) and I_CS and (P_T < P_{T S}), then I_C becomes equal to 1.      Cond.(1)

Here D = R or R_E or R_W and R = (not I_C) and I_CN.

Here, P_T represents the total potential field, P_TS represents potential field in south direction, R represents the active/background pixel pairs in the vertical direction, D represents the danger of collision which is determined by taking logic 'OR' of the current pixel of R with its east (RE) and west (RW) neighbor.

Expansion of the initial contour in the north direction is represented by taking a matrix of 10:10 elements. Figures 8(b), (c) represents the initial contour of 100 pixels and its expanded version in north direction respectively. Observe the pixel values and potential of initial contour highlighted with red box in Figure 8(d), (e) respectively. If the pixel has value 0 and its potential is less than potential in its south direction, then value 1 is assigned to that pixel as represented in Figure 8(f).

Similarly, expressions in other directions can be computed by considering the danger of collision.

Expression in south direction is given by Cond.(2)

If (not D) and I_CN and (P_T < P_TN) then I_C becomes equal to 1.      Cond.(2)

Here D = R or R_E or R_W and R = (not I_C) and I_CS.

Expression in east direction is given by Cond.(3)

If (not D) and I_CW and (P_T < P_TW) then I_C becomes equal to 1.      Cond.(3)

Here D = R or R_N or R_S and R = (not I_C) and I_CE.

Expression in west direction is given by Cond.(4)

If (not D) and I_CE and (P_T < P_TE) then I_C becomes equal to 1.      Cond.(4)

Here D = R or R_N or R_S and R = (not I_C) and I_CW.

Images produced after expansion in N, S, E, W directions are represented by Figure 9(a)-(d).

(6) Inversion

Image produced after expansion in all directions is inverted to ensure contour evolution towards minimum potential. Inversion of the active region produces a new contour shifted by one pixel. So, the inverted image is not simply calculated by (not I_C) but using the following expression.

Inv = (not I_C) or c. Here c = I_C and not (I_CN and I_CS and I_CW and I_CE). Inverted image is represented by Figure 10(a). After inversion, evolution of contour image is again performed in all directions. So, expansion and contraction of active and background regions is performed in each iteration. Also steady direction of forces which are inflating and deflating in nature, can be maintained by inverting balloon potential after each iteration. Figure 10(b)-(e) represents contour expansion in all directions in the second iteration respectively.

3.6.   Removal of noise

In the last stage, small objects (extracted from retinal vasculature obtained after MPLS evolution) having pixels less than 30 are removed. Noise which is present outside the border has been removed by multiplying the final vasculature map with the complement of mask. After that morphological closing with SE disk having size 1 is applied on the image. This is the final vasculature map as shown by Figure 11(a), which can be further used for identification of various diseases.

4.   Results & discussion

Various performance metrics such as SN, SP and Acc have been computed by using extracted vasculature map and ground truth map. Acc of proposed algorithm is better is due to extraction of accurate binary mask of fundus image; better enhancement of image and evolution of vasculature map using MPLS technique in all four cardinal directions. Figure 11(a), (b) represents extracted map and ground truth image of original retinal fundus image.

The algorithm can be applied on all images of the DRIVE database. Figure 12 represents the results of the three normal images of the DRIVE database and their extracted vasculature map respectively.

Table 1 represents comparative analysis of SN, SP and Acc metrics for DRIVE database. For analysis purpose, the proposed method results are compared with the results obtained by Staal ^[29] et al., Soares ^[30] et al., Mendonc-a ^[31] et al., Martinez-Perez ^[32] et al., You ^[33] et al., Fraz ^[34] et al., Ravichandran et al. ^[35], Zhao et al. ^[36], Yin et al. ^[37], Frucci ^[38] et al. and Zhang ^[39] et al., Adapa ^[46], Ma ^[47]. It has been observed that for MPLS, average SN comes out to be better than existing methodologies except ^[47] and SP comes out to be better than existing methodologies except ^[38], because there is a trade-off between SN and SP of image. Acc of proposed methodology is better than Acc of all existing methodologies.

This algorithm has been tested on all test images and pathological images of the DRIVE database. Figure 13 represents the results of the two pathological images of the DRIVE database and their extracted vasculature map respectively. Table 2 represents SN, SP and Acc results for 5 pathological images of the DRIVE database. It has been observed that the average SN, SP and Acc for pathological images is 70.80%, 96.40% and 94.41% respectively. Simulation has also been performed on 20 images of the STARE dataset. Table 3 shows the comparative analysis of average values of SN, SP and Acc for different images of STARE dataset and it has been observed that proposed technique has high Acc even for the STARE dataset also which proves the robust nature of proposed algorithm.

5.   Conclusions

Accurate segmentation of the vasculature map of the fundus image plays a crucial role in the diagnostic procedure of various retinal disorders. In the proposed work, initially the binary mask of fundus image is generated using bimodal masking technique and vasculature map is extracted using global thresholding technique. MPLS technique has been used for evolution of contour in all directions to extract the vasculature map in accurate manner. Simulated results demonstrate that the proposed technique can extract vasculature maps of normal images as well as pathological images accurately. Since the methodology used for extraction of vessels is unsupervised, no training is required. Vessel connectivity has also been done without any danger of collision. Proposed algorithm is an efficient technique because it is used for extraction of vasculature maps from normal as well as pathological images. Further extracted vasculature maps can be used to find the features of retina such as macula or fovea or optic disk or for the automatic identification of pathological elements like hemorrhage, microaneurysms, exudates or lesions accurately. Also the quantitative and objective assessment of arteriovenous nicking can be performed in future.

Acknowledgments

We would like to show our gratitude to Dr. Mausumi Acharyya, AdvenioTechnoSys, India, for sharing their pearls of wisdom with us during this research. The authors would like to thank people who provide the public databases used in this work.

Conflict of interest

The authors declare no conflict of interest in this paper.