1. Introduction
Media coverage, awareness campaign or programs, and public education have played an important and significant role in the control and prevention of the spread of infectious diseases, such as influenza, AIDS/HIV, and SARS. It has been shown that media coverage may change individuals' behavior, while the epidemic is in progress, such as reducing the individuals' contacts or using more safer prevention strategies, to reduce the risk of getting infected [1,2,3,19]. Indeed, people's response to the threat of disease is dependent on their perception of risk, which is influenced by public and private information disseminated widely by the media [33]. In a recent study for outbreaks of infectious diseases with high morbidity and mortality, Mummert and Weiss showed that individuals closely follow media reports of the outbreak, and that many will attempt to minimize contacts with other individuals in order to protect themselves from infection [30]. Therefore, understanding the effects of behavior changes due to influences of media coverage and awareness programs can help guide more effective media plans and strategies on the control and preventions of diseases.
Various mathematical models have been formulated for such purposes. The media coverage and awareness programs can be incorporated into disease transmission models in a more explicit way where an equation or equations for the media coverage or awareness programs are included into compartmental disease models [8,28,29,0]. They can also be incorporated implicitly by being connected to individuals' behavior changes which are expressed in the contact rates or other model terms and therefore the infection or incidence rates [10,30,33,35,36,37]. In the latter case, several types of media influence-dependent incidence rates have been proposed to reflect the influences of media coverage. They include the reduction in contacts due to behavioral change when the number of infectious individuals increases, and have used such forms as e−a1E−a2I−a2H, where H denotes hospitalized individuals, I the infectives, E exposed individuals, with nonnegative constants m,ai,i=1,2,3, [23], 1/(1+mI) [26], βe−mI [10,23,26], and c1−c2f(I), where f(0)=0, f′(I)≥0, and limI→∞f(I)=1, [11,32,0]. Piecewise smooth incidence rates to represent the reduction factor are also used in [36,37].
Employing distinct functions for media coverage in similar disease models can certainly exhibit different model dynamics. The following three distinct functions to present the effects of mass media are identified and compared from various perspectives in [9]
|
f(I,p1)=e−p1γI,f(I,p2)=11+p2I2,f(I,p3)=1−1p3+I.
|
It is demonstrated in [9] that, based on a same SEIR (susceptible-exposed-infectious-recovered) compartmental model, the epidemic curves and key epidemic measurements vary depending on the media functions chosen. In particular, even the models with the distinct media functions have a very similar shape and the same basic reproductive number ℜ0 at the beginning of the epidemic, the entire resulting epidemic curves can vary drastically.
We note that while the influence of media coverage is an important factor in the spread of diseases, it usually does not impact the disease transmissions so rapidly or sensitively as some other factors and thus the reactions to the media coverage from the public are normally slow and delayed. Susceptible individuals may lack the knowledge or information and tend to ignore the media coverage or awareness campaigns when a disease first spreads, especially for those less fatal diseases. As the disease spreads more widely or more severely, the public pays more attention to the media coverage, and individuals then more seriously change their behavior. As a result, the media impact gradually becomes more significant as the infections are clearly increased. Apparently, most of the media functions used in many studies mentioned above, such as e−mI and 1/(1+mI), do not characterize such special features of slow reactions of the public to the media impact appropriately because they both decrease rapidly as I increases. Nevertheless, while function f(I)=1/(1+aI2) is also a decreasing for I≥0, it has such a feature that
|
f″(I){<0,for I<1/√a,>0,for I>1/√a,
|
and may thus be used more appropriately to reflect the individuals slow reactions.
To explore the dynamic features of the disease models with this media function and investigate its possibly different impact on the disease transmissions, we consider an SEI model with media coverage or awareness programs in this paper. We assume that the media coverage or awareness programs directly affect individuals' contact rates. We first present the model system with its basic dynamical properties in Section 2. We then derive a formula for the reproductive number ℜ0, and show the global stability of the disease free equilibrium as ℜ0<1 in Section 3. We prove the uniform persistence of the model for ℜ0>1, determine the existence of endemic equilibria and their stability, and verify the occurrence of Hopf-bifurcation with varying media coverage in section 5, to do that, we will develop the methods and techniques in [10,21,16,22]. Numerical simulations are provided in Section 5 to demonstrate our results, and our findings are briefly discussed in Section 6.
2. The model
Considering the transmission of infectious diseases in some regions, we divide the population into the groups of susceptible individuals, denoted by S(t), individuals exposed to the infection but not yet infectious, denoted by E(t), and infected individuals who are infectious, denoted by I(t). We assume that after their recovery, the infective individuals no longer impose risk to the susceptible individuals. We further assume that the population follows the logistic growth in the absence of infection and then have the following baseline SEI model, in a more general setting, for the transmission dynamics:
|
dSdt=bS(1−SK)−ΛS,dEdt=ΛS−(c+d)E,dIdt=cE−γI,
|
(1)
|
where b is the intrinsic growth rate of the human population, K is the carrying capacity for the human population of a given region, 1/c is the incubating period, d is the natural death rate, γ>d is the removal rate of the infectives which includes the natural death rate, and Λ is the infection rate.
The infection rate is given by
where β is the transmission probability, ξ is the number of contacts per individual per unit of time, and N=S+E+I. We assume random mixing between individuals such that ξ=rN, and the contact factor r characterizes the behavior change of individuals according to the infection level in the region. We then incorporate the influence of media coverage into the model by assuming the contact factor to be a function of the number of infectives with the form of
where m is the maximum effectiveness of the media coverage, and a≥0 measures the sensitivity of individuals to the infection level in the region. Substituting the infection rate into (1), we arrive at the following model system
|
dSdt=bS(1−SK)−μI1+aI2S,dEdt=μI1+aI2S−(c+d)E,dIdt=cE−γI,
|
(2)
|
where we write μ:=βm for convenience.
Define region
|
D:={(S,E,I)∈IR3:S,E,I≥0,S+E+I≤bKl},
|
where l:=min{b,d,γ}. Then D is positively invariant for system (2), and for any given initial condition (S(0),E(0),I(0))∈D with S(0)>0, there exists a unique solution of system (2) with S(t)>0, for all t≥0.
3. Basic reproduction number and system permanence
We first derive a formula for the basic reproduction number, ℜ0, for system (2). Following the procedure introduced in [34], ℜ0=ρ(FV−1), where ρ represents the spectral radius of a matrix, and we have two vectors F and V to represent the new infection term and remaining transfer terms, respectively:
|
F=(μSI1+aI200),V=((c+d)E−cE+γI−bS(1−SK)+μSI1+aI2).
|
The infected compartments are E and I. A straightforward calculation yields
|
FV−1=1γ(c+d)⋅(μKcμK(c+d)00).
|
Hence the basic reproduction number for system (2) is
and then from [34], the disease-free equilibrium E1:=(K,0,0) of system (2) is locally asymptotically stable if ℜ0<1 and unstable if ℜ0>1.
We next show that E1 is globally asymptotically stable as well if ℜ0<1.
Theorem 3.1. For model (2), if ℜ0<1, the disease-free equilibrium E1 is globally asymptotically stable.
Proof. We define a Lyapunov functional for system (2) as
|
U(t):=S(t)−KlnS(t)K−K+E(t)+c+dcI(t).
|
Thus we have U(t)≥0 for t≥0, and U(t)=0 if and only if S(t)=K, E(t)=0, I(t)=0. Differentiating U(t) along the solutions of system (2), we obtain
|
dUdt|(2)=S−KS⋅(bS(1−SK)−μSI1+aI2)+μSI1+aI2−(c+d)E+c+dc⋅(cE−γI)=−bK⋅(S−K)2+μKI1+aI2−γ(c+d)c⋅I=−bK⋅(S−K)2+γ(c+d)c⋅(ℜ01+aI2−1)⋅I≤0.
|
Set
Then U′=0 if and only if
Substituting (3) into the second equation of system (2) then yields E(t)=0. By the LaSalle-Lyapunov theorem ([18], Theorem 3.4.7), the largest compact invariant set of A0 is the singleton point E1. Thus we conclude that E1 is globally attractive in D. Since E1 is locally asymptotically stable, E1 is globally asymptotically stable in D as ℜ0<1.
We further show that system (2) is permanence if the basic reproduction number ℜ0>1.
Theorem 3.2. Assume ℜ0>1. Then there is a positive constant ϵ such that every solution (S(t),E(t),I(t)) of (2) in D satisfies
|
limt→∞inf(S(t),E(t),I(t))≥η:=(ϵ,ϵ,ϵ),
|
and thus system (2) is permanence.
Proof. Define sets
|
X:={(S,E,I):S≥0,E≥0,I≥0},
|
|
X0:={(S,E,I)∈X:S>0,E>0,I>0},
|
and
Let ϕ(t):X→X be the solution semiflow of system (2). As shown above, the solution semiflow ϕ(t) of (2) has a global attractor on X. Since X0 is relatively closed in X and system (2) is positively invariant and point dissipative in D, X0 is positively invariant for ϕ.
Define
We now claim that
|
Ω∂={ϕ(t)∈∂X0:E(t)=0 and I(t)=0,∀t≥0}.
|
(4)
|
Let ϕ(t)∈Ω∂. Without loss of generality, we only need to prove that E(t)=0,∀t≥0.
Assume otherwise. Then there exists nonnegative constant t0 such that E(t0)>0. Following the definition of Ω∂, one must have I(t0)=0. Notice by system (2) that X is invariant for ϕ. Thus by the second equation in (2), we have dE(t)dt≥−(c+d)E(t),∀t≥t0, showing that E(t)>0, ∀t≥t0.
On the other hand, by the last equation in (2), we have dI(t)dt|t=t0=cE(t0)>0. Thus, we get I(t)>0 for any t>t0 and t−t0 sufficiently small. Similarly to the arguments above, we also have I(t)>0, ∀t>t0. Thus we get I(t)>0,E(t)>0, ∀t>t0, which contradicts ϕ(t)∈∂X0,∀t≥0.
We now let
Here Z0 is the global attractor of ϕ(t) restricted to ∂X0. We claim that Ψ0={E0}⋃{E1}. In fact, Ψ0⊆Ω∂={(S(t),0,0)}. From system (2), we obtain S=0 or S=K. Thus E0,E1∈Ψ0.
Since {E0},{E1} are two isolated invariant sets of ϕ(t) in Ω∂, using the similar arguments from Theorem 3.1 and ℜ0>1, we can prove that E1 is asymptotically stable in Ω∂, defined in (4). Hence Ψ0 has an acyclic covering.
Next, we prove that Ws((0,0,0))∩X0=ϕ. Suppose that it is not true. Then for any ϵ1>0, there exists T0>0 such that (S(t),E(t),I(t))<ξ1:=(ϵ1,ϵ1,ϵ1), as t>T0.
By the first equation of (2), we have
|
˙SS=b(1−SK)−μI1+aI2>b(1−ϵ1K)−μϵ1>0, t>T0,
|
where we let a=0 and ϵ1 small enough. Thus S(t)→∞ as t→∞, which leads to a contradiction.
Next, we prove Ws((K,0,0))∩X0=ϕ. Suppose that it is not true. For any ϵ2>0, there exists T1>0 such that (|S(t)−K|,E(t),I(t))<ξ2:=(ϵ2,ϵ2,ϵ2), as t>T1.
By the second equation and the third equation in (2) and a=0, we have
|
(˙E˙I)=(μSI1+aI2−(c+d)EcE−γI)≥(−(c+d)μ(K−ϵ2)c−γ)⋅(EI).
|
Let
The characteristic polynomial of A takes the form
|
|λ+(c+d)−μ(K−ϵ2)−cλ+γ|=λ2+(c+d+γ)λ+(c+d)γ−cμ(K−ϵ2).
|
As ϵ2 small enough and ℜ0=μcKγ(c+d)>1, we have (c+d)γ−cμ(K−ϵ2)7360;0. Thus A has a simple positive eigenvalue. Using the comparison theorem, we have either E(t)→∞ or I(t)→∞, as t→∞. By [39,Theorem 1.3.2], we conclude that there exists ξ>0 such that limt→∞inf(S(t),E(t),I(t))≥ξ. This shows the uniform persistence of solutions of system (2).
4. Equilibria and media impact
Letting the right hand side of (2) equal zero, we find that the origin E0=(0,0,0) is an equilibrium with eigenvalues b,−(c+d),−γ, and model (2) has one disease free equilibrium at E1=(K,0,0). Clearly, E0 is a hyperbolic saddle point.
From model (2), an endemic equilibrium satisfies the following equations:
|
bS(1−SK)=μSI1+aI2=(c+d)γIc,
|
(5)
|
which leads to
where we write α:=(c+d)γc.
Solving (6) for I yields
which is a parabola for S≥αμ. Define
for 0≤S≤K.
Clearly, the curves of functions f1 and f2 intersect once if K2<αμ<K, that is 1<ℜ0≤2. The situation for αμ<K2 could be complex. it follows from (6) and (7) that
|
F(I)=I4+1a(2−ℜ0)I2+μℜ0a2bI+1a2(1−ℜ0)=0.
|
(10)
|
Notice that as ℜ0>1, equation (10) has at least one positive root and has at most three positive roots. More specifically, equation (10) has one positive root as 1<ℜ0≤2. To investigate the existence of multiple endemic equilibria, we only consider the Case ℜ0>2.
We first give a simple lemma for convenience.
Lemma 4.1. The cubic equation
with A, B, and C all positive, has no, one, or two positive solutions if and only if
|
27AC2>4B3, 27AC2=4B3, 27AC2<4B3,
|
respectively.
Proof. Function H has a positive critical point ˉx=√B3A, and then has no, one, or two positive solutions if and only if H(ˉx)>0, H(ˉx)=0, or H(ˉx)<0, respectively. Substituting ˉx into H(ˉx) leads to
|
H(ˉx)=13ˉx(3Aˉx2−B)+13Bˉx−Bˉx+C=C−23Bˉx.
|
Then the conclusion follows directly by substituting ˉx into H(ˉx) again.
Apply Lemma 4.1 to
|
F′(I)=4I3+2a(2−ℜ0)I+μℜ0a2b=0
|
(11)
|
and define
|
ah:=27μ2ℜ208b2(ℜ0−2)3.
|
(12)
|
Then F′(I) has no critical points, and thus F(I) has a unique positive solution if a≤ah.
Assume a>ah. Then F′(I) has two critical points 0<I1<I2; that is, F(I) has two local extreme values at Ik, k=1,2.
We consider the case where F(I)=0 has two positive solutions. To this end, it is necessary to have a unique positive solution to both F(I)=0 and F′(I)=0. Substituting (11) into (10) yields
|
F(I)= I(I3+12a(2−ℜ0)I+μℜ04a2b)+12a(2−ℜ0)I2+3μℜ04a2bI+1a2(1−ℜ0)=12a(2−ℜ0)I2+3μℜ04a2bI+1a2(1−ℜ0):=G(I).
|
It follows from ℜ0>2 that the quadratic equation G(I)=0 has a unique positive solution if and only if
|
(3μℜ04a2b)2=4(12a(2−ℜ0)1a2(1−ℜ0)),
|
that is
|
a=ac:=9μ2ℜ2032b2(2−ℜ0)(1−ℜ0).
|
(13)
|
Under condition (13), the unique positive solution to G(I)=0 is
|
I=3μℜ04a2b2a2(ℜ0−2)=3μℜ04ab(ℜ0−2).
|
(14)
|
Substituting (14) into F′(I)=0 leads to
|
(3μℜ04ab(ℜ0−2))3+2−ℜ02a3μℜ04ab(ℜ0−2)+μℜ04a2b=(3μℜ02ab(ℜ0−2))3−μℜ02a2b=0,
|
or equivalently,
That is, there exists a positive solution to both F(I)=0 and F′(I)=0 if only if a=ac=ah. However, as shown above, F(I) has a unique positive solution if a=ah. Therefore, it is impossible to have two positive solutions to F(I)=0.
Under the assumption of a>ah, there exist two critical points I1<I2 to F(I). If F(I1)F(I2)<0, function F(I) has three positive solutions. In summary, we have
Theorem 4.2. Assume R0>2. Equation (10) has a unique positive solution if a≤ah where ah is given in (12). It is impossible to have two positive solutions to F(I)=0 in any case. If ac>ah, function F(I) has two critical points 0<I1<I2, and if F(I1)F(I2)<0, equation (10) has three positive solutions.
Proposition 1. Consider model (2) with all parameters positive. Clearly we could always find parameter a0=μcbS∗ℜ0+bc(2S∗K−1)(μKℜ0−2μK2ℜ20S∗). If ℜ0>1, then model (2) has one or three positive equilibrium. Furthermore,
∙ if 0<a≤a0, the model has a unique endemic equilibrium;
∙ if a>a0, the model has three endemic equilibria;
4.1. Endemic equilibrium for sufficiently small media impact a
In this section, we study the stability and Hopf bifurcation of the endemic equilibria and determine how the media impact can influence the periods of the oscillations of disease transmissions.
The case a=0 is same as [10], and from [10] we have the following conclusions:
∙ When a=0, model (2) has a unique endemic equilibrium (S∗0,E∗0,I∗0), and the associate characteristic equation of model (2) is
|
λ3+(c+d+γ+bℜ0)λ2+bℜ0(c+d+γ)λ+bγ(c+d)(1−1ℜ0)=0.
|
Let
|
RH0=12[1+(c+d+γ)2γ(c+d)+√1+2(c+d+γ)(2b+c+d+γ)γ(c+d)+(c+d+γ)4γ2(c+d)2].
|
(15)
|
Obviously, for any positive parameters we have RH0>1.
∙ For model (2) with a=0, the endemic equilibrium (S∗0,E∗0,I∗0) is locally asymptotically stable if 1<ℜ0<RH0.
∙ For model (2) with a=0, when ℜ0=RH0, (S∗0,E∗0,I∗0) becomes unstable and model (2) undergoes a Hopf bifurcation.
4.2. Stability for ℜ0 slightly larger than 1
When ℜ0>1 and 0≤a≤a0, model (2) has a unique endemic equilibrium E2=(S∗,E∗,I∗). The Jacobian matrix evaluated at E2 is
|
JE2=(−bS∗K0μKℜ0−2μK2ℜ20S∗b(1−S∗K)−(c+d)−μKℜ0+2μK2ℜ20S∗0c−γ),
|
and the characteristic equation of JE2 is given by
where
|
a2=c+d+γ+bS∗K,a1=bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗.
|
(17)
|
The coordinates of the endemic equilibrium (S∗,E∗,I∗) are smooth functions of a. When 0<a≤a0 is sufficiently small, we can expand the coordinates for S∗ as
where particularly, by (5) we have
|
S∗0=Kℜ0, S∗1=S∗0bμ(1−1ℜ0).
|
(19)
|
Next, we study the impact of the media coverage on the dynamics of the disease transmissions, and consider the case of 0<a≤a0 and sufficiently small.
It is easy to verify that (16) has a pair of purely imaginary roots if and only if a1a2=a0. Let
If Δ=0, the endemic equilibrium has a pair of purely imaginary roots. Now we calculate equation (20) as follows:
|
Δ=a1a2−a0=(c+d+γ+bS∗K)[bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗]−μcbS∗ℜ0−bc(2S∗K−1)(μKℜ0−2μK2ℜ20S∗)=1ℜ20S∗[bℜ20S∗2K(c+d+γ)2+2μcKℜ0S∗(c+d+γ)−2μcK2(c+d+γ)+b2ℜ20S∗3K2(c+d+γ)+bμc(Kℜ0S∗+2KS∗−ℜ0S∗2−2K2)].
|
(21)
|
By (17), (18) and (19), we have
|
Δ=1ℜ50S∗⋅(˜Δ(a,ℜ0)+O(a2)),
|
(22)
|
where
|
˜Δ(a,ℜ0)=bℜ50(c+d+γ)2K[K2ℜ20+2abK2μℜ20(1−1ℜ0)]+2μcKℜ40(c+d+γ)[Kℜ0+abKμℜ0(1−1ℜ0)]−2μcK2ℜ30(c+d+γ)+b2ℜ50(c+d+γ)K2[K3ℜ30+3abK3μℜ30(1−1ℜ0)]+bcμℜ30[(2K+Kℜ0)[Kℜ0+abKμℜ0(1−1ℜ0)]−2K2−ℜ10[K2ℜ20+2abK2μℜ20(1−1ℜ0)]]=ℜ30[bK(c+d+γ)2(1+2abμ)+2cK2ab(c+d+γ)+bcμK2(abμ−1)]+ℜ20[−2ab2K(c+d+γ)2μ+b2K(c+d+γ)(1+3abμ)−2abcK2(c+d+γ)−ab2cK2+bμcK2]+ℜ0[−3ab3K(c+d+γ)μ].
|
(23)
|
It is not difficult to verify that Δ=0 is equivalent to ˜Δ(a,ℜ0)=0. Note that when ˜Δ(a,ℜ0)=0, the endemic equilibrium has a pair of purely imaginary roots λ=±ωi, where
|
ω2=bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗.
|
(24)
|
If the parameters a and ℜ0 satisfy ˜Δ(a,ℜ0)=0, a Hopf bifurcation could occur. Next we investigate the function determined by ˜Δ(a,ℜ0)=0.
Lemma 4.3. Consider ˜Δ(a,ℜ0)=0 for ℜ0>1 and 0<a≤a0. In the neighborhood of (0,RH0), there exists a unique smooth function ℜ0=ℜ0(a) such that ˜Δ(a,ℜ0(a))=0 for 0<a≤a0 sufficiently small. Furthermore, we have
|
ℜ0(a)=RH0+aRH1+O(a2),
|
(25)
|
where RH0 is defined as in (15) and satisfy
|
R2H0γ(c+d)−RH0[(c+d+γ)2+γ(c+d)]−b(c+d+γ)=0
|
(26)
|
and
|
RH1=−R2H0[2b2K(c+d+γ)2μ+2bcK2(c+d+γ)+b2cK2]3RH0[bK(c+d+γ)2−bμcK2]+2[b2K(c+d+γ)+bμcK2]+RH0[2b2K(c+d+γ)2μ−3b3K(c+d+γ)μ+2bcK2(c+d+γ)+b2cK2]3RH0[bK(c+d+γ)2−bμcK2]+2[b2K(c+d+γ)+bμcK2]+3b3K(c+d+γ)μ3RH0[bK(c+d+γ)2−bμcK2]+2[b2K(c+d+γ)+bμcK2].
|
(27)
|
Proof. Note that
|
˜Δ(0,RH0)=R3H0[bK(c+d+γ)2−bcK2μ]+R2H0[b2K(c+d+γ)+bcK2μ]=0
|
where in the neighborhood of (0,RH0), we have
|
∂˜Δ∂ℜ0|a=0,ℜ0=RH0=3R2H0[bK(c+d+γ)2−bcK2μ]+2RH0[b2K(c+d+γ)+bcK2μ]=−RH0[b2K(c+d+γ)+bcK2μ]≠0.
|
(28)
|
then by the Implicit Function Theorem, there exists a unique smooth function ℜ0=ℜ0(a) such that ˜Δ(a,ℜ0(a))=0 for a>0 sufficiently small. If we write the Taylor expansion for ℜ0(a) in terms of a in (25) and bring it into (23), we have
|
˜Δ(a.ℜ0(a))=˜Δ(a,RH0+aRH1+O(a2))=(R3H0+3aR2H0RH1)[bK(c+d+γ)2(1+2abμ)+2cK2ab(c+d+γ)+bcμK2(abμ−1)]+(R2H0+2aRH0RH1)[−2ab2K(c+d+γ)2μ+b2K(c+d+γ)(1+3abμ)−2abcK2(c+d+γ)−ab2cK2+bμcK2]+(RH0+aRH1)[−3ab3K(c+d+γ)μ]=0
|
(29)
|
Equalizing the same power terms of parameter a on both sides in (29), at the same time taking into (26), we have
|
3R2H0RH1[bK(c+d+γ)2−bμcK2]+R3H0[2b2K(c+d+γ)2μ+2bcK2(c+d+γ)+b2cK2]+2RH0RH1[b2K(c+d+γ)+bμcK2]
|
|
+R2H0[−2b2K(c+d+γ)2μ+3b3K(c+d+γ)μ−2bcK2(c+d+γ)−b2cK2]+RH0[−3b3K(c+d+γ)μ]=0
|
(30)
|
thus we solve RH1.
Theorem 4.4. Consider model (2). If 1<ℜ0<ℜ0(a), where ℜ0(a) is defined in (25), then E2=(S∗,E∗,I∗) is locally asymptotically stable.
Proof. When R0>1, if a2>0, a0>0 and a2a1−a0>0, then all eigenvalues of (16) have negative real parts by Routh-Hurwitz criteria [31], we can prove this conclusion. Obviously, a2>0. In the following, we need to prove a0>0 and a2a1−a0>0. By (18) and (19), we have for a>0 small that
|
a0=μcbS∗ℜ0+bc(2S∗K−1)⋅(μKℜ0−2μK2ℜ20S∗)=μcbℜ0S∗⋅(3S∗2−KS∗−4KS∗ℜ0+2K2ℜ0)=μcbK2ℜ20S∗⋅[(1−1ℜ0)(1+2abℜ0μ−abμ)+O(a2)].
|
(31)
|
if 1<ℜ0≤2, obviously a0>0; if 2<ℜ0, from relationship of root and coefficient in (10), we can obtain a<μℜ0b(ℜ0−2), the same as a0>0.
Next, we prove a1a2−a0>0. By (18) and (19), we straightforward calculate
|
a2a1−a0=(c+d+γ+bS∗K)⋅[bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗]−[μcbS∗ℜ0+bc(2S∗K−1)⋅(μKℜ0−2μK2ℜ20S∗)]=bKℜ50S∗⋅[ℜ30(Δ2−μcK+T1a)+ℜ20(bΔ+μcK−T1aT2a)−ℜ0T2a+T2a+O(a2)]=bKℜ50S∗⋅[ℜ30(Δ2−μcK)+ℜ20(bΔ+μcK)+ℜ20T1a(ℜ0−1)+ℜ0T2a(ℜ0−1)]>0
|
(32)
|
where △=c+d+γ, T1=2b(c+d+γ)2μ+2cK(c+d+γ)+bcK and T2=3b2(c+d+γ)μ. Hence according to Routh-Hurwitz criteria [31], E1=(S∗,E∗,I∗) is locally asymptotically stable when 1<ℜ0<ℜ0(a) and a>0 is sufficiently small.
4.3. Hopf bifurcation for ℜ0 larger than some critical value
Theorem 4.5. Consider model (2). If ℜ0=ℜ0(a), 0<a≤a0, then system undergoes a Hopf bifurcation.
Proof. Differentiating (16) with respect μ, we get
where
|
B1=bKλ2+[bK(c+d+γ)+2Kr(c+d)ℜ0S∗2]λ+bγ(c+d)(3K−2Kℜ0S∗2),B2=3λ2+2(c+d+γ+bS∗K)⋅λ+bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗.
|
(34)
|
When ℜ0=ℜ0(a), equation (16) has a pair of purely imaginary roots λ=±ωi with ω2=bS∗K(c+d+r)+2μcKℜ0−2μcK2ℜ20S∗. Note that
|
S∗=γ(c+d)μc+ab2c(K−S∗)2S∗2μK2γ(c+d),
|
so
|
dS∗dμ=−S∗μ+2ab2c(K−S∗)(K−2S∗)S∗μK2γ(c+d)⋅dS∗dμ,
|
Hence we have dS∗dμ<0. Following from (33) and dS∗dμ<0, we get
|
sign{d(Reλ)dμ}λ=iω=sign{Re(dλdμ)}λ=iω=sign{Re(bKω2−[bK(c+d+γ)+2Kγ(c+d)ℜ0S∗2]⋅iω−bγ(c+d)(3K−2Kℜ0S∗2)−3ω2+2(c+d+γ+bS∗K)⋅iω+bS∗K(c+d+γ)+2μcKℜ0−2μcK2ℜ20S∗)}=sign{Re(bKω2−[bK(c+d+γ)+2Kγ(c+d)ℜ0S∗2]⋅iω−bγ(c+d)(3K−2Kℜ0S∗2))×(−2ω2−2(c+d+γ+bS∗K)⋅iω)}=sign{2bKω4+2ω2[bK(γ−c+d2)2+3(c+d)24+cd]+(c+d+γ)b2S∗K2+(c+d+γ+b+bS∗K)2Kγ(c+d)ℜ0S∗2]}>0.
|
(35)
|
Therefore, the system undergoes a Hopf bifurcation when \Re_0=\Re_0(a) and a is small.
5. Numerical simulations
To analyze our results, we provide numerical examples in this section.
We choose parameter a from Table 1. The other parameters K is 5000000 people, b is selected as 0.001 day^{-1}, c is chosen as 0.1 day^{-1}, d is 0.001 day^{-1} and \mu
is selected as 1.2 \times 10^{-8} day^{-1}. We let \gamma and a vary.
Table 1. Endemic equilibrium (S^*, E^*, I^*) when a>0 is varied. In the table, expect for the parameters given in Table 2, here we have \gamma=0.05. In this case, \Re_0=1.1765 and R_{H_{0}}=5.5206 .
| Parameter a | S^* | E^* | I^* |
| a=0 | 4208333 | 6597 | 13194 |
| a=1 \times 10^{-11} | 4215551 | 6548 | 13096 |
| a=1 \times 10^{-10} | 4272153 | 6157 | 12314 |
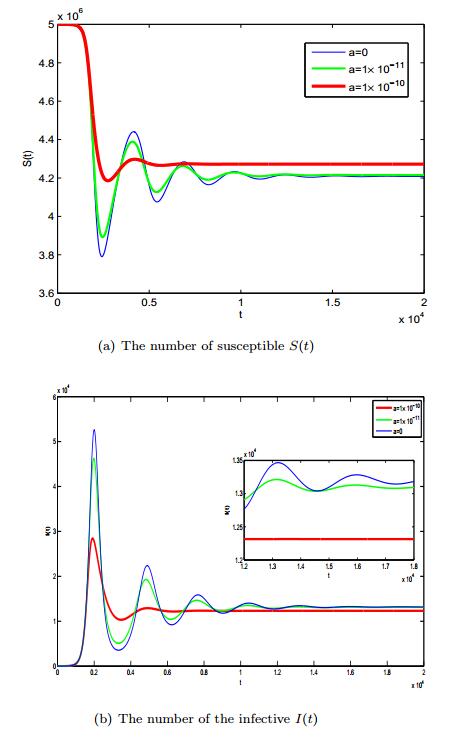
First, we consider the case where the removal rate from the infected compartment is relatively higher, that is \gamma=0.05 day^{-1}. We then \Re_0=1.1765 and R_{H_{0}}=5.5206 . As shown in Fig. 1 (a), (b), the green thin curve represents the case when a=0 , where the application of media was not consider; the blue thick curve and the red thicker curve represent the cases when a=1 \times 10^{-11} and a=1 \times
10^{-10}, respectively. In Table 1, if \gamma=0.05 day^{-1}, \Re_0=1.1765 and R_{H_{0}}=5.5206 , we solve for the solutions of system (2) as a increases from 0 to 1 \times 10^{-11}, to 1 \times 10^ {-10}, and we found that S^* becomes gradually larger and E^*, I^* become smaller when a increases. From Fig. 1 and Table 1, it is not difficult to find that the endemic equilibrium is local asymptotically stable, and the effective media coverage (larger values of a ) not only stabilizes the oscillation but also reduces the number of the infected individuals in the course of transmission.
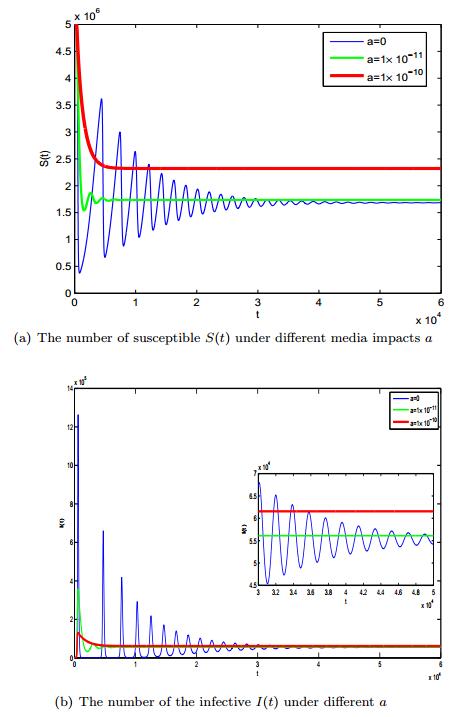
Fig. 2 (a), (b) simulate the media impact to the transmission when \gamma=0.02 day^{-1}. As shown in Fig. 2 (a), (b), the trough of the number of susceptible individuals reduce and come sooner, but the peak rise and retard as the parameters \gamma decreases, simultaneously the trough of the infected individuals also reduce and come sooner, nevertheless the peak of the infected individuals rise and come sooner. The number of the peak and the trough of the susceptible individuals or the infected individuals all improve when the media impact parameter a increases, and when a increases to a specific value, the number of the susceptible individuals and the infected individuals tend to stable, but is less than \gamma=0.05 .
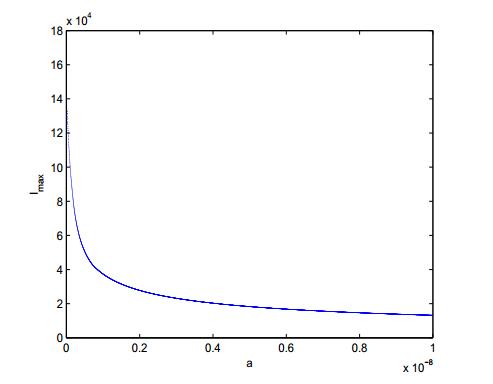
Fig. 3 describes the change of the maximum infected individuals when a increases from 0 to 1 \times 10^ {-8}. It is obvious that the maximum value of infected individuals is from falling sharply to steady reduction as the media impact parameter a increases.
6. Discussion
In this paper, we explore the impact of media coverage a to the transmission of infection diseases. In [10], Cui et al. used a contact transmission rate \beta(I)= \mu e ^{-mI}. However, the contact transmission rate in [10] fails to satisfy that it is unsensitive to the increase of infectious diseases, at least in the early outbreak stage. For further study, we consider the more realistic media function \beta(I)=\frac{\mu SI}{1+aI^2} to reflect the impact of media coverage and alertness. Comparing to contact transmission rate in model [10], our media function is weaken in the beginning period of the outbreak for some infectious diseases, and once the media impact reaches to a certain degree, the declining on the infectives for the contact transmission rate tends to gentle.
We derive formulas for the basic reproductive number of infection \Re_0. If \Re_0 < 1 (Theorem 3.1), the disease free equilibrium E_1 is globally asymptotically stable. If \Re_0 > 1 (Theorem 3.2), system (2) is uniformly persistent with endemic equilibrium. If 0\leq a \leq a_0, the model is shown to have only a unique endemic equilibrium, and system (2) is uniformly persistent with the unique endemic equilibrium. If a>a_0, it is shown that the model may have three endemic equilibria and it is uniformly persistent with the maximum endemic equilibrium. The case of a=0 has been studied by Cui et al. in [10], so we only investigate the case of 0 < a\leq a_0 with a sufficiently small. When 0 < a \leq a_0 and 1 < \Re_0 < \Re_0(a), where \Re_0(a) is defined in 25, then E_2=(S^*, E^*, I^*) is locally asymptotically stable (Theorem 4.4). If \Re_0=\Re_0(a), 0 < a \leq a_0, then system (2) undergoes a Hopf bifurcation (Theorem 4.5).
From the numerical simulations, we obtain that the media coverage a impacts multiple peaks and troughs. In fact, if \Re_0 > 1 and close to R_{H_0}, the disease will be endemic with multiple peaks and troughs when a=0. The time between the two peaks or two troughs can be approximated by
|
T_0=\frac{2\pi }{\omega} =\frac{2\pi }{\sqrt{\frac{b }{\Re_0}(c+d+\gamma)}}.
|
But when the media impact parameter a is introduced, or when 0 <
a\leq a_0 is sufficiently small, if there are multiple peaks and multiple troughs, the time between each of the two peaks or the two troughs can be approximated by
|
T_a=\frac{2\pi }{\sqrt{\frac{b(c+d+\gamma) }{\Re_0}+a\frac{b^2(c+d+\gamma) }
{\mu \Re_0} }
(1-\frac{1}{\Re_0})+\frac{2\mu
cK}{\Re_0}(1-\frac{1}{1+a\frac{b}{\mu}(1-\frac{1}{\Re_0})})}
|
This shows that the media alert shortens the time of the secondary peak and trough of the disease transmission. This effect is also verified by the simulations in Fig. 2 (a), (b).
For the case where \Re_0>2 , because of the complexity of the contact transmission rate, we are unable to calculate the endemic equilibrium of system (2). The stability analysis for each of the solutions seems analytically untractable when system (2) has three endemic equilibria, and further investigations of the impact of parameter a on the model dynamics become more challenging, that we leave in our future work.
Acknowledgments
The authors are grateful to the editor and the anonymous reviewers for their valuable comments and suggestions, based on which they revised this manuscript. XL and SL are supported by the NNSF of China (No. 11471089,11301453) and the Fundamental Research Funds for the Central Universities (Grant No. HIT. IBRSEM. A. 201401). JL is supported partially by U.S. National Science Foundation grant DMS-1118150.









 DownLoad:
DownLoad: