Automatic recognition of giant panda vocalizations using wide spectrum features and deep neural network

1.   Introduction

Solving nonlinear partial differential equations (NLPDEs) has become a useful tool for delineating numerous physical problems that arise in many fields of mathematics and science, which includes describing various types of wave behavior observed in the natural world, with applications such as fluid mechanics to solid-state physics, plasma physics, nonlinear optics, etc. This made the nonlinear wave phenomena a major focus of scientific research in recent decades. Many researchers have diligently developed a wide range of powerful techniques to uncover solutions for NLPDEs both analytically and numerically. For instance, the Korteweg-de Vries (KdV) equation is frequently employed to model small-amplitude, and long waves on various surfaces, including shallow water, ion sound, and longitudinal astigmatic waves. The regularized long-wave (RLW) equation stands as a versatile model encompassing a wide range of physical phenomena. It not only characterizes shallow water waves, but also captures the intricate dynamics of nonlinear dispersive waves, ion-acoustic plasma waves, and magnetohydrodynamic plasma waves. To date, numerous numerical methods have been utilized to simulate solitary waves in the context of the Rosenau-Korteweg-de Vries (R-KdV) and Rosenau-KdV-RLW equations. However, there exists a limited number of numerical schemes specifically designed for the accurate simulation of shock waves in these equations. In this article, we aim to comprehensively address this research gap. To begin, the KdV equation stands as the quintessential model for investigating weakly nonlinear long waves that emerge in physical systems. For instance, it serves as a valuable descriptor for phenomena like shallow water surface waves with long wavelengths and small amplitudes, as well as internal waves within shallow density-stratified fluids. Beyond these examples, the KdV equation finds utility in a multitude of other applications, encompassing plasma waves, Rossby waves, and magma flow ^[1]. Korteweg and de Vries suggested the KdV equation as ^[2,3] :

Within this equation, a real-valued function is denoted as $u$, alongside two real constants, a and b. This equation forms the fundamental basis for exploring and understanding waves of this particular nature^[1,4]. To depict the behavior of dense discrete systems, Philip Rosenau introduced what we now refer to as the Rosenau equation in 1988, which takes the following form ^[5,6]:

In a deeper exploration of nonlinear waves, Zuo ^[7] modified the Rosenau equation (1.2) by adding the viscous term $u_{x x x}$, leading to the what is now known as the R-KdV equation:

The authors effectively obtained solitons and periodic wave solutions for the model by merging the KdV equation and the Rosenau equation, which was achieved by using both the sine-cosine and tanh methods in ^[4,7]. In ^[8], the conservative linear difference scheme was created for the R-KdV equation. The authors introduced the modified variational iteration algorithm-Ⅱ (MVIA-Ⅱ) to obtain numerical solutions of different types of fifth-order KdV equations ^[9]. In ^[10], the authors focus on deriving solitary wave solutions for the generalized Rosenau-KdV equation using the sech-ansatz method. Through the examination of various test problems, these methods showcase both efficiency and reliability in their application. The inclusion of the term $-u_{x x t}$ in Eq (1.3), when $b = 0$, describes an additional characteristic of nonlinear waves, leading to what is commonly referred to as the Rosenau–RLW equation:

This equation represents a significant model in nonlinear wave studies. Furthermore, its extended form is known as the generalized Rosenau–RLW equation:

The generalized Rosenau–RLW equation presents an expanded framework for understanding complex nonlinear wave behaviors, incorporating the effect of $U$ over time within the wave equation's dynamics. This equation holds significance in the realm of nonlinear wave theory, providing a foundation for studying the behaviors and characteristics of waves within different physical systems. In this article, the generalized Rosenau–KDV–RLW (GR–KDV–RLW) equation will be considered, which combines terms from the generalized Rosenau KDV and generalized Rosenau–RLW equations. The provided equation can be represented as follows:

It's important to note that in this context, $p \geq 2, d > 0, a, b^{K d V}, c$, and $e^{R L W}$ are real constants ^[11,12]. We impose specific physical boundary conditions, requiring that $u \rightarrow 0$ as $x \rightarrow \pm \infty$. The variables $x$ and $t$ indicate differentiation with respect to space and time, respectively. To apply our numerical method effectively, we confine our solution to the interval defined by $a \leq x \leq b$. The shallow water wave equation can be represented numerically using the dependent variable \(u(x, t)\), denoting the wave profile concerning spatial position (\(x\)) and time (\(t\)). The equation includes coefficients such as \(a\) for drift effect, \(b\) for third-order dispersion, \(c\) for higher-order dispersion, and \(d\) for nonlinear effects. \(e\) represents the coefficient associated with the term \(u_{xtt}\), contributing to the evolution of shallow water waves. Boundary conditions will be selected from a set of homogeneous conditions for further analysis.

Furthermore, the initial condition is defined as :

Given the known value of $f(x)$, Eq (1.6) combines the general Rosenau-KdV and general Rosenau-RLW equation. By setting $b^{K d V}$ to zero in Eq (1.6), the resulting equation represents the general Rosenau-RLW as follows:

In the Eq (1.9), for $p = 2$, it represents the usual Rosenau-RLW equation, and for $p = 3$, it denotes the modified Rosenau-RLW equation. Moreover, in Eq (1.6) for $p \geq 4$, it signifies the general Rosenau-RLW equation. The Rosenau–KDV–RLW equation has prompted the development of various numerical schemes. However, the generalized form of the Rosenau–KDV–RLW equation has received comparatively less focus owing to its height nonlinearity. Numerous numerical techniques have been put forth to address the Rosenau-KdV equation, including methods where ^[13] introduced an innovative approach merging the Haar wavelet collocation method, a nonstandard finite difference scheme, and quasilinearization to calculate numerical solutions for the given equation effectively. ^[14] proposes semi-discrete and fully-discrete B-spline Galerkin approximations. The approach involves applying a proper orthogonal decomposition (POD) method to a Galerkin finite element (GFE) formulation. ^[15] presents a third-order weighted essentially non-oscillatory (WENO) method combined with a four stage third-order L-stable SSP implicit-explicit Runge-Kutta method (Third-order SSP EXRK method and third-order DIRK method) for spatial and temporal discretization. ^[16] introduces two highly effective numerical schemes that rely on a combination of the B-spline finite element method and time-splitting techniques. ^[17] proposes a meshless algorithm using radial basis function and finite-difference methods to approximate the solution of the equation. In ^[18], a collocation technique based on quintic B-spline basis functions is proposed and they apply the Runge–Kutta method of four stages and third-order (SSP-RK43) to solve the resulting system of equations. ^[19] presents a collocation finite element method based on septic B-splines, which provides better numerical solutions compared to previous methods. ^[20] proposes a two-level implicit fully discrete scheme with third-order accuracy in space and second-order accuracy in time. In both ^[21,22], numerical methods are introduced with a common foundation in B-spline collocation finite element techniques, applied to solve specific equations. ^[23] proposes a three-level linear implicit conservative scheme that is second-order convergent and unconditionally stable. The spectral collocation method has been applied in previous literature as a computational technique, such as shown through ^{[24,25,26,27,28,29,30,31,32,33]}. In this article, the GR–KDV–RLW equation will numerically analyze by employing the fast Fourier transform (FFT) technique combined with the central difference method. The GR–KDV–RLW equation will be addressed and solved across eight different cases, which encompasses the behavior of single solitary waves, interactions among two and three solitary waves, and the evolution of solitons with Gaussian and undular bore initial conditions.

2.   Materials and methods

2.1.   Preliminary

In ^[23], the authors present the following results to ensure the Eqs (1.6)–(1.8) when $c = 1$ are well-posed and satisfy conservation laws, the solution, and its derivatives. When considering the $L_2$ norm, the solution and its derivatives are bounded up to the second order. Also, when considering the $L_{\infty}$ norm, both the solution and its first-order derivative remain confined ^[13]. Equivalent results can be easily obtained for other values of $c$.

Definition 2.1. Let $\Omega = [a, b]$ and $u^{(q)}$ represent the $q$-th order derivative. The Sobolev spaces $H^2(\Omega)$ and $H_0^2(\Omega)$ are defined as follows:

Lemma 2.1. Suppose $u_0 \in H_0^2[a, b]$, then the solution of Eqs (1.6)–(1.8) satisfies

Theorem 2.1. Suppose $u_0 \in H_0^2[a, b]$, then the solution of Eqs (1.6)–(1.8) satisfies

Theorem 2.2. Suppose $u_0 \in H_0^2[a, b]$, then the solution of Eqs (1.6)–(1.8), satisfies $\|u\|_{L_2} \leq C, \left\|u_x\right\|_{L_2} \leq C, \left\|u_{x x}\right\|_{L_2} \leq C$, and, hence $\|u\|_{L_{\infty}} \leq C$ and $\left\|u_x\right\|_{L_{\infty}} \leq C$.

Theorem 2.3. Suppose $u_0 \in H_0^2[a, b]$, then the problem defined by Eqs (1.6)–(1.8) is well-posed.

2.2.   Analysis of the numerical scheme

In the realm of numerical methods, a sophisticated method is developed specifically for tackling the periodic initial value problem that's encountered. This problem is presented with a scenario wherein a function denoted as $u$ is predefined as a prescribed function of $x$ at the initial time point $t = 0$, and, subsequently, the solution exhibits periodic behavior concerning the variable $x$ while being constrained within a fundamental interval defined by $a \leqslant x \leqslant b$. The Eq (1.6) can be written as:

Simplification of Eq (2.3) yields:

where

For a clearer presentation, the spatial period $[a, b]$ will be normalized to $[0, 2\pi]$ via the transformation $x \rightarrow \frac{2\pi(x-a)}{L}$, where $L = b-a$. The normalization process extends to the Fourier space in relation to $x$ and its derivatives or other operators related to $x$. The FFT efficiently performs this process, then, by employing the inverse Fourier transform, expressed as $\frac{\partial^n u}{\partial x^n} = F^{-1}(i k)^n F(u)$ for $n = 1, 2, \ldots$, we proceed to discretize the resulting equations. For any positive integer $N$, we consider grid points $x_j = j\Delta x = \frac{2\pi j}{N}$, where $j = 0, 1, \ldots, N-1$. The solution $u(x, t)$ is subsequently transformed into discrete Fourier space as follows:

The inverse formula is

To simplify, we use the Fourier transform on both sides of Eqs (2.4) and (2.5) to represent them in Fourier space:

Now, all the mathematical operations mentioned earlier will be applied to Eqs (2.4) and (2.5), ultimately reducing them to the following equation:

Let $\boldsymbol{u} = \left[u\left(x_{0}, t\right), u\left(x_{1}, t\right), \ldots, u\left(x_{N-1}, t\right)\right]^{T}$.

The ordinary differential equation (2.11) can be expressed in vector form as:

The function $g(\boldsymbol{u})$ is defined as the righthand side of the equation, which can be solved using various methods from first-order differential equations. Specifically, in this article, the central finite differences method will be employed. Regarding its convergence and stability, its efficacy is discussed in ^[34,35,36]. By utilizing the inverse Fourier transform as defined in Eq (2.7), the next step is to simplify Eq (2.8), resulting in the reduction of the derived equation. Introduce the central difference method as follows:

By applying the scheme to handle the resulting ordinary differential equation in the time domain and, by employing it to advance in time, we achieve the following result:

Finally, in our pursuit of a solution, we employ the inverse Fourier transform to approximate our result. The central difference method necessitates the provision of two distinct initial values, which is fundamental to its operation. To start this process, we define the first of these two levels and start with $u(x, 0)$ to reach $w(x, 0)$, then

To compute the second level of the initial solution denoted as $w(x, \Delta t)$, we utilize a higher-order one-step method, specifically, the fourth-order Runge-Kutta method (RK4).

Following this evaluation, substitute the determined value of $w(x, \Delta t)$ into Eq (2.15) as a pivotal step in our methodology.

To derive the solution $u(x, t)$, Eq (2.12) transforms as follows:

In conclusion, we derive the approximate solution by employing the FFT in MATLAB until evaluating $u(x, t)$ at time $t = n \Delta t$, as outlined precisely in Eq (2.7). It's essential to highlight that the central difference method requires us to provide two sets of initial values.

2.3.   Algorithm

In this section, we outline the algorithm for the proposed methodology related to the GR-KdV-RLW equation (1.6). The steps below encompass the fundamental components of this approach:

● Step 1: Discretize the spatial domain x into spaced grid points.

● Step 2: Apply the Fourier derivative theorem to calculate spatial derivatives in Fourier space, then the inverse to get the initial condition.

● Step 3: Use the RK4 method to calculate the other initial condition for the central difference method.

● Step 4: Thus, we get the solution of (1.6) for various values of $N$ and $t$.

3.   Results and discussion

To assess the effectiveness and precision of the numerical approach, we conducted eight numerical experiments. These experiments included the study of a single solitary wave motion, the interactions of two and interactions of three solitary waves, and the observation of soliton evolution under Gaussian and undular bore initial conditions. This helped us gauge the method's performance and accuracy. To assess solution accuracy, the error norm $L_{2}$ is employed, which is defined as ^[10]:

Also, utilize the error norm $L_\infty$ for assessing solution accuracy.

To calculate the difference between analytical and numerical solutions at some specified times, the two conserved quantities are given as:

Mass conservation (Lemma 2.1)

Energy conservation (Theorem 2.1)

The quantities $I_{M}$ and $I_{E}$ represent the momentum and energy of the shallow water waves, respectively. Throughout the simulation of solitary wave motion, we observe and track these invariants to evaluate the precision and correctness of the numerical algorithm.

3.1.   The motion of the single solitary wave

3.1.1.   Example 1

Given the parameters $a = 1, b = 1, c = 1, d = 0.5, e = 0,$ and $p = 2$ in Eq (1.6), representing the Rosenau-KdV equation considered with the boundary conditions where $U \rightarrow 0$ as $x \rightarrow \pm \infty$ to derive the single solitary wave solution:

such that

The initial condition is as follows:

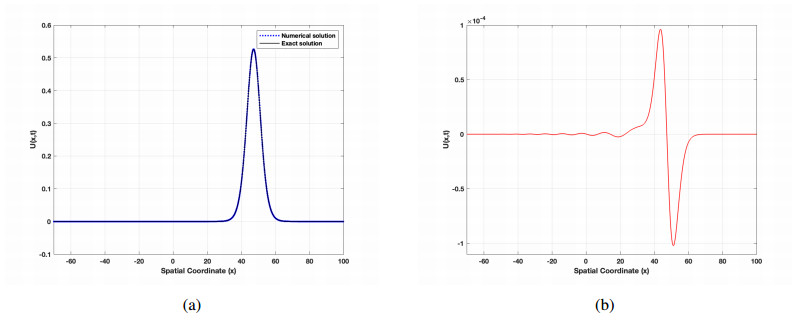
The numerical solutions for a single solitary wave were obtained through the presented method, where $v = 1.18$ considers the variable $x$ within the range $[-70,100]$. The method exhibits an amplitude of $0.5263$ and conducts extensive experimentation when utilizing spatial and temporal step sizes of $\Delta x = 0.1$ and $\Delta t = 0.01$ at time $T = 40$. Figure 1 (a) illustrates a close correspondence between the solitary wave curve and the exact solution. Figure 1 (b), represents the error between the exact and numerical results for solitary waves at time $t = 40$. Figure 2 presents a plan view and a 3D illustration of the motion of a single solitary wave. The method demonstrates the preservation of conserved quantities \(I_M\) and \(I_E\), affirming its capability to accurately uphold the soliton's momentum and energy throughout the simulation while maintaining the amplitude remarkably close to its initial value. Furthermore, Table 1 assesses the performance of the scheme as comparing the error norms \(L_\infty\) and \(L_2\) against results obtained from other numerical approaches. As Table 2 shows, the error norms exhibit a significant reduction (halving) as the parameter $N$ increases (doubles). In addition, the numerical invariants closely approach their corresponding analytical values with increasing $N$, maintaining near-constant values compared to the analytical invariants. The results highlight the superior computational accuracy of the present scheme, as it consistently exhibits the smallest error among the mentioned methods when $N$ increases and $\Delta x$, $\Delta t$ are decreased. These consistently low error values exhibit a high degree of accuracy when compared to alternative methods.

3.1.2.   Example 2

Given the parameters $a = 1, b = 1, c = 1, d = 1, e = 0,$ and $p = 5$ in Eq (1.6), representing the Rosenau-KdV equation, we have

The initial condition was specified as:

This choice yields the exact solitary wave solution:

where

We conducted numerical simulations with specific parameters, considering $x$ within the interval $[-60, 90]$ and $T = 20$. The comparison of the wave graph from the numerical solution is presented in Figure 3. The figure illustrates that the wave amplitude remains nearly identical at different times, suggesting energy conservation. Figure 4 presents a plan view and a 3D illustration of the motion of a single solitary wave. Additionally, a comparison of errors using the $L_\infty$ norm and $L_2$ norm at $T = 20$ is tabulated in Table 3. Table 4 shows that the error norms exhibit a significant reduction (halving) as the parameter $N$ increases (doubles). Also, it's obvious that the computational efficiency of the new scheme highly surpasses that of the methods presented in the comparison methods when $N$ increases and $\Delta x$, $\Delta t$ are decreased. These results provide strong evidence for the energy conservation property of the new scheme.

3.1.3.   Example 3

Consider the parameters $a = 1, b = 1, c = 1, d = 1, e = 0$, and $p = 3$ in Eq (1.6), representing the Rosenau-KdV equation so that, the equation takes the following form:

which is known as the generalized Rosenau KDV equation and its soliton solution is given in ^[10]. For $p = 3$, the exact solution is given by:

where

The initial condition is

Figure 5 displays the comparison of wave amplitude obtained from the numerical solution. The figure reveals that the wave amplitude remains remarkably consistent at different times, implying energy conservation. Furthermore, Figure 6 provides both a plan view and a 3D illustration of the motion of a single solitary wave. Tables 5 provides a comparison of errors using the $L_\infty$ norm and $L_2$ norm at $T = 40$ for $x$ within the interval $[-60, 90]$. Table 6 shows that the error norms exhibit a significant reduction (halving) as the parameter $N$ increases (doubles). As observed in Tables 5 and 6, the error norms obtained by the method are consistently smaller than those of the other comparison methods when $N$ increases and $\Delta x$, $\Delta t$ are decreased.

3.1.4.   Example 4

In this example, considering the parameters $a = 1, b = 1, c = 1, d = 0.5$, $e = 1$, and $p = 2$, Eq (1.6) becomes

The exact solution of the equation is

where

The initial condition is defined as:

In Figure 7, the numerical solutions closely match the exact solutions. These figures demonstrate that the wave amplitude at various time instances remains nearly constant. Figure 8 provides both a plan view and a 3D illustration of the motion of a single solitary wave. Furthermore, the error norms $L_\infty$ and $L_2$ at time $T = 30$ for $x$ within the interval $[-40,100]$ are summarized in Table 7. It is observed from Table 8 that the errors are significantly reduced (halved) as the parameter $N$ increases (doubles), and the resulting error norms are notably good, being smaller than those of the compared methods when $N$ increases and $\Delta x$, $\Delta t$ are decreased.

3.2.   Interaction of two solitary waves

3.2.1.   Example 5

To simulate the interaction between two solitary waves, consider the Eq (1.6) with the following parameters $a = 1$, $b = 1$, $c = 1$, $d = 0.5$, $e = 0$, $h = 0.1$, $\Delta t = 0.01$, $v_1 = 0.3$, $v_2 = 0.5$, $x_1 = -70$, and $x_2 = -35$ across the spatial domain $x \in [-100,400]$, which represents the Rosenau-KdV equation. The initial condition, defined as the linear sum of two well-separated solitary waves with different amplitudes, is expressed as:

such that

where $v_{i}$ and $x_{i}$ are constants. The experiment was conducted up to $t = 250$ for parameters $N = 8192$, illustrating the interaction of two solitary waves at different times, as depicted in Figure 9. The waves originate from positions $x = -70$ and $x = -35$ from left to right, respectively. The taller wave, characterized by a larger amplitude, travels faster than the one with a smaller amplitude. At $t = 80$, the taller wave catches up to the smaller one and merges with it. Two waves interact until around $t = 130$, and this interaction extends until $t = 150$. By $t = 250$, the interaction concludes, and the larger soliton has fully separated. Following this interaction, the waves retain their original shapes and amplitudes. Figure 10 presents a plan view and a 3D illustration of the interaction of two solitary waves. The values of the conserved quantities are denoted as $I_M$ and $I_E$ and have been determined and listed in Table 9. The simulation showed that the invariants remained nearly constant over time.

3.3.   Interaction of three solitary waves

3.3.1.   Example 6

To simulate the interaction of three solitary waves with different amplitudes, consider the Eq (1.6) with the following parameters $a = 1$, $b = 1$, $c = 1$, $d = 0.5$, $e = 0$, $h = 0.1$, $\Delta t = 0.1$, $v_1 = 0.3$, $v_2 = 0.5$, $v_3 = 0.8$, $x_1 = -70$, $x_2 = -40$, and $x_3 = -15$ over the spatial domain $x \in [-100,400]$, which represents the Rosenau-KdV equation, and set an initial condition as follows:

The parameters \(A_i\), \(B_i\), and \(i\) are defined as follows:

such that $v_{i}$ and $x_{i}$ are constants. The simulation is conducted up to time $t = 250$, and our proposed algorithm is executed with $N = 8192$. In Figure 11, the results are illustrated at various time intervals. These waves travel from left to right, and each has a distinct velocity. The figure shows that the tallest wave, characterized by a larger amplitude, moves faster than the smaller waves. The interaction starts at $t = 50$ and persists until around $t = 170$. Throughout this period, the taller wave engages with the two shorter waves reciprocally, and the shorter waves also interact with each other before eventually separating. After this interaction, the waves progress while preserving their original shapes and amplitudes, even after the simulation time of $t = 250$. Figure 12 presents a plan view and a 3D illustration of the interaction of three solitary waves. Table 10 presents the values of conserved quantities throughout the simulation. It is obvious from Table 10 that the calculated invariants maintain remarkable stability during the entire computational process.

3.4.   Evolution of solitons

3.4.1.   Example 7: Gaussian initial condition

The evolution of a train of solitons is governed by Eq (1.6) with the following parameters $a = 1, b = 1,$ $d = 0.5,$ and $e = 0$, which represents the Rosenau-KdV equation. The development of a train of solitons determined by the Rosenau-KdV equation will be evaluated using a Gaussian initial condition:

Consider the boundary condition as:

To explore the behavior of the solution for different values of $c$, consider the impact of these particular $c$ values on its dependence, $c = 0.5, 0.1, 0.05$, and $0.01$, $h = 0.1$, $\Delta t = 0.01$, within the time interval $0 \leq t \leq 14$, and over the spatial domain $x \in [-50,250]$. The numerical computations are performed up to $t = 14$. Figure 13 displays the evolution of the Gaussian initial condition into solitons at $t = 10$. The values of the two invariants of motion are presented in Table 11 for different $c$ values, illustrating the constancy of these invariants as time advances. This demonstrates the presence of oscillating solitons, and the number of oscillating solitons depends on the value of $c$. A decrease in the value of $c$ leads to an increase in the number of oscillating solitons.

3.4.2.   Example 8: Undular bore initial condition

For the evolution of a train of solitons, consider the Eq (1.6) with the following parameters $a = 1$, $b = 1$, $c = 1$, $d = 0.5$, $e = 0$, $v = 1.18$, $h = 0.1$, $\Delta t = 0.01$, $u_0 = 1$, $x_0 = 25$, and $d = 5$, which represents the Rosenau-KdV equation. The equation is examined utilizing the undular bore initial condition expressed as:

The provided boundary condition is expressed as:

To investigate the generation of a train of solitons within the Rosenau-KdV, we examine the impact of parameter $c$. These solitons represent an undular bore, which reflects the water's surface above the equilibrium level at $t = 0$. The computational simulation runs until time $t = 150$. Figure 14 displays that simulation reveals the transformation of the initial perturbation into a train of solitons at specific time intervals. Over time, the evolution becomes evident as six solitons propagate to the right. The numerical results, which include two conserved quantities, are presented in Table 12, showing that these quantities are preserved.

4.   Conclusions

This article presents a combination of the Fourier spectral method and the central difference method. The accuracy and efficiency of the combined scheme were assessed by computing error norms and conservation properties related to the GR-KDV-RLW equation. The numerical results obtained are satisfactory and comparable to other solutions in the literature. The approach exhibits better accuracy compared to the previously presented results when $N$ increases and $\Delta x$, $\Delta t$ are decreased. Furthermore, our method can be applied to similar types of PDEs that model real-life problems, which makes it useful for further research in various scientific fields, such as materials science and engineering.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflicts of interest.