1.
Introduction
This paper has two main ingredients: first, the dynamic geometry software GeoGebra*, and its fork version GeoGebra Discovery (GGD)†, accompanied by other mathematical software with CAS (computer algebra system) capabilities; second, a specific geometry inequality that we refer to—following the terminology of [21]—as the "never-proved" or "never-solved" theorem, problem, inequality... Often we will use the initialism NPT, standing for "never-proved" theorem.
*www.geogebra.org
†https://kovzol.github.io/geogebra-discovery/
This inequality was introduced by Prof. Jiawei Hong in his communication to the IEEE 1986 Symposium on Foundations of Computer Science, where he presented a method ("proving by example") for the automated proving of geometric inequalities. He claimed that, since such inequality "… had never been proved by a mathematician… is proved on a computer lately by my colleagues based on the proving by example method", the "never-proved" (by humans) theorem was a relevant illustration of the successful performance of the proposed method. Let us copy here below the precise statement (labeled as Theorem 5 in [21]) that is at the origin of our work, as Figure 1:
"Theorem 5. (M. O. Tao and J. Z. Zhang) Suppose that P,Q,R are three points on lines AB,BC,CA respectively, and RA+AP=PB+BQ=QC+CR=1/3, then PQ+QR+RP≥1/2."
Let us remark that the mention in [21] to the computer proof of this Theorem 5 can be described, at least, as not well documented. As an example, let us warn the reader that the above statement assumes (but there are no hints about it in the whole article [21]!) that the perimeter of the triangle is 1. This is just a first example of a series of errors and confusions, mostly concerning the references to this statement and some of its variations, that we have thoroughly described in Section 3. We have also tracked the "human-produced" proofs that did exist before Hong's claim and even included a new one resting on some previously published results in [40].
Nevertheless, the goal of this paper is not to bring a "human" proof of the "never-proved" theorem but to focus on the performance of some CAS when attempting to prove it. This includes CAS software newly implemented in GeoGebra Discovery, capable of performing computations in real algebraic geometry such as real quantifier elimination (RQE) and cylindrical algebraic decomposition (CAD). Indeed, our original interest in the NPT arose while testing the ability of these new tools to obtain automatic proofs of statements such as the "never-proved" theorem, or at least, of some modified (and simpler) versions which seemed to be less demanding from a computational point of view.
Even though the current GGD tools did not succeed in proving the "never-proved" theorem in all generality (although they worked well for some restricted versions of the statement), we will see that the 3D graphical tools that this software provides shed light on and helped in understanding the intricacies of this challenging question, driving us to achieve the algorithmic proof of the NPT and/or its variants by using other, more powerful, CAS tools, such us Maple, Mathematica or REDUCE/Redlog, although in a human-driven mode.
Thus, the real objective of the paper is, first, to describe a learning-through-hardship experience, leading us to discover different strategies that can improve formally checking the truth of a given statement (such as considering the advantages of dealing, without loss of generality, with a partial elimination of quantifiers; or considering symmetries in the figure to simplify the computations; or reflecting on the potential computational benefits of beginning by attempting to discover, instead of to prove, the ratio between two magnitudes, etc.).
These strategies are, along the paper, developed as part of a kind of "semi-automated proving" approach, i.e., requiring the merging of human and machine contributions, to solve the problems formulated around the NPT. Yet, we would like to emphasize that our implicit perspective throughout the article, concerning these improvements, focuses on their potential implementation in GeoGebra Discovery in a near future, as part of the fully automated protocol that is now operative in this software.
Leaving aside the Introduction and Conclusions sections, the paper includes five other sections. Section 2 is a presentation of the current automated reasoning tools available in GeoGebra Discovery. Next, in Section 3, we formulate in detail the NPT and explore its antecedents, origins, historical appearances and the various ways that have been used to approach its solution, by both algorithmic and human-driven methods.
In Section 4 we approach the "never-solved" problem from a more computational and actual perspective. First, we present a generalized version of the "never-proved" theorem; see Theorem 3 and its extended formulation, named as Problem 1. After highlighting the involved complexity for obtaining a full automatic proof of this theorem with algebraic tools, we consider some simplified versions—yet non trivial—of this problem (see Problems 2 and 3) in order to check in Section 5 the ability of CAS systems to succeed in these more accessible questions and the need to develop some new approaches to simplify the complexity of the involved computations. Finally, since the "never-solved" problem deals with the perimeter of triangles inscribed in a given one, in Section 6 we state an original result that provides a kind of converse of Problem 2 concerning the space of triangles PQR that can be "inscribed" in the lines that contain the sides of a triangle ABC, requiring again heavy support of CAS symbolic computations.
The article ends providing some reflections and conclusions regarding current and future directions of computer assisted proofs in the realm of geometry and dynamic geometry software, such as GeoGebra Discovery.
2.
GeoGebra's automated reasoning tools
In this section we summarize—providing some relevant references along the way—the core of our initial approach to the "never-solved" problem: the current and on-going implementation of different commands in GeoGebra [18], dealing with the automatic verification or discovery of geometric properties in a figure.
Thus, in 2.1 we will report on the performance of such commands in the standard GeoGebra versions.* Next, in 2.2 we will emphasize some of the characteristics of the advanced automated reasoning tools that are featured in an experimental version of the software named GeoGebra Discovery (GGD) [28]. Finally, we will describe how behind these two versions there are contextual issues that explain, in some sense, our specific interest concerning the "never-proved" theorem.
*Freely downloadable at www.geogebra.org.
2.1. Tools of the standard version
The well known dynamic geometry program GeoGebra includes automated reasoning commands in its standard versions, introduced through the doctoral dissertation [22] of the first author several years ago (for GeoGebra version 5, since September 2014).
Roughly speaking, the Relation command proceeds by systematically considering (internally) a large collection of possible properties holding between some user-selected elements in a geometric construction and providing as output those attributes that are true, in a mathematically rigorously concept of truth, i.e., not just through a visual, probabilistic or numerically approximate verification of a given statement.
On the other hand, the Prove and ProveDetails commands just confirm or deny the true/false character of a user-proposed assertion involving some elements of a construction. Finally, the LocusEquation command suggests some geometric constraints (i.e., an equation) that must be satisfied by a certain point on a construction, so that a given property holds. We could say that this command proceeds by considering a certain thesis (e.g., this triangle is isosceles) and a point (e.g., vertex C) proposed by the user on a geometric figure (e.g., a general triangle ABC), and then it brings a new hypothesis (e.g., place vertex C at the bisector of side AB) that is necessary for the thesis to become true. As this hypothesis could be insufficient, the correction of the new statement (e.g., if C is in the bisector of AB, then triangle ABC is isosceles) should be formally checked through the Prove or ProveDetails commands.
Let us clarify that none of these commands provide any readable justification for their output. Thus, they just declare (for the Relation command) the verification of some property in a figure (e.g., these two lines are parallel) or supply (in the case of the Prove and ProveDetails commands) a yes/no answer about the truth of a conjectured statement and a list of degenerate cases (e.g., triangle ABC, given through its three free vertices, should not collapse to a line or to a single point) that should be discarded for the statement to hold.
Indeed, the algorithms behind these tools proceed by translating the terms (hypotheses H, thesis T) of the given conjecture into algebraic equations and then verify the inclusion of the corresponding solution sets V(H)⊆V(T) using a variety of approaches (see [3] for a detailed description of the implementation) that can be, essentially and very roughly speaking, reduced to two parts:
1. Testing if 1 belongs to the ideal that includes the hypotheses and the negation of the thesis. If so, there will be no instance of the construction where the thesis fails, so the statement will be true (for a precise explanation, see [38]). The test is performed by means of Gröbner basis algorithms through the Giac software, a general-purpose computer algebra program, with a large set of features (but let us remark, for its relevance in our context, that real quantifier elimination is not included) embedded in GeoGebra; see [14,25].
2. Verifying the inclusion V(H)⊆V(T) in a sufficiently large number of cases for establishing its absolute certainty (i.e., not probabilistic, not approximate). See [37] for the theoretical basis of the corresponding GeoGebra algorithm. This is a method that can be called "proving by examples" and arose (with variants such as testing just one, very special example) in the 1980s. See [13], p. 210 and the references therein, in particular those to [21,48]; see also [16] for an early survey on such methods.
Even bearing in mind the lack of readable arguments for the output of the automated reasoning commands, the potential relevance of such GeoGebra tools—turning GeoGebra into a kind of omniscient "oracle, " capable (in principle) of answering whatever geometric queries are posed by the user—in the educational setting has been highlighted in many different publications, including some by the authors and collaborators. See [19,27,29,30,31,32,36], as well as recent papers such as [17] or [34], which explicitly refer to GeoGebra's automated reasoning tools.
2.2. GeoGebra Discovery
GGD [23] is a free experimental version of GeoGebra maintained by the first author and available for download on its GitHub page* or for direct web use.† It includes three new automated reasoning features, if compared with the previously described version:
*GeoGebra Discovery Github repository at https://github.com/kovzol/geogebra-discovery
†Visit https://autgeo.online/geogebra-discovery/.
● A Discover command that addresses an internally implemented list of potential properties involving a given element of a construction, and outputs—both through a message and graphically—all those that are true. Thus, it is a kind of automated extension of the Relation tool that does not require the user to select several elements to analyze relations among them; Discover just requires pointing out one element and takes care of finding relations with all the other elements of the figure. The last versions of GGD even allow turning on an automatic Discover command running over each new element added by the user in a construction. This yields the automatic discovery of a whole set of geometric properties arising after each step of the construction.
● A Compare command that extends the checking of an internally implemented list of potential properties (i.e., the protocol followed in the Relation command for the standard version) by finding new ratios holding between two elements of a given figure. For example, if we Compare the segment from the vertex of a triangle to its barycenter and the segment from the barycenter to the midpoint of the opposite side, we get that the first segment is twice the second one. However, if we attempt to do the same with the orthocenter, the output of Compare is empty, as there is no fixed ratio (equality or inequality) relating both segments.
● More relevantly, GGD is able to deal with inequalities (i.e., not only with equations, a restriction holding for the standard version) between geometric elements (e.g., finding ratios involving sizes, distances, etc.) of a construction. For example, if we try to relate in a triangle ABC with right angle at A the length of the altitude from A and the length of the hypotenuse with the Compare command, in GeoGebra's classic version we just get that both segments are not equal, while in GGD we learn that the altitude is always less than half the hypotenuse.*
*See https://matek.hu/zoltan/blog-20210125.php for more details.
As already remarked, the current developments of GGD rely on the possibility of using a computer algebra subsystem able to work in a real algebraic and semi-algebraic setting, i.e., capable of performing real quantifier elimination (RQE). This functionality is required for conjecturing and proving geometric equalities or inequalities over the reals. This is accomplished in GGD through a double approach: the embedded (also web-available) Tarski software ([8,44]), relying on previous programs such as SACLIB, QEPCAD B [6,11] and MiniSAT [41], and the web service realgeom, working together with Wolfram’s Mathematica's RQE subsystem [45] or with Tarski or QEPCAD B. By default, GGD uses its embedded Tarski subsystem; however, the user can force using realgeom to perform the real geometry computations via Mathematica as well.†
†See https://github.com/kovzol/geogebra-discovery#force-running-realgeom.
Although currently the system and its functionalities are in an early stage of development, many examples of the successful performance of this recent feature are described in [1,7,8,26,28,29,30,31,35,43].
As we will formulate in Theorem 1, the "never-solved" problem includes as thesis a geometric inequality. Therefore, as described above, it is a statement that the standard GeoGebra version is unable to address with automated reasoning tools. Rather, we are interested in testing if the current developments of GGD could provide the suitable tools, at least in principle, to automatically deal with this challenging problem which clearly belongs to the realm of computational real algebraic geometry (the field of application behind Tarski's software package).
A second reason for our specific interest in the "never-solved" problem has to do with our implementation of proving-by-example methods. These methods have been included in GeoGebra’s automated reasoning tools since the beginning and are historically connected to the formulation of the "never-proved" theorem, as we will describe in detail in Section 3.
3.
A journey through the "never-proved" theorem
3.1. Our first contact with the problem
As previously mentioned, in [37] a method for automatically—and rigorously—proving geometric statements through the verification of a finite number of instances was presented. The idea of achieving precise, general information about the truth of a geometric statement by considering just some particular cases emerged in the second half of the past century, subject to diverse restrictions (e.g., only construction steps of a certain kind for the involved geometric figure, or a generic position for its elements, etc.) and far from being accompanied by a good performing, implemented algorithm. Roughly speaking, we can mention that there are two possible mathematical arguments justifying the validity of this approach. One, a uni-variate polynomial has at most as many zeroes as its degree, and thus the polynomial must be zero if it vanishes at a convenient, finite number of points. Two, that the same conclusion holds if the polynomial vanishes over an element of size much greater than that of its coefficients or of absolute size sufficiently smaller than that of the inverse of its coefficients.
In other words, it can be deduced that a given polynomial is identically zero by just evaluating the polynomial over a finite collection of numbers (perhaps over a collection of cardinal only one, if it contains a number of some special kind). It was our previous interest in translating this method to the realm of automatic theorem proving of geometric statements that led us to get in contact with the "never proved" problem.
Indeed, it is the second mathematical argument we have described above—testing the nullity of a polynomial over a single, special number—that is behind the so-called "gap theorem" [21], where it is mentioned that it could be applied to prove geometric inequalities, and it is stated explicitly (see Figure 1 in the Introduction, for the illustration of the statement):
"… By the gap theorem, we can prove inequalities using the proving by example method. The following theorem, which had never been proved by a mathematician* because it is so complicated that no one would take the trouble, is proved on a computer lately by my colleagues based on the proving by example method:
*Italics are ours.
Theorem 5. (M. O. Tao and J. Z. Zhang) Suppose that P,Q,R are three points on lines AB,BC,CA respectively, and RA+AP=PB+BQ=QC+CR=1/3, then PQ+QR+RP≥1/2."
From the hypotheses of Theorem 5, it is easy to conclude that 1=1/3+1/3+1/3=RA+AP+PB+BQ+QC+CR=AB+BC+AC. This means that, in the above formulation, it is assumed that the perimeter of the given triangle is 1. Thus, we can reformulate more generally the theorem as stating that the perimeter of the internal triangle PQ+QR+RP must be greater than or equal to half the perimeter per(ABC) of the external triangle:
Theorem 1 (The "never-proved" Theorem – NPT). Given an arbitrary triangle ABC and three points P,Q,R on the sides AB, BC, CA, respectively (as in Figure 1) such that RA+AP=PB+BQ=QC+CR (thus, equal to per(ABC)/3), PQ+QR+RP≥per(ABC)/2.
Before trying to address this problem using GeoGebra and other tools, let us mention the diverse information relating to the proof of this never-proved theorem.
3.2. Some confusing references
First, it seems that the reference in [21] to this problem is quite fuzzy, declaring that it has been proved on a computer by some colleagues, but the bibliographic reference to this result† is just to appear. Moreover, in the mentioned article, the hints about how to address this problem through one of the described methods (the "gap theorem") are quite light, including a sentence such as "Of course in addition to the [gap‡] principle, some tricks are needed, " but such stratagems are not specified any further. Then, a couple of years later, the survey [16] on the state of the art concerning automated proving in geometry includes, again, a section describing the work of J. Hong in [21]. Yet, concerning its application to inequalities, it is mentioned that
†Tao, M.Q., and J.Z., Zhang, "Proving an geometry inequality by computing some examples" (sic)
‡Italics are ours.
"Jiawei Hong (18)* has proposed a prover which uses the same approach … Hong's `proving by example' method was originally designed to prove theorems … expressible by polynomial equations, … Later Hong discovered a method to prove inequalities over the real numbers for a large class of functions, including polynomials (18). In this paper we will give an account only of the first algorithm."
*This reference in the quotation corresponds to our reference [21].
So, the case of inequalities is, again, not detailed here. Moreover, it seems that there is an error, and the second reference in this quotation should not be (18) but be (19)†. There are two main reasons for supporting this conjecture: first, by considering the pertinence of the title of the paper (19) in the context of the considered sentence; second, because there is not any reference to (19) in the whole paper and the above paragraph seeming to be the most suitable location. Indeed, (19) appears just in the list of References, but we have been unable to find such paper in the J. of Automated Reasoning. Besides, in the popular article by Davis ([13]) published years after the references above, we can see that a slightly modified reference‡ to the same work is included. Again, we have been unable to obtain such report.
†Hong J., Proving inequalities by example. Tech. Rep. Univ. of Chicago, Chicago Ill. (1988). To appear on Journal of Automated Reasoning.
‡Hong, Jiawei and Xiao-nan Tao, Proving inequalities by examples, Courant Institute of Math. 1987.
3.3. Looking for the antecedents of the "never proved"
The concurrence of errors and confusing or missing information seems to be present also if we address a preliminary question concerning the origins of the "never-proved" inequality: Who formulated first such statement? In which context? Why was it declared as "never-proved"? Such questions are not considered in our article of reference [21]; indeed, it seems (see quotation above) that J. Hong attributes the inequality to M. Q. Tao and J. Z. Zhang.
However, we have found a closely related statement in the much earlier monograph on geometric inequalities by Bottema et al. See [5], item 9.12, and see Figure 2.
Let us remark that this item 9.12 refers to another item, 9.1, for notation, but there it is only written that DEF is a triangle inscribed in another triangle ABC. As explicitly declared in the Preface to [5], "this book on geometric inequalities does not contain any drawings." Yet, it is easy to deduce from the notation in 9.12 that D lies on side BC, with E on side CA, F on side AB. For example, to conclude that F lies on the side limited by A and B, we observe that in 9.12 it is written that p=AE+AF, q=BF+BD, etc.
Furthermore, 9.12 ends with the reference to the origin of this inequality, i.e., to [4]. This original paper includes a drawing (labeled in that paper as Figure 2) that is reproduced here as Figure 3. Yet, we see that this figure labels as PQR the vertices of the inscribed triangle, not as DEF. However, it is easy to deduce, following Figure 3 notation, that D=P, E=Q, F=R.
Notice, showing once more the subtleties behind the historical development of this inequality, that this notation does not exactly coincide with that of Figure 1, where P is on side AB, Q on side BC, R on side CA, while in Figure 3, P is on side BC, Q on side CA, R on side AB.
These observations about notation are relevant because we will present below a proof of Theorem 1, based on some results from [40], that follow the notation of Figure 3, not that of Figure 1.
Going beyond notational issues, we must highlight that there is an obvious typo in this inequality 9.12 from Bottema et al., since it introduces some symbols a′, b′, c′ verifying 2a′=b+c, 2b′=a+c, 2c′=b+c, but these symbols play no role in the remainder of the statement. The statement seems to yield the same conclusion as in Theorem 1 but with weaker hypotheses, since those of Theorem 1 (i.e., RA+AP=PB+BQ=QC+CR) correspond just to the case t=p=q=r, that is, when AE+AF=BF+BD=CD+CE=t=(a+b+c)/3=per(ABC)/3, in the formulation of Bottema et al.'s inequality 9.12.
Intrigued by such accumulation of troubling information concerning the inequality we are dealing with, we have consulted the paper by Bollobás [4] that Bottema et al. refers to as the origin of the statement. A look to this article, published in 1967, helps explain the typo in [5]. Indeed, in [4] the hypotheses are (with the notation of [5])
and thus it seems that [5] just forgot to include the primes a′, b′, c′ in the inequalities required for p, q, r.
If this explanation is right, then a new issue arises: Is it possible that in any triangle ABC the inequalities
always hold? Indeed, this is equivalent to
That is, every side must be smaller than the arithmetic mean of the other two. This is obviously false (consider the right triangle with side lengths of 3, 4, 5: 5 is not smaller than (3+4)/2). So, it seems the statement in [4] is wrong… until the reader becomes aware of some (very particular!) remark in that paper, concerning interval notation: For the sake of simplicity the following notation is introduced: x∈[y,z] means that either y≤x≤z or z≤x≤y. Once more, there is some confusing issue associated with this problem: 9.12 in [5] does not just include a typo but has a partial interpretation of the inequalities that the elements p, q, r (as in Figure 2) of the hypotheses should verify, as some of the inequalities could be interpreted in a reversed way.
If these arguments are correct, they confirm that the "never proved" inequality actually corresponds to a special case of 9.12, namely, the one that corresponds to setting t=p=q=r, since now we are not bound—as it looked like at first glance—to impose that t≤a′, t≤b′, t≤c′ (that is not possible in general) but impose that t⋚a′, t⋚b′, t⋚c′, which is no restriction at all!
In conclusion, the "never-proved" inequality (in a more general form) seems to have been already proved by the eminent mathematician B. Bollobás back in 1967! Furthermore, Bollobás declares that one of the goals of his paper is to provide a simpler proof of the given inequality, recognizing that it already had been stated and proved in 1964 by A. Zirakzadeh [49]. We should add that, in our humble opinion, Bollobás's proof is not too simple (it seems that he is more focused on proving when the inequality becomes an equality, and the tools related to convexity that he uses are far from elementary).
Analogously, in [10] it is recognized that this inequality was presented by M. Q. Tao and J-Z. Zhang as Inequality XII, 1.20, p. 347 in the book [33], but also it is declared (confirming Bollobás's perception) that it was already proved by Zirakzadeh in the '60s, although its proof is very difficult (sic). It also mentions that a simpler one was presented in 1989 by [46] (in Chinese).
In this journey around the "never-proved" statement, let us bring some—in a certain sense—more recent information, dealing with the mechanical proof of the same statement appearing in [47], published (in Chinese) in 2010. Its approach, centered in error analysis and using sophisticated computer environments, is quite far from our way—purely symbolic and assuming just the utilization of easily accessible technological tools—to address the same issue.
In summary, it seems that a detailed description of the success concerning the automated proof (or, even, a reasonably accessible proof) of the "never-proved" inequality is not, at best, easy to find. Therefore, the success of such statement in the context of automated proving does not seem to be well documented yet. We consider the result as still challenging to address with current, widely spread in the education world, dynamic geometry software with CAS capabilities, together with other computer algebra systems that shed light on its intricacies.
3.4. A proof of the "never proved"
To finish with some positive output this exploration of the origins and formulation of the "never-proved" problem, we present here a non-automatic proof of this statement, which is based on an elementary (though not simple) solution to a problem that appeared in the journal Crux Mathematicorum and can be openly accessed at its website.
Indeed, a few years after the reference to the "never-solved" problem by [21], Crux Mathematicorum (described as "the best problem solving journal in the world"*) included in [39] the proposal of a problem (number 1849) that, slightly adapting the notation in this journal to that of [4] (see Figure 3), starts by considering the same hypotheses as in Theorem 1 (see Figure 1). However, in the Crux version the reader is asked to prove that (PQ⋅QR+PQ⋅RP+QR⋅RP)≥per(ABC)2/12. A detailed proof, albeit non-elementary since it uses the Finsler-Hadwiger inequality ([33], p. 179), by the proponents of the problem—Shi-Chang Shi and Ji Chen, from Ningbo University—was presented one year later in [40].
*See https://cms.math.ca/publications/crux/
Now, one can observe that the "never-proved" inequality follows quite immediately from the statement of Problem 1849. Indeed, assuming the latter inequality holds, let us expand (PQ+QR+RP)2/3 as
Next, observe that (PQ2+QR2)/2≥PQ⋅QR, since (PQ−QR)2=PQ2+QR2−2PQ⋅QR≥0. Thus, ((PQ2+QR2)/2+2PQ⋅QR)≥3PQ⋅QR, and the same holds for the other blocks, yielding
That is, (PQ+QR+RP)2/3≥per(ABC)2/12. Multiplying both sides by 3 and extracting roots, we finally arrive to the "never-proved" inequality (Theorem 1):
Besides this proof, which relies on the quite involved solution to Problem 1849 described above, we provide later a complete and novel proof for the NPT which requires computer assisted calculations and includes an improvement of the lower bound for the perimeters of the triangles PQR. This lower bound, in a slightly different form, was already obtained in [10].
4.
GeoGebra/CAS approach to the "never-solved" problem
4.1. A generalization of the "never-solved" problem
After putting into historical context the NPT and since different notations were used in its treatment throughout the years and in the previous section (although we already tried to clarify the final notation we are about to use), it is good to start by setting up clearly the notation that will be used for the rest of this article. Thus, we will denote the segment joining two points A, B by AB, while the line containing them will be denoted by ¯AB. To avoid cumbersome notation, AB will also be used to refer to the length of the corresponding segment. Sometimes, to emphasize the difference between choosing a point on the side/segment, or on the line defined by the side, we will talk about "points in the interior, " or R∈AB, when R lies on a side/segment (e.g., segment AB), or "points on the exterior, " if they lay on the line but not on the side (e.g., R∈¯AB but not in AB). A ray with origin at a point P and with direction given by a vector →v will be denoted by (P;→v). We denote the perimeter of a triangle ABC by per(ABC). The basic geometric construction we will be working with consists of a triangle ABC with sides of lengths a=BC, b=AC and c=AB, together with three points P, Q, R chosen on its sides BC, CA, AB, respectively. The interior angles of ABC at vertices A, B, C are denoted correspondingly by α, β, γ (see Figure 3).
In regard to the NPT, it is valuable to make some initial remarks before proceeding any further. If we wish to construct points P, Q, R on the sides of triangle ABC satisfying the conditions AQ+AR=BR+BP=CP+CQ=per(ABC)/3, we soon realize that once we fix point R, the points P and Q will be automatically determined as well.
However, it is easy to observe that such point R cannot be arbitrarily chosen on side AB. It is enough to consider a triangle with very large sides AB, CB and very small side AC and fix a point R on AB very close to A. Then, point Q on AC should verify AQ+AR=per(ABC)/3. It is clear that since AR is small by construction, there is no room for Q on side AC so that the sum AQ+AR is as large as per(ABC)/3. See Figure 4.
This observation means that the choice of R is subject to some inequality constraints. We will see next that such constraints have always a (non-empty interval) solution over side AB.
Proposition 2. Let ABC be a triangle with sides of lengths a=BC, b=AC and c=AB, and choose a point R on the interior of the side AB whose distance from A is given by x>0. Then, we can choose points P, Q on sides BC, CA, respectively, such that AR+AQ=BR+BP=CP+CQ=(a+b+c)/3=k if and only if
Further, the interval (M1,M2) is always non-empty.
Proof. Let us assume first that P, Q, R exist satisfying the conditions of the statement. Then, we have
From (4.1), (4.4) and (4.6), we get x>max(0,c−k,k−b). Similarly, from (4.2), (4.3) and (4.5), we get x<min(c,k,a+c−k).
On the other hand, if we take any value x with M1<x<M2, all inequalities (4.1)–(4.6) are satisfied, and the construction of points P, Q satisfying the required conditions is possible.
Finally, to check that the interval (M1,M2) is always non-empty, it is enough (since all variables appearing in the expressions of M1 and M2 are positive) to verify the inequalities
Inequality (4.7) is equivalent to 2(a+c)>b, which is true by the triangle inequality. In a similar way, inequalities (4.8), (4.9) and (4.10) are equivalent, respectively, to c<2(a+b), a<2(b+c) and 2k<3k and therefore valid. This shows that the interval (M1,M2) is non-empty. This in particular means that it is always possible to choose points R, P, Q on (the interior of) sides AB, BC and CA of an arbitrary triangle ABC so that AR+AQ=BR+BP=CP+CQ, and we are done.* □
*The authors thank J. M. Gamboa for providing a proof for this proposition.
There is a way to overcome these awkward restrictions on the choice of points P, Q, R on the sides of ABC, by means of generalizing our NPT as follows: Let us consider, for example, side AB, and choose a point R on the line ¯AB. Then, the oriented length ARor (respectively, BRor) of the segment AR (BR) is defined positive if the ray (A;→AR) (respectively, (B;→BR)) contains AB; if this is not the case, the oriented segment ARor is considered negative. We define similarly oriented lengths BPor, CPor on ¯BC and CQor, AQor on ¯AC. Then, we can state the following generalization of Theorem 1.
Theorem 3. Given a triangle ABC and three points P, Q, R, respectively, on the sides BC, CA, AB or their prolongations (see Figure 5) such that ARor+APor=BPor+BQor=CQor+CRor, per(PQR)≥per(ABC)/2.
In this new situation the restrictions of Proposition 2 disappear. Indeed, let us set k=per(ABC)/3, choose an arbitrary point R on ¯AB, and set z=ARor. Observe that BRor=c−z. Now, take point P on ¯BC such that x=BPor=k−(c−z), and so CPor=a−x. Choose now Q on ¯AC so that y=CQor=k−(a−x). Now, we have AQor=AC−CQor=b−y. Then, it is clear that
and thus, for any R on ¯AB, we can find points P, Q satisfying the conditions of the statement. Clearly, the truth of Theorem 3 implies readily that of Theorem 1.
From now on, unless otherwise stated, by the "never-proved" theorem we will understand this generalized version of it.
4.2. Our framework and goals
It seems daring, in view of the historical precedents (scientific level of the involved researchers and shown difficulties) described in Section 3, to attempt the mechanical solution of the "never-proved" inequality with GGD. This section describes the framework we have considered regarding this goal, as well as some related ones dealing with simplified—but still challenging—versions of the original problem.
Central Problem: Automatically prove Theorem 1 in all generality.
In this context, let us specify that, by an "automatic proof, " we understand mainly a proof internally performed, without human intervention, by automated reasoning tools such as those currently implemented in GeoGebra (c.f. [8,24,30,32,43]) yielding a symbolically sound answer. Here, we are not particularly interested in obtaining a "human readable" proof, although it is possible to ask for the recorded internal symbolic computation steps justifying this answer. We still consider this an equally valid proof, as declared in [2]:
"The arithmetization of geometry paves the way for the use of algebraic automated deduction methods in synthetic geometry … thanks to the arithmetization of geometry, the proven statements correspond to theorems of any model of Tarski's Euclidean geometry axioms."
Unfortunately, at the present stage of development of CAS systems, these fully automatic procedures are not always successful, even when dealing with such an innocent looking statement as the NPT. Therefore, whenever we have encountered limitations in this ideal computational approach, we have resorted to confronting the situation from a blended perspective, combining a human-driven proof with support from a variety of CAS systems capable of performing the required symbolic computations. The algorithms behind these calculations are fundamentally similar to those implemented in GeoGebra's automated reasoning tools (cf. [3,6,38]), so we expect that in a near future their improvement will allow obtaining better, fully automatic proofs of geometric problems similar to the ones treated here.
It is also interesting to point out that there are two different ways to look for a computational proof of a proposed inequality, such as the one in Theorem 3. One approach consists in asking directly for the proof of the given inequality as it is. That is, to prove Theorem 3 we can ask whether under the given conditions, the inequality per(PQR)≥per(ABC)/2 holds. The computer should answer with a true/false type of response.
On the other hand, we can approach the proof of this statement by asking a more general question, that includes the answer to Theorem 3 as a particular case. Namely, find all possible values for the ratio per(PQR)/per(ABC). Here, the computer algorithm would presumably provide optimal real values M0 and M1 such that M0≤per(PQR)/per(ABC)≤M1 (here, the bounds could become infinity), and these bounds would provide an even more precise answer to our problem.
The parallel consideration of these two approaches is not just whimsical. It has to do with the relevance of a projection process (elimination of quantifiers) behind the implemented algorithms, a process that perhaps is computationally of a similar complexity in both cases. The first one can be described as aiming to decide if the projection of the set of triangles where some inequality holds is the whole space of triangles (so that the NPT holds always true). The second one deals with finding the projection over the r-line of the set of triangles that verify the equation per(PQR)=r⋅per(ABC), yielding an interval for r such as [M0,M1].
Bearing in mind the different aspects we have described in our framework towards approaching the NPT, now we will re-state this inequality in a new, more convenient and scaffolded way:
Problem 1 (The generalized NPT problem). Let ABC be an arbitrary triangle and three points P, Q, R be on the lines ¯BC, ¯CA, ¯AB, respectively, such that AQor+ARor=BRor+BPor=CPor+CQor.
(a) Prove automatically that per(PQR)/per(ABC)≥1/2.
(b) Find automatically all possible values for the ratio per(PQR)/per(ABC).
As we will soon realize in Section 5, the difficulties involved when trying to automatically solve this problem with the assistance of computer software drove us to consider also two simplified, more accessible (but computationally non-trivial) questions closely related to the NPT:
Problem 2 (Inscribed triangles in an equilateral triangle). Let us consider an equilateral triangle ABC and pick three arbitrary points P, Q, R on lines ¯BC, ¯CA, ¯AB.
(a) Prove automatically that per(PQR)/per(ABC)≥1/2.
(b) Find automatically all possible values for the ratio per(PQR)/per(ABC).
Problem 3 (The NPT problem in an equilateral triangle). Let us consider an equilateral triangle ABC and pick three points P, Q, R on lines ¯BC, ¯CA, ¯AB, respectively, such that AQor+ARor=BRor+BPor=CPor+CQor.
(a) Prove automatically that per(PQR)/per(ABC)≥1/2.
(b) Find automatically all possible values for the ratio per(PQR)/per(ABC).
A final ingredient to take into account towards automating the study of problems such as the NPT is the consideration of a full-coordinate approach vs. a coordinate-saving approach to the statement. It has to do, again, with trying to lower the complexity of the involved computations.
Indeed, since GGD was originally conceived as dynamic geometry software, when it attempts to automatically prove a certain proposition, it is required, first, to introduce the hypotheses and thesis through the graphic window, by means of a geometric construction. Internally, GeoGebra assigns symbolic coordinates to the given points and input equations and inequations describing the different steps of the construction. For instance, let us consider Problem 1.
Here, the relevant algebraic information for this statement is handled in GGD by making use of variables representing coordinates of the points which determine the construction (see Figure 6).
Let us work out the algebraic representation of Problem 1 in this full-coordinate setting. Because of the invariance with respect to similarity of our problem, it is usually assumed that A=(0,0) and B=(1,0), to reduce the number of variables involved (but the reduction of variables by fixing some coordinates may have as a side effect the loss of the symmetry inherent to the given geometric construction). Thus, we have the following algebraic relations among the variables that appear in Figure 6:
Under these hypotheses, we would like to decide whether the statement "The perimeter of triangle PQR is at least half of that of triangle ABC" is true or false. This leads us to the quantified formula
Now, the algorithms of real quantifier elimination (implemented through a CAS system such as QEPCAD/Tarski in the current version of GGD, or others such as Maple, Mathematica or REDUCE/Redlog) come into play and should produce either true or false in response to the statement.
On the other hand, if we want to refine our request and ask the computer for obtaining the possible ratios between perimeters per(ABC) and per(PQR), a new variable m representing the ratio (p+q+r)/(a+b+c) is added, and the instruction to be passed to the software changes to
The elimination of the quantified variables would give us a (semialgebraic) formula expressing the possible values that the ratio m=per(PQR)/per(ABC) can take.
It seems that this second option could be computationally more demanding than the first one, since it adds a new variable m and a new hypothesis, before considering the elimination of all variables except m. However, the first option also includes a new inequality (the thesis), with a number 2 as coefficient (while all the others are ±1), and requires elimination of several quantifiers. Our (limited) experience with GGD on this matter shows that sometimes this second option might be less difficult to compute than the first one, even though it yields more complete information and seems more difficult to obtain. All these issues, mathematically or computationally not very complicated to deal with, are to be considered in future versions of GGD.
Finally, let us summarize here an alternate way—looking, again, for less complex and more successful computations—to the full-coordinate approach we have been describing in the previous paragraphs. This new option—again, being considered to be implemented in the near future on GGD—can save an important number of variables by re-formulating the given statement in terms of the variables involved in some projection of the set of hypotheses over a space that includes, at least, the variables involved in the thesis.
That is, a statement H⟹T (with H,T considered as real solution sets of systems of polynomial equations and inequalities, so H⟹T actually means H⊆T) is true if and only if H′⟹T is also true, where H′ describes the projection of H to a space of variables that has to include those in T. For a trivial example, let us consider the statement
and its simplified but equivalent form
This equivalence happens because the projection of the zero set of {a−(x+y+z)=0,b−(x−y−z)=0,a=0,b=0} over the {a,b,c,x} space is just {a=b=x=0} and because the thesis {x=0} contains only a subset of the variables in the projection. Obviously, if {x=0} contains the set {a−(x+y+z)=0,b−(x−y−z)=0,a=0,b=0}, it contains its projection over the variable x, and thus it also contains its projection on the {a,b,c,x} space, namely {a=b=x=0}. Conversely, if {x=0} contains the set {a=b=x=0}, it contains the lifting of this set to the a,b,c,x,y,z-space, and in particular, it contains {a−(x+y+z)=0,b−(x−y−z)=0,a=0,b=0}.
Since the thesis usually involves only some variables that are defined in advanced steps of the construction (e.g., the lengths of some segments) and not the initial variables (e.g., the coordinates of the extremes of the segments) that are used to build the secondary ones, this protocol can be named as coordinate-saving, as it allows handling an equivalent statement involving only the secondary variables.
Yet, it requires computing some intermediate projection, something that would be considered in future versions of GGD; else, this new formulation with fewer variables can be obtained with the use of CAS programs such as Maple or REDUCE/Redlog.
For example, in Problem 1, if we set up oriented lengths
by making use of the Law of Cosines on triangles BPR, CQP, ARQ and ABC, we get, after some symbolic computations,
Now, since the thesis only involves variables {a,b,c,p,q,r}, we can use as hypotheses the above relations between the elements of the hypotheses holding only between the variables {a,b,c,p,q,r,x,y,z}, avoiding the use of {u1,v1,u2,u3,v3,u4,v4}. Thus, instead of formula 4.11 we obtain the simpler quantified expression
and instead of formula 4.12 we obtain
Notice that now the number of variables and equations has decreased, at the expense of getting higher degree polynomial equations.
Let us just mention here that this coordinate-saving approach has some similarities with the successful "area method" (see [20]), as it deals with coordinates representing some geometric quantities, going without auxiliary variables.
In the following section, we will describe the output of our computational attempts to solve Problems 1, 2 and 3 and the encountered difficulties. We will proceed by considering first the most accessible problem, to end up with the most challenging one. From our experience, this means that we will consider the three problems in reverse order to their formulation, so that we will start with Problem 3 and finish with Problem 1.
Notice that Problems 2 and 3 can be affirmatively answered by drawing upon the solution to Fagnano's Problem ([9], §4.5, pp. 88-89) on the minimum perimeter of triangles inscribed in a given acute triangle, but we want to stress here that our interest is in obtaining automatic or semi-automatic proofs based on symbolic computations.
5.
Solving the NPT and variants
5.1. On Problem 3: The NPT for equilateral triangles
5.1.1. GeoGebra Discovery approach
For studying Problem 3 with GGD, we proceed first to describe the geometry construction in the graphical view of the software.*. We start by deploying an equilateral triangle ABC of side length 1 (see Figure 7). Then, we draw lines ¯AB, ¯BC, ¯CA extending the sides of this triangle and place an arbitrary point R on ¯AB. By tracing a parallel line to AC through R and intersecting it with ¯BC, we get point D, and by tracing a parallel line to AB through D, we get the intersection Q on ¯AC. Now, trace a parallel line to BC which meets ¯AB at E and a parallel line to AC which meets ¯BC at point P. The reader can easily check that the inscribed triangle PQR satisfies the conditions AQor+ARor=BRor+BPor=CPor+CQor and that, conversely, any triangle satisfying these conditions can be constructed this way. Notice also that triangle PQR is always equilateral.
*GeoGebra Classic applet accessible at https://www.geogebra.org/classic/r3qyqdrb or at GitHub, https://github.com/carlosueno/NPT-Article
Once we set up the construction, it is time to require from the GGD reasoning tools some answers to see whether it is able to manage Problem 3. To get a response to Problem 3 a), we introduce in the GGD command line the instruction
Prove((3/2)*c<=p+q+r)
and obtain—after increasing the default assigned computing limit time in GGD—the answer true, as expected.
On the other hand, to address Problem 3 b), we introduce the command
Compare(p+q+r, c)
and readily the inequality (3/2)c≤p+q+r shows onscreen, giving a precise answer to our request.
It is worthwhile to mention here that in the current version of GGD, all internal variables, formulas and conversion processes of the geometric information into its algebraic form, as described in Subsection 4.2, are presented through a terminal window at the user's request, for further detailed analysis. In the next section we will deal with such formulas, but, to enlarge our perspective regarding the cooperation between computer algebra systems and dynamic geometry software, we will exemplify the solving of this problem through two well known CAS systems, Maple and REDUCE/Redlog.
5.1.2. Maple/REDUCE approach
We start by recalling the formulas 4.14 and 4.15 in Subsection 4.2 and particularizing them to the special case of this Problem 3, by fixing a=b=c=1. Then, after calling some extra packages to work with semialgebraic sets and real quantifier elimination in the Maple CAS system, we quickly obtain answers to both questions a) and b) of Problem 3:
> with(RegularChains): with(SemiAlgebraicSetTools):
> f := &A [p, q, r, x, y, z], ((((((((z^2 + (1 - y)^2 - z*(1 - y)
= p^2) &and (x^2 + (1 - z)^2 - x*(1 - z) = q^2))
&and (y^2 + (1 - x)^2 - y*(1 - x) = r^2))
&and (0 <= p)) &and (0 <= q)) &and (0 <= r))
&and (x = y)) &and (y = z)) &implies (3 <= 2*p + 2*q + 2*r)
> out := QuantifierElimination(f)
> g := &E [p, q, r, x, y, z], ((((((((z^2 + (1 - y)^2 - z*(1 - y)
= p^2) &and (x^2 + (1 - z)^2 - x*(1 - z) = q^2))
&and (y^2 + (1 - x)^2 - y*(1 - x) = r^2))
&and (0 <= p)) &and (0 <= q)) &and (0 <= r))
&and (x = y)) &and (y = z) &and (m*3=p+q+r))
> out2 := QuantifierElimination(f)
A similar approach can be used with the REDUCE/Redlog CAS system. Here, the translated instructions for tackling Problem 3 a) can be written as follows:
rlset reals;
f:=all({p, q, r, x, y, z}, ((z^2 + (1 - y)^2 - z*(1 - y) = p^2)
and (x^2 + (1 - z)^2 - x*(1 - z) = q^2)
and (y^2 + (1 - x)^2 - y*(1 - x) = r^2)
and (0 <= p) and (0 <= q) and (0 <= r) and (x = y)
and (y = z)) impl (3 <= 2*p + 2*q + 2*r));
rlqe f;
We obtain true as output. To get an answer for Problem 3 b), we should add
g:=ex({p, q, r, x, y, z}, (z^2 + (1 - y)^2 - z*(1 - y) = p^2)
and (x^2 + (1 - z)^2 - x*(1 - z) = q^2)
and (y^2 + (1 - x)^2 - y*(1 - x) = r^2)
and (0 <= p) and (0 <= q) and (0 <= r) and (x = y)
and (y = z) and (3*m = p + q + r));
g1:=rlqe f;
rlcad g1;
This produces as final output the simple formula 2m−1≥0.
5.2. On Problem 2: Inscribed triangles in a given equilateral triangle
After the successful automatic solving of Problem 3, we will attempt here to approach Problem 2. It seems accessible, since its formulation deals, again, with an equilateral triangle, although now there are no restrictions posed on the placement of points P, Q, R. Unfortunately, not only GGD but also powerful mathematical software such as Mathematica or Maple also encounter trouble for automatically proving it. Thus, we end this subsection by including a computer-assisted but human-driven proof of Problem 2.
5.2.1. GeoGebra Discovery approach
In this case, in which no extra conditions are imposed on points P, Q, R apart from being in the corresponding sides of triangle ABC (or their extensions), the geometric construction using the graphical view of GGD is straightforward* (see Figure 8 (a)). Unfortunately, when entering the commands
*GeoGebra Classic applet accessible at https://www.geogebra.org/classic/jptzwsr2 or at GitHub, https://github.com/carlosueno/NPT-Article
Compare(p+q+r, c)
Prove(p+q+r >= (3/2)*c)
no output is produced, and GGD is unable to answer either part (a) or (b) in Problem 2. Even fixing one of the vertices, * let us say P, as the midpoint of BC, we get no answer (Figure 8 (b)). Only when we strongly simplify the initial statement by fixing two of the vertices at the midpoints of their sides† does GGD produce correct answers for both parts of Problem 2.
*GeoGebra Classic applet accessible at https://www.geogebra.org/classic/p5gmekhs or at GitHub, https://github.com/carlosueno/NPT-Article
†GeoGebra Classic applet accessible at https://www.geogebra.org/classic/wp94dchz or at GitHub, https://github.com/carlosueno/NPT-Article
5.2.2. Maple/REDUCE approach and a human-driven proof
After the unsatisfactory behavior of GGD when dealing with Problem 2, we can move to CAS software such as Maple to see whether we are able to succeed performing, at least semi-automatically, in this environment. Comparing with Problem 3, now there are fewer restrictions on the variables x, y, z, and we introduce the following commands for answering part (a) of our problem:
> with(RegularChains): with(SemiAlgebraicSetTools):
> f := &A [p, q, r, x, y, z], ((z^2 + (1 - y)^2 - z*(1 - y)
= p^2) &and (x^2 + (1 - z)^2 - x*(1 - z) = q^2)
&and (y^2 + (1 - x)^2 - y*(1 - x) = r^2)
&and (0 <= p) &and (0 <= q) &and (0 <= r))
&implies (3 <= 2*p + 2*q + 2*r)
> out := QuantifierElimination(f)
With respect to part (b), we introduce
> g := &E [p, q, r, x, y, z], (z^2 + (1 - y)^2 - z*(1 - y)
= p^2) &and (x^2 + (1 - z)^2 - x*(1 - z) = q^2)
&and (y^2 + (1 - x)^2 - y*(1 - x) = r^2)
&and (0 <= p) &and (0 <= q) &and (0 <= r)
&and (m*3=p+q+r))
> out := QuantifierElimination(f)
Unfortunately, even for well established CAS systems such as Maple, we were not able to obtain purely automatic results for Problem 2 stated in these terms!
A similar try with REDUCE/Redlog system also produces no output (at least with our computer specifications). Having in mind that RQE and CAD techniques are quite sensitive to the projections and order of variables which are used in a given problem, we attempt re-writing the quantified formula by means of the changes of variables
and
where p1=p2, q1=q2 and r1=r2. Notice here that the expression
and its symmetric versions are always non-negative, and these substitutions can be safely introduced in this setting (i.e., if always f(x)≥0, then "∃x:p1=f(x)" is equivalent to "∃x:p2=f(x)∧p≥0").
Remark 1. These still "non-automatic" changes are motivated by some projections related to the 3-dimensional (real) algebraic set V⊂R6 given by the set of equations
When working in the space of variables (x,y,z,p1,q1,r1) the "level surfaces" V∩{p1+q1+r1=k} for a given k have worse projections on the spaces (x,y,z) and (p1,q1,r1) than the corresponding projections in the space of variables (x1,y1,z1,p2,q2,r2) (see Figure 9). This intuition led us to make further progress when dealing computationally with Problem 2 and helped us understand in a better way the geometry of the set V. Actually, this was the starting point for obtaining the generic Theorem 5 in Section 6.
In REDUCE/Redlog* the formula
*REDUCE/Redlog file with code described below can be found at GitHub, https://github.com/carlosueno/NPT-Article
f0:=(z^2 + (1 - y)^2 - z*(1 - y) = p1)
and (x^2 + (1 - z)^2 - x*(1 - z) = q1)
and (y^2 + (1 - x)^2 - y*(1 - x) = r1);
is transformed into
f1:=sub({x=x1-y1-z1+1/2, y=x1+2*z1+1/2, z=x1+y1-z1+1/2,
p1=(-3*p2+q2+2*r2)/6, q1=(3*p2+q2+2*r2)/6, r1=(r2-q2)/3}, f0);
Therefore, the quantified formula "ex({x, y, z},f0)" is now "ex({x1, y1, z1},f1)". With these new variables Redlog is capable of performing quantifier elimination without much trouble:
f2:=ex({x1, y1, z1}, f1);
f3:=rlgsn f2; f4:=rlqe f3;
We arrive at the expression
and finally we can retrieve the original variables p, q, r by means of
f5:=sub({p2=-p^2+q^2, q2=p^2+q^2-2*r^2, r2=p^2+q^2+r^2}, f4);
f6:=f5 and p>=0 and q>=0 and r>=0;
In summary, the quantifier-free formula for the expression "ex({x, y, z},f0)" turns out to be f6:
Now, our Problem 2 a) becomes
g1:=all({p, q, r}, f6 impl p+q+r>=3/2);
whose output with the CAD command "rlcad g1;" returns true. With respect to Problem 2 b), the answer to
g2:=ex({p, q, r}, f6 and m=p+q+r);
g3:=rlqe g2; g4:=rltab g3;
returns a rather cumbersome quantifier-free formula in the variable m (see Table 1), which in fact is equivalent to our expected result m≥3/2. This last fact can be deduced with Maple and its QuantifierElimination() command or with other, more specifically CAD-oriented CAS, such as QEPCAD.
Remark 2. After this reformulation by means of changes of variables, which we first implemented in REDUCE/Redlog, we also have been successful with other CAS systems such as Mathematica. After running the code in Table 2, we get as output the clean expression m≥32.
It is worthwhile to mention here that a "fully" human proof for Problem 2 is not too involved, compared to the lengthy and even failed computations required by the automatic procedures based on real quantifier elimination or cylindrical algebraic decomposition seen above. Indeed, because of the similarity invariance of the problem, we can assume ABC is equilateral of side 1, so that {\texttt{per}}(ABC)=3 . With the meanings of our variables x , y , z as in (4.13), we already know that
Now, if u, v\in\mathbb R , the inequality
holds, since
with equality holding when u=v\ge0 . Applying this inequality to our previous expressions, we get
and so
as needed. The equality is achieved when x=y=z=1/2 , that is, when P , Q , R are the midpoints of the sides of ABC .
5.3. On Problem 1: The generalized NPT Problem
5.3.1. GeoGebra Discovery approach
After the difficulties encountered while dealing with Problem 2, confronting the resolution of Problem 1 with GGD becomes an even more challenging task. In the first place, setting up the geometric construction that represents the problem becomes a trickier goal because it involves the computation of intersections of circles and lines, which are of a quadratic nature and represent a technical obstacle in order to define points P , Q , R in the construction. Even though there are ways to overcome these obstacles in GeoGebra that allow a nice geometric representation of the problem, we lose the ability to establish a consistent form of translating the construction into symbolic terms; see Figure 10 (a).* The option of limiting points P , Q , R to the sides BC , CA , AB of the triangle allows for a simpler implementation, † but even in this case the GGD commands {\texttt{Prove()}} and {\texttt{Compare()}} do not succeed in obtaining the desired outputs (see Figure 10 (b)).
*GeoGebra Classic applet available at https://www.geogebra.org/classic/bjgkgnh8 or at GitHub, https://github.com/carlosueno/NPT-Article
†GeoGebra Classic applet available at https://www.geogebra.org/classic/v4n3xdam or at GitHub, https://github.com/carlosueno/NPT-Article
This inability of GGD to deal with Problem 1 was already expected, since this problem is more involved than the preceding one. Thus, in our approach to the NPT, grading the relevance of automation, we observe that we have fully succeeded in the case of Problem 3. We partially succeeded with Problem 2, being required to input in the automatic algorithm some "smart" changes of variables. Finally, in this section we present a highly non-automatic new proof of Theorem 3, which involves heavy trigonometric computations that require the assistance of CAS such as {\texttt{Maple}} and {\texttt{REDUCE}}.
5.3.2. A CAS-assisted human proof
Let us consider an arbitrary triangle ABC . We will make use of the following lemma, which can be found, for example, in [15].
Lemma 1. For any triangle ABC , the inequality
holds, with equality attained only when \alpha=\beta=\gamma=\frac{\pi}{3} .
Proof. By the Law of Sines, we can express a , b , c in terms of the sines of the triangle ABC , so that
So, the inequality is equivalent to
Furthermore, since \alpha+\beta+\gamma=\pi , and all sines are positive,
Notice that the equality holds only when \alpha=\beta=\gamma=\pi/3 . □
Proof of Theorem 3. Choose points P , Q , R , respectively, on lines \overline{BC} , \overline{CA} and \overline{AB} such that AQ^{or}+AR^{or}=BR^{or}+BP^{or}=CP^{or}+CQ^{or}= {\texttt{per}}(ABC)/3 , and set AR^{or}=z , BP^{or}=x , CQ^{or}=y . Notice that with this notation we also have BR^{or}=c-z , CP^{or}=a-x and AR^{or}=b-y . We then have
We can parametrize the variables x , y , z as follows in order to satisfy equalities (5.2):
Observe that, thanks to our generalization of the NPT, the variable t is allowed to take arbitrary real values.
Now, let us express the sides p , q , r in terms of variable t . By applying the Law of Cosines on triangles ARQ , BPR and CQP , we obtain
Now, after using (5.3) to express x, y, z in terms of t and some trigonometric manipulations (a CAS system can provide some help here), we finally arrive at the equalities
Let s(t)=p(t)+q(t)+r(t) denote the perimeter of triangle PQR . We make use now of the inequality
where \delta represents an arbitrary angle. For p(t) , q(t) and r(t) we respectively choose angles
and we get
Now we have, since \alpha+\beta+\gamma=\pi ,
Therefore, the coefficient of t in s_1(t)=p_1(t)+q_1(t)+r_1(t) equals
In other words, s_1(t) does not depend on t , and s(t)\ge s_1(t)=p_1(0)+q_1(0)+r_1(0) . If we use now the Law of Sines, we can express the sides a, b, c of ABC in terms of the angles \alpha, \beta, \gamma so that a=k\sin{\alpha} , b=k\sin{\beta} , c=k\sin{\gamma} , where k is the appropriate proportionality constant. Then,
Finally, we can check (with CAS software if necessary*) that
*{\texttt{Maple}} code available at {\texttt{MapleCloud}} file "NPT – Problem 1 assisted computations" or at GitHub, https://github.com/carlosueno/NPT-Article
Here, the last inequality follows from Lemma 1. Equality only can hold when a=b=c .□
The final step of the previous proof leads us to this bound for the values of the perimeters {\texttt{per}}(PQR) :
Corollary 4. Given an arbitrary triangle ABC and three points P , Q , R on the sides BC , CA , AB , respectively, such that AR^{or}+AQ^{or}=BR^{or}+BP^{or}=CP^{or}+CQ^{or} (thus, equal to {\texttt{per}}(ABC)/3 ),
This lower bound is also obtained in a more elementary way in [10].
6.
The set of inscribed triangles in a given triangle
While attempting to solve Problems 1 through 3, a natural connection arose with the following question: Given a triangle ABC of given sides a , b , c , what are the possible values that the sides p , q , r of a triangle PQR with P , Q , R lying, respectively, on lines \overline{BC} , \overline{CA} and \overline{AB} can take? The authors searched for results in this direction and found no reference in this regard—the closest one goes back to a problem by Steinhaus (see [12,42]), but there, the question is more about which triangles are contained instead of inscribed in ABC . Here, we present a new result (to the best of our knowledge; see Theorem 5 below) on the space of triangles which can be inscribed in an arbitrary, given triangle, where by inscribed we mean that each vertex lies in one of the three lines containing the sides of the given triangle (each vertex in a different line).
Even though at first sight it could seem that this result is not directly related to our "never-proved statement, " a closer look reveals the tight connections that exist between both topics. For instance, Corollary 6 below shows a kind of converse of Problem 2: namely, determining the inequalities that have to be verified by a set of triples (p, q, r) in order to correspond to the sides a triangle PQR inscribed in an equilateral triangle ABC of unit side. The reader is invited to compare this corollary to formula (5.14) in subsection 5.2.
Again, the finding of the statement and the proof of Theorem 5 owe a lot to the assistance of CAS software and, in particular, to the 3D graphical capabilities of GeoGebra and of other mathematical software, which guided us to its final formulation. Through this section, all surfaces and semialgebraic sets to be considered will be restricted to the positive orthant \mathbb R^3_{\ge 0} .
Theorem 5. Let ABC be an arbitrary triangle with an inscribed triangle PQR so that P , Q , R lie, respectively, on lines \overline{BC} , \overline{CA} and \overline{AB} . Set PQ=r , QR=p , RP=q . Let us consider the sets in \mathbb R^3_{\ge 0}
Then, the set \mathcal{S}\subset\mathbb R^3_{\ge 0} of triples (p, q, r) is given by
Proof. Let us consider the space \mathcal T of ordered triples (p, q, r)\in\mathbb R_{\ge0}^3 representing the Euclidean distances of three points P , Q , R on the plane (as usual, we consider p=QR , q=PR and r=PQ ). From the Triangle Inequality, it readily follows that
Now, we have to distinguish five different configurations:
Case 1: The points P , Q R are not collinear, and they form a directly (counterclockwise) oriented triangle PQR .* In this case, the interior angles \alpha' , \beta' and \gamma' at P , Q , R are considered positive (see Figure 11), and (p, q, r) can be written in the form (t\sin\alpha', t\sin\beta', t\sin\gamma') for some t>0 .
*GeoGebra Classic applet available at https://www.geogebra.org/classic/ejtshvav or at GitHub, https://github.com/carlosueno/NPT-Article
Case 2: The points P , Q R are not collinear, and they form an inversely (clockwise) oriented triangle PQR .† In this case, the interior angles \alpha' , \beta' and \gamma' are considered negative (see Figure 12) and (p, q, r)=(-t\sin\alpha', -t\sin\beta', -t\sin\gamma') for some t>0 .
†GeoGebra Classic applet available at https://www.geogebra.org/classic/kcxy2vu7 or at GitHub, https://github.com/carlosueno/NPT-Article
Case 3: The points P , Q , R are collinear and distinct (see Figure 13 (a)). We can consider this case as the one corresponding to a degenerate triangle PQR where one side is the sum of the other two. Here, we can express (p, q, r) in one of the forms (\epsilon t, (1-\epsilon)t, t) , (t, \epsilon t, (1-\epsilon)t) or (\epsilon t, t, (1-\epsilon)t) with 0<\epsilon<1, t>0 , depending on which of the relations r=p+q , p=q+r or q=p+r holds.
Case 4: Two of the points P , Q , R coincide (see Figure 13 (b)). We can think of this case as corresponding to a degenerate triangle PQR with one side equal to zero and the other two equal. Now, (p, q, r) can be expressed as (t, t, 0) , (t, 0, t) or (0, t, t) , with t>0 .
Case 5: All three points P , Q , R coincide. In this case we have a collapsed triangle PQR where P=Q=R .
If we further assume, as we have done in previous sections, that P , Q , R lie, respectively, on the three lines \overline{BC} , \overline{AC} , \overline{AB} containing the sides of a (non-degenerate) triangle ABC , then we can rule out Case 5 above. As in previous sections, we will consider from now on that these restrictions apply to P , Q , R , so that we will be dealing only with Cases 1 through 4.
We proceed now with the proof in several steps:
(i) Understanding the relative positions of the S_i 's.
Let us consider first the surface \partial S_0 —by \partial S_0 we denote the boundary of the semialgebraic set S_0 —with equation
If k represents the scale factor for triangle ABC such that a=k\sin\alpha , b=k\sin\beta , and c=k\sin\gamma , then, dividing equation (6.1) by k^6 , we obtain a normalized equation
where \bar{p}=p/k , \bar{q}=q/k , \bar{r}=r/k have been re-scaled accordingly. From now on, we will be working with this normalized equation, assuming implicitly that the sides of ABC measure \sin\alpha , \sin\beta , \sin\gamma and retrieving the original values a , b , c at the end of the proving process. Similarly, for \partial S_1 we have the normalized equation
which was obtained from simplifying the expression defining the set S_1 after dividing it by k^3\sin\alpha\sin\beta\sin\gamma . In this re-scaled situation, the sets S_0 , S_1 will be denoted by \bar{S}_0 , \bar{S}_1 (notice that the sets S_2 , S_3 , S_4 do not change).
We introduce now the polynomial
Observe that the set \{(\bar{p}, \bar{q}, \bar{r}):j(\bar{p}, \bar{q}, \bar{r})\ge 0\}\subset\mathbb R_{\ge0}^3 is precisely \mathcal T=S_2\cap S_3\cap S_4 (if two of the factors in the expression defining j are negative, it is easily deduced that one of the variables \bar{p} , \bar{q} , \bar{r} is negative).
With the assistance of CAS*, we can verify that the equality
*{\texttt{Maple}} code available at {\texttt{MapleCloud}} file "NPT – Theorem 5 assisted computations" or at GitHub, https://github.com/carlosueno/NPT-Article
holds, and this means that if j(\bar{p}, \bar{q}, \bar{r})<0 , then necessarily \bar{s}_0(\bar{p}, \bar{q}, \bar{r})>0 . Therefore, we must have \bar{S}_0\subset S_2\cap S_3\cap S_4 . Also, the points (\bar{p}, \bar{q}, \bar{r}) lying in the intersection of two of the three surfaces in \{\partial\bar{S} _0, \partial\bar{S}_1, j(\bar{p}, \bar{q}, \bar{r})=0\} must belong to all three of them. In particular, if a point lies in \partial\bar{S}_0\cap\partial\bar{S}_1 , then it also lies on one of the planes \bar{p}=\bar{q}+\bar{r} , \bar{q}=\bar{p}+\bar{r} , \bar{r}=\bar{p}+\bar{q} (see Figure 14 (a)).†
†{\texttt{Maple}} code available at {\texttt{MapleCloud}} file "NPT – Surfaces bounding S_0 , S_1 , \mathcal T " or at GitHub, https://github.com/carlosueno/NPT-Article
Now, let us study the intersections of a ray \Lambda=(O;\vec{\lambda}) —that is, with origin O=(0, 0, 0) and direction vector \vec{\lambda} —contained in \mathcal T with the sets \bar{S}_0 and \bar{S}_1 . When \Lambda lies in the interior of \mathcal T , there is a triple of positive angles (\alpha', \beta', \gamma') in the interval (0, \pi) such that the ray can be expressed as \Lambda=\{(t\sin\alpha', t\sin\beta', t\sin\gamma'), t\ge 0\} . Let us first consider the intersection of \Lambda with \partial S_0 . Substituting the parametrized expression of the ray into (6.2), we obtain a biquadratic equation in t of the form
Here,
In this equation, whenever \alpha, \beta, \gamma, \alpha', \beta', \gamma'\in (0, \pi) , we have
To check that F_2\ge0 , and to shorten the involved expressions, set
By the Law of Cosines,
So,
Collecting terms by considering F_2 as a polynomial in a_2 , we arrive at an expression of the form F_2=G_2a_2^4+G_1a_2^2+G_0 , where
Notice that we can write F_2 as
where D_0 is the discriminant of this polynomial (considered as a quadratic one in a_2^2 ), that is,
Since the triples a_1, b_1, c_1 and a_2, b_2, c_2 are sides of two triangles, this is always non-positive. Further, it can only vanish when b_1c_2-b_2c_1=0 , and by (6.6) we conclude that F_2\ge0 . By considering a symmetric argument taking b_2 and c_2 as main variables in F_2 , we deduce that the equality can only be achieved when
and this only can happen if \alpha'=\alpha , \beta'=\beta , and \gamma'=\gamma .
We also have F_1<0 , since this coefficient can be rewritten as
and for the last factor we have
Finally, the inequality F_0>0 is straightforward.
We proceed now to analyze the real roots of Eq (6.5). The solutions for t^2 are given by
where D represents the discriminant of the associated second-degree equation in t^2 . We claim that both T_0 and T_1 are positive, and
These claims are deduced after running the {\texttt{REDUCE}} code in Tables 3 and 5* (for certain trigonometric computations, {\texttt{Maple}} is less effective, and in these cases we rely on the faster and cleaner outputs that {\texttt{REDUCE}} produces), since there the validity of the stated value for D is verified, as well as the proof that T_0 and T_1 can be expressed as squares of real numbers \tau_0 and \tau_1 , to be defined below.
*{\texttt{REDUCE}} file for Tables 3 through 5 can be found at GitHub, https://github.com/carlosueno/NPT-Article.
From all our previous work, it is now easy to conclude that the intersection of the ray \Lambda with \bar{S}_0 is the segment U_\Lambda V_\Lambda , where U_\Lambda=\sqrt{T_0}(\sin\alpha', \sin\beta', \sin\gamma') is its closest point to the origin, and V_\Lambda=\sqrt{T_1}(\sin\alpha', \sin\beta', \sin\gamma') is the furthest one:
For \alpha'=\alpha , \beta'=\beta , \gamma'=\gamma , from (6.5) and since F_2=0 , in this case we get that this segment becomes the ray (U^*_{\Lambda}; \vec{\lambda}) ,
where U^*_{\Lambda}=\sqrt{T_3}\left(\sin\alpha, \sin\beta, \sin\gamma\right) , and
Remark 3. When (\alpha', \beta', \gamma') approaches (\alpha, \beta, \gamma) , the corresponding U_\Lambda approaches the point U^*_\Lambda . This is because (running the last line of code in Table 5 checks this fact)
and
To simplify notation, we will identify U^*_\Lambda with U_\Lambda for the particular case (\alpha', \beta', \gamma')=(\alpha, \beta, \gamma) .
When \Lambda is contained in the boundary of \mathcal T , we are in one of the degenerate Cases 3, 4. For instance, if we assume that \bar{p}=\bar{q}+\bar{r} , then (\bar{p}, \bar{q}, \bar{r})=(t, \epsilon t, (1-\epsilon)t) . To find the intersection of \Lambda with \partial\bar{S}_0 (we already saw it also coincides with the intersection with \partial\bar{S}_1 ) we can use (6.3) to get the intersection point U^d_\Lambda=\sqrt{T_5}(1, \epsilon, 1-\epsilon) , where
Here, the option 0<\epsilon<1 belongs to Case 3, while the options \epsilon\in\{0, 1\} belong to Case 4. In these degenerate cases, we finally have that \Lambda\cap \bar{S}_0=\{U^d_\Lambda\} and \Lambda\cap \bar{S}_1=(U^d_\Lambda;\vec{\lambda}) . A similar argument can be carried out with the other options \bar{q}=\bar{p}+\bar{r} , \bar{r}=\bar{p}+\bar{q} .
We proceed now to study the intersection of a ray from the origin \Lambda in \mathcal T with the set \bar{S}_1 . If we make the substitutions \bar{p}=t\sin\alpha' , \bar{q}=t\sin\beta' , \bar{r}=t\sin\gamma' in (6.3), we get
but the coefficient of t^2 here is precisely -F_1/(2\sin^2\alpha\sin^2\beta\sin^2\gamma) , so it is positive. Therefore, there exists T_4>0 such that \sqrt{T_4}(\sin\alpha', \sin\beta', \sin\gamma')=W_\Lambda is in \partial \bar{S}_1 , and also we get from this that
In fact, we can check that W_\Lambda lies in \bar{S}_0 . Indeed, if W_\Lambda=(\bar{p}_0, \bar{q}_0, \bar{r}_0)\in\Lambda\subset S_2\cap S_3\cap S_4 , then \bar{s}_1(\bar{p}_0, \bar{q}_0, \bar{r}_0)=0 , and by (6.4) we have \bar{s}_0(\bar{p}_0, \bar{q}_0, \bar{r}_0)\le0 , so that W_\Lambda\in\bar{S}_0 . In particular, from this we get that
(ii) Assume we are in Case 1 above and consider the ray \Lambda=\{t(\sin\alpha', \sin\beta', \sin\gamma'):t\ge0\} , corresponding to triangles PQR directly oriented with p=t\sin\alpha' , q=t\sin\beta' , r=t\sin\gamma' . Then, the set
satisfies \bar{\mathcal S}^+_\Lambda=(U_\Lambda; \vec{\lambda}) .
Let us consider variables x=BP^{or} , y=CQ^{or} , z=AR^{or} . Also, in order to establish some reference vectors to measure angles, consider vectors \vec{u}=\overrightarrow{AB} , \vec{v}=\overrightarrow{BC} , \vec{w}=\overrightarrow{CA} . If \langle \vec{a}, \vec{b}\rangle represents the (oriented) angle formed by the vectors \vec{a} , \vec{b} , let us set
Notice that these angles satisfy the following system of equations (mod 2\pi ):
We can express all angles \delta_i in terms of \delta=\delta_1 as follows:
By using the Law of Sines in triangles ARQ , BPR and CQP and setting x=BP^{or} , y=CQ^{or} , z=AR^{or} , we obtain
From the relation
we can express the value of t in terms of the \delta_i angles and consequently in terms of \delta :
When expressing—by using (6.7)—the denominator in terms of \delta , we get the function
where A_0 and B_0 are trigonometric expressions depending on the angles \alpha, \beta, \gamma, \alpha', \beta', \gamma' . It is a well known trigonometric fact that
and therefore we have
Notice here that a special case would arise if both expressions A_0 , B_0 can be simultaneously zero, but under the assumption of \alpha' , \beta' and \gamma' lying in (0, \pi) , this cannot happen. This comes from the fact (proved with {\texttt{REDUCE}} in Table 3) that
and, since all involved angles lie in (0, \pi) , A_0 can vanish only when \alpha+\alpha'=\pi . However, in case we had started by setting \delta_3 instead of \delta_1 as the parameter for expressing all \delta_i angles, we would infer that \beta+\beta'=\pi , and similarly we should have \gamma+\gamma'=\pi . Adding up these three equalities, we obtain
which is a contradiction.
We claim now that the point (\tau_0\sin\alpha', \tau_0\sin\beta', \tau_0\sin\gamma') is precisely U_\Lambda . Here the trigonometry involved in the computations becomes quite complex, and to prove this fact we have to resort to a CAS system capable of handling (very) long trigonometric expressions. In this respect, {\texttt{REDUCE}} stands out as a great tool to perform the needed computations (see Tables 3 and 5 below).
(iii) Assume we are in Case 2 above and consider the ray \Lambda=\{-t(\sin\alpha', \sin\beta', \sin\gamma'):t\ge0\} , corresponding to triangles PQR inversely oriented with p=-t\sin\alpha' , q=-t\sin\beta' , r=-t\sin\gamma' ( t\ge 0 ). Then, the set
satisfies \bar{\mathcal S}^-_\Lambda=(V_\Lambda; \vec{\lambda}) . For \alpha'=-\alpha , \beta'=-\beta , \gamma'=-\gamma , we have \bar{\mathcal S}^-_\Lambda=\emptyset .
The arguments for proving this run parallel to those in (ii) but having in mind that now angles \alpha' , \beta' and \gamma' lie in (-\pi, 0) . Now, we arrive at a function H_1(\delta)=A_1\cos\delta+B_1\sin\delta and
There is a special case when A_1=B_1=0 , where
which by a similar argument to the previous case leads to \alpha+\alpha'=\beta+\beta'=\gamma+\gamma'=0 . However, now this can take place when \alpha'=-\alpha , \beta'=-\beta , and \gamma'=-\beta , and also with these values we get B_1=0 . See Tables 4 and 5* for the {\texttt{REDUCE}} assisted proof of these facts.
*{\texttt{REDUCE}} file for Tables 3 through 5 can be found at GitHub, https://github.com/carlosueno/NPT-Article.
(iv) The degenerate cases.
When P , Q , R are collinear and distinct points, one of them lies between the other two. Let us say P lies between Q and R , so that the relation p=q+r holds. Setting p=t , q=\epsilon t , r=(1-\epsilon)t ( t>0 ), the equalities in (6.8) become
so that now (6.9) and (6.10) turn into
and
In this case we have
and so the minimum positive value for t is achieved at
Table 6* shows that the point (\tau_2, \epsilon \tau_2, (1-\epsilon)\tau_2) is indeed U^d_\Lambda and lies in the surface \partial S_0 , and so we have proved that
*{\texttt{REDUCE}} file for Table 6 can be found at GitHub, https://github.com/carlosueno/NPT-Article.
Now, we consider the degenerate case in which two of the points P, Q, R do coincide. Let us set P=Q as shown in Figure 13 (b). Then, we can write p=t , q=t and r=0 , and the relations in (6.8) simplify to
So, the condition x+(\sin\alpha-x)+y+(\sin\beta-y)+z+(\sin\gamma-z)=\sin\alpha+\sin\beta+\sin\gamma reduces to
and this time
We set
and it is easy to verify that
Therefore, \tau_3=\sin\alpha\sin\beta , and we have already seen that in fact (\tau_3, \tau_3, 0)=U^d_\Lambda\in \partial S_0 . This proves that
(v) The equality \mathcal S=S_0\cup(S_1\cap S_2\cap S_3\cap S_4) holds.
From step (i) we have seen that a ray \Lambda from the origin and contained in S_2\cap S_3\cap S_4 intersects \bar{S}_0 in a segment bounded by two points U_\Lambda and V_\Lambda , where U_\Lambda represents the closest point to the origin and V_\Lambda the furthest one ( V_\Lambda becomes +\infty for the special ray corresponding to \{(t\sin\alpha, t\sin\beta, t\sin\gamma):t\ge 0\} ). These segments reduce to a point U^d_\Lambda (that we denote here by U_\Lambda as well) in the degenerate cases. On the other hand, \Lambda intersects \bar{S} _1 in a ray with extreme at a point W_\Lambda which lies in the segment U_\Lambda V_\Lambda . Also, from steps (ii), (iii), (iv), we deduce that \bar{\mathcal S}\cap\Lambda=(U_\Lambda; \vec{\lambda}) , and so
Therefore,
If we now retrieve the original variables p, q, r which were valid for an arbitrary triangle ABC without normalizing its size, we end up with the sets \mathcal S , S_0 and S_1 that appear in the original statement of Theorem 5. To gain a better understanding on how \mathcal S looks like, see Figure 14 (b). □
Corollary 6. Let ABC be an equilateral triangle of side 1, with an inscribed triangle PQR so that P , Q , R lie, respectively, on lines \overline{BC} , \overline{CA} and \overline{AB} . Set PQ=r , QR=p , RP=q . Let us consider the sets in \mathbb R^3_{\ge0}
Then, the set \mathcal{R}\subset\mathbb R^3_{\ge 0} of triples (p, q, r) is given by
7.
Conclusions
As we have illustrated through this paper, the "never-solved" problem stands in the middle of an eclectic panorama: early—yet connected with some of our current developments—work on automated theorem proving, old proposals and (human-focused) solutions of involved triangle inequalities, and a large collection of incomplete or wrong data concerning references, deserving clarification, as we have described in section 3, including, in particular, a simple human proof of the "never-solved" problem.
Nevertheless, the relevance of this NPT is not just its curious history but the challenge it poses to both humans and machines and the further explorations that still allows. This challenge has required us to reflect on affordable improvements to be implemented in the near future in the automated reasoning tools currently available in GGD. These improvements have to do with the automatic simplification of the input of statements, through partial elimination of quantifiers, or the discovery of "ratios" as an alternative to "proofs, " or the consideration of symmetries as a source of simplification by means of a change of variables, as described in Sections 4 and 5.
This challenge has required us to propose some simplified variants of the NPT, which have been used as benchmarks for our automated and "partially automated" approaches, as described in detail in Section 5, showing their great performance and, also, the great room for improvement. Yet, it must be remarked that, no matter how relevant is the weight of human intelligence in each case, we find the cooperation of symbolic computation software to be fundamental.
We also have witnessed the difficulties that current CAS systems still have when dealing with trigonometric expressions. Very often we had to resort to our own human-made trigonometric simplifications, in a kind of head-to-head endeavor between human and machine in order to get optimal expressions that would significantly reduce the outputs produced by our personal computers.
Indeed, as a final conclusion, we can still highlight that, even with the use of great computation tools, the human approach still matters.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
First and second authors acknowledge support by the grant PID2020-113192GB-I00 (Mathematical Visualization: Foundations, Algorithms and Applications) from the Spanish MICINN. The authors want to thank Thomas Sturm for his assistance concerning some computations performed with the {\texttt{REDUCE/Redlog}} CAS.
Conflict of interest
The authors declare no conflict of interest whatsoever.
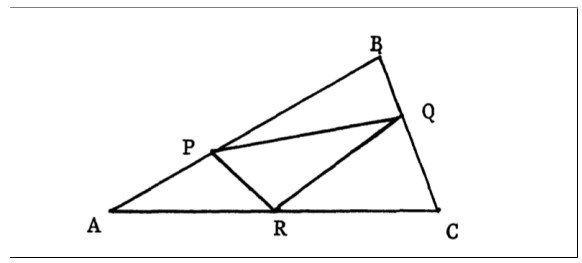









 DownLoad:
DownLoad:
















