Multiplicity results for some fourth-order elliptic equations with combined nonlinearities

1.   Introduction

The novel coronavirus was detected for the first time in Wuhan, China in December 2019 and the epidemic has been spreading ever since. The number of people infected all over the world is 21,040,712 (11 March 2021) and the number of confirmed cases all over the world is 119,107,115 (11 March 2021). COVID-19 gets transmitted from respiratory droplets when someone with the virus coughs, sneezes or talks. Due to severity of the pandemic, it is indeed needed for quick and cost-effective detection of COVID-19.

Recently it is reported that artificial intelligence and machine learning have tremendous potential in health care sector [1]. The SARS-CoV-2 virus in the respiratory tract was usually diagnosed using the reverse transcription-polymerase chain reaction (RT-PCR) by taking naso-pharyngeal samples from the patient [2].

The RT-PCR has a lower potential for contamination and the severity of infection can also be estimated. The RT-PCR has a specificity of 46% and a recall of 87% [3]. Though the test usually takes a few hours, the process of collecting and processing the samples in bulk takes days before the results from a single sample are known from the report.

Although RT-PCR is widely used, it is less sensitive than computed tomography [4]. Chest X-ray is an imaging method to detect COVID-19 done in wards, exclusive to patients with suspected infections. Portable radiology equipments are available for suspected patients. Chest imaging plays an important role in early diagnosis and treatment of patients with COVID-19.

Chest radiography is a faster and comparatively inexpensive imaging method and the previous studies have demonstrated its role in predicting COVID-19 in patients infected with COVID-19 [5]–[7]. The sudden and massive increase in workloads, due to the spread of the COVID-19 pandemic has required the development of additional tools to help manage patients. The algorithm established here is also beneficial in cases where there is shortage of expertise in medical teams.

Mask R-CNN is an important AI-based scheme which has been used before in automatic nucleus segmentation [8], lung nodules detection and segmentation [9],[10], liver segmentation [11], automated blood cell counting [12] and multiorgan segmentation [13]. Face detection and segmentation [14], detection of oral disease [15], hand segmentation [16], segmenting the optic nerve [17], segmentation of early gastric cancer [18],[19] and detection and classification of breast tumors [20] is also performed using Mask R-CNN. However, the Mask R-CNN method for the detection of COVID-19 from chest X-ray images has not been explored to the best of our knowledge.

Imaging in COVID-19 is done by expert radiologists whose role is to screen the images through visual observation and report the findings. Chest X-ray is one of the most commonly and widely applied imaging modality. Healthcare centers and hospitals can be highly benefited in applying our proposed method in practice. It would ease the workflow and the test results can be obtained faster than the RT-PCR and so the spread of the disease can be readily controlled.

Detection methods also include the rapid antigen test which provides immediate results although they have lower sensitivity than RT-PCR. Various medical imaging techniques like X-rays, computed tomography (CT) scans, and magnetic resonance imaging (MRI) are used all over the world for diagnosis of diseases. Deep-learning based AI techniques are used to ensure that the diagnosis is accurate [21],[22]. In this study, we assess the performance of an artificial intelligence (AI) system for the detection of COVID-19.

2.   Materials and methods

2.1.   Datasets

The dataset of images utilized here in this study was collected from COVID-19 image data compiled by Cohen and et al. [23],[24]. The entire dataset of chest X-ray images is a publicly available collection of data and can be obtained from their GitHub repository for further use. The dataset was first made public in February 2020 and is continuously growing ever since. As of now, it contains a total of 542 frontal chest X-ray images from 262 people worldwide of which 408 are standard frontal PA/AP and 134 are AP Supine images [24]. The dataset also contains numerous clinical use cases and tools. Based on these chest X-ray images the deep learning model is evaluated.

2.2.   Deep learning model

The Mask R-CNN is a deep neural network aimed to solve instance segmentation problem in machine learning or computer vision. Mask R-CNN is of enormous importance in medical imaging analysis. Mask R-CNN model is commonly used for object detection and segmentation. Not only it puts a bounding box on the target, but also it creates a mask and classifies the boxes depending on the pixels inside it. It is an extension over the Faster R-CNN model.

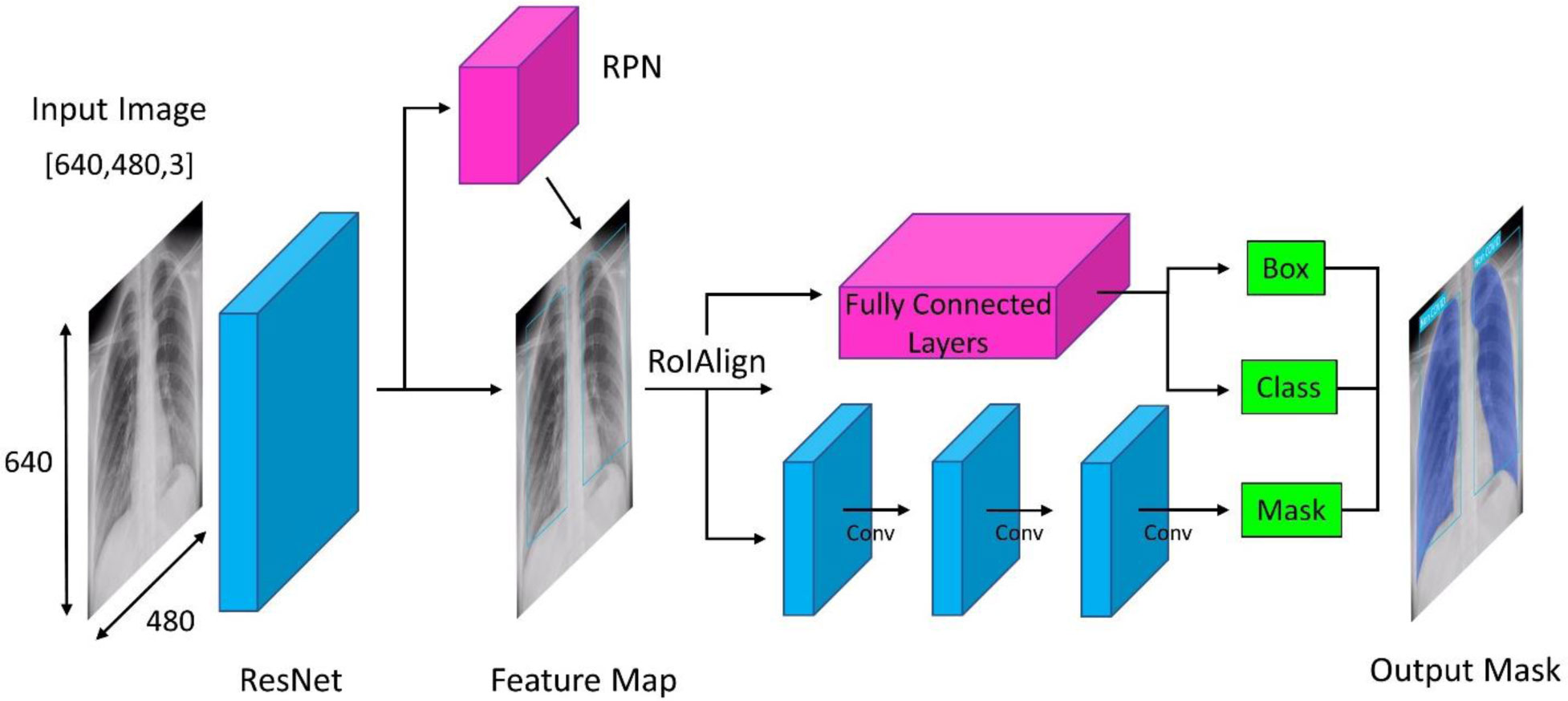
The Mask R-CNN model consists of three primary components which are the backbone, the Region Proposal Network (RPN) and RoIAlign. The architecture of the proposed deep learning model is shown in Figure 1. Backbone is a Feature Pyramid Network style deep neural network which can extract multi-level image features. The ResNet forms the backbone of the Mask R-CNN model. The CNN used here is ResNet41, ResNet50, ResNet65 and ResNet101. The CNN ResNet50 consists of 48 convolution layers along with 1 MaxPool and 1 Average Pool layer. Further, it has 3.8 × 10⁹ floating point operations. The RPN uses a sliding window to scan the input image and detects the infected regions in this study. The RoIAlign then examines the RoIs obtained from the RPN and extends the feature maps from the backbone at various locations. The RoIAlign is responsible for the formation of the precise segmentation masks on the images. The RoIPooling in Faster R-CNN is replaced by a more precise and accurate segmentation using the RoIAlign.

The entire model was buildup using the above deep learning mechanism. The various features of the model are described below. The model is capable of classifying objects into different classes, surround them with bounding boxes and create a mask for the detected objects. The multi-mask loss function for each case is given by:

where L_cls, L_bbx and L_mask are classification loss, bounding box regression loss and mask prediction loss respectively. To minimize the loss function the three components are composed in a specific manner. The classification loss is defined using the following equation:

The classification loss L_cls of each anchor is the log loss of whether the area is a lung is calculated from:

The bounding box regression loss is given by the following equation:

In the above mathematical expressions, i is the index of an anchor and p_i indicates the prediction probability that the anchor is one of the lungs. Ground truth label is denoted by pi* whose value is 1 if anchor indicates one of the lungs and 0 if it doesn't. t_i indicates the predicted four parameterized coordinates of the bounding box and ti* is the vector which represents the ground truth coordinates of the positive anchor. N_cls is the mini-batch size and N_bbx is the number of anchor locations. They are the normalization terms. The smooth L1 loss is used as it is robust for outlier points. The average binary cross-entropy loss is given by L_mask, which is defined by:

where, the label value of a cell (i, j) of a region of m × m size is given by y_ij. y¯ijk is the predicted value of the k^th class of that cell. The minimization of the loss function nearly towards zero is observed during training on the dataset which indicates that the model performs without an overfitting problem.

2.3.   Methodology

At first, the AI-based model was required to train on known results. The chest X-ray images with the best quality were selected for training. The images used were in jpg format. For training, testing and validation dataset, images of different age, gender and orientation were considered.

The system was trained on a pneumonia dataset as well as a COVID-19 dataset [23]. This dataset includes 931 images of which 534 were COVID infected according to the RT-PCR test, 134 were pneumonia and the rest were not specified. The validation set consisted of 150 images (75 per label, equally divided between PA and AP images) that were used to compute the performance during the training process [23],[24]. All of these images were obtained from an open source database as mentioned earlier and the patient anonymity was maintained.

The annotations were done using VGG Image Annotator software. VGG Image Annotator is an open-source image annotation tool used to indicate regions in an image and create text that defines them. These images were annotated by skilled pathologists.

The whole setup was implemented in Windows environment using NVIDIA GTX 1080 4 GB GPU on a system with 8 GB RAM and having Intel Core-i5 7th generation @2.20GHz processor. The entire algorithm was implemented using Python programming language.

3.   Results

The experiments on the deep learning model were performed to detect COVID-19 in chest X-ray images. The Mask R-CNN was trained for 100 epochs. The performance assessment of the methods is tabulated in Table 1. The Accuracy, Specificity, Precision and Recall were compared for the different methods as well as for the method used in this study [25]. The trained neural network was used to classify X-ray images. The parameters used to evaluate the performance are:

The TP, TN, FP and FN are the True Positive, True Negative, False Positive and False Negative respectively. The accuracy, specificity, recall, precision and F1-score for the proposed models are shown in Table 1. These metrics evaluate the performance of the deep learning model on the chest X-ray image dataset.

In order to evaluate the Mask R-CNN model, the 5-fold cross-validation was performed. The first fold was used to test the model while the rest of the dataset was used to train the model. Then the performance was noted from the perspective of a binary classification problem.

The 5-fold cross-validation was performed on all the models of which the ResNet50 proved to be superior than other models. The Confusion Matrix (CM) was computed for the task of binary classification between COVID-19 and Not COVID-19. The results of the CM for all the 5 folds are shown in Figure 2. The performance of the metrics for all 5 folds and their average is illustrated in Table 2. From the Table 2, it is observed that the ResNet50 model has obtained an average accuracy, specificity, precision, recall and F1-score of 96.98%, 97.36%, 96.60%, 97.32% and 96.93% respectively.

4.   Discussion

Among the proposed models the ResNet50 demonstrates a promising amount of accuracy in COVID-19 detection on chest X-ray images. The evaluations indicate that the model is highly capable of accurate detection of the disease. Figure 3 (a) shows the chest X-ray of patients (b) shows the deep learning model prediction with mask.

The biomedical images used are of 640 × 480 for training the model. Our proposed method shows that the infected lungs are obtained with red masks and confined within the bounding boxes. Using our method, the lungs are correctly detected with no false alarms. To obtain better accuracy, experiments are performed extensively on superior quality images of the dataset.

The comparison of the different AI-based COVID-19 detection models is presented in Table 3. From Table 3, it can be seen that our method delivers an accuracy of 96.98% and specificity of 97.36% in COVID-19 detection, which is superior compared to the accuracy of 94.92% and specificity of 92% using SSD proposed by Saiz et al. [21]. Our model is also found to be better in comparison to DeTraC-ResNet18 proposed by Abbas et al. [22], COVIDX-Net proposed by Hemdan et al. [26], COVID-Net proposed by Wang et al. [27] and VGG-19 proposed by Ioannis et al. [28]. Note that VGG-19 has a slightly better specificity than our Mask R-CNN model. In addition to these, our model is also found to be better when it compared with the ResNet50 + SVM model proposed by Sethy and Behera [29] and the shallow Convolutional Neural Network (which contains four layers and lesser number of parameters for more efficient computation) proposed by Mukherjee et al. [30].

The proposed model can also be applied to distinguish COVID-19 pneumonia from other pulmonary diseases such as asthma and bronchitis. The proposed method can also be modified for detecting other abnormalities in the lungs. The advantage of this model is that it provides both bounding box and instance segmentation while the limitation is that larger datasets are required for accurate detection.

5.   Conclusions

The AI-based method, Mask R-CNN for detection of COVID-19 using chest X-ray image as primary dataset is presented in detail. The method, Mask R-CNN is found to be superior in comparison to other AI-based methods for detecting COVID-19. The deep learning model proposed in this study is not only capable to detect but also able to classify COVID-19 infections from chest X-ray study. The method, Mask R-CNN presented here delivers specificity of 97.36% and accuracy of 96.98% and therefore would be a very effective tool in healthcare. Also, it is noticed that the Mask R-CNN method has potential applications in detecting chest related diseases.