Calibrated deep attention model for 3D pose estimation in the wild

1.   Introduction

Decision makers tackle and, despite the complications in every field of life, are in different challenging situations. It is not easy to express the attributed value due to its uncertain nature. Scholars introduce many tools to handle its fuzzy nature. A fuzzy set is a generalized form of a well-defined set, which is known as a truth set having components the members of truth degrees ^[1]. A truth set only has two values $0$, for $(no)$ and $1$ for $(yes)$, so, with the help of the truth set, it cannot be easy, and sometimes solving real-world problems may become impossible. To get a better result, fuzzy set $(FS)$ allows adjustment of truth membership value from $0-1$ instead of only consisting of 0 or 1. Father of fuzzy set theory, Zadeh put forward an idea of the fuzzy set in 1965 ^[2], which is a generalization of a truth set in which entries of a set have different membership values. We know in this generalization no concept of a falsity-membership or negative value is defined. In 1985, Atanassov gave the idea of falsity and truth membership value, which is defined in the form of an intuitionistic fuzzy set $(IFS)$ ^[3] based on having constraint

In this context, the symbols $\alpha$ and ${\beta}$ are used to denote the degree of membership in the concepts of truth and falsehood, respectively. But in ${IFS}$ there are some cases where the sum of truth membership and falsity-membership degrees increases from 1 ^[4]. The Pythagorean fuzzy set was proposed for such cases by Zhang and Xu with new limitations of

which expands the area of uncertainty. Q-rung orthopair fuzzy set was proposed for more generalization by Yager ^[5] with a condition of

For solving real-world problems more generally ^[6] gives an idea of picture fuzzy set $(PFS)$ in which human opinions are of type yes, no, abstain, and refusal is discussed as more sufficient in situations. The $PFS$ gave truth membership, falsity-membership, and abstain degrees as well, with the condition

where

is a refusal degree. Then some fuzzy logic operators — disjunction, conjunction, implication, and complements — were broadened by Coung and Hai.

As $PFS$ well expresses uncertainty and ambiguity to obtain more extension, the concepts of interval-valued spherical fuzzy set $(IVSFS)$ and $IV$ T-spherical fuzzy set $(IVTSFS)$ are introduced along with the condition

which strengthens the idea of $PFS.$ The choice of parameters is increased by $IVTSFS$ and also plays an effective role in real-world issues. Bonferroni mean operators are discussed in ^[7] for $TSFHG,$ and are used to evaluate search and rescue robots performance ^[8]. The strategy used for evaluating the performance of solar cells under uncertain conditions was the multi-attribute group decision-making ($DM$) approach using $IVTSF$ information ^[9].

The graph is the easiest way of graphical representation of different relationships between different elements. The researcher of ^[10] discussed the idea of fuzzy graph $(FG)$ and its structure. He also introduced and highlighted the characteristics of paths, cycles, connectivity, subgraphs, trees, and forests. Parvathi gave the idea of an intuitionistic fuzzy graph $(IFG)$ by increasing the falsity membership value ^[11]. In ^[12], degree, size, and order of $IFG$ are also discussed. The generalization of $IFS$ Pythagorean fuzzy graph $(PyFG)$ is also introduced in ^[13], which also introduces and discuss a number of its properties. By the generalization of $PyFG,$ we get a new concept of a q-rung ortho-pair fuzzy graph ($q$-ROFG) ^[14] and also discussed its applications in soil system ^[15]. In 2019, Zuo proposed a picture fuzzy graph in which truth membership, falsitymembership, and, abstinence degrees are involved ^[16]. In a study conducted by ^[17], a spherical fuzzy graph ($SFG$) was developed, with an exponent increase of two. Similarly, ^[18] presented the notion of a T-spherical fuzzy graph ($TSFG$) based on the work of ^[19], which included an extension of exponent $T.$ In 2011 Akram gave an idea of $IV$ fuzzy graphs $(IVFG)$^[20]. The authors in ^[21] introduced the concept of interval-valued intuitionistic fuzzy graph $(IVIFG)$ due to the expansion of $IV$ fuzzy graphs $(IVFG).$ In ^[22], some certain operations and applications are discussed. The generalized forms of $(IVIFG)$ of $IV$ Pythagorean fuzzy set $(IVPyFG)$ ^[23], $IV$ q-Rung orthopair fuzzy set $(IVqRFG)$ ^[24], $IV$ picture fuzzy graph $(IVPFG)$ ^[25], and $IV$ spherical fuzzy graph $(IVSFG),$ $IV$ T-spherical fuzzy graph $(IVTSFG)$ ^[26]. There are some other topics related to these fuzzy graph theoretical parameters like, metric dimension ^[27,28,29], topological descriptors ^[30,31,32], and their applications ^{[33,34,35,36,37]}.

In chemistry, Gutman introduced ^[38] the idea that the energy of a graph is determined by the interplay between the $\pi$ energy of electrons and the summation of these energies in certain molecules, and also discovered the upper energy limit and lower energy limit of the graph. The energy of a complete graph is usually calculated as 2 times the difference between the total count of nodes (represented by n) and 1. In the case of a graph with no edges, the energy is equal to 0. The energy of splitting graph ^[39] and the energy of shadow graph ^[40]. The authors in ^[41] calculated the Laplacian energy for the graph. If the vertices are adjacent, then the Randić matrix

is defined as

here ${d}_{\chi}$ represents the degree of vertex $\chi$ otherwise

Researchers gave the idea of Randić energy, which can be calculated as the sum of absolute values of eigenvalues^[42]. The Laplacian energy of a fuzzy graph is presented by ^[43]. The intuitionistic fuzzy graphs $IFG$ are started; after that, researcher worked on the Laplacian graph and found the energy of an $IFG$ ^[44]. Akram presents the energy and Laplacian energy of $PFGs;$ the researchers established various $DM$ methods and techniques to tackle the challenges involved in various disciplines. In general, the $IVTSFSs$ are better in comparison to interval-valued intuitionistic fuzzy set ($IVIFS$) and $IVqROFS$ as they also examine the abstinence degree.

When there is more than one method for the solution of a particular problem, to get a more efficient answer, concept of an aggregation operator is more beneficial. Hamacher examined a specific category of t-operators ^[45]. t-norm ($TN$) and Hamacher t-conorm ($TCN$) by Hmacher are a generalization of algebraic $TN$ and $TCN$, and they are highly effective and more flexible. When comparing various notions, it is evident that the interval-valued T-spherical fuzzy Hamacher graphs ($IVTSFHG$) exhibit primarily flexibility and parameterization in representing the perspectives of decision-makers. These are some situations that caused us to write that article. Spectrum graph theory is an inclusive application in branches of mathematics like physics, chemistry, computer science, and many others. Graph spectrum helps in combinatorial optimization problems and has a remarkable role in mathematics. The concept of graph energy comes from energy in chemistry. Multiple mathematical properties of graph energies are being explored.

Another idea of energy, referred to as the $FG$ energy, is introduced in this study. This concept expands upon the existing definitions of energy and Randić energy to include the visualization of $FGs$ and $IV$ $FGs.$ To handle the situation, the modified form of $IVIFS$, $q-ROFSG$, is an effective tool, which is $IVTSFS,$ which can increase the human opinion's flexibility. In this article, the Hamacher aggregation operators have been used to calculate the energy and Randić energy of $IVFG,$ thereby providing a comprehensive assessment of its effect. The article makes a number of contributions: The concept of $IVTSFHG$ is used in the context of the Hamacher $TN$ and $TCN$. In this discourse, we engage in a discussion on the energy associated with the division of $IVTSFHG,$ as well as its corresponding shadow. We provide compelling findings pertaining to this topic. A numerical problem-solving method is provided using $IVTSF$ data. The provided approach has the potential to be employed in many problem-solving scenarios in order to get optimal decision-making outcomes ^[46].

1.1.   Importance, novelty and research gap of the chosen topic

The investigation of Randic energies in the context of $DM$ for human trafficking, using $IVTSFHGs,$ is a novel and influential addition to the domains of graph theory and decision science. The significance of this paper rests in its capacity to provide a comprehensive and adaptable framework for the modeling and analysis of intricate systems, namely within the domain of human trafficking. The new contribution may be delineated as follows:

Multifaceted modeling approach: The use of $IVTSFHGs$ enables a more accurate and adaptable depiction of uncertainties linked to human trafficking data. This comprehensive modeling methodology takes into account both the inherent imprecision of data and the $IV$ attributes, so offering a more nuanced and exact representation of the $DM$ context. Randic energies as descriptors: The integration of Randic energies introduces an additional dimension of structural analysis to the process of $DM$. The research presents a unique approach to quantifying the structural features of networks implicated in people trafficking via the use of graph-based descriptors. This phenomenon has the potential to provide valuable knowledge on the structure, interconnections, and possible weaknesses inherent in human trafficking networks. Decision support system: The incorporation of Randic energies within the context of $IVTSFHGs$ makes a significant contribution to the advancement of a reliable decision support system. The use of this system has the potential to aid policymakers, law enforcement agencies, and many other stakeholders in making well-informed choices. This is achieved by offering a more extensive comprehension of the fundamental structures and dynamics that govern human trafficking networks. Handling uncertainty effectively: The issue of human trafficking is characterized by its intricate and ever-evolving nature, which gives rise to inherent uncertainty. The study places significant importance on $IVTSFHGs,$ demonstrating a very advanced methodology for managing uncertainty. This technique enables decision-makers to efficiently negotiate the intricacies associated with incomplete or inaccurate information. Cross-disciplinary impact: The work presented in this study is characterized by its cross-disciplinary approach, which effectively combines graph theory with decision science. Moreover, the study's focus on the pressing social problem of human trafficking further amplifies its importance. The aforementioned contribution encompasses both theoretical improvements in mathematical modeling and practical implementations, hence bearing immediate consequences for addressing a significant worldwide concern.

The significance of the paper stems from its novel integration of $IVTSFHGs$ and Randic energies, which together provide a robust $DM$ framework within the domain of human trafficking. The new contributions of this study go beyond the conventional uses of graph theory, providing a complete and influential framework for comprehending and tackling intricate social problems.

1.2.   Structure of the study

This study presents an analysis of our notions in a specific structure: Section 2 provides an overview of fundamental ideas. In Section 3, the concept of $IVPFHGs$ was introduced, and an analysis was conducted to determine their respective energy levels. Additionally, the energy associated with the division of $IVTSFHG$ and the shadow $IVTSFHG$ was a topic of discussion. Section 4 made a contribution to the Randić energy calculations of $IVTSFHGs$ and $IVTSFHDGs.$ Section 5 of the paper presents an examination of the use of the $IV$ T-spherical fuzzy Hamacher averaging ($IVTSFHA$) operator and the interval-valued T-spherical fuzzy Hamacher weighted geometric ($IVTSFHWG$) operator. The discussion is supported by the use of numerical examples. In the following part, the conclusion is examined.

2.   Preliminaries

In this section, we will discuss some basic definitions of our research work. In this article, we denote integers by $\mathbb{I}.$

Definition 2.1. A $TSFS$ ${\Gamma}$ on a fixed set $\mathbb{I}$ is defined as:

where $\alpha_{v}({\Upsilon})$ shows the truth membership degree, ${\beta}_{v}({\Upsilon})$ shows abstinence degree, ${\gamma}_{v}({\Upsilon})$ denotes the falsity membership degree.

and

in such a way that

is called the hesitancy degree.

Definition 2.2. Let three $TSFs,$ ${V}_{1}, {V}_{2}$, and ${V}_{3}.$ Then

Definition 2.3. A $TSF$ relation $(TSFR),$ ${A}$ on $\mathbb{I} \times \mathbb{I}$ is defined as:

where, $\alpha_{A}$ denotes truth membership degree, ${\beta}_{A}$ denotes abstinence degree and ${\gamma}_{A}$ represents falsity membership degree.

in such a way that

Definition 2.4. The $TSFPR$ ($TSF$ preference relation) can be explained as: Suppose

be a set of alternatives. A $TSFPR$ on ${ \Theta}$ is symbolized by a matrix

where

for all crisp values of $1\leq a, b\leq{n}$ in $\mathbb{I}.$ The symbol $\alpha_{ab}$ is used to symbolize the extent to which the attribute ${\Upsilon}_{a}$ is chosen in relation to the component ${\Upsilon}_{b}.$ Similarly, ${\beta}_{ab}$ symbolizes the extent to which this ${\Upsilon}_{a}$ is not chosen in relation to ${\Upsilon}_{b}.$ Lastly, ${\gamma}_{ab}$ indicates the degree of stance among the elements ${\Upsilon}_{a}$ and ${\Upsilon}_{b}$ and

is hesitancy degree, which follows the condition ${\alpha_{ab}^{T}}, {{\beta}_{ab}^{T}}, {{\gamma}_{ab}^{T}}\in [0, 1],$

Definition 2.5. For comparing two $TSF$ values ($TSFV$), we also use the score function and accuracy function.

Consider

is a $TSFV.$ The score function $S(\diamondsuit)$ is symbolized and defined as

where $S(\diamondsuit)\in [-1, 1].$

Definition 2.6. Consider $\mathbb{I}$ is a fixed set,

and

are two $TSFVs$ on $\mathbb{I}.$ Then

(ⅰ) If $S({\diamondsuit}_{1})\le S({\diamondsuit}_{2})$ then ${\diamondsuit_{1}}\le {\diamondsuit_{2}};$

(ⅱ) If $S({\diamondsuit}_{1})\ge S({\diamondsuit}_{2})$ then ${\diamondsuit_{1}}\ge {\diamondsuit_{2}}.$

Definition 2.7. Let

is called $TN$, which is a binary function. If $\forall {\Upsilon}, {\zeta}, {n} \in [0, 1]$ meets the observing criteria

(ⅰ) $({\Upsilon}, {\zeta}) = {\Upsilon}$.

(ⅱ) ${\Gamma}({\Upsilon}, {\zeta}) = {\Gamma}({\zeta}, {\Upsilon})$.

(ⅲ) ${\Gamma}({\Upsilon}, {F}({\zeta}, {n})) = ({\Gamma}({\Upsilon}, {\zeta}), n)$.

(ⅳ) ${\Gamma}({\Upsilon}, {\zeta})\leq {\Gamma}({n}, {b})$ if ${\Upsilon}\leq {n}$ and ${b} \geq {\zeta}.$

Definition 2.8. A $TN$ $X$ is said to be a $TCN$ such that

The aforementioned statement of $TN$s along with $TCN$ is established as the Hamacher product and Hamacher sum defined by

and

Definition 2.9. A $TSFS$ X on a fixed set $Z$ is defined as:

where $\alpha_{v}({\Upsilon})$ denotes the truth membership degree, ${\beta}_{v}({\Upsilon})$ denotes the abstinence degree, ${\gamma}_{v}({\Upsilon})$ represents the falsity membership degree ^[47],

in such a way that

is called upper and lower hesitancy degree, respectively.

Definition 2.10. The $TSF$ preference relation $TSFPR$ can be explained as: Suppose

be a set of alternatives. A $TSFPR$ on ${ \Theta}$ is symbolized by a matrix

where

for all crisp values of $1\leq a, b\ \leq n$ from $\mathbb{I}.$ Along with $\alpha_{ab}$ denotes the degree to which the element ${\Upsilon}_{a}$ is close to the element ${\Upsilon}_{b}$ and ${\beta}_{ab}$ denotes the degree to which the element ${\Upsilon}_{a}$ is not selected to the element ${\Upsilon}_{b}$ and ${\gamma}_{ab}$ represents the abstinence degree between the element ${\Upsilon}_{a}$ and ${\Upsilon}_{b}$ and

is a hesitancy degree which follows the condition

3.   Interval-valued T-spherical fuzzy Hamacher graphs $(IVTSFHG)$

During the aforementioned part, we have presented the $IVTSFG$ by using the Hamacher $TN$ and $TCN$. In addition, we determine the energy associated with the variable $IVTSFG$ and analyze its significant characteristics. In this context, we are further curious to see the energy associated with the splitting of $IVTSFG$ and the shadow $IVTSFG.$ It extends traditional fuzzy sets by incorporating interval values for membership, non-membership, abstention, and refusal degrees, offering a richer structure to model uncertainty with four-dimensional information. This makes it particularly suited for scenarios involving complex human judgments.

Definition 3.1. If

is a graph, then by an $IV$ fuzzy relation${B}$on a set$E$we mean an $IV$ fuzzy set such that

for all ${xy} \in {A}$ ^[20].

Definition 3.2. Let

is an $IVTSFHG$ on a fixed set $\mathbb{I},$ where

is an $IVTSFS$ in $\mathbb{I}$ and

is an $IVTSFR$ on $\mathbb{I}$ in such a away that:

$\forall {\Upsilon}, {c} \in \mathbb{I},$ where

Here ${V}$ and ${E}$ are the $IVTSF$ vertex set and $IVTSF$ edge set of $G,$ respectively, where ${A}$ is symmetric $IVTSFR$ on ${V}.$ If ${A}$ is not symmetric on ${V}$, then

is called $IVTSFHDG.$

Definition 3.3. The notion $(AM)$ is used for the adjacency matrix of the

is developed as

which is a square matrix

where ${A}(\alpha_{E, u}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}(\alpha_{E, l}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}({\beta}_{E, u}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}({\beta}_{E, l}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}({\gamma}_{E, u}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}}))$, and ${A}({\gamma}_{E, l}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}}))$ represent the $IV$ truth, abstinence, and falsity membership degree between ${{\Upsilon}_{\chi}}$ and ${{\Upsilon}_{\tau}},$ respectively.

Definition 3.4. Consider an

The adjacency matrix based on the spectrum of an $IVTSFHG {A}(\digamma)$ is developed as $({\chi}, {H}, {Q}),$ given ${\chi}, {H}, {Q}$ are eigenvalues' set of ${A}(\alpha_{A}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}({\beta}_{A}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})), {A}({\gamma}_{A}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})),$ respectively.

Definition 3.5. The energy of an

is developed by:

where ${\phi}_{\chi}\in {\chi}, {\upsilon}\in {H}, {\psi}\in {Q}$.

Theorem 3.1. Suppose

is an $IVTSFHG$ with adjacency matrix $A(\digamma).$ Consider ${\phi}_{1}, {\phi}_{2}, {\phi}_{3}, \dots, {\phi}_{\aleph}$ are the eigenvalues of ${A}(\alpha_{A}({\Upsilon}_{\chi}{\Upsilon}_{\tau}))$ having the condition

are the eigenvalues of ${A}({\beta}_{A}({\Upsilon}_{\chi}{\Upsilon}_{\tau}))$ having the condition

and ${\psi}_{1}, {\psi}_{2}, {\psi}_{3}, \dots, {\psi}_{\aleph}$ are the eigenvalues of ${A}({\gamma}_{A}({\Upsilon}_{\chi}{\Upsilon}_{\tau}))$ having the condition

then

$(i)\sum^{\aleph}_{{\chi} = 1}\bigg[{\phi}_{\chi, u}, {\phi}_{\chi, l}\bigg] = [0, 0], \ \ \ \sum^{\aleph}_{{\chi} = 1}\bigg[{\upsilon}_{\chi, u}, {\upsilon}_{\chi, l}\bigg] = [0, 0], \ \ \ \sum^{\aleph}_{{\chi} = 1}\bigg[{\psi}_{\chi, u}, {\psi}_{\chi, l}\bigg] = [0, 0];$

$(ii)\sum^{\aleph}_{{\chi} = 1}\bigg[{\phi}^{2}_{{\chi}, {u}}, {\phi}^{2}_{{\chi}, {\zeta}}\bigg] = 2\sum_{1\le {\chi} < {\tau}\le m} \bigg[\alpha_{{A}, {u}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}}), \alpha_{{A}, {\zeta}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})\bigg],$

$\quad \sum^{\aleph}_{{\chi} = 1}\bigg[{\upsilon}^{u}_{{\chi}, {u}}, {\upsilon}^{u}_{{\chi}, {\zeta}}\bigg] = 2\sum_{1\le {\chi} < {\tau}\le m} \bigg[{\beta}_{{A}, {u}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}}), {\beta}_{{A}, {\zeta}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})\bigg],$

$\quad \sum^{\aleph}_{{\chi} = 1}\bigg[{\psi}^{2}_{{\chi}, {u}}, {\psi}^{2}_{{\chi}, {\zeta}}\bigg] = 2\sum_{1\le {\chi} < {\tau}\le m} \bigg[{\gamma}_{{A}, {u}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}}), {\gamma}_{{A}, {\zeta}}^{2}({{\Upsilon}_{\chi}}{{\Upsilon}_{\tau}})\bigg];$

where ${\phi}_{{\chi}, {u}}, {\phi}_{{\chi}, {\zeta}} \in {\chi}, {\upsilon}_{{\chi}, {u}}, {\upsilon}_{{\chi}, {\zeta}} \in {H}$ and ${\psi}_{{\chi}, {u}}, {\psi}_{{\chi}, {\zeta}} \in {Q}$.

Proof. $(i)$ It is obvious that the trace of a matrix is the same as the sum of eigenvalues of that matrix, and in the case of simple a graph, diagonal entries of a matrix are always $0.$

$(ii)$ Through the use of the trace properties in the matrix, we've obtained

Hence,

Likewise, we can show that

□

Definition 3.6. A graph in which a new vertex ${\Upsilon}^{\prime}$ is added to each vertex ${\Upsilon},$ such that ${\Upsilon}^{\prime}$ is connected to every vertex that is connected to ${\Upsilon}$ in $\digamma$ with the same truth, abstinence, and falsity membership degree is known as the splitting $IVTSFHG$ ${S}(\digamma)$ of an $IVTSFHG.$

Theorem 3.2. Let ${S}(\digamma)$ be a splitting $IVTSFHG$ of an $IVTSFHG \digamma.$ Then

Consider an $IVTSFHG$ having the vertex sets ${{\Upsilon}_{1}, {\Upsilon}_{2}, \dots, {\Upsilon}_{\aleph}}.$ The ${AM}$ of $\digamma$ is a:

and

Proof. Suppose new vertexs ${\Upsilon}^{\prime}_{1}, {\Upsilon}^{\prime}_{2}, \dots, {\Upsilon}^{\prime}_{{N}}$ corresponding to the vertex ${\Upsilon}_{1}, {\Upsilon}_{2}, \dots, {\Upsilon}_{{N}}$ are built in $\digamma$ to obtain ${S}[{\alpha}_{{{A}, {u}}}({\Upsilon}_{\chi}{\Upsilon}_{\tau}), {\alpha}_{{{A}, {\zeta}}}({\Upsilon}_{\chi}{\Upsilon}_{\tau})](\digamma)$ is in a manner that

along the crisp values of

The notion's ${A}[{\alpha}_{{{A}, {u}}}({\Upsilon}_{\chi}{\Upsilon}_{\tau}), {\alpha}_{{{A}, {\zeta}}}({\Upsilon}_{\chi}{\Upsilon}_{\tau})](\digamma)$ block matrix is shown following:

where

That is,

The eigenvalues of $\left[ \begin{array}{cc} 1 & 1 \\ 1 & 0 \end{array} \right]$ and $[{A}({\alpha}_{{A}, {u}}({\Upsilon}_{\chi}{\Upsilon}_{\tau})), {A}({\alpha}_{{A}, {u}}({\Upsilon}_{\chi}{\Upsilon}_{\tau}))](S(G))$ are $\frac{1\pm \sqrt5}{2}$ and ${\phi}_{\chi},$ where ${\chi} = 1$ where ${\chi}$ is from 1 to $m.$ This implies that

Similarly, we can show that

and

By this, we obtain

□

Definition 3.7. A connected $IVTSFHG$ is said to be a shadow $IVTSFHG$ of ${S}h\left(\digamma\right)$ If it can be shown by making duplicates of $G,$ it is referred to as $G^{\prime}$ and $G^{\prime\prime}.$ Link every Upsilon prime node in $G^{\prime}$ to the nearby residents of the associated $\Upsilon^{\prime}$ node in $G^{\prime}$ using the identical truth, abstinence, and negative degree.

Theorem 3.3. Let ${S}h\left(\digamma\right)$ be a shadow $IVTSFHG$ of an $IVTSFHG\digamma.$ Then

Consider an $IVTSFHG$ having the vertex sets ${{\Upsilon}_{1}, {\Upsilon}_{2}, \dots, {\Upsilon}_{\aleph}}.$ The AM of the graph is a

where,

Proof. Suppose new vertexs ${\Upsilon}^\prime_{1}, {\Upsilon}^\prime_{2}, \dots, {\Upsilon}^\prime_{n}$ corresponding to the vertex ${\Upsilon}_{1}, {\Upsilon}_{2}, \dots, {\Upsilon}_{n}$ are built in $\digamma$ to obtain ${S}h[\left({\alpha}_{ {E, u}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\alpha}_{ {E, l}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)]\left(\digamma\right)$ in such a way that

where

The block matrix of ${A}[\left({\alpha}_{ {E, u}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\alpha}_{ {E, l}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)]\left({S}h\left(\digamma\right)\right)$ is given below:

where

That is,

The eigenvalues of $\left[ \begin{array}{cc} 1 & 1 \\ 1 & 1 \end{array} \right]$ and ${A}[\left({\alpha}_{ {{E, u}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\alpha}_{ {{E, l}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)]\left(\digamma\right)$ are $0, 2$ and ${\phi}_{\chi},$ where ${\chi}$ is from 1 to $m,$ respectively. For that reason,

Similarly, we can also express that

and

The outcome is

□

Definition 3.8. Consider a $TSFHDG,$

The spectrum of the adjacency matrix of a $TSFHDG\ {A}\left(\overrightarrow\digamma\right)$ is explained as $\left({\chi}, {H}, {Q}\right),$ where $P, \ H$ and $Q$ are the eigenvalues of ${A}\left({\alpha}_{\overrightarrow{A}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), {A}\left({\beta}_{\overrightarrow{A}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)$ and ${A}\left({\gamma}_{\overrightarrow{A}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)$, respectively.

Definition 3.9. Consider an $IVTSFHDG,$

The spectrum of the adjacency matrix of an $IVTSFHDG\ {A}\left(\overrightarrow\digamma\right)$ is explained as $\left({\chi}, {H}, {Q}\right),$ where ${\chi}, \ {H}$, and ${Q}$ are the set of eigenvalues of ${A}\left[\left({\alpha}_{\overrightarrow{E, u}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\alpha}_{\overrightarrow{E, l}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)\right], {A}\left[\left({\beta}_{\overrightarrow{E, u}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\beta}_{\overrightarrow{E, l}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)\right]$ and ${A}\left[\left({\gamma}_{\overrightarrow{E, u}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\gamma}_{\overrightarrow{E, l}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)\right],$ respectively.

Definition 3.10. The energy of a $TSFHDG,$

on ${\aleph}$ vertices is formulated as:

where ${t}_{\chi}\in {\chi}, \ {u}_{\chi} \in\ {H}$, and ${v}_{\chi}\in {Q}.$ Record that ${R}e\left({t}_{\chi}\right),$ ${R}e\left({u}_{\chi}\right)$, and ${R}e\left({v}_{\chi}\right)$ denotes the real value of the eigenvalues of ${t}_{\chi},$ ${u}_{\chi}$, and ${v}_{\chi}.$

Definition 3.11. The energy of an $IVTSFHDG,$

on ${\aleph}$ vertices is formulated as:

where ${t}_{\chi, u}, {t}_{\chi, l}\in {\chi}, \ {u}_{\chi, u}, {u}_{\chi, l} \in\ {H}$ and ${v}_{\chi, u}, {v}_{\chi, l}\in {Q}.$ Record that ${R}e\left([{t}_{\chi, u}, {t}_{\chi, l}]\right),$ ${R}e\left([{u}_{\chi, u}, {u}_{\chi, l}]\right)$ and ${R}e\left([{v}_{\chi, u}, {v}_{\chi, l}]\right)$ denotes the real value of the eigenvalues of ${t}_{\chi, u}, {t}_{\chi, l},$ ${u}_{\chi, u}, {u}_{\chi, l}, {v}_{\chi, u}$ and ${v}_{\chi, l}.$

4.   Randić energy of $IVTSFG$

The characteristics and Randić energy of $IVTSFG$ are discussed in this section.

Definition 4.1. Let an

on ${\aleph}$ vertices. An ${\aleph}\times {\aleph}$ matrix

of $\digamma$ is defined as a Randić matrix with these condition:

Definition 4.2. Consider an $IVTSFHG,$

The spectrum of Randić matrix of an $IVTSFHG\ {R}\left(\digamma\right)$ is formulated as $\left({\chi}_{{R}}, {H}_{{R}}, {Q}_{{R}}\right),$ where ${\chi}_{{R}},$ ${H}_{{R}}$, and ${Q}_{{R}}$ are the set of eigenvalues of ${R}[\left({\alpha}_{ {{E, u}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\alpha}_{ {{E, l}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)], \ {R}[\left({\beta}_{ {{E, u}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\beta}_{ {{E, l}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)]$, and ${R}[\left({\gamma}_{ {{E, u}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right), \left({\gamma}_{ {{E, l}}}\left({\Upsilon}_{\chi}{\Upsilon}_{\tau}\right)\right)],$ respectively.

Definition 4.3. The Randić energy of an $IVTSFHG,$

is formulated as:

where ${\phi}_{\chi, u}, {\phi}_{\chi, l} \in {\chi}, \ {\upsilon}_{\chi, u}, {\upsilon}_{\chi, l} \in {H}$ and ${\psi}_{\chi, u}, {\psi}_{\chi, l} \in {Q}.$

Lemma 4.1. Let on $m$ vertices an $IVTSFHG,$

and

be its Randić matrix. Then,

(1) ${\rm Tr}\left({\rm R}\left(\digamma\right)\right) = [0, 0];$

(2) ${\rm Tr}\left({\rm R}^2\left(\digamma\right)\right) = 2 \sum_{ \chi\sim \tau}\left[\frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\chi,\rm u}}\right) {\rm D}_{ \digamma}\left({{\Upsilon}_{\tau, \rm u}}\right)}, \frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\chi, \rm l}}\right) {\rm D}_{ \digamma}\left({{\Upsilon}_{\tau, \rm l}}\right)}\right];$

(3) ${\rm Tr}\left({\rm R}^3\left(\digamma\right)\right) = 2 \sum_{{\chi}\sim {\tau}}\left[\frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\chi, \rm u}}\right) {\rm D}_{ \digamma}\left({{\Upsilon}_{\tau, \rm u}}\right)}\left(\sum_{\text{s}\sim \chi, \text{s}\sim \tau} \frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\text{s}, \rm u}}\right)}\right), \frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\chi, \rm l}}\right) {\rm D}_{ \digamma}\left({{\Upsilon}_{\tau, \rm l}}\right)}\left(\sum_{\text{s}\sim \chi, \text{s}\sim \tau} \frac{1}{{\rm D}_{ \digamma}\left({{\Upsilon}_{\text{s}, \rm l}}\right)}\right)\right];$

(4)

Proof. (1) Due to the fact that ${R}\left(\digamma\right)$'s orthogonal elements add to 0. So,

(2) Furthermore, we establish the ${\rm Tr}\left({\rm R}^2\left(\digamma\right)\right)$ when

when

Additionally, it is useful to state that

Consequently,

(3) For ${R}^3 \left[\left({\alpha}_{\left({\Upsilon}_{\chi, u}{\Upsilon}_{\chi, u}\right)}\right), \left({\alpha}_{\left({\Upsilon}_{\chi, l}{\Upsilon}_{\chi, l}\right)}\right)\right]\left(\digamma\right),$ we have

so,

Additionally, it is useful to state that

and

Hence,

(4) We must locate

Likewise, it is easy to express that

and

The outcome is,

□

Theorem 4.1. Let on $m$ order an $IVTSFHG,$

Then

Additionally, the equality is valid if and only if the graph $G$ is an $IVTSFHG$ with a dsingle degree node and end vertices.

Proof. Let an $IVTSFHG,$

on $m$ vertices. The number's range of variation $|{\phi}_{\chi}|,$ where ${\chi}$ is from 1 to $m,$ is defined as

Further,

Now,

Likewise,

Consequently,

More, if a $IVTSFHG,$

having a single degree node, then ${\phi}_{\chi} = 0$ for all ${\chi}$ is from 1 to $m,$ and thus

so

is an $IVTSFHG$ having no link consequently

If $IVTSFHG$ is $\digamma$ possesses a single degree and a single terminal vertex, then

so the variance of

${\chi}$ is from 1 to $m.$

Therefore,

□

Theorem 4.2. Let an

possessing at least one edge and being on $m$ vertex. Then

Proof. Using the Holder inequality

Here the above inequality holds for any real number $\left[g_{\chi, u}h_{\chi, u}, g_{\chi, l}h_{\chi, l}\right],$ where ${\chi}$ is from 1 to $m.$ Picking

${i} = \frac{3}{2}$ and $j = 3,$ thus, we obtain

All ${\phi}_{\chi}^, s\neq0,$ if there is at least one edge in $G.$ So

along with

and

Likewise,

Consequently,

□

Theorem 4.3. Let

be an $IVTSFHG$ on ${\aleph}$ vertices. Then for any graph $\digamma,$

Proof. Using the convex function specification as a guide, $h\left(a\right) = a^2,$ we will acquire,

Subsequently,

thus,

with ${i} = 2,$ we obtain

Similarly, we can simply say that

The outcome is,

□

Theorem 4.4. If

is a $TSFHG$ with order $m,$ then for any graph $\digamma,$

Proof. Every falsity-negative $[{a}_{1, u}, {a}_{1, l}], [{a}_{2, u}, {a}_{2, l}], \dots, [{a}_{m, u}, {a}_{m, l}]$ holds the inequality

Then,

Consequently,

Similarly, we can also show that

The outcome is

□

Theorem 4.5. If

is a $TSFHG$ with order $m,$ then for any graph $\digamma,$

Proof. We know that

Thus, ${AM}\geq{GM}$ we concluded,

and

Thus,

Likewise, we can also express that,

The outcome is

□

Definition 4.4. Let an $IVTSFHDG,$

on $m$ vertices. An $m\times m$ matrix

of $\overrightarrow{\digamma}$ is explained as a Randić matrix with these conditions

Definition 4.5. Consider an $IVTSFHDG,$

The spectrum of Randić matrix of an $IVTSFHG$ ${R}\left(\overrightarrow{\digamma}\right)$ is formulated as $\left(P_{{R}}, H_{{R}}, Q_{{R}}\right),$ where $P_{{R}},$ $H_{{R}}$, and $Q_{{R}}$ are eigenvalues of

and

respectively.

Definition 4.6. The Randić energy of an $IVTSFHDG,$

is formulated as:

where ${\phi}_{\chi, u}, {\phi}_{\chi, l} \in {\chi}, \ {\upsilon}_{\chi, u}, {\upsilon}_{\chi, l} \in {H}$ and ${\psi}_{\chi, u}, {\psi}_{\chi, l} \in {Q}.$

5.   $DM$ for human trafficking

To check the authenticity and applicability of we formulate an application that deals with human trafficking. We also perform a comparative study for checking its authenticity with the current approach. Begin by imagining a professional who wants to research the issue of human trafficking and assemble a committee of four decision-makers $\{{\Gamma}_{1}, {\Gamma}_{2}, {\Gamma}_{3}, {\Gamma}_{4} \}$ from different countries to select the worst country among the five countries $\{{Y}_{1}, {Y}_{2}, {Y}_{3}, {Y}_{4}, {Y}_{5} \}.$ Decision makers use the criteria of $IVTSFHG$ when comparing five countries in pairs.

Every year, millions of men, women, and children are trafficked worldwide — including right here in the United States, can happen in any community, and victims can be of any age, race, gender, or nationality. Traffickers might use the following methods to lure victims into trafficking situations:

(1) Violence;

(2) Manipulation;

(3) False promises of well-paying jobs.

Language barriers, fear of their traffickers, and/or fear of law enforcement frequently keep victims from seeking help, making human trafficking a hidden crime.

Traffickers look for people who are easy targets for a variety of reasons, including:

(1) Psychological or emotional vulnerability;

(2) Economic hardship;

(3) Lack of a social safety net;

(4) Natural disasters;

(5) Political instability.

The four administrators evaluated every pair of nations, ${Y}_{\chi}$ and $\diamondsuit_{\tau},$ where $\chi$ and $\tau$ possess the values from 1 to 6, separately and given $IVTSFV$

where $b$ is from 1 to 4 with PD $[{\alpha}_{\chi\tau, u}^b, {\alpha}_{\chi\tau, l}^b],$ prioritize ${Y}_{\chi}$ over $\diamondsuit_{\tau}.$ The AD $[{\beta}_{\chi\tau, u}^b, {\beta}_{\chi\tau, l}^b],$ where ${Y}_{\chi},$ $\diamondsuit_{\tau}$ both have the preference. The ND $[{\gamma}_{\chi\tau, u}^b, {\gamma}_{\chi\tau, l}^b],$ because $\diamondsuit_\tau$ is not given preference over $\diamondsuit_\chi.$ The suggested analytical techniques for selecting a country to rank worst are listed here.

5.1.   Algorithm

Input: A unique group of nations

is set of executives

to complete the objective and infrastructure of ${IVTSFHPR}$

for each executive.

Output: Choosing the worst countries to live in.

(1) Initially determine every $IVTSFHDG$'s energy and Randić energy. $Q_{b}$ ($b$ is from 1, to $a$).

(2) Calculate the executive weight vector for the energy and Randi's energy of $IVTSFHDGs$ by using

respectively.

(3) By applying $IVTSFA$ operator and $IVTSFGA$ operator, aggregate all $[{d}_{\chi\tau, u}^{(b)}, {d}_{\chi\tau, l}^{(b)}]$ where ${\tau}$ is from 1 to $m,$ corresponding to the industry ${Y}_{\chi}$ and obtain the T-spherical fuzzy elements $(IVTSFE),$ ${d}_{\chi}^{(b)}$ of the country ${Y}_{\chi}$ on the whole the all other countries for the executives.

(4) Compute the collective $IVTSFE$ ${d}_{\chi}$ for countries ${Y}_{\chi}$ by aggregating all ${d}_{\chi\tau}^{(b)}$ ($b$ is from 1, to $a$) using the $IVTSFWA$ operator and the $IVTSFWG$ operator.

(5) Calculate the score function $S({b}_{\chi, u}, {b}_{\chi, l})$ of ${b}_{\chi}$ where ${\chi}$ is from 1 to $m.$

(6) Rank all the countries ${Y}_{\chi}$ where ${\chi}$ is from 1 to $m.$

(7) Output the suitable country.

The $TSFPRs$

($b$ is from 1 to $4$) are shown as follows:

The energy of each $IVTSFHDG$ is formulated below:

$E({Q_1}) = ([3.890641, 3.3108107], [3.944952, 3.493447], [3.508376, 2.75356]),$

$E(Q_2) = ([3.928878, 3.431376], [3.853645, 3.1132687], [3.70876, 3.406579]),$

$E(Q_3) = ([3.183152, 2.732871], [3.789294, 3.341306], [3.852292, 3.0448514]),$

$E(Q_4) = ([3.856494, 3.358533], [4.0919205, 3.5953166], [3.661323, 3.168921]).$

The weight vector of each executive can be calculated as:

The $IVTSFHA$ operator is formulated as:

For $\diamond = 1$ the $IVTSFHA$ operator is $d_{\chi}^{(b)}:$

All the Tables 1–4 and 6–9 are the values from theorems and definitions of results section. The aggregation results are computed in Table 5.

The $TSFHWA$ operator is formulated as:

For $\diamond = 1$ the $IVTSFHWA$ operator is $d_{\chi}^{(b)}$:

The cumulative $IVTSFE$ applying $IVTSFHWA$ operator are formulated as:

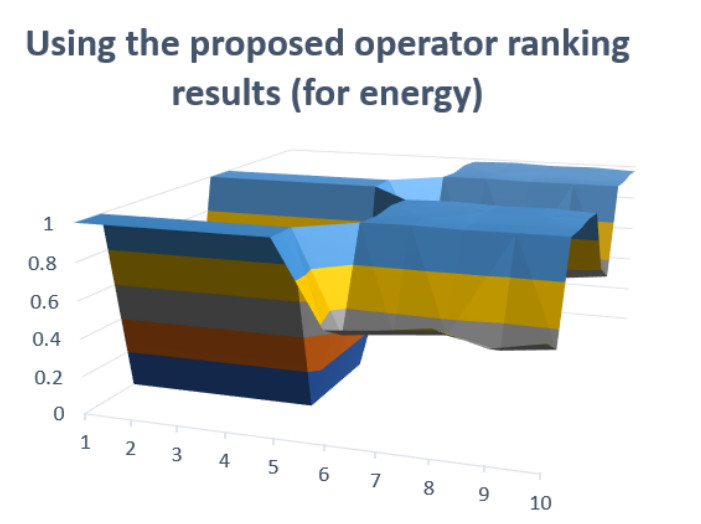
The graphical depiction shown in the Figure 1.

The score function $S\left(d_{\chi}\right)$ of $d_{\chi}$, where ${\chi}$ is from 1 to $5,$ is calculated as:

The worst country with respect to human trafficking is $\diamondsuit_{3}.$

Then, similarly, with the same procedure using the above $(IVTSFHG)$ operator, we obtain these results:

The score function $S\left(d_{\chi}\right)$ of $d_{\chi}$, where ${\chi}$ is from 1 to $5,$ is calculated as:

The worst country regarding human trafficking is $\diamondsuit_{5}.$

The $IVTSFHG$ operator is formulated as:

The Randić matrix of the $IVTSFPRs$

where ($b$ is from 1, to $4$) are shown as follows:

The Randić energy of each $IVTSFHDG$ is formulated below:

The weight vector of each executive can be calculated as:

Weight vector of four executive $x_{b}$ where ($b$ is from 1, to $4$) is:

The $IVTSFHA$ operator is formulated as:

The aggregation result is computed in Table 10.

The cumulative $IVTSFE$ applying $IVTSFHWA$ operator is formulated as:

The score function $S\left(d_{\chi}\right)$ of $d_{\chi}$, where $\chi$ is from 1 to 6, si calculated as:

Then,

The worst country is$\diamondsuit_{2}.$ The $IVTSFHG$ operator is formulated as:

Then, similarly, with the same procedure using the above $(IVTSFHG)$ operator, we obtain these results:

The score function $S\left(d_{\chi}\right)$ of $d_{\chi}$, where $\chi$ is from 1 to 6, is calculated as:

so this implies $\diamondsuit_{3}$ is the worst country among all.

5.2.   Comparitive study

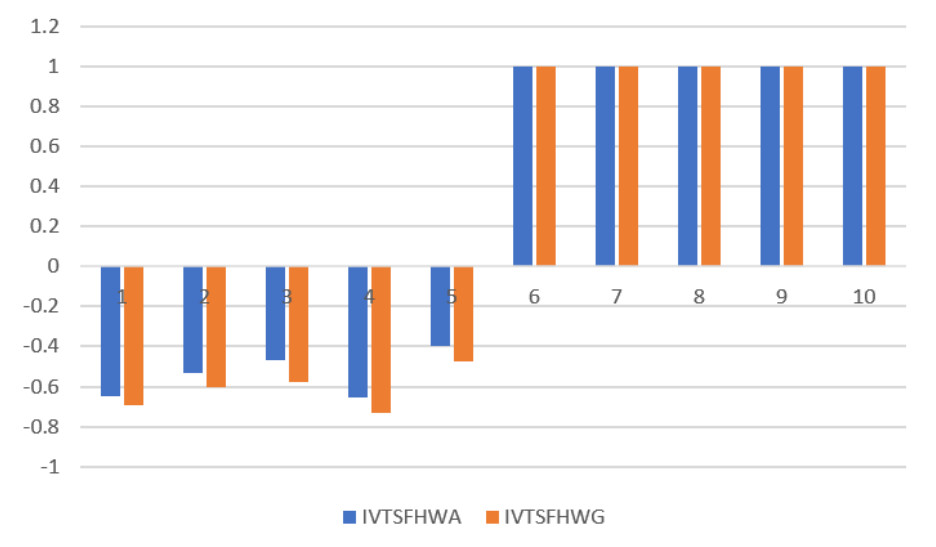
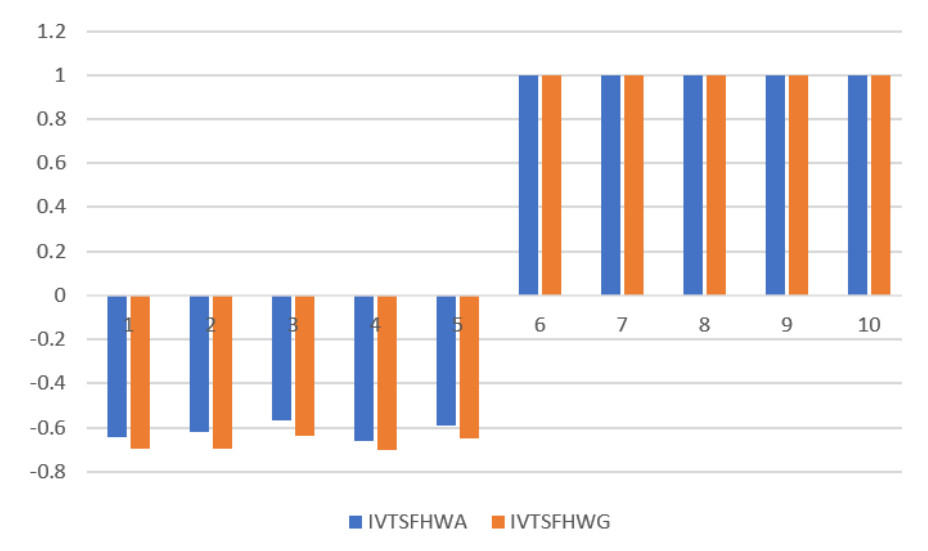
This subsection presents the results of the previous numerical example using specifically established operators. The $IVTSF$ Dombi weighted arithmetic $(IVTSFDWA)$ and $IVTSF$ Dombi weighted geometry $(IVTSFDWG)$ operators are utilized to compare the outputs of the currently employed model. The rankings generated by these operators are summarized in Tables 11 and 12. Table 11 confirms that our proposed method aligns with the rankings obtained from the $IVTSFDWA$ of energy, thus validating our approach's effectiveness. However, the results in Table 12 do not align with our approach. This discrepancy results from Randic's energy and the energy of $IVTSFHG$ being calculated using various aggregation techniques or slightly changing the value produced by the scoring function.

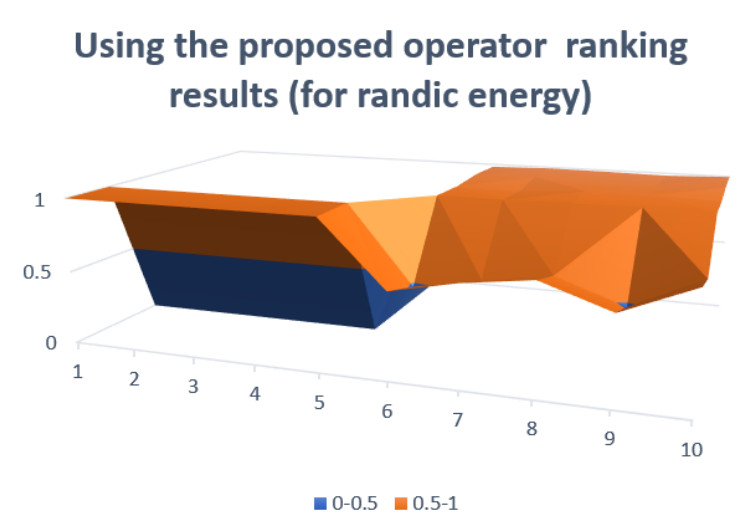
Figures 2–4 show graphical representations to contrast the suggested technique with the current approach. To generalize algebraic operations, it is essential to use the $TN$s and $TCN$s developed by Hamacher and Einstein. The Hamacher operator can be either an algebraic $TN$ or $TCN$ depending on the value of parameter 1, and it can be either an Einstein's $TN$ or $TCN$ depending on the value of parameter 2.

5.3.   Comparative experiments with existing methods

The Hamacher parameter $\mu$ plays a crucial role in the aggregation process. We propose analyzing its impact through:

Table 13 shows how varying $\mu$ affects the decision outcomes:

The analysis reveals that while absolute scores vary with $\mu,$ the relative ranking remains stable, demonstrating the robustness of our method.

Comparative analysis. We compare $IVTSFHG$ with $IVIFS$ and IVPFS approaches using the same dataset shown in the Table 14:

5.4.   Discussion

Interval-valued T-spherical $(IVT-spherical)$ serves as an enhanced version of the spherical fuzzy set $(SFS)$ model, which provides greater flexibility in handling spaces with larger values. When considering truth order $({\alpha}),$ abstinence order $({\beta}),$ and negative order $({\gamma}),$ the constraint ${\alpha, u}^{ {T}} + {\beta, u}^{ {T}} + {\gamma, u}^{ {T}}\leq 1\ (T\geq 1)$ in the $TSFS$ model facilitates more precise value definitions. In the $PFS$ model, the energy and Randić energy cannot be computed using the $HWA$ and $HWG$ operators, resulting in an inability to rank the outcomes. This occurs when the sum of $PD,$ $AD,$ and $ND$ exceeds 1. Tables 11 and 12 display the rankings of energy and Randić energy achieved through the $PFS,$ $SFS,$ and $TSF$ models. Due to the sum of squares of $PD,$ $AD,$ and $ND$ being greater than 1, analysis using the $PFS$ model is impractical. Nevertheless, the calculation is feasible when $T = 3.$ Specifically, $TSFS$ is $PFV$ for $T = 1$ and $SFV$ for $T = 2.$ As $T$ increases, so does the space and its corresponding value. For instance, $(0.9, 0.4, 0.5)$ represents a $3-SFV.$ In the case of

but

and

Consequently, the $PFS$ and $SFS$ models lack the capability to handle this data adequately. Hence, $(0.9) + (0.4) + (0.5)$ is neither $SFV$ nor $PFV.$ Thus, all $PFV$s are $SFV$s and $TSFS.$ However, the $PFS$ and $SFS$ classes do not fall under the $TSF$ category. The assessment of the energy and Randić energy in $TSFHDG$ designates Y3 as the least favorable country.

6.   Conclusions

In order to enhance the efficacy of our methodology, we incorporated investigations on data mining, encompassing topics such as human trafficking, as well as algorithms. The $IVTSF$ Hamarcher operator was employed in the study to ascertain the energy values of both $IVTSFG$ energy and Randić energy. The arrangement of characteristics is contingent upon the Randić energy and the energy of $IVTSFHDG.$ The optimal choice is the variable $\diamondsuit,$ as it remains consistent across all circumstances. The study yields a novel way for addressing challenges encountered in the data management process, while also facilitating the establishment of new frameworks for measuring information.

The current state of the discourse about $DM$ frequently exhibits characteristics of illogicality and ambiguity. The accurate prediction of future outcomes may be hindered by the presence of insufficient knowledge. The concept of $IVFS$ offers a theoretical foundation for effectively managing the provided data. The effectiveness of $IVTSFG$ surpasses that of $IVIFS$, $IVPFS,$ $PFS,$ and $IFS$ due to its ability to address a diverse range of real-world problems based on triplets. We have introduced a novel notion, denoted as $IVTSFHG,$ by employing the Hamacher operator. This idea allows us to investigate the Randić energy as well as the energy associated with $IVTSFHG.$ In addition, the division of $IVTSFHG$ and the allocation of shadow $IVTSFHG$ energy are established. In addition, our discussion also encompassed the examination of the energy of the molecular structure denoted as $IVTSFHG,$ as well as the Randić energy associated with $IVTSFHG.$

6.1.   Future research directions

● Conduct systematic sensitivity analysis of the Hamacher parameter $\mu$ to understand its impact on decision outcomes.

● Extend the methodology to other complex decision-making problems beyond human trafficking assessment.

● Develop hybrid models combining $IVTSFHG$ with machine learning techniques for enhanced predictive capabilities.

● Investigate the scalability of the approach for high-dimensional decision problems.

6.2.   Limitations of the existing methodologies

Limitations of the existing methodologies are summarized as follows:

(1) $q$-ROFG, $IV q$-ROFG were considered good additions in the fuzzy world, but these concepts are not sufficient to symbolize human opinion properly due to the statistics of the scenario which will have an element of hesitant degree in a variety of issues and applications. In such situations, the decision-makers are not sure to give results according to the provided data.

(2) The scenario we discussed in this article gave data in the form of all four fuzzy components, which makes it unsolvable for either an $IVIFG,$ $IVTFS$, or $IVPyFG.$

(3) Furthermore, the $q$-ROFG, $IV q$-ROFG and their operations which are currently used to solve real-world issues are not enough to deal with the information having a refusal degree as well.

(4) $SFS,$ $TSFS$ are comparatively more convenient ways to solve complex real-world problems. But $IVTSFS$ is much better than these two methods.

Author contributions

Ali Ahmad: conceptualization, methodology, investigation, writing — original draft, funding acquisition; Humera Rashid: conceptualization, methodology, software, data curation, writing — review & editing; Hamdan Alshehri: project administration, supervision, writing — review & editing, funding acquisition; Muhammad Kamran Jamil: data curation, investigation, validation, verification, writing — original draft; Haitham Assiri: formal analysis, investigation, resources, visualization, writing — original draft. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors gratefully acknowledge the funding of the Deanship of Graduate Studies and Scientific Research, Jazan University, Saudi Arabia, through project number: RG24-M039.

Conflict of interest

The authors declare that there are no conflicts of interest.