1.
Introduction
Discrete models, also known as discrete maps, serve as mathematical representations to describe how a system evolves at specific time intervals [1]. In contrast to continuous models that employ differential equations to describe a system's behavior over time continuously, discrete maps use iterative equations. The simplicity of discrete models, owing to the absence of calculus or differential equations, makes them more accessible for comprehension, implementation, and analysis [2]. Their computational efficiency allows them to need fewer computational resources than solving intricate differential equations. These discrete models have many applications in diverse scientific and engineering fields. They can be used to study population dynamics [3], such as animal population growth and infectious disease spread, as well as in economic and financial systems [4,5]. Moreover, discrete maps can be used for exploring chaotic behavior in various systems wherein simple equations can yield unpredictable and intricate trajectories [6,7].
Discrete models have offered valuable insights into the dynamic behavior of neural networks [8]. The simplicity of discrete models makes them suitable for understanding the complex interactions and dynamics of neural networks. These models facilitate investigation of various cognitive functions, sensory processing, and information propagation within the brain [1]. By discretely representing neural activity, researchers can analyze complex neural phenomena with more efficiency, leading to a deeper understanding of network behaviors. One significant application of discrete models in neuroscience is the study of synchrony and collective patterns in networks [9,10,11,12]. For example, Bashkirtseva et al. [10] studied the synchronization in the map-based Chialvo neuron model and reported a critical noise value for the synchronization of neurons. Sausedo-Solorio [11] studied the synchronization of Rulkov neurons with memory and synaptic delay. They found that anticipation or lag synchronization may emerge relying on delay time. Moreover, discrete models have been used for exploring phenomena such as neural firing patterns and synaptic plasticity [13,14,15]. For example, He et al. [14] described a new discrete neuron model based on the Huber-Braun neuron and discussed the effects of temperature-dependent ion channels on the firing patterns. Wang et al. [15] analyzed the dynamics of a discrete-time Chialvo neuron model through bifurcation diagrams and Lyapunov exponents.
The discovery of the fourth electrical component, named memristor, has led many scientists to modify the existing dynamical system or suggest new systems [16]. As a result, numerous memristive continuous or discrete time systems have been introduced with various distinctive features, such as amplitude control [17,18]. Incorporating memristor in neural models helps reproduce the neural behaviors more accurately [19]. The memristor is an electrical component connecting the charge and magnetic flux [20,21]. Therefore, it can be used for considering the effects of electromagnetic induction [22]. The variation of neurons' membrane voltage can change the distribution of the electromagnetic field around the membrane, which significantly impacts the neuron's activities. Moreover, the memristors have memory, making them suitable for modeling the synaptic strengths of biological neurons [23]. The synaptic connections play a crucial role in information processing and learning [24]. Consequently, the neural network models have been improved using the memristor [25,26].
Several researchers have explored the effect of memristors on neuron models [27]. Xu et al. [28] introduced a 3D memristor-based Wilson neuron model that could represent asymmetric coexisting electrical activities and antimonotonicity. Qiao and Gao [29] used a Filippov-type Wilson neuron model to examine the effect of temperature and magnetic induction. They presented a complete analysis on the model by applying multiple nonlinear dynamic tools. Li et al. [30] represented different coexisting periodic and chaotic attractors in the memristive Hindmarsh-Rose model. Lai et al. [31] proposed a new memristive neuron model with special chaotic properties and showed its application in image encryption. Gao et al. [32] improved a four-dimensional Filippov Hindmash-Rose with considering a memristive autapse with the threshold control strategy, which could cause the occurrence of sliding bursting, sliding limit cycle and coexisting attractors. In another study [33], they applied the analysis on a 4D Filippov hybrid neuron model and found the local stability and bifurcation conditions.
The presence of memristors in neural networks can also influence their collective behaviors. Synchronization is the most important behavior in complex networks [34,35,36]. Hence, a large number of studies have been devoted to the study of synchronization in memristive neural networks [37,38,39]. Besides, other partial synchronization patterns, such as chimera state [40,41] and cluster synchronization [42,43], have special associations with neural processes [44]. Li et al. [45] studied the synchronization of two Rulkov maps coupled with a memristor synapse and showed complete and lag synchronization behaviors. Ramakrishnan et al. [46] found different collective behaviors such as imperfect synchronization, solitary state, cluster synchronization, and chimera states in coupled memristive neuron maps. Wang et al. [47] investigated the synchronization of memristive HR maps with electrical synapses, chemical synapses, inner linking functions, and hybrid synapses. They found that coupled maps could get synchronized via electrical and mixed synapses.
In this paper, we investigate the effects of electromagnetic induction on the dynamics of a neural map model by adding the memristor to the model. The considered neural map model is a behavioral model proposed based on some physiological facts about the attention control mechanism and chaos intermittency. The model's coefficients are related to the brain synapses' weights regulated by the release of different neurotransmitters. Analyzing this model can help recognize inhibitory problems in people with Attention Deficit Disorder. Motivated by previous studies that suggest the advantages of memristors on neuron and neural models, we study this model with a memristor. We consider its dynamics under magnetic induction, which can help in studying the alternation of attention levels in different cases. To this aim, the bifurcation diagrams are plotted for different magnetic induction strengths and the dynamics is considered. The impact of the initial conditions and the coexisting dynamics is also explored. Besides the single map model, the dynamical behavior of coupled memristive neural maps is studied by applying different synapses such electrical, chemical and magnetic couplings. Various network patterns such the synchronization, cluster synchronization and chimera states are shown.
2.
Model
We consider a discrete neural model, which was introduced by Baghdadi et al. in 2015 [48]. This model is described as follows,
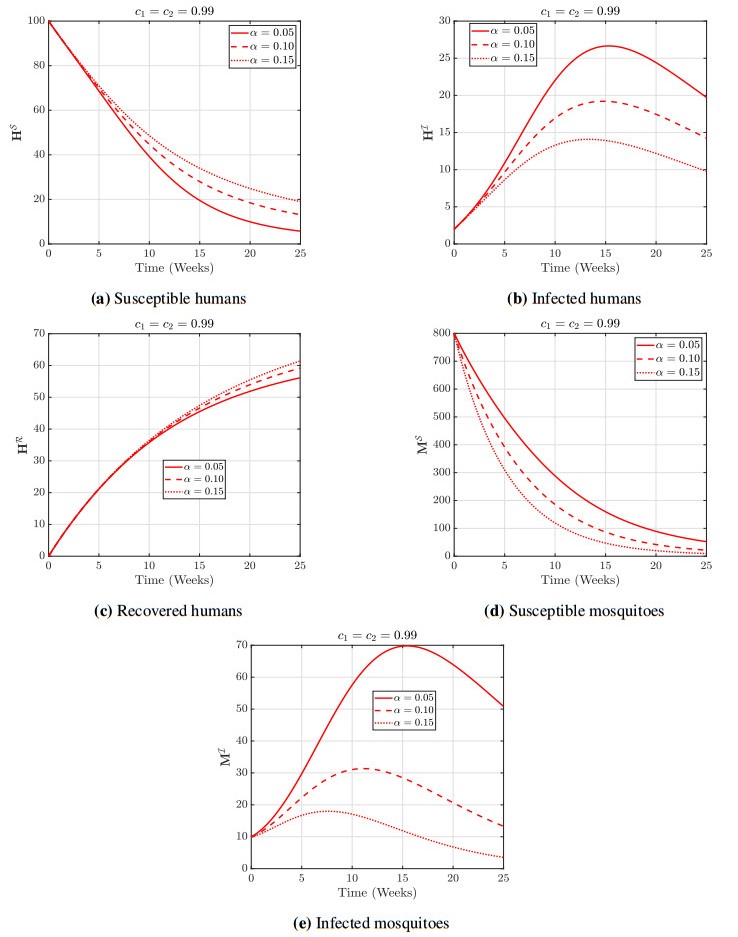
where A, B, w1, and w2 are the parameters by adjusting which the model represents a variety of dynamical behaviors. By setting B=5.821, w1=1.487, w2=0.2223, the bifurcation diagram according to A is shown in Figure 1(a). It should be noted that the system has coexisting attractors in some values of the parameter A. In this figure, the red and blue colors correspond to the negative and positive initial conditions, respectively.
A voltage-controlled memristor is generally described as,
where iM is the electromagnetic induction current, vM is the neuron's membrane potential, and W(ϕ) is the memristor memductance function. The neuron's activation function is monotonically differentiable and bounded above and below. Hence, the hyperbolic tangent function has been widely used as the neuron's activation function [49,50,51]. Therefore, W(ϕ)=tanh(ϕ).
The discrete model for the memristor can be obtained by applying the continuous discretization method to the continuous flux-controlled memristor models. A discrete memristor model was presented by [52] as,
where ϕ is the flux variable and v and i are the memristor's voltage and current. More details about this memristor and its fingerprints can be found in [52]. Since the memristor contains nonlinearity and possesses memory effects, it complies with real memristive properties and can be used for the representation of more accurate neural dynamics and synaptic plasticity processes.
Using the defined memristor, the memristive neural map model can be defined as,
where μ is the magnetic induction strength and ε=1 is set. In the following, we analyze the dynamics of the memristive map model and the collective behavior of coupled memristive maps.
3.
Dynamics of the memristive model
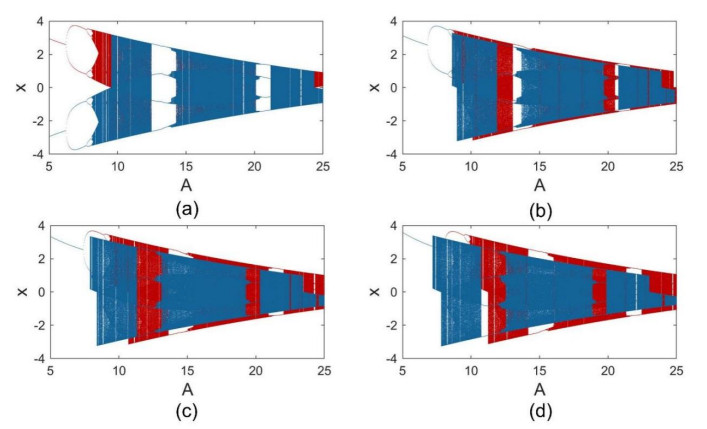
The magnetic flux effects through the memristor can considerably influence the model dynamics. The bifurcation diagrams of the memristive model for different magnetic induction strengths (μ), according to the parameter A, are shown in Figure 1(b)–(d). To obtain the bifurcation diagrams the attractor-following method [33,53] is used, where the result of each iteration serves as the initial value of the next iteration. The forward and backward continuations are shown by red and blue colors. Comparing the bifurcation diagrams in presence of memristor with the original model (Figure 1(a)) suggests that as the magnetic flux strengthens, the region of multistability is extended. The coexisting attractors of the main model exist in the range A<9.556 and A>24.35, while in the memristive version, the coexisting attractors are visible for almost all A values as A>8.63 for μ=0.1, A>7.9 for μ=0.2 and A>7.18 for μ=0.3. Therefore, existence of the memristor promote multistability property.
The presence of multiple stable states in multistability can provide different cognitive or perceptual interpretations, and studying the transitions between these states can provide valuable insights into the brain's information processing and behavior generation. An important application of multistability is in understanding perceptual phenomena, where an ambiguous sensory input can cause oscillations between different interpretations [54]. Additionally, multistability is also relevant in decision-making processes, as the coexistence of multiple stable states corresponds to alternative decisions or choices [55]. Another example is the cognitive flexibility in which the brain is able to switch rapidly between different mental states or cognitive processes [56]. The transition between several stable states helps to the brain's adaptation to varying external demands.
In the following, the dynamics of the memristive model are investigated by setting A=8. Figure 2 shows the bifurcation diagram according to μ. The blue, red, and cyan colors are related to [−1,0], [1,0], and [−5,4], respectively. It is seen that varying μ can considerably change the dynamics of the model. Moreover, the dynamics are highly dependent on the initial conditions. However, the probability of observing periodic dynamics is higher for stronger magnetic induction. The bifurcation diagram obtained by the forward continuation for two initial conditions [1,0] and [-1, 0] are shown in Figure 2(b). It is notable that the bifurcation obtained with the fixed initial condition [1,0] is the same as one obtained by its forward continuation. Figure 3 illustrates the dynamics of the original model in A=8 (Figure 3(a)) and A=9 (Figure 3(b)), and its variation under magnetic induction. In parts (a1) and (b1), the response of the original model is depicted where it is periodic in A=8 and is chaotic in A=9. In parts (a2–a4) and (b2–b4), the magnetic induction is μ=0.02, μ=0.05, and μ=0.1, respectively. It is observed that in the case of A=8, adding the memristor can increase the period of time series or induce chaos. Similarly, for A=9, the memristor can change the chaotic dynamics and lead to different periodic behaviors and also different chaotic dynamics. Therefore, the dynamics are considerably affected by the memristor; however, increasing its strength has a different impact and is dependent on the original dynamics.
Another notable point is that the basin of attraction of coexisting attractors is dependent on the strength of the magnetic induction. In order to show this, two basins of attraction corresponding to the periodic (blue) and chaotic dynamics (red) is depicted in Figure 4. In part (a), μ=0.1, and in part (b), μ=0.25 is set. In smaller induction strengths, the basins are less dependent on ϕ0. As induction strength increases, the basins change and have more relation with the initial condition of the magnetic flux variable. The coexisting dynamics of the model for A=8 and for different μ values are shown in Figure 5. In parts (a)–(c), the value of μ is set to μ=0.1, μ=0.2, and μ=0.51. The left panel refers to the initial condition [1,0], and the right to[−1,0]. For μ=0.1, a chaotic and a periodic pattern coexist, while for μ=0.2, two periodic dynamics with different patterns and periods coexist. By setting μ=0.51, the coexistence of period dynamics and a fixed point is observed.
4.
Coupled memristive neural maps
In addition to the dynamics of the neural map model, the memristor can remarkably change the collective behavior of the coupled maps. A network of non-locally coupled neural maps can be described by,
where N=100. The network is considered to be a ring of neural maps with non-local coupling where each map is connected to its P=10 nearest neighbors from right and left. ge, gc, and gm represent the coupling strength for the electrical, chemical, and magnetic coupling. The effect of each coupling type is investigated separately. Three different scenarios are considered: 1) the coupling is electrical (gc=gm=0), 2) the coupling is magnetic (ge=gc=0), 3) the coupling is chemical (ge=gm=0). At first, the complete synchronization is examined by computing the numerical error:
Besides the synchronization error, a statistical factor of synchronization (R) [57] is also computed which is based on the mean field theory, as follows:
where <·> denotes the time average. The synchronization can be detected when this synchronization factor is equal to 1.
The synchronization is investigated by varying μ and the coupling strength. The results for different coupling types are shown in Figure 6, where in the first row P=10 and in the second row P=25. The dark blue color indicates the synchronous area, and the black shows the instability. Figure 6(a1) represents the synchronization error by varying the electrical coupling strength (gm=gc=0) for different μ values. There are some small synchronization regions in smaller coupling strengths. In part (b1), the magnetic coupling (ge=gc=0) is examined. This figure has a synchronous area referring to very small μ values. In contrast to the two mentioned couplings, chemical coupling (ge=gm=0)) results in a larger synchronization area (Figure 6(c1)). Consequently, it can be concluded that synchronization is achievable in wider regions of parameters through chemical coupling. Comparing the first and the second rows shows that changing the network structure has a small impact on the results. By increasing P, the synchronization is still reached in a small area via electrical coupling (Figure 6(a2)). Moreover, the instability occurs in smaller couplings. In the case of magnetic coupling (Figure 6(b2)), increasing P has a small effect and the synchronization happens only in small μ values, and instability occurs in smaller couplings. For chemical coupling (Figure 6(c2)), the synchronization area is significantly larger than other couplings. Parts (d)–(f) of Figure 6 shows the synchronization factor R in red, computed for three coupling types and for μ=0.5. The synchronization error is also shown in blue color. It is seen that for electrical coupling, synchronization happens in a small region in 0.004<ge<0.0095. In contrast, for chemical coupling R factor equals 1 in 0.0005<gc<0.0045 and 0.021<gc<0.05 representing synchronization in larger area. In magnetic coupling, some coupling strength (gm) results in R=1, however the synchronization error is not zero. The reason is that in these coupling strength values, the systems are attracted by two fixed points. Hence, R=1 do not represent complete synchronization.
In the next step, we search for the collective behaviors in coupled maps before reaching complete synchrony. The initial conditions for the x state variables of all systems are set to x(0)=−1, while the initials of the ϕ are randomly chosen from [01]. In Figure 7, the map models are coupled with electrical coupling. In Figure 7(a), a chimera pattern is shown for μ=0.4 and ge=0.007. In this pattern, most systems are located in two clusters, and a few are not synchronous with the clusters. Figure 7(b) shows that while the synchronous clusters have periodic dynamics, the asynchronous systems are chaotic. For a bit stronger coupling, the asynchronous systems disappear and two clusters are formed. A two-cluster state is shown in Figure 7(c). The periodic time series of the clusters are shown in Figure 7(d).
Figure 8 shows two cluster synchronization states when the systems are coupled with magnetic coupling. In part (a), the systems form four different clusters for μ=0.1 and gm=0.03; the time series are shown in part (b). By raising the coupling strength, four clusters are converted to two clusters. Figure 8(c) shows the pattern for gm=0.08 with the corresponding time series of the clusters shown in part (d). Figure 9 represents the network's magnetic coupling pattern for other μ values (μ=0.5). In this case, for low magnetic inductions, the systems are attracted by the fixed points, and oscillation death happens. Therefore, the pattern can be called chimera death (Figure 9(a)). The systems are returned to chaotic oscillating for larger induction strengths. Figure 9(c) shows an example of asynchronous chaotic oscillation for gm=0.07. The time series of the chaotic firing is shown in Figure 9(d).
Finally, the patterns obtained with chemical coupling are shown in Figure 10. In Figure 10, μ is set to 0.1. In this case, for very small chemical coupling, synchronous clusters are organized (Figure 10(a), (b)). By slightly increasing the coupling, the systems are all synchronous, as shown in Figure 10(c) for gc=0.005, and have periodic behavior (Figure 10(d)). For stronger couplings, some of the systems are oscillating periodically, and some of them are attracted to a fixed point. An example of this state is shown in Figure 11(a), (b) forgc=0.04. Finally, by increasing the coupling, the systems are again synchronous and oscillate periodically. Other than the synchronous and cluster synchronous states, the chemically coupled systems can represent the chimera state. Figure 11(c) shows a chimera state for μ=0.4 and gc=0.03. It can be observed that there are synchronous and asynchronous groups. The time series corresponding to the synchronous and asynchronous groups are shown in Figure 11(d).
5.
Conclusions
This paper presented a modified memristive neural map model using a hyperbolic memductance function. By introducing the memristor to a neuron model, the magnetic induction effects can be considered, which remarkably affect the model's behavior. Hence, in this paper, the dynamics of the neural model were investigated according to the magnetic induction strength. It was shown that varying the magnetic induction strength changes the dynamics, so its increment leads to the extension of multistable regions. The memristive model showed multistability in some parameter values where the original model was not multistable. Different regions' basins also varied as the magnetic induction was strengthened. The collective dynamics of the coupled memristive maps were also examined under electrical, chemical, and magnetic coupling. The behavior of the network was also under consideration in the asynchronized areas. The chimera state and the cluster synchronization state were observed for the electrical coupling and the chemical coupling. In contrast, cluster synchronization and chimera death states emerged for magnetic coupling. Finally, it was demonstrated that chemical coupling leads to a larger synchronization region. However, the considered chemical synapse contained a simplification of ignoring the time delay. We will consider the time delay and investigate its effects in our future work. Moreover, we assumed the network free of noise, which can affect the neural activities remarkably. For example, it can lead to occurrence of phenomena like coherence resonance [58,59]. In coherence resonance phenomenon, a specific noise intensity can lead to a maximized regularity in the network. In the future works, we will consider the proposed memristive model under noisy disturbance and study its impacts.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is partially funded by Centre for Nonlinear Systems, Chennai Institute of Technology, India vide funding number CIT/CNS/2023/RP/009, the Natural Science Foundation of China (No. 61901530, 62071496), the Natural Science Foundation of Hunan Province (No.2020JJ5767).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: