1. Introduction
Attributed to the strong sp2 C-C bonds, graphene possesses superior mechanical properties such as high elastic modulus (1TPa) and fracture strength (125GPa) [1,2], and is considered taking advantages over carbon nanotube in terms of enhancing materials as reinforcements in composites because of its two-dimensional morphology that favors load transfer and preventing atomic diffusion at elevated temperatures. Consequently, extensive investigations (e.g., [3,4,5,6,7]) have been performed on the use of graphene to strengthen polymers, ceramics and metals. Inclusion of graphene into composites is either through in-situ synthesis [8] or via adding graphene nanoflakes or graphene oxides (GO) [9,10,11,12,13]. Comparatively, GNFs, which is composed of multiple layers of graphene and has similar properties as single-layered one, is more suitable than in-situ synthesis for producing bulk composites and outperforms GO which induces considerable structural defects [14].
Aluminum (Al) matrix composites are lightweight materials that have great potential for applications in automobile, aeronautical and aerospace industries [15,16]. With successful applications of GNFs to strengthen polymers and ceramics [17,18], there have been investigations on the incorporation of GNFs to improve the properties of aluminum, although the challenge is evident due to the significant differences in density between GNFs and aluminum as well as the high processing temperatures. While density differences give rise to difficulties for distributing GNFs relatively uniform in Al matrix, potentially leading to poorly-dispersed GNFs acting as defect sites, the high processing temperature causes unfavorable chemical reactions such as the transformation of GNFs to carbides that would undermine the role of GNFs as reinforcements [19]. The recent processing technologies, though exhibiting differences in specific routes, tend to employ powder metallurgy to fabricate Al-GNFs composites [19,6,20,21], and this has led to significant improvements in composite yield strength. However, existing investigations generally examined quasi-static properties of composites manufactured, and the dynamic behavior, which is critically important for practical applications, was usually overlooked. As dynamic loading introduces transient stress wave and noticeable temperature rise that potentially trigger deformation and fracture mechanisms [22,23,24] distinct from those associate with static loading, a study of material dynamic behavior is necessary to assess the capability of materials to fulfil a variety of demand under various rates of load and the effectiveness of material processing technology.
The present work investigated the behavior of GNFs-reinforced Al composites under various strain rates and attempted to elucidate the mechanisms regarding the effects of strain rate and GNFs on deformation behavior of the composites. The knowledge acquired from the present work lays foundation for design of Al-GNFs composites aiming to sustain load of various rates in complex serving environment.
2. Experimental
2.1. Composite Synthesis
The components of composites include Al matrix with 1.5wt.%Mg and 3.9wt.%Cu, silicon carbide and GNFs. Al alloy powders were prepared by means of close coupled gas atomization in the atmosphere of nitrogen and the diameter of Al alloy powder obtained was less than 50 µm. GNFs were converted from graphene oxides of a few atomic layers by hydrazine hydrate, and the size of SiC is around 5µm. The weight percentages of GNFs and SiC within composites were respectively 1% and 10%. Synthesis of composites takes four main steps: firstly, powders of all components were mixed and ball milled; secondly, the mixture was processed by hot isostatic pressing, producing consolidated rod; thirdly, hot extrusion was applied to the rod; finally, the extruded rod was solution treated, followed by water quenching. Detailed processing parameters regarding the four steps can be found in Ref. [20].
2.2. Stress-strain Behavior
Stress-strain behavior of the composites were examined at various strain rates, and for each strain rate, three specimens were used. Quasi-static behavior of the composites was tested using Instron Universal Testing machine, according to ASTM standard E9-89a. Specimens were 5 mm in diameter and 4 mm in thickness. The planar surfaces of specimens were polished and molybdenum disulphide grease was applied to reduce the friction between contact surfaces of specimens and the machine.
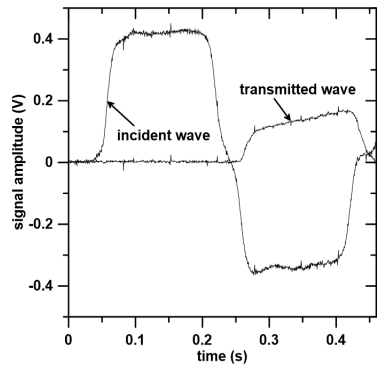
Dynamic stress-strain behavior was determined via split Hopkinson Pressure Bar (SHPB) system, of which the striker, incident and transmission bars were made of steel and 13mm in diameter. During each test, the specimen, with the same size as quasi-static sample, was sandwiched between incident and transmission bars, and then strikers were propelled by pressurized nitrogen to induce deformation to specimens. Strain gauges were mounted respectively to incident and transmission bars to measure the corresponding amount of strain, denoted by εi and εt. Figure 1 is an example of the signals recorded for stress waves along incident and transmission bars, and the engineering strain rate (${{\dot \varepsilon }_S}$), strain (εS) and stress (σS) for specimens were calculated by Eq 1 [25].
|
$
˙εS=2c0LS(εi−εt),εS=2c0LSt∫0(εi−εt)dt,σS=AEεtAS.
$
|
(1)
|
where c0, A and E represent the stress wave velocity, cross-sectional area and Young's modulus regarding the incident bar; AS and LS stand for the cross-sectional area and initial thickness of the specimen; t denotes elapse of time during an impact event.
In order to achieve a variety of strain rates for specimens, the length and initial velocity of strikers were adjusted, and true strain (εSt) and true stress (sSt) for specimens were determined by Eq 2.
|
$
εtS=ln(1+εS),σtS=(1+εS)σS
$
|
(2)
|
2.3. Micro-hardness Tests
The Vickers micro-hardness of deformed samples was measured using a Matsuzawa MXT50 micro-hardness tester. An indentation load of 50 gf was applied and maintained for 15 seconds. Care was taken to ensure that the diagonal length of each indentation was no larger than 1/5 the sample size, and that all indentations were sufficiently far from each other, as well as from the sample edges.
2.4. Microstructure Characterization
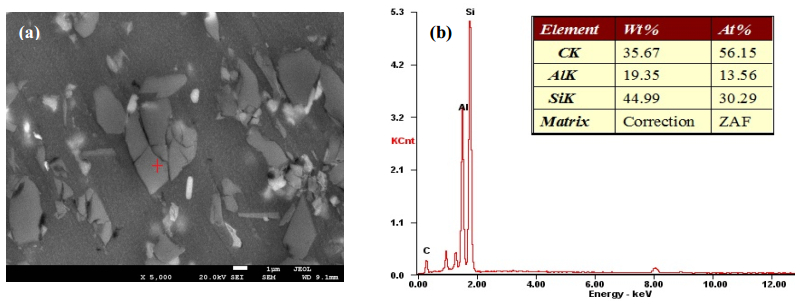
A JEOL scanning electron microscopy (SEM) equipped with an energy-dispersive X-ray spectroscopy (EDX) was employed to examine the microstructure of specimens, which were polished before subjected to microstructure characterization.
3. Results and discussion
GNFs-reinforced Al Composites versus Unreinforced Al.
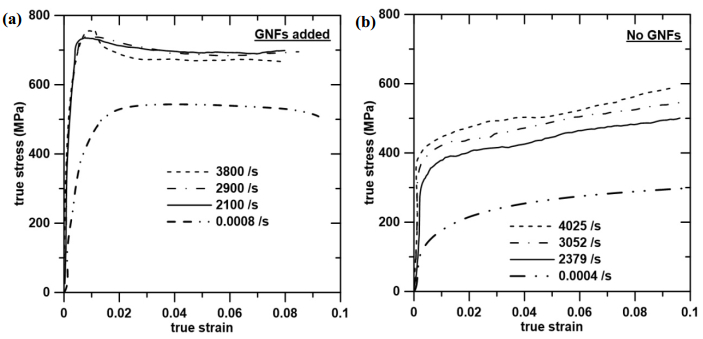
Figure 2a shows the stress-strain responses of GNFs-reinforced composites under various strain rates. It is observed that dynamic strength of the composites is significantly higher than the static strength. With an increase in strain rate, composite yield strength tends to increase, but this trend is insignificant for dynamic loading. A noticeable feature is the decrease in stress after reaching the maxima, indicating a weakened strain hardening rates as compared with conventional metallic materials such as copper [22]. As a reference, Figure 2b displays the stress-strain behavior of unreinforced alloys. Similar to the composites, unreinforced alloys exhibit a rise in flow stress with strain rate, but seems to be more sensitive to the change in strain rate, particularly for dynamic loading. Moreover, strain hardening is obviously demonstrated at all strain rates by unreinforced alloy, although the strength is considerably lower than the composite counterpart. It is thus concluded that the incorporation of GNFs can effectively strength aluminum, but meanwhile leads to weakened strain hardening and declined sensitivity to strain rate at high strain rates.
3.1. Yield Strength
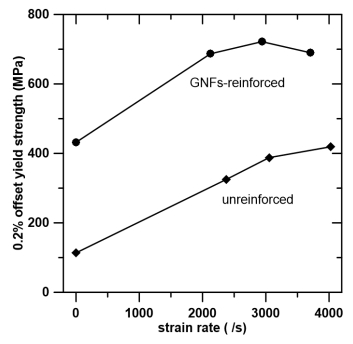
The strengthening effects of GNFs is manifested by Figure 3, which shows that an addition of GNFs leads to an increase in 0.2% offset yield strength (denoted by σY), by around 300 MPa, regardless of the magnitude of strain rates (${\dot \varepsilon }$). According to the earlier study [26], 10 wt.% of SiC caused an increase in Al yield strength by only about 100 MPa. Hence, 100–200 MPa enhancement of the present composite strength was connected with the addition of GNFs. Although the yield strength for GNFs-reinforced composites shows a decline when strain rate exceeds 3000/s, it remains significantly higher than that for unreinforced Al at similar strain rate. Note in Figure 2a that the maximum strength of reinforced Al at strain rate of 3800/s outnumbers those at lower strain rates; hence, the slight decrease in yield strength in Figure 3 does not negate the enhancing effects of GNFs.
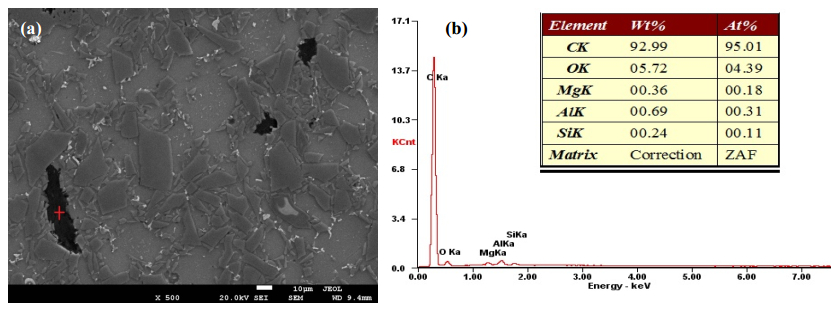
Figure 4 shows the distribution of GNFs within the fabricated composites. The darker regions correspond to GNFs in the form of graphene agglomerates, as evidenced by the EDX data. GNFs are either close to equiaxed or elongated in geometry and the border with Al matrix is irregularly shaped. As the interfacial bonding is sufficiently strong for the present processing approach [20], load transfer plays an important role in strengthening Al, due to the high strength of GNFs. The increase in composite yield strength resulting from load transfer can be calculated by Eq 3 [12], where pr and fr represent aspect ratio and volume fraction of GNFs and σAl denotes the yield strength of Al matrix. Eq 3 suggests that enhancement of yield strength increases with volume or weight fraction of GNFs, and this is consistent with the present and existing investigations [6], for which weight percentages of GNFs are respectively 1% and 0.3%, corresponding to increments of yield strengths by 300 MPa and 95 MPa.
|
$
\Delta {{\rm{ \mathsf{ σ} }}_{LT}} = {p_r}{f_r}{{\rm{ \mathsf{ σ} }}_{Al}}
$
|
(3)
|
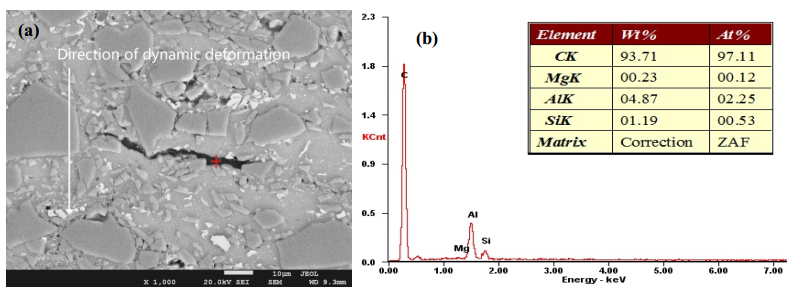
Figure 5 illustrates the feature of GNFs upon dynamic deformation. Compared with GNFs in un-deformed composites (Figure 4), those in impacted ones are obviously elongated, along with the macroscopic expansion of materials in lateral direction, i.e. the aspect ratio has increased upon impact deformation. This suggests an increase in the value of pr, and hence results in an enhanced load transfer, as indicated by Eq 3.
3.2. Strain Hardening Rate
Microstructural analysis was employed to investigate the mechanisms concerning weakened strain rate hardening, as demonstrated by Figure 2. Figure 6 is a representative SEM image of the impacted specimen. Cracks are clearly observed and EDX analysis implies that the damaged phase is silicon carbide, which has been widely used as reinforcements [27,28,29]. Although it is effective in enhancing material strength, the brittle nature also brings about reduction in material strength, particularly at relatively large strains and high strain rates.
The aforementioned mechanism associate with cracking of silicon carbon can also been inferred from hardness tests of unreinforced and GNFs-reinforced Al before and after deformation. Figure 7a shows the changes in hardness of unreinforced Al after deformed to fracture, and demonstrates that plastic deformation does not lead to an increase in hardness as it takes place for conventional metallic materials due to generation and storage of dislocations during deformation [22,23], because micro-cracks within deformed material results in a decline in strength, which cancels out the enhancing effects arising from dislocation accumulation. This suggests that micro-cracking is a significant effect leading to decrease of material strength. As for GNFs-reinforced Al, such weakening effect is more pronounced as indicated by Figure 7a, with material hardness decreasing dramatically after deformation, because cracking of silicon carbide in GNFs-reinforced composites occurs at relative low strains in comparison with ductile Al matrix and promotes the drop in material strength. Figure 7b depicts the morphology of fracture surfaces for GNFs-reinforced composites deformed to fracture. The fracture of silicon carbide is evident and shows a feature distinct from that for the matrix.
3.3. Effects of Strain Rate
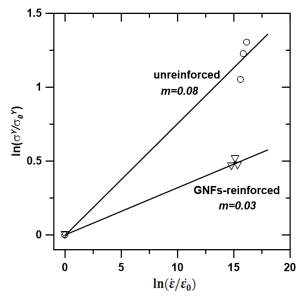
Strain rate sensitivity of materials is usually represented by the exponent m in a power law relationship as shown in Eq 4 [30], where σ and ${\dot \varepsilon }$ denote respectively flow stress and strain rate, and σ0 is the reference flow stress at strain rate of ${{\dot \varepsilon }_0}$. Taking quasi-static test as the reference strain rate and using yield strength in Figure 2 as the flow stress, a linear line is fitted to the scattered data in Figure 8 and the values of m are determined as 0.08 and 0.03 respectively for unreinforced and GNFs-reinforced Al, which are in the same order of magnitude as that for coarse-grained metals [31,32]. The drop in m value due to addition of GNFs reflects the inhomogeneity of material microstructure and deformation that could not provide enough resistance to softening mechanism like localized deformation and is presumably due to the decrease in grain size, caused by involvement of reinforcements as grain refiner, that helps to activate the mechanism of cutting forest dislocations associate with the operation of Peierls barriers [33].
|
$
{\rm{ \mathsf{ σ} }} = {\sigma _0}{\left( {\frac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}} \right)^m}
$
|
(4)
|
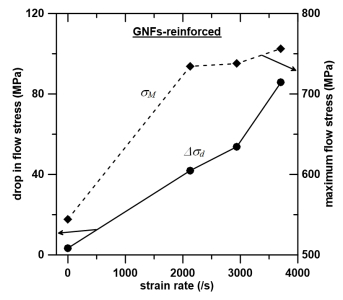
The effect of strain rate is also manifested by a noticeable drop in flow stress, particularly at dynamic strain rates. Figure 9 depicts the variation of drop in flow stress (Dsd) with strain rate, which is calculated by Eq. 5, with σM and σsa representing respectively the maximum and saturated stress. The increase Δσd of with strain rate is mainly caused by two reasons. Firstly, the rise in strain rate results in a higher temperature rise due to the conversion of plastic work into heat [22,23,24,] and hence softens materials in a greater degree. Secondly, nucleation and propagation of cracks in silicon carbide is strain rate dependent [34], and higher strain rate causes more severe stress concentration at the tip of cracks that accelerates the propagation of cracks, leading to a larger drop in stress. However, the maximum flow stress remains larger for higher strain rates, as shown in Figure 9, because shorter duration of deformation process indicates a higher rates of crack nucleation that requires greater stress to accomplish [35].
The effect of strain rate is also manifested by a noticeable drop in flow stress, particularly at dynamic strain rates. Figure 9 depicts the variation of drop in flow stress (Dsd) with strain rate, which is calculated by Eq. 5, with σM and σsa representing respectively the maximum and saturated stress. The increase Δσd of with strain rate is mainly caused by two reasons. Firstly, the rise in strain rate results in a higher temperature rise due to the conversion of plastic work into heat [22,23,24,] and hence softens materials in a greater degree. Secondly, nucleation and propagation of cracks in silicon carbide is strain rate dependent [34], and higher strain rate causes more severe stress concentration at the tip of cracks that accelerates the propagation of cracks, leading to a larger drop in stress. However, the maximum flow stress remains larger for higher strain rates, as shown in Figure 9, because shorter duration of deformation process indicates a higher rates of crack nucleation that requires greater stress to accomplish [35].
The effect of strain rate is also manifested by a noticeable drop in flow stress, particularly at dynamic strain rates. Figure 9 depicts the variation of drop in flow stress (Dsd) with strain rate, which is calculated by Eq. 5, with σM and σsa representing respectively the maximum and saturated stress. The increase Δσd of with strain rate is mainly caused by two reasons. Firstly, the rise in strain rate results in a higher temperature rise due to the conversion of plastic work into heat [22,23,24,] and hence softens materials in a greater degree. Secondly, nucleation and propagation of cracks in silicon carbide is strain rate dependent [34], and higher strain rate causes more severe stress concentration at the tip of cracks that accelerates the propagation of cracks, leading to a larger drop in stress. However, the maximum flow stress remains larger for higher strain rates, as shown in Figure 9, because shorter duration of deformation process indicates a higher rates of crack nucleation that requires greater stress to accomplish [35].
|
$
\Delta {{\rm{ \mathsf{ σ} }}_d} = {{\rm{ \mathsf{ σ} }}_M} - {{\rm{ \mathsf{ σ} }}_{sa}}
$
|
(5)
|
4. Conclusion
Aluminum (Al) matrix composites containing graphene nanoflakes (GNFs) and silicon carbide was synthesized by a processing approach combining hot isostatic pressing, hot extrusion with heat treatment. Compared with unreinforced aluminum, GNFs-added composites possessed yield strength around three times higher upon quasi-static loading, and the yield strength at dynamic strain rates was elevated by more than 300MPa. Transfer of load from Al matrix to GNFs was considered the main mechanism accounting for improved strength for GNFs-reinforced composites. On the other hand, decreased strain hardening rate and declined strain rate sensitivity were resulted, and cracking of silicon carbide and its propagation was the underlying reason, although it helped to enhance the composites. Despite the drop of flow stress particularly at dynamic strain rates, the maximum flow stress of composites remained exhibiting an upward trend with the increase in strain rate, because nucleation of micro-cracks was strain rate dependent and required greater stress at higher strain rates.
Acknowledgements
The authors are grateful to the support from the National Natural Science Foundation of China (Grant No.: 51701197).









 DownLoad:
DownLoad: