1.
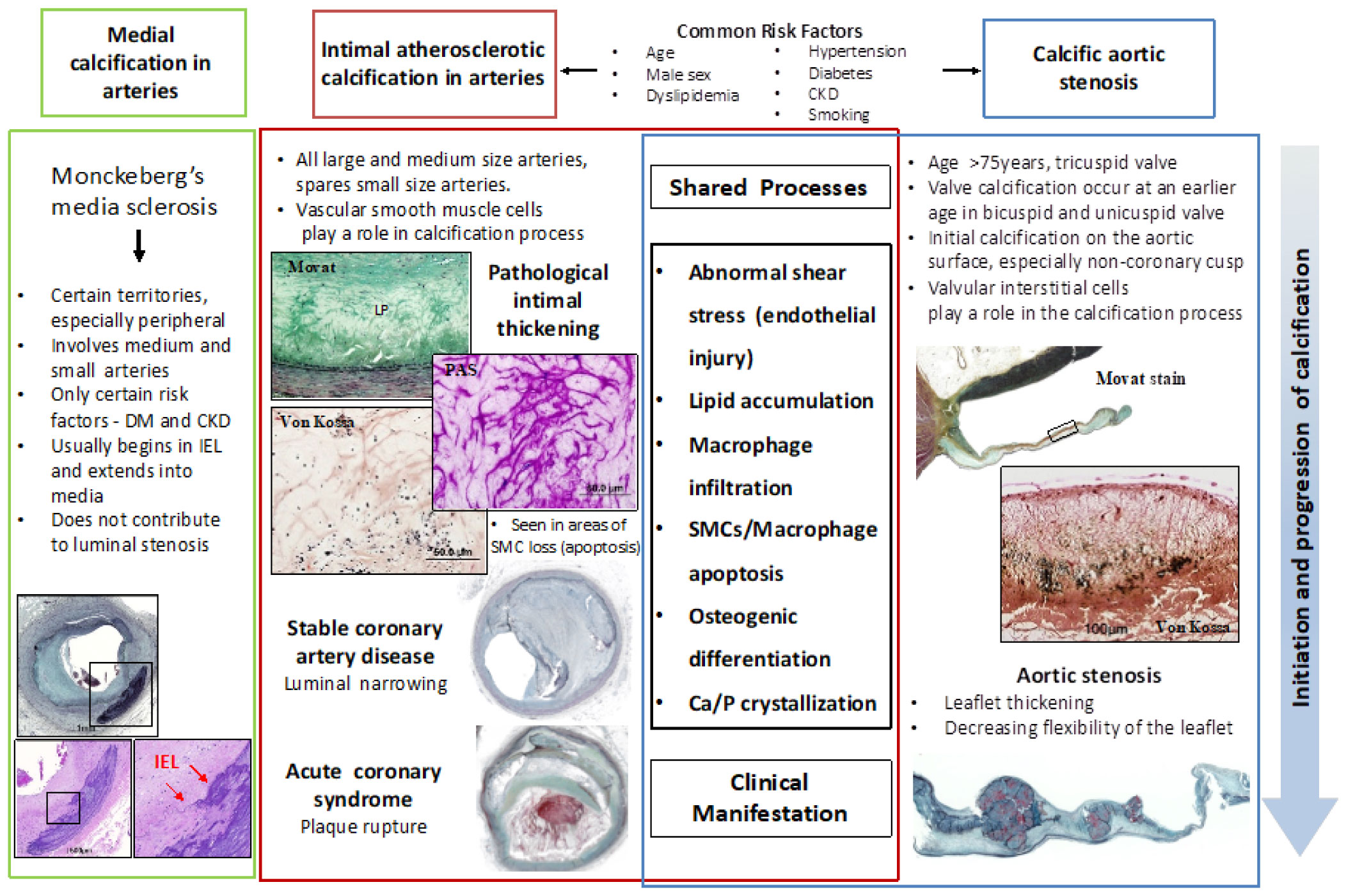
Introduction
Treatments for coronary artery disease and structural heart disease have evolved dramatically over the past decade and contributed to improving outcomes and quality of life in patients with cardiovascular disease. However, the mechanisms of vascular and valvular calcification are still not well understood. Due to this lack of understanding, there are few treatment options for vascular and valvular calcifications. Vascular and valvular calcifications hamper surgical and transcatheter treatments for these diseases and also portend worse clinical outcomes [1],[2]. A deeper understanding of vascular and valvular calcification is needed in order to better risk stratify patients with atherosclerotic and valvular disease and to improve prognosis in these patients. Vascular calcification is categorized into two different forms, intimal and medial calcification, depending on the location of the calcification within the vessel. In coronary arteries, intimal calcification is the major type of calcification whereas the peripheral arteries of the lower extremities are subject to both medial and intimal calcification. Although medial calcification can lead to a loss of elasticity, it minimally contributes to luminal stenosis. Valvular calcification generally occurs in aortic valve leaflets and causes aortic stenosis. The prevalence of aortic stenosis has increased in recent years because of population aging [3]. The mechanism of valvular calcification is still unclear, and the only treatments for aortic stenosis are surgical or transcatheter replacement [4]. In this review, we will focus on intimal calcification in coronary and lower extremity peripheral arteries and aortic valve calcification.
2.
Coronary artery disease (CAD)
2.1. Initiation of coronary artery calcification and definitions in pathology
Initiation of coronary artery calcification has been proposed to occur to four major mechanisms, some of which may be more relevant to the process of medial rather than intimal calcification [5]: (1) inflammatory cell apoptosis with the release of apoptotic bodies and necrotic debris that contribute nucleating sites for calcium phosphate crystal formation in atheroma; (2) matrix vesicles released nucleation complexes that contribute sites for calcium complex crystallization; (3) reduced local expression of mineralization inhibitors, such as Matrix Gla protein (MGP), pyrophosphate, fetuin-A, osteopontin (OPN), Klotho, and osteoprotegerin (OPG); and (4) Induction of bone formation resulting from differentiation of pericytes and/or vascular smooth muscle cells (VSMCs). In addition, elevated Ca or phosphorus (P) can result in apatite nucleation and growth of crystals which promotes vascular calcification via so-called thermodynamic mechanisms.
Coronary arterial calcification can be seen in pathological intimal thickening, which is the earliest form of progressive atherosclerotic lesions [6]. The innermost layer of the arterial wall is the intima. The intima contains three sublayers: (1) the endothelium, (2) subendothelial layer, and (3) the internal elastic lamina [7]. Resident smooth muscle cells in tunica media dedifferentiate and migrate into intima [8]. Such cells can undergo osteogenic transformation into phenotypically distinct osteoblast-like cells that are capable of expressing and releasing osteochondrogenic proteins [9]. Other studies suggest that circulating progenitor cells with osteogenic markers may also contribute to vascular calcification but their exact role and contribution to the process of vascular calcification in human remains poorly defined [10].
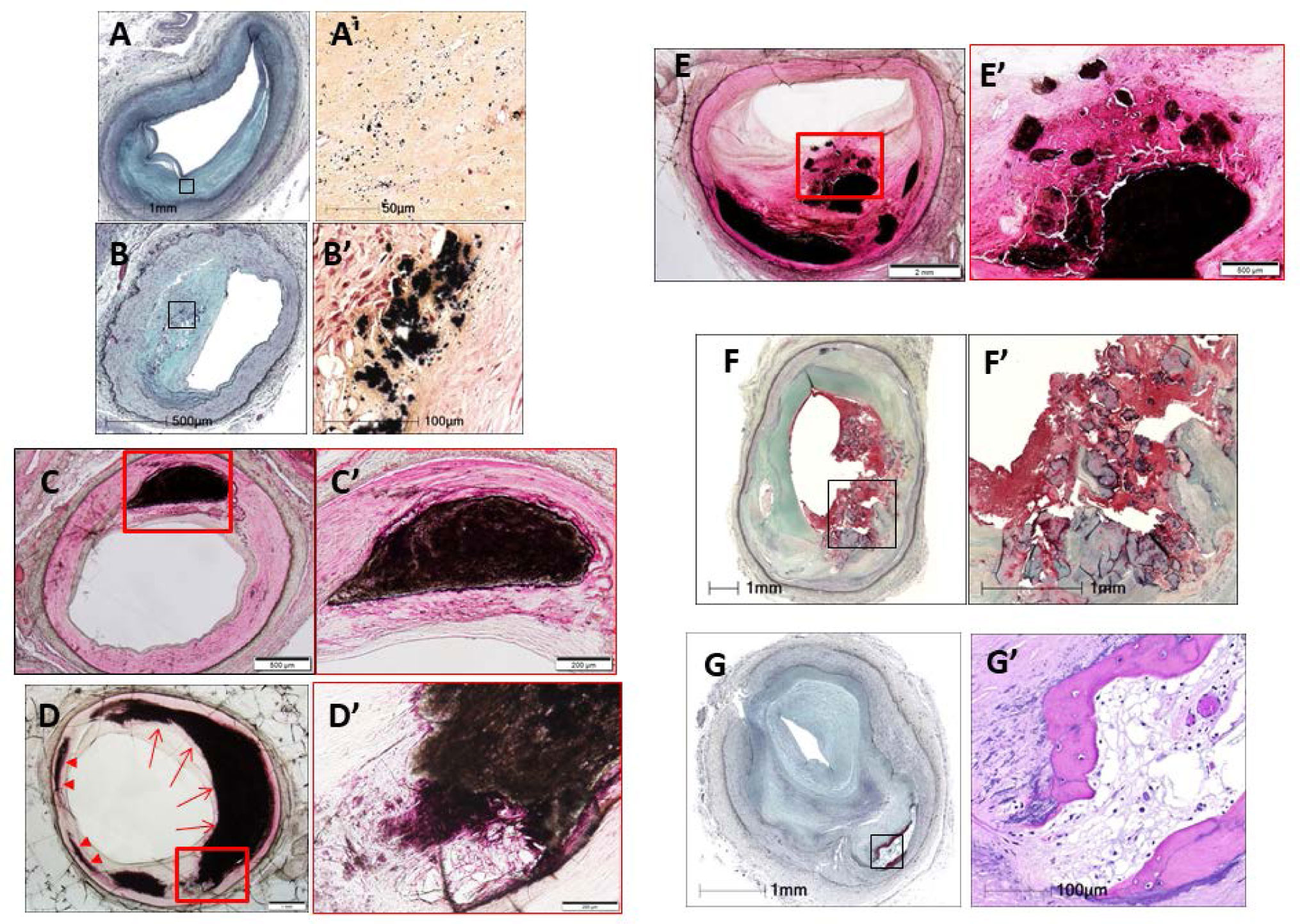
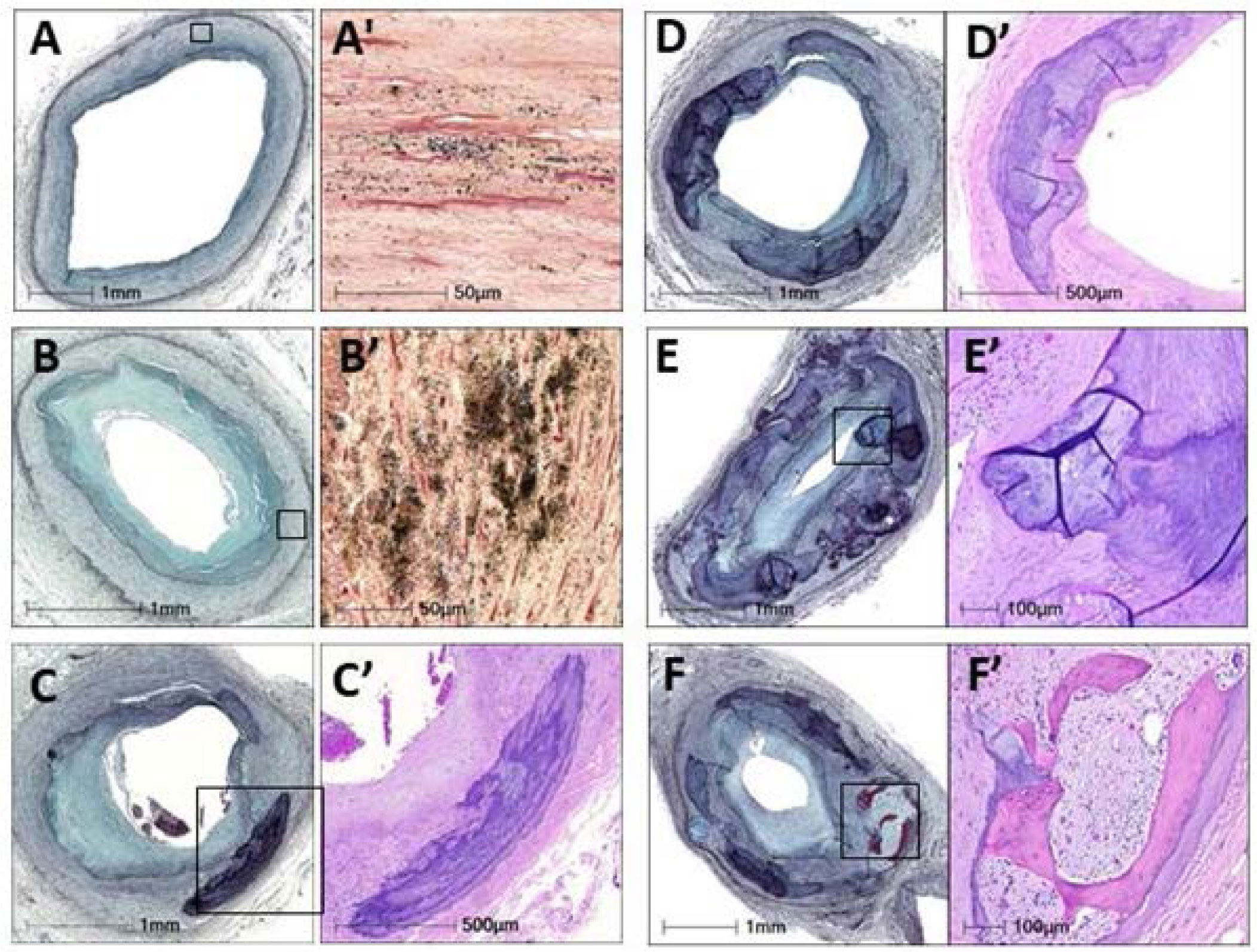
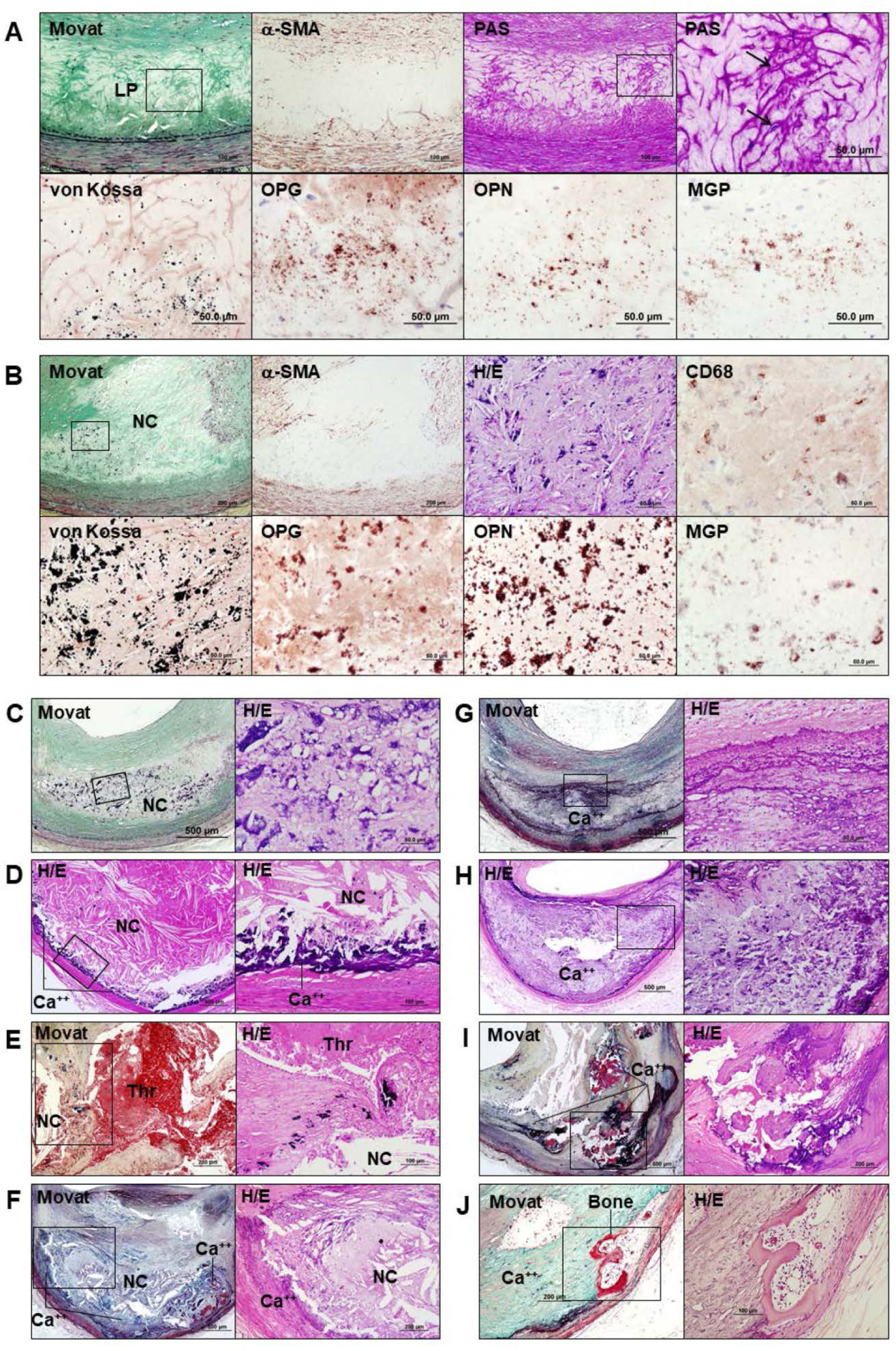
Calcification is classified according to the size and morphology. Microcalcifications, the initial form of calcification, are seen in lesions with pathological intimal thickening and are defined as calcium particles varying in size from over 0.5 µm to less than 15 µm in diameter in cross-sectional histologic sections; these are thought to result from apoptotic smooth muscle cell death (Figure 1). Punctate calcification occurs as calcium deposits ≥15 µm but less than 1 mm and is commonly seen in more advanced lesions such as fibroatheromas. Macrophages releasing matrix vesicles or macrophage apoptosis also contribute to initiate micro and punctate calcification. These macrophages are derived from circulating monocytes, which are attracted to lipid accumulation in the plaque [5],[6]. Fragmented calcification occurs when deposits become ≥1 mm and can be observed at the edge of necrotic cores. The mechanism for this type of calcification is still unclear. Sheet calcification is noted when more than 1 quadrant of the vessel demonstrates calcification or is 3 mm in size or greater and is thought to be consistent with plaque stabilization. Nodular calcification is least frequently seen and is mainly confined to tortuous arteries. The components of nodular calcification are nodular calcium deposits and fibrin with intact fibrous cap. When such a lesion protrudes through the fibrous cap into the lumen, and there is attached luminal thrombus, it is called calcified nodule. Ossification with intervening marrow formation is rarely observed in the coronary artery but is seen in peripheral arteries. These definitions are adapted not only to coronary arteries but also to peripheral arteries and may describe forms of both intimal and medial calcification.
2.2. Plaque type and progression of calcification
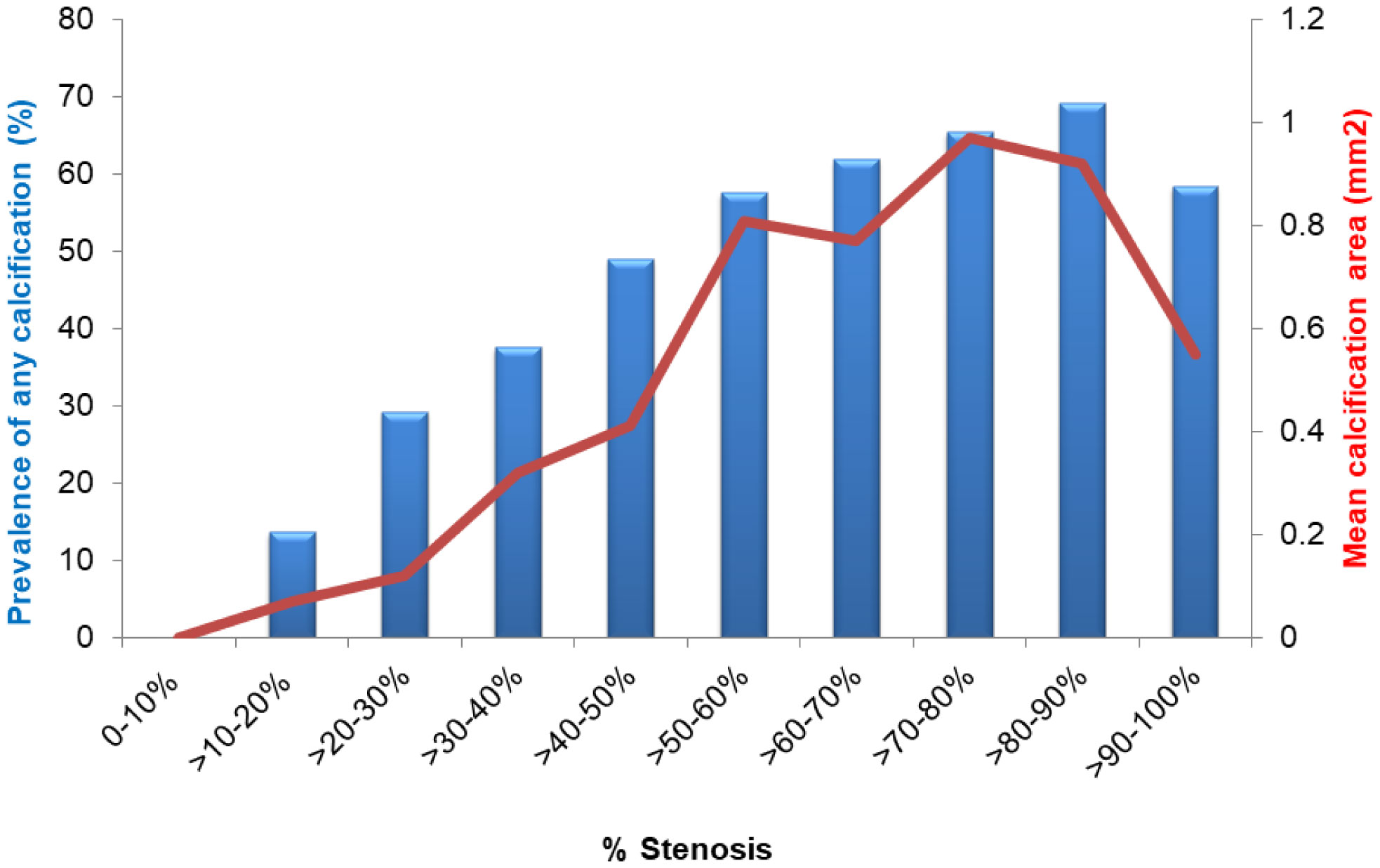
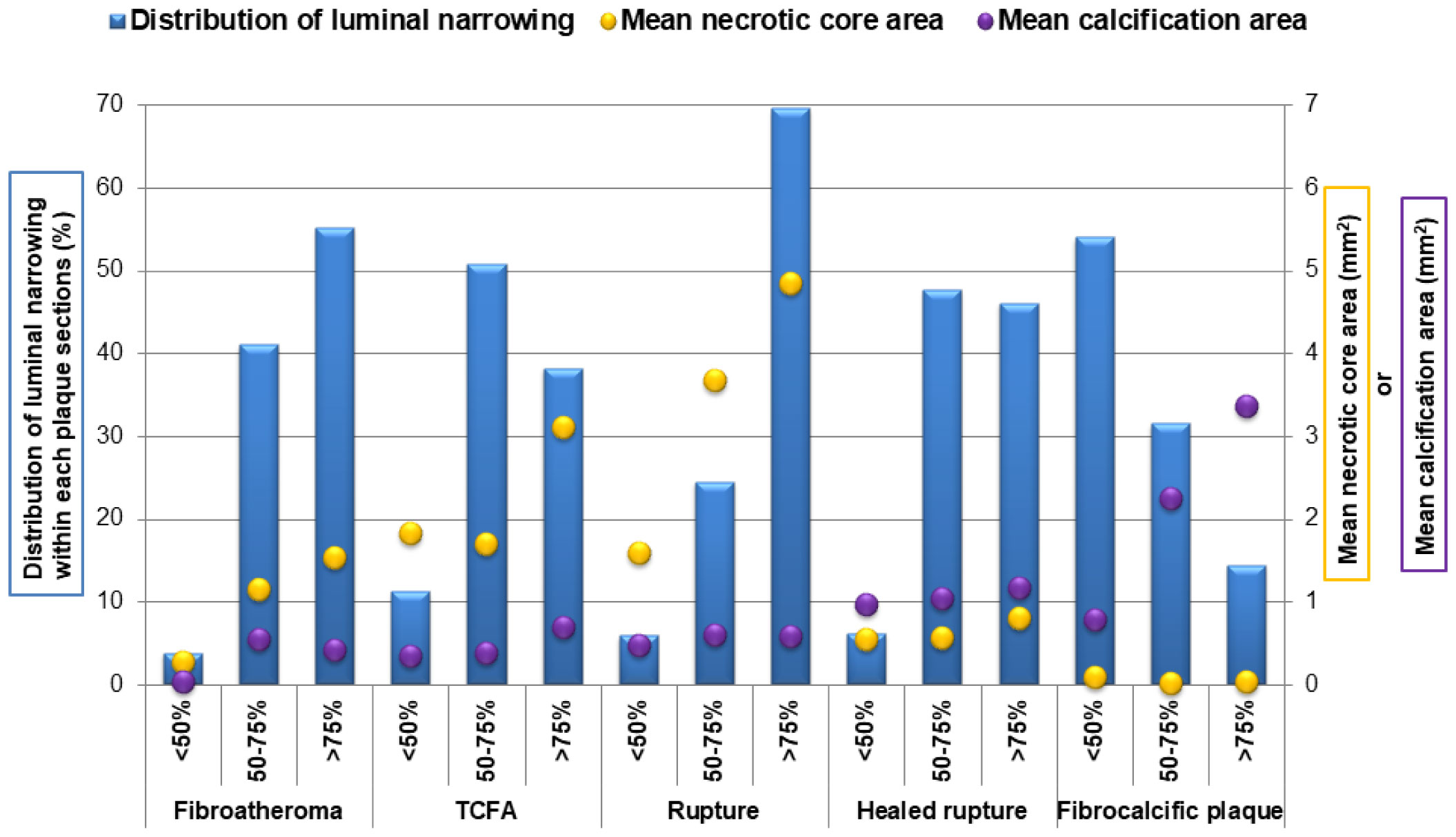
The severity of luminal stenosis correlates with calcification burden (Figure 2a) [11]. In early lesions such as adaptive intimal thickening or pathological intimal thickening, calcification is rarely seen. While in progressive lesions, the presence of coronary calcification is not binary but rather depends on the type of calcification. The mean area of calcification diverges according to plaque types (Figure 2b) [12]. Fibrocalcific plaque tends to have the greatest amount of calcification, followed by healed ruptures, plaque ruptures, thin cap fibroatheroma, and then fibroatheroma. Although the mean area of necrotic core area in fibroatheroma, thin-cap fibroatheroma, and rupture increases with percent stenosis, the mean area of calcification did not show a proportionate increase. Spotty calcification seems to correlate with plaque instability, while dense calcification seems to correlate with overall plaque burden. On the other hand, calcification in healed ruptures and fibrocalcific plaques exceeds that of necrotic core area as the vessel narrows. Interestingly, arterial calcification correlates with plaque burden, whereas there is no correlation between calcification and lumen area [13]. Because the lumen area does not decrease unless percent plaque reaches up to 40% due to vessel positive remodeling, that is the reason for the non-correlation between the luminal area and atrial calcification [14]. Taken together, these studies show that calcium burden is greatest in stable plaque compared to unstable plaques, and there is an inverse relationship between necrotic core area and calcification burden.
2.3. The difference of calcification in age, sex, and race
We reported the relationship between coronary calcification and age in individuals dying with severe coronary disease. Based on radiography, calcification in coronary artery was seen in 46% of individuals aged <40 years, 79% of those aged 50–60 years, and 100% of those aged >60 years [15].
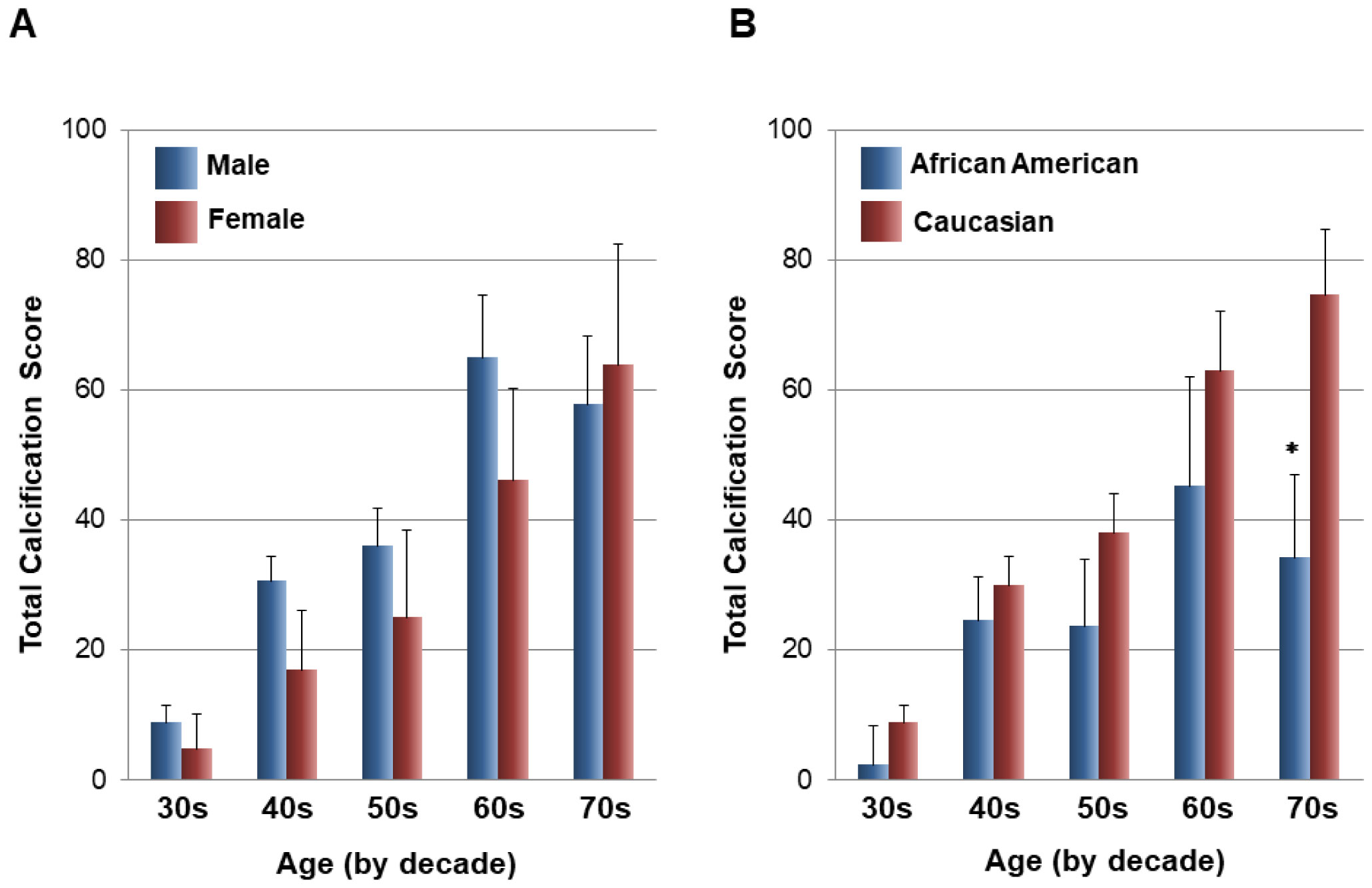
Sex differences also contribute to the prevalence of coronary arterial calcification. Atherosclerotic coronary artery disease in females is delayed by 10–15 years as compared to males because of estrogen exposure in the pre-menopausal years, which is likely to afford protective effects against the development of atherosclerosis [16]. In our autopsy registry, a total of 108 human hearts from victims of sudden cardiac death, 70 men and 38 women were enrolled to evaluate the extent of calcification by radiography [17]. The total calcification semi-quantitative score was greater in males than in females up to the sixties (Figure 3A). However, in the seventies, the difference between males and females was not obvious, which suggests an effect of the post-menopausal state promoting rapid progression of calcification and atherosclerosis in females. When females were divided into pre- and post-menopausal groups, the degree of calcification was three times greater in post-menopausal females than in pre-menopausal females [18]. The sub-study of the Women's Health Initiative (WHI) trial—which enrolled 50–59 years old women who had undergone hysterectomy and compared estrogen therapy group with placebo group—evaluated the effect of estrogen therapy on coronary calcification. In that study, the extent of coronary artery calcification was significantly less in the estrogen therapy group than in the placebo group [19].
The difference in the extent of calcification has also been observed among races. In the MESA (Multi-Ethnic Study of Atherosclerosis) study, a total of 6,814 people aged 45–84 years without clinical cardiovascular disease were evaluated for coronary calcification by computed tomography [20]. After adjusting for clinical factors, the relative risks for having coronary calcification were significantly less in African Americans (0.78 (95% confidential interval [CI], 0.74 to 0.82)), Hispanics (0.85 (95% CI, 0.79 to 0.91)), and Chinese (0.92 (95% CI, 0.85 to 0.99)) compared to Caucasians. In our autopsy registry, a total of 108 human hearts from victims of sudden cardiac death, 70 men and 38 women were enrolled to evaluate the extent of calcification by radiography [21]. We reported that Caucasians showed more significant coronary calcification as compared to African Americans regardless of age, which is consistent with previous clinical studies (Figure 3B) [20],[22]. Racial differences were also observed in the younger adult population. A total of 3,043 people aged 18–30 years old were enrolled in the prospective CARDIA (Coronary Artery Risk Development in Young Adults) study, and coronary artery calcification was assessed at a 15-year follow-up. Overall, 9.6% adults had any coronary artery calcification, with a greater prevalence among men than woman (15.0% vs. 5.1%), a greater prevalence among Caucasian than African American men (17.6% vs. 11.3%), and a greater prevalence among those aged 40–45 years than 33–39 years (13.3% vs. 5.5%) [23]. Although the reason for the racial differences in coronary arterial calcification remains unknown, several potential mechanisms have been proposed. A past study reported that bone loss might contribute to the calcification of abdominal aorta [24]. Less bone mineral density was more frequently seen in Caucasians than in African Americans, which suggested that lower bone turnover may contribute to a lesser degree of vascular calcification [25]. Genetic predisposition might also affect vascular calcification in Caucasians and African Americans. Huang et al. reported that the expression of GAB2, a molecular adaptor that associates with the pro-calcific receptor activator of nuclear factor kappa beta (NF-kB) and its ligand receptor activator of NF-B ligand (RANKL), is more frequently seen in Caucasians than in African Americans [26]. From the CARDIA study, Fornage et al. reported that Arg287Gln polymorphisms in the soluble epoxide hydrolase gene were related to lower calcification in African Americans but not Caucasians [27].
2.4. Influence of comorbidities on coronary calcification: diabetes mellitus and chronic kidney disease
Diabetes mellitus (DM) is a risk factor for coronary calcification, as well as a larger plaque burden and worse clinical outcomes [28],[29]. Carson et al. evaluated the relationship between hemoglobin A1c (HbA1c) and the progression of calcification in a total of 2,076 patients by non-contrast CT at baseline and at 5-year follow-up [30]. Patients with higher HbA1c showed significantly greater progression of calcification. In our autopsy study, patients with DM showed more significant total plaque burden than those without DM. This result was driven by the higher number of healed plaque ruptures in patients with DM vs. without DM (2.6 vs. 1.9; p = 0.04) [31]. The mean percent calcified area was also higher in patients with DM versus those without DM (12.1% vs. 11.4%; p = 0.05) [32].
Patients with chronic kidney disease (CKD) show higher risk for cardiovascular disease and its associated morbidity and mortality than the general population, which could partially be due to extensive cardiovascular calcification. A combination of atherosclerotic disease and an imbalance in calcium and phosphorus homeostasis causes calcification in both intimal and medial wall in patients with CKD. Even in the younger population, patients under 30 years old on hemodialysis showed a high prevalence of calcification [33]. There is an inverse correlation between estimated glomerular filtration and the prevalence of calcification [34]. Other studies support these findings [35]–[37]. Among patients on hemodialysis, the degree of calcification is proportionate to age, duration of dialysis, presence of DM, abnormalities of mineral metabolism, and the use and dose of calcium-based phosphate-binding medications [33],[37]–[41]. Hyperphosphatemia is associated with the degree of calcification, all-cause death, and cardiovascular death among patients with CKD. Even in patients without CKD, all-cause death and cardiovascular death are associated with hyperphosphatemia [42]–[44]. Thus, hyperphosphatemia and its treatment (e.g., sevelamer, calcimimetic agents, and calcium-containing phosphate binders) can affect clinical outcomes in patients on dialysis. However, a meta-analysis that included 12,562 patients with CKD from 77 trials failed to show any benefit of phosphate-binder treatment in terms of clinical outcomes, and few differences were observed in the progression of vascular calcification [45].
Recently, Raggi et al. conducted a randomized controlled trial, which included 274 patients with end-stage kidney disease receiving hemodialysis, to investigate the effect of a calcification inhibitor (Myo-inositol hexaphosphate: SNF472) in addition to standard treatment for the management of mineral metabolism imbalances in end-stage kidney disease [46]. The mean change of coronary artery calcium volume score at 52 weeks was smaller in the treatment group than in the placebo group (11% (95% CI, 7–15) vs. 20% (95% CI, 14–26), p = 0.016). Interestingly, the mean change of coronary calcium volume score in the placebo group in the current study was smaller than the placebo group in previous studies (35–40%) [40],[47],[48]. It means that standard treatments for hyperphosphatemia have also been progressed over time. However, it remains unknown whether the treatment for the progression of coronary artery calcification is a surrogate marker of clinical outcome in patients with maintenance hemodialysis.
3.
Peripheral artery disease (PAD) of the lower extremity
3.1. Pathology of PAD
3.1.1. Above the knee artery
There are limited studies evaluating the extent and characteristics of peripheral artery disease of the lower extremities. Sawabe et al. reported that a total 1,074 autopsy cases, including an equal number of males and females aged from 60 to 90 years who died from various causes, were evaluated for the progression of disease in each artery. The progression of disease was most rapid in the aorta, followed by coronary, femoral, and the least rapid in the carotid and intracerebral arteries [49]. Dalager et al. reported a similar study which included coronary, superficial femoral, and carotid arteries from 100 autopsy cases (70 men; 20 to 82 years of age), of whom 27 died from coronary atherosclerosis [50]. They modified the American Heart Association (AHA) classification of atherosclerotic lesions and used in this study. Our classification, based on coronary experience, can also be applied to their PAD cases [51]. The study showed that the progression of plaque burden was associated with aging for all vascular beds, and atherosclerotic patterns were different depending on the type of the artery. Plaques in carotid and coronary arteries often contained foam cells and lipid cores, and these plaques were located most frequently in the left anterior descending coronary artery and carotid arterial bifurcation. On the other hand, the femoral arteries showed mainly fibrous plaques and fewer foam cell lesions. These results suggested that atherosclerotic progression in the femoral artery was slower than coronary and carotid arteries; however, this study did not include the patients with symptomatic PAD.
Histological studies of femoral arterial plaque were conducted using endarterectomy specimens. Herisson et al. reported that a total of 88 plaques (45 carotid and 43 femoral samples: mean age, 69.7 ± 1.65 years and 69.2 ± 1.5 years, respectively) collected from endarterectomy specimens [52]. Carotid arteries frequently showed fibroatheromas, while femoral arteries dominantly showed fibrocalcific plaques, and the extent of calcification was greater in femoral arteries than carotid arteries. Derksen et al. reported that there were differences in plaque composition between the common femoral artery (CFA) and the superficial femoral artery (SFA). A total of 217 samples (CFA 124 and SFA 93) from patients with symptoms were assessed after endarterectomy. In a histopathological evaluation, SFA plaque showed more significant amount of collagen (69% vs. 31% for CFA, p < 0.001) and smooth muscle cells (64% vs. 36% for CFA, p < 0.001) [53].
3.1.2. Below the knee arteries
Soor et al. reported a histomorphological assessment of 58 consecutive patients who underwent a lower limb amputation ranging in age from 43 to 95 years (mean 68.7 ± 12.5 years). Thirty-three out of 58 (57%) were below-the-knee, and 25 (43%) were above-the-knee lesions. Most of the lesions (218 of 261 segments (84%)) showed atherosclerotic plaques with mean luminal stenosis of 68 ± 29%; severe luminal narrowing (76 to 100%) was seen in 48% of the vessel segments. Medial calcification was noted in 199 segments (76%), which involved 55 ± 37% of the medial circumference of the vessel, and severe calcification (>75% involvement) was observed in 37% of the vessel segments. Concomitant medial calcification and atherosclerotic disease were observed in 168 (77%) of the 218 arterial segments. Interestingly, the degree of medial calcification did not correlate with the degree of atherosclerosis [54].
3.1.3. Mönckeberg's disease; medial calcification
Medial calcification, also known as Mönckeberg's disease, is a feature of peripheral artery disease but is not seen in the coronary artery. The media in small- or medium-sized muscular arteries become calcified without an association with atherosclerosis, the etiology of which is still unclear. In the early stages of the disease, hydroxyapatite crystal deposition occurs in the elastic lamina, followed by the adjacent medial wall where there are abundant smooth muscle cells. Mönckeberg's disease does not affect the intimal layer or adventitia, and does not occur in luminal stenosis. In general, there is no inflammatory reaction in the medial wall, and medial calcification is not associated with necrotic core, smooth muscle cells, or collagen. A plain radiograph finding of medial calcification is the appearance of “railroad tracks” along the outline of the arterial wall [53] (Because medial calcification occurs at the edges of artery, it looks like a double line similar to a railroad track). The known risk factors of medial calcification were reported as aging, end-stage renal disease, autonomic neuropathies, osteoporosis, and DM [55]–[57]. Even among young adults, medial calcification was observed in up to 50% in the lower extremities [57]. The mechanism of medial calcification remains unknown, however, there is likely an association between lower serum levels of bone-related proteins (MGP and OPN) and higher levels of alkaline phosphatase, bone sialoprotein, and collagen type II [56]. Both OPN and MGP knock out mice (OPN-/-, MGP-/-) showed more progressive arterial calcification as compared to single knockout (OPN+/+, MGP-/-) mice [56].
3.1.4. Detailed histopathological studies of the patients with PAD and critical limb ischemia (CLI)
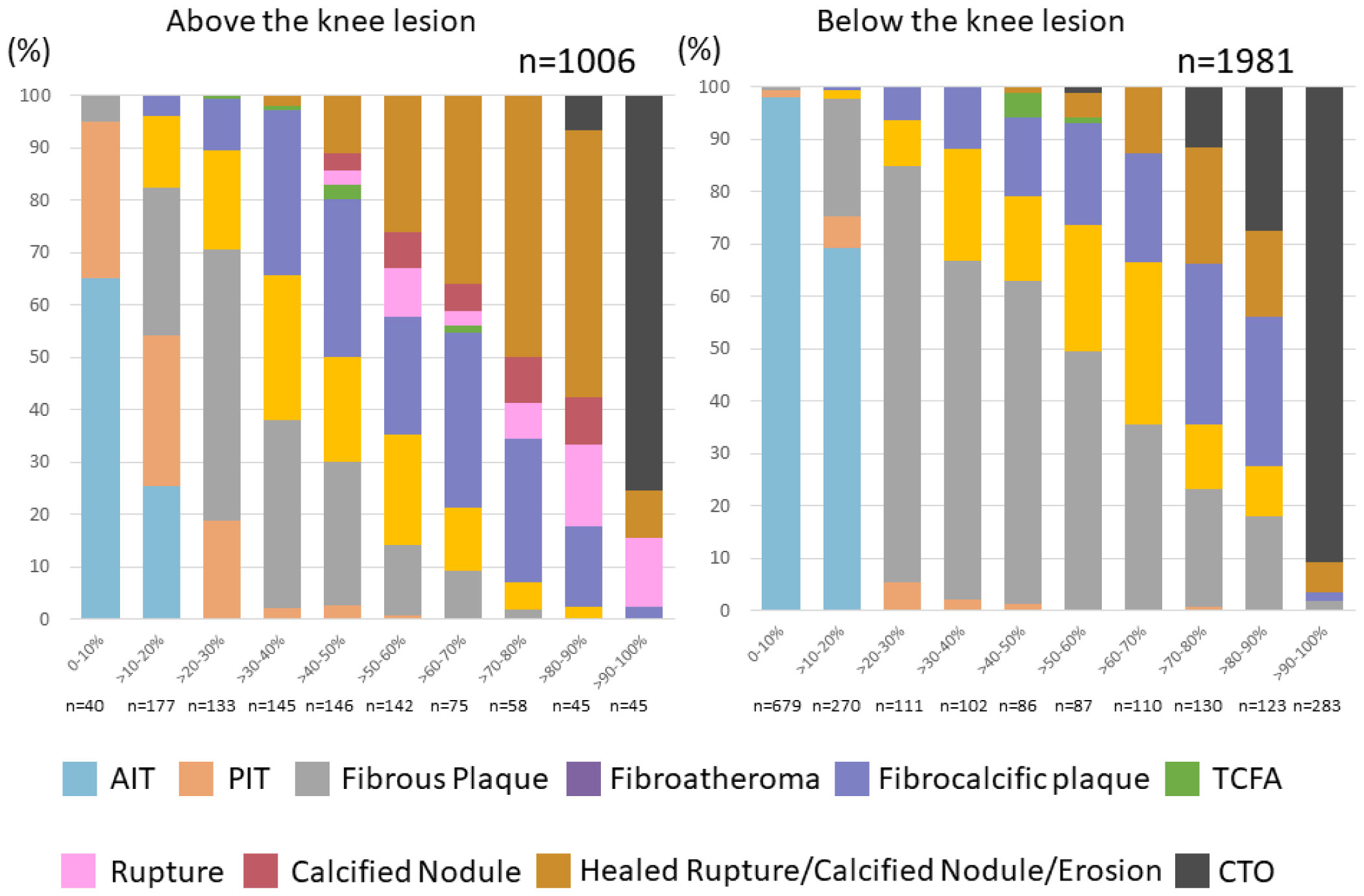
Recently we conducted a systematic pathological study characterizing PAD in the lower extremities. A total of 12 legs from 8 victims dying with abundant risk factors (median age, 82 years; 6 men) were evaluated [58]. Peripheral atherosclerotic plaques were classified using the modified American Heart Association classification proposed for coronary atherosclerotic lesions (Figure 4). Atherosclerotic lesions were more frequently detected in above-knee arteries (92.9%) than below-knee arteries (56.9%). The prevalence of calcified nodule was greater in above-knee arteries than coronary arteries (2 to 7%) (51) and carotid arteries (4 to 14%) [59]. All eight above-knee arteries showed lesion with acute thrombus, three cases had plaque rupture, and five cases had calcified nodule. Intimal and medial calcifications were frequently observed (75.3% and 86.2%, respectively) (Figure 5a). The progression of intimal calcification was associated with the presence of stenosis in above-knee arteries, while there was no correlation between the progression of medial calcification and the presence of stenosis (Figure 5b).
The most serious complication of PAD is critical limb ischemia (CLI), which is strongly associated with worse clinical outcomes [60]. Narula et al. reported a histopathological study of 239 lower extremity arteries collected from patients who underwent amputation due to CLI [61]. Atherosclerosis was more frequently seen in femoral and popliteal arteries (FEM-POP) than infrapopliteal arteries (INFRA-POP; anterior and posterior tibial, peroneal, and dorsalis pedis) (67.6% vs. 38.5%). Their study also revealed that only 69% of arteries showed >70% luminal stenosis. The presence of chronic total occlusion (CTO) was greater in INFRA-POP than FEM-POP arteries without significant atherosclerosis. In contrast, acute thrombi were more frequently seen in FEM-POP than INFRA-POP, which suggested more frequent thromboembolic etiology in INFRA-POP CLI.
3.2. The prevalence of peripheral arterial calcification
There are limited studies about the prevalence of femoropopliteal artery calcification in the general population because of the lack of data from younger and healthier individuals and the difficulty of conducting a longitudinally study in humans. Kamenskiy et al. evaluated human femoropopliteal arteries histological sections from 431 tissue donors aged 13 to 82 years (mean age, 53 ± 16 years) [62]. Medial calcification was identified in almost half of these cases (46%). Although arteries in older individual showed greater calcification, tiny calcium deposits in media were observed even in arteries in the case of an 18 year old. The prevalence of femoropopliteal artery calcification increased with age: <20 years old (7%), 21–30 years old (17%), 31–40 years old (16%), 41–50 years old (48%), 51–60 years old (46%), 61–70 years old (64%), and in subjects >71 years old (61%). Sex differences did not affect the calcification burden.
Although the relationship between peripheral arterial calcification and age, CKD, and type II DM was previously described [63]–[65], no consensus was established in the literature regarding the association between peripheral arterial calcification and risk factors. Kroger et al. reported that there was no correlation between arterial calcification and Framingham risk factors (age, DM, systolic blood pressure, low-density lipoprotein cholesterol, high-density lipoprotein cholesterol, smoking, and renal function) [66]. Vasuri et al. also found no correlation between calcification and any risk factor except hypertension from a histological study which enrolled 36 arteries [67]. Nevertheless, Kamenskiy et al. reported that positive correlations were observed between calcification and DM, dyslipidemia, coronary artery disease, and body mass index as well as hypertension [62]. Other studies also found associations between risk factors for atherosclerosis and calcification, especially DM and CKD [63]–[65].
3.3. DM and calcification in lower extremity PAD
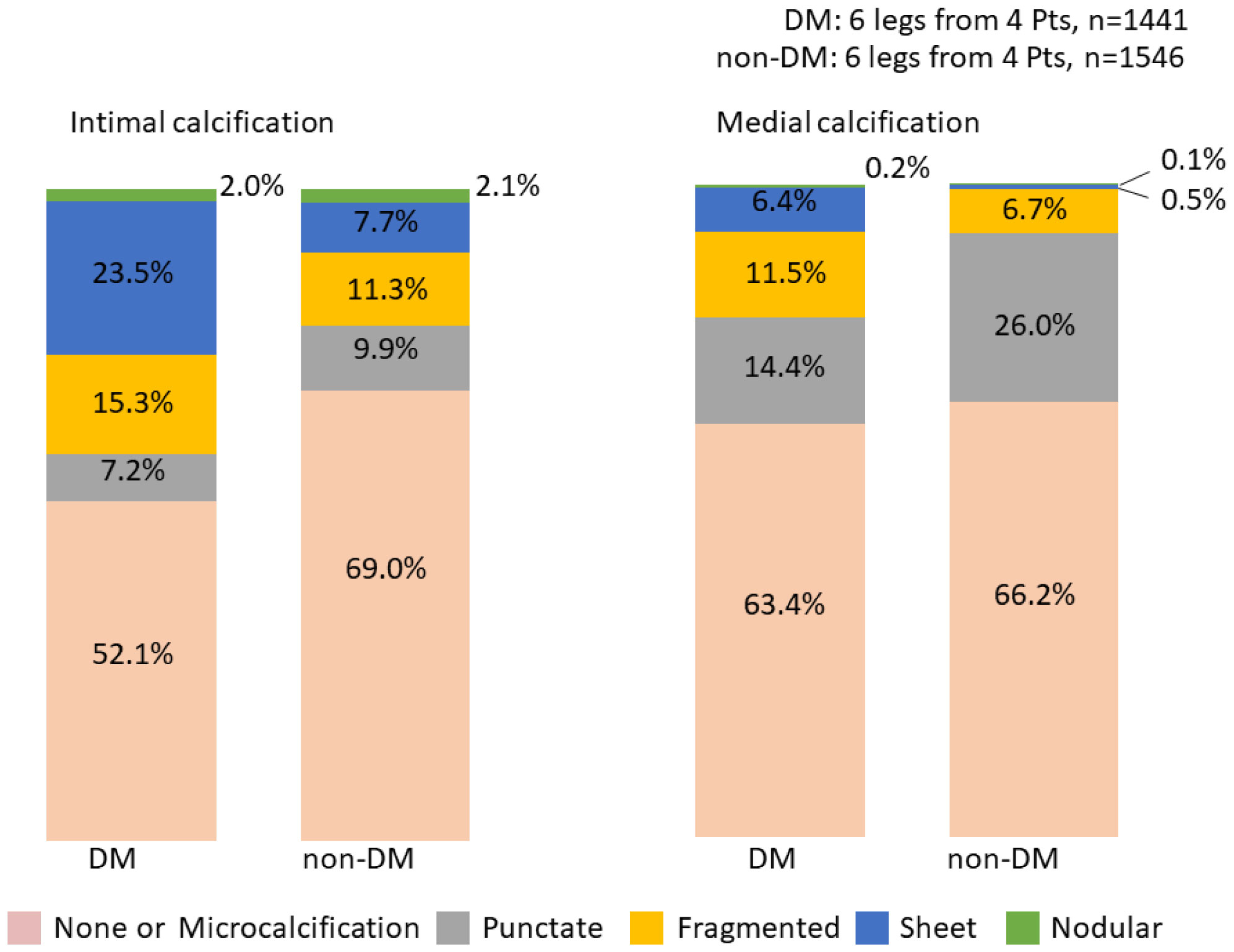
DM is a well-known independent risk factor of PAD [68], but the prevalence of intimal and medial calcification has not been reported. In patients with lower extremity PAD, intimal and medial calcifications were more frequently seen in arteries from patients with DM as compared to those without DM (Figure 6) [58]. In intimal calcification, patients with DM showed 47.9% of sections with calcification characterized as punctate (7.2%), fragmented (15.3%), sheet (23.5%), and nodular (2.0%), whereas in patients without DM, 31.0% showed calcification characterized as punctate (9.9%), fragmented (11.3%), sheet (7.7%), and nodular (2.1%). Also, patients with DM showed a greater prevalence of progressive medial calcification (fragmented = 11.5%, sheet = 6.4%, nodular = 0.2%) than those without DM (fragmented = 6.7%, sheet = 0.5%, nodular = 0.1%).
4.
Aortic valve (AV)
4.1. Structure of aortic valve
The normal aortic valve consists of three semicircular cusps (i.e., left, right, and non-coronary cusp), which are attached to the annulus of ascending aorta at the three commissures. The cusps have a thin and translucent shape with a thickness of less than 1 mm. The histologic structure of the aortic valve cusps is composed of three layers: a fibroelastic layer on the ventricular surface (ventricularis), a proteoglycan rich layer (spongiosa) in the middle, and dense collagen with a thin fibroelastic layer on the aortic surface (fibrosa). The thickness of cusps increased with age <20 years (0.67 ± 0.21 mm), 20–59 years (0.87 ± 0.27 mm), and is greatest in individuals >60 years (1.42 ± 0.51 mm). Non-coronary cusps were thicker than the right and left cusps in the advanced age group [69].
4.2. Degenerative aortic valve calcification (tricuspid)
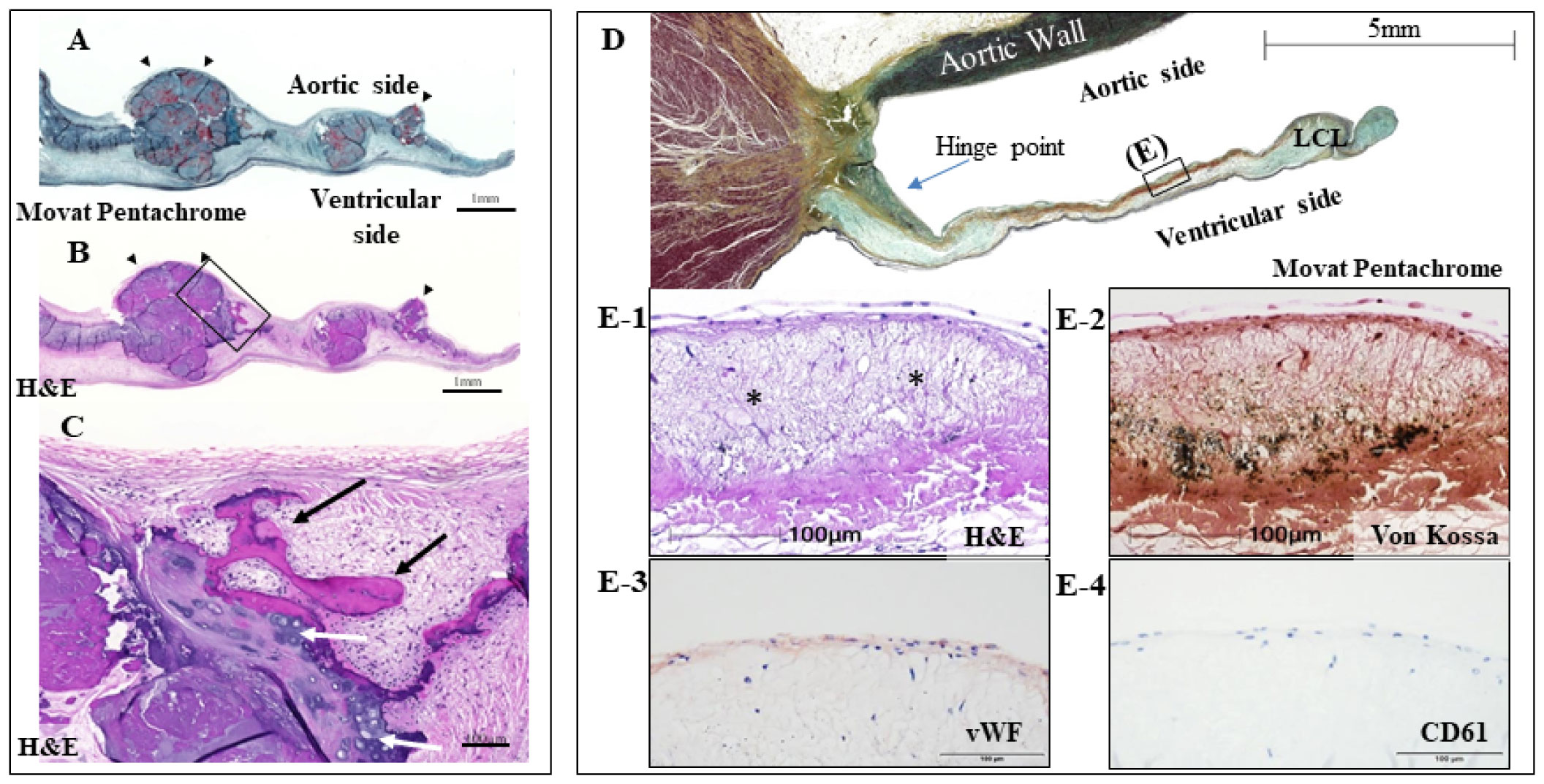
The prevalence of degenerative calcific aortic stenosis was reported at approximately 0.4% in the general population and 1.7% in the population aged over 65 years in developed countries [70]. Calcific aortic valve stenosis is a progressive disease with pathologic findings ranging from minimal fibrocalcific changes in early disease to end-stage lesions characterized by fibrotic thickening and nodular calcification (Figure 7) [71]. Early valve calcification is similar to atherosclerotic changes, tiny stippled microcalcification or small nodular concretions with lipid insudation are observed in fibrosa on the aortic surface of the cusp (Figure 7). These changes were most frequently seen in the hinge area of the aortic cusps near the attachment of the aortic root and in an area just below the line of valve closure, possibly because of higher mechanical stress. After endothelial cell damage and lipid insudation, calcification begins in the interstitial cells in the fibrosa, gradually merges into larger complex nodules, and then extends towards the middle portion of the cusp, sparing the free margin, and may protrude into the aortic surface during the progression. Butany et al. conducted a histopathological study including 247 surgically excised aortic valves (mean age 64.1 ± 13.4 years). Approximately 70% of valves were tricuspid, 27% were bicuspid, 2.4% were unicuspid, and 0.4% valve was quadricuspid. Almost 70% of valves showed grade 3 or 4 calcification, and ulceration of the calcific nodules was seen in 42% of valves which have severe calcification [72]. At the beginning of degenerative change, mild fibrous thickening without left ventricular outflow obstruction is seen. Fibrous thickening and calcification increase gradually; eventually, irregular calcific nodules are formed on the aortic side of the cusps causing aortic valve obstruction (Figure 7 C–E). The degree of leaflet calcification is usually more significant in the non-coronary cusp as compared to the other cusps. One of the reasons reported was that non-coronary cusp receives greater stress during diastole than the right and left coronary cusps due to the absence of coronary arteries [73].
Aortic valve calcification and atherosclerosis share risk factors, including age, male gender, smoking, elevated cholesterol level, lipoprotein (a), hypertension, DM including metabolic syndrome, and CKD. In the Multi-Ethnic Study of Atherosclerosis (MESA), aortic valve calcification was quantified from serial computed tomographic images from 5,880 patients, and 5142 patients did not have aortic valve calcification on the baseline CT [74]. During a mean follow-up of 2.4 ± 0.9 years, 210 out of 5,142 patients developed aortic valve calcification. Risk factors for incident aortic valve calcification were age, male gender, body mass index, current smoking, and the use of lipid-lowering and antihypertensive medications. Of the 738 patients with valve calcification at baseline, the median rate of progression of aortic valve calcification was two Agatston units/year (interquartile range −21 to 37). Baseline Agatston score, male sex, and lower diastolic pressure were independent predictors of progression.
Formerly, aortic stenosis was regarded as a passive degenerative disease. However, current studies suggest that aortic stenosis is an active disease and may be related to lipid deposition, inflammation, osteogenic differentiation of valvular interstitial cells (VIC), and oxidative stress. Mohler et al. reported that 256 surgically excised aortic valves were examined histologically, and mature lamellar bone with hematopoietic elements and active bone remodeling were identified in 34 valves [75]. Brien et al. conducted a histological study that included 18 tricuspid aortic valves ranging from normal to stenotic and found that apolipoproteins were identified in early to late phase of aortic stenosis, but were not found in the leaflets considered histologically normal [76]. Zheng et al. conducted a prospective study including 145 patients with aortic stenosis (a peak aortic jet velocity > 2 m/sec). They revealed that patients in the top lipoprotein (a) tertile at baseline had increased valve calcification activity as compared to those in lower tertiles by positron emission tomography (n = 79; 18F-NaF tissue-to-background ratio of the most diseased segment: 2.16 vs. 1.97; p = 0.043). During the follow-up period, the top lipoprotein (a) tertile showed increased progression of valvular CT calcium score (n = 51; 309 AU/year (IQR: 142 to 483 AU/year) vs. 93 AU/year (IQR: 56 to 296 AU/year; p = 0.015), faster hemodynamic progression on echocardiography (n = 129; 0.23 ± 0.20 m/s/year vs. 0.14 ± 0.20 m/s/year) p = 0.019), and increased risk for aortic valve replacement and death (n = 145; hazard ratio: 1.87; 95% CI: 1.13 to 3.08; p = 0.014). Although effective pharmacological treatments are limited and surgical- or catheter-based aortic valve replacement is the only effective option at present, these studies suggest a target of the treatment of aortic stenosis.
Calcific aortic valve stenosis and atherosclerotic calcification share some risk factors and cellular mechanisms [77]. Mechanical and shear stress initiate endothelial damage and accumulation of lipoproteins, triggering inflammatory events and attracting inflammatory cells, and calcification. However, there are some discrepancies between the two diseases. Smooth muscle cells are mainly involved in atherosclerosis, whereas in aortic valve calcification, smooth muscle cells are not seen and valvular interstitial cells play a role in the aortic valve calcification [77]. In aortic valve, pulsatile shear stress on the ventricular side and low and reciprocating shear stress on the aortic side are observed. Whereas the artery is exposed to sustained laminar flow [78]. Malformations of the aortic valves, such as bicuspid aortic valve, contribute to valve calcification, which is also different from atherosclerosis. Calcific aortic valve stenosis is characterized by gradual leaflet thickness and outflow obstruction, while events in patients with coronary atherosclerosis are mainly acute luminal thrombotic obstruction or narrowing. Therefore, treatment and prevention for these diseases are also different. Figure 8 summarizes common and uncommon characteristics of vascular calcification and valvular calcification.
5.
Conclusions
The progression of plaque burden was associated with aging for all vascular beds, while atherosclerotic patterns were different depending on the type of artery. In the coronary artery, vascular calcification burden correlates with the severity of luminal stenosis. However, in progressive lesions, the presence of coronary calcification is not binary but depends on the type of calcification. The peripheral arteries of the lower extremities are influenced by both medial and intimal calcification, and the former minimally contributes to luminal stenosis. Valvular calcification mainly occurs in aortic valves and has many similarities with vascular calcification. Because of the lack of understanding of vascular and valvular calcification, treatment options remain limited. Thus, more studies are needed to understand the mechanisms of vascular and valvular calcification.









 DownLoad:
DownLoad: