Starting from the correspondence between the Cattaneo hyperbolic heat equation and the stochastic formulation based on Poisson-Kac processes, that holds solely for one-dimensional spatial models, this article analyzes three paradigmatic problems in the hyperbolic theory of heat and mass transport. The problems considered involve unbounded, semi-bounded and bounded domains, and are aimed at : (i) highlighting analogies and differences between the two approaches (Cattaneo vs Poisson-Kac), (ii) addressing the role of a bounded propagation velocity in order to regularize the properties of the solutions of heat/mass transport problems. A typical example of the latter phenomenology is expressed by boundary-layer regulatization of interfacial fluxes. The case of transport in bounded domains permits to pinpoint unambiguously the need of a stochastic interpretation of the transport equation in order to unveil the occurrence of physical inconsistencies that may occur in the linear Cattaneo hyperbolic model in some range of parameter values.
1.
Introduction
Thermal and heat transport problems have recently become a fertile and exciting field of theoretical and applied research due to advances in phononics and in the miniaturization of microelectromechanical systems [1,2]. New effects have been discovered (e.g. thermal rectification) and new devices tested (thermal diodes and transistors) [3]. On equal footing, the analysis of microscale thermal problem has questioned the application of classical phenomenological laws, such as the Fourier law, and more generally the formulation of transport equations in out-of-equilibrium conditions. There is enough experimental and theoretical work indicating that the classical Fourier constitutive equation, leading to parabolic heat transport models, is not completely adequate for processes evolving at small length and short time scales [4,5].
The natural physical candidate for a generalization of the Fourier law is represented by the hyperbolic models defined by constitutive equations with memory for the heat flux. The archetype of this class of models is the Cattaneo heat transfer equation [6,7], ∂T(x,t)/∂t+τ∂2T(x,t)/∂t2=D∇2T(x,t), where D is the thermal diffusivity, and τ>0 a characteristic relaxation time, that provides the evolution of thermal fronts possessing finite propagation velocity [8,9]. Hyperbolic transport models and heat waves have found a variety of applications in several physical problems (second-sound in helium, phonon-assisted thermal transport, etc.) [4,5,10], and recently they have been extensively applied and further elaborated for micro- and nanoscale applications [13,14,15]. A further generalization of the Cattaneo model is represented by the theory developed by Guyer and Krumhansl [11,12] based on a linearized Boltzmann equation for phonon-assisted heat transfer.
Following parallel pathways, mass (solute) transport in 17ic systems displays phenomenologically clear deviations for a pure Fickian behavior, referred to as "case Ⅱ diffusion" in the mass transport literature [16,17]. The origin of this anomalous behavior stems from the swelling of the 17ic matrix, causing the coupling between mass (solute) transport and viscoelastic stress relaxation [18,19]. The use of hyperbolic and Cattaneo-based models encompasses also biomedical applications of controlled release of active principles [20].
In a more general perspective, the mathematical structure of the Cattaneo equation has been embedded in a consistent thermodynamic theory of non-equilibrium phenomena thanks to the seminal work by Müller and Ruggeri [21] that is commonly referred to as "extended theory of thermodynamics". Extended thermodynamics generalizes the classical approach of irreversible thermodynamics [22] by including, in the definition of the thermodynamic variables, the explicit contribution of the fluxes that vanish in equilibrium conditions. This approach has been further elaborated and extended by the contribution of Jou, Casas-Vazquez, Lebon, any many others [23,24,25].
There is however a formal bottleneck in all the hyperbolic formulations of thermodynamic and transport models grounded on the Cattaneo equation deriving from the fact that the latter does not preserve positivity (of the local concentrations) in space dimensions greater than one. This has been reported in [26] by considering the Green function for the two-dimensional Cattaneo heat equation.
It should be clearly stated that this does not inficiate neither the reach of extended thermodynamic theories nor the validity of many of the results found within this approach. Similar problems involving the deprecated occurrence of negative density values arise in the application of Grad's 13 moment expansion, and are ultimately a consequence of the approximations (essentially a truncated power-series expansion) underlying these approaches [27]. However, the positivity issue remains as a standing problem requiring a formal solution in the development of the theory.
Recently, in order to overcome the positivity issue, a stochastic approach to hyperbolic transport problems has been proposed, applicable in any space dimension, via the concept of Generalized Poisson-Kac (GPK) processes [28,29,30,31]. These developments originate from the work by Mark Kac that in a series of lectures, (dated 1956 and subsequently reprinted in 1974), showed that the one-dimensional Cattaneo equation represents the evolution equation for the probability density function associated with a simple stochastic differential equation driven by Poissonian fluctuations [32,33]. The trajectories of the process introduced by Kac are almost everywhere smooth, contrarily to Wiener fluctuations, usually considered in statistical physics, that are characterized by almost nowhere differential trajectories possessing fractal character [34,35]. The transport equations originating for GPK theory are indeed hyperbolic and involve only the first-order derivatives with respect to time and space coordinates, but require a vector-valued system of partial probability density functions [28,29,30,31]. This vector-valued description of the concentration, parametrized with respect to the state of the stochastic perturbation, physically corresponds to a spinorial description of the concentration fields [36], and is conceptually similar to the 4-wave formulation of the Dirac's equation compared to its non-relativistic counterpart (the Schrödinger equation). It is convenient to refer to it as the "partial-wave formulation" of a hyperbolic transport problem possessing finite propagation velocity (see Section 2). The importance of this kind of models has been envisaged by Rosenau in an illuminating article on kinetic theory [37].
Albeit the stochastic theory indicates that the original Cattaneo equation and the stochastic partial-wave formulation are equivalent in one spatial dimension (see Section 2 for details), there are indeed subtle issues that arise whenever transport problems in bounded domains (intervals) are considered, associated with the setting of proper boundary conditions accounting for the wave-like propagation of the partial concentration waves [38]. While the Cattaneo model admits a stochastic explanation, at least for one-dimensional spatial problems, the Guyer-Krumhansl model does not correspond to any underlting stochastic dynamics, and even in one-dimensional problems the associated Green function may attain negative values [39,40]. For this reason this model and its generalizations are not considered in the present work.
Due to the practical interest in the development of hyperbolic transport models at nanoscale, and their theoretical relevance (as only a hyperbolic model can be relativistically covariant, i.e., consistent with the space-time structure emerging from special relativity [21,41]), this article analyzes the mathematical description and some physical implications of the partial wave representation of hyperbolic transport models of heat and mass transport, focusing on the physical advantages of this approach compared with the classical one based exclusively on the evolution of the overall concentration/temperature and on the connection between finite propagation and the flux regularity. One-dimensional paradigmatic problems are considered, since only in this case the partial-wave representation can be compared with the corresponding Cattaneo equation for the overall concentration/temperature field (see Section 5).
It should be mentioned that some of the results obtained may have also some interest in the formulation of transport equations (continuous hydrodynamic limit) of anomalous transport processes, e.g. derived from the Continuous Time Random Walk paradigm [42,43,44], as they suggest that the stochastic spinorial (partial-wave) description of a process may capture finer details that cannot be enucleated when solely the evolution equation for the overall concentration is considered.
The article is organized as follows. Section 2 defines the setting of the problem and the different representations of a linear hyperbolic transport equation in one spatial dimension, based either on the Cattaneo equation for the overall concentration or on the partial-wave formulation derived from the undelying stochastic dynamics. Section 3 develops the closed-form expression for the spinorial Green function in the partial-wave representation. Section 4 analyzes heat transport problems arising from boundary layer theory in order to show how the occurrence of a finite propagation velocity regularizes the behavior of interfacial fluxes still maintaining the long-term large-distance properties that can be derived from the corresponding parabolic models. Finally, Section 5 addresses the simplest conceivable problem in heat transport: the stationary temperature distribution in a material slab kept at two different temperatures at the endpoints. Albeit its apparent "triviality", the analysis of this problem is physically enlightning, as it indicates the relevance of the partial-wave formulation, and the possible occurrence of negative temperature values in particular (and extreme) situations, that cannot be revealed using an approach exclusively based on the overall concentration (temperature) fields. The case of boundary conditions on the fluxes, corresponding in parabolic schemes to the Neumann boundary conditions, has been analyzed in [38] within the partial-wave formulation of hyperbolic transport models. The analysis is not repeated here and the reader is referred to [38] for details.
2.
Setting of the problem
Consider the simplest stochastic motion X(t) possessing finite propagation velocity b, defined by the evolution equation
where b>0 is a constant velocity, and χ(t,λ) a Poisson process characterized by the transition rate λ>0. This is the classical model proposed by M. Kac in order to derive the telegraphers' equation from stochastic grounds [33].
Its statistical description involves two partial probability densities p±(x,t) where p±(x,t)=Prob[X(t)∈(x,x+dx),(−1)χ(t,λ)=±1], (henceforth X(t) denotes the stochastic process at time t and x(t) a realization of it), that are solutions of the hyperbolic system of equations
By analogy, it is possible to infer from this class of stochastic dynamics undulatory transport models for mass, momentum and energy [31]. Throughout this article we refer mainly to the heat transfer case, but the analysis of mass transport problems would be completely analogous.
Eq. (2.2) suggests that a one-dimensional heat-transfer model possessing finite propagation velocity, and fulfilling the positivity requirement (the temperature, viewed as absolute temperature, cannot attain negative values) would require two scalar fields T+(x,t) and T−(x,t) possessing the physical dimension of temperature and evolving according to eq. (2.2), i.e.,
with the same meaning for b and λ as above. The system's temperature is the sum of these two fields
It should be stressed that the physical meaning of the two temperatures T±(x,t) corresponds to the temperatures associated with the two disjoint particle sub-ensembles characterized by a positive ("+") or negative ("-") orientation of the local velocity at time t and position x, respectively. As eq. (2.2) represents the evolution of two waves moving in opposite directions and recombining with each other at rate λ, the two fields T±(x,t) will be simply referred to as the "partial heat waves".
Considering absolute temperatures expressed in Kelvin, it follows that
that henceforth will be referred to as the positivity requirement for the two partial heat waves. With reference to the waves T±(x,t), the local heat flux Jq(x,t) is defined by the equation
Alternatively, given T(x,t) and Jq(x,t), the two partial waves can be simply recovered from the relations
The temperature T(x,t) is a solution of the balance equation
where the heat flux is defined by the constitutive equation
where D0=b2/2λ that, in a heat-conduction problem, corresponds to the ratio k/ρcp, where k is the thermal conductivity, ρ the density and cp the specific heat at constant pressure. In order to keep strict the analogy with mass transfer problems, stemming from the mathematically equivalent formulation of the Fourier and Fick equations for conductive/diffusive fluxes, we have defined the heat flux Jq(x,t) in eq. (2.6) in a rather uncoventional way, namely as the classical heat flux divided by ρcp. Equation (2.9) corresponds to a constitutive equation of Cattaneo type, and from eqs. (2.8)-(2.9) it follows that T(x,t) is a solution of the Cattaneo equation
Alternatively, one can explicit the heat flux from eq. (2.9), namely
where τc=1/2λ, the symbol "∗" indicates convolution with respect to the time variable from time t=0 to the actual time t, and D(t)=D0e−λ/τc. With this notation, the temperature field is also a solution of the equation
that is formally analogous to the convolution-type equation used for describing anomalous transport problems using fractional operators (Riemann-Liouville derivatives) [43,44,45].
Therefore, T(x,t) can be viewed as a solution of each of the three equations (2.3)-(2.4), (2.10) and (2.12), that are mathematically equivalent. We refer to eqs. (2.3)-(2.4) as the Poisson-Kac formulation, to eq. (2.10) as the Cattaneo formulation and to eq. (2.12) as the memory kernel formulation of one and the same heat transfer problem. The mathematical equivalence between these three formulations for the evolution equation of the temperature profile T(x,t) does not mean that the solutions of the three above mentioned problems should be physically equivalent. This apparent paradox becomes conceptually clear if one considers that any balance equation is complemented with a system of initial and boundary conditions that defines a particular solution uniquely. The way initial and boundary conditions are expressed depends significantly on the choice of the primitive quantities used to formalize a transport problem. Let us give an elementary example, as regards the initial conditions.
In the Poisson-Kac formulation of the problem, the basic (primitive) quantities are the two partial heat waves T±(x,t), and the initial conditions are simply the values attained by these two fields at t=0
where T±,0(x) are arbitrary non-negative functions of the position x. Eqs. (2.13) define uniquely the overall initial temperature T(x,0) and the initial heat flux Jq(x,0) via eqs. (2.4) and (2.6)
In the Cattaneo formulation, it is natural to express the initial condition in two ways: either (ⅰ) by fixing the initial temperature profile T(x,0)=T0(x) and the initial heat flux Jq(x,0)=J0(x), or (ⅱ) by imposing the initial temperature T(x,0), and its time-derivative at t=0, ∂T(x,t)/∂t|t=0=θ0(x). In the latter case, the initial heat flux can be derived from eq. (2.8) as
where x∗ is some reference position. The initial flux Jq(x,0) is unambiguously defined in the case of unbounded propagation, i.e., x∈(−∞,∞), as regularity conditions at infinity dictate lim|x|→∞Jq(x,0)=0, so that, setting x∗=−∞, eq. (2.14) becomes
However, the situation is different in bounded domains x∈(0,L), where e.g. the heat balance equation is equipped at the boundaries with Dirichlet-type conditions. In this case, θ0(x) defines the initial flux Jq(x,0) modulo an additive constant equal to the value of the flux at some point x∗∈[0,L].
As regards the boundary conditions, each transport formulation implies some natural setting of the boundary conditions. For example, in the Poisson-Kac formulation, this implies to fix the values either of T+(x,t), of T−(x,0) or of the superposition of the partial waves at the endpoints of the intervals, enforcing the positivity requirements. Such a setting provides a simple and elegant interpretation of apparently strange physical phenomenologies arising in the solution of the Cattaneo equation such as the occurrence of the maximum-flux condition [46,47], as addressed in [38].
With respect to all the other formulations, the Poisson-Kac description, involving the system of two partial waves T±(x,t) enforces a more stringent physical condition on the temperature field, namely that both T±(x,t) should be greater than zero (positivity requirement) and not solely the overall temperature
as in the Cattaneo or in the memory-kernel formulation. The effect of this more restrictive requirement will become clear in Section 5, in connection with the simplest problem of stationary heat conduction in a finite domain.
3.
Green functions for the Poisson-Kac formulation
In this Section, we consider the propagation of the Poisson-Kac equations (2.2) over the real line, x∈(−∞,∞), and the representation of the Green functions for the partial probability waves p±(x,t). This is apparently a rather simple problem, as the Green function for the Cattaneo equation 2.10) is known [48,49]. Nevertheless, this problem presents some interesting physical issues, by considering that the fundamental solution for the Cattaneo equation involves the initial values for p(x,t) and its time derivative ∂p(x,t)/∂t, and some technical problems arise when this information is transferred into the partial-wave representation.
In point of fact, the latter (partial-wave) representation is physically interesting from several points of view:
● it enables a fully local description of the transport problem, in that solely the values of p+(x,t) and p−(x,t) at any initial time instant t=t0 are needed in order to predict its future evolution. Conversely, in the Cattaneo formulation one need to specify p(x,t0) and ∂p(x,t)/∂t|t=t0, namely its first-order time derivative;
● imbedding Poisson-Kac processes in the Minkowski space-time of special relativity (in the present case when only a single spatial coordinate is considered), the partial probability waves transform as probabilistic spinorial quantities [36], and the associated Green function can be therefore referred to as the spinorial Green functions of the problem.
By considering that the spinorial Green function has never been explicited and physically discussed, it justifies the content of the present Section.
In deriving the analytical expression for the spinorial Green function G(x,t), we refer to the probabilistic notation, namely p±(x,t), p(x,t)=p+(x,t)+p−(x,t) and J(x,t)=b[p+(x,t)−p−(x,t)]. The transposition to a heat-transfer problem, simply requires the substitution of p±(x,t) with T±(x,t).
Consider the Cattaneo formulation associated with the Poisson-Kac process (2.1)-(2.2) for x∈R, namely eq. (2.10) with T(x,t) substituted by p(x,t), equipped with the initial conditions
and with regularity conditions at infinity. The general solution of this problem admits a closed-form solution [48]
where "*" indicates here convolution with respect to the spatial coordinate, h(x)∗k(x)=∫∞−∞h(x−ξ)k(ξ)dξ=k(x)∗h(x), and the kernels Kh(x,t), h=1,2 are defined in the Appendix.
Since ∂p(x,t)/∂t=−∂J(x,t)/∂x, where J(x,t) is the probability flux, the initial conditions (3.1) can be expressed in terms of the partial waves as
In deriving the second eq. (3.3), the extension of the balance equation at t=0+=limε→0ε, ε>0 has been enforced, i.e., ∂p(x,t)/∂t|t=0+=−∂J(x,t)/∂x|t=0+=−b[∂p+(x,t)/∂x−∂p−(x,t)/∂x]t=0+. From the regularity at infinity, that holds strictly in the present case, as the kernels possess compact support, it follows that the probability flux J(x,t) can be expressed as
and consequently the flux J(x,t) attains the convolutional expression
where
Substituting the expression for f(x), g(x) in terms of the initial condition for the partial waves p0±(x) it follows that
and analogously for J(x,t) in eq. (3.5). Consider a generic convolutional integral involving the spatial derivative of the initial profile of the partial probability waves. Enforcing regularity at infinity, it follows that
and the evolution equations for p(x,t) and J(x,t) can be expressed as a spatial convolution of the initial concentration p0(x)=p0+(x)+p0−(x) and of the initial flux J0(x)=b[p0+(x)−p0−(x)] as
The expression for −∂H2(x,t)/∂x is straightforward since
and is explicitly reported in the Appendix. In turn, it is much more cumbersome to derive the expression for H1(x,t) starting from its definition (3.6). For this reason, it is suitable to follow a more "physically oriented" approach to this problem.
To begin with, observe that the flux J(x,t) satisfies the same equation as p(x,t), i.e.,
Next, consider two transport problems, differing from each other in the initial conditions, as depicted in Figure 1:
● Case (1): Symmetric initial conditions for the partial probability waves, i.e.,
which implies
● Case (2): Antisymmetric initial conditions for the partial probability waves, i.e.,
and therefore,
Let p(1)(x,t) and p(2)(x,t) be the solutions of the two above defined problems, and J(h)(x,t) the associated fluxes. From eq. (3.9) it follows that
In the antisymmetric case, the solution p(2)(x,t) is nothing but the normalized flux J(1)(x,t)/b associated with Case (1). This follows from the fact that J(x,t) is a solution of the same equation, and that eq. (3.15) are the initial conditions for the flux in Case (1). Therefore,
But from eq. (3.9), substituting the initial conditions for Case (1), one obtains that
From eqs. (3.17)-(3.18) the expression for H1(x,t) follows
Therefore, expressing p(x,t) and J(x,t) in terms of the partial waves p±(x,t), eq. (3.9) takes the form
in which the matrix-valued kernel is expressed in terms of K1(x,t) and of the first derivatives of K2(x,t). In eq. (3.20) the functional dependence of the kernels on x and t has been omitted, for lightening the notation. Expliciting with respect to p±(x,t), the spinorial Green function G(x,t) for the partial probability waves,
follows
where ∂xK2=∂K2(x,t)/∂x, ∂tK2=∂K2(x,t)/∂t. Performing the algebraic manipulations, and using the expressions for the kernels and their derivatives reported in the Appendix, a compact expression for G(x,t) can be derived: the spinorial Green function G(x,t) is the superposition of two contributions,
where G(δ)(x,t) is an impulsive kernel,
and G(c)(x,t) is the continuous, compactly supported part,
where z=√t2−x2/b2, and η(ξ) is the Heaviside step function, η(ξ)=1 for ξ>0 and η(ξ)=0 for ξ<0.
Expressed with respect to the partial probability waves, the spinorial Green function G(x,t) is represented by a symmetric matrix attaining a very compact form. Modulo the prefactor A(x,t)=λe−λtη(bt−|x|)/(2b), the diagonal entries G(c)1,1(x,t), G(c)2,2(x,t) can be expressed in terms of a single function G(x,t;b,λ)=(t+x/b)I1(λz)/z, depending on the parameters b and λ characterizing the stochastic process,
where only the sign of the velocity ±b changes. This is related to the fact that p+(x,t) represents a forwardly propagating wave, while p−(x,t) propagates backward in space. As a consequence of this, p+(x,t) admits solely an impulsive contribution centered at x=bt, while the Dirac-delta impulse for p−(x,t) is located at x=−bt.
The analytical expressions (3.21)-(3.25) obtained for p±(x,t) can be compared with the stochastic simulations of the random-walk process (2.1). In the simulations, an ensemble of Np=5×106 particles is considered, initially located at x=0, and evolving in space according to eq. (2.1). As initial condition for the stochastic perturbation, let ¯p0+=Prob[(−1)χ(0,λ)=1] and ¯p0−=1−¯p0+, which imply that p±(x,0)=¯p0±δ(x).
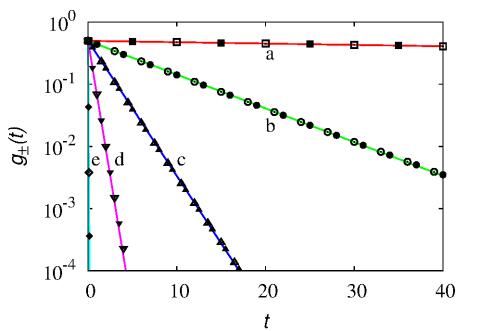
To begin with, consider balanced initial conditions, namely ¯p0+=¯p0−=1/2, setting D0=1 and varying b. From eqs. (3.21)-(3.25) the partial-wave profiles are given in this case by the expressions
Let g±(t) be the amplitudes of the impulsive contributions for the two partial waves. Figure 2 depicts the time evolution of g±(t) for several values of b obtained from stochastic simulations (symbols) compared with the analytical result that predicts g±(t)=e−λt/2. Since D0=1 a.u. is kept fixed, different values of b determine different λ's, i.e., g±(t)=exp(−b2t/2D0)/2, and therefore the relaxation of the impulsive contribution is faster for higher velocities b.
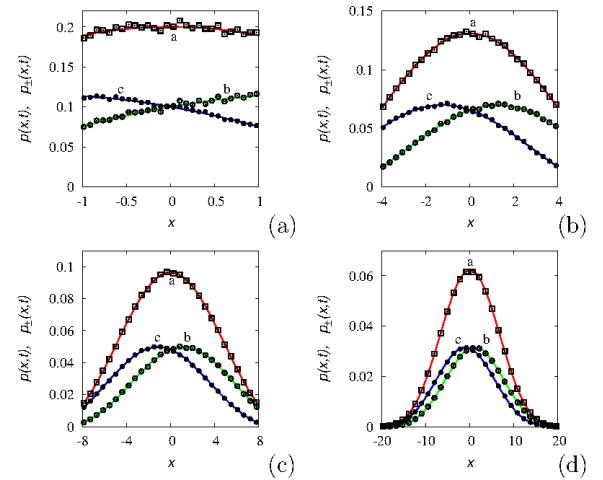
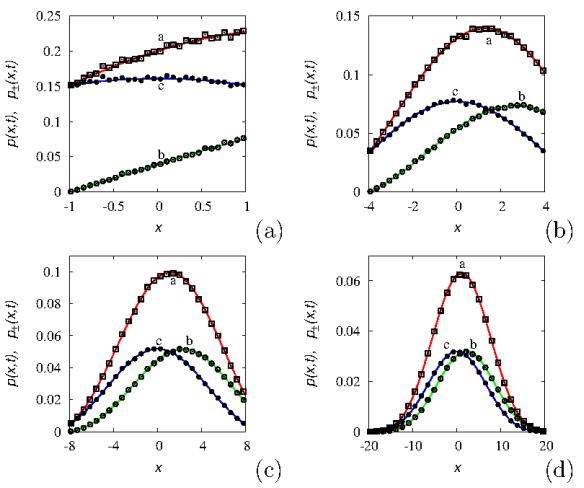
Figure 3 reports the comparison of the continuous (smooth) part of the partial-wave profiles and of the overall density p(x,t), in the balanced case obtained from stochastic simulations (symbols) and from the analytical expressions (3.21), (3.22), (3.25) at several time instants. An analogous plot is reported in Figure 4 in the unbalanced case where ¯p0+=1, ¯p0−=0.
In both cases the agreement between stochastic simulations and the analytical expression is excellent, and the small fluctuations at short time scales (panels (a) in Figures 3-4) derive from the relatively small number Np of particles considered in the stochastic simulations.
4.
Regularization of boundary-layer problems
In this Section we consider simple boundary-layer problems approached within the hyperbolic model described in Section 2, in order to show that the constraint of a finite propagation velocity, characteristic of eq. (2.3), regularizes the singularities often appearing in boundary-layer analysis associated with the interfacial fluxes.
Consider the conduction problem eq. (2.3) on the semi-infinite line x∈(0,∞), filled with a material phase at rest, characterized by the thermal diffusivity D0, and assume the presence of an interface (wall) at x=0. Without loss of generality, suppose to shift the temperatures so that the initial temperature is equal to zero,
while the wall temperature at x=0 is kept constant at a given value T0>0,
This problem can be conveniently approached in the Laplace domain, indicating with s the Laplace variable, and with a "hat", ˆf(s) the Laplace transform of a function f(t) of time t, ˆf(s)=L[f(t)]. From eqs. (2.8)-(2.9) one obtains
where ˆT(x,s) and ˆJq(x,s) are the Laplace transforms of T(x,t) and Jq(x,t), respectively. It follows from eq. (4.3) that ˆT(x,s) satisfies the second-order equation
where D0=b2/2λ is the thermal diffusivity. Taking into account the regularity conditions at infinity (x→∞), and enforcing the boundary condition (4.2), the Laplace transform of the normalized thermal profile q(x,t)=T(x,t)/T0 is given by
Considering that [50]
where, as in the previous Section, η(ξ) is the Heaviside step function, I1(ξ) the modified Bessel function of the first kind and order 1, and α=x/b, c=b2/2D0=λ, it follows from eqs. (4.5)-(4.6) that
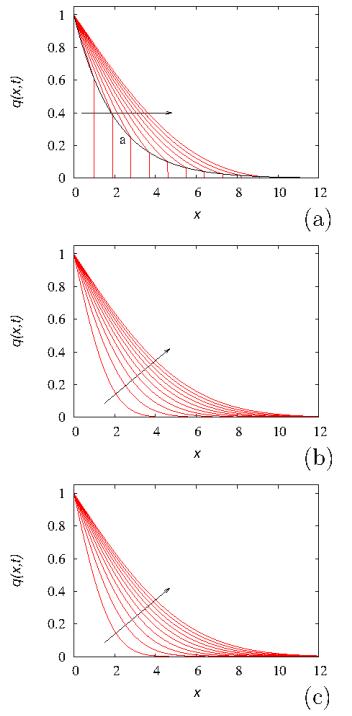
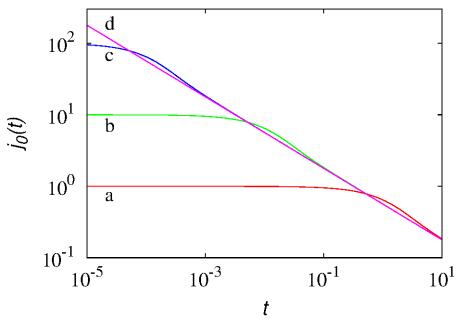
Figure 5 panels (a) and (b) depict the normalized thermal front q(x,t) vs x at several time instants obtained from (4.7) at two different values of the propagation velocity: b=1 a.u. (panel a), and b=10 a.u. (panel b), keeping fixed D0=1 a.u.
Observe that the Poisson-Kac (Cattaneo) model is characterized by a discontinuity of temperature profile at the moving front edge x∗(t)=bt, since from eq. (4.7) it follows that q(x∗−,t)=limε→0q(x∗−ε)=e−cx∗/b=e−bx∗/2D0, ε>0, while q(x∗+,t)=limε→0q(x∗+ε)=0. This edge discontinuity can be clearly observed from the data at lower values of b (such as b=1 in panel (a)), and decreases exponentially as the front propagates. Panel (c) in figure 5 corresponds to the Kac-limit solution of the Poisson-Kac (Cattaneo) model when b,λ→∞, keeping fixed the group D0=b2/2λ, that provides the classical parabolic model
equipped with the same initial and boundary conditions, that in the present case is given by T(x,t)=T0erfc(x/2√D0t), where erfc(ξ) is the complementary error function of argument ξ.
Next, consider the interfacial flux. From the second equation (4.3) and from (4.5) it follows that
so that the Laplace transform of the normalized interfacial flux j0(t)=Jq(0,t)/T0 is given by
the inverse Laplace transform of which takes the expression [50]
where I0(ξ) is the modified Bessel function of the first kind and order 0. Let us comment the physical properties underlying these expressions.
● Since I0(0)=1, it follows from eq. (4.11) that
i.e., the interfacial flux in a transport model possessing finite propagation velocity is always a smooth and bounded function of time, even at t=0. Divergence of J0(t=0) can occur only if one let b→∞, such as in the Kac limit of the model leading to the parabolic heat equation (4.8). In point of fact, the interfacial flux deriving from the solution of the parabolic transport model is expressed by
and displays the characteristic power-law singularity j0(t)∼t−1/2 for t→0.
● From the asymptotic expansion of the Bessel function for large arguments ξ>>1, I0(ξ)=eξ[1+O(1/ξ)]/√2πξ, one obtains for b2t/2D0>1,
implying that, for any values of D0 and b, the long-time scaling behaviour of the interfacial flux coincides with that of the corresponding parabolic transport model. This phenomenon is depicted in Figure 6.
● In a heat transport model possessing finite propagation velocity the invariant rescaling, T(x,t)=ϕ(x/√t) characterizing the parabolic limit (4.8) does not hold true, other than in the asymptotic limit, i.e., for large time scales.
The regularization effects induced by a finite propagation velocity, shown above with the aid of a simple example, arise also for more general boundary-layer problems. Indeed this is a generic property, dictated by the fact that the fluxes in this class of models are necessarily bounded due to the constitutive equation (2.6) whenever the the initial temperature field T(x,t=0) is bounded and the boundary-conditions are non-singular function of time.
In higher dimensional problems, the analogy between the Cattaneo equation and stochastic models of transport possessing finite propagation velocity breaks down [29], but the qualitative result of a flux regularization applies also to the Generalized Poisson-Kac (GPK) formulation of the (heat) transport equations. For details on the GPK formulation of transport models see [31].
Below, we address another classical two-dimensional problem that, under some simplifying assumptions, involves a one-dimensional formulation of the stochastic perturbation. Consider a two-dimensional straight channel of width W, in which a stationary velocity field v(x)=(vx(y),0) is defined (x is the axial coordinate, and y the transversal coordinate). The inlet fluid stream enters at constant temperature Tin, while the solid walls of the channel are kept at constant temperature Tw. This is the classical Leveque problem [51], that under the simplifying assuption of negligible axial conduction, is described by the equation [52]
equipped with some initial condition T|t=0=Tin(x,y), and with the inlet and wall conditions
In the Leveque boundary-layer problem one is mainly interested to the stationary heat flux at the solid walls, that is related to the width of the thermal boundary layer that develops along the channel for axial lengthscales shorther than the width of the channel itself.
The corresponding Poisson-Kac (Cattaneo) formulation of the problem involves two partial temperature waves T±(x,y,t). This is due to basic simplifying assumption of neglecting axial conduction, meaning that the unique source of "stochasticity" is related to transversal heat conduction. The balance equations for T±(x,y,t) are thus given by
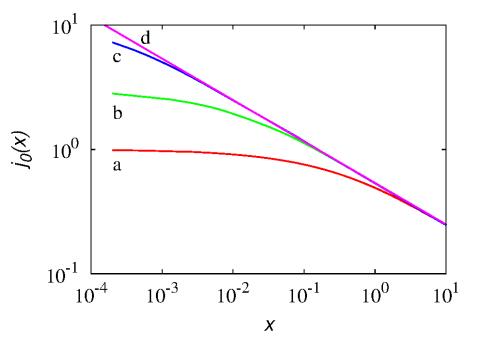
We consider a shear flow, vx(y)=y, W=20, D0=1 and Tw=1, Tin=0 a.u., and solve eqs. (4.17) with a finite-difference scheme in a channel possessing a length L that is much larger than W, L=100. From the stationary solutions T∗±(x,y)=limt→∞T±(x,y,t), the normalized wall flux j0(x)=b[T∗+(x,0)−T∗−(x,0)]/[Tw−Tin] is obtained, and its graph is depicted in Figure 7 for different values of the "stochastic" velocity b. These data should be compared with the boundary-layer solution of the parabolic eq. (4.15) that provides the classical Leveque scaling for a shear flow (i.e., for a flow vanishing at the wall, and locally linear in the neighbourhood of y=0),
Also in this case, the Poisson-Kac solution possesses the same qualitative features envisaged in the previous boundary-layer problem, namely: (ⅰ) the finite propagation velocity regularizes the behaviour of the flux at the interface, and (ⅱ) the asymptotics (in the present case, the large-distance properties) of the Poisson-Kac solution converges to that of the corresponding (limit) parabolic transport model.
5.
Stationary solutions with Dirichlet conditions: positivity
Consider the simplest heat transfer model on the interval [0,L], where the temperature is kept fixed at the endpoints at two constant values T0,TL>0,
Without loss of generality, suppose TL>T0. From the Cattaneo and from the memory-kernel formulations, one derives immediately that at steady-state, for sufficiently long times (t→∞), d2T(x)/dx2=0, thus
as one would obtain by enforcing the Fourier law with a constant heat conductivity.
Let us analyze the same problem within the Poisson-Kac formulation. This formulation differs from the other two in that, from physical reasons, a detailed positivity requirement should be enforced on each T±(x) separately, as expressed by (2.5). Consider the Poisson-Kac heat transport model (2.3). From the overall balance eq. (2.8) at steady state it follows that Jq(x)=J0=constant, and from eq. (2.3) one obtains
where B=J0/2D0. Therefore,
Imposing the Dirichlet boundary conditions (5.1) to T(x)=T+(x)+T−(x), one obtains
which implies that B=(T0−TL)/2L<0. Consequently, the stationary profiles for T±(x) can be expressed as
where C is a parameter to be determined. Before expliciting C as a function of the other physical parameters, it is important to stress that the detailed positivity requirement reduces in the present case, (as TL>T0, by hypothesis), to T±(x)|x=0≥0, and implies C≥0, T0−C≥0, i.e.,
Condition (5.7) can be interpreted as follows: there is a C∞-family of solutions of the stationary partial wave equations (2.3), parametrized with respect to the real-valued parameter C, such that, if C satisfies the inequalities (5.7), the resulting stationary profiles T±(x) satisfy the detailed positivity requirement (2.5).
The constant C entering eqs. (5.6) is not independent of the flux J0, that in turn is related to T±(x) by J0=b[T+(x)−T−(x)]. Therefore,
which returns
Condition C≥0 is always satisfied while, C≤T0 implies that
This means that for any positive value of T0, there exists a critical value T∗L of TL, expressed by eq. (5.10), i.e., T∗L=T0r∗, such that if TL>T∗L then the stationary partial temperature waves attain negative values.
This result can be easily derived within the Poisson-Kac formulation of the transport problem, in which the basic quantities are the partial temperature waves T±(x) propagating at constant velocity b in the two opposite directions, while it is hidden within the Cattaneo and in the memory-kernel formulations which consider exclusively the overall temperature field T(x,t). Of course, due to the equivalence between these three formulations in one-dimensional spatial problems, one would in principle derive this result from the Cattaneo formulation, by imposing as a consistency requirements the conditions
that corresponds to eq. (2.7). But, the positivity requirement of the quantities in eq. (5.11) cannot be easily derived within the Cattaneo approach, as it is an intrinsic by-product of the stochastic formulation of the process in terms of partial waves.
In order to avoid misunderstandings, it is important to stress out that the critical ratio r∗, can hardly be met in real physical experiments. The ratio r∗ is proportional, modulo an additive unit constant, to the ratio of the velocity of the thermal wave b times the characteristic length of the specimen, divided by the "thermal diffusivity" D0. For a metallic object (say brass), D0=3×10−5 m2/s, and b=5.5×103 m/s, for silicon D0=9.4×10−5 m2/s and b=9.7×103 m/s [53]. If one consider a specimen of length L=1 cm, it follows that r∗≥106 in both cases. Therefore, if one side of the sample is kept at constant temperature T0=1 K, the critical temperature at the other endpoints is higher than T∗L=106 K, which is approximately the order of magnitude of temperature of the convective zone of the sun, the upper layer of the sun's interior. Therefore, one should not be worried about the violation of positivity requirement when using the one-dimensional Cattaneo model in real-world heat transfer experiments, as for such high temperature differences, other physical phenomena enter into play (changes of state), and the simple (linear) formulation of the heat transfer problem becomes meaningless.
Nevertheless, the conceptual and theoretical importance of this result is rather clear: it indicates a criticality in the heat transport model based on the Cattaneo equation (breakdown of positivity of the partial temperature waves) that can be discovered only within the stochastic (partial wave) formulation of the problem.
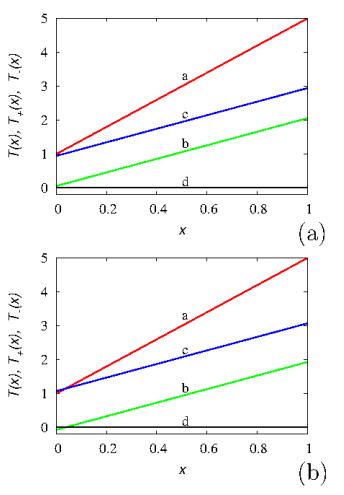
To give a numerical example, set D0=L=T0=1 a.u., TL=5 a.u. and vary the velocity b. Figure 8 depicts the steady-state profiles above (b=4.5, panel a) and below (b=3.5, panel b) the threshold b∗ defined by eq. (5.10). Fixing TL, T0, D0, and L, the threshold in the velocity is given by b∗=D0(TL−T0−1)/L, and negative partial temperature profiles are expected for b<b∗. In the present case b∗=4. Below the threshold b∗ (panel b), while the overall temperature profile reproduces, as expected, the linear behavior ranging from T0 to TL, the partial temperature T+(x) attains small but negative values in the neighbourhood of x=0. The occurrence of negative values becomes progressively amplified as TL/T0 increases above the threshold given by 1+bL/D0.
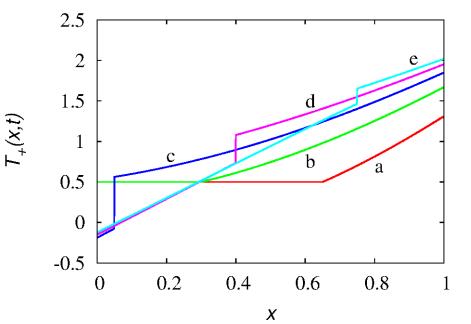
The time evolution of T+(x,t) in the case b=3.5 (i.e., above the threshold ensuring positivity) is depicted in Figure 9. The initial condition is set uniform, T(x,0)=T0 and T+(x,0)=T−(x,0)=T0/2. The occurrence of negative values of T+(x,t) stems from the recombination dynamics with the backpropagating wave T−(x,t) originating from x=L=1, which is characterized by the highest value of boundary temperature TL, and appears starting from the time instant tc=L/b>0.2 (just before the time instant corresponding to line (c) in figure 9), when the effects of the backpropagating partial wave reach the other endpoint x=0, determining negative values of T+(0,t) just to compensate the fact that T−(0,t)>T0.
From this analysis it follows that, in the setting of a linear hyperbolic transport scheme on an interval, the Dirichlet boundary conditions (5.1) should be modified in order to ensure the fulfillment of positivity requirements. The simplest way to modify eq. (5.1) is to consider
and
where [ξ] indicates the positive truncation of its argument ξ, namely [ξ]=ξη(ξ), where η(ξ) is the Heaviside step function, [ξ]=ξ for ξ>0, [ξ]=0 for ξ≤0. Observe from eqs. (5.12) that the boundary condition at x=0 defines the value at this endpoint of the forward propagating wave T+(x,t), given the external temperature T0 and the value of the partial temperature deriving from the backpropagating wave T−(x,t) incoming from positive x-value. The same argument with reversed orientation applies to (5.13) at the other endpoint x=L.
From eqs. (5.3) and (5.12)-(5.13) it follows that at steady state
where T+0 and T−L are the actual values of T+(x) and T−(x) at x=0 and x=L, respectively.
From TL>T0, it follows that J0<0 which implies that T+(x)<T−(x). Therefore T−L+BL−T+0>0, and thus T−L−T+(L)>0. Therefore, T−L=TL, so that the boundary condition at x=L is of regular Dirichlet type, namely T−|x=L=TL−T+|x=L.
This means that positivity issues can arise solely in the neighborhood of x=0, as also observed from the graphs of the temperature profiles depicted in figures 8 and 9. Enforcing eq. (5.2), two cases can occur:
● either T0−T−(0)>0, so that T+(0)+T−(0)=T0, and this occurs if condition eq. (5.10) is satisfied. In this case the regular profile (5.2) is observed at steady state;
● or T0−T−(0)<0, so that T+0=0, and correspondingly T(0)=T−0>T0. This means that the stationary profiles of the partial temperature waves are given by
and the value of the constant B follows from the condition
that implies
so that the temperature value at x=0+ is given by
In this case, the difference between the actual value of T(0+) and the value T0 externally imposed is
It is rather clear the physical phenomenology originating the possible occurrence of negative values at x=0, or the discontinuity at x=0 between reservoir temperature and the actually temperature at x=0+. If the endpoint temperature TL is sufficiently high, the backpropagating wave T−(x) may attain at x=0 values greater then T0. From this observation, it follows that a mismatch (discontinuity) will always arise at x=0 if T0=0. Using the boundary conditions (5.12), the Poisson-Kac formulation of the hyperbolic heat transfer would predict at x=0+ a value of temperature T(0+) expressed by eq. (5.18). While T=0 [K] is a limit temperature value that cannot be physically reached, the transposition of the same problem to a mass-transport situation is physically relevant. It indicates that, in the case of hyperbolic transport, the Dirichlet problem when one of the endpoints (x=0) is kept at vanishing concentration (corresponding to the case of a perfectly absorbing boundary) may not admit solution in which the partial concentrations are strictly non negative, or better to say, it may admit a solution satisfying the positivity requirement, by applying the modified boundary conditions (5.12)-(5.13), in which a sudden concentration jump occurs at one boundary as predicted by eq. (5.19).
6.
Concluding remarks
In this article, several prototypical problems involving heat/mass transport models possessing finite propagation velocity (hyperbolic models) have been solved in closed form, and their physical implications thoroughly discussed. Two qualitative results are worth of special attention.
The finite propagation velocity induces as a by-product the regularization of the associated fluxes (in the meaning that it eliminates the singularities that may characterize the initial temporal/spatial scaling of the fluxes associated with a classical parabolic transport model involving Fourier/Fick constitutive equations), still maintaining a perfectly analogous long-term behavior observed in their parabolic counterparts. This is a nice and physically consistent result, as it indicates that the occurrence of singularities in boundary-layer problems analyzed within the paradigm of parabolic transport models, are essentially - to quote Müller [21] - an artifact of the oversimplified assumption of strictly Fickian/Fourier constitutive models at very short time scales. In principle, it would be possible to verify experimentally this claim, although it is rather clear that any experimental falsification of this property, would automatically question the basic assumptions of special relativity, as with reference to the problem treated in Section 4, |J(0,t)|≤cT0, where c is the velocity of light in vacuo.
The second general observation that follows from the present analysis is that, although formally equivalent, the Cattaneo and the Poisson-Kac (stochastic) formulation of a heat/mass transport problem in one spatial dimension display conceptual differences when boundary value problems over finite domains (intervals) are considered. This depends on the physical information that is implicitly imbedded into the decomposition of a concentration field (say T(x,t)), solution of a one-dimensional Cattaneo equation, into partial concentration waves (T±(x,t)), each of which, separately, should satisfy a physically grounded positivity requirement, T±(x,t)≥0.
These observation can be conceptually extended to non-linear transport models and to higher dimensional systems. In the latter case, it is sufficient to consider for the stochastic-based formulation the generalization of the Poisson-Kac models developed in [29,30,31]. Of course, the connection with the Cattaneo model in the latter case cannot be performed as the Cattaneo equation in higher dimensions violates the positivity requirements and cannot be recovered from any stochastic model.
The extension of the analysis developed in this article for the spinorial Green function of the one-dimensional Poisson-Kac model can be in principle extended to spatial dimensions higher than one, starting from the mathematical works by Kolesnik [54,55,56] for some classes of Generalized Poisson-Kac processes.
Appendix: Explicit representation of Green-function kernels
In this Appendix, the analytical expressions for the kernels necessary to explicit in closed form the spinorial Green function G(x,t) are reviewed. Setting
the kernels K1(x,t), K2(x,t) entering the general solution of the Cattaneo transport scheme are given by
where I0(z), I1(z) are the modified Bessel functions of the first kind of order 0 and 1, respectively. Consequently,
and
where the properties I0(0)=0, dI0(z)/dz=I1(z) have been enforced.
Ackowledgments
One of the author (M.G.) thanks Alexander Kolesnik for useful and stimulating discussions during his stay at the Institute of Mathematics and Computer Science of the Kishinev University.
Conflict of interest
The authors declare no conflict of interest.
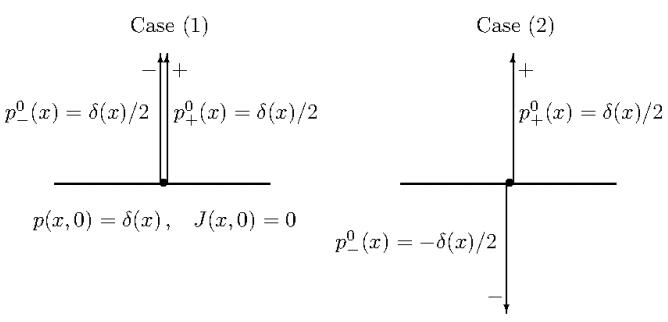









 DownLoad:
DownLoad: