Stability and Hopf bifurcation of an HIV infection model with two time delays

Yu Yang; Gang Huang; Yueping Dong; Yu Yang; Gang Huang; Yueping Dong

doi:10.3934/mbe.2023089

Mathematical Biosciences and Engineering

2023, Volume 20, Issue 2: 1938-1959. doi: 10.3934/mbe.2023089

Previous Article Next Article

Research article Special Issues

Stability and Hopf bifurcation of an HIV infection model with two time delays

1.
School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China
2.
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China

Academic Editor: Xiang-Sheng Wang

Received: 04 September 2022 Revised: 25 October 2022 Accepted: 30 October 2022 Published: 09 November 2022

This work focuses on an HIV infection model with intracellular delay and immune response delay, in which the former delay refers to the time it takes for healthy cells to become infectious after infection, and the latter delay refers to the time when immune cells are activated and induced by infected cells. By investigating the properties of the associated characteristic equation, we derive sufficient criteria for the asymptotic stability of the equilibria and the existence of Hopf bifurcation to the delayed model. Based on normal form theory and center manifold theorem, the stability and the direction of the Hopf bifurcating periodic solutions are studied. The results reveal that the intracellular delay cannot affect the stability of the immunity-present equilibrium, but the immune response delay can destabilize the stable immunity-present equilibrium through the Hopf bifurcation. Numerical simulations are provided to support the theoretical results.

Keywords:

Citation: Yu Yang, Gang Huang, Yueping Dong. Stability and Hopf bifurcation of an HIV infection model with two time delays[J]. Mathematical Biosciences and Engineering, 2023, 20(2): 1938-1959. doi: 10.3934/mbe.2023089

Related Papers:

[1]	Yousef Jawarneh, Humaira Yasmin, Abdul Hamid Ganie, M. Mossa Al-Sawalha, Amjid Ali . Unification of Adomian decomposition method and ZZ transformation for exploring the dynamics of fractional Kersten-Krasil'shchik coupled KdV-mKdV systems. AIMS Mathematics, 2024, 9(1): 371-390. doi: 10.3934/math.2024021
[2]	Ihsan Ullah, Aman Ullah, Shabir Ahmad, Hijaz Ahmad, Taher A. Nofal . A survey of KdV-CDG equations via nonsingular fractional operators. AIMS Mathematics, 2023, 8(8): 18964-18981. doi: 10.3934/math.2023966
[3]	Rasool Shah, Abd-Allah Hyder, Naveed Iqbal, Thongchai Botmart . Fractional view evaluation system of Schrödinger-KdV equation by a comparative analysis. AIMS Mathematics, 2022, 7(11): 19846-19864. doi: 10.3934/math.20221087
[4]	Aslı Alkan, Halil Anaç . The novel numerical solutions for time-fractional Fornberg-Whitham equation by using fractional natural transform decomposition method. AIMS Mathematics, 2024, 9(9): 25333-25359. doi: 10.3934/math.20241237
[5]	Maysaa Al-Qurashi, Saima Rashid, Fahd Jarad, Madeeha Tahir, Abdullah M. Alsharif . New computations for the two-mode version of the fractional Zakharov-Kuznetsov model in plasma fluid by means of the Shehu decomposition method. AIMS Mathematics, 2022, 7(2): 2044-2060. doi: 10.3934/math.2022117
[6]	Saleh Baqer, Theodoros P. Horikis, Dimitrios J. Frantzeskakis . Physical vs mathematical origin of the extended KdV and mKdV equations. AIMS Mathematics, 2025, 10(4): 9295-9309. doi: 10.3934/math.2025427
[7]	Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon . On the solution of nonlinear fractional-order shock wave equation via analytical method. AIMS Mathematics, 2022, 7(10): 19325-19343. doi: 10.3934/math.20221061
[8]	M. S. Alqurashi, Saima Rashid, Bushra Kanwal, Fahd Jarad, S. K. Elagan . A novel formulation of the fuzzy hybrid transform for dealing nonlinear partial differential equations via fuzzy fractional derivative involving general order. AIMS Mathematics, 2022, 7(8): 14946-14974. doi: 10.3934/math.2022819
[9]	Amjad Ali, Iyad Suwan, Thabet Abdeljawad, Abdullah . Numerical simulation of time partial fractional diffusion model by Laplace transform. AIMS Mathematics, 2022, 7(2): 2878-2890. doi: 10.3934/math.2022159
[10]	Hilal Aydemir, Mehmet Merdan, Ümit Demir . A new approach to solving local fractional Riccati differential equations using the Adomian-Elzaki method. AIMS Mathematics, 2025, 10(4): 9122-9149. doi: 10.3934/math.2025420

Abstract

1. Introduction

Due to its broad relevance and propensity to incorporate many repercussions of actual concerns, the idea of fractional calculus (FC) has garnered considerable prominence in previous decades. Classical calculus has remained a small segment of FC, despite the fact that it can demonstrate numerous critical challenges and assist us in forecasting the behaviour of intricate occurrences in impulsive integro-differential equations ^[1], neural networking ^[2], thermal energy ^[3], non-Newtonian fluids ^[4] and heat flux ^[5]. Despite the fact that innovators offer numerous novel concepts, several aspects should always be deduced in order to guarantee all categories of phenomenon, that will be accomplished by conquering the restrictions posed by mathematicians and scientists. This is highly pertinent when investigating of MHD electro-osmotically flow ^[6], epidemics ^[7,8,9], stability and instability of special functions ^{[10,11,12,13]}, inequalities ^[14,15,16] as well as other disciplines. When it tends to arrive to the exploration of repercussions that assist in resolving major difficulties (such as the current global challenges), there is always room for improvements, innovation, creativeness, and extensions in analysis, and so many investigators have inferred provoking outcomes with the assistance of FC, and by incorporating efficacious methodologies with the assistance of underlying FC findings ^[17,18,19].

Numerical models investigation and analysis of corresponding features are often a high priority in mathematical modeling when the relevant techniques are implemented. This is certainly pertinent in epidemic research, bifurcation, thermodynamics, electrostatistics modeling, fluid flow, plasma physics, and other fields. Several approaches, including N-solitons ^{[20,21,22,23]}, solitary waves ^{[24,25,26,27]}, Tan-Cot function method ^[28], Adomian decomposition method ^[29], homotopy perturbation method ^[30], q-homotopy analysis method ^[31], variation iteration method ^[32], collocation-shooting method ^[33], $G/G^{'}$ expansion method ^[34], improved tan $(\phi(\tau)/2)$ -expansion method ^[35], Lie symmetry analysis method ^[36], wavelet method ^[37] have been employed and refined by researchers to achieve the analytic, semi-analytic, and numerical solution of nonlinear PDEs. The Adomian decomposition method ^[29,38] is one of them, and it offers an efficient approach for exact-analytical solutions across a broad and comprehensive domain of specific aspects that simulate real-world issues. This strategy transforms a basic, incredibly straightforward problem into the complicated problem under investigation, and when combined with Adomian components, it offers a tremendous mathematical instrument. Numerous aspects of the Adomian decomposition method have also received considerable focus recently.

In this analysis, we examine a nonlinear framework that explains powerful interactions between interior disturbances in the water. The Korteweg de-Vries (KdV) equations are frequently utilized to illustrate acoustic wave behaviour and its physical relevance. Due to the immense amplitude of lengthy longitudinal waves and prolonged rotating impacts, we employ a modified KdV equation. We now evaluate the following models using the isopycnic surface $\mathcal{W}(x, t)$ , which dipicts the KdV and modified KdV equations ^[39], respectively:

$\begin{eqnarray} \frac{\partial\mathcal{W}(x, t)}{\partial t}+a_{1}\mathcal{W}(x, t)\frac{\partial\mathcal{W}(x, t)}{\partial x}+a_{2}\mathcal{W}^{2}(x, t)\frac{\partial\mathcal{W}(x, t)}{\partial x}+b_{1}\frac{\partial^{3}\mathcal{W}(x, t)}{\partial x^{3}} = 0, \end{eqnarray}$

(1.1)

where $a_{1}$ and $a_{2}$ signifies the quadratic and cubic non-linear coefficients, respectively. Also, the coefficient of small-scale dispersion is denoted by $b_{1}.$ Here, $a_{1}$ and $a_{1}$ presents the proportional factors associating in the aforsaid equation, and is due to the nonlinear hydrodynamic system, and it appears classically, see^[40,41].

Furthermore, we compute the exact-analytical solution of nonlinear dispersive equations $K(n, n):$

$\begin{eqnarray} \frac{\partial\mathcal{W}(x, t)}{\partial t}+\frac{\partial}{\partial x}\big(\mathcal{W}^{n}\big)+\frac{\partial^{3}}{\partial x^{3}}\big(\mathcal{W}^{n}\big) = 0, \; \; \; n > 1. \end{eqnarray}$

(1.2)

Equation (1.2) is the evolutionary model for compactons. Compactons are characterized as solitons with bounded wave lengths or solitons without exponential tails in solitary wave theory (Rosenau and Hyma, 1993). Compactons are formed by the intricate coupling of nonlinear convection $\frac{\partial}{\partial x}\big(\mathcal{W}^{n}\big)$ and nonlinear dispersion $\frac{\partial^{3}}{\partial x^{3}}\big(\mathcal{W}^{n}\big)$ in (1.2).

Amidst Gorge Adomian's massive boost in 1980, the Adomian decomposition method introduced a well-noted terminology. It has been intensively implemented for a diverse set of nonlinear PDEs, for instance, the Korteweg-De Vries model ^[42], Fisher's model ^[43], Zakharov–Kuznetsov equation ^[44] and so on. The ADM was determined to be significantly related to a variety of integral transforms, including Laplace, Swai, Mohand, Aboodh, Elzaki, and others. Humanity is continuously striving to improve performance and minimizing the method's intricacy through invention, modernity, and experimentation. In connection with this, Jafari ^[45] propounded a well-known integral transform which is known to generalized integral transform. The dominant feature of this transformation is that it has the ability to recapture several existing transformations, see Remark 1.

Motivated by the above propensity, we aim to establish a semi-analytical approach by mingling the Jafari transform with the Adomian decomposition method, namely the Jafari decompostion method (JDM). With the assistance of fractional derivative operators, we constructed the approximate-analytical solutions for KdV, MKdV, K(2,2) and K(3,3). The suggested methodology helps us increase flexibility in determining the initial conditions, and its novelty is that it has a straightforward solution technique. This approach is straightforward and encompasses all of JDM accomplishments, as well as encouraging several scholars to investigate a broad spectrum of applications and processes. The tool to overcome computational complexity without any constraints, perturbations, or transformations from nonlinear to linear, or partial to ordinary differential equations, is the distinctive characteristic of the proposed approach. Furthermore, it is connected to factors that are extremely useful in bringing the findings to a favourable conclusion. It also is coupled to well-posed transformation, which tries to diminish the technique's intricacy while increasing its application and dependability.

2. Preliminaries

In this section, we evoke some essential concepts, notions, and definitions concerning fractional derivative operators depending on power and Mittag-Leffer as a kernel, along with the detailed consequences of the Jafari transform.

Definition 2.1. (^[17]) The Caputo fractional derivative $(CFD)$ is described as follows:

$\begin{eqnarray} \, _{0}^{c}{\bf{D}}_{t}^{\lambda} = \begin{cases} \frac{1}{\Gamma(r-\lambda)}\int\limits_{0}^{t}\frac{\mathcal{W}^{(r)}(x)}{(t-x)^{\lambda+1-r}}dx, \; \; r-1 < \lambda < r, \\ \frac{d^{r}}{dt^{r}}\mathcal{W}(t), \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \lambda = r. \end{cases} \end{eqnarray}$

(2.1)

Definition 2.2. (^[18]) The Atangana-Baleanu fractional derivative operator in the Caputo form $(ABC)$ is stated as follows:

$\begin{eqnarray} \, _{\eta_{1}}^{ABC}{\bf{D}}_{t}^{\lambda}\big(\mathcal{W}(t)\big) = \frac{\mathbb{A}(\lambda)}{1-\lambda}\int\limits_{\eta_{1}}^{t}\mathcal{W}^{\prime}(t)E_{\lambda}\Big[-\frac{\lambda(t-x)^{\lambda}}{1-\lambda}\Big]dx, \end{eqnarray}$

(2.2)

where $\mathcal{W}\in\mathcal{H}^{1}(a_{1}, a_{2}) (Sobolev \; space), \; a_{1} < a_{2}, \lambda\in[0, 1]$ and $\mathbb{A}(\lambda)$ signifies a normalization function as $\mathbb{A}(\lambda) = \mathbb{A}(0) = \mathbb{A}(1) = 1.$

Definition 2.3. (^[18]) The fractional integral of the $ABC$ -operator is described as follows:

$\begin{eqnarray} \, _{\eta_{1}}^{ABC}\mathcal{I}_{t}^{\lambda}\big(\mathcal{W}(t)\big) = \frac{1-\lambda}{\mathbb{A}(\lambda)}\mathcal{W}(t)+\frac{\lambda}{\Gamma(\lambda)\mathbb{A}(\lambda)}\int\limits_{\eta_{1}}^{t}\mathcal{W}(x)(t-x)^{\lambda-1}dx. \end{eqnarray}$

(2.3)

Definition 2.4. (^[45]) Consider an integrable mapping $\mathcal{W}(t)$ defined on a set $\mathcal{P},$ then

$\begin{eqnarray} \mathcal{P} = \Big\{\mathcal{W}(t):\exists\; M > 0, \kappa > 0, \big\vert\mathcal{W}(t)\big\vert < M\exp({\kappa t}), \; if\; t\geq0\Big\}. \end{eqnarray}$

(2.4)

Definition 2.5. (^[45]) Suppose the mappings $\phi(\mathfrak{s}), \psi(\mathfrak{s}):\mathbb{R}^{+}\mapsto\mathbb{R}^{+}$ such that $\varphi(\mathfrak{s})\neq0\; \forall\mathfrak{s}\in\mathbb{R}^{+}.$ The Jafari transform of the mapping $\mathcal{W}(t)$ presented by ${\bf{Q}}(\mathfrak{s})$ is described as

$\begin{eqnarray} \mathbb{J}\big\{\mathcal{W}(t), \mathfrak{s}\big\} = {\bf{Q}}(\mathfrak{s}) = \phi(s_{1})\int\limits_{0}^{\infty}\mathcal{W}(t)\exp(-\psi(\mathfrak{s})t)dt. \end{eqnarray}$

(2.5)

Theorem 2.6. (^[45]) (Convolution property). For Jafari transform, the subsequent holds true:

$\begin{eqnarray} \mathbb{J}\big\{\mathcal{W}_{1}\ast\mathcal{W}_{2}\big\} = \frac{1}{\phi(\mathfrak{s})}{\bf{Q}}_{1}(\mathfrak{s})\ast{\bf{Q}}_{2}(\mathfrak{s}). \end{eqnarray}$

(2.6)

Definition 2.7. The Jafari transform of the CFD operator is stated as follows:

$\begin{eqnarray} \mathbb{J}\Big\{\, _{0}^{c}{\bf{D}}_{t}^{\lambda}\big(\mathcal{W}(t)\big), \mathfrak{s}\Big\} = \psi^{\lambda}(\mathfrak{s}){\bf{Q}}(s_{1})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{\lambda-1}\psi^{\lambda-\kappa-1}(s_{1})\mathcal{W}^{(\kappa)}(0), \; \; r-1 < \lambda < r, \; \phi, \psi > 0. \end{eqnarray}$

(2.7)

Remark 1. Definition 2.7 leads to the following conclusions:

1) Taking $\phi(\mathfrak{s}) = 1$ and $\psi(\mathfrak{s}) = \mathfrak{s},$ then we acquire the Laplace transform ^[46].

2) Taking $\phi(\mathfrak{s})\frac{1}{\mathfrak{s}}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the $\alpha$ -Laplace transform ^[47].

3) Taking $\phi(\mathfrak{s}) = \frac{1}{\mathfrak{s}}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the Sumudu transform ^[48].

4) Taking $\phi(\mathfrak{s}) = \frac{1}{\mathfrak{s}}$ and $\psi(\mathfrak{s}) = 1,$ then we acquire the Aboodh transform ^[49].

5) Taking $\phi(\mathfrak{s}) = \mathfrak{s}$ and $\psi(\mathfrak{s}) = \mathfrak{s}^{2},$ then we acquire the Pourreza transform ^[50,51].

6) Taking $\phi(\mathfrak{s}) = \mathfrak{s}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the Elzaki transform ^[52].

7) Taking $\phi(\mathfrak{s}) = {\bf{u}}_{2}$ and $\psi(\mathfrak{s}) = \frac{\mathfrak{s}}{{\bf{u}}_{2}},$ then we acquire the Natural transform ^[53].

8) Taking $\phi(\mathfrak{s}) = \mathfrak{s}^{2}$ and $\psi(\mathfrak{s}) = {\mathfrak{s}},$ then we acquire the Mohand transform ^[54].

9) Taking $\phi(\mathfrak{s}) = \frac{1}{\mathfrak{s}^{2}}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the Swai transform ^[55].

10) Taking $\phi(\mathfrak{s}) = 1$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we get the Kamal transform ^[56].

11) Taking $\phi(\mathfrak{s}) = \mathfrak{s}^{\alpha}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the $G_{-}$ transform ^[57,58].

Definition 2.8. (^[59]) The Jafari transform of the $ABC$ fractional derivative operator is described as:

$\begin{eqnarray} \mathbb{J}\Big\{\, _{0}^{ABC}{\bf{D}}_{t}^{\lambda}\big(\mathcal{W}(t)\big), \mathfrak{s}\Big\}(\lambda) = \frac{\mathbb{A}(\lambda)\psi^{\lambda}(\mathfrak{s})}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\bigg({\bf{Q}}(\mathfrak{s})-\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(0)\bigg). \end{eqnarray}$

(2.8)

Remark 2. Definition 2.8 leads to the following conclusions:

1) Taking $\phi(\mathfrak{s}) = 1$ and $\psi(\mathfrak{s}) = \mathfrak{s},$ then we acquire the Laplace transform of ABC fractional derivative operator ^[60,61].

2) Taking $\phi(\mathfrak{s}) = \mathfrak{s}$ and $\psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we acquire the Elzaki transform of ABC fractional derivative operator ^[62].

3) Taking $\phi(\mathfrak{s}) = \psi(\mathfrak{s}) = \frac{1}{\mathfrak{s}},$ then we get the Sumudu transform of ABC fractional derivative operator ^[63].

4) Taking $\phi(\mathfrak{s}) = 1$ and $\psi(\mathfrak{s}) = \mathfrak{s}/{\bf{u}}_{2},$ then we get the Shehu transform of ABC fractional derivative operator ^[63].

Definition 2.9. (^[64]) The Mittag-Leffler function for single parameter is described as

$\begin{eqnarray} E_{\lambda}(z) = \sum\limits_{\kappa = 0}^{\infty}\frac{z_{1}^{\kappa}}{\Gamma(\kappa\lambda+1)}, \; \; \lambda, z_{1}\in\mathbb{C}, \; \Re(\lambda)\geq0. \end{eqnarray}$

(2.9)

3. Description of the Jafari decomposition method involving singular and nonsingular kernels

Consider the generic fractional form of PDE:

$\begin{eqnarray} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t) = \mathcal{F}(x, t), \; t > 0, \; 0 < \lambda\leq1 \end{eqnarray}$

(3.1)

with ICs

$\begin{eqnarray} \mathcal{W}(x, 0) = \mathcal{G}(x), \end{eqnarray}$

(3.2)

where ${\bf{D}}_{t}^{\lambda} = \frac{\partial^{\lambda}\mathcal{W}(x, t)}{\partial t^{\lambda}}$ symbolizes the Caputo and ABC fractional derivative of order $\lambda\in(0, 1]$ while $\mathfrak{L}$ and $\mathfrak{N}$ denotes the linear and nonlinear factors, respectively. Also, $\mathcal{F}(x, t)$ represents the source term.

Taking into account the Jafari transform to (3.1), and we acquire

$\begin{eqnarray*} \mathbb{J}\big[{\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t)\big] = \mathbb{J}\big[\mathcal{F}(x, t)\big]. \end{eqnarray*}$

Firstly, applying the differentiation rule of Jafari transform with respect to CFD, then we apply the ABC fractional derivativ operator as follows:

$\begin{eqnarray} &&\psi^{\lambda}(\mathfrak{s})\mathcal{U}(x, \mathfrak{s}) = \phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{\ell-1}\psi^{\lambda-1-\kappa}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0)+\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t)\big]+\mathbb{J}\big[\mathcal{F}(x, t)\big], \end{eqnarray}$

(3.3)

and

$\begin{eqnarray} &&\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{W}(0)+\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t)\big]+\mathbb{J}\big[\mathcal{F}(x, t)\big].\\ \end{eqnarray}$

(3.4)

The inverse Jafari transform of (3.3) and (3.4) yields

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\bigg[\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{\ell-1}\psi(\mathfrak{s})^{\lambda-\kappa-1}\mathcal{W}^{(\kappa)}(0)+\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathcal{F}(x, t)\big]\bigg]-\mathbb{J}^{-1}\bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t)\big]\bigg]. \end{eqnarray}$

(3.5)

and

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(0)+\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\big[\mathcal{F}(x, t)\big]\bigg]-\mathbb{J}^{-1}\bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\mathfrak{N}\mathcal{W}(x, t)\big]\bigg]. \end{eqnarray}$

(3.6)

The generalized decomposition method solution $\mathcal{W}(x, t)$ is represented by the following infinite series

$\begin{eqnarray} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray}$

(3.7)

Thus, the nonlinear term ${\mathfrak{N}}(x, t)$ can be evaluated by the Adomian decomposition method prescribed as

$\begin{eqnarray} {\mathfrak{N}}\mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\tilde{A}_{\ell}(\mathcal{W}_{0}, \mathcal{W}_{1}, ...), \; \ell = 0, 1, ...\; , \end{eqnarray}$

(3.8)

where

$\tilde{A}_{\ell}(\mathcal{W}_{0}, \mathcal{W}_{1}, ...) = \frac{1}{\ell!}\bigg[\frac{d^{\ell}}{d\varsigma^{\ell}}{\mathfrak{N}}\bigg(\sum\limits_{\jmath = 0}^{\infty}\varsigma^{\jmath}\mathcal{W}_{\jmath}\bigg)\bigg]_{\varsigma = 0}, \; \; \ell > 0.$

Inserting (3.7) and (3.8) into (3.5) and (3.6), respectively, we have

$\begin{eqnarray} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t)&& = \mathcal{G}(x)+\tilde{\mathcal{G}}(x)-\mathbb{J}^{-1}\bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\sum\limits_{\ell = 0}^{\infty}\tilde{A}_{\ell}\big]\bigg] \end{eqnarray}$

(3.9)

and

$\begin{eqnarray} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t)&& = \mathcal{G}(x)+\tilde{\mathcal{G}}(x)-\mathbb{J}^{-1}\bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\mathbb{A}(\lambda)\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathfrak{L}\mathcal{W}(x, t)+\sum\limits_{\ell = 0}^{\infty}\tilde{A}_{\ell}\big]\bigg]. \end{eqnarray}$

(3.10)

Consequently, the recursive technique for (3.9) and (3.10) are established as:

$\begin{eqnarray} \mathcal{W}_{0}(x, t)&& = \mathcal{G}(x)+\tilde{\mathcal{G}}(x), \; \; \ell = 0, \\\mathcal{W}_{\ell+1}(x, t)&& = -\mathbb{J}^{-1}\bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathfrak{L}\big(\mathcal{W}_{\ell}(x, t)\big)+\sum\limits_{\ell = 0}^{\infty}\tilde{A}_{\ell}\big]\bigg], \; \; \ell\geq1, \\\mathcal{W}_{\ell+1}(x, t)&& = -\mathbb{J}^{-1}\bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\mathbb{A}(\lambda)\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\big[\mathfrak{L}\big(\mathcal{W}_{\ell}(x, t)\big)+\sum\limits_{\ell = 0}^{\infty}\tilde{A}_{\ell}\big]\bigg], \; \; \ell\geq1. \end{eqnarray}$

(3.11)

4. Physical interpretation of Jafari decomposition method

In what follows, we present the various kinds of partial differential equations with the CFD and AB-frctional derivative operators, respectively.

4.1. Fractional KdV equation

Example 4.1. Assume that the time-fractional KdV equation

$\begin{eqnarray} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)-6\mathcal{W}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t) = 0, \end{eqnarray}$

(4.1)

with IC:

$\begin{eqnarray} \mathcal{W}_{0}(x, 0) = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}. \end{eqnarray}$

(4.2)

Proof. Foremost, we provide the solution of (4.1) in two general cases.

Case Ⅰ. Firstly, we apply the Caputo fractional derivative operator coupled with the Jafari transform and Adomian decomposition method. Applying the Jafari transform to (4.1).

$\begin{eqnarray} &&\psi^{\lambda}(\mathfrak{s})\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0) = \mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.3)

Taking into consideration the IC given in (4.2), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)+\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)+\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.4)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = -2\mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}\Big]\nonumber\\&& = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}. \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}(\mathcal{W})$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}(\mathcal{W}) = \mathcal{W}\mathcal{W}_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{A}_{\ell}, \end{eqnarray*}$

where $\mathcal{W}_{\ell}(x, t)$ will be evaluated recurrently, and $\mathcal{A}_{\ell}$ is the so-called polynomial of $\mathcal{W}_{0}, \mathcal{W}_{1}, ..., \mathcal{W}_{\ell}$ established by ^[65].

$\begin{eqnarray*} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell+1}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\sum\limits_{\ell = 0}^{\infty}(\mathcal{A})_{\ell}+\sum\limits_{\ell = 0}^{\infty}(\mathcal{W}_{xxx})_{\ell}\bigg]\Bigg], \; \; \ell = 0, 1, 2, ...\; . \end{eqnarray*}$

The first few Adomian polynomials are presented as follows:

$\begin{eqnarray} \mathcal{A}_{\ell}(\mathcal{W}\mathcal{W}_{x}) = &&\begin{cases}\mathcal{W}_{0}\mathcal{W}_{0x}, \; \; \ell = 0, \\\mathcal{W}_{0x}\mathcal{W}_{1}+\mathcal{W}_{1x}\mathcal{W}_{0}, \; \; \ell = 1, \\\mathcal{W}_{2}\mathcal{W}_{0x}+\mathcal{W}_{1}\mathcal{W}_{1x}+\mathcal{W}_{0}\mathcal{W}_{2x}, \; \; \ell = 2, \end{cases} \end{eqnarray}$

(4.5)

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{A}_{0}+\mathcal{W}_{0xxx}\bigg]\Bigg]\nonumber\\&& = -2\frac{\sigma^{5}\exp(\sigma x)(\exp(\sigma x)-1)}{(1+\exp(\sigma x_{1}))^{3}}\frac{t^{\lambda}}{\Gamma(\lambda+1)}, \nonumber\\ \mathcal{W}_{2}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{A}_{1}+\mathcal{W}_{1xxx}\bigg]\Bigg]\nonumber\\&& = -2\frac{\sigma^{8}\exp(\sigma x)(\exp(2\sigma x)-4\exp(\sigma x)+1)}{(1+\exp(\sigma x_{1}))^{4}}\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}, \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.1 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}-2\frac{\sigma^{5}\exp(\sigma x)(\exp(\sigma x)-1)}{(1+\exp(\sigma x_{1}))^{3}}\frac{t^{\lambda}}{\Gamma(\lambda+1)}\\&&\quad-2\frac{\sigma^{8}\exp(\sigma x)(\exp(2\sigma x)-4\exp(\sigma x)+1)}{(1+\exp(\sigma x_{1}))^{4}}\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}+...\; . \end{eqnarray}$

(4.6)

Case Ⅱ. Here, we surmise ABC fractional derivative operator coupled with the Jafari transform and Adomian decomposition method. Applying the Jafari transform for Example 4.1.

$\begin{eqnarray} &&\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0) = \mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.7)

Taking into consideration the IC given in (4.2), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)+\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)+\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{W}\mathcal{W}_{x}(x, t)-\mathcal{W}_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.8)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = -2\mathbb{J}^{-1}\Big[\frac{\psi(s_{1})}{\phi(\mathfrak{s})}\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}\Big]\nonumber\\&& = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}. \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}_{1}(\mathcal{W})$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}_{1}(\mathcal{W}) = \mathcal{W}\mathcal{W}_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{A}_{\ell}, \end{eqnarray*}$

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{A}_{0}+\mathcal{W}_{0xxx}\bigg]\Bigg]\nonumber\\&& = -\frac{2}{\mathbb{A}(\lambda)}\frac{\sigma^{5}\exp(\sigma x)(\exp(\sigma x)-1)}{(1+\exp(\sigma x_{1}))^{3}}\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg], \nonumber\\ \mathcal{W}_{2}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{A}_{1}+\mathcal{W}_{1xxx}\bigg]\Bigg]\nonumber\\&& = -\frac{2}{\mathbb{A}^{2}(\lambda)}\frac{\sigma^{8}\exp(\sigma x)(\exp(2\sigma x)-4\exp(\sigma x)+1)}{(1+\exp(\sigma x_{1}))^{4}}\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg], \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.1 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}-2\frac{\sigma^{5}\exp(\sigma x)(\exp(\sigma x)-1)}{{\mathbb{A}(\lambda)}(1+\exp(\sigma x_{1}))^{3}}\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg]\\&&\quad-2\frac{\sigma^{8}\exp(\sigma x)(\exp(2\sigma x)-4\exp(\sigma x)+1)}{{\mathbb{A}^{2}(\lambda)}(1+\exp(\sigma x_{1}))^{4}}\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg]+...\; . \end{eqnarray}$

(4.9)

For $\lambda = 1,$ we obtained the exact solution of Example 4.1 as

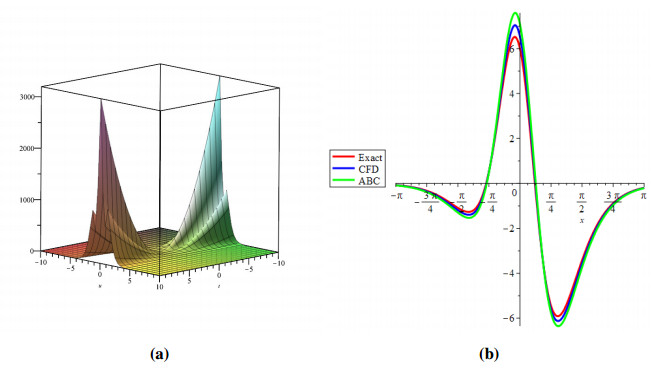
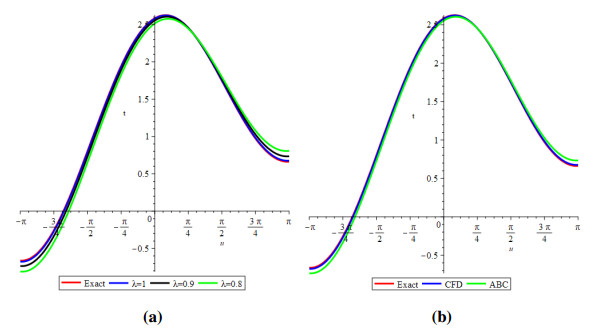
$\begin{eqnarray*} \mathcal{W}(x, t) = -\frac{\sigma^{2}}{2}\sec h^{2}\frac{\sigma}{2}(x-\sigma^{2}t). \end{eqnarray*}$

shows the evolutionary outcomes for the explicit and approximate solutions of Example 4.1 for the particular instance $\lambda = 1$ . The result generated by the proposed technique is remarkably similar to the exact solution, as shown in Figure 1.

Figure 1. Three-dimensional illustration of the exact and approximate solution of Example 4.1 when

$\lambda = 1,$ and

$\sigma = 0.05$ .

DownLoad: Full-Size Img PowerPoint

Then, by considering only the first few elements of the linear equations features are integrated, we can deduce that we have accomplished a reasonable estimation with the numerical solutions of the problem. It is obvious that by adding additional components to the decomposition series (4.6) and (4.9), the cumulative error can be diminished.

Analogously, we demonstrate the two-dimensional view of the change in fractional values of the order. We depict the response in Figure 2. It is remarkable that pairwise collisions of particle-like phenomena (including solitary waves and breathers) are fundamental mechanisms in the production of condensed soliton gas dynamics. Deep water waves, shallow groundwater waves, internally waves in a segmented sea, and fibre optics are all manifestations of these waves.

Figure 2. Three-dimensional illustration of the absolute error plot and 2D-approximations of Example 4.1 when

$\lambda = 1, \; \; \sigma = 0.05 = 0,$ and

$t = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Remark 3. It is remarkable that equivalent version of the KdV equation is presented as

$\begin{eqnarray*} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+6\mathcal{W}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t) = 0, \end{eqnarray*}$

with IC:

$\begin{eqnarray*} \mathcal{W}_{0}(x, 0) = -2\frac{\sigma^{2}\exp(\sigma x)}{(1+\exp(\sigma x))^{2}}. \end{eqnarray*}$

has the solitary wave solution, when $\lambda = 1,$ then

$\begin{eqnarray*} \mathcal{W}(x, t) = \frac{\sigma^{2}}{2}\sec h^{2}\frac{\sigma}{2}(x-\sigma^{2}t). \end{eqnarray*}$

4.2. Fractional modified KdV equation

Example 4.2. Assume that the time-fractional modified KdV equation

$\begin{eqnarray} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t) = 0, \end{eqnarray}$

(4.10)

with IC:

$\begin{eqnarray} \mathcal{W}_{0}(x, 0) = 2\frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}. \end{eqnarray}$

(4.11)

Proof. Foremost, we provide the solution of (4.10) in two general cases.

Case Ⅰ. Firstly, we apply the Caputo fractional derivative operator coupled with the Jafari transform and Adomian decomposition method.

Applying the Jafari transform to (4.10).

$\begin{eqnarray} &&\psi^{\lambda}(\mathfrak{s})\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0) = -\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.12)

Taking into consideration the IC given in (4.11), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.13)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}\Big]\nonumber\\&& = 2\frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}. \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}(\mathcal{W})$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}(\mathcal{W}) = \mathcal{W}^{2}\mathcal{W}_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{B}_{\ell}, \end{eqnarray*}$

where $\mathcal{W}_{\ell}(x, t)$ will be evaluated recurrently, and $\mathcal{B}_{\ell}$ is the so-called polynomial of $\mathcal{W}_{0}, \mathcal{W}_{1}, ..., \mathcal{W}_{\ell}$ established by ^[65].

$\begin{eqnarray*} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell+1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\sum\limits_{\ell = 0}^{\infty}(\mathcal{B})_{\ell}+\sum\limits_{\ell = 0}^{\infty}(\mathcal{W}_{xxx})_{\ell}\bigg]\Bigg], \; \; \ell = 0, 1, 2, ...\; . \end{eqnarray*}$

The first few Adomian polynomials are presented as follows:

$\begin{eqnarray} \mathcal{B}_{\ell}(\mathcal{W}^{2}\mathcal{W}_{x}) = &&\begin{cases}\mathcal{W}^{2}_{0}\mathcal{W}_{0x}, \; \; \ell = 0, \\\mathcal{W}_{0x}(2\mathcal{W}_{0}\mathcal{W}_{1})+\mathcal{W}_{1x}\mathcal{W}_{0}^{2}, \; \; \ell = 1, \\(2\mathcal{W}_{2}\mathcal{W}_{0}+\mathcal{W}_{1}^{2})\mathcal{W}_{0x}+(2\mathcal{W}_{0}\mathcal{W}_{1})\mathcal{W}_{1x}+\mathcal{W}_{0}^{2}\mathcal{W}_{2x}, \; \; \ell = 2, \end{cases} \end{eqnarray}$

(4.14)

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{B}_{0}+\mathcal{W}_{0xxx}\bigg]\Bigg]\nonumber\\&& = -2\frac{\sigma^{4}\exp(\sigma x)(1-\exp(2\sigma x))}{(1+\exp(2\sigma x_{1}))^{2}}\frac{t^{\lambda}}{\Gamma(\lambda+1)}, \nonumber\\ \mathcal{W}_{2}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[6\mathcal{B}_{1}+\mathcal{W}_{1xxx}\bigg]\Bigg]\nonumber\\&& = 2\frac{\sigma^{7}\exp(\sigma x)(1-6\exp(2\sigma x)+\exp(4\sigma x))}{(1+\exp(2\sigma x_{1}))^{3}}\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}, \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.2 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = 2\frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}-2\frac{\sigma^{4}\exp(\sigma x)(1-\exp(2\sigma x))}{(1+\exp(2\sigma x_{1})^{2}}\frac{t^{\lambda}}{\Gamma(\lambda+1)}\\&&\quad+2\frac{\sigma^{7}\exp(\sigma x)(1-6\exp(2\sigma x)+\exp(4\sigma x))}{(1+\exp(2\sigma x_{1})^{3}}\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}+...\; . \end{eqnarray}$

(4.15)

Case Ⅱ. Here, we surmise ABC fractional derivative operator coupled with the Jafari transform and Adomian decomposition method.

Applying the Jafari transform on (4.10).

$\begin{eqnarray} &&\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0)\\&& = -\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.16)

Taking into consideration the IC given in (4.11), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{W}^{2}\mathcal{W}_{x}(x, t)+\mathcal{W}_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.17)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\psi(s_{1})}{\phi(\mathfrak{s})}\frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}\Big]\nonumber\\&& = \frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}. \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}(\mathcal{W}),$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}_{1}(\mathcal{W}) = \mathcal{W}^{2}\mathcal{W}_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{B}_{\ell}, \end{eqnarray*}$

where $\mathcal{W}_{\ell}(x, t)$ will be evaluated recurrently, and $\mathcal{B}_{\ell}$ is the so-called polynomial of $\mathcal{W}_{0}, \mathcal{W}_{1}, ..., \mathcal{W}_{\ell}$ defined in (4.14).

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{B}_{0}+\mathcal{W}_{0xxx}\bigg]\Bigg]\nonumber\\&& = -\frac{2}{\mathbb{A}(\lambda)}\frac{\sigma^{4}\exp(\sigma x)(1-\exp(2\sigma x))}{(1+\exp(2\sigma x_{1})^{2}}\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg], \nonumber\\ \mathcal{W}_{2}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[6\mathcal{A}_{1}+\mathcal{W}_{1xxx}\bigg]\Bigg]\nonumber\\&& = \frac{2}{\mathbb{A}^{2}(\lambda)}\frac{\sigma^{7}\exp(\sigma x)(1-6\exp(2\sigma x)+\exp(4\sigma x))}{(1+\exp(2\sigma x_{1}))^{3}}\nonumber\\&&\quad\times\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg], \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.2 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = \frac{\sigma\exp(\sigma x)}{1+\exp(2\sigma x)}-2\frac{\sigma^{4}\exp(\sigma x)(1-\exp(2\sigma x))}{{\mathbb{A}(\lambda)}(1+\exp(2\sigma x_{1}))^{2}}\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg]\\&&\quad+2\frac{\sigma^{7}\exp(\sigma x)(1-6\exp(2\sigma x)+\exp(4\sigma x))}{{\mathbb{A}^{2}(\lambda)}(1+\exp(2\sigma x_{1}))^{3}}\\&&\quad\times\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg]+...\; . \end{eqnarray}$

(4.18)

For $\lambda = 1,$ we obtained the exact solution of Example 4.2 as

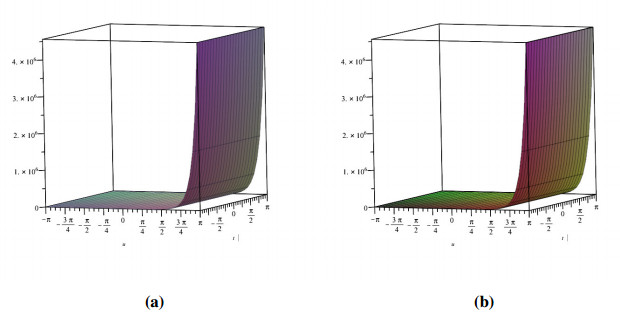
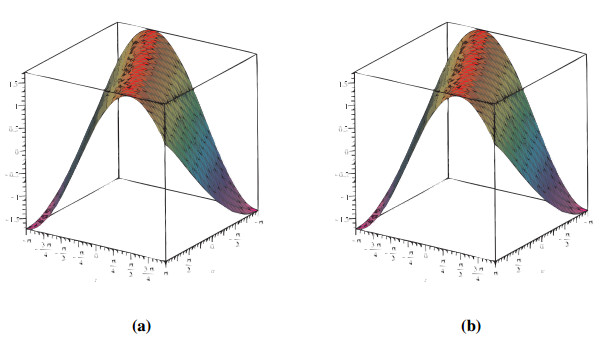
$\begin{eqnarray*} \mathcal{W}(x, t) = \pm\sigma\sec h {\sigma}(x-\sigma^{2}t). \end{eqnarray*}$

shows the evolutionary outcomes for the explicit and approximate solutions of Example 4.2 for the particular instance $\lambda = 1$ . The result generated by the proposed technique is remarkably similar to the exact solution, as shown in Figure 3.

Figure 3. Three-dimensional illustration of the exact and approximate solution of Example 4.2 when

$\lambda = 1,$ and

$\sigma = 0.5$ .

DownLoad: Full-Size Img PowerPoint

Then, by considering only the first few elements of the nonlinear equations features are integrated, we can deduce that we have accomplished a reasonable estimation with the numerical solutions of the problem. It is obvious that by adding additional components to the decomposition series (4.15) and (4.18), the cumulative error can be diminished.

Analogously, we demonstrate the two-dimensional view of the change in fractional values of the order. Figure 4 depicts the response for exact CFD and AB fractional derivative operators. It is remarkable that pairwise collisions of particle-like phenomena (including solitary waves and breathers) are fundamental mechanisms in the production of condensed soliton gas dynamics. Deep water waves, shallow groundwater waves, internally waves in a segmented sea, and fibre optics are all manifestations of these waves.

Figure 4. Two-dimensional illustration for change in fractional values of the order of Example 4.2 when

$\sigma = 0.05$ and

$t = 0.5$ .

DownLoad: Full-Size Img PowerPoint

4.3. Fractional K(2,2) equation

Example 4.3. Assume that the time-fractional K(2,2) equation

$\begin{eqnarray} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t) = 0, \end{eqnarray}$

(4.19)

with IC:

$\begin{eqnarray} \mathcal{W}_{0}(x, 0) = \frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big). \end{eqnarray}$

(4.20)

Proof. Foremost, we provide the solution of (4.19) in two general cases.

Case Ⅰ. Firstly, we apply the Caputo fractional derivative operator coupled with the Jafari transform and Adomian decomposition method.

Applying the Jafari transform on (4.19).

$\begin{eqnarray} &&\psi^{\lambda}(\mathfrak{s})\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0) = -\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.21)

Taking into consideration the IC given in (4.20), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.22)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big)\Big]\nonumber\\&& = \frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big). \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearities $\mathcal{F}_{1}(\mathcal{W})$ and $\mathcal{F}_{2}(\mathcal{W})$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}_{1}(\mathcal{W}) = (\mathcal{W}^{2})_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{D}_{\ell}, \; \; \; \; \; \mathcal{F}_{2}(\mathcal{W}) = (\mathcal{W}^{2})_{xxx} = \sum\limits_{\ell = 0}^{\infty}\mathcal{E}_{\ell}, \end{eqnarray*}$

where $\mathcal{W}_{\ell}(x, t)$ will be evaluated recurrently, and $\mathcal{D}_{\ell}$ and $\mathcal{E}_{\ell}$ are the so-called polynomial of $\mathcal{W}_{0}, \mathcal{W}_{1}, ..., \mathcal{W}_{\ell}$ established by ^[65].

$\begin{eqnarray*} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell+1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\sum\limits_{\ell = 0}^{\infty}(\mathcal{D})_{\ell}+\sum\limits_{\ell = 0}^{\infty}(\mathcal{E})_{\ell}\bigg]\Bigg], \; \; \ell = 0, 1, 2, ...\; . \end{eqnarray*}$

The first few Adomian polynomials are presented as follows:

$\begin{eqnarray} \mathcal{D}_{\ell}((\mathcal{W}^{2})_{x})& = &\begin{cases}\mathcal{W}^{2}_{0x}, \; \; \ell = 0, \\(2\mathcal{W}_{0}\mathcal{W}_{1})_{x}, \; \; \ell = 1, \\(2\mathcal{W}_{2}\mathcal{W}_{0}+\mathcal{W}_{1}^{2})_{x}, \; \; \ell = 2, \end{cases}\\\mathcal{E}_{\ell}((\mathcal{W}^{2})_{xxx})& = &\begin{cases}\mathcal{W}^{2}_{0xxx}, \; \; \ell = 0, \\(2\mathcal{W}_{0}\mathcal{W}_{1})_{xxx}, \; \; \ell = 1, \\(2\mathcal{W}_{2}\mathcal{W}_{0}+\mathcal{W}_{1}^{2})_{xxx}, \; \; \ell = 2, \end{cases} \end{eqnarray}$

(4.23)

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{D}_{0}+\mathcal{E}_{0}\bigg]\Bigg] = \frac{\sigma^{2}}{3}\sin\Big(\frac{x}{2}\Big)\frac{t^{\lambda}}{\Gamma(\lambda+1)}, \nonumber\\ \mathcal{W}_{2}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{D}_{1}+\mathcal{E}_{1}\bigg]\Bigg] = -\frac{\sigma^{3}}{6}\sin\Big(\frac{x}{2}\Big)\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}, \nonumber\\ \mathcal{W}_{3}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{D}_{2}+\mathcal{E}_{2}\bigg]\Bigg] = -\frac{\sigma^{4}}{12}\sin\Big(\frac{x}{2}\Big)\frac{t^{3\lambda}}{\Gamma(3\lambda+1)}\nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.3 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = \frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big)+\frac{\sigma^{2}}{3}\sin\Big(\frac{x}{2}\Big)\frac{t^{\lambda}}{\Gamma(\lambda+1)}\\&&\quad-\frac{\sigma^{3}}{6}\sin\Big(\frac{x}{2}\Big)\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}-\frac{\sigma^{4}}{12}\sin\Big(\frac{x}{2}\Big)\frac{t^{3\lambda}}{\Gamma(3\lambda+1)}+...\; . \end{eqnarray}$

(4.24)

Case Ⅱ. Here, we surmise ABC fractional derivative operator coupled with the Jafari transform and Adomian decomposition method. Applying the Jafari transform for Example 4.19.

$\begin{eqnarray} &&\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0)\\&& = -\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.25)

Taking into consideration the IC given in (4.20), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[(\mathcal{W}^{2})_{x}(x, t)+(\mathcal{W}^{2})_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.26)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\psi(s_{1})}{\phi(\mathfrak{s})}\frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big)\Big]\nonumber\\&& = \frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big). \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}_{\jmath}(\mathcal{W}), \; \jmath = 1, 2$ can be decomposed by an infinite series of polynomials represented by

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[\mathcal{D}_{0}+\mathcal{E}_{0}\bigg]\Bigg]\nonumber\\&& = \frac{\sigma^{2}}{3{\mathbb{A}(\lambda)}}\sin\Big(\frac{x}{2}\Big)\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg], \nonumber\\ \mathcal{W}_{2}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[\mathcal{D}_{1}+\mathcal{E}_{1}\bigg]\Bigg]\nonumber\\&& = -\frac{\sigma^{3}}{6{\mathbb{A}^{2}(\lambda)}}\sin\Big(\frac{x}{2}\Big)\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg], \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.3 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = \frac{4}{3}\sigma\cos^{2}\Big(\frac{x}{4}\Big)+\frac{\sigma^{2}}{3{\mathbb{A}(\lambda)}}\sin\Big(\frac{x}{2}\Big)\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg]\\&&\quad-\frac{\sigma^{3}}{6{\mathbb{A}^{2}(\lambda)}}\sin\Big(\frac{x}{2}\Big)\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg]+...\; . \end{eqnarray}$

(4.27)

For $\lambda = 1,$ we obtained the closed form solution of Example 4.3 as

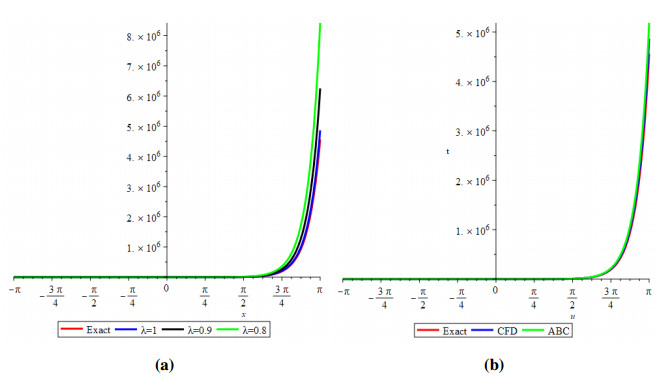
$\begin{eqnarray*} \mathcal{W}(x, t) = \begin{cases}\frac{4}{3}\sigma\cos^{2}\Big(\frac{x-\sigma t}{4}\Big), \; \; \; \vert x-\sigma t\vert\leq2\pi, \\0, \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; otherwise.\end{cases}. \end{eqnarray*}$

shows the evolutionary outcomes for the explicit and approximate solutions of Example 4.3 for the particular instance $\lambda = 1$ . The result generated by the proposed technique is remarkably similar to the exact solution, as shown in Figure 5.

Figure 5. Three-dimensional illustration of the exact and approximate solution of Example 4.3 when

$\lambda = 1$ and

$\sigma = 0.05$ .

DownLoad: Full-Size Img PowerPoint

Then, by considering only the first few elements of the nonlinear equations features are integrated, we can deduce that we have accomplished a reasonable estimation with the numerical solutions of the problem. It is obvious that by adding additional components to the decomposition series (4.24) and (4.27), the cumulative error can be diminished.

Analogously, we demonstrate the two-dimensional view of the change in fractional values of the order. Figure 6 depicts the response for exact CFD and AB fractional derivative operators.

Figure 6. Two-dimensional illustration of the exact and approximate solution for the change in fractional values of the order of Example 4.3 when

$\lambda = 1, \sigma = 0.05$ and

$t = 0.5$ .

DownLoad: Full-Size Img PowerPoint

For a variation of the K(2,2) equation, constrained traveling-wave solutions are achieved. We acquire hump-shaped and valley-shaped solitary-wave solutions, as well as some periodic solutions, for the focusing branch. It is worth noting that optimal focusing provides the aggregate of the frequency and amplitude of the originating waves in the engaging phase, as illustrated in reference ^[66].

4.4. Fractional K(3,3) equation

Example 4.4. Assume that the time-fractional K(3,3) equation

$\begin{eqnarray} {\bf{D}}_{t}^{\lambda}\mathcal{W}(x, t)+(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t) = 0, \end{eqnarray}$

(4.28)

with IC:

$\begin{eqnarray} \mathcal{W}_{0}(x, 0) = \sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big). \end{eqnarray}$

(4.29)

Proof. Foremost, we provide the solution of (4.28) in two general cases.

Case Ⅰ. Firstly, we apply the Caputo fractional derivative operator coupled with the Jafari transform and Adomian decomposition method.

Applying the Jafari transform on (4.28).

$\begin{eqnarray} &&\psi^{\lambda}(\mathfrak{s})\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0) = -\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.30)

Taking into consideration the IC given in (4.29), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.31)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big)\Big]\nonumber\\&& = \sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big). \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearities $\mathcal{F}_{1}(\mathcal{W})$ and $\mathcal{F}_{2}(\mathcal{W})$ can be decomposed by an infinite series of polynomials represented by

$\begin{eqnarray*} \mathcal{F}_{1}(\mathcal{W}) = (\mathcal{W}^{3})_{x} = \sum\limits_{\ell = 0}^{\infty}\mathcal{G}_{\ell}, \; \; \; \; \; \mathcal{F}_{2}(\mathcal{W}) = (\mathcal{W}^{3})_{xxx} = \sum\limits_{\ell = 0}^{\infty}\mathcal{H}_{\ell}, \end{eqnarray*}$

where $\mathcal{W}_{\ell}(x, t)$ will be evaluated recurrently, and $\mathcal{G}_{\ell}$ and $\mathcal{H}_{\ell}$ are the so-called polynomial of $\mathcal{W}_{0}, \mathcal{W}_{1}, ..., \mathcal{W}_{\ell}$ established by ^[65].

$\begin{eqnarray*} \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell+1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\sum\limits_{\ell = 0}^{\infty}(\mathcal{G})_{\ell}+\sum\limits_{\ell = 0}^{\infty}(\mathcal{H})_{\ell}\bigg]\Bigg], \; \; \ell = 0, 1, 2, ...\; . \end{eqnarray*}$

The first few Adomian polynomials are presented as follows:

$\begin{eqnarray} \mathcal{G}_{\ell}((\mathcal{W}^{3})_{x})& = &\begin{cases}\mathcal{W}^{3}_{0x}, \; \; \ell = 0, \\(3\mathcal{W}_{0}^{2}\mathcal{W}_{1})_{x}, \; \; \ell = 1, \\(3\mathcal{W}_{2}\mathcal{W}_{0}^{2}+3\mathcal{W}_{1}^{2}\mathcal{W}_{0})_{x}, \; \; \ell = 2, \end{cases}\\\mathcal{E}_{\ell}((\mathcal{W}^{3})_{xxx})& = &\begin{cases}\mathcal{W}^{2}_{0xxx}, \; \; \ell = 0, \\(3\mathcal{W}_{0}^{2}\mathcal{W}_{1})_{xxx}, \; \; \ell = 1, \\(3\mathcal{W}_{2}\mathcal{W}^{2}_{0}+3\mathcal{W}_{1}^{2}\mathcal{W}_{0})_{xxx}, \; \; \ell = 2, \end{cases} \end{eqnarray}$

(4.32)

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{G}_{0}+\mathcal{H}_{0}\bigg]\Bigg] = \frac{\sqrt{6\sigma^{3}}}{6}\sin\Big(\frac{x}{3}\Big)\frac{t^{\lambda}}{\Gamma(\lambda+1)}, \nonumber\\ \mathcal{W}_{2}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{G}_{1}+\mathcal{H}_{1}\bigg]\Bigg] = -\frac{\sqrt{6\sigma^{5}}}{18}\sin\Big(\frac{x}{3}\Big)\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}, \nonumber\\ \mathcal{W}_{3}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{1}{\psi^{\lambda}(\mathfrak{s})}\mathbb{J}\bigg[\mathcal{G}_{2}+\mathcal{H}_{2}\bigg]\Bigg] = -\frac{\sqrt{6\sigma^{7}}}{54}\sin\Big(\frac{x}{3}\Big)\frac{t^{3\lambda}}{\Gamma(3\lambda+1)}\nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.4 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = \sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big)+\frac{\sqrt{6\sigma^{3}}}{6}\sin\Big(\frac{x}{3}\Big)\frac{t^{\lambda}}{\Gamma(\lambda+1)}\\&&\quad-\frac{\sqrt{6\sigma^{5}}}{18}\sin\Big(\frac{x}{3}\Big)\frac{t^{2\lambda}}{\Gamma(2\lambda+1)}-\frac{\sqrt{6\sigma^{7}}}{54}\sin\Big(\frac{x}{3}\Big)\frac{t^{3\lambda}}{\Gamma(3\lambda+1)}+...\; . \end{eqnarray}$

(4.33)

Case Ⅱ. Here, we surmise ABC fractional derivative operator coupled with the Jafari transform and Adomian decomposition method. Applying the Jafari transform for Example 4.28.

$\begin{eqnarray} &&\frac{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}\mathcal{U}(x, \mathfrak{s})-\phi(\mathfrak{s})\sum\limits_{\kappa = 0}^{m-1}\psi^{\lambda-\kappa-1}(\mathfrak{s})\mathcal{W}^{(\kappa)}(0)\\&& = -\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg].\\ \end{eqnarray}$

(4.34)

Taking into consideration the IC given in (4.29), we have

$\begin{eqnarray*} \mathcal{U}(x, \mathfrak{s}) = \frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg]. \end{eqnarray*}$

Employing the inverse Jafari transform, we obtain

$\begin{eqnarray} \mathcal{W}(x, t) = \mathbb{J}^{-1}\Bigg[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)-\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[(\mathcal{W}^{3})_{x}(x, t)+(\mathcal{W}^{3})_{xxx}(x, t)\bigg]\Bigg]. \end{eqnarray}$

(4.35)

Thanks to the JDM, we find

$\begin{eqnarray*} \mathcal{W}_{0}(x, t)&& = \mathbb{J}^{-1}\Big[\frac{\phi(\mathfrak{s})}{\psi(\mathfrak{s})}\mathcal{W}(x, 0)\Big] = 2\mathbb{J}^{-1}\Big[\frac{\psi(s_{1})}{\phi(\mathfrak{s})}\sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big)\Big]\nonumber\\&& = \sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big). \end{eqnarray*}$

Here, we surmise that the unknown function $\mathcal{W}(x, t)$ can be written by an infinite series of the form

$\begin{eqnarray*} \mathcal{W}(x, t) = \sum\limits_{\ell = 0}^{\infty}\mathcal{W}_{\ell}(x, t). \end{eqnarray*}$

Also, the non-linearity $\mathcal{F}_{\jmath}(\mathcal{W}), \; \jmath = 1, 2$ can be decomposed by an infinite series of polynomials represented by

For $\ell = 0, 1, 2, 3, ...$

$\begin{eqnarray*} \mathcal{W}_{1}(x, t)&& = -\mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[\mathcal{G}_{0}+\mathcal{H}_{0}\bigg]\Bigg]\nonumber\\&& = \frac{\sqrt{6\sigma^{3}}}{6{\mathbb{A}(\lambda)}}\sin\Big(\frac{x}{3}\Big)\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg], \nonumber\\ \mathcal{W}_{2}(x, t)&& = \mathbb{J}^{-1}\Bigg[\frac{\lambda+(1-\lambda)\psi^{\lambda}(\mathfrak{s})}{\psi^{\lambda}(\mathfrak{s})\mathbb{A}(\lambda)}\mathbb{J}\bigg[\mathcal{G}_{1}+\mathcal{H}_{1}\bigg]\Bigg]\nonumber\\&& = -\frac{\sqrt{6\sigma^{5}}}{18{\mathbb{A}^{2}(\lambda)}}\sin\Big(\frac{x}{3}\Big)\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg], \nonumber\\ \vdots. \end{eqnarray*}$

The approximate solution for Example 4.4 is expressed as:

$\begin{eqnarray} \mathcal{W}(x, t)&& = \mathcal{W}_{0}(x, t)+\mathcal{W}_{1}(x, t)+\mathcal{W}_{2}(x, t)+\mathcal{W}_{3}(x, t)+..., \\&& = \sqrt{\frac{3\sigma}{2}}\cos\Big(\frac{x}{3}\Big)+\frac{\sqrt{6\sigma^{3}}}{6{\mathbb{A}(\lambda)}}\sin\Big(\frac{x}{3}\Big)\bigg[\frac{\lambda t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)\bigg]\\&&\quad-\frac{\sqrt{6\sigma^{5}}}{18{\mathbb{A}^{2}(\lambda)}}\sin\Big(\frac{x}{3}\Big)\bigg[\frac{\lambda^{2}t^{2\lambda}}{\Gamma(2\lambda+1)}+2\lambda(1-\lambda)\frac{t^{\lambda}}{\Gamma(\lambda+1)}+(1-\lambda)^{2}\bigg]+...\; . \end{eqnarray}$

(4.36)

For $\lambda = 1,$ we obtained the closed form solution of Example 4.4 as

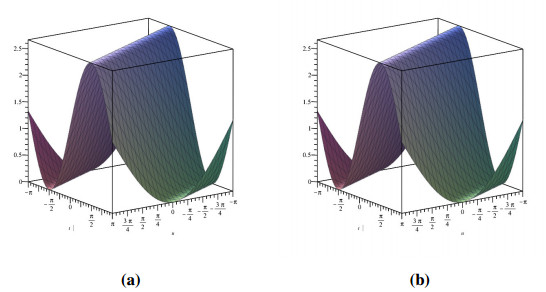
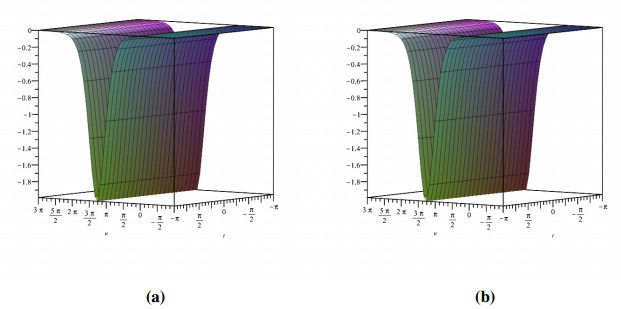
$\begin{eqnarray*} \mathcal{W}(x, t) = \begin{cases}\frac{\sqrt{6\sigma}}{2}\sigma\cos\Big(\frac{x-\sigma t}{3}\Big), \; \; \; \vert x-\sigma t\vert\leq\frac{3\pi}{2}, \\0, \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; otherwise.\end{cases}. \end{eqnarray*}$

shows the evolutionary outcomes for the explicit and approximate solutions of Example 4.4 for the particular instance $\lambda = 1$ . The result generated by the proposed technique is remarkably similar to the exact solution, as shown in Figure 7.

Figure 7. Three-dimensional illustration of the exact and approximate solution of Example 4.4 when

$\lambda = 1$ and

$\sigma = 0.05$ .

DownLoad: Full-Size Img PowerPoint

Then, by considering only the first few elements of the nonlinear equations features are integrated, we can deduce that we have accomplished a reasonable estimation with the numerical solutions of the problem. It is obvious that by adding additional components to the decomposition series (4.33) and (4.36), the cumulative error can be diminished.

Analogously, we demonstrate the two-dimensional view of the change in fractional values of the order. Figure 8 depicts the response for exact CFD and AB fractional derivative operators.

Figure 8. Two-dimensional illustration of the exact and approximate solution of change in fractional values of the order of Example 4.4 when

$\lambda = 1, \sigma = 0.5$ and

$t = 0.5$ .

DownLoad: Full-Size Img PowerPoint

For a variation of the K(3,3) equation, constrained traveling-wave solutions are achieved. We acquire hump-shaped and valley-shaped solitary-wave solutions, as well as some periodic solutions, for the focusing branch. It is worth noting that optimal focusing provides the aggregate of the frequency and amplitude of the originating waves in the engaging phase, as illustrated in reference ^[66].

5. Conclusions

In this paper, we conducted a novel algorithm based on the Jafari transform and Adomin decomposition method, known as the Jafari decomposition method. In the time-fractional technique, we investigated several models such as KdV, mKdV, K (2,2), and K (3,3). To comprehend their physical interpretation, we researched and examined several novel families of solutions and their simulation studies, presented in two-dimensional and three-dimensional plots. The new discoveries concerned the hyperbolic function, trigonometric function, exponential function, and constant function. These new solutions and results might be appreciated in the laser, plasma sciences and wave pattern. To summarise, the suggested method stated above was determined to solve this collection of challenges by utilizing successive fast converging approximations without any limiting requirements or manipulations that changed the physical attributes of the concerns. Also, increasing the recursive procedure leads to the closed form solution of the governing equation.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	E. A. Hernandez-Vargas, R. H. Middleton, Modeling the three stages in HIV infection, J. Theor. Biol., 320 (2013), 33–40. https://doi.org/10.1016/j.jtbi.2012.11.028 doi: 10.1016/j.jtbi.2012.11.028
[2]	K. A. Lythgoe, L. Pellis, C. Fraser, Is HIV short-sighted? Insights from a multistrain nested model, Evolution, 67 (2013), 2769–2782. https://doi.org/10.1111/evo.12166 doi: 10.1111/evo.12166
[3]	M. A. Nowak, C. R. M. Bangham, Population dynamics of immune responses to persistent viruses, Science, 272 (1996), 74–79. https://doi.org/10.1126/science.272.5258.74 doi: 10.1126/science.272.5258.74
[4]	M. A. Nowak, R. M. May, K. Sigmund, Immune responses against multiple epitopes, J. Theor. Biol., 175 (1995), 325–353. https://doi.org/10.1006/jtbi.1995.0146 doi: 10.1006/jtbi.1995.0146
[5]	M. A. Nowak, R. M. May, Virus Dynamics, Oxford University Press, Oxford, 2000.
[6]	R. A. Arnaout, M. A. Nowak, D. Wodarz, HIV-1 dynamics revisited: biphasic decay by cytotoxic T lymphocyte killing, Proc. Biol. Sci., 267 (2000), 1347–1354. https://doi.org/10.1098/rspb.2000.1149 doi: 10.1098/rspb.2000.1149
[7]	X. Lai, X. Zou, Modeling cell-to-cell spread of HIV-1 with logistic target cell growth, J. Math. Anal. Appl., 426 (2015), 563–584. https://doi.org/10.1016/j.jmaa.2014.10.086 doi: 10.1016/j.jmaa.2014.10.086
[8]	Y. Yang, L. Zou, S. Ruan, Global dynamics of a delayed within-host viral infection model with both virus-to-cell and cell-to-cell transmissions, Math. Biosci., 270 (2015), 183–191. https://doi.org/10.1016/j.mbs.2015.05.001 doi: 10.1016/j.mbs.2015.05.001
[9]	A. V. Herz, S. Bonhoeffer, R. M. Anderson, R. M. May, M. A. Nowak, Viral dynamics in vivo: limitations on estimations on intracellular delay and virus decay, Proc. Natl. Acad. Sci., 93 (1996), 7247–7251. https://doi.org/10.1073/pnas.93.14.7247 doi: 10.1073/pnas.93.14.7247
[10]	G. Huang, Y. Takeuchi, W. Ma, Lyapunov functionals for delay differential equations model of viral infections, SIAM J. Appl. Math., 70 (2010), 2693–2708. https://doi.org/10.1137/090780821 doi: 10.1137/090780821
[11]	Y. Jiang, T. Zhang, Global stability of a cytokine-enhanced viral infection model with nonlinear incidence rate and time delays, Appl. Math. Lett., 132 (2022), 108110. https://doi.org/10.1016/j.aml.2022.108110 doi: 10.1016/j.aml.2022.108110
[12]	J. Wang, H. Shi, L. Xu, L. Zang, Hopf bifurcation and chaos of tumor-Lymphatic model with two time delays, Chaos Solitons Fractals, 157 (2022), 111922. https://doi.org/10.1016/j.chaos.2022.111922 doi: 10.1016/j.chaos.2022.111922
[13]	K. Wang, W. Wang, X. Liu, Global stability in a viral infection model with lytic and nonlytic immune responses, Comput. Math. Appl., 51 (2006), 1593–1610. https://doi.org/10.1016/j.camwa.2005.07.020 doi: 10.1016/j.camwa.2005.07.020
[14]	P. Borrow, A. Tishon, S. Lee, J. Xu, I. S. Grewal, M. B. Oldstone, et al., CD40L-deficient mice show deficits in antiviral immunity and have an impaired memory CD8+ CTL response, J. Exp. Med., 183 (1996), 2129–2142. https://doi.org/10.1084/jem.183.5.2129 doi: 10.1084/jem.183.5.2129
[15]	R. V. Culshaw, S. Ruan, R. J. Spiteri, Optimal HIV treatment by maximising immune response, J. Math. Biol., 48 (2004), 545–562. https://doi.org/10.1007/s00285-003-0245-3 doi: 10.1007/s00285-003-0245-3
[16]	A. R. Thomsen, A. Nansen, J. P. Christensen, S. O. Andreasen, O. Marker, CD40 ligand is pivotal to efficient control of virus replication in mice infected with lymphocytic choriomeningitis virus, J. Immunol., 161 (1998), 4583–4590.
[17]	H. Zhu, Y. Luo, M. Chen, Stability and Hopf bifurcation of a HIV infection model with CTL-response delay, Comput. Math. Appl., 62 (2011), 3091–3102. https://doi.org/10.1016/j.camwa.2011.08.022 doi: 10.1016/j.camwa.2011.08.022
[18]	G. Huang, Y. Takeuchi, A. Korobeinikov, HIV evolution and progression of the infection to AIDS, J. Theor. Biol., 307 (2012), 149–159. https://doi.org/10.1016/j.jtbi.2012.05.013 doi: 10.1016/j.jtbi.2012.05.013
[19]	A. M. Elaiw, A. A. Raezah, Stability of general virus dynamics models with both cellular and viral infections and delays, Math. Methods Appl. Sci., 40 (2017), 5863–5880. https://doi.org/10.1002/mma.4436 doi: 10.1002/mma.4436
[20]	G. Huang, H. Yokoi, Y. Takeuchi, T. Kajiwara, T. Sasaki, Impact of intracellular delay, immune activation delay andnonlinear incidence on viral dynamics, Japan. J. Indust. Appl. Math., 28 (2011), 383–411. https://doi.org/10.1007/s13160-011-0045-x doi: 10.1007/s13160-011-0045-x
[21]	M. L. Mann Manyombe, J. Mbang, G. Chendjou, Stability and Hopf bifurcation of a CTL-inclusive HIV-1 infection model with both viral and cellular infections, and three delays, Chaos Solitons Fractals, 144 (2021), 110695. https://doi.org/10.1016/j.chaos.2021.110695 doi: 10.1016/j.chaos.2021.110695
[22]	H. Miao, Z. Teng, X. Abdurahman, Stability and Hopf bifurcation for five-dimensional virus infection model with Beddington-DeAngelis incidence and three delays, J. Biol. Dyn., 12 (2018), 146–170. https://doi.org/10.1080/17513758.2017.1408861 doi: 10.1080/17513758.2017.1408861
[23]	H. Miao, Z. Teng, C. Kang, Stability and Hopf bifurcation of an HIV infection model with saturation incidence and two delays, Discrete Contin. Dyn. Syst. - B, 22 (2017), 2365–2387. https://doi.org/10.3934/dcdsb.2017121 doi: 10.3934/dcdsb.2017121
[24]	H. Shu, L. Wang, J. Watmough, Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses, SIAM J. Appl. Math., 73 (2013), 1280–1302. https://doi.org/10.1137/120896463 doi: 10.1137/120896463
[25]	J. Wang, C. Qin, Y. Chen, X. Wang, Hopf bifurcation in a CTL-inclusive HIV-1 infection model with two time delays, Math. Biosci. Eng., 16 (2019), 2587–2612. https://doi.org/10.3934/mbe.2019130 doi: 10.3934/mbe.2019130
[26]	J. Xu, Y. Zhou, Bifurcation analysis of HIV-1 infection model with cell-to-cell transmission and immune response delay, Math. Biosci. Eng., 13 (2016), 343–367. https://doi.org/10.3934/mbe.2015006 doi: 10.3934/mbe.2015006
[27]	K. Wang, W. Wang, H. Pang, X. Liu, Complex dynamic behavior in a viral model with delayed immune response, Physica D, 226 (2007), 197–208. https://doi.org/10.1016/j.physd.2006.12.001 doi: 10.1016/j.physd.2006.12.001
[28]	J. K. Hale, S. M. Verduyn Lunel, Introduction to Functional Differential Equations, Springer, New York, 1993.
[29]	H. L. Smith, Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems, Amer. Math. Soc., Mathematical Surveys and Monographs, Providence, Rhode Island, 41 (1995). https://doi.org/10.1090/surv/041
[30]	Y. Tian, Y. Yuan, Effect of time delays in an HIV virotherapy model with nonlinear incidence, Proc. Math. Phys. Eng. Sci., 472 (2016), 20150626. https://doi.org/10.1098/rspa.2015.0626 doi: 10.1098/rspa.2015.0626
[31]	S. Ruan, J. Wei, On the zeros of a third degree exponential polynomial with applications to a delayed model for the control of testosterone secretion, IMA J. Math. Appl. Med. Biol., 18 (2001), 41–52.
[32]	M. Y. Li, H. Shu, Multiple stable periodic oscillations in a mathematical model of CTL response to HTLV-I infection, Bull. Math. Biol., 73 (2011), 1774–1793. https://doi.org/10.1007/s11538-010-9591-7 doi: 10.1007/s11538-010-9591-7
[33]	B. Hassard, N. Kazarinoff, Y. Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, 1981.
[34]	Q. An, E. Beretta, Y. Kuang, C. Wang, H. Wang, Geometric stability switch criteria in delay differential equations with two delays and delay dependent parameters, J. Differ. Equations, 266 (2019), 7073–7100. https://doi.org/10.1016/j.jde.2018.11.025 doi: 10.1016/j.jde.2018.11.025
[35]	X. Lin, H. Wang, Stability analysis of delay differential equations with two discrete delays, Can. Appl. Math. Q., 20 (2012), 519–533. Available from: https://www.math.ualberta.ca/hwang/TwoDelayCAMQ.pdf.
[36]	P. Wu, Z. He, A. Khan, Dynamical analysis and optimal control of an age-since infection HIV model at individuals and population levels, Appl. Math. Modell., 106 (2022), 325–342. https://doi.org/10.1016/j.apm.2022.02.008 doi: 10.1016/j.apm.2022.02.008
[37]	P. Wu, H. Zhao, Mathematical analysis of an age-structured HIV/AIDS epidemic model with HAART and spatial diffusion, Nonlinear Anal. Real World Appl., 60 (2021), 103289. https://doi.org/10.1016/j.nonrwa.2021.103289 doi: 10.1016/j.nonrwa.2021.103289
[38]	R. Xu, C. Song, Dynamics of an HIV infection model with virus diffusion and latently infected cell activation, Nonlinear Anal. Real World Appl., 67 (2022), 103618. https://doi.org/10.1016/j.nonrwa.2022.103618 doi: 10.1016/j.nonrwa.2022.103618

This article has been cited by:

1.	Saima Rashid, Muhammad Kashif Iqbal, Ahmed M. Alshehri, Rehana Ashraf, Fahd Jarad, A comprehensive analysis of the stochastic fractal–fractional tuberculosis model via Mittag-Leffler kernel and white noise, 2022, 39, 22113797, 105764, 10.1016/j.rinp.2022.105764
2.	Pooyan Alinaghi Hosseinabadi, Ali Soltani Sharif Abadi, Hemanshu Pota, Sundarapandian Vaidyanathan, Saad Mekhilef, Kamal Shah, Adaptive Finite-Time Sliding Mode Backstepping Controller for Double-Integrator Systems with Mismatched Uncertainties and External Disturbances, 2022, 2022, 1607-887X, 1, 10.1155/2022/3758220
3.	Saima Rashid, Fahd Jarad, Stochastic dynamics of the fractal-fractional Ebola epidemic model combining a fear and environmental spreading mechanism, 2023, 8, 2473-6988, 3634, 10.3934/math.2023183
4.	Timilehin Kingsley Akinfe, Adedapo Chris Loyinmi, An improved differential transform scheme implementation on the generalized Allen–Cahn equation governing oil pollution dynamics in oceanography, 2022, 6, 26668181, 100416, 10.1016/j.padiff.2022.100416
5.	Maysaa Al-Qurashi, Sobia Sultana, Shazia Karim, Saima Rashid, Fahd Jarad, Mohammed Shaaf Alharthi, Identification of numerical solutions of a fractal-fractional divorce epidemic model of nonlinear systems via anti-divorce counseling, 2022, 8, 2473-6988, 5233, 10.3934/math.2023263
6.	Jarunee Soontharanon, Muhammad Aamir Ali, Hüseyin Budak, Pinar Kösem, Kamsing Nonlaopon, Thanin Sitthiwirattham, Behrouz Parsa Moghaddam, Some New Generalized Fractional Newton’s Type Inequalities for Convex Functions, 2022, 2022, 2314-8888, 1, 10.1155/2022/6261970
7.	Saima Rashid, Saad Ihsan Butt, Zakia Hammouch, Ebenezer Bonyah, Alexander Meskhi, An Efficient Method for Solving Fractional Black-Scholes Model with Index and Exponential Decay Kernels, 2022, 2022, 2314-8888, 1, 10.1155/2022/2613133
8.	Saima Rashid, Fahd Jarad, Hajid Alsubaie, Ayman A. Aly, Ahmed Alotaibi, A novel numerical dynamics of fractional derivatives involving singular and nonsingular kernels: designing a stochastic cholera epidemic model, 2023, 8, 2473-6988, 3484, 10.3934/math.2023178
9.	Khadija Aayadi, Khalid Akhlil, Sultana Ben Aadi, Hicham Mahdioui, Weak solutions to the time-fractional g-Bénard equations, 2022, 2022, 1687-2770, 10.1186/s13661-022-01649-3
10.	Saima Rashid, Bushra Kanwal, Muhammad Attique, Ebenezer Bonyah, Ibrahim Mahariq, An Efficient Technique for Time-Fractional Water Dynamics Arising in Physical Systems Pertaining to Generalized Fractional Derivative Operators, 2022, 2022, 1563-5147, 1, 10.1155/2022/7852507
11.	Haresh P. Jani, Twinkle R. Singh, Study of concentration arising in longitudinal dispersion phenomenon by Aboodh transform homotopy perturbation method, 2022, 8, 2349-5103, 10.1007/s40819-022-01363-9
12.	Maysaa Al Qurashi, Saima Rashid, Fahd Jarad, A computational study of a stochastic fractal-fractional hepatitis B virus infection incorporating delayed immune reactions via the exponential decay, 2022, 19, 1551-0018, 12950, 10.3934/mbe.2022605
13.	Kingsley Timilehin Akinfe, A reliable analytic technique for the modified prototypical Kelvin–Voigt viscoelastic fluid model by means of the hyperbolic tangent function, 2023, 7, 26668181, 100523, 10.1016/j.padiff.2023.100523
14.	Rachid Belgacem, Ahmed Bokhari, Dumitru Baleanu, Salih Djilali, New generalized integral transform via Dzherbashian--Nersesian fractional operator, 2024, 14, 2146-5703, 90, 10.11121/ijocta.1449
15.	Emmanuel Kengne, Conformable derivative in a nonlinear dispersive electrical transmission network, 2024, 112, 0924-090X, 2139, 10.1007/s11071-023-09121-2
16.	Nan Jiang, Research on stability and control strategies of fractional-order differential equations in nonlinear dynamic systems, 2025, 1472-7978, 10.1177/14727978251346078

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)