Primitivoids of curves in Minkowski plane

1.   Introduction

Einstein presented work on general relativity as a theory of space, time and gravitation in pseudo-Euclidean space in 1915. Even so, this topic has stayed immobile for much of its rich history because its conception requires advanced mathematics awareness. Since the end of the twentieth century, pseudo-Euclidean geometry has been an energetic area of mathematical research, and it has been applied to a variety of subjects relating to geometry and relativity.

A lot of vital outcomes in the theory of curves in $\mathbb{R}^{3}$ were started by Monge, and Darboux pioneered the moving frame concept. Subsequently, Serret-Frenet equations had a vital role in these topics. It is well known that Einstein's concept paved the way to learning about other types of geometries. One of the most important of these geometries is Minkowski geometry.

The concept of a singularity is a vital point in nonlinear studies. Specially, it has been widely used in categorizations of singularities correlating with some topics in different spaces (see ^[1,2]).

In the early 18th century, pedal curves were presented by Collin Maclaurin as the position of the foot of the orthogonal from the certain point to the tangent to a specific curve. In ^[3], T. Nishimura gave the meaning and the categorizations of the singularities of pedal curves of regular curves in the unit sphere. In ^[4], Božek and Foltán discussed the relations among singular points of the pedal curves and inflection points of regular curves in the Euclidean plane. If the curve is not regular at any point, we are not able to define the pedal curve at this point as in the traditional method. Fukunaga and Takahashi have studied frontals (sometimes known as fronts) in the Euclidean plane and also investigated Legendrian curves in the unit tangent bundle of $\mathbb{R}^{2}$ (see^[5,6,7]). Legendrian curves are also known as Legendrian immersions. In ^[8,9], authors studied some geometric properties of the frontal. Also, Li and Pei have achieved some work related to pedal curves of fronts in the sphere. They recognized the pedal curves of fronts and introduced the classification of singularities of the pedal curves of fronts in the sphere. Moreover, some of the latest connected studies can be seen in ^{[10,11,12,13,14,15,16]}. The main variation between a regular curve and a frontal is that the frontal might have singular points. A key instrument for investigation of the frontal is said to be a moving frame realized in the unit tangent bundle. With the use of the moving frame, one can express a new definition of the pedal curve of the frontal. When the curve is a regular one, this new idea of the pedal curve is compatible with the traditional one.

This work aims to present the concept of the anti-pedal of a curve in which its singularities also coincide with the inflection points of the main curve. Further, we demonstrate that the primitive is the same as the anti-pedal of the inversion image of the given curve. There is one more idea, which is introduced as the notion of primitivoids of a curve in the Minkowski plane, which are relatives of the primitive. There are two methods to determine primitivoids. One is known as a parallel primitivoid and the other is a slant primitivoid. At last, we treat these concepts for frontal curves and establish the relationships. The main results are in sections 3–6. During this work, we assume that $\boldsymbol{\zeta}$ is a timelike curve, and all maps are class $C^{\infty}$.

2.   Geometric meanings and basis concepts

In this part, we present some geometric properties of the Minkowski plane. More details can be seen in ^{[10,11,12,13]}. The Minkowski plane $\mathbb{R}_{1}^{2}$ is the Euclidean plane $\mathbb{R}^{2}$ with the metric $\langle {\mathbf{x}}, {\mathbf{y}}\rangle = -x_{1}y_{1}+x_{2}y_{2}$, where ${\mathbf{x}} = (x_{1}, x_{2})$, and ${\mathbf{y}} = (y_{1}, y_{2})$. A non-zero vector ${\mathbf{x}}$ in $\mathbb{R}_{1}^{2}$ is spacelike, lightlike or timelike if $\langle {\mathbf{x}}, {\mathbf{x}}\rangle > 0$, $\langle {\mathbf{x}}, {\mathbf{x}}\rangle = 0$ or $\langle {\mathbf{x}}, {\mathbf{x}}\rangle < 0$, respectively. The norm of a vector ${\mathbf{x}} = (x_{1}, x_{2})\in\mathbb{R}_{1}^{2}$ is denoted by $\rVert {\mathbf{x}}\lVert = \sqrt{\lvert\langle {\mathbf{x}}, {\mathbf{x}} \rangle \rvert}$. We express by ${\mathbf{x}}^{\bot}$ the vector denoted by ${\mathbf{x}}^{\bot} = (x_{2}, x_{1})$. It is easy to see that ${\mathbf{x}}^{\bot}$ is orthogonal to ${\mathbf{x}}$ $(i.e., \langle {\mathbf{x}}, {\mathbf{x}}^{\bot} \rangle = 0)$, and $\rVert {\mathbf{x}}\lVert = \rVert {\mathbf{x}}^{\bot}\lVert$. We find ${\mathbf{x}}^{\bot} = \pm {\mathbf{x}}$ if and only if ${\mathbf{x}}$ is lightlike, and ${\mathbf{x}}^{\bot}$ is timelike (respectively, spacelike) if and only if ${\mathbf{x}}$ is spacelike (respectively, timelike).

Furthermore, we indicate three types of pseudo-circle in $\mathbb{R}_1^2$, which have the center $\mathit{\boldsymbol{v}}\in\mathbb{R}_1^2$ and radius $r\geq0$.

Suppose $\mathit{\boldsymbol{\zeta}}:I\rightarrow \mathbb{R}_1^2$ is a smooth curve in $\mathbb{R}_1^2$. The curve $\mathit{\boldsymbol{\zeta}}$ is said to be $spacelike$, $timelike$ or $lightlike$ if $\mathit{\boldsymbol{\zeta}}'(t) = \frac{d\mathit{\boldsymbol{\zeta}}}{dt}(t)$ is spacelike, timelike or lightlike for any $t\in \mathbb{R}$, respectively. Also, ${\boldsymbol \zeta}$ is non-lightlike if ${\boldsymbol \zeta}$ is timelike or spacelike.

Let the curve $\boldsymbol{\zeta} :I\longrightarrow \mathbb{R}_{1}^{2}$ be a non-lightlike. Here, $s$ is the arc-length parameter. Then, this leads to $\rVert \boldsymbol{\zeta}'(s)\lVert = 1$ for all $s\in I$, where $\boldsymbol{\zeta}'(s) = (d\boldsymbol{\zeta}/ds)(s)$. We refer by $\mathbf{e}_{1}(s)$ and $\mathbf{e}_{2}(s)$ to the unit tangent and normal vectors to $\boldsymbol{\zeta}(s)$, respectively, such that $\left\lbrace \mathbf{e}_{1}(s), \mathbf{e}_{2}(s) \right\rbrace$ is oriented anti-clockwise. In fact, $\mathbf{e}_{1}(s) = \boldsymbol{\zeta}'(s)$, and $\mathbf{e}_{2}(s) = (-1)^{w+1}\boldsymbol{\zeta}'(s)^{\perp}$, such that $w = 1$ if $\boldsymbol{\zeta}$ is timelike, and $w = 2$ if $\boldsymbol{\zeta}$ is spacelike.Thus, we find the Serret-Frenet equations:

where $\kappa(s)$ is the curvature of $\boldsymbol{\zeta}$. Therefore,

Even if $\boldsymbol{\zeta}$ is not parameterized by the arc-length, and $t$ denotes the parameter, then $\left\lbrace \mathbf{e}_{1}(t), \mathbf{e}_{2}(t) \right\rbrace$ are expressed as

This leads to

and the curvature function is denoted by $\kappa(t) = \langle \ddot{\boldsymbol{\zeta}}(t), \dot{\boldsymbol{\zeta}}(t)^{\perp} \rangle/\lVert \dot{\boldsymbol{\zeta}}(t)\rVert^{3}$ (see^[17,18]).

We call $\mathit{\boldsymbol{\zeta}} : I \rightarrow \mathbb{R}_1^2$ a spacelike frontal in $\mathbb{R}_{1}^{2}$ if there exists a smooth map $\boldsymbol \nu: I \rightarrow H_0^1(\mathit{\boldsymbol{\zeta}})$ where the pair $(\mathit{\boldsymbol{\zeta}}, \boldsymbol \nu) : I \rightarrow \mathbb{R}_1^2 \times H_0^1(\mathit{\boldsymbol{\zeta}})$ is a spacelike Legendrian curve, that is, $(\mathit{\boldsymbol{\zeta}}(t), \boldsymbol \nu(t))^{\ast}\theta = 0$ for each $t \in I$, where $\theta$ is a canonical contact structure on $T_1 \mathbb{R}_1^2 = \mathbb{R}_1^2\times H_0^1(\mathit{\boldsymbol{\zeta}})$. Note that the second condition is tantamount to $\dot{ \mathit{\boldsymbol{\zeta}}}(t) \cdot \boldsymbol \nu(t) = 0$ for each $t \in I$. Furthermore, if $(\mathit{\boldsymbol{\zeta}}, \boldsymbol \nu) : I \rightarrow \mathbb{R}_1^2 \times H_0^1(\mathit{\boldsymbol{\zeta}})$ is a spacelike Legendrian immersion, that is, $(\dot{ \mathit{\boldsymbol{\zeta}}}(t), \dot{\boldsymbol \nu}(t)) \neq (0, 0)$ for each $t \in I$, we regard $\mathit{\boldsymbol{\zeta}} : I \rightarrow \mathbb{R}_1^2$ as a spacelike front (or a spacelike wave front) in $\mathbb{R}_{1}^{2}$. Otherwise, $(\mathit{\boldsymbol{\zeta}}, \boldsymbol \nu)$ is said to be a timelike Legendrian curve; that is, $(\mathit{\boldsymbol{\zeta}}(t), \boldsymbol \nu(t))^{\ast}\theta = 0$ for each $t \in I$, then $\mathit{\boldsymbol{\zeta}}$ is called a timelike frontal. Hence, $(\mathit{\boldsymbol{\zeta}}, \boldsymbol \nu)$ is said to be a non-lightlike Legendrian curve, if $(\mathit{\boldsymbol{\zeta}}, \boldsymbol \nu)$ is a spacelike Legendrian curve or a timelike Legendrian curve. Here, we only consider non-lightlike Legendrian curves in $\mathbb{R}_{1}^{2}$.

Let $(\boldsymbol \zeta, \boldsymbol \nu) : I \rightarrow \mathbb{R}_1^2 \times S_1^1$(or $H_0^1$) be a non-lightlike Legendrian curve. Then, in the light of orthonormal frame $\{\boldsymbol \nu(t), \boldsymbol \mu(t)\}$ along ${\boldsymbol \zeta}(t)$, there are Frenet type formulae:

Further, we find $\beta(t)$ where $\dot{\boldsymbol \zeta}(t) = \beta(t)\boldsymbol \mu(t)$ for any $t \in I$. The pair $\left(\ell, \beta\right)$ is said to be the curvature of $(\boldsymbol \zeta, \boldsymbol \nu)$. (See for more details, ^[5,19,20]).

3.   Pedals, anti-pedals and primitives

Here, we present the notion of anti-pedals, which plays a vital role in this work. More details can be seen in ^{[8,9,10,11,12,13,18,21,22]}. The pedal curve of $\boldsymbol{\zeta}$ is given by $Pe_{\boldsymbol{\zeta}}(s) = -\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \mathbf{e}_{2}(s)$, where $\mathbf{e}_{2}(s) = J\mathbf{e}_{1}(s)$ is the unit normal, and we refer to the Jacobian matrix by $J$. After some manipulations, we get

The singular point of the pedal of $\boldsymbol{\zeta}$ is the point $s_{0}$ where $\boldsymbol{\zeta}(s_{0}) = 0$ or $\kappa(s_{0}) = 0$ (i.e., $s_{0}$ is the inflection point of $\boldsymbol{\zeta}$). If we suppose that $\boldsymbol{\zeta}$ does not pass through the origin, then by definition, $Pe_{\boldsymbol{\zeta}}(s)$ is the point on the tangent line through $\boldsymbol{\zeta}(s)$, which is denoted by the projection image of $\boldsymbol{\zeta}(s)$ of the normal direction. Therefore, $Pe_{\boldsymbol{\zeta}}(s)-\boldsymbol{\zeta}(s)$ produces the tangent line at $\boldsymbol{\zeta}(s)$.

Let $\boldsymbol{\zeta}: I\longrightarrow \mathbb{R}_{1}^{2}\backslash\lbrace0 \rbrace$ be a unit speed plane curve, and then we give a family of functions $\mathcal{H}:I\times(\mathbb{R}_{1}^{2}\backslash\lbrace0 \rbrace)\longrightarrow \mathbb{R}_{1}^{2}$ by $\mathcal{H}(s, \mathbf{u}) = \langle \mathbf{u}-\boldsymbol{\zeta}(s), \boldsymbol{\zeta}(s)\rangle$. For any fixed $s\in I$, $h_{s}(\mathbf{u}) = \mathcal{H}(s, \mathbf{u}) = 0$ is the line through $\boldsymbol{\zeta}(s)$ and orthogonal to the position vector $\boldsymbol{\zeta}(s)$. The envelope of the family of the lines $\left\lbrace h^{-1}_{s}(0)\right\rbrace _{s\in I}$ is the primitive of $\boldsymbol{\zeta}(s)$. Since $\partial \mathcal{H}/\partial s(s, \mathbf{u}) = \langle \mathbf{u}-2\boldsymbol{\zeta}(s), \mathbf{e}_{1}(s)\rangle$, $\left\lbrace \mathbf{e}_{1}(s), \mathbf{e}_{2}(s)\right\rbrace$ is an orthonormal basis of $\mathbb{R}_{1}^{2}$, and therefore, we can write $\mathbf{u} = \lambda\mathbf{e}_{1}(s)+\mu\mathbf{e}_{2}(s)$. From

we have

The primitive $Pr_{\boldsymbol{\zeta}}: I\longrightarrow \mathbb{R}_{1}^{2}\backslash\lbrace0 \rbrace$ of $\boldsymbol{\zeta}$ is

Assume that $Pe_{\boldsymbol{\zeta}}(s)$ and $Pr_{\boldsymbol{\zeta}}(s)$ are regular curves. Therefore, we have $Pr_{Pe_{\boldsymbol{\zeta}}}(s) = Pe_{Pr_{\boldsymbol{\zeta}}}(s) = \boldsymbol{\zeta}(s)$.

Even though the concept of a pedal is interpreted in $\mathbb{R}_{1}^{2}$, we choose the origin. Therefore, the pedal is stated as the envelope of a family of pseudo-circles:

Let $\mathcal{G}:I\times\mathbb{R}_{1}^{2}\longrightarrow \mathbb{R}_{1}^{2}$ be a function given by

Arranging this equation, we obtain

If we fix $s_{0}\in I$, then $\mathcal{G}(s_{0}, \mathbf{u}) = 0$ is a pseudo-circle which has the center $\frac{1}{2}\boldsymbol{\zeta}(s_{0})$ and passes through the origin.

For a fixed $s\in I$, $g_{s}(\mathbf{u}) = \mathcal{G}(s, \mathbf{u}) = 0$ is a pseudo-circle through the origin. Then, the inversion image of it is a line. If we recognize the inversion $\Psi:\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ at the origin with respect to the unit circle by $\Psi(\mathbf{u}) = \dfrac{\mathbf{u}}{\lVert\mathbf{u}\rVert^{2}}$, we get $\Psi(g^{-1}_{s}(0)) = \left\lbrace \mathbf{u}\mid \langle \mathbf{u}, \boldsymbol{\zeta}(s)\rangle = 1\right\rbrace$. Therefore, we define a family of functions $\mathcal{F}:I\times\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace \longrightarrow \mathbb{R}$ by $\mathcal{F}(s, \mathbf{u}) = \langle \mathbf{u}, \boldsymbol{\zeta}(s)\rangle-1$. Then $\partial \mathcal{F}/\partial s(s, \mathbf{u}) = \langle \mathbf{u}, \mathbf{e}_{1}(s)\rangle$, and we get $\mathcal{F}(s, \mathbf{u}) = \partial \mathcal{F}/\partial s(s, \mathbf{u}) = 0$ if and only if

Thereafter, a mapping $APe_{\boldsymbol{\zeta}}:I\times\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace \longrightarrow \mathbb{R}$ which is expressed as

is known as an anti-pedal curve of $\boldsymbol{\zeta}$. Therefore, we find $\Psi\circ APe_{\boldsymbol{\zeta}} = Pe_{\boldsymbol{\zeta}}$, and $\Psi\circ Pe_{\boldsymbol{\zeta}} = APe_{\boldsymbol{\zeta}}$.

Proposition 3.1. Assume that $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ is a unit speed plane curve. Therefore, we find

Proof. According to the properties of $\left\lbrace h^{-1}_{s}(0)\right\rbrace _{s\in I}$, since $\mathcal{H}(s, \mathbf{u}) = \langle \mathbf{u}, \boldsymbol{\zeta}(s)\rangle -\lVert\boldsymbol{\zeta}(s)\rVert^{2},$ $\mathcal{H}(s, \mathbf{u}) = 0$ if and only if $\langle \mathbf{u}, \Psi\circ\boldsymbol{\zeta}(s)\rangle = 1$. Subsequently, the envelope of the family of lines $\left\lbrace h^{-1}_{s}(0)\right\rbrace _{s\in I}$ is equal to the anti-pedal of $\Psi\circ\boldsymbol{\zeta}$. This leads to $Pr_{\boldsymbol{\zeta}}(s) = APe_{\Psi\circ\boldsymbol{\zeta}}(s)$. Since $\Psi\circ\Psi = 1_{\mathbb{R}_{1}^{2}\setminus \left\lbrace 0\right\rbrace }$, we obtain

which leads to the required result.

Since $\Psi$ is a diffeomorphism, the pedal $Pe_{\boldsymbol{\zeta}}$ and the anti-pedal $APe_{\boldsymbol{\zeta}} = \Psi\circ Pe_{\boldsymbol{\zeta}}(s)$ have the same singularities, which correspond to the inflection points of $\boldsymbol{\zeta}$. Thus, the singularities of the primitive $Pr_{\boldsymbol{\zeta}}(s) = APe_{\Psi\circ\boldsymbol{\zeta}}$ correspond to the inflections of the inversion curve $\Psi\circ\boldsymbol{\zeta}$. Now, we compute the curvature of $\Psi\circ\boldsymbol{\zeta}$.

Proposition 3.2. Let $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ be a unit speed curve. Then, the curvature of $\Psi\circ\boldsymbol{\zeta}$ at $s\in I$ is $\kappa_{\Psi\circ\boldsymbol{\zeta}}(s) = -\kappa(s)\lVert\boldsymbol{\zeta}(s)\rVert^{2}+2\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle$.

Proof. Since $\boldsymbol{\alpha}(s) = \Psi\circ\boldsymbol{\zeta}(s) = \dfrac{\boldsymbol{\zeta}(s)}{\lVert\boldsymbol{\zeta}(s)\rVert^{2}}$,

Assume $\sigma$ is the arc-length parameter of $\boldsymbol{\alpha}(s)$. Therefore, $d\sigma/ds = 1/\lVert\boldsymbol{\zeta}\rVert^{2}$.

Moreover,

and from relations

we get

By the Frenet formula and from Eqs (3.4) and (3.5), we get

and then we have

It follows that

and

which completes the proof.

Therefore, we have the result:

Corollary 3.1. Let $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ be a unit speed curve, and from Eq (3.6), we have

Then, $\kappa'(s) = 0$ if and only if $\kappa'_{\Psi\circ\boldsymbol{\zeta}}(s) = 0$.

We say that the point $s_{0}\in I$ with $\kappa'(s_{0}) = 0$ is a vertex of $\boldsymbol{\zeta}$. Therefore, the previous result confirms that the vertices of $\boldsymbol{\zeta}$ and $\Psi\circ\boldsymbol{\zeta}$ are identical. Also, the point $s_{0}\in I$ is an inflection point of $\boldsymbol{\zeta}$ if and only if $\kappa(s_{0}) = 0$.

4.   Parallel primitivoids in Minkowski plane

Now, we investigate a family of functions $\mathcal{H}:(I\times\mathbb{R}_{1}^{2} \setminus\left\lbrace 0\right\rbrace) \longrightarrow\mathbb{R}$ given by $\mathcal{H}(s, \mathbf{u}) = \langle\mathbf{u}-r\boldsymbol{\zeta}(s), \boldsymbol{\zeta}(s)\rangle$. More details can be seen in ^{[8,9,10,11,12,13,18,21,22]}. Therefore, $\left\lbrace h_{s}^{-1}(0) \right\rbrace_{s\in I}$ is a family of lines which are orthogonal to $\boldsymbol{\zeta}(s)$ through $r\boldsymbol{\zeta}(s)$, where $h_{s}(\mathbf{u}) = \mathcal{H}(s, \mathbf{u})$. Therefore, by definition, the envelope of these lines is the $r$-parallel primitivoid of $\boldsymbol{\zeta}$. Since $\left\lbrace\mathbf{e}_{1}(s), \mathbf{e}_{2}(s) \right\rbrace$ is an orthonormal frame along $\boldsymbol{\zeta}$, then there exist $\lambda, \mu\in\mathbb{R}$ such that $\mathbf{u}-r\boldsymbol{\zeta}(s) = \lambda\mathbf{e}_{1}(s)+\mu\mathbf{e}_{2}(s)$. Thus, we obtain

Then,

since $\partial \mathcal{H}/\partial s(s, \mathbf{u}) = 0$ if and only if $\lambda = -r\langle\boldsymbol{\zeta}(s), \mathbf{e}_{1}(s)\rangle$, and $\mathcal{F}(s, \mathbf{u}) = 0$ if and only if $\langle\lambda\mathbf{e}_{1}(s)+\mu\mathbf{e}_{2}(s), \boldsymbol{\zeta}(s)\rangle = 0$, which means that

or, in the another form,

Then,

If $\langle \mathbf{e}_{2}(s), \boldsymbol{\zeta}(s) \rangle\neq0$, then we get $\mathcal{F}(s, \mathbf{u}) = \partial \mathcal{H}/\partial s(s, \mathbf{u}) = 0$ if and only if

From Eq (3.5), the last equation becomes

Therefore, the parametrization of the $r$-parallel primitivoid is obtained as follows

and is given by $r$-$Pr_{\boldsymbol{\zeta}}(s)$.

Since

we obtain the following result:

Theorem 4.1. Assume $\langle \mathbf{e}_{2}(s), \boldsymbol{\zeta}(s) \rangle\neq0$. Then, $r$-$Pr_{\boldsymbol{\zeta}}(s) = rPr_{\boldsymbol{\zeta}}(s) = Pr_{r\boldsymbol{\zeta}}(s).$

Proof. For $rPr_{\boldsymbol{\zeta}}(s)$, the unit tangent vector is $r\mathbf{e}_{1}(s)/\lVert r\mathbf{e}_{1}(s)\rVert^{2} = \mathbf{e}_{1}(s)$, and therefore $\mathbf{e}_{2}(s)$ is the unit normal vector of $rPr_{\boldsymbol{\zeta}}(s)$. Hence, we get

which is our required result.

5.   Slant primitivoids

The definition of primitivoids of Euclidean plane curves was introduced by Izumiya and Takeuchi (2019) (see ^[21]). More related studies can be seen in ^{[10,11,12,13,14,15,16,22]}. Analogous to their notions in Euclidean plane, we can give the $\psi$-slant primitivoid as the envelope of the family of lines with the constant angle $\psi$ to the position vector of the curve. Therefore, we introduce the following accurate definition:

Consider $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ to be a unit speed curve, and we find $\boldsymbol{\zeta}(s) = -\langle \boldsymbol{\zeta}(s), \mathbf{e}_{1}(s)\rangle \mathbf{e}_{1}(s)+\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \mathbf{e}_{2}(s)$. Therefore, the $\pi/2$ couterclockwise-rotated vector is $J\boldsymbol{\zeta}(s) = -\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \mathbf{e}_{1}(s)+\langle \boldsymbol{\zeta}(s), \mathbf{e}_{1}(s)\rangle \mathbf{e}_{2}(s)$. For $\psi\in\mathbb{R}$, we present the definition

Now, we evaluate a function $\mathcal{F}:(I\times\mathbb{R}_{1}^{2} \setminus\left\lbrace 0\right\rbrace) \longrightarrow\mathbb{R}$ given by $\mathcal{F}(s, \mathbf{u}) = \langle\mathbf{u}-\boldsymbol{\zeta}(s), \mathbb{N}[\psi](s)\rangle$. For $s\in I$, $f_{s}(\mathbf{u}) = \mathcal{F}(s, \mathbf{u}) = 0$ is an equation of the line through $\boldsymbol{\zeta}(s)$ orthogonal to $\mathbb{N}[\psi](s)$, and the angle between the line and the position vector $\boldsymbol{\zeta}(s)$ is $\psi+\pi/2$. The envelope of the family of lines $\left\lbrace f_{s}^{-1}(0) \right\rbrace_{s\in I}$ is called a $\psi$-slant primitivoid of $\boldsymbol{\zeta}$. We consider a parametrization of the $\psi$-slant primitivoid of $\boldsymbol{\zeta}$. The $\psi$-slant primitivoid of $\boldsymbol{\zeta}$ is given by $Pr[\psi]_{\boldsymbol{\zeta}}(s)$.

Theorem 5.1. Let $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ be a unit speed curve such that $\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \neq0$. Then, we obtain

Proof. Since $\mathbb{N}[\psi](s) = \cosh\psi\boldsymbol{\zeta}(s)+\sinh\psi J\boldsymbol{\zeta}(s)$, we have $\mathbb{N}[\psi]'(s) = \cosh\psi\mathbf{e}_{1}(s)+\sinh\psi J\mathbf{e}_{1}(s) = \cosh\psi\mathbf{e}_{1}(s)+\sinh\psi \mathbf{e}_{2}(s)$. Then, $\mathcal{F}(s, \mathbf{u}) = 0$ if and only if there exits $\lambda\in\mathbb{R}$ such that $\mathbf{u}-\boldsymbol{\zeta}(s) = \lambda\left(\cosh\psi J\boldsymbol{\zeta}(s)+\sinh\psi \boldsymbol{\zeta}(s)\right)$. From relations $\boldsymbol{\zeta} = -\langle \boldsymbol{\zeta}, \mathbf{e}_{1}\rangle \mathbf{e}_{1}+\langle \boldsymbol{\zeta}, \mathbf{e}_{2}\rangle \mathbf{e}_{2}$, and $J\boldsymbol{\zeta} = -\langle \boldsymbol{\zeta}, \mathbf{e}_{2}\rangle \mathbf{e}_{1}+\langle \boldsymbol{\zeta}, \mathbf{e}_{1}\rangle \mathbf{e}_{2}$, we note that $\langle J\boldsymbol{\zeta}, \mathbf{e}_{2}\rangle = \langle \boldsymbol{\zeta}, J^{t}\mathbf{e}_{2}\rangle = - \langle \boldsymbol{\zeta}, J\mathbf{e}_{2}\rangle = \langle \boldsymbol{\zeta}, \mathbf{e}_{1}\rangle$ and $\langle J\boldsymbol{\zeta}, \mathbf{e}_{1}\rangle = \langle \boldsymbol{\zeta}, J^{t}\mathbf{e}_{1}\rangle = \langle \boldsymbol{\zeta}, J\mathbf{e}_{1}\rangle = \langle \boldsymbol{\zeta}, \mathbf{e}_{2}\rangle$. Also, we obtain $\langle \boldsymbol{\zeta}, \boldsymbol{\zeta}\rangle = -\langle J\boldsymbol{\zeta}, J\boldsymbol{\zeta}\rangle$. With the condition $\mathcal{F}(s, \mathbf{u}) = 0$, we get

Thereby, $\mathcal{F}(s, \mathbf{u}) = \partial \mathcal{F}(s, \mathbf{u})/\partial s = 0$ if and only if

and then

From Eq (3.5), and the relation $J\boldsymbol{\zeta}(s) = -\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \mathbf{e}_{1}(s)+\langle \boldsymbol{\zeta}(s), \mathbf{e}_{1}(s)\rangle \mathbf{e}_{2}(s)$, we find

and then

Where $Pr_{\boldsymbol{\zeta}}(s) = 2\boldsymbol{\zeta}(s)-\dfrac{\lVert\boldsymbol{\zeta}(s)\rVert^{2}}{\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle}\mathbf{e}_{2}(s)$, $J\boldsymbol{\zeta}(s)$ is a unit speed curve such that the tangent vector is $J\mathbf{e}_{1}(s) = \mathbf{e}_{2}(s)$, and the normal vector is $J\mathbf{e}_{2}(s) = J J \mathbf{e}_{1}(s) = -\mathbf{e}_{1}(s)$, which yields that

Thus, we arrive at

which is our desired conclusion.

Corollary 5.1. Consider a unit speed curve is given by $\boldsymbol{\zeta}:I \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$, such that $\langle \boldsymbol{\zeta}(s), \mathbf{e}_{2}(s)\rangle \neq0$. Therefore, we obtain

Proof. Since

from Theorem 5.1, we find

and the proof is completed.

Theorem 5.2. With the same notations as above, we conclude

Proof. According to Theorem 5.1 and Corollary 5.1, we get

where $I$ is the identity matrix, and then we find

where $R(\psi) = \cosh\psi I+\sinh\psi J$. This leads to our required result.

Hereafter, we investigate the relations between primitivoids and pedals. For $\lambda\in\mathbb{R}\setminus\left\lbrace 0\right\rbrace$, we give $\lambda\boldsymbol{\zeta}(s)$. Since $(\lambda\boldsymbol{\zeta})'(s) = \lambda\mathbf{e}_{1}(s),$ $\lVert\lambda\mathbf{e}_{1}(s)\rVert = -\lvert\lambda\rvert$, so $\mathbf{e_{1}}_{\lambda\boldsymbol{\zeta}}(s) = \mathbf{e}_{1}(s)$ for $\lambda < 0$, and $\mathbf{e_{2}}_{\lambda\boldsymbol{\zeta}}(s) = J\mathbf{e}_{1}(s) = \mathbf{e}_{2}(s)$. Also, we have $\mathbf{e_{1}}_{\lambda\boldsymbol{\zeta}}(s) = -\mathbf{e}_{1}(s)$ for $\lambda > 0$ and $\mathbf{e_{2}}_{\lambda\boldsymbol{\zeta}}(s) = J(-\mathbf{e}_{1}(s)) = -\mathbf{e}_{2}(s)$. Therefore, we find $Pe_{\lambda\boldsymbol{\zeta}}(s) = \lambda Pe_{\boldsymbol{\zeta}}(s)$. Then, we arrive at the following result:

Proposition 5.1. Assume that $Pe_{\boldsymbol{\zeta}}$ and $Pr[\psi]_{\boldsymbol{\zeta}}$ are regular curves. Therefore,

Proof. By the aforementioned information and Theorem 5.2, we obtain

and

which is the required result.

Now, we investigate the relations of primitivoids with anti-pedals and parallel primitivoids.

Proposition 5.2. Consider a unit speed curve $\boldsymbol{\zeta} :I\longrightarrow\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ such that $\langle \mathbf{e}_{2}(s), \boldsymbol{\zeta}(s)\rangle \neq0$. Therefore,

Proof. According to Proposition 3.1 and Theorem 5.2, we get

By Theorem 4.1, we obtain

which leads to the desired result.

6.   Pedals and primitivoids of frontals in Minkowski plane

In this part, we propagate the concept of primitivoids and pedals of certain singular curves. The pedal of non-lightlike frontal $\boldsymbol{\zeta}$ is denoted by $\mathcal{P}e_{\boldsymbol{\zeta}}(t) = \langle \boldsymbol{\zeta}(t), \mathit{\boldsymbol{\nu}}(t)\rangle\mathit{\boldsymbol{\nu}}(t)$ (for more details, see ^[18,22,23]). Furthermore, the anti-pedal of $\boldsymbol{\zeta}$ is construed to be

As we noted for a regular curve $\boldsymbol{\zeta}$ in $\S 3$, the anti-pedal of a non-lightlike frontal $\boldsymbol{\zeta}$ is the envelope of the family of lines $\left\lbrace \mathbf{u}\mid \langle \mathbf{u}, \boldsymbol{\zeta}(t)\rangle = 1\right\rbrace_{t\in I}$.

Otherwise, for a non-lightlike frontal $\boldsymbol{\zeta}$ with $\langle \boldsymbol{\zeta}(t), \mathit{\boldsymbol{\nu}}(t)\rangle\neq0$, we recognize the primitive of $\boldsymbol{\zeta}$ by

We notice that the primitive of $\boldsymbol{\zeta}$ is the envelope of the family of lines

Because $\langle \mathbf{u}-\boldsymbol{\zeta}(t), \boldsymbol{\zeta}(t)\rangle = 0$ if and only if $\langle \mathbf{u}, \Psi\circ\boldsymbol{\zeta}(t)\rangle -1 = 0$, where $\Psi:\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace \longrightarrow \mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ is the inversion defined by $\Psi(\mathbf{u}) = \dfrac{\mathbf{u}}{\lVert\mathbf{u}\rVert^{2}}$. We obtain the following lemma:

Lemma 6.1. Let $(\boldsymbol \zeta, \boldsymbol \nu)$ be a non-lightlike Legendrian curve with the curvature $(\ell, \beta)$ in a Minkowski plane. Then, we obtain

Then, we conclude the following lemma.

Lemma 6.2. Let $(\boldsymbol \zeta, \boldsymbol \nu)$ be a non-lightlike Legendrian curve with the curvature $(\ell, \beta)$ in a Minkowski plane. Then, the primitive $\mathcal{P}e_{\boldsymbol{\zeta}}$ of $\boldsymbol{\zeta}$ is a non-lightlike frontal.

Proof. Because $\boldsymbol{\zeta}(t)\neq0$, $\Psi\circ\boldsymbol{\zeta}$ is well defined, and it is not equal to the origin. $\mathcal{P}e_{\Psi\circ\boldsymbol{\zeta}}$ is a non-lightlike frontal. By Lemma 6.1, we find $\mathcal{P}r_{\boldsymbol{\zeta}}(t) = \Psi\circ\mathcal{P}e_{\Psi\circ\boldsymbol{\zeta}}(t)$. Since, $\Psi$ is a diffeomorphism, $\Psi\circ\mathcal{P}e_{\Psi\circ\boldsymbol{\zeta}}(t)$ is a non-lightlike frontal.

After getting the parametrization of primitivoids of regular curves, we can propagate these concepts for non-lightlike frontals to get $\psi$-slant primitivoid $\mathcal{P}r_{\boldsymbol{\zeta}}[\psi]$ of the non-lightlike frontal $\boldsymbol{\zeta}$ as

In the following theorem, we define the $r$-parallel primitivoid of a non-lightlike frontal $\boldsymbol{\zeta}$.

Theorem 6.1. Suppose $\langle\boldsymbol{\zeta}(t), \mathit{\boldsymbol{\nu}}(t) \rangle\neq0$. Then, we get $r$-$\mathcal{P}r_{\boldsymbol{\zeta}}(t) = r\mathcal{P}r_{\boldsymbol{\zeta}}(t).$

Proof. For $r\mathcal{P}r_{\boldsymbol{\zeta}}(t)$, the unit tangent vector is $r\mathit{\boldsymbol{\eta}}_{1}(t)/\lVert r\mathit{\boldsymbol{\eta}}_{1}(t)\rVert^{2} = \mathit{\boldsymbol{\eta}}_{1}(t)$, so that $\mathit{\boldsymbol{\nu}}(t)$ is the unit normal vector of $r\mathcal{P}r_{\boldsymbol{\zeta}}(t)$. Hence, we obtain

and the proof is completed.

Also, we define the $\psi$-slant primitivoid of a non-lightlike frontal $\boldsymbol{\zeta}$ with the same method of a regular curve as

Since $\langle R(\psi)\boldsymbol{\zeta}(t), R(\psi)\mathit{\boldsymbol{\nu}}(t)\rangle = \langle \boldsymbol{\zeta}(t), \mathit{\boldsymbol{\nu}}(t)\rangle$, we find

A rotated frontal $\boldsymbol{\zeta}_{\psi}$ is defined to be $\boldsymbol{\zeta}_{\psi}(t) = R(\psi)\boldsymbol{\zeta}(t)$. Therefore, we obtain $R(\psi) \mathcal{P}r_{\boldsymbol{\zeta}}(t) = \mathcal{P}r_{\boldsymbol{\zeta}_{\psi}}(t)$. Thus, we conclude the following results.

Theorem 6.2. Let $(\boldsymbol \zeta, \boldsymbol \nu)$ be a non-lightlike Legendrian curve with the curvature $(\ell, \beta)$ in a Minkowski plane. Then, both of the $r$-parallel primitivoid $r$-$\mathcal{P}r_{\boldsymbol{\zeta}}(t)$ and the $\psi$-slant primitivoid $\mathcal{P}r[\psi]_{\boldsymbol{\zeta}}(t)$ of $\boldsymbol{\zeta}$ are non-lightlike frontals.

Proof. According to Lemma 6.2, $\mathcal{P}r_{\boldsymbol{\zeta}}$ is a non-lightlike frontal. Because $\cosh\psi R(\psi):\mathbb{R}_{1}^{2}\longrightarrow\mathbb{R}_{1}^{2}$ is a diffeomorphism, $\mathcal{P}r[\psi]_{\boldsymbol{\zeta}} = \cosh\psi R(\psi)\mathcal{P}r_{\boldsymbol{\zeta}}$ is a non-lightlike frontal. Also, if there exists $t_{0}\in I$ such that $\mathcal{P}r_{\boldsymbol{\zeta}}(t_{0}) = 0$, we find

Since $\lVert\mathit{\boldsymbol{\nu}}(t_{0})\rVert = 1$, we get $\lVert\boldsymbol{\zeta}(t_{0})\rVert = 2\lvert\langle \boldsymbol{\zeta}(t_{0}), \mathit{\boldsymbol{\nu}}(t_{0})\rangle \rvert$. This leads to

such that $\boldsymbol{\zeta}(t_{0}) = 2\langle \boldsymbol{\zeta}(t_{0}), \mathit{\boldsymbol{\nu}}(t_{0}) \rangle\mathit{\boldsymbol{\nu}}(t_{0})$. Hence, we obtain $\langle \boldsymbol{\zeta}(t_{0}), \mathit{\boldsymbol{\nu}}(t_{0}) \rangle = 2\langle \boldsymbol{\zeta}(t_{0}), \mathit{\boldsymbol{\nu}}(t_{0}) \rangle$. This contradicts the assumption $\langle \boldsymbol{\zeta}(t), \mathit{\boldsymbol{\nu}}(t) \rangle\neq0$. Then, $\mathcal{P}r_{\boldsymbol{\zeta}}(t) \neq0$. Here, we define $\Pi_{r}:\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace \longrightarrow\mathbb{R}_{1}^{2}\setminus\left\lbrace 0\right\rbrace$ by $\Pi_{r}(\mathbf{u}) = r\mathbf{u}$. Thus, $\Pi_{r}$ is a diffeomorphism, and $\Pi_{r}\circ\mathcal{P}r_{\boldsymbol{\zeta}} = r$-$\mathcal{P}r_{\boldsymbol{\zeta}}$. Therefore, we find that $r$-$\mathcal{P}r_{\boldsymbol{\zeta}}$ is a non-lightlike frontal.

7.   Computational examples

Now, we give two computational examples to confirm some properties of the primitivoids for the regular and frontal.

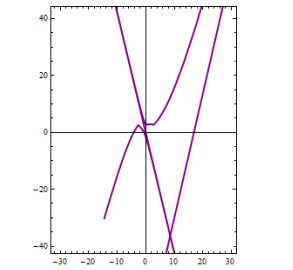
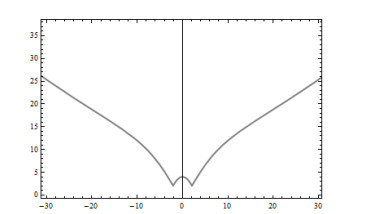
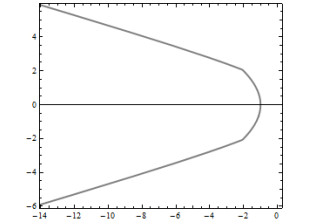
Example 7.1. Assume a curve $\boldsymbol{\zeta}:I\longrightarrow\mathbb{R}_{1}^{2}$, $I\in \mathbb{R}$, which is defined by $\boldsymbol{\zeta}(t) = \left(t^{3}+\sinh t, \cosh t\right)$. From Eq (2.2), we get

and then

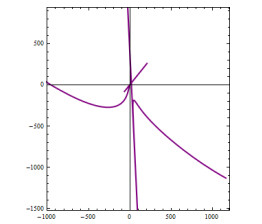
By considering the above equations, we see that $\boldsymbol{\zeta}(t)$ is a regular curve, and there are no lightlike points. Also, it is a timelike curve. From Eq (3.1), we get the primitive $Pr_{\boldsymbol{\zeta}}$ of the regular curve $\boldsymbol{\zeta}(t)$ as

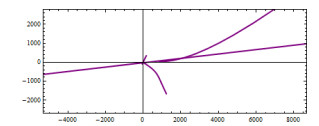
and from Eq (5.2), the primitive $Pr_{J\boldsymbol{\zeta}}$ of a regular curve $J\boldsymbol{\zeta}(t)$ is given as

Also, from Eq (5.1), the $\psi$-slant primitivoid of $\boldsymbol{\zeta}$ is given by

where

The figures of the example can be seen in Figures 1–5.

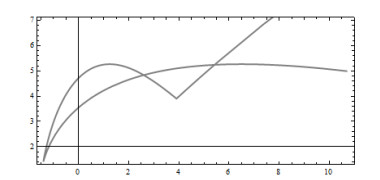
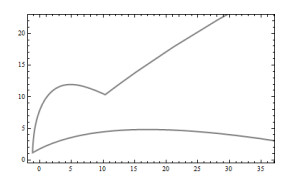
Example 7.2. We consider a curve $\boldsymbol{\delta}:I\longrightarrow\mathbb{R}_{1}^{2}$, $I\in \mathbb{R}$, which is expressed as

and we have

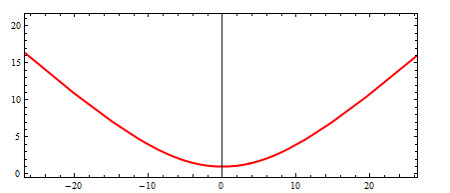
From the previous equations, we see that $\boldsymbol{\delta}(t)$ is a timelike frontal curve. The primitive curve $\mathcal{P}r_{\boldsymbol{\delta}}$ of the frontal curve $\boldsymbol{\delta}(t)$ is obtained as

where

The primitive $\mathcal{P}r_{J\boldsymbol{\delta}}$ of the frontal curve $J\boldsymbol{\delta}(t)$ is expressed as

where

Therefore, the $\psi$-slant primitivoid of the frontal timelike curve $\boldsymbol{\delta}$ is given by

The figures of the example can be seen in Figures 6–10.

8.   Conclusions

In a Minkowski plane, the differential geometry of pedal and primitive curves have been investigated. Relatives of the primitive of a plane curve which we call primitivoids have been considered. Also, the relationship between primitivoids and pedals of plane curves has been obtained. Meanwhile, we have illustrated the convenience and efficiency of this approach by some representative examples. The main results of the paper are in sections 3-6. Furthermore, interdisciplinary research can provide valuable new insights, but synthesizing articles across disciplines with highly varied standards, formats, terminology, and methods requires an adapted approach. Recently, many interesting papers have been written related to symmetry, molecular cluster geometry analysis, submanifold theory, singularity theory, eigenproblems, etc. ^{[24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]}. In future works, we plan to study the primitivoids of curves in a Minkowski plane for different queries and further improve the results in this paper, combined with the techniques and results in ^{[24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]}. We intend to explore new methods to find more results and theorems related to the singularity and symmetry properties of this topic in our following papers.

Acknowledgments

We gratefully acknowledge the constructive comments from the editor and the anonymous referees. This work was funded by the National Natural Science Foundation of China (Grant No. 12101168), Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ22A010014).

Conflict of interest

The authors declare no conflicts of interest.