1.
Introduction
In the context of phase field modeling, the equations that are often used to describe phase-separation in micro and nano-structure evolution of materials are in the form of higher order parabolic nonlinear partial differential equations (PDEs). The Cahn Hilliard (CH) equation originally proposed in 1958 to model phase separation in binary alloys [1], has found many other applications in physical processes related to block-copolymers, crystal growth, drug delivery, tumor growth, and image processing [2,3,4,5,6]. For the extended applications of the CH equation, full material separation is prevented leading to micro-phase separation, which is a result of interfacial energy interactions of the materials. For such models, different pattern formations are possible, which are often related to key structural properties of the materials [7].
The classic CH equation with constant mobility is a fourth order nonlinear PDE that derives from an energy functional that penalizes sharp transitions and selects minima related to the two materials in the mixture. There have been a number of numerical methods which have been proposed to solve the CH equation using finite differences, finite elements, finite volume methods, and spectral methods [8,9,10,11,12]. An extended version of the CH equation equation is found in the block copolymer (BCP) equation, which was proposed by Ohta and Kawasaki [13] to model BCP microstructure evolution. The energy functional for the BCP equation is similar to the one used in the CH equation but there is an added term to account for polymer stretching. Another extension for the CH equation is the phase field crystal (PFC) equation proposed by Elder and Grant [14]. Computational approaches for CH, BCP, and PFC equations can be found in [9,10,13,15,16].
Another very important equation in the phase field modeling area is the Functionalized Cahn-Hilliard (FCH) equation [17], which has been used to model micro-phase separation in ternary systems (oil-water-surfactant). The FCH equation is a sixth order parabolic PDE for which explicit methods are not practical since they would require very small steps for numerical stability (h≤Odx6), where h is the time step and dx is the grid spacing in one dimension. On the other hand, fully implicit methods would ensure stability, but can be computationally expensive for problems in more than one dimension. The FCH equation is a more challenging problem compared to the previous mentioned extensions of the CH equation. The challenges are due to the wide variations in space and time scales that need to be captured. The high PDE order makes the time evolution of spatial discretizations very stiff. Some progress has been made in the numerical solutions to the FCH equation [18], but more work needs to be done. Recent numerical approaches have been proposed in [19] using the (scalar auxiliary variable) SAV method. In our approach, we extend the ideas of the bi-harmonic modified (BHM) [20] method and introduce a parameter M3 for the FCH equation that allows for all nonlinear terms in the equation to be computed explicitly. This in turn gives an efficient implementation for the numerical solution at each time step. Numerical examples using the tri-harmonic modified (THM) approach are presented and compared to the work presented in [19] to demonstrate the efficiency, convergence properties, and ease of implementation of the proposed methodology. The purpose of this paper is to provide a numerical approach for the FCH equation that is efficient, accurate, and that is easy to implement with complexity similar to the original convexity-splitting (CS) approach [21] and the BHM approach [20].
In this paper, we utilize the THM approach as the basis for the new algorithms, which are coupled with different linear extrapolation and higher order time discretization techniques. In Section 2, we introduce the main mathematical model for the FCH equation to be considered in the first part of the numerical experiments. In Section 3, we explain how the THM approach can be applied to this version of the FCH equation and we provide a stability analysis of the proposed scheme. In Section 4, we introduce a series of benchmark problems for the FCH equation and we directly compare the performance of the THM approach versus the SAV methodology in terms of accuracy and order of convergence. Section 5 introduces a more complicated version of the FCH equation and we explain the adaptability of the THM approach to such models. In addition, we also show the adaptability of the THM approach with a higher order time stepping technique using an implicit-explicit (IMEX) Runge-Kutta (RK) formulation.
2.
Mathematical formulation
The FCH free energy is given in the form [17],
where W(u) is a symmetric double well function given by W(u)=14(u2−1)2. Here, η>0 is a parameter that represents the properties of amphiphilic phase at the interface (η<0 defines the Cahn-Hilliard-Willmore (CHW) energy [19], which is not considered in this paper), and ϵ is a parameter that characterizes the thickness of the diffusive interface.
The FCH equation is obtained as the H−1 gradient flow of the free energy (2.1)
where μ is the chemical potential, W′(u)=u3−u, W″(u)=3u2−1 and M is the mobility constant. Considering periodic boundary conditions, the scalar solution u(x,t) will evolve into configurations in a way that the FCH energy is always nonincreasing, that is dE(u)dt≤0. Numerical solutions of the FCH must retain this energy decreasing property. We note that this means that the scheme should produce numerical solutions in which the energy is either constant or decreasing but not increasing over time.
3.
Computational approach
The approach that we will consider for this problem relies in the extension of the BHM approach [20]. One of the goals for this formulation is maximum simplicity. We rewrite the Eqs (2.2)–(2.4) as
Having S(u) defined by (3.2) allows for us to write a single equation in the form
We note that (3.3) is identical to the FCH equation given by Eqs (2.2)–(2.4). The advantage of writing the FCH in this way is that now we can consider a splitting approach by extending the ideas of the BHM method proposed by Bertozzi [20]. Equation (3.3) is expanded by distributing the divergence operator to give
which now is suitable for introducing a constant M3 and rewriting Eq (3.4) as
which leads to the form of the FCH equation with a tri-harmonic splitting parameter M3.
We denote the discretized approximations to the solution u by u(xi,tn)≈Un,i, where the time step h is given by tn+1=tn+h. Accounting for the first order approximation of the left-hand side of (3.5) and treating the linear part of right-hand side in (3.5) implicitly gives the following semi-implicit scheme
where Ψ(u)=M3ϵ4Δ3u and Φ(u)=(M−M3)ϵ4Δ3u+MΔS(u). We note that Eq (3.5) is the general form of the splitting that accounts for a variable mobility case (M=M(u)), but this case is not considered in the present problem. For problems with variable mobility, the interested reader is referred to [22,23]. For the class of sixth order parabolic problems, the scheme given by (3.6) could also be referred to as the THM method. With regards to splitting approaches, a well-known CS approach was proposed by Eyre [21] and several others have been used in the variable mobility CH equation [20]. In addition and more recently, the PFC equation has been computed with a stabilizing parameter [19]. Equation (3.6) can be understood as a class of splitting methods for phase field models.
We will use Fourier pseudo-spectral methods [24] for our numerical simulations. The CH equation and related phase field models have been implemented with Fourier spectral methods in the past [25,26,27,28,29]. More recently, the FCH was implemented using Fourier spectral method in the work of Wise et al [19] which is one of the main reasons for us to consider the same type of implementation for our paper.
We include additional details about the spatial discretization for (3.6). The two-dimensional discrete Fourier transform of U can be written as
Consequently, the Fourier transforms of the harmonic, bi-harmonic and tri-harmonic operators can be expressed as ^ΔU=−k2ˆU, ^Δ2U=k4ˆU, and ^Δ3U=−k6ˆU where k2=k2x+k2y. Applying the Fourier spectral method to (3.6), gives the the following expression:
which provides an efficient formula for obtaining ˆUn+1, and then the inverse transform is applied to obtain Un+1.
For the stability criteria of the THM method given by (3.6), we will use the approach presented in [30]. Equation (3.3) is of the form ut=G(u), where G(u)=Ψ(u)+Φ(u). Using the expression ^Φ(Un)=^G(Un)−^Ψ(Un) in (3.7) gives the following:
To analyze the conditions for linear stability, we consider highest order terms in G(u) to arrive at the approximation ^G(Un+en)≈^G(Un+en)−C0ϵ4k6^en, which is then used in (3.8) to obtain the amplification factor associated with the growth of the errors in Un. The amplification factor is given by
The conditions to guarantee stability of the THM scheme require that |σ|<1, so one gets
Given the quantities considered in this formulation, the less-than-zero inequality is satisfied so one works with
which can be further reduced by rearranging the terms to arrive at the following inequality
In order to guarantee stability (|σ|<1), we satisfy the above inequality with the requirement that (C0−2M3)<0 which gives M3>C0/2. In the context of a constant mobility case, we can set C0=M, which gives a minimum value for the splitting parameter in the THM method (3.6). We note that in the analysis performed in [20], a criteria of M1>M (M1 is the splitting parameter for fourth order equations with constant mobility) was obtained for the original BHM approach. Following the approach in [30], we are able to get an improved criteria for this splitting parameter threshold. We will use M3>M/2 for all the simulations presented in this paper.
Remark 1. We emphasize that the THM approach is different than the original CS approach since the THM approach does not require splitting of the energy into convex and concave parts. The similarities with our approach and the CS approach are only in the shared simplicity of the splitting which leads to fast computations. In addition, we also make a note that the THM approach is an extension of the original BHM approach and many benefits in terms of efficiency and ease of implementation are inherited. Finally, in the next section we will present numerical experiments in which we show that the THM approach leads to good numerical results when compared to the SAV formulation.
4.
Numerical experiments and simulations: Part Ⅰ
Our numerical experiments will be presented in two parts: The first part will be related to the simpler version of the FCH equation and second part of the numerical experiments will include the more general and complicated verson of the FCH equation.
Since we are proposing a new THM method, it is important for us to understand how the method compares to the recently developed schemes for the FCH equation using a SAV formulation. We are interested in order of convergence, accuracy and ease of implementation for the THM approach. For the order of convergence and computing errors, there are several different forms such tests can take:
(ⅰ) We can construct a reference solution [9] using a very small time step h for a corresponding simulation final time tf. Then simulation runs using different h values reaching tf can be compared against this reference solution in order to compute errors and order of convergence.
(ⅱ) We can define an exact solution [31] and insert it into the FCH equation which will produce a modified version of the equation. We can then apply our methods to the modified FCH and for different choices of h we are able to compute the error since we have defined our exact solution.
In order to directly compare the performance of our schemes with those schemes presented in [19], in particular their SAV-BDF1 (scalar auxiliary variable backward differentiation formula of order 1) schemes, we will use a numerical test of the type (ⅱ) for the first few test problems. We note that SAV-BDF1 and the THM method presented in this paper are implemented using the same Fourier pseudo-spectral approach so that we can present a fair comparison of their performance.
We can consider an exact solution, whenever available, or accurate reference solution Uref(x,y,t) which is constructed with a small time step size of h=10−7 and a final time configuration of tf. We then compute the numerical solution using the THM scheme with difference choices of h, and compare against the reference solution at tf, and compute the L2 error with the formula
4.1. Test problem 1
We first investigate the convergence properties for our numerical approach by solving Eq (3.3) on Ω=[0,L]2 subject to periodic boundary conditions. For simplicity, all test problems will be considered with periodic boundary conditions. We use Fourier pseudo-spectral discretizations in space using N Fourier modes in each space direction [24,32]. We note that other discretizations are certainly possible (finite differences, finite elements, finite volume). The numerical solution is obtained by solving (3.3) with initial condition u0(x,y,t=0)=sinxcosy, parameter values M=1, M3=5, ϵ=0.1, η=ϵ2, L=4π, and with 2562 Fourier modes. The solution is evolved to a final time tf and compared against the exact solution given by
Equation (4.2) is the solution to the forced FCH equation which is obtained by inserting (4.2) into (3.3), resulting in a forcing term that is used to modify the original equation [19]. To be concrete, the form of the forced FCH equation is given by
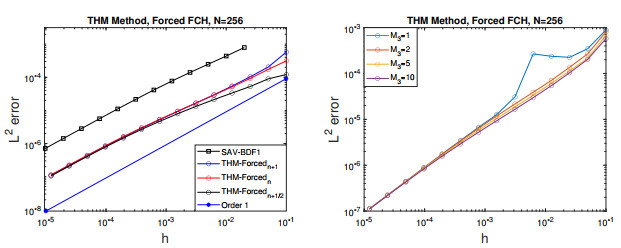
where F(x,y,t)=cos(y)sin(x)(1.9404cos(t)+cos(t)3(5.775−5.955cos(2y)+cos(2x) (5.955+16.965cos(2y)))−sin(t)+cos(t)5(−60cos(x)2 cos(y)4sin(x)2+sin(x)4(30cos(y)4−15sin(2y)2))). We compute the errors in the L2 norm. Here, we consider 3 cases for the computation of the forcing term F(x,y,t), the implicit time level (n+1), explicit (n), and semi-implicit (n+1/2). In addition, we compare our errors to the first order scheme SAV-BDF1 introduced in [19] to solve the FCH equation. For a comprehensive review of SAV methods, which were introduced by Shen [12] to efficiently solve gradient flow problems, we recommend the review-paper on SAV methods [33]. Our numerical results using the THM method are presented in Figure 1. It can be seen that the new method produces small errors for all possible evaluations of the forcing term, and, in addition, the errors from THM are found to be smaller than those from the SAV-BDF1 method [19]. Table 1 shows that the THM method reaches first order convergence with no problems and it is capable to perform well when compared to the SAV formulaton. Figure 1 (right) contains the error curves with several choices of the splitting parameter M3. For problems using a stabilization or splitting parameter, it is possible to introduce instability if the parameter is chosen very small (M3≈0, which defines a fully explicit problem). For the current benchmark problem, we tested several cases and found our lowest value of M3 to be M3≈1. For this case, we can see errors increasing for the range of values centered at h=10−2. On the other hand, when M3≥2, solutions remain accurate, numerical instability is suppressed, and the scheme performs with the expected level of accuracy (see Figure 1, right).
4.2. Test problem 2
To test the performance of the proposed method for longer runs, we considered a benchmark problem used for the FCH equation which can be found in the work done by Wise et al [19] that also traces back to the problems tested in [34]. We solve the FCH equation given by (3.3) with the following initial condition
with parameters values M=1, M3=5, ϵ=0.18, η=ϵ2, L=2π and with 1282 Fourier modes. The simulation snapshots are taken at values for t=0;and t=4 (see Figure 2). We test the numerical convergence of the method by following the numerical procedure (ⅰ), that is we construct a reference solution for this problem using a small time step h=10−6 using the THM method with a simple linear extrapolation [9] and compute the L2 errors for different choices of h. Figure 3 (left) shows the error curves for several values of M3. Local truncation errors are noticeable in this simulation and they can be spotted for h>10−2. To improve accuracy, we coupled the THM scheme (3.6) with a simple linear extrapolation which is given by
where we have now introduced the need of knowing two consecutive steps initially. However, this is easily accomplished since this is only required to be done during the initialization of the numerical procedure which allows for the computation cost of the linear extrapolation technique to be very efficient. We note that a linear extrapolation technique allows for a better choice of the initial condition and it is known to improve accuracy of numerical solutions [9]. In particular, the work presented in [9] is related to the classic CH equation and the PFC equation. For a detailed formulation using linear extrapolation and nonlinear extrapolation (not considered in this paper) applied to phase field models, we refer the readers to the work presented in [9]. We label the scheme given by (4.5) as the THM scheme with linear extrapolation as THMLX. Computational results given by THMLX allow for errors to be reduced and remain accurate while allowing larger time steps (h≈10−1.5). The error plots for this problem suggests h=0.01 to be a time step that will offer sufficient accuracy for the THM method, which coincides with the step size proposed in [19] for their SAV-BDF1 method. Figure 3 (right) shows the energy decreasing property for THM and THMLX schemes using h=0.01 and M3=5. We also demonstrate the performance of our methods by running longer simulations. Figure 4 displays the extended dynamics for test problem 2 by using the THM method with h=0.001 and M3=5. The energy decreasing property is preserved for the entire duration of the simulation (see Figure 5). We note that the extended dynamics simulation results are in agreement with the results presented in [19].
4.3. Test problem 3
Our third test problem is aimed at testing our numerical approach with regards to correctly capturing the meandering instability [35]. We set our initial condition to
with the rest of the parameters the same as in the previous test problem except for η=0.2 and L=4π. We note that this type of initial condition has been used by different authors [19,36] and a smoothing procedure has been implemented in order to avoid the Gibbs phenomena. Details of the smoothing procedure can be found in [19]. It is also worth mentioning that smoothing procedures are standard in the context of spectral methods [24,32]. We treated our initial condition with a smoothing function found in MATLAB. In particular, we used a Gaussian filter on the initial condition with a standard deviation of 2 which provided a smooth enough initial configuration for our schemes to run. The function used was imgaussfilt(u0,σ), where sigma is the standard deviation. The main goal of the smoothing process is that the spectral computations do not initially blow-up due to numerical instability [24]. We implement the THM method using 256×256 Fourier modes with h=0.001 and M3=5. The computed dynamics capturing the meandering instability are presented in Figure 6 matching results in [19]. Corresponding energy evolution with the decreasing property is shown in Figure 7.
4.4. Test problem 4
We set up our final test problem from this section by using a random initial state, which is connected to the modeling of a bilayer structure [19]. In this case, the solution to the FCH equaton represents an amphiphilic binary mixture undergoing phase separation [37]. We let our initial condition take the form of u(x,y,t=0)=0.5+0.001rand(x,y) and u(x,y,z,t=0)=0.5+0.001rand(x,y,z) for the 2D and 3D cases, respectively. Simulations are presented in Figures 8–11 using the THM method with ϵ=0.1, η=ϵ2, and Ω=[0,4π]d with d=2,3 for 2D and 3D, respectively. It can be seen that our schemes are able to correctly capture the dynamics for the FCH equation [19] in either 2D and 3D and they do so with an ease of implementation and efficiency provided by the THM approach. The energy decreasing property was retained for the entire duration of the simulations (see Figures 9 and 11).
5.
Numerical experiments and simulations: Part Ⅱ
Test problem 5 : pearling instability
Now that we have tested the performance of the THM method by solving the benchmark problems given by test problems 1–4, we introduce a more complicated version of the FCH equation which is given by the following energy [17,19,35]:
where ϵ is a parameter associated with thickness of the interface, and η1>0 and η2 are parameters related to the properties of the amphiphilic materials. The H−1 gradient flow for the above functional gives the following:
where ˜W(u) is a double well-potential of unequal well depths given by
which implies that ˜W′(u)=(u+1)(u+τ)(u−1) and ˜W″(u)=(u+1)(u−1)+2u(u+τ).
The THM approach applied to this version of the FCH equation (5.2) gives the following scheme,
where ˜Ψ(u)=M3ϵ4Δ3u, ˜Φ(u)=(M−M3)ϵ4Δ3u+MΔP(u) and similar to the previous formulation there is an associated term analogous to S(u) which is labeled as P(u) for this version of the FCH equation and it is given by
In addition to the THM approach, we also incorporate a higher order time stepping approach based on IMEX-RK schemes for the equation ut=˜Ψ(Un+1)+˜Φ(Un). The THM-IMEX2 schemes read as,
We note that several phase field models have been adapted with the IMEX approach in the past in order to increase accuracy. The classic CH equation was implemented with an IMEX scheme in the work presented in [10]. Ceniceros presented a numerical procedure for the variable CH equation using IMEX time stepping [23] technique. More recently a higher order IMEX scheme was used for the PFC equation in [38]. Our current THM-IMEX2 scheme differs from all the ones mentioned since to the best of our knowledge the THM approach has not been implemented before for the FCH equation.
We will test the numerical convergence of the method by following procedure (ⅰ), that is, we construct a reference solution using a small time step h=10−7 and evolve the solution to tf=1.0. An initial condition that illustrates the pearling instability is used in the form of an elliptical annulus which is given by
where g(x,y)=√(x−L/2)2+0.5(y−L/2)2. Similar to the case of meandering instability, we filter our initial condition with a Gaussian filter to obtain a smooth initial configuration. To observe the pearling instability, we evolve the filtered initial condition to a final configuration using tf=1 for which the instability is visible on the longer sides of the ellipse (see Figure 12). The rest of the parameters used in this simulation are given by L=4π,M=1,M3=5,ϵ=0.1,η1=1.45ϵ,η2=2ϵ, and τ=0.125.
The THM-BE (which refers to the THM approach coupled with a backward Euler (BE) approximation for the time derivative) and THM-IMEX2 computed errors are shown in Figure 13. The errors are able to reach 1st order accuracy and reach second order accuracy for small enough choices of the time step h. We note that the THM-IMEX2 with M3=5 scheme requires h<0.01 in order to produce stable results. For these range of values of the time step h, the THM-IMEX2 generates smaller errors than THM-BE, which well justifies the formulation. It is common for the splitting parameter in these type of formulations to influence the stability of the numerical results [9,12,19,33,36]. For this reason, we tried M3=10,15 and we noticed that the THM-IMEX2 scheme was able to generate stable results with larger time steps h, but this came at the expense of losing accuracy. Overall, we found that THM-IMEX2 increased the accuracy of our THM method which can be seen in Figure 13. This improvement in accuracy demonstrates that the THM approach can be adapted with a time stepping technique and generate accurate and stable results with the benefits of ease of implementation. Of course, here the method of choice will be based on the preference of the user in which a smaller time step h could be chosen to implement a slightly more efficient THM scheme to generate accurate results. The other option is to consider a few more computations to implement the THM-IMEX2 scheme with the benefits of added accuracy. We now test the performance of the new THM-IMEX2 method for longer simulation runs using the same initial condition. We note that both schemes are very efficient and are able to run in a modest laptop. Simulation plots are presented in Figure 14 where it can be seen that the pearling instability has fully dominated the ellipse by time t=10 but this is followed by a reconnecting of the pearls/dots to then evolve into a configuration that fully reconnects around t=15 and then follows a meandering instability for t≥20. The computed energy for this simulation is presented in Figure 15 where the energy decreasing property is displayed.
Finally, we demonstrate the performance of the new methods by solving the FCH in full 3D space variables by using parameters associated with the different solutions that the FCH equation is intended to model in mixtures of amphiphilic molecules in solvent [17,35,39]. We set our initial condition to u(x,y,z,t=0)=0.65+0.001rand(x,y,z) and run the simulations using THM-IMEX2 on Ω=[0,2π]3 with h=0.001,M=1,M3=5,ϵ=0.1,η1=5ϵ,τ=−0.4 and tf=4. We then vary η2=6ϵ,4ϵ,−ϵ,−3ϵ. Simulation results are shown in Figure 16 in which level sets of the solutions have been labeled for (u=0.4) and (u=0.45) with the colors yellow and purple, respectively. The solution structures are related to a highly branched pore network η2=6ϵ, a pore network η2=4ϵ, a pearled pore and micelle mixture η2=−ϵ, and isolated micelles η2=−3ϵ, which are given from left to right and top to bottom in Figure 16. The simulation results computed with our new proposed approach are in agreement with the results presented in [39].
6.
Conclusions
A THM numerical approach for solving the FCH equation was proposed and the convergence properties of the scheme were investigated using relevant benchmark problems in the phase field community. Our methods retain the energy decreasing property and reach first and second order convergence while producing small errors. In particular, the errors produced using the THM method are found to be smaller than those provided by the SAV formulation [19], by way of a direct comparison. The main advantage of our approach is that the computations are very efficient since all nonlinearities in the equation are computed at the explicit time level. The computation cost for the THM method is similar to the original BHM method, which was originally developed for variable mobility problems. The THM shares a comparable ease of implementation to the original CS method, which was originally developed for the constant mobility CH equation. One additional advantage of the THM method is found on its simplicity. A simple splitting allows for accurate implementation of the FCH equation under the THM approach. We note that the SAV formulation [19,33] requires additional stabilizer parameters for their methods to produce accurate results. In fact, two different SAV formulations had to be derived in order to handle the two versions of the FCH equation in [19] which gives an edge to the THM method in ease of implementation. The THM method requires only one simple splitting on the tri-harmonic term that relies on a single parameter M3 and does not suffer for the required additional steps and reformulation of the energy as the SAV method [12,19,33]. In addition to efficiency, our method is easy to implement and can run in a modest laptop for 2D and 3D implementations in the course of a few hours. In addition to numerical convergence, we tested our method for longer time runs with and without linear extrapolation in which dynamics for the FCH equation were properly displayed by capturing the microstructure evolution of material and the more challenging meandering type of instability. To demonstrate the robustness of the THM method, we applied the method to a more complicated form of the FCH equation and we also coupled our method with an IMEX time stepping technique to improve errors and to capture the pearling instability dynamics. Additionally, we tested the performance of the THM-IMEX2 scheme in full 3D to capture more complex dynamics associated with the more complicated version of the FCH equation. The THM approach provides a simple and efficient implementation for the FCH equation and it produces small errors. We believe that the proposed THM approach could serve as a powerful tool, that is easy to implement, to study not only the FCH equation but also a general class of sixth order phase field models and a class of 4th order problems [30,40], for which the original BHM approach remains applicable. The work presented in this numerical investigation can be viewed as preliminary results and formulations of improved/extended numerical schemes that will lead to further studies and rigorous numerical analysis. Future research work will include theoretical analysis of the energy stability and the convergence analysis of the scheme with constant and variable mobility. We will also study the applicability of the new approach to systems of CH equations in 2D and 3D related to the modeling of biomedical applications.
Author contributions
All authors contributed equally for the completion of the manuscript. All authors have read and approved the final version of the manuscript for publication.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
S. Orizaga is grateful for the support from New Mexico IDeA Networks of Biomedical Research Excellence (NM-INBRE) and from the 2024 NM-INBRE NIRF Faculty Fellowship award. S. Orizaga thanks Professors Snezna Rogelj and Sally Pias for summer funding opportunities. We thank the anonymous reviewers who provided valuable feedback resulting in an improved version of this paper.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









 DownLoad:
DownLoad: