Machine fault detection methods based on machine learning algorithms: A review

Giuseppe Ciaburro; Giuseppe Ciaburro

doi:10.3934/mbe.2022534

Mathematical Biosciences and Engineering

2022, Volume 19, Issue 11: 11453-11490. doi: 10.3934/mbe.2022534

Previous Article Next Article

Review

Machine fault detection methods based on machine learning algorithms: A review

Giuseppe Ciaburro ^,

Department of Architecture and Industrial Design, Università degli Studi della Campania LuigiVanvitelli, Borgo San Lorenzo - 81031 Aversa (Ce), Italy

Received: 29 April 2022 Revised: 20 June 2022 Accepted: 18 July 2022 Published: 10 August 2022

Preventive identification of mechanical parts failures has always played a crucial role in machine maintenance. Over time, as the processing cycles are repeated, the machinery in the production system is subject to wear with a consequent loss of technical efficiency compared to optimal conditions. These conditions can, in some cases, lead to the breakage of the elements with consequent stoppage of the production process pending the replacement of the element. This situation entails a large loss of turnover on the part of the company. For this reason, it is crucial to be able to predict failures in advance to try to replace the element before its wear can cause a reduction in machine performance. Several systems have recently been developed for the preventive faults detection that use a combination of low-cost sensors and algorithms based on machine learning. In this work the different methodologies for the identification of the most common mechanical failures are examined and the most widely applied algorithms based on machine learning are analyzed: Support Vector Machine (SVM) solutions, Artificial Neural Network (ANN) algorithms, Convolutional Neural Network (CNN) model, Recurrent Neural Network (RNN) applications, and Deep Generative Systems. These topics have been described in detail and the works most appreciated by the scientific community have been reviewed to highlight the strengths in identifying faults and to outline the directions for future challenges.

Keywords:

Citation: Giuseppe Ciaburro. Machine fault detection methods based on machine learning algorithms: A review[J]. Mathematical Biosciences and Engineering, 2022, 19(11): 11453-11490. doi: 10.3934/mbe.2022534

Related Papers:

[1]	Ngo Thai Hung . Equity market integration of China and Southeast Asian countries: further evidence from MGARCH-ADCC and wavelet coherence analysis. Quantitative Finance and Economics, 2019, 3(2): 201-220. doi: 10.3934/QFE.2019.2.201
[2]	Chikashi Tsuji . The historical transition of return transmission, volatility spillovers, and dynamic conditional correlations: A fresh perspective and new evidence from the US, UK, and Japanese stock markets. Quantitative Finance and Economics, 2024, 8(2): 410-436. doi: 10.3934/QFE.2024016
[3]	Emmanuel Assifuah-Nunoo, Peterson Owusu Junior, Anokye Mohammed Adam, Ahmed Bossman . Assessing the safe haven properties of oil in African stock markets amid the COVID-19 pandemic: a quantile regression analysis. Quantitative Finance and Economics, 2022, 6(2): 244-269. doi: 10.3934/QFE.2022011
[4]	Samuel Kwaku Agyei, Ahmed Bossman . Investor sentiment and the interdependence structure of GIIPS stock market returns: A multiscale approach. Quantitative Finance and Economics, 2023, 7(1): 87-116. doi: 10.3934/QFE.2023005
[5]	Yue Liu, Gaoke Liao . The Measurement and Asymmetry Tests of Business Cycle: Evidence from China. Quantitative Finance and Economics, 2017, 1(2): 205-218. doi: 10.3934/QFE.2017.2.205
[6]	Albert A. Agyemang-Badu, Fernando Gallardo Olmedo, José María Mella Márquez . Conditional macroeconomic and stock market volatility under regime switching: Empirical evidence from Africa. Quantitative Finance and Economics, 2024, 8(2): 255-285. doi: 10.3934/QFE.2024010
[7]	Fredrik Hobbelhagen, Ioannis Diamantis . A comparative study of symbolic aggregate approximation and topological data analysis. Quantitative Finance and Economics, 2024, 8(4): 705-732. doi: 10.3934/QFE.2024027
[8]	Fangzhou Huang, Jiao Song, Nick J. Taylor . The impact of business conditions and commodity market on US stock returns: An asset pricing modelling experiment. Quantitative Finance and Economics, 2022, 6(3): 433-458. doi: 10.3934/QFE.2022019
[9]	Nan Zhang, Li Zhu . Structural changes in China's flow of funds (1992–2022): A Who-to-Whom model. Quantitative Finance and Economics, 2025, 9(1): 167-201. doi: 10.3934/QFE.2025006
[10]	David G. McMillan . The information content of the stock and bond return correlation. Quantitative Finance and Economics, 2018, 2(3): 757-775. doi: 10.3934/QFE.2018.3.757

Abstract

1. Introduction

This paper investigates the macro-financial underlying of the time-varying co-movements among stock market returns in G7 and BRICS-T countries. For this purpose, firstly, we decompose the dynamic conditional correlations among the daily stock market returns of the countries in the sample into the short-term (daily) and the long-term (quarterly) components using the DCC-MIDAS (Dynamic Conditional Correlation-Mixed Data Sampling) method proposed by Colacito et al. (2011). Then, we estimate the relationship between the long-term dynamic conditional correlations derived from the DCC-MIDAS models and the macroeconomic variables that represent economic-financial proximity between country pairs via the dynamic panel data methodology.

Since the emergence of globalization in the 1980s, the removal of obstacles to international trade and the liberalization of capital movements have gradually led to highly integrated economic and financial systems across the world. News on market conditions spread more quickly and effectively due to significant developments in information and communication technologies, particularly in the last two decades. Thanks to cheaper costs of information market participants can respond to news in the global markets more rapidly, thereby facilitating the acceleration of international capital flows. This process has given rise to the internationalization of stock markets all over the world, and has brought about increased interdependence among stock markets. Particularly, after the adverse effects of the 2008 global financial crisis and the European sovereign debt crisis in global financial markets, the analysis of co-movements among international stock markets have become popular and intriguing issues for researchers, policy makers and investors. In the related literature, the issues on the co-movements among stock markets have been examined by several studies using different methods, country groups, time periods and data frequencies (Hamao et al., 1990; Arouri et al., 2010; Zhou et al., 2012; Dimitriou et al., 2013; Jung and Maderitsch, 2014; Liu et al., 2017 and Das et al., 2018). Although there is a considerable literature on how integration among stock markets occurs, a limited number of studies investigate the macro-financial factors behind integration among stock markets. Furthermore, understanding the major macro-financial dynamics behind the co-movements among stock markets is also crucial as well as knowing whether these relationships exist.

In general, the majority of studies that investigate the reasons of the co-movement among stock markets follow a two-stage procedure. These studies initially examine the interaction among stock markets, and then investigate the causes of this interaction. To explain the interaction among stock markets, these studies use various economic, financial and social variables including bilateral trade, foreign portfolio investments, inflation rate, interest rate, economic growth rate, exchange rate regime-volatility, stock market size, distances between financial centers and cultural effects (Bracker et al., 1999; Pretorius, 2002; Walti, 2005; Tavares, 2009; Asgharian et al., 2013; Mobarek et al., 2016 and Thomas et al., 2019). Stock markets are expected to be highly correlated with each other due to both the strong financial relations between countries and the similarities of economic policies in these countries. The stock market performances of countries that have similar macroeconomic indicators are supposed to converge towards each other, otherwise it is supposed to diverge from each other (Pretorius, 2002). In other words, the low absolute value of the difference between economic indicators from two countries is an indication of having high co-movements between the stock markets of those countries (Luchtenberg and Vu, 2015; Mobarek et al., 2016; Vithessonthi and Kumarasinghe, 2016 and Nitoi and Pochea, 2019). In addition, if there is a strong bilateral trade relationship between two countries, stock markets of those countries are expected to be highly interrelated (Walti, 2011). In the same vein, the empirical results put forward that there is a positive relationship between bilateral trade and stock market co-movements (Pretorius, 2002; Tavares, 2009 and Beine and Candelon, 2011). On the contrary, some studies suggest that there is not a significant relationship between bilateral trade and stock market co-movements (Didier et al., 2012; Vithessonthi and Kumarasinghe, 2016 and Thomas et al., 2019). Besides, it known that the co-movements between stock markets of countries with a similar language and culture in the nearby geography are higher than the co-movements between stock markets of countries with different languages and cultures in the distant geography (Walti, 2005 and Lucey and Zhang, 2010). On this backdrop, an attempt to investigate the macro-financial dynamics of the time-varying co-movements among stock markets is crucial to shed light on financial institutions, financial analysts, portfolio managers and global investors.

The seminal paper of Colacito et al. (2011) puts forward that the fundamental causes of time-varying conditional correlations can be captured by slowly moving processes of dynamic conditional correlations. Thus, economic and financial factors that represent the economic-financial proximity between countries are expected to be connected with slowly moving long-term components rather than rapidly moving short-term components of dynamic conditional correlations between stock market returns. Whereas, in the vast majority of studies in the related literature, dynamic conditional correlations between stock markets have not been decomposed into the short- and long-term components, but instead, the relationships between dynamic conditional correlations and macroeconomic indicators have been directly analyzed without any decomposition (Narayan et al., 2014; Thomas et al., 2019 and Wang and Guo, 2020). However, it is inconvenient to examine the relationships between dynamic conditional correlations and macroeconomic fundamentals without such decomposition. On the contrary to the other econometric time series models, the DCC-MIDAS approach decomposes the short- and long-term components of the dynamic conditional correlations between stock market returns of two countries. By this way, this approach can remove rapidly moving (temporary) effects in the dynamic conditional correlations. It enables us to focus on the relationship between the slowly moving long-term components of dynamic conditional correlations among stock markets and macroeconomic variables.

The central question of this paper is whether the economic-financial proximity between G7 and BRICS-T countries have an impact on the time-varying co-movements between stock markets of those countries. This broad sample enables us to examine the relationships both among advanced economies and among emerging economies as well as the relationships between advanced and emerging economies. By this way, as opposed to the common approach in the literature, this paper considers the relationships among all possible pairs of stock markets instead of keeping just the stock markets of the USA at the center. The empirical analysis of this paper consists of two stages. In the first stage, the DCC-MIDAS method is used to decompose the short (daily) and long-term (quarterly) dynamic conditional correlations among stock market returns. This method enables us to regress the long-term (quarterly) components of dynamic conditional correlations between stock markets of G7 and BRICS-T countries with the quarterly macroeconomic variables that represent the macro-financial proximity between each country pairs. In the second stage of the empirical analysis, the dynamic panel data methodology (the System GMM method) is employed unlike the majority of the literature in order to take the dynamic structure of the dataset into account. From a methodological perspective, one of our contributions is to estimate the DCC-MIDAS models based on the GARCH-MIDAS model with rolling window realized volatility. However, up until now the literature, including Colacito et al. (2011), has estimated the DCC-MIDAS models based on the GARCH-MIDAS model with fixed window realized volatility. To the best our knowledge, this study is the first attempt to investigate the macro-financial dynamics of the time-varying co-movements between the daily stock market returns of G7 and BRICS-T countries.

The remainder of this study structured as follows: Section 2 presents the DCC-MIDAS model; Section 3 reports the data and variables; Section 4 discusses the empirical results; and Section 5 concludes the study.

2. The DCC-MIDAS model

We use the DCC (Dynamic Conditional Correlation)-MIDAS (Mixed Data Sampling) model proposed by Colacito et al. (2011) to decompose the short- and the long-term components of the dynamic conditional correlations between stock market returns of two countries. This model is a multivariate extension of the GARCH-MIDAS model (Engle et al., 2006) which is based on dynamic conditional correlations. In the GARCH-MIDAS model, two components of volatility are distilled, one relating to short-term fluctuations, and the other relating to a secular component. The univariate GARCH-MIDAS process can be written as follows:

${r}_{i, t} = \mu +\sqrt{{\tau }_{t}\times {g}_{i, t}}{\xi }_{i, t}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \forall i = 1, \dots, {N}_{t}$

(1)

where ${\xi }_{i, t}|{\mathrm{\Omega }}_{i-1, t}\sim N\left(\mathrm{0, 1}\right)$ , and ${\mathrm{\Omega }}_{i-1, t}$ is the information set up to day $(i-1)$ of period $t$ . ${r}_{i, t}$ is the return of an asset on day $i$ in period $t$ (month, quarter, biannual etc.), ${g}_{i, t}$ is the short-term variance component which explains daily fluctuations, and ${\tau }_{t}$ is the slowly moving long-term component. The short-term component ${g}_{i, t}$ is presumed to follow a GARCH (1, 1) model:

${g}_{i, t} = \left(1-\alpha -\beta \right)+\alpha \frac{{\left({r}_{i-1, t}-\mu \right)}^{2}}{{\tau }_{t}}+\beta {g}_{i-1, t}$

(2)

with restrictions $\alpha >0$ , $\beta \ge 0$ , and $\alpha +\beta < 1$ . The long-term component ${\tau }_{t}$ is modeled using the MIDAS regression:

${\tau }_{t} = m +\theta \sum _{k = 1}^{K}{\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right){RV}_{t-k}$

(3)

${RV}_{t} = \sum _{i = 1}^{{N}_{t}}{r}_{i, t}^{2}$

(4)

where ${RV}_{t}$ is the realized volatility, and ${\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right)$ indicates the MIDAS weighting scheme. There are two specifications for the long-term component ${\tau }_{t}$ . The first one is the component $\tau$ which is fixed on days $i$ in a period $t$ and the second one is the component $\tau$ which is varied on days $i$ in a period $t$ . Equation (3) represents the GARCH-MIDAS model with fixed time span RV (realized volatility) and Equation (5) indicates the GARCH-MIDAS model with rolling window RV (realized volatility).

${\tau }_{i}^{\left(rw\right)} = {m}^{\left(rw\right)}+{\theta }^{\left(rw\right)}\sum _{k = 1}^{K}{\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right){RV}_{i-k}^{\left(rw\right)}$

(5)

${RV}_{i}^{\left(rw\right)} = \sum _{j = 1}^{{N}^{'}}{r}_{i-j}^{2}$

(6)

The MIDAS weighting scheme ${\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right)$ used in Equation (3) and Equation (5) defined by a beta lag polynomial in Equation (7) and an exponentially weighted in Equation (8).

${\vartheta }_{k}\left(\omega \right) = \frac{{(k/K)}^{{\omega }_{1-}1}{(1-k/K)}^{{\omega }_{2}-1}}{{\sum }_{j = 1}^{K}{(j/K)}^{{\omega }_{1}-1}{(1-j/K)}^{{\omega }_{2}-1}}$

(7)

${\vartheta }_{k}\left(\omega \right) = {\omega }^{k}/\left({\sum }_{j = 1}^{K}{\omega }^{j}\right)$

(8)

In the DCC-MIDAS model, the dynamic conditional correlations are decomposed into short-term and slowly moving secular component with the same logic to the GARCH-MIDAS model. We follow a two-stage procedure to estimate the parameters of the DCC-MIDAS model. In the first stage, the parameters of the univariate GARCH-MIDAS model are estimated, and then the DCC-MIDAS model is estimated by using the Quasi-Maximum Likelihood method. The multivariate DCC-MIDAS process can be written as follows:

${q}_{xy, t} = {\stackrel{-}{\rho }}_{xy, t}\left(1-a-b\right)+a{\xi }_{x, t-1}{\xi }_{y, t-1}+b{q}_{xy, t-1}$

(9)

where ${\xi }_{x, t-1}$ and ${\xi }_{y, t-1}$ are the standardized residuals from the univariate GARCH-MIDAS model. The ${q}_{xy, t}$ term is the short-term correlation component, while ${\stackrel{-}{\rho }}_{xy, t}$ is the slowly moving long-term component of the dynamic conditional correlations between assets $x$ and $y$ . The parameters $a$ and $b$ must satisfy the stability conditions which are $a, b>0$ and $a+b<1$ . The long-term correlation component is defined as:

${\stackrel{-}{\rho }}_{xy, t} = \sum _{k = 1}^{K}{\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right){c}_{xy, t-1}$

(10)

${c}_{xy, t} = \frac{\sum _{t}^{k = t-N}{\xi }_{x, k}{\xi }_{y, k}}{\sqrt{\sum _{t}^{k = t-N}{\xi }_{x, k}^{2}}\sqrt{\sum _{t}^{k = t-N}{\xi }_{y, k}^{2}}}$

(11)

where ${c}_{xy, t}$ is the realized correlation, and ${\vartheta }_{k}\left({\omega }_{1}, {\omega }_{2}\right)$ denotes the MIDAS weighting scheme. The correlations can be calculated as:

${\rho }_{xy, t} = \frac{{q}_{xy, t}}{\sqrt{{q}_{xx, t}}\sqrt{{q}_{yy, t}}}$

(12)

where ${\rho }_{xy, t}$ indicates the dynamic conditional correlations between assets $x$ and $y$ .

3. Data

The data set consists of two parts. In the first part, we make use of daily stock market indices of G7 (USA, Germany, United Kingdom, France, Italia, Japan, Canada) and BRICS-T countries (Brazil, Russia, India, China, South Africa, Turkey) for the period from January 2nd, 2002 to September 19th, 2018^1. The return series are calculated using:

¹The sample period starts from January 2nd, 2002 in order to keep away from the unstable periods of emerging economies during the 1990s and early 2000s.

${r}_{i, t} = 100\times \left[ln{(P}_{i, t})-ln{(P}_{i, t-1})\right]$

(13)

Table 1 shows the descriptive statistics of logarithmic returns of daily stock market indices. All of the log-returns have negative skewness. Besides, all of them have leptokurtic distribution as regards to their kurtosis.

Table 1. Descriptive statistics of the daily stock returns.

	Mean	Min	Max	Std. Dev.	Skewness	Kurtosis	Observations
S & P 500	0.0213	−9.4695	10.957	1.1602	−0.2611	13.617	4361
DAX 30	0.0197	−7.4335	10.797	1.4389	−0.0058	8.2199	4361
FTSE	0.0059	−11.750	12.198	1.3560	−0.2598	13.341	4361
CAC 40	0.0035	−9.4715	10.594	1.4085	−0.0048	8.9249	4361
FTSE MIB	−0.0095	−13.331	10.876	1.5021	−0.2054	8.5680	4361
NIKKEI 225	0.0185	−12.111	13.234	1.4430	−0.4737	10.822	4361
S & P/TSE	0.0170	−9.7880	9.3703	1.0185	−0.6833	15.260	4361
BOVESPA	0.0401	−12.096	13.679	1.6898	−0.0996	7.8687	4361
RTS	0.0337	−21.199	20.203	2.0383	−0.4528	14.298	4361
NIFTY 500	0.0599	−12.884	15.034	1.3436	−0.5355	14.207	4361
SHANGHAI	0.0116	−9.2561	9.0345	1.5451	−0.4318	8.1483	4361
FTSE/JSE	0.0386	−7.5807	6.8340	1.1519	−0.1492	6.7317	4361
BIST 100	0.0446	−13.340	12.127	1.7729	−0.1495	7.8664	4361

| Show Table

DownLoad: CSV

In the second part, we employ quarterly macroeconomic and financial variables to represent the economic-financial proximity between each country pair, for the period of January, 2006 to August, 2018. The reason why the data set starts with the year of 2006 rather than the year of 2002 in the second stage is the initial observations used for the prediction of the MIDAS weighting scheme in the DCC-MIDAS analysis. To be more precise, we use up to forty-five MIDAS lags for the DCC process for each model. Besides, the country-specific dataset has twenty-two daily observations (N = 22) for each month. Thus, the DCC MIDAS method makes use of up to 990 initial observations (22 × 45 = 990), which corresponds to the first four years of daily stock returns, for prediction of the MIDAS weighting scheme. All the data are compiled from the Thomson Reuters Datastream database. Table 2 provides the definitions of the variables used in the empirical analysis.

Table 2. Definitions of the variables.

Variable names	Definition
Panel A: Dependent variable
Dccmidascorr	Dccmidascorr shows the long-term (quarterly) dynamic conditional correlations between stock markets of countries x and y. These correlations are calculated using the DCC-MIDAS model. We then employ the Fisher-Z transformation to adjust the potential problem of non-normality in the dynamic conditional correlation. ${\stackrel{'}{\rho }}_{xy, t}=(1/2)\mathrm{I}\mathrm{n}\left[\right(1+{\rho }_{xy, t})/(1-{\rho }_{xy, t}\left)\right]$ For similar analysis, see (Beine and Candelon, 2011; Colacito et al., 2011)
Panel B: Explanatory variables (economic)
Bilateral trade	Bilateral trade indicates the quarterly average bilateral trade between countries x and y. Calculated as: $\left[\right({X}_{xy, t}/{X}_{x, t})+{(M}_{xy, t}/{M}_{x, t})+({X}_{yx, t}/{X}_{y, t})+({M}_{yx, t}/{M}_{y, t})]/4$ where ${X}_{xy, t}$ and ${M}_{xy, t}$ are exports and imports from country $x$ to country $y$ during quarter $t$ . ${X}_{yx, t}$ and ${M}_{yx, t}$ are exports and imports from country $y$ to country $x$ during quarter $t$ . ${X}_{x, t}, {M}_{x, t}$ and ${X}_{y, t}, {M}_{y, t}$ indicate the total exports and total imports of country $x$ and country $y$ during quarter $t,$ respectively. For similar analysis, see (Bracker et al., 1999; Mobarek et al., 2016)
GDP growth rate	GDP growth rate indicates the logarithmic transformation of the absolute differences between the GDP growth rate of country $x$ and country $y$ , during quarter $t$ . $ln\left\|{∆GDP}_{x, t}-{∆GDP}_{y, t}\right\|.$ For similar analysis, see (Johnson and Soenen, 2002; Beine and Candelon, 2011)
Inflation rate	Inflation rate shows the logarithmic transformation of the absolute differences between the inflation rate of country $x$ and country $y$ , during quarter $t$ . $ln\left\|{\pi }_{x, t}-{\pi }_{y, t}\right\|$ For similar analysis, see (Bracker et al., 1999; Pretorius, 2002)
EPU	EPU² shows the logarithmic transformation of the absolute differences between the economic policy uncertainty index of country $x$ and country $y$ , during quarter $t$ . $ln\left\|{EPU}_{x, t}-{EPU}_{y, t}\right\|$ For similar analysis, see (Peng et al., 2018)
Panel C: Explanatory variables (financial)
Term spread	Term spread represents the logarithmic transformation of the absolute differences between term spread rate of country $x$ and country $y$ , during quarter $t$ . Term spread rate is defined by the differences between the long-term 10-year government bond yield and the 3-month interbank rate. $ln\left\|{ts}_{x, t}-{ts}_{y, t}\right\|.$ For similar analysis, see (Mobarek et al., 2016)
CDS risk premium	CDS risk premium represents the logarithmic transformation of the absolute differences between the five-year CDS risk premium of country $x$ and country $y$ , during quarter $t$ . $ln\left\|{CDS}_{x, t}-{CDS}_{y, t}\right\|$ For similar analysis, see (Min and Hwang, 2012)
Volatility ratio	Volatility ratio shows the ratio of the stock market volatilities of country $x$ and country $y$ , during quarter $t$ . $\left[ \right({Vol}_{x, t})/ ({Vol}_{y, t}\left)\right]$ For similar analysis, see (Pretorius, 2002)
Panel D: Control variables (USA factors)
S & P 500 volatility	S & P 500 volatility indicates the volatility of the S & P 500 index during quarter $t$ . $\left({Vol}_{S\&P 500, t}\right)$ Related references: (Kim et al., 2015)
Global financial crisis	This is the dummy variable which takes value 1 for the period from 2007 q3 to 2009 q3, else the value is 0. Related references: (Romer, 2012)

| Show Table

DownLoad: CSV

²The EPU variables are not calculated for the country pairs that includes either Turkey or South Africa due to the lack of data.

Broadly, there are three main explanations on why time-varying co-movements among stock markets exist. The first one is the contagion effect that cannot be explained by economic fundamentals, the second one is economic integration which means that if two economies are more integrated then their stock markets will be more interdependent. Finally, the third one is stock market characteristics that affect the extent of interdependence among stock markets. Economic integration contains not only the co-movement in economic factors that affect stock market returns, such as inflation rate, economic growth rate, and interest rate, but also bilateral trade relations. The stronger bilateral trade links between two countries, the higher co-movements between their stock markets. Moreover, according to the cash flow model, various macroeconomic factors, namely inflation rate, economic growth rate, and interest rate, affect the stock market performance (Pretorius, 2002). Since these macroeconomic variables affect stock market returns, the proximity between macroeconomic variables of different countries will impact the co-movement between their stock markets. In other words, as the macroeconomic indicators of two countries approach each other, the co-movement between the stock markets of these countries is expected to increase. In this regard, it is plausible to expect that there is a negative relationship between the time-varying co-movements among stock market returns and the differences in GDP growth rate, inflation rate, term spread, and economic policy uncertainty index. So far, the differences in the economic policy uncertainty indices between country pairs have not been used as regressors in the related literature. The inclusion of those absolute differences is also one of our contributions into the related literature. Besides, as a global factor, the S & P 500 volatility is used in order to take into account possible effects of the US stock market.

In addition, Naifar (2012) puts forward that there is a positive relationship between the stock market volatility and the CDS risk premium. This empirical result implies that an increase in CDS risk premium leads to a rise in stock market volatility. In this regard, the rise in stock market volatility of two countries is expected to increase the co-movement among those stock markets (Min and Hwang, 2012). On this backdrop, we benefit from the differences in five-year CDS risk premium between country pairs in order to apprehend the time-varying co-movements among stock markets. Based on the related literature, our expectation is to have a positive relationship between the five-year risk premium and the stock market co-movements.

Table 3 presents the descriptive statistics of dependent and explanatory variables for the different country pairs. The sample contains 78 country pairs in which 21 of them are the G7 country pairs, 15 of them are the BRICS-T country pairs, and 42 of them are the G7 and BRICS-T country pairs. The long-term dynamic conditional correlations (mean) and the bilateral trade (mean) are higher in the G7 country pairs than in the G7 & BRICS-T and the BRICS-T country pairs. Besides, the highest GDP growth rate and the term spread differences (mean) belong to the BRICS-T country pairs and the highest CDS risk premium difference (mean) pertains to the G7 & BRICS-T country pairs. On the other hand, the lowest inflation rate and the EPU (Economic Policy Uncertainty) index differences belong to the G7 country pairs.

Table 3. Descriptive statistics of the dependent and explanatory variables.

	Mean	Min	Max	Std. Dev.	Skewness	Kurtosis	Observations	Country Pairs
All country pairs
Dccmidascorr	0.402	−0.017	0.968	0.201	0.500	2.752	3978	78
Bilateral trade	0.040	0.0009	0.450	0.052	4.631	31.36	3978	78
GDP growth rate	4.452	0.010	32.37	5.473	2.137	7.895	3978	78
Inflation rate	3.737	0.010	16.47	3.208	1.085	3.851	3978	78
Term spread	1.565	0.013	12.61	1.428	2.359	12.15	3978	78
CDS risk premium	97.41	0.354	663.13	91.12	1.804	8.425	2769	78
EPU	79.79	1.020	609.16	77.47	2.404	10.34	2805	55
Volatility ratio	1.002	0.145	5.144	0.604	1.541	5.982	3978	78
S & P 500 volatility	0.040	0.010	0.191	0.040	2.646	9.659	3978	78
G7 country pairs
Dccmidascorr	0.553	0.163	0.968	0.210	0.133	1.990	1071	21
Bilateral trade	0.063	0.006	0.450	0.084	3.128	13.05	1071	21
GDP growth	0.753	0.010	4.220	0.627	1.529	6.217	1071	21
Inflation rate	1.094	0.010	5.064	0.852	1.208	4.561	1071	21
Term spread	0.936	0.013	4.719	0.807	1.821	7.173	1071	21
CDS risk premium	42.03	0.715	366.31	61.84	2.815	11.88	783	21
EPU	76.77	1.020	561.95	80.99	2.503	10.64	1071	21
Volatility ratio	1.166	0.271	5.144	0.617	1.464	5.436	1071	21
S & P 500 volatility	0.040	0.010	0.191	0.040	2.646	9.659	1071	21
G7 & BRICS-Tcountry pairs
Dccmidascorr	0.363	−0.017	0.770	0.171	0.194	2.292	2142	42
Bilateral trade	0.032	0.001	0.159	0.029	2.257	8.665	2142	42
GDP growth	5.529	0.010	30.32	5.744	1.943	6.830	2142	42
Inflation rate	5.054	0.051	16.47	3.261	0.688	3.329	2142	42
Term spread	1.635	0.048	11.33	1.397	2.392	12.85	2142	42
CDS risk premium	130.03	0.354	663.13	94.09	1.767	8.647	1493	42
EPU	80.49	2.930	609.16	74.38	2.394	10.60	1428	28
Volatility ratio	0.788	0.145	3.374	0.416	1.228	4.844	2142	42
S & P 500 volatility	0.040	0.010	0.191	0.040	2.646	9.659	2142	42
Notes: Dccmidascorr is the dependent variable. Bilateral trade shows the ratio of total mutual trade between countries to their total foreign trade volume. GDP growth rate indicates the absolute difference between the GDP growth rates, inflation rate indicates the absolute difference between the inflation rates, term spread indicates the absolute difference between the term spreads, CDS risk premium indicates the absolute difference between the five-year CDS risk premiums, and finally, EPU shows the absolute difference between economy policy uncertainty indices of country $x$ and country $y$ . For detailed definitions, see Table 2.

| Show Table

DownLoad: CSV

4. Empirical results

The central question of this study is whether the economic-financial proximity between G7 and BRICS-T countries have an impact on the time-varying co-movements between stock markets of those countries. The empirical analysis of this study is composed of two stages. In the first stage, we estimate the DCC-MIDAS model based on the GARCH-MIDAS model with rolling window realized volatility to investigate the time-varying co-movements between the stock markets of G7 and BRICS-T countries. To check the robustness of these results, we re-estimate the DCC-MIDAS model based on the GARCH-MIDAS model with fixed window realized volatility. In the second stage, we estimate both the POLS (Pooled Ordinary Least Squares) models and the System GMM (Generalized Method of Moments) models for all country pairs (full sample) including the G7 country pairs, the BRICS-T country pairs, and the G7 & BRICS-T country pairs to quantify the macro-financial underlying of the time-varying co-movements among stock markets of those countries. To check the robustness of these results, we re-estimate both the POLS models and the System GMM models for two distinct subsample country pairs which are the G7 country pairs and the G7 & BRICS-T country pairs.

4.1. The time-varying co-movements between G7 & BRICS-T stock markets

First of all, we decompose the dynamic conditional correlations between log-returns of daily stock market indices of G7 and BRICS-T countries into the short-term (daily) and the long-term (quarterly) components with the help of the DCC-MIDAS model for the period January 2nd, 2002 to September 19th, 2018. The DCC-MIDAS models are separately estimated for 78 country pairs in which 21 of them are country pairs between G7 countries, 15 of them are country pairs between BRICS-T countries and 42 of them are country pairs between G7 and BRICS-T countries. Furthermore, to check the robustness of results, we estimate the DCC-MIDAS model based on both the GARCH-MIDAS model with rolling window realized volatility and the GARCH-MIDAS model with fixed window realized volatility. The estimation results of those models are almost identical. Thus, we only present the estimation results of the DCC-MIDAS models based on the GARCH-MIDAS model with rolling window realized volatility³.

³All estimation results related to the DCC-MIDAS models are included in the Appendix B.

Table 4 shows the descriptive statistics of the DCC-MIDAS correlations for the G7, European, G7 & BRICS-T and BRICS-T country pairs. The DCC-MIDAS correlations (mean) between the stock markets of G7 countries are higher than the DCC-MIDAS correlations (mean) between the stock markets of G7 & BRICS-T countries and between the stock markets of BRICS-T countries. Furthermore, the highest DCC-MIDAS correlations (mean) among the G7 country pairs belong to the European country pairs.

Table 4. Descriptive statistics of the DCC-MIDAS correlations.

	G7 pairs	European pairs	G7 & BRICS-T pairs	BRICS-T pairs
Mean	0.5535	0.7967	0.3630	0.3021
Min	0.1633	0.4102	−0.0179	−0.0058
Max	0.9682	0.9682	0.7702	0.7454
Std. dev.	0.2105	0.1202	0.1716	0.1442
Skewness	0.1339	−1.0128	0.1946	0.4075
Kurtosis	1.9905	3.4721	2.2926	2.7751
Country pairs	21	7	42	15
Observations	1071	306	2142	765

| Show Table

DownLoad: CSV

As an illustration, we select three country pairs from the G7 sample. Figure 1 presents the fluctuations of the short- and long-term components of the dynamic conditional correlations over the time for each country pair; USA-Germany, Italia-Canada and UK-France. In Figure 1, the red lines show rapidly moving short-term components of the DCCs between stock markets returns, and the black lines indicate slowly moving long-term components of the DCCs between stock markets returns. As shown in Figure 1, we find that the evolution of the short- and long-term components of the DCCs between stock markets returns are similar, while the long-term DCCs are flatter than the short-term DCCs. Figure 1 also shows that the average long-term DCCs between the log-returns of S & P 500 and DAX 30 are 0.58 for the USA-Germany country pair and the average long-term DCCs between the log-returns of FTSE MIB and S & P/TSE are 0.47 for the Italia-Canada county pair. Lastly, Figure 1 exhibits that the average long-term DCCs between the log-returns of FTSE and CAC 40 are 0.72 for the UK-France country pair.

Figure 1. The short- and long-term DCC-MIDAS correlations for selected G7 country pairs. The red lines indicate the short-term correlations and the black lines indicate the long-term correlations.

DownLoad: Full-Size Img PowerPoint

provides the estimation results of the DCC-MIDAS model for the selected G7 country pairs. The results of the S & P 500-DAX 30 pair, the FTSE MIB-S & P/TSE pair, and the FTSE-CAC 40 are given in the first, the second, and the third column, respectively. As shown in , all parameters are statistically significant at 1% level, except for the weighting parameter. In addition, the stationarity conditions, $a>0$ , $b>0$ , and $a+b < 1$ , are satisfied, and the weighting parameter $\omega$ is larger than one. This means that the weighting function is rapidly decreasing. The lag numbers of the MIDAS weights in the models are determined according to the values that minimize AIC and BIC.

Table 5. Parameter estimates of the DCC-MIDAS models for selected G7 country pairs.

Dcc-Midas parameters	S & P 500 vs. DAX 30	FTSE MIB vs. S & P/TSE	FTSE vs. CAC 40
$a$	0.019***(0.002)	0.016***(0.005)	0.066***(0.005)
$b$	0.963***(0.006)	0.972***(0.007)	0.901***(0.011)
$\omega$	2.163***(0.825)	1.035**(0.510)	1.428***(0.432)
$LL$	−8476.01	−8815.05	−8990.73
$AIC$	16958.1	17626.1	17987.5
$BIC$	16977.1	17635.1	18006.5
Notes: The numbers in the parentheses are standard errors. *, indicate statistical significance at the 1%, 5% level, respectively. LL is the logarithmic likelihood, AIC is the Akaike information criterion and BIC is the Bayesian information criterion.

| Show Table

DownLoad: CSV

To illustrate, we also select three country pairs from the G7 & BRICS-T sample. Figure 2 presents the fluctuations of the short- and long-term components of the dynamic conditional correlations over the time for each country pair; Germany-South Africa, Japan-Russia and Canada-Brazil. Figure 2 indicates that the short- and long-term components of the DCCs between stock markets returns follow a similar trend while the long-term DCCs are smoother. Moreover, the average long-term DCCs between the log-returns of DAX 30 and FTSE/JSE, between log-returns of the NIKKEI 225 and RTS, and between the log-returns of the S & P/TSE and BOVESPA are 0.56, 0.22, and 0.54 for the country pairs of Germany-South Africa, Japan-Russia, and Canada-Brazil, respectively.

Figure 2. The short- and long-term DCC-MIDAS correlations for selected G7 & BRICS-T country pairs. The red lines indicate the short-term correlations and the black lines indicate the long-term correlations.

DownLoad: Full-Size Img PowerPoint

presents the estimation results of the DCC-MIDAS models for selected G7 & BRICS-T country pairs. The results of the DAX 30-FTSE/JSE pair, the NIKKEI 225-RTS pair, and the S & P/TSE-BOVESPA pair are provided in the first, the second, and the third column, respectively. In , all parameters are statistically significant at 1% level, except for the weighting parameter. Besides, the stationarity conditions are satisfied and the weighting parameter $\omega$ is larger than one.

Table 6. Parameter estimates of the DCC-MIDAS models for selected G7 & BRICS-T country pairs.

Dcc-Midas parameters	DAX 30 vs. FTSE/JSE	NIKKEI 225 vs. RTS	S & P/TSE vs. BOVESPA
$a$	0.030***(0.005)	0.013***(0.004)	0.037***(0.007)
$b$	0.951***(0.011)	0.969***(0.014)	0.910***(0.021)
$\omega$	1.497*(0.875)	1.051***(0.095)	1.042***(0.039)
$LL$	−8813.93	−9495.93	−9503.77
$AIC$	17633.9	18997.9	19013.5
$BIC$	17652.9	19016.7	19032.4
Notes: The numbers in the parentheses are standard errors. **, indicate statistical significance at the 1%, 10% level, respectively. LL is the logarithmic likelihood, AIC is the Akaike information criterion and BIC is the Bayesian information criterion.

| Show Table

DownLoad: CSV

To illustrate, we also choose three country pairs from the BRICS-T sample. Figure 3 shows the fluctuations of the short- and long-term components of the dynamic conditional correlations over the time for each country pair; Russia-China, South Africa-Turkey and India-China. Figure 3 shows that the short- and long-term components of the DCCs between stock markets returns follow a similar pattern while the long-term DCCs are flatter than the short-term DCCs.

Figure 3. The short- and long-term DCC-MIDAS correlations for selected BRICS-T country pairs. The red lines indicate the short-term correlations and the black lines indicate the long-term correlations.

DownLoad: Full-Size Img PowerPoint

Furthermore, Figure 3 shows that the average long-term DCCs between the log-returns of RTS and SHANGHAI, and between FTSE/JSE and BIST 100, and between NIFTY 500 and SHANGHAI are 0.19, 0.39, and 0.21 for the country pairs of Russia-China, South Africa-Turkey, and India-China, respectively.

presents the estimation results of the DCC-MIDAS model for selected BRICS-T country pairs. The results of the RTS-SHANGHAI pair, the FTSE/JSE-BIST 100 pair, and the NIFTY 500-SHANGHAI pair are given the first, the second, and the third column, respectively. As shown in , all parameters are statistically significant. Besides, the stationarity conditions are satisfied, and the weighting parameter $\omega$ is larger than one.

Table 7. Parameter estimates of the DCC-MIDAS models for selected BRICS-T country pairs.

Dcc-Midas parameters	RTS vs. SHANGHAI	FTSE/JSE vs. BIST 100	NIFTY 500 vs. SHANGHAI
$a$	0.024***(0.007)	0.026***(0.005)	0.020**(0.008)
$b$	0.894***(0.047)	0.958***(0.011)	0.900***(0.062)
$\omega$	1.969***(0.838)	1.062* (0.606)	1.292** (0.551)
$LL$	−9398.61	−9380.68	−8993.86
$AIC$	18803.2	18767.4	17993.7
$BIC$	18822.1	18786.3	18012.5
Notes: The numbers in the parentheses are standard errors. *, and * indicate statistical significance at the 1%, 5% and 10% level, respectively. LL is the logarithmic likelihood, AIC is the Akaike information criterion and BIC is the Bayesian information criterion.

| Show Table

DownLoad: CSV

4.2. Determinants of the time-varying co-movements between G7and BRICS-T stock markets

To investigate macroeconomic determinants of the time-varying co-movements between the stock markets of G7 and BRICS-T countries, we make use of both the POLS (Pooled Ordinary Least Squares) method and the System GMM (Generalized Method of Moments) method for the period of January, 2006 to August, 2018. Equation (14) shows the benchmark model. Equations (14–16) are estimated by the pooled OLS method. The dependent variables of these models are quarterly long-term dynamic conditional correlations obtained from the DCC-MIDAS models in previous part. Additionally, we benefit from various quarterly economic and financial variables that represent the economic-financial proximity between countries as explanatory variables explained in Table 2.

${\rho }_{xy, t} = a+{\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+{\beta }_{3}{Inflation \ rate}_{xy, t}+\\ {\beta }_{4}{Term \ spread}_{xy, t}+ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+{ \varepsilon }_{xy, t}$

(14)

${\rho }_{xy, t} = a+{\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+{\beta }_{3}{Inflation \ rate}_{xy, t}+\\ {\beta }_{4}{Term \ spread}_{xy, t}+\delta {CDS \ risk \ premium}_{xy, t}+\gamma {EPU}_{xy, t}+ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+\\ { \varepsilon }_{xy, t}$

(15)

${\rho }_{xy, t} = a+{\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+{\beta }_{3}{Inflation \ rate}_{xy, t}+\\ {\beta }_{4}{Term \ spread}_{xy, t}+\delta \ {CDS \ risk \ premium}_{xy, t}+\gamma \ {EPU}_{xy, t}+\theta \ {Volatility \ ratio}_{xy, t}+\\ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+{ \varepsilon }_{xy, t}$

(16)

In all equations, ${Bilateral \ trade}_{xy, t}$ represents the ratio of total mutual trade between countries $x$ and $y$ , at time $t$ to their total foreign trade volume, ${GDP \ growth \ rate}_{xy, t}$ shows the absolute values of the quarterly GDP growth rate differences between countries $x$ and $y$ , at time $t$ , ${Inflation \ rate}_{xy, t}$ indicates the absolute values of the quarterly inflation rates differences between countries $x$ and $y$ , at time $t$ , ${Term \ spread}_{xy, t}$ indicates the absolute values of the quarterly term spread rate differences between countries $x$ and $y$ , at time $t$ , ${CDS \ risk \ premium}_{xy, t}$ shows the absolute values of the quarterly five-years CDS risk premium differences between countries $x$ and $y$ , at time $t$ , ${EPU}_{xy, t}$ represents the absolute values of the quarterly Economic Policy Uncertainty Index differences between countries $x$ and $y$ , at time $t$ , ${Volatility \ ratio}_{xy, t}$ represents the ratio of the stock market volatilities of countries $x$ and $y$ , at time $t$ , ${S\&P \ 500 \ volatility}_{t}$ indicates the volatility of the S & P 500 index at time $t$ , ${GFC}_{t}$ displays Global Financial Crisis dummy variable for the period from 2007 q3 to 2009 q3, and ${ \varepsilon }_{xy, t}$ shows the error term.

The estimation results of the POLS models are summarized in Table 8, where Model 1, Model 2, and Model 3 correspond to Equations (14), (15), and (16), respectively. As shown in Table 8, the coefficient estimates for bilateral trade are positive and statistically significant in all models. These results are consistent with the studies by Pretorius (2002), Tavares (2009) and Beine and Candelon (2011) which document a positive relationship between bilateral trade and stock market co-movements. These findings indicate that the stronger the bilateral trade links between two countries, the higher the dynamic conditional correlations among their stock markets. Furthermore, we find that the estimated coefficients of GDP growth rate, inflation rate, and term spread' differences are negative and statistically significant in all models. These results are consistent with the findings of Mobarek et al. (2016), Vithessonthi and Kumarasinghe (2016), and Nitoi and Pochea (2019). These results show that the lower the differences in GDP growth rates, inflation rates and term spreads between two countries, the higher the time-varying co-movements between their stock market. We also use the differences in five-year CDS risk premium between country pairs for the determinants of time-varying co-movements between stock market returns. Compatible with expectations, the coefficient estimates for five-year CDS risk premium differences are positive and statistically significant for the Model 2 and the Model 3. Moreover, we investigate the influence of the S & P 500 volatility on the long-term DCCs between G7 and BRICS-T countries' stock markets. The coefficient estimate for the volatility of the S & P 500 is positive and statistically significant for the Model 1. This finding shows that an increase in the volatility of the S & P 500 leads to an increase the long-term DCCs between stock market returns. However, the estimated coefficient for the volatility of the S & P 500 is statistically insignificant in the Model 3 which includes the five-year CDS risk premium. Besides, the volatility ratio is negative and statistically significant which is in line with findings of Thomas et al. (2019). Lastly, we find that the EPU (Economic Policy Uncertainty) index differences between country pairs do not have a statistically significant impact on the time-varying co-movements between stock market returns. For the robustness controls, we also estimate the POLS models for the G7 country pairs and the G7 & BRICS-T country pairs. The estimation results of the POLS models for the G7 country pairs and the G7 & BRICS-T country pairs are given in the Table A1 and the Table A2 in the Appendix A, respectively. The estimation results of those models have resemblance to each other qualitatively, however those models differ numerically.

Table 8. Estimation results of the POLS models for all country pairs.

Dccmidascorr	Model 1	Model 2	Model 3
Bilateral trade	0.4150***(0.046)	0.5624***(0.064)	0.5509*** (0.064)
GDP growth rate	−0.0360***(0.001)	−0.0458***(0.002)	−0.0468***(0.002)
Inflation rate	−0.0095***(0.002)	−0.0174***(0.003)	−0.0174***(0.003)
Term spread	−0.0138***(0.002)	−0.0365***(0.003)	−0.0373***(0.003)
CDS risk premium		0.0253***(0.003)	0.0233***(0.003)
Economic policy uncertainty		0.0035(0.004)	0.0035(0.004)
S&P 500 volatility	0.8657***(0.070)		0.1735(0.128)
Volatility ratio			−0.0249***(0.006)
Global financial crisis dummy	−0.0262***(0.008)	−0.0853***(0.013)	−0.0941*** (0.015)
Trend	−0.0010***(0.0001)	−0.0068***(0.0003)	−0.0065***(0.0004)
Constant	0.3845***(0.006)	0.4998***(0.022)	0.5159***(0.023)
Number of country pairs	78	55	55
Number of observations	3978	1905	1905
Adjusted ${R}^{2}$	0.209	0.336	0.340
$F$ statistics	151.33***	121.42***	99.29***
Notes: Dccmidascorr is the dependent variable. Bilateral trade shows the ratio of total mutual trade between countries to their total foreign trade volume. GDP growth rate indicates the log transformation of the GDP growth rate differences, inflation rate indicates the log transformation of the inflation rate differences, term spread indicates the log transformation of the term spread differences, CDS risk premium indicates the log transformation of the five-year CDS risk premium differences, and finally, EPU shows the log transformation of the economy policy uncertainty index differences between country $x$ and country $y$ . The numbers in the parentheses are standard errors. *** indicates statistical significance at the 1% level. For detailed definitions, see Table 2.

| Show Table

DownLoad: CSV

In the POLS (Pooled Ordinary Least Squares) method, all observations are collected in a pool and use the OLS method to estimate an equation without considering a cross section and time dimension of a dataset. The properties of the time series should be taken into consideration in the case of having a panel data set in which dynamic structure is dominant. Since the co-movement among stock markets is a dynamic process, the model specifications should contain lagged values of the dynamic conditional correlations Thomas et al. (2019). Therefore, we make use of the System GMM (Generalized Method of Moments) method developed by Arellano and Bover (1995) and Blundell and Bond (1998) to investigate the determinants of the long-term DCCs among stock markets. This methodology is appropriate to handle the dynamic structure of the co-movements among stock markets. Additionally, this methodology also deals with the problem of endogeneity between the explanatory variables. We estimate the following model specifications:

${\rho }_{xy, t} = a+\sum _{k = 1}^{3}{\delta }_{k}{\rho }_{xy, t-k}{+\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+\\ {\beta }_{3}{Inflation \ rate}_{xy, t}+{\beta }_{4}{Term \ spread}_{xy, t}+ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+{ \varepsilon }_{xy, t}$

(17)

${\rho }_{xy, t} = a+{\sum _{k = 1}^{3}{\delta }_{k}{\rho }_{xy, t-k}+\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+\\ {\beta }_{3}{Inflation \ rate}_{xy, t}+{\beta }_{4}{Term \ spread}_{xy, t}+\psi {CDS \ risk \ premium}_{xy, t}+\gamma {EPU}_{xy, t}+ \\ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+{ \varepsilon }_{xy, t}$

(18)

${\rho }_{xy, t} = a+\sum _{k = 1}^{3}{\delta }_{k}{\rho }_{xy, t-k}+{\beta }_{1}{Bilateral \ trade}_{xy, t}+{\beta }_{2}{GDP \ growth \ rate}_{xy, t}+\\ {\beta }_{3}{Inflation \ rate}_{xy, t}+{\beta }_{4}{Term \ spread}_{xy, t}+\psi {CDS \ risk \ premium}_{xy, t}+\gamma {EPU}_{xy, t}+\\ \theta {Volatility \ ratio}_{xy, t}+ \varphi {S\&P \ 500 \ volatility}_{t}+\lambda {GFC}_{t}+{ \varepsilon }_{xy, t}$

(19)

where ${ \ \rho }_{xy, t}$ represents long-term (quarterly) dynamic conditional correlations between stock markets of countries $x$ and $y$ , at time $t$ and $\sum _{k = 1}^{3}{\delta }_{k}{\rho }_{xy, t-k}$ indicates the lagged values of the dependent variable ${ \ \rho }_{xy, t}$ .

The estimation results of the System GMM models are shown in Table 9, where Model 1, Model 2, and Model 3 correspond to Equations (17), (18), and (19), respectively. According to the estimation results in Table 9, the most important factors explaining the long-term DCCs between stock market returns of G7 and BRICS-T countries are the differences in GDP growth rates, five-year CDS risk premiums, and EPU (Economy Policy Uncertainty) indices between country pairs. Overall, the coefficient estimates for GDP growth rate differences are negative and statistically significant for all models. These results are consistent with the findings of Mobarek et al. (2016) and Nitoi and Pochea (2019). This result indicates that as the differences in GDP growth rates between country pairs decrease, the long-term DCCs between stock market returns rise. Moreover, we find that the coefficient estimates for inflation rate difference are negative and statistically significant for the Model 1 and the Model 2. These findings are compatible with the results of Alotaibi and Mishra (2015) and Nitoi and Pochea (2019). Furthermore, according to the estimation results of the Model 1 and Model 3, the estimated coefficients for term spread difference are negative and statistically significant in accordance with the findings of Mobarek et al. (2016) and Vithessonthi and Kumarasinghe (2016). Taken together, these results show that the time-varying co-movements between stock markets of countries with similar inflation rate and term spread are high. Besides, we find that the differences in five-year CDS risk premium between country pairs are positively related to the long-term DCCs among stock market returns in consistent with the results of Min and Hwang (2012) and Güngör and Güngör (2020). We also utilize the differences in EPU (Economic Policy Uncertainty) indices between country pairs as determinants of the time-varying co-movements among stock markets. In line with expectations, the differences in economic policy indices are negative and statistically significant for the Model 2 and the Model 3. These findings show that as the economic policy uncertainty index differences between two counties increase, the long-term DCCs among the stock markets of those countries decline.

Table 9. Estimation results of the system GMM models for all country pairs.

${\left(\mathrm{D}\mathrm{c}\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\right)}_{\mathrm{t}}$	Model 1	Model 2	Model 3
${\left(\mathrm{D}\mathrm{c}\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}\right)}_{t-1}$	1.2794***(0.008)	1.3618***(0.008)	1.3456***(0.010)
$({\mathrm{D}\mathrm{c}\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r} \ )}_{t-2}$	−0.4515***(0.014)	−0.4873***(0.015)	−0.4704***(0.019)
$({\mathrm{D}\mathrm{c}\mathrm{c}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r} \ )}_{t-3}$	0.0871***(0.011)	0.0914***(0.008)	0.0799***(0.013)
Bilateral trade	−0.0666(0.065)	−0.0191(0.092)	0.0183(0.084)
GDP growth rate	−0.0011***(0.0001)	−0.0024***(0.0001)	−0.0025***(0.0001)
Inflation rate	−0.0009***(0.0002)	−0.0008***(0.0002)	0.00008(0.0002)
Term spread	−0.0009***(0.0002)	−0.0005(0.0003)	−0.0010***(0.0004)
CDS risk premium		0.0093***(0.0004)	0.0067***(0.0004)
Economic policy uncertainty		−0.0013***(0.0003)	−0.0016***(0.0004)
S & P 500 volatility	0.0904***(0.003)		0.1421***(0.012)
Volatility ratio			−0.0057***(0.001)
Global financial crisis dummy	−0.0021***(0.0004)	0.0012***(0.0004)	−0.0098***(0.0009)
Trend	−0.0002***(0.0001)	−0.0002***(0.00003)	−0.0001***(0.00004)
Constant	0.0869***(0.010)	−0.0076(0.006)	0.0032(0.004)
Number of country pairs	78	55	55
Number of observations	3978	1905	1905
Number of instruments	150	96	98
Wald statistics	1.80e + 06***	336501.38***	2.28e + 06***
AR(1) Arellano-Bond prob	0.000	0.000	0.000
AR(2) Arellano-Bond prob	0.121	0.173	0.134
AR(3) Arellano-Bond prob	0.123	0.118	0.123
Sargan test prob	0.999	0.999	0.998
Notes: Dccmidascorr is the dependent variable. Bilateral trade shows the ratio of total mutual trade between countries to their total foreign trade volume. GDP growth rate indicates the log transformation of the GDP growth rate differences, inflation rate indicates the log transformation of the inflation rate differences, term spread indicates the log transformation of the term spread differences, CDS risk premium indicates the log transformation of the five-year CDS risk premium differences, and finally, EPU shows the log transformation of the economy policy uncertainty index differences between country $x$ and country $y$ . The numbers in the parentheses are standard errors. *** indicates statistical significance at the 1% level. For detailed definitions, see Table 2.

| Show Table

DownLoad: CSV

Furthermore, we examine impact of the S & P 500 volatility on long-term DCCs between the stock markets of G7 and BRICS-T countries. As expected, the coefficient estimates of the S & P 500 volatility are positive and statistically significant for the Model 1 and the Model 3. These results indicate that a rise in the volatility of the S & P 500 leads to an increase in the long-term DCCs among stock markets. In addition, we find that the volatility ratio is negatively related to the time-varying co-movements among stock market returns in accordance with the findings of Thomas et al. (2019). Empirical findings suggest that as volatility of stock markets gets closer to each other, the time-varying co-movements between those markets increase. In line with the findings of (Didier et al., 2012; Vithessonthi and Kumarasinghe, 2016 and Thomas et al., 2019), we also find that there is a statistically insignificant relationship between the bilateral trade and the long-term DCCs among stock markets. For the robustness controls, we also estimate the System GMM models for the G7 country pairs and the G7 & BRICS-T country pairs. The estimation results of the System GMM models for the G7 country pairs and the G7 & BRICS-T country pairs are given in the Table A3 and the Table A4 in the Appendix A, respectively. The estimation results of those models have resemblance to each other qualitatively, however those models differ numerically.

5. Conclusions

This paper analyzes the macroeconomic factors expounding the time-varying co-movements between stock market returns of G7 and BRICS-T countries. For this purpose, first DCC-MIDAS models are estimated for 78 country pairs, and then, the dynamic conditional correlations among the daily stock market returns of the countries in the sample are decomposed into the short-term (daily) component and the long-term (quarterly) components. According to the estimation results of the DCC-MIDAS models, it is found that the highest DCC-MIDAS correlations among 78 country pairs belong to the stock markets of G7 country pairs. In addition, the stock market pairs of European countries have the highest DCC-MIDAS correlations among the stock market pairs of G7 countries. Colacito et al. (2011) put forward that fundamental causes of time-varying conditional correlations are captured by slowly moving processes of DCCs. In this respect, economic and financial factors that represent economic-financial proximity between countries are expected to be connected with slowly moving long-term components rather than rapidly moving short-term components of DCCs among stock market returns. Thus, this study examines the relationship between the long-term component of DCCs between G7 and BRICS-T countries' stock markets and macroeconomic variables that represent economic-financial proximity between those countries using the System GMM method for the period from January, 2006 to August, 2018. For this purpose, we use bilateral trade, GDP growth rate, inflation rate, term spread, five-year CDS risk premium and economy policy uncertainty index, volatility of the S & P 500 and volatility rates of stock markets as regressors to analyze the DCC-MIDAS correlations between stock market returns of countries. Furthermore, we also estimate the System GMM models for the G7 country pairs and the G7 & BRICS-T country pairs in addition to all country pairs for the robustness controls. These robustness checks enable us to separately examine the relationships both between advanced countries and between advanced and emerging countries.

Empirical results suggest that the most important factors that explain long-term DCCs between stock market returns of G7 and BRICS-T countries are the differences in GDP growth rates, five-year CDS risk premiums, and EPU (Economy Policy Uncertainty) indices between country pairs. The estimated coefficients of the differences in GDP growth rates and economic policy uncertainty indices between country pairs are negative while the differences in five-year CDS risk premiums between country pairs are positive. These findings imply that as the differences in GDP growth rates and EPU indices between country pairs decrease, the long-term DCCs between stock market returns increase. According to the empirical results from the G7 country pairs, the most important variables expounding the DCC-MIDAS correlations among stock market returns of those countries are the differences in term spreads, inflation rates, and five-year CDS risk premiums between G7 country pairs. These results indicate that as the differences in term spreads and inflation rates between G7 country pairs get closer to each other, the time-varying co-movements among those stock markets tend to rise. In addition, the estimation results for the G7 & BRICS-T country pairs show that the most significant variables expressing the long-term DCCs between stock market returns of those countries are the differences in GDP growth rates, term spreads, and five-year CDS risk premiums between G7 & BRICS-T country pairs. These results indicate that as the differences in GDP growth rates and term spreads between G7 & BRICS-T country pairs increase, the DCC-MIDAS correlations between stock markets of those countries decline.

The results of this paper offer important implications for policy makers, financial institutions, financial analysts, portfolio managers and global investors. The higher co-movement between stock markets of two countries will potentially reduce the benefits from portfolio diversification. Thus, global investors and portfolio managers should comprehend the macro-financial dynamics of the time-varying co-movements among stock markets to take efficient investment decisions. Besides, the higher co-movement between stock market of two countries might make these stock markets vulnerable to the same kind of economic and financial shocks. Therefore, the knowledge of policy makers on the determinant factors of co-movement among stock markets will definitely ease to construct a suitable policy to sustain their financial stabilization.

Conflict of interest

The authors declare no conflict of interest.

References

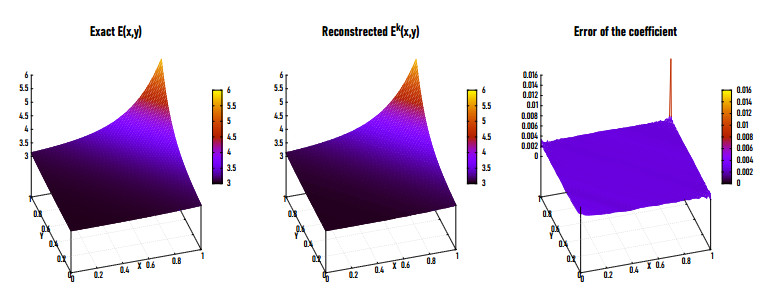
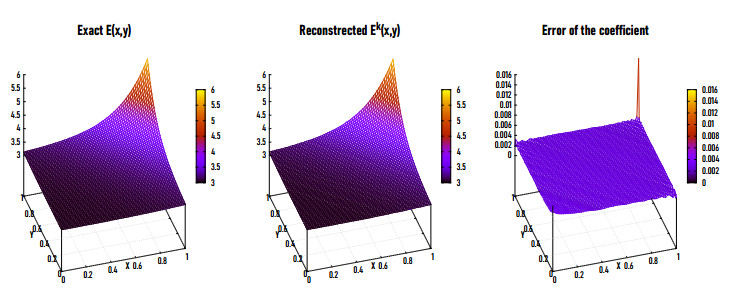
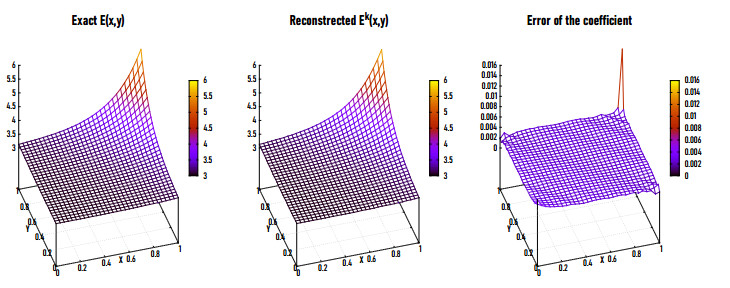
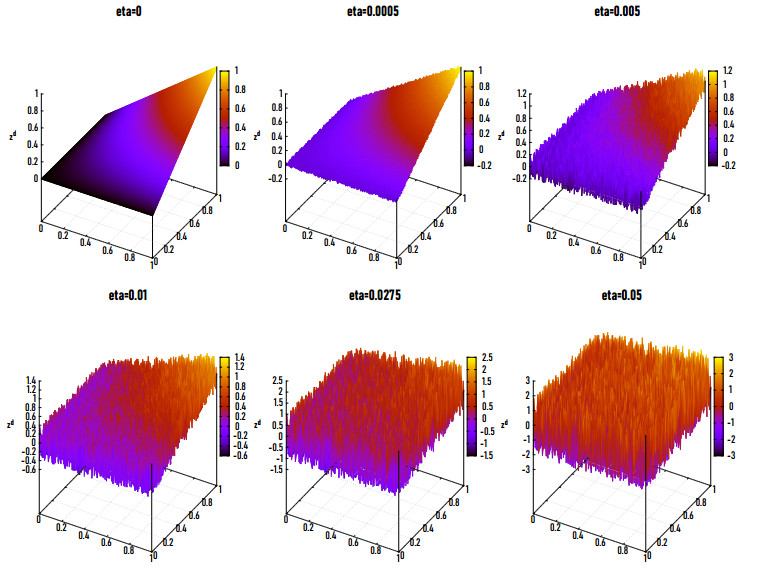
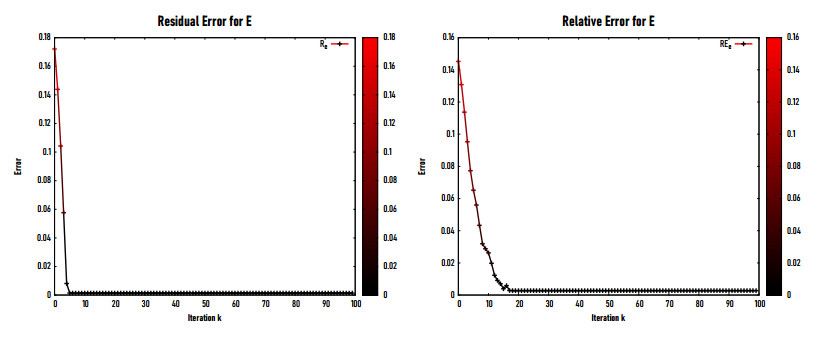
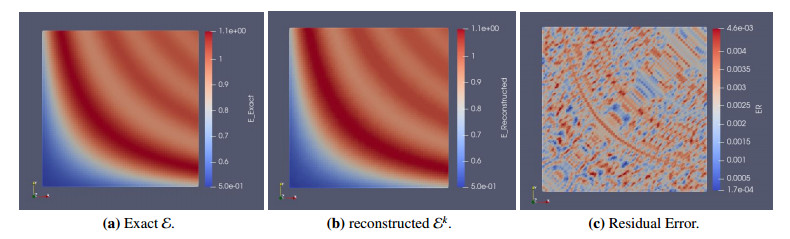
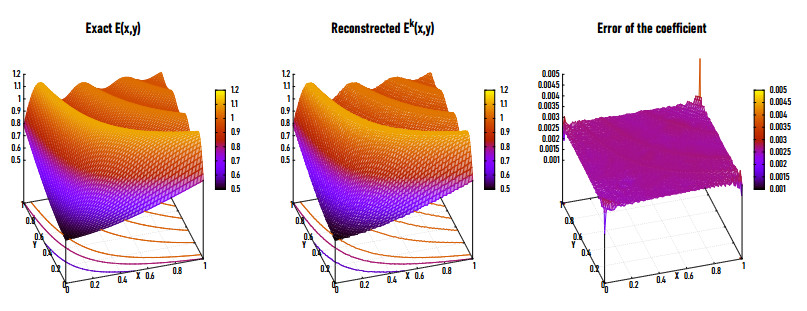
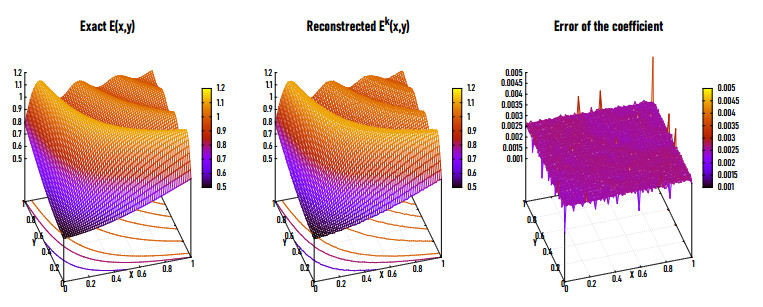
[1]	A. Muller, A. C. Marquez, B. Iung, On the concept of e-maintenance: Review and current research, Reliab. Eng. Syst. Saf., 93 (2008), 1165–1187. https://doi.org/10.1016/j.ress.2007.08.006 doi: 10.1016/j.ress.2007.08.006
[2]	K. Gandhi, A. H. Ng, Machine maintenance decision support system: a systematic literature review, in Advances in Manufacturing Technology XXXⅡ: Proceedings of the 16th International Conference on Manufacturing Research, incorporating the 33rd National Conference on Manufacturing Research, September 11–13, University of Skö vde, IOS Press, Sweden, 8 (2018), 349.
[3]	A. Garg, S. G. Deshmukh, Maintenance management: literature review and directions, J. Qual. Maint. Eng., 12 (2006), 205–238. https://doi.org/10.1108/13552510610685075 doi: 10.1108/13552510610685075
[4]	D. Sherwin, A review of overall models for maintenance management, J. Qual. Maint. Eng., 6 (2000), 138–164. https://doi.org/10.1108/13552510010341171 doi: 10.1108/13552510010341171
[5]	K. C. Ng, G. G. G. Goh, U. C. Eze, Critical success factors of total productive maintenance implementation: a review, in 2011 IEEE international conference on industrial engineering and engineering management, IEEE, Singapore, 269–273. https://doi.org/10.1109/IEEM.2011.6117920
[6]	E. Sisinni, A. Saifullah, S. Han, U. Jennehag, M. Gidlund, Industrial internet of things: Challenges, opportunities, and directions, IEEE Trans. Ind. Inf., 14 (2018), 4724–4734. https://doi.org/10.1109/TⅡ.2018.2852491 doi: 10.1109/TⅡ.2018.2852491
[7]	H. Boyes, B. Hallaq, J. Cunningham, T. Watson, The industrial internet of things (ⅡoT): An analysis framework, Comput. Ind., 101 (2018), 1–12. https://doi.org/10.1016/j.compind.2018.04.015 doi: 10.1016/j.compind.2018.04.015
[8]	J. Wan, S. Tang, Z. Shu, D. Li, S. Wang, M. Imran, et al., Software-defined industrial internet of things in the context of industry 4.0, IEEE Sens. J., 16 (2016), 7373–7380. https://doi.org/10.1109/JSEN.2016.2565621 doi: 10.1109/JSEN.2016.2565621
[9]	Y. Liao, E. D. F. R. Loures, F. Deschamps, Industrial Internet of Things: A systematic literature review and insights, IEEE Internet Things J., 5 (2018), 4515–4525. https://doi.org/10.1109/JIOT.2018.2834151 doi: 10.1109/JIOT.2018.2834151
[10]	M. Hartmann, B. Halecker, Management of innovation in the industrial internet of things, in The International Society for Professional Innovation Management ISPIM Conference Proceedings, 2015.
[11]	M. Mohri, A. Rostamizadeh, A. Talwalkar, Foundations of Machine Learning, MIT press, 2018.
[12]	C. Sammut, G. I. Webb, Encyclopedia of Machine Learning, Springer Science & Business Media, 2011.
[13]	G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, et al., Machine learning and the physical sciences, Rev. Mod. Phys., 91 (2019), 045002. https://doi.org/10.1103/RevModPhys.91.045002 doi: 10.1103/RevModPhys.91.045002
[14]	M. Du, N. Liu, X. Hu, Techniques for interpretable machine learning, Commun. ACM, 63 (2019), 68–77. https://doi.org/10.1145/3359786 doi: 10.1145/3359786
[15]	H. Sahli, An introduction to machine learning, in TORUS 1-Toward an Open Resource Using Services: Cloud Computing for Environmental Data, (2020), 61–74. https://doi.org/10.1002/9781119720492.ch7
[16]	R. H. P. M. Arts, G. M. Knapp, L. Mann, Some aspects of measuring maintenance performance in the process industry, J. Qual. Maint. Eng., 4 (1998) 6–11. https://doi.org/10.1108/13552519810201520 doi: 10.1108/13552519810201520
[17]	C. Stenströ m, P. Norrbin, A. Parida, U. Kumar, Preventive and corrective maintenance-cost comparison and cost-benefit analysis, Struct. Infrastruct. Eng., 12 (2016), 603–617. https://doi.org/10.1080/15732479.2015.1032983 doi: 10.1080/15732479.2015.1032983
[18]	H. P. Bahrick, L. K. Hall, Preventive and corrective maintenance of access to knowledge, Appl. Cognit. Psychol., 5 (1991), 1–18. https://doi.org/10.1002/acp.2350050102 doi: 10.1002/acp.2350050102
[19]	J. Shin, H. Jun, On condition based maintenance policy, J. Comput. Des. Eng., 2 (2015), 119–127. https://doi.org/10.1016/j.jcde.2014.12.006 doi: 10.1016/j.jcde.2014.12.006
[20]	R. Ahmad, S. Kamaruddin, An overview of time-based and condition-based maintenance in industrial application, Comput. Ind. Eng., 63 (2012), 135–149. https://doi.org/10.1016/j.cie.2012.02.002 doi: 10.1016/j.cie.2012.02.002
[21]	J. H. Williams, A. Davies, P. R. Drake, Condition-Based Maintenance and Machine Diagnostics, Springer Science & Business Media, 1994.
[22]	R. K. Mobley, An Introduction to Predictive Maintenance, 2nd edition, Elsevier, 2002. https://doi.org/10.1016/B978-0-7506-7531-4.X5000-3
[23]	C. Scheffer, P. Girdhar, Practical Machinery Vibration Analysis and Predictive Maintenance, Elsevier, 2004.
[24]	K. Efthymiou, N. Papakostas, D. Mourtzis, G. Chryssolouris, On a predictive maintenance platform for production systems, Procedia CIRP, 3 (2012), 221–226. https://doi.org/10.1016/j.procir.2012.07.039 doi: 10.1016/j.procir.2012.07.039
[25]	G. A. Susto, A. Schirru, S. Pampuri, S. McLoone, A. Beghi, Machine learning for predictive maintenance: A multiple classifier approach, IEEE Trans. Ind. Inf., 11 (2014), 812–820. https://doi.org/10.1109/TⅡ.2014.2349359 doi: 10.1109/TⅡ.2014.2349359
[26]	R. Isermann, Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance, Springer Science & Business Media, 2005.
[27]	Z. Gao, C. Cecati, S. X. Ding, A survey of fault diagnosis and fault-tolerant techniques—Part I: Fault diagnosis with model-based and signal-based approaches, IEEE Trans. Ind. Electron., 62 (2015), 3757–3767. https://doi.org/10.1109/TIE.2015.2417501 doi: 10.1109/TIE.2015.2417501
[28]	S. Leonhardt, M. Ayoubi, Methods of fault diagnosis, Control Eng. Pract., 5 (1997), 683–692. https://doi.org/10.1016/S0967-0661(97)00050-6 doi: 10.1016/S0967-0661(97)00050-6
[29]	R. J. Patton, P. M. Frank, R. N Clark, Issues of Fault Diagnosis for Dynamic Systems, Springer Science & Business Media, 2013.
[30]	M. I. Jordan, T. M. Mitchell, Machine learning: Trends, perspectives, and prospects, Science, 349 (2015), 255–260. https://doi.org/10.1126/science.aaa8415 doi: 10.1126/science.aaa8415
[31]	U. S. Shanthamallu, A. Spanias, C. Tepedelenlioglu, M. Stanley, A brief survey of machine learning methods and their sensor and IoT applications, in 2017 8th International Conference on Information, Intelligence, Systems & Applications (ⅡSA), IEEE, (2017), 1–8. https://doi.org/10.1109/ⅡSA.2017.8316459
[32]	D. A. Pisner, D. M. Schnyer, Support vector machine, in Machine Learning, Academic Press, (2020), 101–121. https://doi.org/10.1016/B978-0-12-815739-8.00006-7
[33]	W. S. Noble, What is a support vector machine, Nat. Biotechnol., 24 (2006), 1565–1567. https://doi.org/10.1038/nbt1206-1565 doi: 10.1038/nbt1206-1565
[34]	L. Wang, Support Vector Machines: Theory and Applications, Springer Science & Business Media, 2005. https://doi.org/10.1007/b95439
[35]	S. I. Amari, S. Wu, Improving support vector machine classifiers by modifying kernel functions, Neural Networks, 12 (1999), 783–789. https://doi.org/10.1016/S0893-6080(99)00032-5 doi: 10.1016/S0893-6080(99)00032-5
[36]	O. L. Mangasarian, D. R. Musicant, Lagrangian support vector machines, J. Mach. Learn. Res., 1 (2001), 161–177.
[37]	A. Widodo, B. S. Yang, Support vector machine in machine condition monitoring and fault diagnosis, Mech. Syst. Sig. Process., 21 (2007), 2560–2574. https://doi.org/10.1016/j.ymssp.2006.12.007 doi: 10.1016/j.ymssp.2006.12.007
[38]	S. W. Fei, X. B. Zhang, Fault diagnosis of power transformer based on support vector machine with genetic algorithm, Expert Syst. Appl., 36 (2009), 11352–11357. https://doi.org/10.1016/j.eswa.2009.03.022 doi: 10.1016/j.eswa.2009.03.022
[39]	S. D. Wu, P. H. Wu, C. W. Wu, J. J. Ding, C. C. Wang, Bearing fault diagnosis based on multiscale permutation entropy and support vector machine, Entropy, 14 (2012), 1343–1356. https://doi.org/10.3390/e14081343 doi: 10.3390/e14081343
[40]	W. Aziz, M. Arif, Multiscale permutation entropy of physiological time series, in 2005 Pakistan Section Multitopic Conference, IEEE, (2005), 1–6. https://doi.org/10.1109/INMIC.2005.334494
[41]	B. Tang, T. Song, F. Li, L. Deng, Fault diagnosis for a wind turbine transmission system based on manifold learning and Shannon wavelet support vector machine, Renewable Energy, 62 (2014), 1–9. https://doi.org/10.1016/j.renene.2013.06.025 doi: 10.1016/j.renene.2013.06.025
[42]	Z. Wang, L. Yao, Y. Cai, J. Zhang, Mahalanobis semi-supervised mapping and beetle antennae search based support vector machine for wind turbine rolling bearings fault diagnosis, Renewable Energy, 155 (2020), 1312–1327. https://doi.org/10.1016/j.renene.2020.04.041 doi: 10.1016/j.renene.2020.04.041
[43]	L. Yao, Z. Fang, Y. Xiao, J. Hou, Z. Fu, An intelligent fault diagnosis method for lithium battery systems based on grid search support vector machine, Energy, 214 (2021), 118866. https://doi.org/10.1016/j.energy.2020.118866 doi: 10.1016/j.energy.2020.118866
[44]	Y. P. Zhao, J. J. Wang, X. Y. Li, G. J. Peng, Z. Yang, Extended least squares support vector machine with applications to fault diagnosis of aircraft engine, ISA Trans., 97 (2020), 189–201. https://doi.org/10.1016/j.isatra.2019.08.036 doi: 10.1016/j.isatra.2019.08.036
[45]	F. Marini, B. Walczak, Particle swarm optimization (PSO). A tutorial, Chemom. Intell. Lab. Syst., 149 (2015), 153–165. https://doi.org/10.1016/j.chemolab.2015.08.020 doi: 10.1016/j.chemolab.2015.08.020
[46]	M. Van, D. T. Hoang, H. J. Kang, Bearing fault diagnosis using a particle swarm optimization-least squares wavelet support vector machine classifier, Sensors, 20 (2020), 3422. https://doi.org/10.3390/s20123422 doi: 10.3390/s20123422
[47]	X. Li, S. Wu, X. Li, H. Yuan, D. Zhao, Particle swarm optimization-support vector machine model for machinery fault diagnoses in high-voltage circuit breakers, Chin. J. Mech. Eng., 33 (2020), 1–10. https://doi.org/10.1186/s10033-019-0428-5 doi: 10.1186/s10033-019-0428-5
[48]	Y. Fan, C. Zhang, Y. Xue, J. Wang, F. Gu, A bearing fault diagnosis using a support vector machine optimised by the self-regulating particle swarm, Shock Vib., 2020 (2020). https://doi.org/10.1155/2020/9096852 doi: 10.1155/2020/9096852
[49]	E. Mirakhorli, Fault diagnosis in a distillation column using a support vector machine based classifier, Int. J. Smart Electr. Eng., 8 (2020), 105–113.
[50]	S. Gao, C. Zhou, Z. Zhang, J. Geng, R. He, Q. Yin, C. Xing, Mechanical fault diagnosis of an on-load tap changer by applying cuckoo search algorithm-based fuzzy weighted least squares support vector machine, Math. Probl. Eng., 2020 (2020). https://doi.org/10.1155/2020/3432409 doi: 10.1155/2020/3432409
[51]	X. Huang, X. Huang, B. Wang, Z. Xie, Fault diagnosis of transformer based on modified grey wolf optimization algorithm and support vector machine, IEEJ Trans. Electr. Electron. Eng., 15 (2020), 409–417. https://doi.org/10.1002/tee.23069 doi: 10.1002/tee.23069
[52]	Y. Zhang, J. Li, X. Fan, J. Liu, H. Zhang, Moisture prediction of transformer oil-immersed polymer insulation by applying a support vector machine combined with a genetic algorithm, Polymers, 12 (2020), 1579. https://doi.org/10.3390/polym12071579 doi: 10.3390/polym12071579
[53]	Y. Liu, H. Chen, L. Zhang, X. Wu, X. J. Wang, Energy consumption prediction and diagnosis of public buildings based on support vector machine learning: A case study in China, J. Cleaner Prod., 272 (2020), 122542. https://doi.org/10.1016/j.jclepro.2020.122542 doi: 10.1016/j.jclepro.2020.122542
[54]	S. K. Ibrahim, A. Ahmed, M. A. E. Zeidan, I. E. Ziedan, Machine learning techniques for satellite fault diagnosis, Ain Shams Eng. J., 11 (2020), 45–56. https://doi.org/10.1016/j.asej.2019.08.006 doi: 10.1016/j.asej.2019.08.006
[55]	Y. P. Zhao, G. Huang, Q. K. Hu, B. Li, An improved weighted one class support vector machine for turboshaft engine fault detection, Eng. Appl. Artif. Intell., 94 (2020), 103796. https://doi.org/10.1016/j.engappai.2020.103796 doi: 10.1016/j.engappai.2020.103796
[56]	M. Guo, L. Xie, S. Q. Wang, J. M. Zhang, Research on an integrated ICA-SVM based framework for fault diagnosis, in SMC'03 Conference Proceedings. 2003 IEEE International Conference on Systems, Man and Cybernetics. Conference Theme-System Security and Assurance (Cat. No. 03CH37483), IEEE, 3 (2003), 2710–2715. https://doi.org/10.1109/ICSMC.2003.1244294
[57]	S. Poyhonen, P. Jover, H. Hyotyniemi, Signal processing of vibrations for condition monitoring of an induction motor, in First International Symposium on Control, Communications and Signal Processing, IEEE, Tunisia, (2004), 499–502. https://doi.org/10.1109/ISCCSP.2004.1296338
[58]	M. C. Moura, E. Zio, I. D. Lins, E. Droguett, Failure and reliability prediction by support vector machines regression of time series data, Reliab. Eng. Syst. Saf., 96 (2011), 1527–1534. https://doi.org/10.1016/j.ress.2011.06.006 doi: 10.1016/j.ress.2011.06.006
[59]	K. Y. Chen, L. S. Chen, M. C. Chen, C. L. Lee, Using SVM based method for equipment fault detection in a thermal power plant, Comput. Ind., 62 (2011), 42–50. https://doi.org/10.1016/j.compind.2010.05.013 doi: 10.1016/j.compind.2010.05.013
[60]	K. He, X. Li, A quantitative estimation technique for welding quality using local mean decomposition and support vector machine, J. Intell. Manuf., 27 (2016), 525–533. https://doi.org/10.1007/s10845-014-0885-8 doi: 10.1007/s10845-014-0885-8
[61]	K. Yan, C. Zhong, Z. Ji, J. Huang, Semi-supervised learning for early detection and diagnosis of various air handling unit faults, Energy Build., 181 (2018), 75–83. https://doi.org/10.1016/j.enbuild.2018.10.016 doi: 10.1016/j.enbuild.2018.10.016
[62]	Z. Yin, J. Hou, Recent advances on SVM based fault diagnosis and process monitoring in complicated industrial processes, Neurocomputing, 174 (2016), 643–650. https://doi.org/10.1016/j.neucom.2015.09.081 doi: 10.1016/j.neucom.2015.09.081
[63]	M. M. Islam, J. M. Kim, Reliable multiple combined fault diagnosis of bearings using heterogeneous feature models and multiclass support vector Machines, Reliab. Eng. Syst. Saf., 184 (2019), 55–66. https://doi.org/10.1016/j.ress.2018.02.012 doi: 10.1016/j.ress.2018.02.012
[64]	R. P. Monteiro, M. Cerrada, D. R. Cabrera, R. V. Sánchez, C. J. Bastos-Filho, Using a support vector machine based decision stage to improve the fault diagnosis on gearboxes, Comput. Intell. Neurosci., 2019 (2019). https://doi.org/10.1155/2019/1383752 doi: 10.1155/2019/1383752
[65]	D. Yang, J. Miao, F. Zhang, J. Tao, G. Wang, Y. Shen, Bearing fault diagnosis using a support vector machine optimized by an improved ant lion optimizer, Shock Vib., 2019 (2019). https://doi.org/10.1155/2019/9303676 doi: 10.1155/2019/9303676
[66]	S. Mirjalili, The ant lion optimizer, Adv. Eng. Software, 83 (2015), 80–98. https://doi.org/10.1016/j.advengsoft.2015.01.010 doi: 10.1016/j.advengsoft.2015.01.010
[67]	L. You, W. Fan, Z. Li, Y. Liang, M. Fang, J. Wang, A fault diagnosis model for rotating machinery using VWC and MSFLA-SVM based on vibration signal analysis, Shock Vib., 2019 (2019). https://doi.org/10.1155/2019/1908485 doi: 10.1155/2019/1908485
[68]	A. Kumar, R. Kumar, Time-frequency analysis and support vector machine in automatic detection of defect from vibration signal of centrifugal pump, Measurement, 108 (2017), 119–133. https://doi.org/10.1016/j.measurement.2017.04.041 doi: 10.1016/j.measurement.2017.04.041
[69]	Z. Chen, F. Zhao, J. Zhou, P. Huang, X. Zhang, Fault diagnosis of loader gearbox based on an Ica and SVM algorithm, Int. J. Environ. Res. Public Health, 16 (2019), 4868. https://doi.org/10.3390/ijerph16234868 doi: 10.3390/ijerph16234868
[70]	T. W. Lee, Independent component analysis, in Independent Component Analysis, Springer, Boston, (1998), 27–66. https://doi.org/10.1007/978-1-4757-2851-4_2
[71]	W. Liu, Z. Wang, J. Han, G. Wang, Wind turbine fault diagnosis method based on diagonal spectrum and clustering binary tree SVM, Renewable Energy, 50 (2013), 1–6. https://doi.org/10.1016/j.renene.2012.06.013 doi: 10.1016/j.renene.2012.06.013
[72]	M. A. Djeziri, O. Djedidi, N. Morati, J. L. Seguin, M. Bendahan, T. Contaret, A temporal-based SVM approach for the detection and identification of pollutant gases in a gas mixture, Appl. Intell., 52 (2022), 6065–6078. https://doi.org/10.1007/s10489-021-02761-0 doi: 10.1007/s10489-021-02761-0
[73]	G. Ciaburro, G. Iannace, J. Passaro, A. Bifulco, D. Marano, M. Guida, et al., Artificial neural network-based models for predicting the sound absorption coefficient of electrospun poly (vinyl pyrrolidone)/silica composite, Appl. Acoust., 169 (2020), 107472. https://doi.org/10.1016/j.apacoust.2020.107472 doi: 10.1016/j.apacoust.2020.107472
[74]	S. Agatonovic-Kustrin, R. Beresford, Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research, J. Pharm. Biomed. Anal., 22 (2000), 717–727. https://doi.org/10.1016/S0731-7085(99)00272-1 doi: 10.1016/S0731-7085(99)00272-1
[75]	G. Ciaburro, G. Iannace, M. Ali, A. Alabdulkarem, A. Nuhait, An artificial neural network approach to modelling absorbent asphalts acoustic properties, J. King Saud Univ. Eng. Sci., 33 (2021), 213–220. https://doi.org/10.1016/j.jksues.2020.07.002 doi: 10.1016/j.jksues.2020.07.002
[76]	J. Misra, I. Saha, Artificial neural networks in hardware: A survey of two decades of progress, Neurocomputing, 74 (2010), 239–255. https://doi.org/10.1016/j.neucom.2010.03.021 doi: 10.1016/j.neucom.2010.03.021
[77]	Z. Zhang, K. Friedrich, Artificial neural networks applied to polymer composites: a review, Compos. Sci. Technol., 63 (2003), 2029–2044. https://doi.org/10.1016/S0266-3538(03)00106-4 doi: 10.1016/S0266-3538(03)00106-4
[78]	G. Iannace, G. Ciaburro, A. Trematerra, Modelling sound absorption properties of broom fibers using artificial neural networks, Appl. Acoust., 163 (2020), 107239. https://doi.org/10.1016/j.apacoust.2020.107239 doi: 10.1016/j.apacoust.2020.107239
[79]	K. P. Singh, A. Basant, A. Malik, G. Jain, Artificial neural network modeling of the river water quality—a case study, Ecol. Modell., 220 (2009), 888–895. https://doi.org/10.1016/j.ecolmodel.2009.01.004 doi: 10.1016/j.ecolmodel.2009.01.004
[80]	H. Zhu, X. Li, Q. Sun, L. Nie, J. Yao, G. Zhao, A power prediction method for photovoltaic power plant based on wavelet decomposition and artificial neural networks, Energies, 9 (2015), 1–15. https://doi.org/10.3390/en9010011 doi: 10.3390/en9010011
[81]	V. P. Romero, L. Maffei, G. Brambilla, G. Ciaburro, Modelling the soundscape quality of urban waterfronts by artificial neural networks, Appl. Acoust., 111 (2016), 121–128. https://doi.org/10.1016/j.apacoust.2016.04.019 doi: 10.1016/j.apacoust.2016.04.019
[82]	S. Fabio, D. N. Giovanni, P. Mariano, Airborne sound insulation prediction of masonry walls using artificial neural networks, Build. Acoust., 28 (2021), 391–409. https://doi.org/10.1177/1351010X21994462 doi: 10.1177/1351010X21994462
[83]	Y. Zhang, X. Ding, Y. Liu, P. J. Griffin, An artificial neural network approach to transformer fault diagnosis, IEEE Trans. Power Delivery, 11 (1996), 1836–1841. https://doi.org/10.1109/61.544265 doi: 10.1109/61.544265
[84]	J. C. Hoskins, K. M. Kaliyur, D. M. Himmelblau, Fault diagnosis in complex chemical plants using artificial neural networks, AIChE J., 37 (1991), 137–141. https://doi.org/10.1002/aic.690370112 doi: 10.1002/aic.690370112
[85]	J. B. Ali, N. Fnaiech, L. Saidi, B. Chebel-Morello, F. Fnaiech, Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals, Appl. Acoust., 89 (2015), 16–27. https://doi.org/10.1016/j.apacoust.2014.08.016 doi: 10.1016/j.apacoust.2014.08.016
[86]	T. Sorsa, H. N. Koivo, Application of artificial neural networks in process fault diagnosis, Automatica, 29 (1993), 843–849. https://doi.org/10.1016/0005-1098(93)90090-G doi: 10.1016/0005-1098(93)90090-G
[87]	N. Saravanan, K. I. Ramachandran, Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN), Expert Syst. Appl., 37 (2010), 4168–4181. https://doi.org/10.1016/j.eswa.2009.11.006 doi: 10.1016/j.eswa.2009.11.006
[88]	W. Chine, A. Mellit, V. Lughi, A. Malek, G. Sulligoi, A. M. Pavan, A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks, Renewable Energy, 90 (2016), 501–512. https://doi.org/10.1016/j.renene.2016.01.036 doi: 10.1016/j.renene.2016.01.036
[89]	B. Li, M. Y. Chow, Y. Tipsuwan, J. C. Hung, Neural-network-based motor rolling bearing fault diagnosis, IEEE Trans. Ind. Electron., 47 (2000), 1060–1069. https://doi.org/10.1109/41.873214 doi: 10.1109/41.873214
[90]	B. Samanta, K. R. Al-Balushi, S. A. Al-Araimi, Artificial neural networks and genetic algorithm for bearing fault detection, Soft Comput., 10 (2006), 264–271. https://doi.org/10.1007/s00500-005-0481-0 doi: 10.1007/s00500-005-0481-0
[91]	T. Han, B. S. Yang, W. H. Choi, J. S. Kim, Fault diagnosis system of induction motors based on neural network and genetic algorithm using stator current signals, Int. J. Rotating Mach., 2006 (2006). https://doi.org/10.1155/IJRM/2006/61690 doi: 10.1155/IJRM/2006/61690
[92]	H. Wang, P. Chen, Intelligent diagnosis method for rolling element bearing faults using possibility theory and neural network, Comput. Ind. Eng., 60 (2011), 511–518. https://doi.org/10.1016/j.cie.2010.12.004 doi: 10.1016/j.cie.2010.12.004
[93]	M. A. Hashim, M. H. Nasef, A. E. Kabeel, N. M. Ghazaly, Combustion fault detection technique of spark ignition engine based on wavelet packet transform and artificial neural network, Alexandria Eng. J., 59 (2020), 3687–3697. https://doi.org/10.1016/j.aej.2020.06.023 doi: 10.1016/j.aej.2020.06.023
[94]	G. Iannace, G. Ciaburro, A. Trematerra, Fault diagnosis for UAV blades using artificial neural network, Robotics, 8 (2019), 59. https://doi.org/10.3390/robotics8030059 doi: 10.3390/robotics8030059
[95]	M. Kordestani, M. F. Samadi, M. Saif, K. Khorasani, A new fault diagnosis of multifunctional spoiler system using integrated artificial neural network and discrete wavelet transform methods, IEEE Sens. J., 18 (2018), 4990–5001. https://doi.org/10.1109/JSEN.2018.2829345 doi: 10.1109/JSEN.2018.2829345
[96]	S. Shi, G. Li, H. Chen, J. Liu, Y. Hu, L. Xing, et al., Refrigerant charge fault diagnosis in the VRF system using Bayesian artificial neural network combined with ReliefF filter, Appl. Therm. Eng., 112 (2017), 698–706. https://doi.org/10.1016/j.applthermaleng.2016.10.043 doi: 10.1016/j.applthermaleng.2016.10.043
[97]	X. Xu, D. Cao, Y. Zhou, J. Gao, Application of neural network algorithm in fault diagnosis of mechanical intelligence, Mech. Syst. Sig. Process., 141 (2020), 106625. https://doi.org/10.1016/j.ymssp.2020.106625 doi: 10.1016/j.ymssp.2020.106625
[98]	A. Viveros-Wacher, J. E. Rayas-Sánchez, Analog fault identification in RF circuits using artificial neural networks and constrained parameter extraction, in 2018 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), IEEE, (2018), 1–3. https://doi.org/10.1109/NEMO.2018.8503117
[99]	S. Heo, J. H. Lee, Fault detection and classification using artificial neural networks, IFAC-PapersOnLine, 51 (2018), 470–475. https://doi.org/10.1016/j.ifacol.2018.09.380 doi: 10.1016/j.ifacol.2018.09.380
[100]	P. Agrawal, P. Jayaswal, Diagnosis and classifications of bearing faults using artificial neural network and support vector machine, J. Inst. Eng. (India): Ser. C, 101 (2020), 61–72. https://doi.org/10.1007/s40032-019-00519-9 doi: 10.1007/s40032-019-00519-9
[101]	Y. LeCun, B. E. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. E. Hubbard, et al., Handwritten digit recognition with a back-propagation network, in Advances in Neural Information Processing Systems, (1990), 396–404.
[102]	T. Chen, Y. Sun, T. H. Li, A semi-parametric estimation method for the quantile spectrum with an application to earthquake classification using convolutional neural network, Comput. Stat. Data Anal., 154 (2021), 107069. https://doi.org/10.1016/j.csda.2020.107069 doi: 10.1016/j.csda.2020.107069
[103]	F. Perla, R. Richman, S. Scognamiglio, M. V. Wüthrich, Time-series forecasting of mortality rates using deep learning, Scand. Actuarial J., 2021 (2021), 1–27. https://doi.org/10.1080/03461238.2020.1867232 doi: 10.1080/03461238.2020.1867232
[104]	G. Ciaburro, G. Iannace, V. Puyana-Romero, A. Trematerra, A comparison between numerical simulation models for the prediction of acoustic behavior of giant reeds shredded, Appl. Sci., 10 (2020), 6881. https://doi.org/10.3390/app10196881 doi: 10.3390/app10196881
[105]	C. Yildiz, H. Acikgoz, D. Korkmaz, U. Budak, An improved residual-based convolutional neural network for very short-term wind power forecasting, Energy Convers. Manage., 228 (2021), 113731. https://doi.org/10.1016/j.enconman.2020.113731 doi: 10.1016/j.enconman.2020.113731
[106]	G. Ciaburro, Sound event detection in underground parking garage using convolutional neural network, Big Data Cognit. Comput., 4 (2020), 20. https://doi.org/10.3390/bdcc4030020 doi: 10.3390/bdcc4030020
[107]	R. Ye, Q. Dai, Implementing transfer learning across different datasets for time series forecasting, Pattern Recognit., 109 (2021), 107617. https://doi.org/10.1016/j.patcog.2020.107617 doi: 10.1016/j.patcog.2020.107617
[108]	J. Han, L. Shi, Q. Yang, K. Huang, Y. Zha, J. Yu, Real-time detection of rice phenology through convolutional neural network using handheld camera images, Precis. Agric., 22 (2021), 154–178. https://doi.org/10.1016/j.patcog.2020.107617 doi: 10.1016/j.patcog.2020.107617
[109]	G. Ciaburro, G. Iannace, Improving smart cities safety using sound events detection based on deep neural network algorithms, Informatics, 7 (2020), 23. https://doi.org/10.3390/informatics7030023 doi: 10.3390/informatics7030023
[110]	L. Wen, X. Li, L. Gao, Y. Zhang, A new convolutional neural network-based data-driven fault diagnosis method, IEEE Trans. Ind. Electron., 65 (2017), 5990–5998. https://doi.org/10.1109/TIE.2017.2774777 doi: 10.1109/TIE.2017.2774777
[111]	Y. LeCun, LeNet-5, Convolutional Neural Networks, 2015, Available from: http://yann.lecun.com/exdb/lenet/, Accessed date: 28 April 2022.
[112]	H. Wu, J. Zhao, Deep convolutional neural network model based chemical process fault diagnosis, Comput. Chem. Eng., 115 (2018), 185–197. https://doi.org/10.1016/j.compchemeng.2018.04.009 doi: 10.1016/j.compchemeng.2018.04.009
[113]	W. Zhang, C. Li, G. Peng, Y. Chen, Z. Zhang, A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load, Mech. Syst. Sig. Process., 100 (2018), 439–453. https://doi.org/10.1016/j.ymssp.2017.06.022 doi: 10.1016/j.ymssp.2017.06.022
[114]	L. Jing, M. Zhao, P. Li, X. Xu, A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox, Measurement, 111 (2017), 1–10. https://doi.org/10.1016/j.measurement.2017.07.017 doi: 10.1016/j.measurement.2017.07.017
[115]	Z. Chen, C. Li, R. V. Sanchez, Gearbox fault identification and classification with convolutional neural networks, Shock Vib., 2015 (2015). https://doi.org/10.1155/2015/390134 doi: 10.1155/2015/390134
[116]	X. Guo, L. Chen, C. Shen, Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis, Measurement, 93 (2016), 490–502. https://doi.org/10.1016/j.measurement.2016.07.054 doi: 10.1016/j.measurement.2016.07.054
[117]	O. Janssens, V. Slavkovikj, B. Vervisch, K. Stockman, M. Loccufier, S. Verstockt, et al., Convolutional neural network based fault detection for rotating machinery, J. Sound Vib., 377 (2016), 331–345. https://doi.org/10.1016/j.jsv.2016.05.027 doi: 10.1016/j.jsv.2016.05.027
[118]	W. Zhang, G. Peng, C. Li, Y. Chen, Z. Zhang, A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals, Sensors, 17 (2017), 425. https://doi.org/10.3390/s17020425 doi: 10.3390/s17020425
[119]	Y. Li, N. Wang, J. Shi, X. Hou, J. Liu, Adaptive batch normalization for practical domain adaptation, Pattern Recognit., 80 (2018), 109–117. https://doi.org/10.1016/j.patcog.2018.03.005 doi: 10.1016/j.patcog.2018.03.005
[120]	T. Ince, S. Kiranyaz, L. Eren, M. Askar, M. Gabbouj, Real-time motor fault detection by 1-D convolutional neural networks, IEEE Trans. Ind. Electron., 63 (2016), 7067–7075. https://doi.org/10.1109/TIE.2016.2582729 doi: 10.1109/TIE.2016.2582729
[121]	Y. Zhang, K. Xing, R. Bai, D. Sun, Z. Meng, An enhanced convolutional neural network for bearing fault diagnosis based on time-frequency image, Measurement, 157 (2020), 107667. https://doi.org/10.1016/j.measurement.2020.107667 doi: 10.1016/j.measurement.2020.107667
[122]	M. Azamfar, J. Singh, I. Bravo-Imaz, J. Lee, . Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis, Mech. Syst. Sig. Process., 144 (2020), 106861. https://doi.org/10.1016/j.ymssp.2020.106861 doi: 10.1016/j.ymssp.2020.106861
[123]	Q. Zhou, Y. Li, Y. Tian, L. Jiang, A novel method based on nonlinear auto-regression neural network and convolutional neural network for imbalanced fault diagnosis of rotating machinery, Measurement, 161 (2020), 107880. https://doi.org/10.1016/j.measurement.2020.107880 doi: 10.1016/j.measurement.2020.107880
[124]	K. Zhang, J. Chen, T. Zhang, Z. Zhou, A compact convolutional neural network augmented with multiscale feature extraction of acquired monitoring data for mechanical intelligent fault diagnosis, J. Manuf. Syst., 55 (2020), 273–284. https://doi.org/10.1016/j.jmsy.2020.04.016 doi: 10.1016/j.jmsy.2020.04.016
[125]	Y. Li, X. Du, F. Wan, X. Wang, H. Yu, Rotating machinery fault diagnosis based on convolutional neural network and infrared thermal imaging, Chin. J. Aeronaut., 33 (2020), 427–438. https://doi.org/10.1016/j.cja.2019.08.014 doi: 10.1016/j.cja.2019.08.014
[126]	Z. Chen, A. Mauricio, W. Li, K. Gryllias, A deep learning method for bearing fault diagnosis based on cyclic spectral coherence and convolutional neural networks, Mech. Syst. Sig. Process., 140 (2020), 106683. https://doi.org/10.1016/j.ymssp.2020.106683 doi: 10.1016/j.ymssp.2020.106683
[127]	J. Antoni, Cyclic spectral analysis in practice, Mech. Syst. Sig. Process., 21 (2007), 597–630. https://doi.org/10.1016/j.ymssp.2006.08.007 doi: 10.1016/j.ymssp.2006.08.007
[128]	D. Zhou, Q. Yao, H. Wu, S. Ma, H. Zhang, Fault diagnosis of gas turbine based on partly interpretable convolutional neural networks, Energy, 200 (2020), 117467. https://doi.org/10.1016/j.energy.2020.117467 doi: 10.1016/j.energy.2020.117467
[129]	T. Chen, T. He, M. Benesty, V. Khotilovich, Y. Tang, H. Cho, Xgboost: extreme gradient boosting, R package version 0.4-2, 1 (2015), 1–4.
[130]	X. Li, J. Zheng, M. Li, W. Ma, Y. Hu, Frequency-domain fusing convolutional neural network: A unified architecture improving effect of domain adaptation for fault diagnosis, Sensors, 21 (2021), 450. https://doi.org/10.3390/s21020450 doi: 10.3390/s21020450
[131]	C. C. Chen, Z. Liu, G. Yang, C. C. Wu, Q. Ye, An improved fault diagnosis using 1D-convolutional neural network model, electronics, 10 (2021), 59. https://doi.org/10.3390/electronics10010059
[132]	Y. Liu, Y. Yang, T. Feng, Y. Sun, X. Zhang, Research on rotating machinery fault diagnosis method based on energy spectrum matrix and adaptive convolutional neural network, Processes, 9 (2021), 69. https://doi.org/10.3390/pr9010069 doi: 10.3390/pr9010069
[133]	D. T. Hoang, X. T. Tran, M. Van, H. J. Kang, A deep neural network-based feature fusion for bearing fault diagnosis, Sensors, 21 (2021), 244. https://doi.org/10.3390/s21010244 doi: 10.3390/s21010244
[134]	T. Mikolov, M. Karafiát, L. Burget, J. Černocký, S. Khudanpur, Recurrent neural network based language model, in Eleventh Annual Conference of the International Speech Communication Association, 2010.
[135]	K. Gregor, I. Danihelka, A. Graves, D. Rezende, D. Wierstra, Draw: A recurrent neural network for image generation, in International Conference on Machine Learning (PMLR), 37 (2015), 1462–1471.
[136]	T. Mikolov, G. Zweig, Context dependent recurrent neural network language model, in 2012 IEEE Spoken Language Technology Workshop (SLT), IEEE, (2012), 234–239. https://doi.org/10.1109/SLT.2012.6424228
[137]	G. Ciaburro, Time series data analysis using deep learning methods for smart cities monitoring, in Big Data Intelligence for Smart Applications, Springer, Cham, (2022), 93–116. https://doi.org/10.1007/978-3-030-87954-9_4
[138]	H. Sak, A. W. Senior, F. Beaufays, Long short-term memory recurrent neural network architectures for large scale acoustic modeling, Interspeech, (2014), 338–342. https://doi.org/10.21437/Interspeech.2014-80 doi: 10.21437/Interspeech.2014-80
[139]	J. Kim, J. Kim, H. L. T. Thu, H. Kim, Long short term memory recurrent neural network classifier for intrusion detection, in 2016 International Conference on Platform Technology and Service (PlatCon), IEEE, (2016), 1–5. https://doi.org/10.1109/PlatCon.2016.7456805
[140]	Y. Tian, L. Pan, Predicting short-term traffic flow by long short-term memory recurrent neural network, in 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), IEEE, (2015), 153–158. https://doi.org/10.1109/SmartCity.2015.63
[141]	H. Jiang, X. Li, H. Shao, K. Zhao, Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network, Meas. Sci. Technol., 29 (2018), 065107. https://doi.org/10.1088/1361-6501/aab945 doi: 10.1088/1361-6501/aab945
[142]	T. De Bruin, K. Verbert, R. Babuška, Railway track circuit fault diagnosis using recurrent neural networks, IEEE Trans. Neural Networks Learn. Syst., 28 (2016), 523–533. https://doi.org/10.1109/TNNLS.2016.2551940 doi: 10.1109/TNNLS.2016.2551940
[143]	R. Yang, M. Huang, Q. Lu, M. Zhong, Rotating machinery fault diagnosis using long-short-term memory recurrent neural network, IFAC-PapersOnLine, 51 (2018), 228–232. https://doi.org/10.1016/j.ifacol.2018.09.582 doi: 10.1016/j.ifacol.2018.09.582
[144]	H. A. Talebi, K. Khorasani, S. Tafazoli, A recurrent neural-network-based sensor and actuator fault detection and isolation for nonlinear systems with application to the satellite's attitude control subsystem, IEEE Trans. Neural Networks, 20 (2008), 45–60. https://doi.org/10.1109/TNN.2008.2004373 doi: 10.1109/TNN.2008.2004373
[145]	S. Zhang, K. Bi, T. Qiu, Bidirectional recurrent neural network-based chemical process fault diagnosis, Ind. Eng. Chem. Res., 59 (2019), 824–834. https://doi.org/10.1021/acs.iecr.9b05885 doi: 10.1021/acs.iecr.9b05885
[146]	Z. An, S. Li, J. Wang, X. Jiang, A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network, ISA Trans., 100 (2020), 155–170. https://doi.org/10.1016/j.isatra.2019.11.010 doi: 10.1016/j.isatra.2019.11.010
[147]	W. Liu, P. Guo, L. Ye, A low-delay lightweight recurrent neural network (LLRNN) for rotating machinery fault diagnosis, Sensors, 19 (2019), 3109. https://doi.org/10.3390/s19143109 doi: 10.3390/s19143109
[148]	K. Liang, N. Qin, D. Huang, Y. Fu, Convolutional recurrent neural network for fault diagnosis of high-speed train bogie, Complexity, 2018 (2018). https://doi.org/10.1155/2018/4501952 doi: 10.1155/2018/4501952
[149]	D. Huang, Y. Fu, N. Qin, S. Gao, Fault diagnosis of high-speed train bogie based on LSTM neural network, Sci. Chin. Inf. Sci., 64 (2021), 1–3. https://doi.org/10.1007/s11432-018-9543-8 doi: 10.1007/s11432-018-9543-8
[150]	H. Shahnazari, P. Mhaskar, J. M. House, T. I. Salsbury, Modeling and fault diagnosis design for HVAC systems using recurrent neural networks, Comput. Chem. Eng., 126 (2019), 189–203. https://doi.org/10.1016/j.compchemeng.2019.04.011 doi: 10.1016/j.compchemeng.2019.04.011
[151]	H. Shahnazari, Fault diagnosis of nonlinear systems using recurrent neural networks, Chem. Eng. Res. Des., 153 (2020), 233–245. https://doi.org/10.1016/j.cherd.2019.09.026 doi: 10.1016/j.cherd.2019.09.026
[152]	L. Guo, N. Li, F. Jia, Y. Lei, J. Lin, A recurrent neural network based health indicator for remaining useful life prediction of bearings, Neurocomputing, 240 (2017), 98–109. https://doi.org/10.1016/j.neucom.2017.02.045 doi: 10.1016/j.neucom.2017.02.045
[153]	M. Yuan, Y. Wu, L. Lin, Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network, in 2016 IEEE international conference on aircraft utility systems (AUS), IEEE, (2016), 135–140. https://doi.org/10.1109/AUS.2016.7748035
[154]	Z. Wu, H. Jiang, K. Zhao, X. Li, An adaptive deep transfer learning method for bearing fault diagnosis, Measurement, 151 (2020), 107227. https://doi.org/10.1016/j.measurement.2019.107227 doi: 10.1016/j.measurement.2019.107227
[155]	A. Yin, Y. Yan, Z. Zhang, C. Li, R. V. Sánchez, Fault diagnosis of wind turbine gearbox based on the optimized LSTM neural network with cosine loss, Sensors, 20 (2020), 2339. https://doi.org/10.3390/s20082339 doi: 10.3390/s20082339
[156]	M. Xia, X. Zheng, M. Imran, M. Shoaib, Data-driven prognosis method using hybrid deep recurrent neural network, Appl. Soft Comput., 93 (2020), 106351. https://doi.org/10.1016/j.asoc.2020.106351 doi: 10.1016/j.asoc.2020.106351
[157]	Z. Wang, Y. Dong, W. Liu, Z. Ma, A novel fault diagnosis approach for chillers based on 1-D convolutional neural network and gated recurrent unit, Sensors, 20 (2020), 2458. https://doi.org/10.3390/s20092458 doi: 10.3390/s20092458
[158]	R. Salakhutdinov, Learning deep generative models, Annu. Rev. Stat. Appl., 2 (2015), 361–385. https://doi.org/10.1146/annurev-statistics-010814-020120 doi: 10.1146/annurev-statistics-010814-020120
[159]	A. Gupta, A. Agarwal, P. Singh, P. Rai, A deep generative framework for paraphrase generation, in Proceedings of the AAAI Conference on Artificial Intelligence, 32 (2018). https://doi.org/10.1609/aaai.v32i1.11956
[160]	I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, et al., Generative adversarial networks, 2014, preprint, arXiv: 1406.2661.
[161]	L. Metz, B. Poole, D. Pfau, J. Sohl-Dickstein, Unrolled generative adversarial networks, 2016, preprint, arXiv: 1611.02163.
[162]	G. Ciaburro, Security systems for smart cities based on acoustic sensors and machine learning applications, in Machine Intelligence and Data Analytics for Sustainable Future Smart Cities, Springer, Cham, (2021), 369–393. https://doi.org/10.1007/978-3-030-72065-0_20
[163]	X. Hou, L. Shen, K. Sun, G. Qiu, Deep feature consistent variational autoencoder, in 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), IEEE, (2017), 1133–1141. https://doi.org/10.1109/WACV.2017.131
[164]	M. J. Kusner, B. Paige, J. M. Hernández-Lobato, Grammar variational autoencoder, in International Conference on Machine Learning (PMLR), 70 (2017), 1945–1954.
[165]	Y. Pu, Z. Gan, R. Henao, X. Yuan, C. Li, A. Stevens, et al., Variational autoencoder for deep learning of images, labels and captions, 2016, preprint, arXiv: 1609.08976.
[166]	A. Makhzani, J. Shlens, N. Jaitly, I. Goodfellow, B. Frey, Adversarial autoencoders, 2015, preprint, arXiv: 1511.05644.
[167]	Z. Zhang, Y. Song, H. Qi, Age progression/regression by conditional adversarial autoencoder, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (2017), 5810–5818. https://doi.org/10.1109/CVPR.2017.463
[168]	H. Liu, J. Zhou, Y. Xu, Y. Zheng, X. Peng, W. Jiang, Unsupervised fault diagnosis of rolling bearings using a deep neural network based on generative adversarial networks, Neurocomputing, 315 (2018), 412–424. https://doi.org/10.1016/j.neucom.2018.07.034 doi: 10.1016/j.neucom.2018.07.034
[169]	S. Shao, P. Wang, R. Yan, Generative adversarial networks for data augmentation in machine fault diagnosis, Comput. Ind., 106 (2019), 85–93. https://doi.org/10.1016/j.compind.2019.01.001 doi: 10.1016/j.compind.2019.01.001
[170]	W. Zhang, X. Li, X. D. Jia, H. Ma, Z. Luo, X. Li, Machinery fault diagnosis with imbalanced data using deep generative adversarial networks, Measurement, 152 (2020), 107377. https://doi.org/10.1016/j.measurement.2019.107377 doi: 10.1016/j.measurement.2019.107377
[171]	Z. Wang, J. Wang, Y. Wang, An intelligent diagnosis scheme based on generative adversarial learning deep neural networks and its application to planetary gearbox fault pattern recognition, Neurocomputing, 310 (2018), 213–222. https://doi.org/10.1016/j.neucom.2018.05.024 doi: 10.1016/j.neucom.2018.05.024
[172]	P. Vincent, H. Larochelle, I. Lajoie, Y. Bengio, P. A. Manzagol, L. Bottou, Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion, J. Mach. Learn. Res., 11 (2010), 3371–3408.
[173]	Q. Li, L. Chen, C. Shen, B. Yang, Z. Zhu, Enhanced generative adversarial networks for fault diagnosis of rotating machinery with imbalanced data, Meas. Sci. Technol., 30 (2019), 115005. https://doi.org/10.1088/1361-6501/ab3072 doi: 10.1088/1361-6501/ab3072
[174]	J. Wang, S. Li, B. Han, Z. An, H. Bao, S. Ji, Generalization of deep neural networks for imbalanced fault classification of machinery using generative adversarial networks, IEEE Access, 7 (2019), 111168–111180. https://doi.org/10.1109/ACCESS.2019.2924003 doi: 10.1109/ACCESS.2019.2924003
[175]	Y. Xie, T. Zhang, Imbalanced learning for fault diagnosis problem of rotating machinery based on generative adversarial networks, in 2018 37th Chinese Control Conference (CCC), IEEE, (2018), 6017–6022. https://doi.org/10.23919/ChiCC.2018.8483334
[176]	C. Zhong, K. Yan, Y. Dai, N. Jin, B. Lou, Energy efficiency solutions for buildings: Automated fault diagnosis of air handling units using generative adversarial networks, Energies, 12 (2019), 527. https://doi.org/10.3390/en12030527 doi: 10.3390/en12030527
[177]	D. Zhao, S. Liu, D. Gu, X. Sun, L. Wang, Y. Wei, et al., Enhanced data-driven fault diagnosis for machines with small and unbalanced data based on variational auto-encoder, Meas. Sci. Technol., 31 (2019), 035004. https://doi.org/10.1088/1361-6501/ab55f8 doi: 10.1088/1361-6501/ab55f8
[178]	J. An, S. Cho, Variational autoencoder based anomaly detection using reconstruction probability, Spec. Lect. IE, 2 (2015), 1–18.
[179]	G. San Martin, E. López Droguett, V. Meruane, M. das Chagas Moura, Deep variational auto-encoders: A promising tool for dimensionality reduction and ball bearing elements fault diagnosis, Struct. Health Monit., 18 (2019), 1092–1128. https://doi.org/10.1177/1475921718788299 doi: 10.1177/1475921718788299
[180]	Y. Kawachi, Y. Koizumi, N. Harada, Complementary set variational autoencoder for supervised anomaly detection, in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, (2018), 2366–2370. https://doi.org/10.1109/ICASSP.2018.8462181
[181]	D. Park, Y. Hoshi, C. C. Kemp, A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder, IEEE Rob. Autom. Lett., 3 (2018), 1544–1551. https://doi.org/10.1109/LRA.2018.2801475 doi: 10.1109/LRA.2018.2801475
[182]	S. Lee, M. Kwak, K. L. Tsui, S. B. Kim, Process monitoring using variational autoencoder for high-dimensional nonlinear processes, Eng. Appl. Artif. Intell., 83 (2019), 13–27. https://doi.org/10.1016/j.engappai.2019.04.013 doi: 10.1016/j.engappai.2019.04.013
[183]	K. Wang, M. G. Forbes, B. Gopaluni, J. Chen, Z. Song, Systematic development of a new variational autoencoder model based on uncertain data for monitoring nonlinear processes, IEEE Access, 7 (2019), 22554–22565. https://doi.org/10.1109/ACCESS.2019.2894764 doi: 10.1109/ACCESS.2019.2894764
[184]	G. Ping, J. Chen, T. Pan, J. Pan, Degradation feature extraction using multi-source monitoring data via logarithmic normal distribution based variational auto-encoder, Comput. Ind., 109 (2019), 72–82. https://doi.org/10.1016/j.compind.2019.04.013 doi: 10.1016/j.compind.2019.04.013
[185]	J. Wu, Z. Zhao, C. Sun, R. Yan, X. Chen, Fault-attention generative probabilistic adversarial autoencoder for machine anomaly detection, IEEE Trans. Ind. Inf., 16 (2020), 7479–7488. https://doi.org/10.1109/TⅡ.2020.2976752 doi: 10.1109/TⅡ.2020.2976752
[186]	G. Ciaburro, An ensemble classifier approach for thyroid disease diagnosis using the AdaBoostM algorithm, in Machine Learning, Big Data, and IoT for Medical Informatics, Academic Press, (2021), 365–387. https://doi.org/10.1016/B978-0-12-821777-1.00002-1
[187]	Z. Gao, C. Cecati, S. X. Ding, A survey of fault diagnosis and fault-tolerant techniques—Part I: fault diagnosis with model-based and signal-based approaches, IEEE Trans. Ind. Electron., 62 (2015), 3757–3767. https://doi.org/10.1109/TIE.2015.2417501 doi: 10.1109/TIE.2015.2417501
[188]	M. Djeziri, O. Djedidi, S. Benmoussa, M. Bendahan, J. L. Seguin, Failure prognosis based on relevant measurements identification and data-driven trend-modeling: Application to a fuel cell system, Processes, 9 (2021), 328. https://doi.org/10.3390/pr9020328 doi: 10.3390/pr9020328
[189]	M. Aliramezani, C. R. Koch, M. Shahbakhti, Modeling, diagnostics, optimization, and control of internal combustion engines via modern machine learning techniques: A review and future directions, Prog. Energy Combust. Sci., 88 (2022), 100967. https://doi.org/10.1016/j.pecs.2021.100967 doi: 10.1016/j.pecs.2021.100967
[190]	D. Passos, P. Mishra, A tutorial on automatic hyperparameter tuning of deep spectral modelling for regression and classification tasks, Chemom. Intell. Lab. Syst., 233 (2022), 104520. https://doi.org/10.1016/j.chemolab.2022.104520 doi: 10.1016/j.chemolab.2022.104520
[191]	A. Zakaria, F. B. Ismail, M. H. Lipu, M. A. Hannan, Uncertainty models for stochastic optimization in renewable energy applications, Renewable Energy, 145 (2020), 1543–1571. https://doi.org/10.1016/j.renene.2019.07.081 doi: 10.1016/j.renene.2019.07.081
[192]	M. H. Lin, J. F. Tsai, C. S. Yu, A review of deterministic optimization methods in engineering and management, Math. Probl. Eng., 2012 (2012). https://doi.org/10.1155/2012/756023 doi: 10.1155/2012/756023

This article has been cited by:

1.	Wenhui Li, Qi Zhu, Fenghua Wen, Normaziah Mohd Nor, The evolution of day-of-the-week and the implications in crude oil market, 2022, 106, 01409883, 105817, 10.1016/j.eneco.2022.105817
2.	Weiwen Li, Yijiang Zhou, Xingan Dai, Fang Hu, Evaluation of Rural Tourism Landscape Resources in Terms of Carbon Neutrality and Rural Revitalization, 2022, 14, 2071-1050, 2863, 10.3390/su14052863
3.	Juan Meng, Sisi Hu, Bin Mo, Dynamic tail dependence on China's carbon market and EU carbon market, 2021, 1, 2769-2140, 393, 10.3934/DSFE.2021021
4.	Liu Hong, Li Lin, Xiaohang Ren, Evaluation of Interest Balance of Low-carbon Collaborative Innovation Subjects, 2022, 2022, 1563-5147, 1, 10.1155/2022/8270712
5.	Mei-Jing Zhou, Jian-Bai Huang, Jin-Yu Chen, Time and frequency spillovers between political risk and the stock returns of China's rare earths, 2022, 75, 03014207, 102464, 10.1016/j.resourpol.2021.102464
6.	Xiong Wang, Jingyao Li, Xiaohang Ren, Ruijun Bu, Fredj Jawadi, Economic policy uncertainty and dynamic correlations in energy markets: Assessment and solutions, 2023, 117, 01409883, 106475, 10.1016/j.eneco.2022.106475
7.	Zi-sheng Ouyang, Meng-tian Liu, Su-su Huang, Ting Yao, Does the source of oil price shocks matter for the systemic risk?, 2022, 109, 01409883, 105958, 10.1016/j.eneco.2022.105958
8.	Min Zhou, Xiaoqun Liu, Overnight-Intraday Mispricing of Chinese Energy Stocks: A View from Financial Anomalies, 2022, 9, 2296-598X, 10.3389/fenrg.2021.807881
9.	Xu Gong, Yi Sun, Zhili Du, Geopolitical risk and China's oil security, 2022, 163, 03014215, 112856, 10.1016/j.enpol.2022.112856
10.	Xiaowei Lin, Zijun Ding, Aihua Chen, Huaizhi Shi, Internal whistleblowing and stock price crash risk, 2022, 84, 10575219, 102378, 10.1016/j.irfa.2022.102378
11.	Isabelle Cadoret, Jacques Minlend, Tovonony Razafindrabe, Uncertainty diffusion across commodity markets, 2022, 0003-6846, 1, 10.1080/00036846.2022.2129041
12.	YUNXIA TAN, HAFEEZ ULLAH, XIAOYUE CHENG, FAN ZHANG, ZHUQUAN WANG, MULTIDIMENSIONAL PERSPECTIVE OF FINANCIAL RISK ANALYSIS: EVIDENCE FROM CHINA, 2022, 0217-5908, 1, 10.1142/S0217590822500680
13.	Fenghua Wen, Minzhi Zhang, Jihong Xiao, Wei Yue, The impact of oil price shocks on the risk-return relation in the Chinese stock market, 2022, 47, 15446123, 102788, 10.1016/j.frl.2022.102788
14.	Xu Gong, Jun Xu, Geopolitical risk and dynamic connectedness between commodity markets, 2022, 110, 01409883, 106028, 10.1016/j.eneco.2022.106028
15.	Lin Chen, Fenghua Wen, Yun Zhang, Xiao Miao, Oil supply expectations and corporate social responsibility, 2023, 87, 10575219, 102638, 10.1016/j.irfa.2023.102638
16.	Wuyi Ye, Chenglong Hu, Ranran Guo, Tail risk network of Chinese green-related stocks market, 2024, 67, 15446123, 105802, 10.1016/j.frl.2024.105802
17.	Marco Tronzano, What Drives Asset Returns Comovements? Some Empirical Evidence from US Dollar and Global Stock Returns (2000–2023), 2024, 17, 1911-8074, 167, 10.3390/jrfm17040167
18.	Raghav Goyal, Sandro Steinbach, Edouard Romeo Mensah, The Interplay of Geopolitics and Agricultural Commodity Prices, 2024, 1556-5068, 10.2139/ssrn.4888749
19.	Ilyes Abid, Abderrazak Dhaoui, Olfa Kaabia, Salma Tarchella, Geopolitical risk on energy, agriculture, livestock, precious and industrial metals: New insights from a Markov Switching model, 2023, 85, 03014207, 103925, 10.1016/j.resourpol.2023.103925
20.	Hiroyuki Imai, Jong-Min Kim, Foreign investors, rebalancing trades, and increases in U.S.-Japan stock market correlations, 2024, 56, 0003-6846, 5634, 10.1080/00036846.2023.2257929
21.	Raghav Goyal, Edouard Mensah, Sandro Steinbach, The interplay of geopolitics and agricultural commodity prices, 2024, 46, 2040-5790, 1533, 10.1002/aepp.13481
22.	Nasir Khan, Sami Mejri, Shawkat Hammoudeh, How do global commodities react to increasing geopolitical risks? New insights into the Russia-Ukraine and Palestine-Israel conflicts, 2024, 138, 01409883, 107812, 10.1016/j.eneco.2024.107812
23.	Kelleb Mloyi, Edson Vengesai, The impact of global risk aversion and domestic macroeconomic factors on the dynamic conditional correlations of South African financial markets, 2024, 12, 2332-2039, 10.1080/23322039.2024.2431543
24.	Najib Shrydeh, Mohammed Shahateet, Suleiman Mohammad, Mohammad Sumadi, A revised approach to testing for asymmetric intermarket spillover effects, 2025, 13, 2332-2039, 10.1080/23322039.2024.2440440

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)