1.
Introduction
The dramatic effect of infectious diseases in health, social and economic aspects of human society is highlighted by epidemics and most notable the recent COVID-19 pandemic. In this respect, mathematical modeling is a valuable tool (ⅰ) to understand the transmission and impact of a disease to a population (ⅱ) to make predictions for a disease future evolvement and (ⅲ) to develop strategies for controlling a disease (e.g. by enforcing social distances or by vaccination). The corresponding models can be classified to zero-dimensional ones (no spatial consideration) and to distributed ones (with spatial consideration). The distributed models in most of the cases focus on pattern formation (e.g., network modeling [1,2,3]) but also there are several models which assume the spatial transmission of a disease as a diffusion process [4]. A general review of mathematical modeling of epidemics can be found in [5] and [6] whereas a very interesting and comprehensive work in spatial modeling of the transmission in terms of Chemical Reaction Engineering can be found in [7]. In the present work the discussion is restricted to zero dimensional models (i.e. spatially well-mixed population). A different approach than that introduced by Chemical Reaction Engineering in [7] for the homogeneous problem is proposed here.
Zero dimensional models can be classified into three categories. The first category includes all models based on a system of Ordinary Differential Equations (ODEs). This type of modeling is the most extensively used in epidemiology literature and practice [8], (i.e. the well-known SIR model standing for Susceptible, Infected and Recovered individuals). These models use time as the independent variable and as dependent variables employ the different possible states of individuals with respect to the disease. Several extensions of the model by considering additional states of individuals can be found in literature. A few of such models are the SEIR, SEIRS, SIRS, SEI, SEIS, SIS, SEIRIS, where E denotes the Exposed individuals [9,10,11]. Another extension was made by considering Asymptomatic, Hospitalized and Dead individuals [7]. Several additional states like classification of the infected and recovered individuals depending on their response to the disease have been also considered. Consideration of reinfection leads to the addition of whole new branches to the models repeating the states of the first infection [10]. A slight modification with respect to the ODEs models is the time delayed models accounting for a time-delay between the infection of an individual and the time to become infectious [12,13].
The second category of the zero-dimensional epidemic models is the age-structured models. This type of models classifies the population according to age. Such models in the case that infection dynamics are fast with respect to the population ageing time scale, consist of ordinary differential equations with dependent variables distributed among age classes [14]. However, for time scales comparable to population age, the mathematical model consists of hyperbolic type partial differential equations having as continuous dependent variable the age of individuals [15]. A detailed mathematical analysis and a review on this type of models (which are also known as demographic models) can be found in [16].
The third category of the zero-dimensional epidemic models refers to time scales much smaller than the age of population and accounts for variation in the transmission behavior depending on the time of infection of each individual. These models are much more powerful than those employing a single time delay since they permit calculation of the complete distribution of infection age of the infected population [17]. Detailed mathematical analysis of these type of models can be found in several literature sources (e.g. [18]).
Parameters in all categories of models are rate constants. These can be assumed to vary across a population in a discrete (compartmentalization) way [19,20] or in a continuous way [21]. Kinetic rate expressions are common in many fields of medical, industrial, and engineering research to describe interactions between physical conditions and interferences originating from multiphase dependencies [22]. Of course, in the general case the rate constants are time dependent, and this dependency must be determined by fitting to experimental (empirical) data. Very sophisticated approaches exist for this purpose [23].
The above analysis refers to classical developments in epidemiological models field. The recent outbreak of COVID-19 yielded a wealth of empirical data for disease spreading which combined with significant funding led to the development of many new epidemiological models [24]. In [24] 100 recent papers (published in the first 12 months of emergency) on epidemiological models are reviewed. A more general review on mathematical modeling related to COVID-19 covering not only epidemiology but also drug repurposing and vaccine design can be found in [25]. A comprehensive view point on the COVID-19 related mathematical modeling is given in [26].
The extensive application of quarantine and the social distancing measures applied for first time in history at this extend motivated the creation of a new generation of epidemiological models. Some of them (belonging to class (ⅰ) of the spatially homogeneous models) are reviewed here. The SVIAKUR model and its generalization employing fractional derivatives is developed in [27]. In this case, V, A, K, U stands for Vulnerable, Asymptomatics, Quarantined and Under treatment individuals, respectively. A large number of models has been developed, mathematically analyzed and calibrated using data from several regions of India. Among these we refer to the SAIU [28], SAIUQR [29] and SEAIHR [30] models, where U, Q, H designate Unreported symptomatic, Quarantined and Hospitalized individuals, respectively. It is noted that in the presence of A and U, then I includes only reported symptomatic individuals. Somewhat more sophisticated are the SSqAIIqR [31] and SEIs, Ia, Q, Ah, Al, H [32] models where Sq, Iq, Is, Ia, Ah, Al are the Susceptible quarantined, Infected isolated, Infected symptomatic, Infected asymptomatic, Highly Active aware and Less Active aware individuals. A very important extension of the above models is the incorporation of the effect of media awareness [33] and social media advertisement [34]. An excellent example of using optimal control theory to extract the optimal intervention strategies in terms of efficiency and cost can be found in [35]. An extension of the above described deterministic epidemiological models arises by adding to them stochastic terms and transforming them to the so called stochastic epidemic models [36,37].
In the present work an alternative progressive way to model the spread of an epidemic is explored. The key feature is that the transition time from the state of infection to the state of recovery is not dictated by a rate coefficient, but it is a property assigned to every individual (prescribed by his organic and physical conditions). Apart from this transition time, other response features of individuals to the disease can also be handled in this way, defining a multidimensional probability function of these features among the population. The computation of the evolution of this function in time is the main scope of the proposed framework. Despite the simplicity of the idea and of the multitude of disease spread models in mathematical biology, it appears that this idea has never been exploited/adopted before.
The main motivation of the proposed approach is the need to overcome the increasing number of kinetic constants appearing in the typical ODEs epidemiological models and replace them by probability density functions over the population. So, issues such as severity of the disease, duration of the disease, amount of virus in stools etc can be more efficiently and sophisticated parameterized than simply increasing the number of ODEs and adding rate coefficients to the ODEs model. A further motivation is the need for a model where vaccination appears as a modifier of the severity of the disease distribution and not as a means of transition from Susceptible to Recovered compartments being typically the case in ODEs models.
Based on the above idea, a model that is mathematically and numerically simple as the conventional ODEs models is developed. This new model admits the calculation of infection age distribution and of properties variability across the population whereas it avoids the explicit reformulation and addition of dependent variables required for each extension of the classical ODEs model.
The structure of the present work is the following: At first (Sections 2.1, 2.2) the modification of the standard SIR model to account for an infection age distribution with sharp cut-off aspect is illustrated. In the next section (Section 2.3), the new model is presented using a top-bottom approach; from the more general with generalized coordinates describing the state of the population to the more specific situation of a set of three completely correlated variables based on their significance. Finally, several indicative results are presented to demonstrate the features of the new model.
2.
Model formulation
2.1. The standard SIR model
The new model is presented in a stepwise way focusing on novel characteristics. The original SIR model divides the population in Susceptible, Infected and Recovered individuals (their number is denoted as S, I, R, respectively). The evolution equations for the three populations are
where t is time, N is the total population number (N = S + I + R) and cs, cI are model parameters.
In chemical reaction terms the above scheme can be represented by the reaction S→I→R where the first from the two consecutive reactions is an autocatalytic one (i.e. its rate depends not only on the reactant but on the product, too [38]). The meaning of the parameters cS, cI has been extensively discussed [5,6] so it will not be repeated here.
Let us attempt to further simplify the mathematical problem. It is observed that R can be found by postprocessing of I, i.e., there is one way coupling between R and variables S and I. This means that only the first two equations of the system need to be solved at a first stage. In addition, if a weak spread of the disease (in terms of fraction of the total population i.e. I + R << N) is considered, the value of S can be assumed to be constant and equal to N (the term "weak spread" henceforth implies this situation). In this case the evolution of infection can be described by the simple equation
which leads to exponential increase or decrease of I depending on the sign of the quantity cs-cI (or equivalently by the relative value of constants cs, cI). A further simplification refers to the period of no disease spread (complete lockdown or hospitalized patients). Then the model describes just the recovery process and it can be written as
2.2. Introducing infection age with sharp cut-off
Let us introduce here the concept of infection age to the model development. The governing equation for pure recovery dynamics (replacing Eq (5) in the case of no disease spread) takes the form:
where I(τ, t) is the number of infected individuals having infection age τ at time t. The function b(τ) determines the rate of recovery. The above equation yields a distribution of infection times for the recovered individuals. This distribution cannot be written explicitly but depends implicitly on the function b(τ).
The first feature of the proposed approach (at least in the present context) is to replace the above recovery term by a strict one corresponding to an exact duration of infection time Τ for all individuals. The governing equation is in this case:
The parameter cI is defined as the inverse infection time, that is, cI = 1/T. Assuming an initial number of infected individuals Io the solution of the lumped Eq (5) is I = Ioexp(-t/T) whereas the solution of the distributed Eq (7) is I(τ, t) = Io(τ-t) (for t < Τ) where Io(τ) = I(τ, 0) is the initial infection age distribution. The total number of infected individuals I in the distributed case is given as It(t)=∫T−t0Io(τ)dτ.
Comparing I(t) and It(τ) the following inferences are made: 1) The computation of It(t) needs the complete initial infection age distribution of the infected individuals Io. 2)The evolution of I is always exponential but the evolution of It can take several shapes depending on the shape of Io(τ) (with the exponential being one of them). Some limiting cases are: i) uniform Io(τ) leading to It/Io = 1-t/T (for t < T), (ⅱ) initially all individuals being at the inception stage (Io = δ(0) where δ is the Dirac function) of infection leading to sudden end of the disease at t = T (ⅲ) initially all individuals being at the end of infection (Io = δ(T)) leading to sudden end of disease at t = 0. This variety of behaviors adds versatility to the model at the cost of additional input data.
The next step is to consider the new model in the presence of a weak spread of the disease. The governing equations take the form
It will be shown that the above equation has asymptotic solutions (i.e., self-similar ones) where the shape of the distribution with respect to τ remains the same and only the total number of infected individuals varies in time. This variation is exponential (increasing or decreasing depending on the values of parameters T and cs). Let us assume that Eq (8) has a solution of the form I(τ, t) = M(t)F(τ) where M(t) is the total number of infected individuals at time t and ∫T0F(τ)dτ=1. Introducing these terms in Eq (8) and (9) leads to
Taking the integral with respect to τ of all terms of Eq (10) from τ = 0 το τ = Τ gives:
Denoting F(T) as k, one can find by combining Eq (11) and (12) and integrating:
Solving Eq (10) for the time derivative of M, substitution in Eq (12) and integration employing Eq (11) as initial condition leads to
Applying the above equation at τ = T leads to
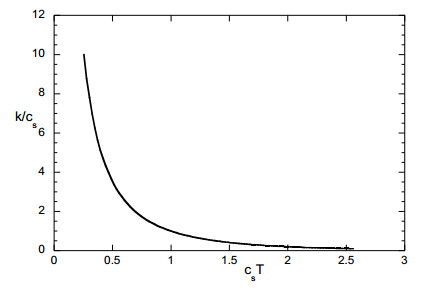
Integrating F(τ) in Eq (13b) for τ between zero and T and using Eq (13c), it confirms that the requirement of the integral of F(τ) to be equal to unity holds. Eq (13c) is a transcendental one giving the value of k as a function of cs and T. This algebraic equation can be set in a universal basis by considering the new variables k/cs and csT. The universal relation between these two variables is shown in Figure 1. In case of csT values larger than unity the ratio k/cs is smaller than unity, which means that the number of infected individuals increases exponentially with time. On the contrary, for csT values smaller than unity the number of infected individuals decreases exponentially. In this model the number Ro = csT is the basic reproduction number denoting the effective number of secondary infections produced by a single infection [39]. The distribution F(τ) decreases or increases exponentially in the opposite direction from the total number M(t). Furthermore, one can add that the shape of function F(τ) is always the aforementioned asymptotic one except in periods of external forcing. Such a period is the initial one when the distribution is affected by its initial prescribed form. The asymptotic distribution is reached fast after a short transient. As the initial distribution is closer to the asymptotic one, the transient becomes shorter and it totally vanishes when the initial distribution equals the asymptotic one. Except from the initial period, the system loses its similarity when becomes non-autonomous (i.e. time dependence of the parameters). As an example, let us assume a disease at the self-similar growing regime. A change in the parameter cs occurs leading to the decreasing regime of the infection. After this change, the distribution F(τ) exhibits a transient between its two self-similar asymptotes corresponding to the two cs values.
A nice feature of the sharp cut off model is that the equation for R takes the following simple form
2.3. Introducing a generalized parametric population dependence
2.3.1. Generalized formulation
The second innovation in the present modeling effort is the description of the whole population in terms of its response to the disease. Let us say that α is an n-dimensional vector containing all the parameters defining the response of a particular individual to the specific disease. For each individual, this could include for example the severity of the disease (native immune response; vaccination induced response will be dealt in a next section), the duration of the disease, the virus load in the body etc. The probability of an individual to have a specific value of α is described through the joint probability density function P(α). The state of the population is described in this case by the functions S(α, t), I(α, τ, t), R(α, t) for susceptible, infected and recovered population, respectively. The mathematical problem for these functions takes the following form:
where Ω(α) is a generalized function of the vector α (in the simplest case it refers to a single coordination of the vector) and Y(α) is the subdomain of the n-dimensional space of α designating the infected individuals which can transmit the decease. The double integral in Eq (15c) reminds the collision integral of the Boltzmann Eq [40] or the first of the two integrals in the coagulation Eq [41]. The function K is the rate of infection transmission from an infected individual with state vector α' and infection age τ to a susceptible individual with state vector α. The time dependence in K stands for seasonal changes and for external (non-autonomous) contributions (e.g., lockdown, change of social behavior etc). The initial condition for the above system is S(α, 0) = P(α), R(α, 0) = 0. Some initial seeding is needed for the function I but as discussed in the previous section (in the context of self-similar behavior) the solution of the system is (after a short initial transient) independent from the initial condition.
The nice attribute of the above model is that it can be expanded without additional differential equations coupled to it, contrary to the typical case for extensions of the SIR model (e.g. [10]).
Let us say that the model must be augmented for computation of the number of deaths D(t). Let us define as Y(α) the subdomain corresponding to individuals with fatal effect of infection. Then the equation for deaths is simply:
In this case, the subdomain Y(α) must be excluded from the domain of application of Eq (15d) for recovered individuals. Other categories of population can be found in an even simpler way by simply post-processing the function I(α, τ, t). As a matter of fact, the whole required information is contained in this function. In order to find the number of hospitalized individuals H(t) one has to integrate the function I at the subdomain of α and τ characterizing hospitalization O(α, τ):
In principle, the methodology can handle different modes of transmission at different exposure conditions, e.g. hospitalized patients. Although several airborne diseases may be transmitted in hospitals, e.g. COVID-19 at infectious stages, there are also diseases, e.g. bacterial pneumonias, that may not be transmitted. This has to be accounted in the integration domain of Eq (15c). The subdomain O(α, τ) has to be subtracted from the integration domain of Eq (15c).
A discussion exists in literature on the possibility of estimating the spread of the disease in the population (not only temporal [42] but also spatial [43]) based on the analysis of virus parts concentration in wastewaters. Thus, it is important for an epidemic spread model to has as output the expected evolution of total shedding rate of virus parts.
The shedding rate of virus parts (fragments) in stool (highest amount from all other human excreta) per individual is a strong function of infection age as it has been extensively discussed in [44]. This function, in general, varies across the population. Let us denote this function as C(α, τ). To be precise, in practice C depends only on some components of vector α but we leave the particular notation to account for the most general case. The evolution of shedding rate of VP (virus parts) in the wastewater of a city can be found as:
where the domain Φ(α) is selected equal to Υ(α) if all the infected people contribute to shedding rate or to a subset of this if, for example, the unprocessed wastewater of hospitals does not end up at the city sewerage system. In order to decrease the number of parameters in the problem, the parametrization of S(τ) introduced in [41] has been employed. It is noted that other expressions for C proposed in literature, e.g. [45,46], can be easily incorporated in the present model. The employed equations following [44] are:
where s(τ; τa, Τ) is
where stool amount produced by a person per day is denoted as A (gramsstool/day) and the maximum virus concentration in stool along the total duration of infection is denoted as B (gramsvirus/gramsstool). The value of τa denotes the day of the infection (infection age) corresponding to the maximum shedding rate of an individual and T is the total duration of the infection for an individual. In the general case A, B, τa, T are components of vector α.
2.3.2. A specific 3 parameters example
In order to illustrate the benefits of the above analysis an example in 3-dimensional parameter space is presented. The three parameters are: 1) a parameter α denoting the response of a person to a disease. It takes values between 0 and 1. Its values smaller than α1 denote asymptomatic response, values larger than α2 denote hospitalization and values larger than α3 denote a fatal end of the infected person. 2) a parameter B denoting the maximum concentration of virus parts in the stool of an individual and 3) the duration T of the disease (total infection period) for an individual. Considering a distribution of the above three parameters over the population implies that constant values are taken for all other possible parameters (e.g., A, τa). These values are average ones over the whole population. It must be mentioned that regarding shedding rates in stool the parameters A, τa vary much less than B across the population so taking constant values is a satisfactory educated guess.
The joint probability density function describing the population is P(α, Β, Τ). The unknown functions are S(α, Β, Τ, t), Ι(α, Β, Τ, τ, t), R(α, Β, Τ, t), H(t), D(t) (as defined previously). The governing equations are
The initial conditions for R and S is zero and S(α, Β, Τ, 0) = P(α, Β, Τ)
The basic reproduction number for this model can be found at any moment in time by the product KαυTαυ where Kαυ is the average value of function K and Tαυ is the average value of infection duration over the state of the population at the particular moment in time.
Several other unknown functions are found by simply post-processing the distribution I. In this respect, the hospitalized number is given as (it is assumed that an individual stays in hospital for α > α2 and τ > τ1):
The function Θ in Eq (22c) puts restrictions on the transmission frequency. In the specific case that transmission from hospitalized individuals is ignored, it takes the form Θ = 0 for α > α2 and τ > τ1, Θ = 1 elsewhere. As τ1 is designated the infection age for hospitalization of an infected person. The structure of function K suggests that the direct effects of B and T in the transmission process have been ignored. Yet, the T values affect indirectly the transmission process through the higher possibility of contact induced by the extended duration of disease.
The number of asymptomatic infected people A(t) can be easily computed as
The shedding rate in stool is given as
The above mathematical problem is defined in a 5-dimensional space. Even a coarse discretization for its numerical solution leads to several millions of algebraic equations. The immense computational effort needed restricts its usefulness. On the other hand, the problem is well-suited to a Monte Carlo stochastic solution approach. This is even more so since the Monte Carlo method scales linearly to the problem dimensionality so additional parameters can be easily considered (e.g. the day of hospitalization τ1, the day of maximum shedding rate τa etc). However, here we seek a computationally efficient deterministic model so we will proceed in the opposite way of reducing the problem dimensionality.
2.3.3. Reduced order problem
Let us assume that the function P has such a form that for each value of α it takes non-zero values only for a narrow range of B and T. In this case the function P can be (quite accurately) approximated by the form
It is reminded that δ takes non-zero values only when its argument equals to zero. The above definition implies that the information included in the three-dimensional function P can be approximated by three one dimensional functions Ji (i = 1, 2, 3) (only the first one is a probability density function whereas the other two are simple functions). From the physical point of view, this means that the severity of the disease for an individual (including all possible native factors e.g. virus replication) completely determines the duration of his infection and his virus parts shedding rate in stool.
The evolution of the disease is described by the functions S(α, t), I(α, τ, t), R(α, t), D(t), H(t), A(t). The evolution of these functions can be calculated by solving the following mathematical problem:
The initial conditions for R and S is zero and S(α, 0) = J1(α). The rest of the unknown functions are calculated by a simple post processing of I:
The virus parts shedding rate in stool is computed as
The above modelling approach is ideally suited to be extended to cover additional phenomena. Typically, a possible second infection can be modeled by adding a first order derivative term (age of recovery) to the equation of recovered individuals [10]. Using the present approach, the time spent in recovery can be registered for each individual and the transition to second infection is rendered when the effect of the first infection is eliminated. The time required for this can be different for different individuals. The equation for the evolution of function R(α, τ, t) standing for the recovered from the first infection people takes the form (τ is the time being in recovery)
Let us say that the time needed to become susceptible to a second infection is a function of parameter α i.e., τv = J4(α). The reversion of recovered people to susceptible status is described by modifying the corresponding equation to
The third innovation of the proposed approach is that the employed scheme automatically considers any number of reinfections and no explicit consideration of this number is needed. This is in contrast to the standard procedure in which new variables are introduced for each number of re-infections.
Let us introduce the variable τI which is the number of days from the infection to its registration (day of performing medical test). It is reasonable that it would be a function of α since it depends on the intensity of the disease symptoms. It is assumed that τI = J4(α). The number of officially registered infections every day L(t) is
The basic reproduction number Ro is given through the product of Kαυ and Tαυ which in the present case takes the form:
The typical way to model a vaccination campaign is through a first order reaction term with susceptible people as reactant and recovered people as product (e.g. [20]). More advanced models of vaccination include age dependent efficiency [47] or dependency of the vaccination efficiency from the time elapsed from vaccination [48].
The scheme proposed here allows a more sophisticated treatment of vaccination. In many cases (e.g. COVID-19) vaccination does not yield complete immunity but affects the temporal variation of individuals on the acquisition and severity of the infection based on the type of vaccine, pathogen and pathogen evolution. The fourth innovation of the proposed approach is that such behavior can be represented as a modification of the distribution of α among the susceptible population. Let us say that the effect of vaccination is to reduce the value of α for a person, for a constant quantity αm. Persons with α less than zero are no more susceptible to infection. If a vaccination campaign proceeds at constant rate such that the whole initial population is vaccinated at time τv the governing equation for S(α, t) takes the form (the following equations hold only during vaccination period):
where S1 and S2 refers to the non-vaccinated and vaccinated susceptible individuals, respectively. The function U is a step function equal to 1 for positive argument and 0 for negative argument.
The second right hand term in Eq (36) ensures that the reduction of S1 occurs only when its value is non-zero. The outcome of S1 is equal to the income in S2 with the variable α shifted by the quantity αm. The mathematical representation of the vaccination process in this scheme is by far not trivial, and it is an essential feature of the present modeling approach. A good handling of vaccination modeling is essential to optimize vaccination strategy. As an example in [49] the effect of vaccination strategy with respect to the risk group ordering is considered. Further research regarding the formulation of vaccination in the present framework is needed.
In summary, the algorithm behind the new approach is the following:
1) Assign multidimensional probability density function to the population.
2) Apply the vaccination operator to the probability density function of the susceptible population.
3) Follow in time the evolution of the probability density function corresponding to infected population.
4) Post-process the infected population probability density function in order to infer number of individuals in other compartments.
3.
Indicative results
In general, the governing equations of the model must be solved numerically. The main equation for function I has a hyperbolic form and so it must be discretized properly. The approach followed in literature is to transform it to a set of ordinary differential equations in time by applying a first order finite discretization with respect to infection age variable τ [17]. However, it is well known that this type of discretization leads to a numerical diffusion problem [50]. A different numerical approach is introduced here which in fact constitutes the fifth innovation of the proposed approach. The problem has a natural time scale for both variables t and τ, namely, that of a day. So, applying a combination of forward in time t and backward in infection age τ first order finite difference discretization, the main hyperbolic equation of the problem takes the quite simple form
where i, j, k are the discretization indices of the corresponding variables. This simple treatment of the hyperbolic partial differential equation renders the whole problem amenable to explicit integration techniques (i.e. the Euler method is used for the differential equations and trapezoidal or orthogonal rules for the evaluation of the integrals). It is very important to stress that the above approach is the only one (and only for the specific hyperbolic equation), which is free of both numerical diffusion and dispersion errors typical for discretization of first order hyperbolic partial differential equations. The approach can accurately trace any discontinuity of the initial distribution and it was proved successful in the past for the mathematically similar problem of simulating cell cycles [51,52,53]. In principle, the required mathematical effort can be further reduced by using approximating techniques for the solution of population balances equation (e.g. method of moments [54,55]). This reduction has meaning only for the extension of the model to spatially distributed scenarios since for the present homogeneous case the numerical effort is quite affordable. The discretized system which arises here is just a set of differential equations which can be solved explicitly. The calculations are implemented in the VisualBasic programming language. The running time of the presented calculations in this work is of the order of 10 seconds.
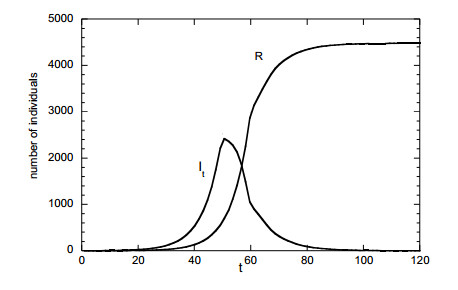
The first example refers to a problem described by Eq (8) and (9). An initial seed of value I = 1 with τ = 5 is employed (the seed patients supposedly arrived from a different place and are all on the 5th day of disease). The absolute value of I has no special meaning since all the models presented here are linear in I so their values can be rescaled by properly rescaling the initial condition. The total duration of disease is assumed as T = 10 days. The parameter cs has initially the value 0.2 but at t = 50 (i.e., 50th day after the seed patient's arrival) it suddenly drops to 0.05, e.g. due to a lockdown. The evolution of the total number of infected individuals It and of the number of recovered R is shown in Figure 2. The delay of the recovered with respect to infected patients is obvious.
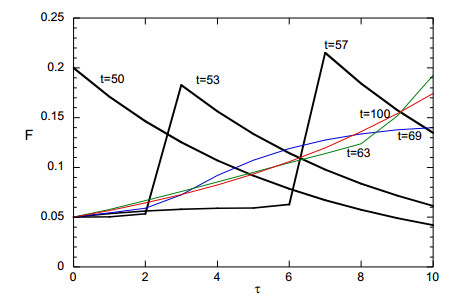
After an initial transient of more than 15 days, self-similar exponential profiles both in time and in infection age are captured. The initial transient period is long because the monodisperse initial distribution in τ varies strongly from the exponential asymptotic one. After t = 70 a new self-similar, exponential distribution decreasing in τ, is gradually approached. Of great significance is the period i between t = 50 and t = 70 where most of the transition between the two self-similar distributions occurs. The evolution of the shape of the function F(τ) between the two asymptotic shapes appears in Figure 3. It is noticed that the transition between the two shapes is never smooth. Instead, a singularity appears and proceeds along the τ domain. Oscillations decaying in time t appears at the edge t = T. It is noted that the two numerical asymptotic distributions differ from the analytical solution described by Eq (13a), (13b), (13c) by less than 1%.
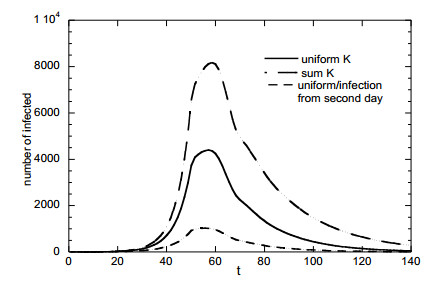
The next example refers to the reduced problem described in section 2.3.3. The probability density function has the parabolic form J1(α) = 6α(1-α). The function J2(α) = 10 + 10α is also considered (i.e., the higher the value of α the larger the duration of the disease for an individual). Finally, the function J3(α) = Βο(1+10α) (i.e., the virus load of an individual increase with the value of α). The parameter Bo is just a normalization factor employed to keep the problem dimensionless. The values of α for asymptomatic cases, hospitalized patients and deaths are taken as α1 = 0.3, α2 = 0.7 and α3 = 0.9, respectively. The mathematical model is described by Eq (27-30). In this particular example it is assumed that hospitalized individuals contribute to both the spread of disease and to shedding rate in wastewater. Three different shapes for the kernel K are considered: (ⅰ) uniform K, (ⅱ) sum type K (proportional to α+α') which implies that the possibility of infection increases with the α value of two persons in contact, (ⅲ) the otherwise uniform kernel denotes that the disease is transmitted only after the second day of infection. In all three cases the kernels are multiplied by 0.18 and 0.04 before and after the day t = 50, respectively, to account for transmission reduction.
The evolution of the total number of infected people Ιt for the three kernels is shown in Figure 4. The sum kernel (despite it has an average value of K equal to the constant one) leads to higher number of infections. On the contrary, the assumption that the infection is transmitted only after the second day leads to much smaller number of infections. It is apparent that the spread of the disease is very sensitive not only to the average value but also to the shape of the function K with respect to its arguments.
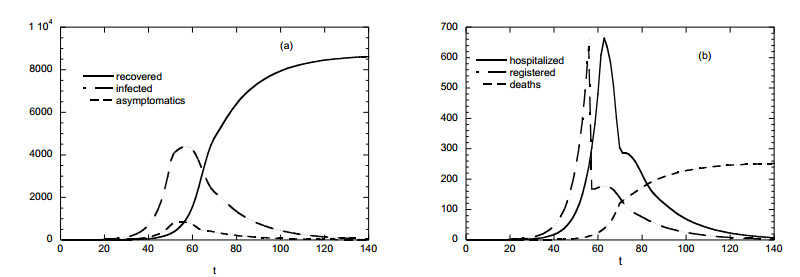
It is assumed that J4(α) = tr = 6 implying that the disease is registered (by medical testing) at the 6th day of infection. The evolution of the numbers of total infected people, It, asymptomatic cases A, and recovered individuals, R, is shown in Figure 5a (for the uniform kernel case indicated above). The evolution of the number of hospitalized patients, registered and dead individuals appear in Figure 5b. It is clear that all the above indices exhibit a delay in recognizing the sudden reduction (e.g., lockdown) occurring at t = 50. The delay is smaller for the registered individuals (equal to 6 days which is the time between infection and registration). In case of a uniform kernel, the dependence of I on α is uniform in time and it has the shape of J1(α). This means that the distribution I(α, τ, t) acquires a self-similar shape during the spread of the disease. The shape of I in two dimensions (a and τ) can be seen in Figure 6a. In the case of a kernel depending on α (e.g., the sum kernel) the α-dependence evolves in time. Computations show that I also acquires a self-similar shape during the spread of the disease. The dependence of I on α for uniform and sum kernels Κ is showed in Figure 6b. The distribution appears to be skewed at large α for the sum kernel in contrast to the symmetric distribution for the constant kernel.
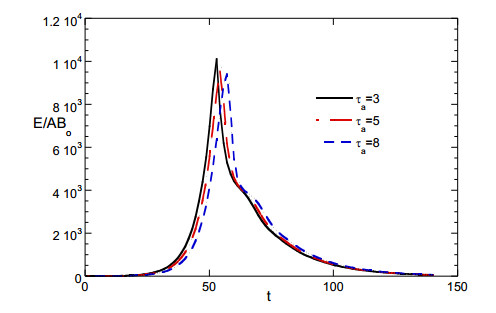
The evolution of virus parts shedding rate in wastewater normalized to the quantity ABo for several values of the parameter τa is shown in Figure 7. The maximum in the curves is sharper than the one of total infected people but less sharp that the number of registered individuals. The relative position of the maximum to the time of sharp reduction of transmission (e.g., lockdown) depends strongly on the parameter τa (+3, +5 and +7 days for τa = 3, 5, 8 respectively). The peak position of the registered individuals depends on τr. So, the relative position of peaks of shedding rate and registered infections is mainly determined by the difference τa-τr.
Next, let us study the implementation of a vaccination strategy. In the case of weak spreading of the disease considered here, the first term of the righthand side of Eq (36) can be ignored. The parameter αm is assumed to take the value 0.3, i.e., vaccination decreases the α value of an individual by 0.3. Negative α values implies that a person is not prone to the disease. One can proceed analytically in the derivation of the functions S1 and S2. The final result reached after some algebra is (where t' is the time elapsed from starting of vaccination):
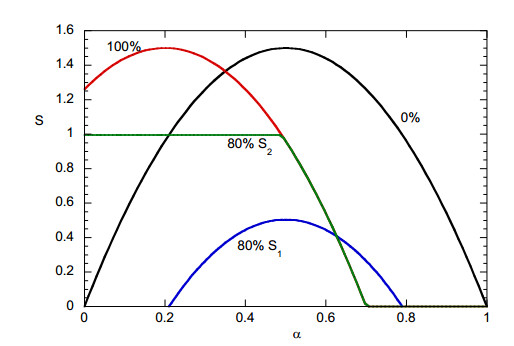
The shapes of function S for no vaccination and complete vaccination along with the shapes of S1 and S2 for 80% vaccination of the population are shown in Figure 8. During the vaccination period, a transition between zero and complete vaccination curves occurs as described by the above model.
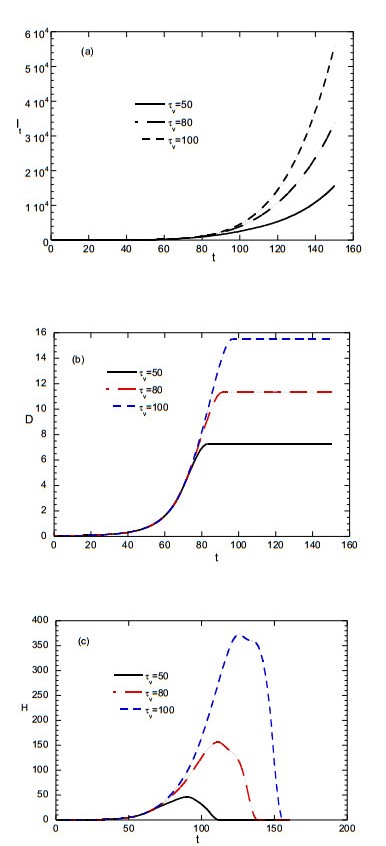
In the example of vaccination, no lockdown is accounted whereas K is considered constant and equal to 0.12. According to the scenario examined, the vaccination starts at day 50. The effect of vaccination rate is examined by assuming three different vaccination scenarios such that the total population is vaccinated in 50, 80 and 100 days, respectively. It must be stressed that the above selection of vaccination days is only to illustrate discrepancies for different vaccination rates and are not typical of real life infectious diseases. The evolution of the total infected people is presented in Figure 9(a). The vaccination cannot suppress the disease since most of the vaccinated people are amenable to it. However, the rate of vaccination strongly reduces the spreading rate of the disease. One should note that according to the employed scenario in the absence of vaccination the number of infected individuals at t = 150 would be equal to 800000. The corresponding number of deaths appears in Figure 9(b). In all cases of vaccination, the deaths stop at a time between t = 50 and t = 100 day (the higher the vaccination rate the smaller this time). The vaccination for this specific example almost eliminates deaths (which in absence of vaccination would be 5000 at t = 150).
Finally, in Figure 9(c) the evolution of the number of hospitalized individuals (assuming that they are admitted in the hospital at day 10 of infection) is presented. The curves display a bell shape with larger area for smaller rate of vaccination. The specific model parameters suggest that the number of deaths and hospitalization can be completely eliminated at the end of vaccination whereas the number of infected individuals continues to grow. This is an essential improvement from the typical epidemiological models based on ordinary differential equations which cannot incorporate such a behavior.
It is noted here that the new approach although being mathematically simple has as unknown several multidimensional functions (i.e., initial probability distribution among the population, transmission kernel) and constraints (i.e., conditions for asymptomatic cases, hospitalized cases etc). In this respect, its direct use to fit existing data and predict the near future is not possible. Its main use is that it allows parametric study of several scenarios and performance of sensitivity analysis. On the other hand, the unique implementation of the vaccination process, offers the possibility to optimize the vaccination strategy by selecting in a specified way the order by which individuals should be vaccinated (instead of randomly). The ambition for the future, that personal (medical and physical) record of individuals will be registered in big databases related to national security, health insurance etc, is that the α value of each individual for a specific disease will be directly estimated by employing its personal record. It is noted that after the completion of the present work a quite similar approach was found in the very recent literature [56]. In that work, the main idea is alike (proving its novel character), however the way of development, presentation and implementation differs. For example, in [56] the vector α is restricted to just one dimension and moreover the disease time does not depend on α. In addition, their partial focus is on the evaluation of numerical solution schemes for the solution of the resulting system of partial differential equations. The latter is not a priority in our work and has been overcome by defining the period of a day as the standard discretization period. Instead, our goal is about quantifying the effect of prominent epidemiological parameters and determining the sensitivity of the model on their variation.
4.
Conclusions, limitations and further research
A new framework for epidemiological modeling is proposed here. The basic element of the new approach is the infection age-structured model with a sharp definition of infection duration for each individual. The population is characterized by distributed properties such as the total duration of infection per individual, being more representative than simple process rate constants. Any degree of sophistication can be accommodated by retaining the main model structure and adding more independent variables (in contrast to dependent variables needed for the extension of the typical epidemiological ODEs model). The new model is naturally discretized with respect to a time increment of one day leading to a very simple replacement (yet, very accurate) of the governing partial differential equation to a set of explicit difference equations. Finally, the new model admits a much more general treatment of vaccination response of individuals than the one accounted by the typical ODEs methods (first order transition from Susceptible to Recovered). Several simple cases are examined using the new framework and several elementary results are presented to demonstrate the versatility and benefits of the proposed approach. The proposed approach can be served as the basis for the development of a new class of epidemic models. However, there is a limitation regarding its use since the model parameters are not only scalars but also functions. Their determination from empirical data is difficult. The true power of the approach is associated to the (possible in future) independent estimation of the functions determining the state of the population. The next step in the new approach development will be the generalization of the vaccination modeling.
Conflicts of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: