1.
Introduction
Uterine cervical cancer is a worldwide health problem but it is especially concerning in developing countries. It is the first or second most common cancer in women [1]. It is estimated that the probability of a person being infected with human papillomavirus (HPV) in their lifetime reaches 70 to 80% [2], and the total infection rate in the global population is as high as 11.7% [3]. An estimated 233,000 deaths were attributed to HPV infection in the year 2000 [4]. There were approximately 500,000 cases and 275,000 deaths due to cervical cancer worldwide in 2002, equivalent to about a tenth of all deaths in women due to cancer [5]. The burden of cervical cancer is disproportionately high (>80%) in the developing world [6].
HPV was discovered to be the causative agent of cervical cancer in the 1970s by the Zur Hausen group [7]. Usually, the infecting papillomavirus is eliminated from individuals; however, some individuals retain the virus. Persistent infection with oncogenic HPV is recognized as the major cause of uterine cervical cancer [8]. Cervical carcinogenesis is a complex stepwise process over a continuum of increasingly severe precancerous changes known collectively as cervical intraepithelial neoplasia (CIN) [9]. The spectrum of CIN is traditionally divided into three histopathological categories: CIN1, CIN2 and CIN3. In CIN1, cells with malignant changes are limited to the superficial layer of the cervical epithelium. Most CIN1 lesions are likely to disappear without treatment. However, a small percentage may progress to high-grade CINs (i.e., CIN2 and CIN3). The risk of progression to invasive cervical cancer increases significantly with worsening CIN grades [10,11].
Pap cytology screening for the early detection of cervical neoplasia has been successful in reducing cervical cancer incidence and mortality [12]. In unscreened populations, the risk of invasive cervical cancer occurs earlier than of most adult cancers, peaking or reaching a plateau between about 35 and 55 years of age [13]. This distribution is because cervical cancers originate mainly from HPV infections transmitted sexually in late adolescence and early adulthood [14]. HPV transmission can be reduced through the use of condoms [15]. Some studies have reported that smoking [16], multiparity [17], and long-term use of oral contraceptives [18] can double or triple the risk of precancer and cancer among women infected with carcinogenic types of HPV. There are two major kinds of anti-HPV vaccines approved for use to protect newly sexually active individuals against some of the most common HPV types and boost immunity, namely, therapeutic vaccines and prophylactic vaccines [7]. A few years after receiving a prophylactic vaccine, the individual must be revaccinated because the vaccine loses its preventive effect. Progress in the development of therapeutic vaccines for HPV has been slow [7]. In summary, there is currently no specific treatment for HPV infection [19]. There are three major treatments for cervical cancer: surgery (such as total hysterectomy and subtotal hysterectomy), radiotherapy, and chemotherapy. Among these, surgery and radiotherapy are the main treatment methods [19].
Mathematical modeling is a useful tool for assessing the potential impact of intervention strategies against HPV spread among humans [20,21,22,23,24]. A number of authors have reported the use of mathematical modeling to evaluate the impact of HPV vaccination. Al-arydah [20] developed a two-sex, age-structured model to describe a vaccination program for the administration of an HPV vaccine. Malik et al. [11] presented an age-structured mathematical model that incorporated sex structure and Pap screening cytology. Sharomi and Malik [21] developed a two-sex HPV vaccination model to study the effect of vaccine compliance on HPV infection and cervical cancer. Omame [22] developed a two-sex deterministic model for HPV that assessed the impact of treatment and vaccination. Elbasha [23] presented a two-sex, deterministic model for assessing the potential impact of a prophylactic HPV vaccine with several properties.
Based on the above research and understanding of HPV pathology, we develop an ordinary differential equation model with precautionary measures such as screening, which are rarely considered in previous studies, and analyze the potential effects of multiple factors on HPV transmission. The model is formulated in section 2. In section 3, the equilibria, basic reproduction number, and global stability are analyzed. We report the sensitivity analysis of the model through the partial rank correlation coefficient (PRCC) method and identify the key factors in the model in section 4. In section 5, we set the vaccination rate and screening rate as control variables and analyze an optimal control problem that minimizes vaccination and screening cost. Section 6 concludes the article. Through extensive numerical simulations with MATLAB, we obtained results to verify our conclusions.
2.
An HPV model with vaccination and screening
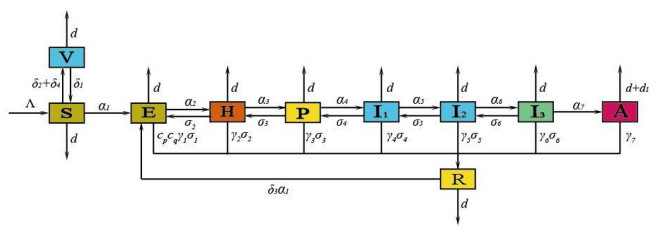
The total individual population at time t is divided into 10 mutually exclusive subpopulations of susceptible individuals S(t), vaccinated individuals V(t), infectious individuals without disease symptoms E(t), infectious individuals with disease symptoms H(t), individuals with persistent HPV infection P(t), CIN1 symptomatic individuals I1(t), CIN2 symptomatic individuals I2(t), CIN3 symptomatic individuals I3(t), cancer-infected individuals A(t) and recovered individuals R(t). As such, the total population is
Susceptible individuals acquire HPV infection, following effective contact with infected individuals (i.e., those in the E, H, P, I1, I2 and I3 classes) at the rate α1 as follows
It follows that the model for the transmission of HPV is given by the following system of differential equations.
Tables 1 and 2 list the associated state variables and parameters of model (2). Figure 1 shows the flow diagram of the model. We emphasize that the vaccine mentioned in model (2) is a prophylactic vaccine. In the following section, model (2) is qualitatively analyzed to derive insights into its dynamical features.
3.
Analysis of the model
3.1. Basic properties
3.1.1. Positivity and boundedness of solutions
Model (2) is epidemiologically and mathematically well-posed in the epidemiologically valid domain
Theorem 3.1 Assuming that the initial condition lies in domain D, then the solutions (V,S,E,H,P,I1,I2,I3,A,R) of model (2) remain in D for all time t≥0. Furthermore
Proof. We note that along the edges of D, the time derivatives all lead the solution into the invariant domain [25]
Furthermore, adding all the equations in the differential equation system of model (2) gives
It follows from Eq (3) that
Therefore
and
as required.
3.1.2. Invariant regions
Model (2) is analyzed in a biologically-feasible region as follows [26]. We first show that model (2) is dissipative (i.e., all feasible solutions are uniformly bounded in a proper subset Ω⊂R10+). Consider the region
The following steps establish the positive invariance of Ω (i.e., solutions in Ω remain in Ωt≥0). It follows from Eq (3) that
A standard comparison theorem can then be used to show that
In particular
Thus, the region Ω is positively invariant. Hence, it is sufficient to consider the dynamics of the flow generated by model (2) in Ω. In this region, the model can be considered as being epidemiologically and mathematically well-posed [27]. Thus, every solution of model (2) with initial conditions in Ω remains in Ω for all t>0. Therefore, the ω-limit sets of model (2) are contained in Ω. This result is summarized below.
Lemma 3.1 The region Ω is positively invariant for model (2) with initial conditions in R10+.
3.2. Local stability of the disease-free equilibrium (DFE)
Model (2) has a DFE, which is obtained by setting the right-hand sides of the equations in the model to zero, given by
Let X=(V,S,E,H,P,I1,I2,I3,A,R)T. Using the notation from [28], the model consists of nonnegative initial conditions together with the following system of equations:
where
and it follows that
The matrices F and VΔ for the new infection terms and the remaining transfer terms are respectively given by
where
We obtain
where
Consequently, it follows from Theorem 2 of [28].
Lemma 3.2 The DFE of model (2), given by (4), is locally asymptotically stable (LAS) when R0 < 1 and unstable if R0 > 1.
3.3. Backward bifurcation
The epidemiological significance of forward bifurcation is that the disease will eventually disappear if the basic reproduction number is less than one. The public health significance of backward bifurcation is that the classical requirement of R0 < 1 although necessary is no longer sufficient for effective disease control. Therefore, the presence of backward bifurcation in HPV transmission dynamics makes its effective control more difficult.
3.3.1. Existence of backward bifurcation
First, the possible equilibrium solutions that model (2) can have are determined as follows. Let
be any arbitrary equilibrium of model (2). Further, let
be the associated force of infection at a steady state.
Setting the right-hand sides of model (2) to zero (steady state) gives
where
Substituting (7) into the expressions for α1∗ in (6) gives
so
where
and
Quadratic Eq (9) can be analyzed for the possibility of multiple endemic equilibria. It is worth noting that the coefficient a is always positive, and c is positive (negative) if R0 is less than (greater than) one. Hence, the following result is established.
Theorem 3.2 Model (2) (details in Appendix A (Table A1)) has the following.
ⅰ. A unique endemic equilibrium if c<0⇔R0>1;
ⅱ. A unique endemic equilibrium if b<0, and c=0 or b2−4ac=0;
ⅲ. Two endemic equilibria if c>0,b<0 and b2−4ac>0;
ⅳ. No endemic equilibrium otherwise.
Case (ⅲ) of Theorem 3.2 indicates the possibility of backward bifurcation in model (2) when R0<1. To check for this, by setting
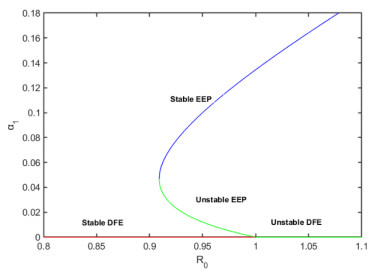
it can be shown that backward bifurcation occurs for values of R1<R0<1. This phenomenon is illustrated by simulating model (2). The parameter values are presented in Table 3. Let M∈[0.35,0.5]. It should be mentioned that the aforementioned parameter values may not all be epidemiologically realistic.
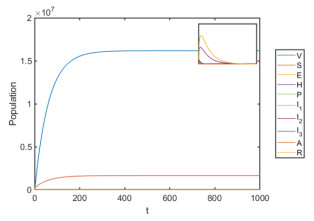
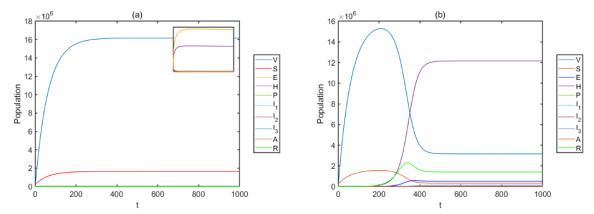
The associated backward bifurcation diagram, depicted in Figure 2, shows that the model has a DFE (corresponding to Figure 3) and two endemic equilibria: One of the endemic equilibria is LAS (corresponding to Figure 4a); the other is unstable (a saddle); and the disease-free equilibrium is LAS. This clearly shows the coexistence of two stable equilibria when R0<1, confirming that the model exhibits backward bifurcation for R1<R0<1. This result is summarized below for model (2) (a more rigorous proof of the backward bifurcation phenomenon of the model, using the center manifold theory is given in Appendix B).
Theorem 3.3 Model (2) exhibits backward bifurcation when Case (ⅲ) of Theorem 3.2 holds and R1<R0<1.
3.3.2. Effect of perfect protection after recovery on backward bifurcation
Consider model (2) with perfect protection after recovery (that is, δ3=0). In such a case, the basic reproduction number is R′0=R0|δ3=0. It follows from Eq (9) that if δ3=0, the coefficients a=0 and b>0, so quadratic Eq (9) reduces to a linear equation in α1∗ (with α1∗=−c/b). In this case, model (2) has a unique endemic equilibrium if c<0 (i.e.,
R′0>1), ruling out backward bifurcation in the model for this case (the presence of two endemic equilibria when R′0<1 is necessary for the existence of backward bifurcation). Furthermore, it follows that c=0 when R′0=1. Thus, in such a case (with a=c=0), quadratic Eq (9) has only the trivial solution α1∗=0 (which corresponds to the DFE ε0). This result is summarized below.
Lemma 3.3 Consider the case where the protection after recovery is perfect (δ3=0). Model (2) has a unique endemic equilibrium whenever R′0>1 and no endemic equilibrium otherwise.
3.4. Global stability of the DFE
Theorem 3.4 In the first quadrant, there is no limit cycle in model (2).
Proof We consider the Dulac function as B(S,E)=1SE. Let
Hence Q≥E and N≥R. Therefore,
Then,
Therefore, by the Dulac−Bendixson theorem [29], there is no periodic orbit for model (2). Moreover, ε0 is the unique positive equilibrium point in R10+ if δ3=0, and it is also locally asymptotically stable for R0<1. Hence, every positive solution actually approaches ε0. Thus, ε0 is globally asymptotically stable if δ3=0 and R0<1.
4.
Efficacy of interventions and sensitivity analysis
In this section, we performed a numerical simulation to enhance the understanding of model (2).
4.1. Efficacy of interventions
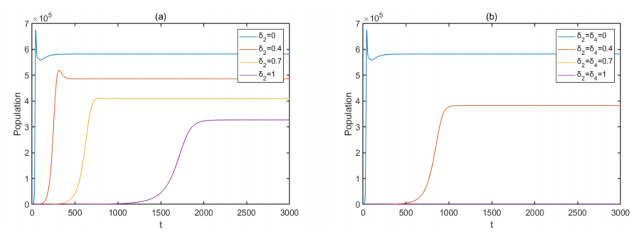
To examine the possible impact of interventions on disease infections we plot the number of infected individuals (E) with various vaccination rates and revaccination rates.
This analysis shows that an increasing vaccination rate persistently decreases the peak value, as shown in Figure 5. Increasing the vaccination rate δ2 by 1.75 times (increase from 0.4 to 0.7) or 1.43 times (increased from 0.7 to 1) will lead to a reduction in the peak value in the number of E by 20.21% or by 15.67%, respectively. In addition, the peak value of the number of people infected with δ2=1 decreased by 43.82% compared with the number of people infected with δ2=0.
On the premise that the vaccine's protective effect will end after a few years, we consider the situation of vaccination and revaccination. Figure 5b indicates that increasing δ2 and δ4 from 0 to 0.4 will lead to a reduction in the peak value in the number of E by 34.16%. In addition, the peak value of the number of people infected with δ2=δ4=0.7 decreased by 100% compared with the number of people infected with δ2=δ4=0.
4.2. Sensitivity analysis of R0 to parameters
To identify the factors associated with a certain intervention that markedly affect the rate of new infections, we performed sensitivity analysis of the basic reproduction number.
LHS belongs to the MC class of sampling methods; it was introduced by Mckay et al.
[30]. LHS allows an unbiased estimate of the average model output and has the advantage that it requires fewer samples than simple random sampling to achieve the same accuracy. For nonlinear but monotonic relationships between outputs and inputs, measures that work well are based on rank transforms such as the partial rank correlation coefficient, and standardized rank regression coefficient.
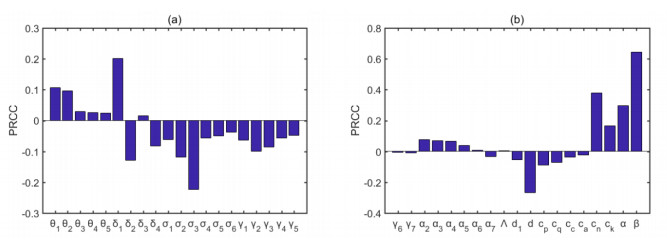
Model (2) has 39 parameters. To identify the key factors, following [30], we performed a Latin hypercube sampling on the parameters that appear in R0 and calculated the PRCC. The parameters of the model were set as input variables, and R0 was the output variable. Generally, in PRCC analysis, the parameters with large PRCC values and corresponding small p values are deemed to be the most influential parameters in the model.
Detailed inspection of Table C1 (Appendix C) and Figure 6 indicates that in terms of reducing the value of R0, except σ3 (control the disease and reduce the number of persistent infections) and d, the vaccination rate δ2 is the most sensitive parameter with a leading PRCC value, followed by γ2,γ3,σ2,δ4. This implies that enhancing the vaccination rate is the most effective intervention for lowering HPV new infections. Moreover, in the treatment of patients in stages H, P, I1, I2 and I3, the effect of treatments γ2,γ3,γ4,γ5 and γ6 on R0 decreases successively. That is, the same treatment intervention is more effective in the earlier stages. This means that more attention should be paid to patients in the early stages of infection. As asymptomatic patients are unable to diagnose themselves, regular screening for HPV should be strengthened. Smoking, overuse of contraceptive drugs, and unsafe sexual life will increase the value of R0, thus promoting the spread of HPV.
5.
Optimal control in an extended model
In this section, an optimal control model for the transmission dynamics of HPV is formulated by extending model (2) to include control functions. Our goal here is to study the optimal control strategies to curtail the epidemic and minimize cost.
5.1. An extended HPV model
The optimal vaccination and screening strategy can be formulated as the following optimal control problem (P) with inequality constraints and free terminal states defined over the prescribed interval [0,tf] [31]:
where tf∈R+ is the fixed terminal time, the coefficients C1,C2,C3,C4,C5,C6,B1 and B2 represent the corresponding weight constants, and these weights are balancing cost factors related to the size and importance of the parts of the objective function. The control function u1(t) is the fraction of the population of susceptible individuals who enters the vaccination compartment. The control function u2(t) is the fraction of the population of infectious individuals with no symptoms who undergo HPV screening, and they are Lebesgue integrable.
5.2. Characterization of optimal control
The inequality constraints in problem (P) can be transformed into equality ones with the help of some non-negative parametric parameters, that is, ηi(i=1,2,3,4), as
Hence, the Hamiltonian function for problem (P) is obtained as follows:
where λ=[λV,λS,λE,λH,λP,λI1,λI2,λI3,λA,λR]T are adjoint variables, and μ=[μ1,μ2,μ3,μ4]T are non-negative penalty multipliers [32].
Theorem 5.1 There exists an optimal control (u∗1(t),u∗2(t)) and corresponding solution V, S, E, H, P, I1,I2,I3,A, and R that minimize J(u1(t),u2(t)) over Ω. Furthermore, there exist adjoint functions λV,λS,λE,λH,λP,λI1,λI2,λI3,λA and λR, such that
with transversality conditions
The following characterization holds
Proof.
The existence of an optimal control can be obtained owing to the convexity of the integrand of J(u1(t),u2(t)) with respect to (u1(t),u2(t)) [33], a priori boundedness of the state solutions, and the Lipschitz property of the state system with respect to the state variables.
By Pontryagin's maximum principle [34], the optimal conditions with respect to the state, costate, and parametric variables result in a two-point boundary value problem coupled with a nonlinear complementarity problem as follows:
and
evaluated at the optimal control and corresponding states results in the stated adjoint system (13) with transversality (14).
The optimality conditions with respect to the control variables are
By solving Eq (17), the optimal control can be expressed as
To determine an explicit expression of the optimal control without μ1, we consider the following three cases:
ⅰ. On the set {t∣0<u∗1<u1max}, we have μ1=μ2=0. Hence, u∗1(t)=S(λS−λV)2B1.
ⅱ. On the set {t∣u∗1=u1max}, we have μ2=0. Hence, u∗1(t)=u1max=S(λS−λV)+μ12B1. As μ1≥0, it is determined that u1max≥S(λS−λV)2B1.
ⅲ. On the set {t∣u∗1=0}, we have μ1=0. Hence, u∗1(t)=0=S(λS−λV)−μ22B1. As μ2≥0, it is determined that S(λS−λV)2B1≥0.
Combining the above three cases, the optimal control u∗1 is characterized as
Using similar arguments, we can characterize the optimal control u∗2 as
5.3. Numerical simulations
An analytical expression of the optimal vaccination rate and screening rate was derived in Eq (15). However, an effective algorithm is still required to solve the nonlinear constrained optimal control problem numerically. Based on the generating function method, Peng et al. developed a series of symplectic methods for nonlinear optimal control problems [35,36,37,38]. Such symplectic methods have good precision and efficiency because of the structure-preserved property. Recently, Wang et al. improved the symplectic methods by incorporating the local pseudospectral discretization scheme [39,40,41,42]. Such symplectic pseudospectral methods (SPMs) have been successfully applied to solve optimal control problems in various mechanical systems [43,44]. In this paper, the SPM developed in [45] was adopted.
In the following simulation, the weights in the objective function (meaning the minimization of the number of patients at each stage has different importance) are C1=4.5e−2,C2=1e−7,C3=1e−4,C4=1e−5,C5=2e−4, and C6=1e−4. Let M=1. The initial values for the states and other parameters are listed in Table 4. Unless otherwise stated, the parameters used in each case were as listed in Table 3.
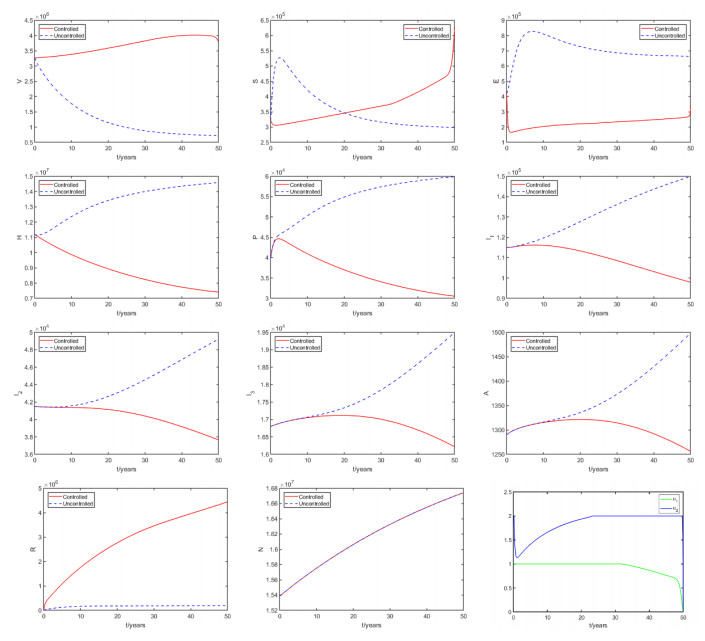
The controlled solutions together with the solutions for the uncontrolled case are presented in Figure 7. It can be seen that the control strategy is effective. Vaccinated individuals increase steadily and reach almost 400% at the terminal end. Susceptible individuals keep increasing and then stabilize during the whole period. The number of infected individuals decreases significantly when optimal control strategies are used compared to the number in the absence of control strategies.
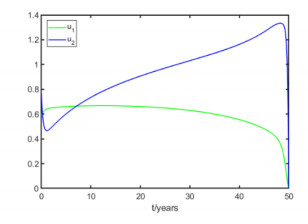
We considered another set of weights, the simulation results are shown in Figure 8. A higher focus on the control strategies leads to a drop in the importance of the vaccination and screening strategies. As the number of asymptomatic individuals depends on the immunity of the susceptible individuals and the protection of the susceptible population, we should consider strengthening their immunity or implement regular cost-effective screening to control HPV transmission.
6.
Conclusions
The human papillomavirus is among the most common sexually transmitted infections. Following infection, cervical carcinogenesis is a complex stepwise process characterized by slow progression. According to the known pathology, we represented the CIN stages with three corresponding components in the model. Our model accounted for the fact that preventive vaccines become ineffective over time. We derived three types of equilibria and their conditions of existence, analyzed the stability of the equilibria, and characterized the threshold condition as backward bifurcation for the stable fixed points. We also obtained the conditions for the elimination of the disease. We found that the possibility of HPV transmission to lead to endemic disease can be reduced by strengthening the protection after cure. We then simulated and compared practical mitigation strategies and performed sensitivity analysis to illustrate the key factors for the threshold condition. The results show that increasing the vaccination rate is the most effective way to reduce the basic reproduction number. The effect of optimal control was illustrated numerically, and a comparison of HPV infection was presented under different control strategies.
Acknowledgements
This work was supported by the Fundamental Research Funds for the Central Universities (31920200037; 31920200070), the Research Fund for Humanities and Social Sciences of the Ministry of Education(20XJAZH006), the Program for Young Talent of State Ethnic Affairs Commission of China (No. [2014]121), the Innovation Team of Intelligent Computing and Dynamical System Analysis and Application.
Conflict of interest
The authors declare that no conflict of interest.
Appendix.
A
Appendix.
B
Here, we explore the existence of backward bifurcation using the center manifold theory [46,47]. To apply this theory, it is necessary to carry out the following change of variables.
V=x10, so that
Further, using the vector notation
Model (2) can be rewritten in the form
as follows:
with
Consider the case when R0=1. Suppose, further, that δ2 is chosen as a bifurcation parameter.
Solving for δ2=δ2∗ from R0 gives
The Jacobian of model (B.1) evaluated at the DFE is given as
where
It is easy to verify that the transformed model (B.1), with δ2=δ2∗, has a hyperbolic equilibrium point (i.e., the linearized system has a simple eigenvalue with zero real part, and all other eigenvalues have negative real parts). Hence, the center manifold theory can be used to analyse the dynamics of model (B.1) near δ2=δ2∗.
It can be shown that the Jacobian of model (B.1) at δ2=δ2∗ has a right eigenvector (associated with the zero eigenvalue) given by w=(w1,w2,w3,w4,w5,w6,w7,w8,w9,w10)T, where
The components of the left eigenvector of Jε0|δ2=δ2∗,v=(v1,v2,v3,v4,v5,v6,v7,v8,v9,v10), satisfying v⋅w=1 are
It follows from [26]:
are computed to be
Thus, we have made the following conclusions
Theorem A.1 Model (B.1) (or, equivalently, model (2)) undergoes a backward bifurcation at R0=1 if all parameters are positive.
Appendix.
C









 DownLoad:
DownLoad: