Thermoelectric Generators (TEGs) modules—Optimum electrical configurations and performance determination

1.   Introdution

The work of Markowitz ^[1] stands as one of the pioneering works on portfolio theory ^[2] and details Markowitz's major contributions to the rising modern portfolio theory. Besides providing criterious description of Markowitz's model of portfolio choice ^[3], the work in ^[1] traced future research directions explored by other scientists like the suggestion to replace variance with semi-variance as a measure of risk, recommendations on the maximization of the expected logarithmic utility of return, and the outlining of a market model developed in depth by Sharpe ^[4].

However, Markowitz's portfolio selection framework relies on the premise that one can measure asset's return variance as emphasized by the statement that "examples of rapidly increasing variances are of mostly academic interest" ^[1]. This restriction brings concerns related to the framework suitability in a scenario where heavy-tailed distributions better model assets return by allowing fast varying volatilities resulting from extreme events. We can find evidences in literature that financial data is better modelled by $\alpha$-stable processes (heavy-tailed alternative to Brownian motion ^[5]) or by heavy-tailed time series models ^[6,7]. Although in this work we rely on the general hypothesis that logarithmic returns in financial data follow an $\alpha$-stable process with parameter $0 < \alpha < 2$ ^[8] (which implies that variance of return is undefined), without loss of generality, we use results from extreme value theory (EVT) regarding generalized extreme value (GEV) distribution ^[9] as an alternative to $\alpha$-stable distributions. This approach can be considered valid since the GEV distribution has fat-tailed behaviour and can be used as a proxy of various fat-tailed distributions.

From an economic point of view, it is well known that extreme share returns on stock markets can have important implications for financial risk management and several studies have successfully applied GEV to model financial data ^[10]. For example, Gettinby et al. ^[11] characterized the distribution of extreme returns for a UK share index over the years 1975 to 2000. They considered the suitability of several distributions, being the weekly maxima and minima of daily return best modelled by the GEV and the Generalised Logistic distributions. For the UK case, Generalised Logistic was a better choice overall. On the other hand, GEV has presented a similar modelling capability as well as presenting some important properties due to EVT. Also, Hussain & Li ^[12] studied the distribution of the extreme daily returns of the Shanghai Stock Exchange (SSE) Composite Index. They modelled the SSE Composite index returns based on the data from 1991 to 2013, which indicated that the Generalized Logistic distribution is a better fit for the minima series and that the GEV distribution is a better fit for the maxima series of the returns for the Chinese stock market.

EVT is a branch of probability and statistics that deals with the modeling of extreme events that are related to maximums and minimums of independent random samples. Applications of this theory are found in finance ^[13], natural catastrophes, and equipment failures, among others. The books ^[6,14,15,16] provide extensive coverage that allows for a detailed study of EVT.

Furthermore, EVT provides a theoretical basis and framework to deal with extreme deviations from the mean of distribution functions (DFs) by restricting the behavior of the DFs in the tails. It focuses on the study of the possible limiting distributions and their properties for the normalized maximum.

Specifically, let $X_1, X_2, \cdots, X_n$ be a sequence of independent and identically distributed (i.i.d.) random variables (RVs) with common distribution function $F$ and set $M_n = \max\{X_1, \cdots, X_n\}$. The theory is concerned with properties of $F$ and of the possible non-degenerate distribution functions $G$ satisfying

for sequences of constants $a_n > 0$ and $b_n\in\mathbb{R}$ ($n = 1, 2, \cdots)$, suitably chosen, where $C(G)$ denotes the set of continuity points of $G$.

The possible distribution functions $G$ satisfying (1.1) have been known for some time ^[17] and have been extensively studied by several authors from then on. They are also known as max-stable laws (or max-stable distributions) and can only be of three well-known types: Fréchet, Weibull or Gumbel.

Goncu et al. ^[18] used the EVT to model the extreme return behaviour of the Istanbul Stock Exchange (ISE), Turkey. They considered Gumbel, Fréchet and Weibull distributions for modelling extreme returns over different investment horizons. Their results indicate that when the Value at Risk (VaR) is computed with the proposed distributions, backtesting results indicate that the EVT provides superior risk management in all the sub-intervals considered compared to the VaR estimation under the assumption of a normal distribution.

For statistical applications, the max-stable distributions can be summarized in a single distribution function called generalized extreme value (GEV) distribution. Essentially, the GEV distribution has the cumulative distribution function (CDF) given by

where $\gamma$ is the shape parameter.

Our interest in this work is the property of stress-strength probability which, in general terms, consists of the study of the probability of failure of a system or component based on the comparison of the applied stress to the strength of the system. Let stress $Y$ and strength $X$ be independent continuous RVs with probability density function (PDF) $f_{Y}$ and CDF $F_{X}$, respectively. The stress-strength probability (or reliability) is defined as

There are several applications of this theory such as in engineering and manufacturing, aerospace and defense, automotive industry, energy sector, healthcare, and electronics, among others. See ^[19] for more details.

The stress-strength reliability framework is versatile and finds various applications in economics. Besides this contribution regarding financial data, previous works researched economic inequality ^[19,20]. Regarding financial data, the authors explored stress-strength reliability framework in ^{[21,22,23,24]}.

The stress-strength probability for the extreme Fréchet, Weibull, and Gumbel distributions has been widely studied in the literature. Nadarajah ^[25] considered the class of extreme value distributions and derived the corresponding forms for the reliability $R$ in terms of special functions. Confidence limits for $R$ involving Weibull models were presented in ^[26]. Kundu & Raqab ^[27] proposed a modified maximum likelihood estimator of $R$ and obtained the asymptotic distribution of the modified maximum likelihood estimators, which was used to construct the confidence interval of $R$. The previous results of $R$ for Weibull distribution were generalized by Nojosa & Rathie ^[28], where $R$ was expressed in terms of $H$-functions. Bayesian estimation of $R$ for Fréchet and Weibull distributions has also been explored ^[29,30].

The goal of this paper is to present an asset selection approach based on the probability $R = P(X < Y)$ when both $X$ and $Y$ present the distributions of returns of two assets. In particular, we seek to derive an expression of $R$ when $X$ and $Y$ have three-parameter GEV distributions and to propose an estimation procedure of $R$ by not using transformations in the data and with as fewer parameter restrictions as possible.

The paper is organized as follows: In Section 2, we define the $H$-function, $\mathbb{H}$-function and the three-parameter GEV distribution. Section 3 deals with the derivation of $R$ when $X$ and $Y$ are independent GEV RVs. The maximum likelihood estimation for $R$ is presented in Section 4. In Section 5, we present Monte-Carlo simulations for the estimation of $R$ and also deal with two real situations involving log-returns of stock prices and different-length carbon fibers. The last section deals with the conclusions and the Appendix presents the correlation matrices of the data set modeled in Section 5.

2.   Preliminaries

In this section, we present definitions and results on which our contributions are based.

2.1.   Special functions

Recently, Rathie et al. ^[31] introduced the extreme-value $\mathbb{H}$-function as:

where $\Re (a_1), \Re (a_2), \Re (a_4) \in\mathbb{R}_+, a_3, a_5\in\mathbb{C}$, not both $\Re (a_1)$ and $\Re (a_2)$ can be equal to zero at the same time, $\Re (a_6) > -1$ when $a_1 \neq 0$ or $a_1 = 0$ and $\text{sign} (a_3) = \text{sign} (a_5)$, $\Re (a_6) < -1$ when $a_1 = 0$ and $\text{sign} (a_3) \neq \text{sign} (a_5)$. In this paper, $\mathbb{R}$, $\mathbb{C}$ and $\Re$ denote the real numbers, complex numbers and the real part of a complex number, respectively.

In this work, we are interested in the case $a_6 = 0$. Thus, we omit such a parameter from the representation and denote only:

In the following sections, we prove that all stress-strength probabilities involving three-parameter GEV distribution with shape parameters of equal sign can be written as $\mathbb{H}$-functions.

Note that (2.1) generalizes some important cases of the $H$-function (cf. ^[32]) defined by

where $0 \leq m \leq q$, $0 \leq n \leq p$ (not both $m$ and $n$ simultaneously zero), $A_j > 0$ ($j = 1, \cdots, p$), $B_k > 0$ ($k = 1, \cdots, q$), $a_j$ and $b_k$ are complex numbers such that no poles of $\Gamma (b_k + B_k s)$ ($k = 1, \cdots, m)$ coincide with poles of $\Gamma (1-a_j - A_j s)$ ($j = 1, \cdots, n)$. $L$ is a suitable contour $w -i \infty$ to $w + i \infty$, $w\in\mathbb{R}$, separating the poles of the two types mentioned above. For more details, see ^[32].

An important special case of this function is obtained by taking $a_4 = 0$, which represents an upper (or lower) bound for its value depending on the sign of $a_5$. This case is, therefore, an extreme value of the function and can be written in terms of the $H$-function as ^[31]:

when $\text{sign} (a_3) = \text{sign} (a_5)$ and:

otherwise.

2.2.   Three-parameter GEV distribution

The three-parameter GEV distribution is obtained by taking CDF of the same type of the standard GEV $G$ defined in (1.2). That means, $G(x; \mu, \sigma, \gamma) = G\left(\frac{x-\mu}{\sigma}\right)$. We denote by $X\sim GEV(\mu, \sigma, \gamma)$, $\mu, \gamma\in\mathbb{R}$ and $\sigma\in\mathbb{R}_+$, an RV with CDF given by

where $\mu$ is the location parameter, $\sigma$ is the scale parameter and $\gamma$ is the shape parameter. The corresponding probability density function (PDF) is given by

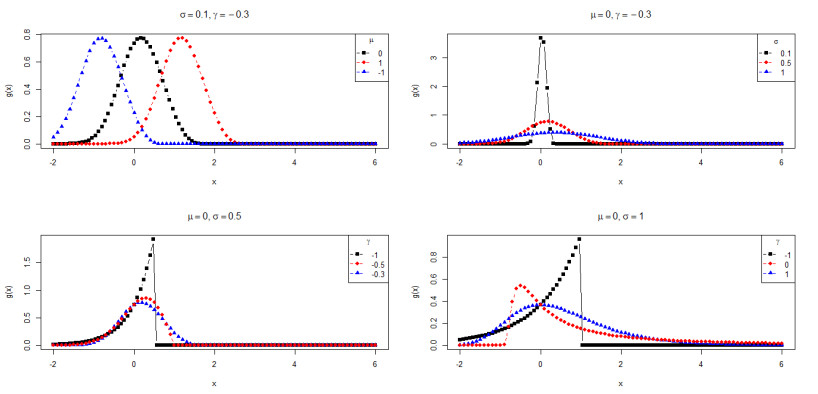
Figure 1 shows the behavior of $g$ for some parameter choices. Note that the location parameter shifts the curve, the scale controls dispersion, and the density changes according to the sign of the shape parameter.

3.   Main results

In this section, the reliability of two independent three-parameter GEV RVs is derived in terms of the $\mathbb{H}$-function. In addition, with suitable parameter restrictions, representations of $R$ as an $H$-function and an explicit form are obtained. We consider the case of two independent GEV distributions with different shape parameters (but of the same sign). Cases of opposite signs of shape parameters are not normally of interest, as it would indicate that random variables with incompatible support are being compared. Therefore, these cases are not treated in the present paper.

Theorem 3.1. Let $Y$ and $X$ be independent RVs, respectively, with distribution $GEV(\mu_1, \sigma_1, \gamma_1)$ and $GEV(\mu_2, \sigma_2, \gamma_2)$, $\mu\in\mathbb{R}$, $\sigma_j\in \mathbb{R}_+$, $\gamma_j\in \mathbb{R} \; (\gamma_j\neq 0)$, $j = 1, 2$. Then

● When $\gamma_j > 0$, $j = 1, 2$:

provided that $\mu_1-\frac{\sigma_1}{\gamma_1}\geq\mu_2-\frac{\sigma_2}{\gamma_2}$. When $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$:

● When $\gamma_j < 0$, $j = 1, 2$:

provided that $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$. When $\mu_1-\frac{\sigma_1}{\gamma_1}\geq\mu_2-\frac{\sigma_2}{\gamma_2}$:

In particular, if $\mu_1-\frac{\sigma_1}{\gamma_1} = \mu_2-\frac{\sigma_2}{\gamma_2}$, we have

Proof. Set $\mu_j\in\mathbb{R}$, $\sigma_j, \gamma_j\in\mathbb{R}_{+}$ ($j = 1, 2$). Then

where $M = \max\left\{ \mu_1-\frac{\sigma_1}{\gamma_1}, \mu_2-\frac{\sigma_2}{\gamma_2}\right\}$. Substituting $y = \left[1+\frac{\gamma_1}{\sigma_1}(x-\mu_1)\right]^{-\frac{1}{\gamma_1}}$ and taking $M = \mu_1-\frac{\sigma_1}{\gamma_1}$, we can rewrite (3.6) as

Hence, (3.1) follows from (2.1) and (3.7). For the case where $\gamma_j > 0$, $j = 1, 2$ and $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$, it suffices to notice that $P(X < Y) = 1-P(Y < X)$ and the result in (3.1) is applied with interchanged sub-indices. For the cases where $\gamma_j < 0$, $j = 1, 2$, the same rationale can be applied, just noticing that in such cases $x$ mostly takes negative values. The case where $\gamma_j = 0$, $j = 1, 2$, can be obtained as a limiting procedure and shall be explicitly explored later on the present paper. In addition, applying (2.4) with $\mu_1-\frac{\sigma_1}{\gamma_1} = \mu_2-\frac{\sigma_2}{\gamma_2}$, we obtain (3.5). □

Remark 3.2. In a practical scenario, the estimates $(\hat{\mu}_1, \hat{\sigma}_1, \hat{\gamma}_1, \hat{\mu}_2, \hat{\sigma}_2, \hat{\gamma}_2)$ should be obtained. Then, if $sign(\hat{\gamma}_1) = sign(\hat{\gamma}_2)$, the conditions $\mu_1-\frac{\sigma_1}{\gamma_1}\geq\mu_2-\frac{\sigma_2}{\gamma_2}$ or $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$ must be verified and the corresponding $R$ expression should be used.

Next, we consider some special cases of two independent GEV random variables. We have the following immediate consequence of Theorem 3.1:

Corollary 3.3. Let $Y\sim GEV(\mu_1, \sigma_1, \gamma_1)$ and $X\sim GEV(\mu_2, \sigma_2, \gamma_2)$ be independent RVs, with $\gamma_1 = \gamma_2 = \gamma\in\mathbb{R}, \gamma\neq0$, $\mu_1, \mu_2\in\mathbb{R}$, $\sigma_1, \sigma_2\in\mathbb{R}_+$ and $\mu_1-\mu_2 = \frac{\sigma_1}{\gamma}-\frac{\sigma_2}{\gamma}$. Then, we have

Lastly, we consider the cases of two independent GEV with $\gamma_1 = \gamma_2 = 0$.

Theorem 3.4. Let $Y$ and $X$ be independent RVs, respectively, with distribution $GEV(\mu_1, \sigma_1, 0)$ and $GEV(\mu_2, \sigma_2, 0)$, $\mu_j\in\mathbb{R}$, $\sigma_j\in\mathbb{R}_+$, $j = 1, 2$. Then

Proof. Set $\mu_j\in\mathbb{R}$ and $\sigma_j\in\mathbb{R}_+$ ($j = 1, 2$). Then

Substituting $y = \exp\{-x/\sigma_1\}$, we can rewrite (3.10) as

Hence, (3.9) follows from (2.1) and (3.11). □

We have the immediate consequence of Theorem 3.4.

Corollary 3.5. Let $Y\sim GEV(\mu_1, \sigma_1, 0)$ and $X\sim GEV(\mu_2, \sigma_2, 0)$ be independent RVs, with $\sigma_1 = \sigma_2 = \sigma\in\mathbb{R}_+$. Then, we have

The results presented in Theorems 3.1 and 3.4 are more general than that presented in the literature. The $\mathbb{H}$-function allows us to write the probability $R$ with as little parameter restrictions as possible. Table 1 lists related studies and their parameter restrictions.

Remark 3.6. The particular case of GEV while $sign(\gamma) = -1$ (cf. ^[14]) is called reversed Weibull. The Weibull distribution studied by the authors cited in Table 1 is obtained as the limit of a normalized minimum of i.i.d. RVs. That is, the Weibull distribution is obtained by

where $X_1, \cdots, X_n$ are i.i.d. RVs of $F$ and $a_n$ and $b_n$ are suitable sequences of constants (see Theorem 2.1.5 in ^[14]).

3.1.   Multicomponent system reliability

Let $X_1, \cdots, X_n$ be i.i.d. RVs with distribution $GEV(\mu_2, \sigma_2, \gamma_2)$ and $Y$ be an independent RV with distribution $GEV(\mu_1, \sigma_1, \gamma_1)$. Set $M_n = \max\{X_1, \cdots, X_n\}$. Then, $P(M_n\leq u) = G^n(u; \mu_2, \sigma_2, \gamma_2)$ and we have

Closed expressions for (3.14) are presented in the following result. Its proof follows the same steps of Theorems 3.1 and 3.4 and it will be omitted.

Theorem 3.7. Let $X_1, \cdots, X_n$ be i.i.d. RVs with distribution $GEV(\mu_2, \sigma_2, \gamma_2)$ and $Y$ be an independent RV with distribution $GEV(\mu_1, \sigma_1, \gamma_1)$. Then

● When $\gamma_j > 0$, $j = 1, 2$:

provided that $\mu_1-\frac{\sigma_1}{\gamma_1}\geq\mu_2-\frac{\sigma_2}{\gamma_2}$. When $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$:

● When $\gamma_j < 0$, $j = 1, 2$:

provided that $\mu_1-\frac{\sigma_1}{\gamma_1}\leq\mu_2-\frac{\sigma_2}{\gamma_2}$. When $\mu_1-\frac{\sigma_1}{\gamma_1}\geq\mu_2-\frac{\sigma_2}{\gamma_2}$:

● When $\gamma_1 = \gamma_2 = 0$:

Remark 3.8. In a broader k-out-of-n multicomponent reliability context, consider independent RVs $Y, X_1, \cdots, X_k$ with $Y\sim GEV(\mu_1, \sigma_1, \gamma_1)$ and $X_j\sim GEV(\mu_2, \sigma_2, \gamma_2)$, for $j = 1, \cdots, k$ ($X_j's$ are i.i.d.). The reliability for this kind of model is given by

Using a binomial expansion, we obtain

Note that the integral terms in (3.20) are particular cases of (3.14) provided that $n = k-r$. Therefore,

4.   Estimation

This section deals with parameter estimation for $R = P(X < Y)$ given two independent GEV RVs. The literature presents some maximum likelihood estimators for $R$ considering explicit forms of $R$ obtained by strong parameter restrictions on extreme value distributions (such as ^[27,29,30]). Those approaches require the estimation of the parameters to be done jointly in the two samples. In our case, we release any requirements about having the same parameters between different samples, since we deal with expressions of $R$ in terms of functions $\mathbb{H}$.

Consider the PDF $g(\cdot; \mu, \sigma, \gamma)$ defined in (2.7). Take $\mathbf{X} = (X_1, \cdots, X_n)$ as a sample of $n$ observations. The likelihood function for the $GEV(\cdot; \mu, \sigma, \gamma)$ is given by:

where $\mathbb{1}_A$ denotes the indicator function on the set $A$. Note that $\prod_{i = 1}^n\mathbb{1}_{[1+\gamma(X_i-\mu)/\sigma > 0]} > 0$ if and only if $x_i\in supp\; g(\cdot; \mu, \sigma, \gamma)$ for all $i = 1, \cdots, n$. Here, $supp\; g$ denotes the support of the function $g$. Then, if $\gamma\neq0$, we are not able to obtain the MLE explicitly, so an additional numeric procedure is required in the likelihood maximization (see ^[6] for a more detailed discussion).

Remark 4.1. Set $\mathbf{X} = (X_1, \cdots, X_n)$, a random sample of $GEV(\mu_2, \sigma_2, \gamma_2)$, and $\mathbf{Y} = (Y_1, \cdots, Y_m)$, a random sample of $GEV(\mu_1, \sigma_1, \gamma_1)$, with $\gamma_j > 0$, $j = 1, 2$ and $\mu_1-\sigma_1/\gamma_1 \geq \mu_2-\sigma_2/\gamma_2$ (or $\gamma_j < 0$, $j = 1, 2$ and $\mu_1-\sigma_1/\gamma_1 \leq \mu_2-\sigma_2/\gamma_2$). Let $\hat{\mu}_i, \hat{\sigma}_i, \hat{\gamma}_i$ ($i = 1, 2$) be the estimates of $\mu_i, \sigma_i, \gamma_i$. We are able to estimate $R$ by the invariance property of MLE, as follows:

Alternatively, whenever $\gamma_j > 0$, $j = 1, 2$ and $\mu_1-\sigma_1/\gamma_1 \leq \mu_2-\sigma_2/\gamma_2$ (or $\gamma_j < 0$, $j = 1, 2$ and $\mu_1-\sigma_1/\gamma_1 \geq \mu_2-\sigma_2/\gamma_2$), the same invariance property can be applied, leading to:

This is due to the Theorems 3.1 and 3.4 that describe $R$ in terms of the function $\mathbb{H}$ (which is an integral, hence a continuous and measurable function).

Whenever a single set of realizations of the random variables involved is available, the MLE approach above is of utmost importance. This is the case, for example, of asset selection, when a single time series of observed returns is available for each asset.

On the other hand, to illustrate the suitability of the analytical closed-form expressions hereby derived, a direct simulation approach can be carried out. In such case, several samples of size $n$ can be drawn from each random variable, which are then used to estimate the empirical value of $R$ and can be repeated several times. Both approaches will be explored in the next section.

5.   Application

5.1.   Simulation study

To evaluate the correctness of the closed-form expression for $R$ given in Theorem 3.1, we generate $N$ Monte-Carlo samples, each of which is size $n$, of the random variables $GEV(\mu_2, \sigma_2, \gamma_2)$ and $GEV(\mu_1, \sigma_1, \gamma_1)$. In these cases, the values of $\mu_2, \sigma_2, \gamma_2, \mu_1, \sigma_1, \gamma_1$ are pre-specified.

The GEV distribution with negative shape parameter is treated in Tables 2 and 3 where we analyze the estimates $\hat{R}$, bias and root mean squared error (RMSE). Table 4 deals with positive shape parameter.

For the simulation, for each line in the Tables 2–4, the following procedure was carried out:

(1) for each Monte-Carlo sample, the estimate $\hat{R}$ is computed empirically, simply as $n^{-1} \sum_{i} I(x_i < y_i)$, where $I(.)$ is an indicator function, which is 1 for true arguments and 0 otherwise;

(2) $\hat{R}_{MC}$ is evaluated by taking the sample mean of the Monte-Carlo samples $\hat{R}$;

(3) the bias is computed as the difference between the value obtained by Theorem 3.1 and $\hat{R}_{MC}$. The same follows for the RMSE, which also considers the true value as the analytically obtained one.

As expected, Tables 2 and 3 illustrate that the analytical results obtained match the empirical ones. This is a clear evidence of the correctness of the new expressions hereby derived. Besides, it is clear that increasing the sample size $n$ leads to more precise estimations of $R$, indicating reduced bias and greater consistency. In Table 4 we observe the same good behavior of the estimator characterized by low bias and RMSE.

5.2.   Brazil stock market

In order to evaluate the proposed framework, we modeled stock prices log-returns as GEV and compare them in a reliability sense. For this, we assume that the returns are independent. To meet independence requirements, we take stock log-returns that are not correlated and correlations are measured using Pearson, Kendal and Spearman methods.

Denote $X_1, X_2, X_3$ and $X_4$ the stock price log-returns of BBAS3, ITUB4, VALE3 and VIIA3, respectively. The data sets are retrieved directly through the software R ^[34] by the command

quantmod::getSymbols("BBAS3.SA", src = "yahoo", auto.assign = FALSE, from = '2022-01-01', to = '2023-04-30', return.class = 'xts').

The data sets have information in Brazilian currency (R＄, BRL).

Summary statistics for the data sets $X_1, X_2, X_3$ and $X_4$ are presented in Table 5. A boxplot is presented in Figure 2 showing the symmetry around zero of the log-returns and that $X_4$ has more dispersion than the others.

Maximum likelihood (ML) estimates and Kolmogorov-Smirnov (KS) p-values are given in Table 6. Figure 3 shows histograms and the fit of the GEV model to $X_1, X_2, X_3$ and $X_4$. For each data set, the empirical CDF (ECDF) is compared to the theoretical model in Figure 4.

Although the p-value of the Kolmogorov-Smirnov test is small for the BBAS3 ($X_1$), the graphical analysis does not invalidate the good fit of the distribution to the data.

Aiming at estimating probabilities of the type $R = P(X < Y)$ via Theorems 3.1–3.4, we need $X$ and $Y$ to be independent RVs. In this sense, we analyzed the dependency structures of $X_1, \cdots, X_4$ using the Pearson, Kendal and Spearman correlation matrices, and the results are presented in the Appendix. The pairs chosen to be compared are $X_3-X_2$, $X_3-X_4$ and $X_3-X_1$.

Reliability measures of the type $R = P(X < Y)$ appear in a decision process of an investor. In summary, when $X$ and $Y$ represent profit RVs and $R < 1/2$, it is advisable that the investor chooses the variable $X$. If $R > 1/2$, the opposite occurs. The case $R = 1/2$ is inconclusive. Thus, knowing how to evaluate $R$ accurately is important to support the decision process. In this sense, Table 7 presents the estimates of $P(X_3 < X_1)$, $P(X_3 < X_2)$ and $P(X_3 < X_4)$ and the $95\%$ bootstrap confidence intervals (CI). For all subsequent Tables, $\hat{R}$ is the estimate obtained by first fitting the dataset to a GEV distribution and using the results from Remark 4.1 (invariance property of MLE of the parameters and the analytical expression obtained for $R$). Also, $\hat{R}_{NP}$ is a non-parametric estimation of $R$, which considers a similar approach as in the simulation study (uses an indicator function to compare samples from the two distributions). Finally, $\hat{R}_{Boot}$ is the mean value of the bootstrap estimation of $R$ using the non-parametric approach and the CI reported is for such mean.

The estimates of $R$ indicate that, within the analyzed time period, VALE3 would be preferred over BBAS3 and ITUB4, while VIIA3 would be preferred over VALE3. On the other hand, the bootstrap CI estimates indicate that only the case $P(X_3 < X_4)$ was conclusive since $0.5$ does not belong to the estimated confidence interval.

It is important to compare different distributions as candidate models for the log-returns modelling. Considering previous results in the literature ^[11], we compared the performance of the GEV and generalized logistic distributions as models for daily returns, as presented in Table 8.

It is possible to see that both GEV and generalized logistic provided quite similar modelling capabilities (about the same log-likelihood values). Since the two distributions considered have three parameters, there is no need to consider information criteria.

5.2.1.   Considering weekly maximum log-returns

Instead of considering the log-returns for the closing prices, as in the previous analyses, one may study how the weekly maximums (or minimums) behave. This has a direct economic interpretation: a proxy for greater profits (or greater losses, i.e., shortfalls and values-at-risk) and has been explored in the literature ^[11,12,18].

Following previous studies ^[12], it is of interest to explore the modelling scenario where the maximum returns are considered GEV random variables. Table 9 show the GEV ML estimates for such case.

Table 9 indicates that the GEV random variable is adequate for every case considered, which is expected as the EVT predicts such convergence. Now that the parameters have been obtained, Table 10 presents the reliability calculations.

Since $R = 0.5$ is within the confidence intervals, the metric becomes inconclusive. It is possible to notice, on the other hand, that if $\hat{R}$ is considered as a metric by itself, it would precisely reflect the high volatility of VIIA3, which suffered severe instability and losses during the time window analyzed.

Besides the direct application to financial assets selection, some engineering applications can also benefit from the new relations hereby defined. One application is illustrated in the next subsection.

5.3.   Carbon fibers

Stress-strength reliability can be also applied to the modelling and comparison of carbon fibers of lengths 10 and 20 mm. The data represent the strength data measured in GPa (gigapascal), for single carbon fibers tested under tension. The data are frequently used in the literature and are also presented below (e.g., ^[28]).

Carbon fibers of length 20 mm:

Carbon fibers of length 10 mm:

Table 11 and Figure 5 show the summary statistics of $X$ and $Y$ in which it is possible to observe that $Y$ (carbon fibers of length 10 mm) tend to have greater strength values than $X$ (carbon fibers of length 20 mm).

ML estimates and KS p-values for the GEV model are presented in Table 12 and the good fit can be observed in Figure 6.

The estimates of stress-strength reliability and bootstrap $95\%$ CI are $\hat{R} = 0.774$ and $(0.699, 0.851)$, respectively. It is easy to conclude that since $P(X < Y) > 1/2$ and 0.5 is not within the CI, that $X < Y$ statistically, i.e., the fibers with length of 10 mm have statistically greater strength values than the ones of length of 20 mm.

6.   Conclusions

Despite its significant limitations, Markowitz's modern portfolio theory is still relied upon by many practitioners because of its user-friendly simplicity. This way, studying alternative approaches that are also of straightforward comprehension is of utmost importance.

In this paper, we studied the stress-strength reliability $R = P(X < Y)$ when both $X$ and $Y$ follow three-parameter GEV distributions. In summary, when $X$ and $Y$ represent return RVs and $R < 1/2$, it is advisable that the investor chooses the variable $X$. If $R > 1/2$, the opposite occurs. The case $R = 1/2$ is inconclusive. Thus, exact expressions for $R$ have been obtained in terms of the extreme-value $\mathbb{H}$-function with minimal parameter restrictions. With additional restrictions, it was shown that $R$ can be calculated in terms of $H$-functions and even in terms of standard functions (such as exponential functions).

Monte-Carlo simulations attested to the performance of the analytical closed-form expressions hereby derived. By applying our methodology to real-world financial data, we could orient a stock selection procedure by calculating $P(X < Y)$ when both $X$ and $Y$ represent stock returns. Besides, an engineering application was also described, where carbon fibers tested under tension were modelled in a stress-strength reliability sense.

Appendix

In this appendix, we present the correlation matrices of the data sets (log-returns) modeled in Section 5. Thus, Tables 13–15 give the correlations of Pearson, Spearman and Kendal, respectively.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors acknowledge the support provided by the University of Brasilia (UnB). Additionally, M.O. acknowledges the Coordination for the Improvement of Higher Education Personnel (CAPES) for awarding him a scholarship for a Master of Science program.

Conflict of interest

The authors declare no conflicts of interest.