Collecting silences: creating value by assetizing carbon emission mitigations and energy demand reductions

1.   Introduction

Currently, the study of non-linear fractional differential equations (NLFDEs) play a key role in the arena of solitary wave theory. The analysis of such models ^[1,2,3], is significant to understand the everyday physical phenomena in non-linear evolution models. Nowadays technological developments have exposed that, fractional calculus have developed as a dominant instrument in numerous fields of applied sciences and engineering ^[4,5]. A big advantage of fractional models is that their narrative is more suitable than the ordinary models ^[6]. These properties motivate our interest to yield consideration in a noteworthy and appropriate model for (4+1)-dimensional fractional-order non-linear Fokas equation. Non-linear Fokas equation is one of the well-known physical models ^[7,8] that defines a huge diversity of phenomena, such as non-linear optics, fluid mechanics, condensed matter, and plasmas. The properties of fractional derivatives are complex, therefore, it is not easy to solve fractional-order problems using novel derivatives. As for as we know, there is no regular scheme to answer the fractional-order non-linear models. A number of novel arithmetical and analytical schemes ^{[9,10,11,12,13,14,15,16,17,18,19,20]}, are suggested for fractional-order models by using ordinary calculus, however, it's static task for the scholars. Fokas ^[21] improved the Lax couples of integrable non-linear KP and DS equations, and consequent the simple wave equation. In wave systems, DS and KP models are proposed to define the surface and internal waves in canals with altering depth and breadth ^[22,23]. The Fokas equation has many applications in quantum mechanics and plasma physics to explore the transmission of solitons. The important applications of the Fokas equation lie in real world problems considered as a higher dimensional integrable model in mathematical physics. The importance of the Fokas equation suggests that the idea of complexifying time can be investigated in the context of modern field theories via the existence of integrable nonlinear equations in four spatial dimensions involving complex time ^[24,25]. In this paper, we deal the non-linear fractional-order (4+1)-dimensional Fokas equation (FE),

where $u$ is a function and wave velocity physically also $0 < \alpha < 1$. While $\alpha = 1$ then Eq (1.1) converts to simple (4+1)-dimensional FE. Assume this general Eq (1.1) to designate the gesture of waves in multifaceted broadcasting. It shows the distortion or dispersion of the external wave. So, various types of solution of FE will offer us proposals to instruct the multifaceted system of DS and KD models. Also, according above-stated evidences and the significant uses of the FE, it is crucial to discover the innovative solitons solutions of Eq (1.1). In recent times, physicists and mathematicians have great concern to discover the Eq (1.1), such as Zhang et al. ^[26] applied the sub-equation method (SM) to determine the solution of Eq (1.1) using some derivative in the form of rational, trigonometric, and functions of hyperbolic. Zhang et al. ^[27] utilized the new SM, in fractional form of $(G0 = G)$-expansion scheme. Choi et al. ^[28] applied the SM using different schemes and attained the novel analytical solutions of Eq (1.1). Zhang ^[29] used Exp-function method to explore the solitary wave solution of Eq (1.1). Zhao et al.^[30] suggested the improved fractional $(G0 = G)$-expansion scheme and acquire the exact solutions. Solitons are used to denote the particle-like properties of non-linear pulses. The significance of solitons is due to their existence in a variety of non-linear differential equations representing many complex nonlinear phenomena, such as acoustics, optics, convictive fluids, condensed matter, and solid-state physics. There are numerous type of solitary wave and solitons solutions ^{[31,32,33,34,35,36,37,38,39,40,41]}.

The study of non-linear PDEs has become much significant in pure and applied mathematics from many years. Through the aid of computer technology, the new horizons are opened in the field of applied sciences for the mathematicians. There has been a growing interest in PDEs which are frequently used in engineering sciences and mathematical physics. The PDEs arise commonly in biological and physical sciences as well. Many problems of physics, chemistry, and engineering lead naturally to the resolution of PDEs. In the light of the literature review, there are various models of PDEs, particularly, PDEs whose exact solutions need to be discussed. The application of non-linear PDEs in mathematical modeling has induced a motivation for research in the field of differential problems.

The prominent concern of this existing study is to utilize the novel meanings of fractional-order derivative, named conformable derivative, for space-time fractional-order $(4+1)$-dimensional FE. As our best knowledge the considered methods have not been utilized for such model in the literature. Several type of solutions in the form of bright soliton, dark soliton, combined dark-bright soliton, periodic soliton and general solitary waves solutions of FE are missing in the literature. As compared our obtained results with previous existing results in literature, some of results are not available in literature with other methods lies in ^{[42,43,44,45,46]}. In this article our goal is to discover novel various soliton solutions of (4+1)-dimensional fractional-order non-linear Fokas equation using Sardar-subequation ^[47,48] and new extended hyperbolic function method ^{[49,50,51,52]}. As a result, novel soliton solutions are more generalized and in different form which have never been obtained before. To the best of our knowledge, these novel properties and interesting structures are investigated for the first time in (4+1)-dimensional Fokas equation. Our results enrich the variety of the dynamics of higher-dimensional non-linear wave field. It is hoped that these results will provide some valuable information in the higher-dimensional non-linear field.

The layouts of this paper are: Section 2 contains the governing model. Section 3 consists on the analysis of the methods. In section 4 the applications of the proposed methods are presented. Section 5 describes results and discussion and conclusion of this work is presented in section 6.

2.   Conformable derivative

Progress in fractional-calculus is more beneficial for scholars to express the physical phenomena with novel techniques. Newly, Caputo et al. ^[53] modified the Caputo derivative ^[54], Atangana-Baleanu (AB) presented a novel fractional derivative (FD), known as AB derivative ^[55]. In 2014, Khalil et al. ^[56] proposed a conformable derivative. The Caputo, Riemann-Liouville (RL) ^[57,58], and further derivatives do not follow the simple instructions, which are supposed by Newtonian kind simple derivative. Such as:

(1) For RL derivative, $D_t^{\alpha}P\neq 0$, $P$ is any constant.

(2) For Caputo and RL derivative,

(3) For Caputo and RL derivative,

Definition 2.1: ^[56] The FD of a function $k = k(t):\; [0, \infty)\longrightarrow \Re$ of order $\varsigma > 0$ is described as

At $\varsigma = 1$, the fractional-order derivative converted to integer-order derivative.

Theorem 2.2: We have the following properties when $\varsigma\in(0, 1]$ and $k, \; k_1$ are conformable functions as follows:

$\bullet D_t^{\varsigma}k(t) = t^{1-\varsigma}\frac{dk(t)}{dt}$.

$\bullet D_t^{\varsigma}t^h = ht^{n-\varsigma}, \forall h\in R$.

$\bullet D_t^{\varsigma}c = 0$, $\forall$ constant functions $k(t) = 0$.

$\bullet D_t^{\varsigma}(p_1*k(t)+p_2*k_1(t)) = p_1*D_t^{\varsigma}k(t)+p_2*D_t^{\varsigma}k_1(t), \; \; \forall p_1, p_2 \in R$.

$\bullet D_t^{\varsigma}(k(t)k_1(t)) = k(t)D_t^{\varsigma}k_1(t)+k_1(t)D_t^{\varsigma}h(t)$.

$\bullet \frac{D_t^{\varsigma}k(t)}{k_1(t)} = \frac{k_1(t)D_t^{\varsigma}-k(t)D_t^{\varsigma}k_1(t)}{k_1(t)^2}$.

$\bullet D_t^{\varsigma}(k \; o\; k_1)(t) = t^{1-\varsigma}k'_1(t)k'(k_1(t))$.

3.   Analysis of the methods

In this section, we have analyzed two methods that are applied to construct novel solitons solutions of the given model.

3.1.   Sardar-subequation method

In this section, we describe the offered methods to solve the fractional model, we assume the proposed model as

where $u$ is a function. Using following wave transformations in (3.1)

here $v$ is frequency while $\beta_1, \; \beta_2, \; \beta_3, \; \beta_4$ are wave lengths, respectively. Using (3.2) into (3.1), we yield an ODE as follows

Where $U'$, $U''$ and $U'''$ are the first, second and the third derivatives of $U$, respectively w. r. t $\eta$ and so on.

where $F_j$ are constants and $\Phi(\eta)$ accept the (3.7) as follows

here $\epsilon$ and $\delta$ are constants.

Case 1: When $\delta > 0\; and\; \epsilon = 0$, then

where, $sech_{pq}(\eta) = \frac{2}{pe^{\eta}+qe^{-\eta}}, \; csch_{pq}(\eta) = \frac{2}{pe^{\eta}-qe^{-\eta}}$.

Case 2: When $\delta < 0\; and\; \epsilon = 0$, then

where, $sec_{pq}(\eta) = \frac{2}{pe^{\iota \eta}+qe^{-\iota \eta}}, \; csc_{pq}(\eta) = \frac{2\iota}{pe^{\iota \eta}-qe^{-\iota \eta}}$.

Case 3: When $\delta < 0\; and\; \epsilon = \frac{\delta^2}{4b}$, then

where, $tanh_{pq}(\eta) = \frac{pe^{\eta}-qe^{-\eta}}{pe^{\eta}+qe^{-\eta}}, \; coth_{pq}(\eta) = \frac{pe^{ \eta}+qe^{-\eta}}{pe^{ \eta}-qe^{-\eta}}$.

Case 4: When $\delta > 0\; and\; \epsilon = \frac{\delta^2}{4}$, then

where, $tan_{pq}(\eta) = -\iota\frac{pe^{\iota \eta}-qe^{-\iota \eta}}{pe^{\iota \eta}+qe^{-\iota \eta}}, \; cot_{pq}(\eta) = \iota\frac{pe^{\iota \eta}+qe^{-\iota \eta}}{pe^{\iota \eta}-qe^{-\iota \eta}}$.

3.2.   New EHFM

The new EHFM has two phases as follows.

Form 1: Consider FPDE is taken in (3.1) and using the wave transformations in (3.2) to obtain (3.3). Assume (3.3) admits the solution as follows:

where $F_j$ are constants and $\Phi(\eta)$ accept the (3.7)

On balancing in (3.3) the value of $N$ is obtained. Inserting (3.6) into (3.3) along with (3.7), yields a set of equations. By resolving the equations, we get the solutions that accepts (3.5), as

Set 1: When $\Lambda > 0$ and $\Delta > 0$,

Set 2: When $\Lambda < 0$ and $\Delta > 0$,

Set 3: When $\Lambda > 0$ and $\Delta < 0$,

Set 4: When $\Lambda < 0$ and $\Delta > 0$,

Set 5: When $\Lambda > 0$ and $\Delta = 0$,

Set 6: When $\Lambda < 0$ and $\Delta = 0$,

Set 7: When $\Lambda = 0$ and $\Delta > 0$,

Set 8: When $\Lambda = 0$ and $\Delta < 0$,

Form 2: Adopting the procedure as earlier, consider that $\Phi(\eta)$ accept the following ODE as

Substituting (3.6) into (3.3) along with (3.16), gets a set of equations with the values of $F_j\; (j = 1, \; 2, \; \; 3, ...M)$. We assume that (3.5) has solutions as

Set 1: When $\Lambda \Delta > 0$,

Set 2: When $\Lambda \Delta > 0$,

Set 3: When $\Lambda \Delta < 0$,

Set 4: When $\Lambda \Delta < 0$,

Set 5: When $\Lambda = 0$ and $\Delta > 0$,

Set 6: When $\Lambda \in R$ and $\Delta = 0$,

Note: $sn$ is well-known sign function.

4.   Application

Here, we construct the solitons solutions of fractional-order Fokas equation. The Eq (1.1) with Eq (3.2) becomes

4.1.   Application of the SSM

Now, we apply the SSM to solve the (4+1)-dimensional FE. Using balance method on (4.1), gets $M = 2$, so (3.6) decreases to

where $F_0$, $F_1$ and $F_2$ are constants. Inserting (4.2) into (4.1) and comparing the coefficients of $\Phi(\eta)$ to zero, we get a set of equations in $F_0, \; F_1, \; F_2, \; \epsilon\; and\; v$.

Working on the set of equations, yields

Case 1: When $\delta > 0\; and\; \epsilon = 0$, then

Case 2: When $\delta < 0\; and\; \epsilon = 0$, then

Case 3: When $\delta < 0\; and\; \epsilon = \frac{\delta^2}{4b}$, then

Case 4: When $\delta > 0\; and\; \epsilon = \frac{\delta^2}{4}$, then

4.2.   Application of the new EHFM

Form 1: Now, we apply the new EHFM to solve the (4+1)-dimensional FE. Using balance method in (4.1), yields $M = 2$, so (3.6) changes to

where $F_0$, $F_1$ and $F_2$ are constants. Inserting (4.18) into (4.1) and associating the constants of $\Phi(\eta)$ with zero, we yield the equations in $F_0, \; F_1, \; F_2, \; \Lambda\; and \; \Delta$.

On working set of equations, we achieve

Set 1: When $\Lambda > 0$ and $\Delta > 0$,

Set 2: When $\Lambda < 0$ and $\Delta > 0$,

Set 3: When $\Lambda > 0$ and $\Delta < 0$,

Set 4: When $\Lambda < 0$ and $\Delta < 0$,

Set 5: When $\Lambda > 0$ and $\Delta = 0$,

Set 6: When $\Lambda < 0$ and $\Delta = 0$,

Set 7: When $\Lambda = 0$ and $\Delta > 0$,

Set 8: When $\Lambda = 0$ and $\Delta < 0$,

where $\eta = \beta_1\frac{x^\alpha}{\alpha}+\beta_2 \frac {y^\alpha}{\alpha}+\beta_3\frac{z^\alpha}{\alpha}+\beta_4\frac{w^\alpha}{\alpha}-v\frac{t^\alpha}{\alpha}$.

Form 2: Utilizing balance method in (4.1), gives $M = 2$, so (3.6) converts to

where $F_0$, $F_1$ and $F_2$ are numbers. Inserting (4.28) into (4.1) and associating the constants of $\Phi(\eta)$ with zero, we attain set of equations in $F_0, \; F_1, \; F_2, \; \Lambda, \; and \; \Delta$.

On working the set of equations, we achieve

Set 1: When $\Lambda \Delta > 0$,

Set 2: When $\Lambda \Delta > 0$,

Set 3: When $\Lambda \Delta < 0$,

Set 4: When $\Lambda \Delta < 0$,

Set 5: When $\Lambda = 0$ and $\Delta > 0$,

Set 6: When $\Lambda \in R$ and $\Delta = 0$,

where $\chi = sgn(\Lambda)$, $\eta = \beta_1\frac{x^\alpha}{\alpha}+\beta_2 \frac {y^\alpha}{\alpha}+\beta_3\frac{z^\alpha}{\alpha}+\beta_4\frac{w^\alpha}{\alpha}-v\frac{t^\alpha}{\alpha}$.

5.   Results and discussion

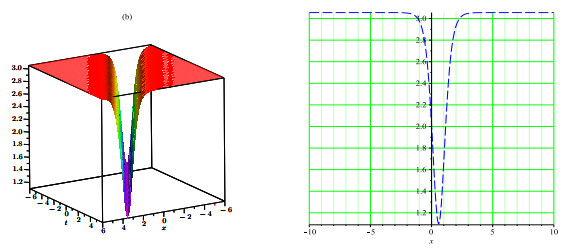
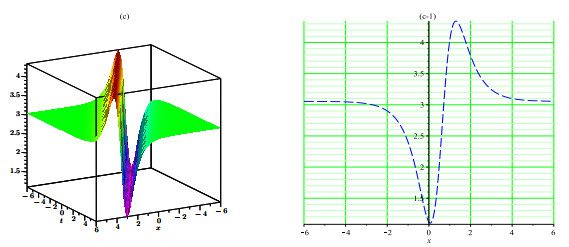
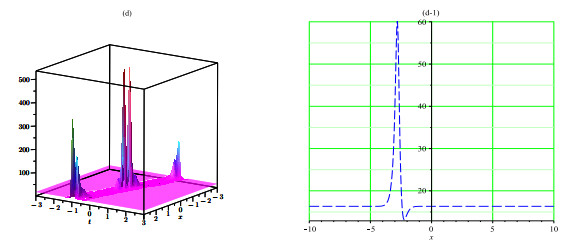
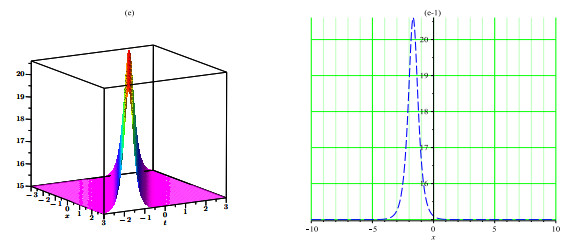
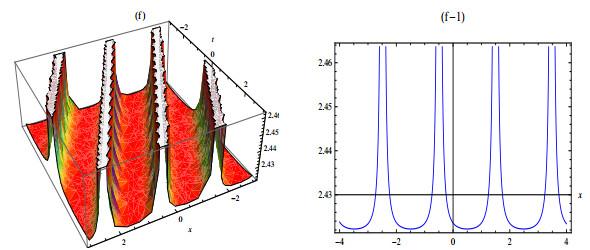
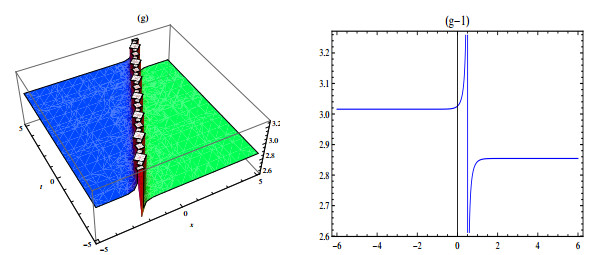
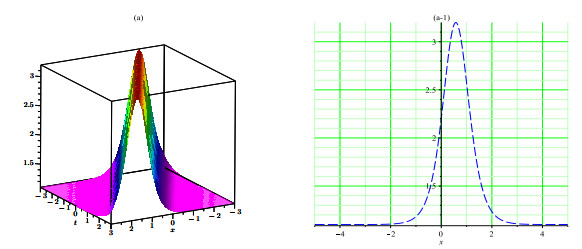
Herein study, we have successfully built various solitons solutions for the (4+1)-dimensional Fokas equation applying SSM and new EHFM. The proposed methods are measured most efficient techniques in this field and that are not applied to this model previous. To analyze physically, 3D and 2D graphs of some selected results are added with suitable parameters. These obtained solutions determine their applications in propagation to carry information since solitons have the competency to mobile long spaces without drop and shifting their systems. In this study, we added only certain figures (see Figures 1–7) to dodge overloading the document. Absolutely the achieved results are fresh and different from that reported results.

6.   Conclusions

We have constructed novel multi solitons solutions for the nonlinear fractional-order Fokas equation by applying the SSM and new EHFM. From results we obtained multi solitons solutions such as dark, singular, bright and periodic solitons. By the purpose of describe the behavior of achieved solutions of the model, we plotted some particular solutions by assigning the suitable values to the parameters involved. The obtained results may have much inspiration in various fields of physical sciences. From obtained results, we can know that the under study techniques are proficient, consistent and beneficial for rescuing the exact solutions of nonlinear FPDEs in a wide range. Also, these results are supportive to learn the dynamics of nonlinear waves in optics, hydrodynamics, solid state physics, and plasma. In future, we anticipate that this study is a step towards the solutions of such kinds of higher dimensional problems by using the proposed methods in this study. This work may be extended for a novel fractional order Fokas dynamical model in future.

Acknowledgments

The work in this paper has been supported by the Polish National Science Centre under the grant OPUS 14 No. 2017/27/B/ST8/01330.

Conflict of interest

The authors declare that they have no conflicts of interest.