Stability analysis and optimal control of COVID-19 with quarantine and media awareness

1.   Introduction

The year 2020 will be an extraordinary year. Since December 31, 2019, the 27 case of unknown pneumonia were reported in Wuhan City of Hubei Privince in South China ^[1]. The virus has been gradually discovered around the world after that, which is a new strain of coronavirus that has never been found in humans before. The new virus that caused the outbreak of pneumonia in Wuhan was originally known as coronavirus. On January 12, 2020, the World Health Organization (WHO) provisionally named the virus 2019-nCoV. Subsequently, on February 11, the WHO held a press conference in Geneva to announce the official designation of the infectious virus COVID-19. The Coronavirus Study Group (CSG) formally recognizes this virus as a sister to severe acute respiratory syndrome coronviruses (SARS-CoVs) of the species Severe acute respiratory syndrome-related coronavirus and designates it as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) ^[2].

Infectious diseases have been threatening people's health all over the world, and many researchers focus their attention on the study of epidemic models. The basic SIR models are used widely to investigate epidemic diseases ^[3,4,5,6], however, diseases like urticaria, tuberculosis and AIDS have a long-time infectious process, therefore SIR model is improved to SEIR model ^[7,8,9]. In the general prevention and treatment of infectious diseases, besides the usual hospitalization for drug treatment, there are measures such as vaccination, artificial isolation, spraying disinfectant, and media coverage. According to the characteristics of infectious diseases, various models of infectious diseases have been established and studied with different control measures. With isolation as a control, an epidemic model is studied and some possible impact on the susceptible individuals is discussed by Jana ^[10]. With the rampant spreading of infectious diseases, it is necessary to allocate the resources on prevention and treatment rational, so as to minimize financial, material and human resources for reducing the burden of the country. Therefore, investigation of the optimal control problem of infectious disease model is necessary. Gao ^[11] considered three intervention strategies in a TB model, including vaccination of susceptible, treatment of both latent and infectious individuals. With the increasing influence of media publicity, more investigations are focused on revealing the impact of media coverage on disease transmission. People will consciously conduct disease isolation under the influence of media publicity, and hygiene will also reduce the risk of disease through media coverage frequent hand washing. In addition, media coverage will enable susceptible people to timely detect the early symptoms of infectious diseases and acquire some therapeutic tips, so as to have a positive impact on disease prevention and control. However, excessive and inappropriate media coverage not only consume lots of financial resources, but also causes unnecessary social troubles. Therefore, the optimal control strategy for media is also worth studying. Das ^[12] proposed and analyzed a tuberculosis transmission mathematical model to consider the social awareness effects during an epidemic, and they proved the existence and obtained the characterization of the optimal media control. In addition, considering the saturation incidence and treatment function, Kar studied the optimal control of an SEIR infectious disease model to evaluate the impact of media and treatment control ^[13].

There has been considerable research on COVID-19. However the origin of infection is still not found, and the disease was first discovered at a seafood market in Wuhan, China, therefore it is thought that the disease spread from bats to humans. Chen ^[14] developed a Bats-Hosts-Reservoir-People transmission network model for simulating the phase-based transmissibility of the disease, and it is showed that the transmissibility of SARS-CoV-2 was higher than Middle East respiratory syndrome in the Middle East countries, similar to severe acute respiratory syndrome but lower than MERS in the Republic of Korea by calculating the basic reproduction number. Khan ^[15] proposed a mathematical model for coronavirus (2019-nCoV) and analyzed the dynamics behaviors of the disease by describing the brief details of interaction among the bats and unknown hosts. General SEIR-type epidemiological models incorporating appropriate compartments relevant to interventions such as quarantine, isolation and treatment are investigated ^[16,17]. Up till now, as no practical vaccine has been developed, the impact of media coverage on society is particularly important while actively cooperating with hospital treatment. In this paper, the saturation treatment function is introduced to the model ^[16], and we explore the influence of optimal control on the model by taking treatment and media coverage as control parameters. The novel coronavirus elimination condition and the optimal control scheme are obtained by using dynamic analysis, calculation of basic reproduction number and investigation of optimal control. In this paper, the critical threshold of the system is calculated, and the conditions for the global stability of the equilibrium are obtained. Therefore, it is found that the global stability is closely related to the total number of initial susceptible groups. When the susceptible population is in a given condition, the disease will not disappear completely, and the virus will change from pandemic to local epidemic. In the long run, the development trend and optimize the control of the disease are estimated through the stability and optimization analysis of the disease dynamics system.

The paper is organized as follows. In Section 2, we developed the SEIR model by introducing the saturation treatment function and media parameter. In Section 3, qualitative analysis are done to the developed system. In Section 4, a control model is proposed to investigate the optimal control on treatment and media coverage. Finally, in Section 5, several numerical simulations are given to verify the conclusions, and the conclusions are included in Section 6.

2.   The mathematical model

Assume that $S(t)$ are susceptible, $E(t)$ are exposed individuals, $A(t)$ denote infected individuals but not yet symptomatic, $I(t)$ are those infected individuals with symptoms, $H(t)$ are hospitalized individuals, $R(t)$ are recovered individuals, $S_q(t)$ are quarantined susceptible, and $E_q(t)$ are isolated exposed individuals. Considering that interventions such as quarantine, isolation and treatment, Tang and Wang ^[16] proposed a nonlinear 2019-nCoV model system as follows:

From ^[16], the treatment rate increases as infected cases increase. However, due to the limited therapeutic capacity, the rate of treatment tends to be constant even with further increase in infections. Following ^[13], we have the following assumptions:

(i) The treatment function is taken in saturated form as $\frac{buH}{1+\gamma uH}$. With the elapse of time, the treatment rate will gradually increase. However, due to the shortage of treatment resources and limited treatment capacity, the treatment rate will eventually tend to a constant.

(ii) Due to the needs of economic development, The inflow of population is limited to a fixed constant, which is considered as recruitment rate $S_0$.

(iii) The media effect $M$ is introduced. It is assumed that under the influence of media publicity, some susceptible people directly transition to the rehabilitation group at the rate of $pSM$.

Based on the above assumptions, system (2.1) is developed to the following model with media effect and saturation treatment function:

Since the variable $R$ of system $(2.2)$ does not appear in the first seven equations, which implies that the influence individuals in the recovery subclass does not transmit infection. In the subsequent analysis, we only consider the following subsystem:

with the initial conditions as:

3.   Dynamics analysis

First, we study the boundedness and the basic reproduction number, and then we try to find the endemic equilibrium and its stability.

3.1.   Uniform boundedness of model

From system (2.3), we have

The above rates are all non-negative over the boundary planes of the non-negative cone of $R_+^7$. Therefore, for all nonnegative initial value points, the solutions of the system are positively bounded. $\frac{dI}{dt}|_{[S > 0, E\geq0, I = 0, A\geq0, S_q\geq0, E_q\geq0, H\geq0]}\geq0$ and $\frac{dA}{dt}|_{[S > 0, E\geq0, I\geq0, A = 0, S_q\geq0, E_q\geq0, H\geq0]}\geq0$ mean that the existence of individuals with symptomatic or asymptomatic infection can lead to the spread of the disease. $\frac{dH}{dt}|_{[S > 0, E\geq0, I\geq0, A\geq0, S_q\geq0, E_q\geq0, H = 0]}\geq0$ means that sufficient quarantine can promote the decrease of hospitalized individuals.

Next, we prove that solutions are bounded in the nonnegative cone of $R_+^7$. For system (2.3), as $S_q\leq S$, we have

Then we have

so $\frac{dI}{dt} < \sigma\varrho \mathcal{M}-(\delta_I+\alpha+\gamma_I)I$ and $\frac{dA}{dt} < \sigma(1-\varrho) \mathcal{M}-\gamma_A A$, then we have $I(t) < \frac{\sigma\varrho \mathcal{M}}{\delta_I+\alpha+\gamma_I}\triangleq \mathcal{N}$, $A(t) < \frac{\sigma(1-\varrho) \mathcal{M}}{\gamma_A}$.

Because of

for all $t > 0$, $H(t)$ is bounded as well, that is $H(t) < \frac{\delta_I \mathcal{N}+\delta_q\mathcal{M}}{\alpha}$. Therefore, system (2.3) is well posed and the solutions are bounded for all time, which is summarized in the following theorem.

Theorem 1. The solutions of system (2.3) with initial value (2.4) remain positive in $R_+^7$ as $t > 0$, and uniformly bounded in the region $\Gamma = \{(S, E, \cdots, H)\in R_+^7:(S+E+S_q+E_q)(t)\leq\mathcal{M}, I(t) < \mathcal{N}, A(t) < \frac{\sigma(1-\varrho) \mathcal{M}}{\gamma_A}, H(t) < \frac{\delta_I \mathcal{N}+\delta_q\mathcal{M}}{\alpha}\}$.

3.2.   Basic reproduction number

Basic reproduction number is the number of new infections induced by a single infected individual during the whole time period per day, it is critical to the spread of the infectious diseases. Obviously, system (2.3) has a disease-free equilibrium $P_0 = (\frac{S_0}{pM}, 0, \cdots, 0)$. To calculate the basic reproduction number $R_0$, the next-generation matrix method is used in the paper studied by van den Driessche and Watmough ^[18].

Let us write the system (2.3) as $\frac{d\chi}{dt} = \mathcal{F}-\mathcal{V}$, where $\chi = (E, E_q, I, A, H, S, S_q)^T$, $\mathcal{F} = \left(\begin{array}{c} \beta c(1-q)S(I+\theta A)\\ \beta cqS(I+\theta A)\\0\\0\\0\\0\\0 \end{array}\right)$, and $\mathcal{V} = \left(\begin{array}{c} \sigma E\\ \delta_q E_q\\(\delta_I+\alpha+\gamma_I)I-\sigma\varrho E\\ \gamma_A A-\sigma(1-\varrho)E\\ \alpha H+\frac{buH}{1+\gamma uH}-\delta_I I-\delta_q E_q\\ \frac{(\beta c+cq(1-\beta))S(I+\theta A)}{1+\alpha(I+\theta A)}-\lambda S_q+pSM-S_0\\ \lambda S_q-(1-\beta)cqS(I+\theta A) \end{array}\right)$.

The jacobian matrices of $\mathcal{F}$ and $\mathcal{V}$ at $P_0$ are given by

where $F = \left(\begin{array}{cccc} 0 & 0 & \frac{S_0\beta c(1-q)}{pM} & \frac{S_0\beta c(1-q)\theta}{pM}\\ 0 & 0 & \frac{S_0\beta cq}{pM} & \frac{S_0\beta cq\theta}{pM}\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{array}\right)$, $V = \left(\begin{array}{cccc} \sigma & 0 & 0 & 0\\ 0 & \delta_q & 0 & 0\\ -\sigma\varrho & 0 & \delta_I+\alpha+\gamma_I & 0\\ -\sigma(1-\varrho) & 0 & 0 & \gamma_A \end{array}\right)$.

According to the Theorem 2 in ^[17], the basic reproduction number is the spectral radius $\rho$ of the matrix $FV^{-1}$, and it is $R_0 = \rho(FV^{-1}) = \frac{S_0\beta c(1-q)}{pM}[\frac{(1-\varrho)\theta}{\gamma_A}+\frac{\varrho}{\delta_I+\alpha+\gamma_I}]$.

3.3.   Equilibrium points

The model always has a disease-free equilibrium (DFE) $P_0 = (\frac{S_0}{pM}, 0, \cdots, 0)$. To get an endemic equilibrium $P^* = (S^*, E^*, \cdots, H^*)$, we compute that

In addition, $H$ satisfies

so there exists a unique $H^*$. And $E$ satisfies $S_0-\frac{\sigma E}{1-q}-pSM = 0$, so we obtain that $E = \frac{(1-q)S_0(R_0-1)}{\sigma R_0}$, then when $R_0 > 1$, we have $E^* = \frac{(1-q)S_0(R_0-1)}{\sigma R_0}$.

Theorem 2. The model system (2.3) always exists a disease-free equilibrium point $P_0 = (\frac{S_0}{pM}, 0, 0, \cdots, 0)$, and exists an endemic equilibrium point $P^* = (S^*, E^*, \cdots, H^*)$ when $R_0 > 1$. There exists no endemic equilibrium point when $R_0\leq1$.

3.4.   Stability of the equilibrium point

Since the last two equations of system (2.3) are independent from the others, for stability analysis purpose we omit the last two equations, but to investigate the optimal control problem we will consider all these equations. The jacobian matrix $J$ is given by

Theorem 3. The disease-free equilibrium ($P_0$) is locally asymptotically stable(unstable) if $R_0 < 1\; (R_0 > 1)$.

Proof. The eigenvalues of the above jacobian matrix at $P_0$ have $-\alpha-bu$, $-\delta_q$, $-pM$, $-\lambda$, and the other three eigenvalues are the roots of the following equation:

when $R_0 > 1$, the eigenvalues have at least one positive root, so it is unstable as $R_0 > 1$.

when $R_0 < 1$, note that

$a_0 = \gamma_A\sigma(\delta_I+\alpha+\gamma_I)(1-R_0)$, $a_1 = (\sigma+\gamma_A)(\delta_I+\alpha+\gamma_I)+\gamma_A\sigma-\frac{S_0\beta c(1-q)\sigma}{pM}(\varrho+\theta(1-\varrho)$, $a_2 = \sigma+\delta_I+\alpha+\gamma_I+\gamma_A$, $a_3 = 1$,

The characteristic roots of Eq (3.3) are either real negative or with negative real parts if it satisfies Routh-Hurwitz criterion $a_0 > 0$, $a_2 > 0$, $a_3 > 0$ and $a_1a_2-a_0a_3 > 0$. For Eq (3.3), we have

according to the practical significance of infectious diseases, we have $\delta_I+\alpha+\gamma_I > \gamma_A$, then

Therefore the disease-free equilibrium is locally asymptotically stable when $R_0 < 1$.

Next, we construct a Lyapunov function

Differentiating with respect to t, we have

By Lyapunov LaSalle's theorem, we have

Theorem 4. When $R_0\leq1$, the disease-free equilibrium $P_0$ is globally asymptotically stable in the interior of $\Gamma$ of system (2.3) if $\frac{\beta c+cq(1-\beta)}{pM}S_0 < \min\{\alpha+\gamma_I, \frac{\gamma_A}{\theta}\}$.

Theorem 5. When $R_0 > 1$, the unique endemic equilibrium point $E^*$ is globally asymptotically stable in the interior of $\Gamma$ of system (2.3) if

and

Proof. To prove global stability of the unique endemic equilibrium point, we construct a Lyapunov function

Differentiating with respect to t, we have

Using Theorem 1 and the bounds of the populations, it can be found that if inequality (Eq 3.4) hold, then $\frac{dL_2}{dt} < 0$, and $\frac{dL_2}{dt} = 0$ iff $S = S^*$, $E = E^*$, $I = I^*$, $A = A^*$, $S_q = S_q^*$, $E_q = E_q^*$, $H = H^*$ in $\Gamma$. By Lyapunov LaSalle's theorem, $E^*$ is globally asymptotically stable in the interior of $\Gamma$.

Note 1. According to Theorem 5, in the absence of vaccine, in order to control disease stability, expanding media coverage and actively doing a good job in quarantine and prevention is needed.

Note 2. As $R_0 = 1$, Theorem 4 gives the condition of global stability of disease-free equilibrium. Following Theorems 2 and 3, system (2.3) has an endemic equilibrium when $R_0 > 1$ and there exists no endemic equilibrium point when $R_0\leq1$, therefore it undergoes the forward bifurcation of transcritical bifurcation. We use numerical simulation to verify the stability in the Section 5.

Note 3. Let $S_0 = 1.5 \times 10^4$, $c = 0.22781$, $\beta = 0.03$, $q = 4.18887\times10^{-5}$, $b = 0.1$, $u = 0.5$, $\theta = 4.5$, $\lambda = 20$, $p = 0.88$, $M = 300$, $\sigma = 4$, $\varrho = 0.09998$, $\delta_I = 0.13266$, $\gamma_I = 2.2029$, $\alpha = 200$, $\gamma_A = 1.0013978$, $\delta_q = 125.9$, $\gamma = 0.014$, then inequality (Eq 3.4) in Theorem 5 holds, which is not an empty set. Therefore, from Theorem 5, we have that there are appropriate parameters to make the endemic equilibrium globally stable.

3.5.   Sensitivity analysis

Form the above discussion, if reducing the basic reproduction number $R_0$ to less than 1, COVID-19 will be eliminated. Therefore, it is reasonable to investigate the influence of parameters on the basic reproduction number ($R_0$). We now analyze the sensitivity of the parameters using the method given by Chitnis ^[4] to examine the robustness of $R_0$.

Definition. The normalized forward sensitivity index for the variable $c$ is denoted by $\Gamma_c^{R_0}$, and $\Gamma_c^{R_0}$ is defined as $\Gamma_c^{R_0} = \frac{\partial R_0}{\partial c}\times\frac{c}{R_0}$.

For the sensitivity analysis of system (2.3), the parameter estimates obtained from ^[13,14,16], as well as the normalized forward sensitivity index of $R_0$, are given in Table 1.

As is shown in Table 1, probability of transmission per contact $\beta$, contact rate $c$ and media control parameter $M$ are the most sensitive parameters. The least sensitive parameter is the quarantined rate $q$. Therefore, in order to reduce the basic reproduction number and thereby control the spread of the disease, it is the most effective way to reduce contact with individuals (decrease $c$), reduce the possibility of transmission (decrease $\beta$), and increase media coverage (increase $M$), such as maintaining an even greater distance, avoiding crowds, and wearing a mask. The epidemic information should be open, accurate and transparent in time, and the progress and common sense of the epidemic situation should be popularized.

4.   The optimal control

Considering the costs and expenses of quarantine, treatment and media awareness program, it is urgent to find out the optimal strategy. We construct the objective functional as follows according to ^[11,13]:

$B_1, B_2$ are the per capita losses caused by the presence of symptomatic infected individuals and ineffective treatment prognosis, respectively. The weight corresponding to the square of treatment and media awareness control is taken as $B_3, B_4$ respectively, which represent the cost due to treatment and media publicity. We need to find a pair of optimal control $(u^*, M^*)$ such that

where $\phi = \{(u, M)|u, M$ is Lebesugue measure and $0\leq u(t), M(t)\leq 1\; for\; t\in[0, t_1]\}$ is the control set.

To obtain the optimal control solution $(u^*, M^*)$, we now use Pontryagin's Maximum Principle ^[13,19,20]. Then Hamiltonian $\mathcal{L}$ is as follows:

Here, $(\lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5, \lambda_6, \lambda_7)\in R^5$ is known as adjoint variable, which is determined by solving the following equations

with transversality conditions $\lambda_i(t_1) = 0$, for $i = 1, 2, \cdots, 7$.

Note that the solution of system (4.1) is $(\bar{\lambda}_1, \bar{\lambda}_2, \dots, \bar{\lambda}_7)$, then we verify the existence of optimal control pair.

Theorem 6. There exists a pair of optimal control $(u^*, M^*)$ satisfied

Proof. To verify the existence, the following properties is needed ^[20,21]:

1) The set of controls and corresponding state variables is non-empty.

2) The control $\phi$ set is closed and convex.

3) The RHS of the state system is bounded by a linear function in the state and control variables.

4) The integrand of the objective functional is concave on $\phi$.

5) There exist constants $c_1, c_2 > 0$ and $\zeta > 1$ such that the integrand of the objective functional is bounded above by $c_2-c_1(\left|u_1(t)\right|^2+\left|u_2(t)\right|^2)^{\zeta/2}$.

Then we have

1) The system (2.3) has bounded coefficients, following Lukes ^[22], we have the boundness of solution of system (2.3).

2) From the practical meaning of control set, $\phi$ is closed and convex.

3) As $1+\gamma uH > 0$, the right side of the equations in system (2.3) is continuous. Again, it can be calculated by using the property of upper bounds(super-solutions) $\hat{S}, \hat{E}, \cdots, \hat{H}$ of the following equations:

Following Theorem 1, $S(t)\leq\mathcal{M}$($\mathcal{M}$ is a constant), then the above system can be written in vector form:

It is a linear system and the time interval is finite, then the super-solutions are uniformly bounded. In addition, system (2.3) is bilinear in control and in the following vector form:

where $\boldsymbol{x} = [S(t), E(t), \cdots, H(t)]^T$, $\boldsymbol{u} = [u(t), M(t)]^T$, and $\boldsymbol{v}$ is a constant coefficient vector valued function about $\boldsymbol{x}$.

Using the boundness of the solutions, we have

where $Q$ depends on the coefficients of the system.

4) Note the objective functional

Now we prove $(1-q)\boldsymbol{Z}(t, \boldsymbol{x}, \boldsymbol{u})+q\boldsymbol{Z}(t, \boldsymbol{x}, \boldsymbol{v})\leq\boldsymbol{Z}(t, \boldsymbol{x}, (1-q)\boldsymbol{u}+q\boldsymbol{v})$.

As

and

$\boldsymbol{Z}(t, \boldsymbol{x}, (1-q)\boldsymbol{u}+q\boldsymbol{v}) = S(t)-B_1I(t)-B_2A(t)-B_3[(1-q)u_1(t)+qu_2(t)]^2-B_4[(1-q)M_1(t)+qM_2(t)]^2.$ Then we have

Hence, the function $\boldsymbol{Z}(t, \boldsymbol{x}, \boldsymbol{u})$ is concave in the control set $\phi$.

5) We have $S(t)-B_1I(t)-B_2A(t)-B_3u^2(t)-B_4M^2(t)\leq S(t)-B_3u^2(t)-B_4M^2(t)\leq c_2-c_1(u^2(t)+M^2(t))^{\zeta/2}$, where $c_2$ is an upper bound of $S(t)$ with $c_1 = \min\{B_3, B_4\}, \zeta = 2$.

Therefore, there exists a pair of optimal control $(u^*, M^*)$ such as the objective functional (4.1) is the maximum.

Remark. The specific form of the optimality system is as follows:

where $S(0), E(0), I(0), A(0), S_q(0), E_q(0), H(0)\geq0,$ and $\lambda_i(t_1) = 0, i = 1, 2, ..., 7.$

Theorem 7. The optimal controls $(u^*, M^*)$ with corresponding solutions to the state system $\bar{S}$, $\bar{E}$, $\cdots$, $\bar{H}$, which minimizes $J$ over the region $\phi$, is given by

where $\bar{u} = \frac{1}{3\gamma\bar{H}}(\frac{2B_3^{1/3}}{(B+6\bar{H}\sqrt{C})^{1/3}}+\frac{(B+6\bar{H}\sqrt{C})^{1/3}}{2B_3^{1/3}}-2), \; \; \bar{M} = -\frac{\bar{\lambda}_1 p\bar{S}}{2B_4}$,

with $B = 8B_3-54\gamma\bar{\lambda}_7b\bar{H}^2, \; \; \; C = 81\bar{\lambda}_7^2b^2\bar{H}^2\gamma^2-24\bar{\lambda}_7b\gamma B_3$.

Proof. The controls $\bar{u}$ and $\bar{M}$ satisfy the optimality conditions $\frac{\partial L}{\partial u} = 0$ and $\frac{\partial L}{\partial M} = 0$.

From $\frac{\partial L}{\partial M} = 0$, we have $\bar{M} = -\frac{\bar{\lambda}_1 p\bar{S}}{2B_4}$, then $\bar{\lambda}_1 < 0$.

From $\frac{\partial L}{\partial u} = 0$, we have $2B_3u(1+\gamma uH)^2 = -\lambda_7bH$, so $\lambda_7 < 0$. we obtain $2B_3\gamma^2H^2u^3+4B_3\gamma Hu^2+2B_3u+\lambda_7bH = 0$, and it has only one real root $\bar{u} = \frac{1}{3\gamma\bar{H}}(\frac{2B_3^{1/3}}{(B+6\bar{H}\sqrt{C})^{1/3}}+\frac{(B+6\bar{H}\sqrt{C})^{1/3}}{2B_3^{1/3}}-2), \; \; \bar{M} = -\frac{\bar{\lambda}_1 p\bar{S}}{2B_4}$, where $B$ and $C$ are given.

As the two controls are bounded, and the upper and the lower bounds are $0$ and $1$, respectively. Then we have the optimal control pair.

Due to the bounds of the state system, the adjoint system has bounded coefficients which is linear in every variable. Therefore, the adjoint system (4.2) is bounded which is dependent on the final time $t_1$. For convenience, we consider the coefficient $\gamma = 0$ and then simplify $\frac{buH}{1+\gamma uH}$ into $buH$. Now we use the method in ^[11,23] to solve the uniqueness of the optimality system (4.3) for the small time window as follows:

Theorem 8. For $t_1$ sufficiently small, the solution to the system (4.3) is unique.

Proof. Suppose $(S, E, I, A, S_q, E_q, H, \lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5, \lambda_6, \lambda_7)$ and ($\widetilde{S}$, $\widetilde{E}$, $\widetilde{I}$, $\widetilde{A}$, $\widetilde{S}_q$, $\widetilde{E}_q$, $\widetilde{H}$, $\widetilde{\lambda}_1$, $\widetilde{\lambda}_2$, $\widetilde{\lambda}_3$, $\widetilde{\lambda}_4$, $\widetilde{\lambda}_5$, $\widetilde{\lambda}_6$, $\widetilde{\lambda}_7$) are two distinct solutions to the optimal system (4.3).

For $\mu > 0$, let

and the optimality conditions become

with $B = 16B^3_3\gamma^3H^3-108B^2_3\gamma^4\lambda_7bH^5,$ $C = 256B^6_3\gamma^6H^6$, $\widetilde{B} = 16B^3_3\gamma^3\widetilde{H}^3-108B^2_3\gamma^4\widetilde{\lambda}_7b\widetilde{H}^5,$ $\widetilde{C} = 256B^6_3\gamma^6\widetilde{H}^6$ and $\lambda_1, \widetilde{\lambda}_1, \lambda_7, \widetilde{\lambda}_7 < 0$.

From the first equation of system (4.3), we have

and

Next, we subtract the above two equations, multiply them by $x-\widetilde{x}$ on both sides, and then integrate both sides from 0 to $t_1$ to get the following result:

In order to simplify the inequality, we have

where $C$ depends on bounds for $x$, $\widetilde{y}$.

For $B\leq B+\sqrt{B^2-C}\leq 2B$ and $16B^3_3\gamma^3H^3\leq B\leq C_1^{3}(H+1)^6$($C_1$ is a positive constant), we have

As $H, \widetilde{H}$ is bounded, then there is a positive constant $C_2$, $C_3$ such that $(H-\widetilde{H})^2 = e^{2\mu t}(w-\widetilde{w})^2\leq e^{2\mu t_1}(w-\widetilde{w})^2 = C_3^2$ and

where $C_4 = \frac{(C_2+C_3)^2e^{2\mu t_1}}{9C_3}$.

It is easy to obtain that

where $C_5$ depends on bounds for $f$, $\widetilde{x}$.

Based on the above inequalities, we have

Similarly, we have

where $M_i(i = 1, 2, \dots, 7)$ and $N_j(j = 1, 2, \dots, 10)$ depend on the coefficients and the bounds of the state variables and co-state variables.

Now from the above conclusions, we obtain

Let the coefficients of system (4.4) be positive. For example, $\mu-(M_1+M_2+M_4+M_6+M_7)e^{\mu t_1}-(N_1+N_5) > 0$, then $\mu > M_1+M_2+M_4+M_6+M_7-N_1-N_5$, and $t_1 < \frac{1}{\mu}ln\frac{\mu+N_1+N_5}{M_1+M_2+M_4+M_6+M_7}$. Similarity, we obtain all of the other $\mu_i$ and $t_{1i}\; (i = 1, 2, \dots, 14)$. Take $\mu = \max\{\mu_i\}$, $t_{1} = \min\{t_{1i}\}$. Then we have

and

Hence the solution of system (4.3) is unique for small time.

Remark. If we choose a sufficiency large $\mu$ and a sufficiently small $t_1$, the solution of system (4.3) is unique, and then we can find the unique optimal control of system (4.2).

5.   Numerical simulations

This section of numerical simulation is obtained by using MATLAB software. At the beginning of the virus outbreak, large influx of population pour in Wuhan as it is just the Chinese new year vocation, and the size is about $S_0 = 2\times10^5$ ^[14]. Let these parameters $\{\lambda, \sigma, \alpha, \delta_q\} = \{1/14, 1/7, 1.7826\times10^{-5}, 0.1259\}$, the initial values are set as follows:

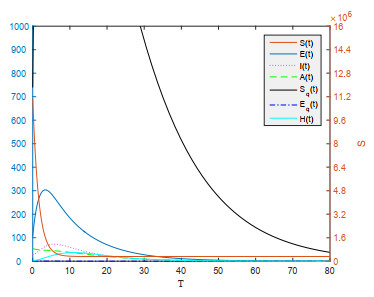
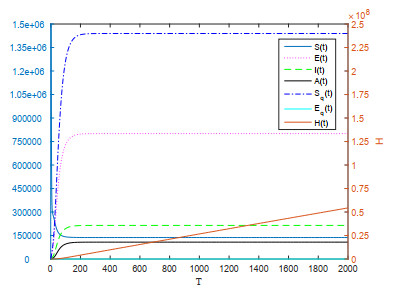
from Markov Chain Monte Carlo (MCMC) and WHO ^[17]. Now, we set several parameters related to treatment and media influence as $\{p, \gamma, b, u\} = \{0.78, 0.014, 0.5, 0.5\}$ ^[13]. Combining the data in Table 1, we have Figure 1, and it is shown that when $R_0 < 1$, the disease-free equilibrium point is stable. In addition, as shown in Figure 2, we increase $\beta$ to $2.1011\times10^{-7}$, the endemic equilibrium point appears and it is stable when $R_0 > 1$. Therefore only by controlling basic reproduction number below 1, the disease can be completely eliminated.

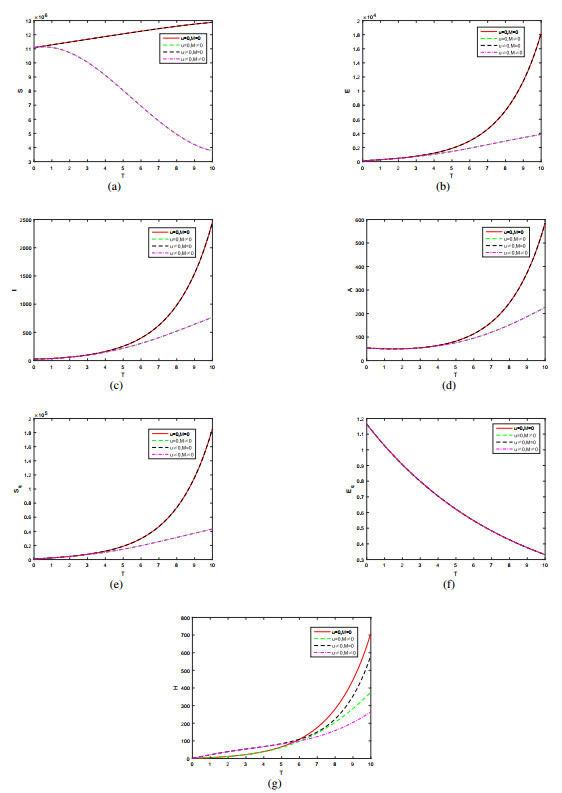
We still use the initial values of the outbreak area to simulate the optimal solution, the weights of the objective function are set to $B_3 = 150$, $B_4 = 10,000$. It is shown in Figure 3 that the media has a particularly large impact on disease prevention, control and treatment, which also verifies our previous sensitivity analysis. From $(a)$–$(f)$ of Figure 3, it is shown that while $u = 0, M = 0$ and $u\neq0, M = 0$, the lines overlap. While $u = 0, M\neq0$ and $u\neq0, M\neq0$, the lines also overlap. Therefore, we conclude that treatment has basically no effect on the spread of infectious diseases. Only by strengthening media publicity, the individuals will isolate themselves consciously, thus resulting in the decrease of the disease transmission rate, therefore media coverage has played a great role in disease prevention and control. However, it is shown in $(g)$ of Figure 3 that when $u\neq0, M\neq0$, the rate of increase in number of hospitalized individuals is becoming slower while compared with those short of controls, so media and treatment control co-function have a great effect on the hospitalized individuals. This provides us with an optimal strategy for disease prevention and control.

6.   Conclusions

The media campaign is particularly important when there is no vaccine or vaccines are not universal. In this paper, an improved COVID-19 model is given to investigate the influence of the treatment and media awareness. A nonlinear saturated treatment function is introduced in the model to lay stress on the limited medical conditions. Model analysis shows that the model has only two equilibrium points, namely disease-free equilibrium point and endemic equilibrium point. When $R_0 < 1$, the disease-free equilibrium point is stable, but when $R_0 > 1$, the disease-free equilibrium point becomes unstable. If $R_0 > 1$, the system begins to appear an endemic equilibrium point, and it is stable, which undergoes the forward bifurcation at $R_0 = 1$. An object function is constructed by taking treatment and media coverage as control parameters, and optimal control is used to guide the degree of execution of treatment and media awareness. Numerical analysis shown that media coverage is useful to prevent and control diseases, strengthening media coverage to reduce the contact rate is important for the disease control. The co-function of treatment and media campaign show great effect on reducing the number of hospitalized individuals, therefore beside media coverage, increasing the treatment rate to reduce the number of hospitalized individuals (such as setting up new hospitals, mobilization of doctors, etc.) is also important for the disease spreading. The values of optimal control are calculated to guide the control degree. The investigations show that controlling the media campaign is of great importance to prevent and control of COVID-19 after the outbreak.

With the development and popularization of vaccine, the COVID-19 model with vaccine and nonlinear transmission rate will be further studied. Under the influence of multiple parameters, bifurcation phenomena and limit cycles under multiple codimension will occur. These problems are interesting and worth studying, and we leave them for future research.

Acknowledgments

This research is supported by Natural Science Foundation of Beijing Municipality (No. 4202025).

Conflict of interest

The authors declare there is no conflict of interest.