Development and bioevaluation of controlled release 5-aminoisoquinoline nanocomposite: a synergistic anticancer activity against human colon cancer

1.   Introduction

Enormous interest has been focused on developing smart delivery vehicles capable of targeting and controlling the release of chemotherapeutic agents. Controlled drug release is very attractive as it overcomes various drawbacks of conventional chemotherapy. Limitations of using chemotherapy with subsequent adverse outcomes on healthy tissues can be attributed to incompatible pharmacokinetics as well as narrow therapeutic indices [1]. Recently, the utilization of smart polymers showed great potential for controlling drug release when subjected to external stimuli such as temperature, PH, electric/magnetic field, light, etc. [1]. Among the various thermoresponsive polymers, Poly(N-isopropyl acrylamide)(PNIPAAm) is the most extensively used candidate.

The current study reported the design of a core-shell drug loaded platform, in which SPIONs constitute the core that acts as the heat source, and PNIPAAm acts as the thermoresponsive shell, together they constitute the core shell magnetic thermoresponsive nanocomposite (MTN). 5-aminoisoquinoline (5-AIQ) acts as a PARP inhibitor loaded on MTN. This drug loaded magnetic thermoresponsive nanocomposite (MTN.5-AIQ) can be intravenously injected and targeted to the tumor site by a magnetic field gradient. An alternating magnetic field (AMF) then triggers heat production by the SPION cores, which consequently triggers drug release. The elevated temperature along with the chemotherapeutic agent are awaited to play synergistic roles in tumor treatment.

The thermoresponsive Poly(N-isopropylacrylamide) (PNIPAAm) is frequently used for drug delivery owing to its convenient coil to globule transition temperature; the effect that can favor its use over other alternatives in a multitude of biomedical applications [1],[2]. This polymer exhibits thermally reversible coil-to-globule phase transition when the temperature changes around the LCST of the polymer. At temperatures below its LCST, PNIPAAm becomes hydrophilic as it swells and extends in virtue of the intermolecular hydrogen bonds formed between polymer chains and water molecules. Whereas, above LCST, the polymer chain collapses, releases much of the water content and eventually shrinks. These reversible shrinking and water release of PNIPAAm are exploited for drug loading and release. The hydrophilicity of the polymer can be modified by association of SPIONs and drug loading resulting in an increase LCST. The high temperature generated by induction heating leads to coil-to-globule transition of the composite, followed by expulsion of the loaded drug in a controlled manner.

SPIONs act as tiny antennae that generate heat upon exposure to alternating magnetic field (AMF). They exhibit superparamagnetic behavior at room temperature, which implies that they can be magnetized by applying magnetic field and lose their magnetization when the field is removed [3]. Heat dissipation from these superparamagnetic nanoparticles is caused by two relaxation mechanisms; the rotation of the moments within the particle (Néel relaxation) and the physical rotation of the particle itself (Brownian or viscous loss) [4] upon exposure to AMF. Néel (τ_N) and Brownian (τ_B) magnetic relaxation times of a particle are given by Equation 1 and Equation 2 [5] respectively; where τ_N is the Néel relaxation time, τ_B is the Brownian relaxation time, V_m is the volume of the magnetic core, K is the anisotropy constant, k_B is the Boltzmann constant, T is the absolute temperature, f_° is an attempt frequency for changes in the dipole direction, η is the viscosity of the carrier fluid and V_hyd is the hydrodynamic volume of the particle.

PARP-1 belongs to the superfamily of more than seventeen enzymes that catalyzes the transfer of ADP-ribose units from its substrate NAD⁺ to several protein acceptors as single-strand break repair and base excision repair factors which contribute to DNA repair [6]. In general, PARP inhibitors act through competitive blocking of the NAD⁺ binding domain of the enzyme [7]; the effect which inhibits the repair of damaged DNA and facilitates apoptosis-dependent death of tumor cells [8]. 5-aminoisoquinoline (5-AIQ) is an active, water soluble inhibitor of Poly (ADP-ribose) polymerase-1 (PARP-1) that adjunctly promotes radiotherapy and chemotherapy of various cancer types [9]. The elevated mortality associated with metastatic colon cancer is attributed to further development of resistant microenvironments towards current drugs [10]–[12]. Today, different techniques are dedicated to prognose these types of resistance and the progress of their treatment regimens [13]. Latest chemotherapeutic protocols for colon cancer include DNA-modifying pharmaceuticals, like oxaliplatin or irinotecan, combined with 5-fluorouracil [14]. Furthermore, many studies revealed the anti-cancer effect of the natural flavonoids in treatment of colorectal cancers [15]–[17]. Such treatment regimens are initially successful in numerous patients, but ultimately, the majority of patients become resistant. A significant interpretation of this resistance in colon cancer is the frequent DNA repair mechanism-linked to high expression of PARPs enzymes [18]. Previous studies investigated the use of commercially available PARP-1 inhibitors like Olaparib alone or in combination with the chemotherapeutic agents , the latter was accepted as a promising candidate for treatment of colon cancer [19]. Magnetite coated with thermoresponsive polymer and its derivatives was previously synthesized for drug delivery and controlled drug release applications. Doxorubicin was loaded on the magnetite thermoresponsive nanocomposite and used as the anticancer model drug [20]–[22]. In addition, indomethacin was loaded on thermo-responsive magnetic nanoclusters grafted with Poly(N-isopropylacrylamide) and PNIPAAm-co-PEGMA copolymers and was used as the anticancer model drug [23]. The current work investigates the feasibility of loading 5-aminoioquinoline drug (5-AIQ) on the magnetic thermoresponsive polymer and its release kinetics.

2.   Materials and methods

2.1.   Chemicals

Ferric chloride hexahydrate (FeCl₃.6H₂O, 97%), ferrous chloride Tetrahydrate (FeCl₂.4H₂O, 98%), sodium hydroxide pellets (NaOH, 98%) and ammonium persulfate (APS, 98%) were purchased from LOBA CHEMIE PVT.LTD. While, N, isopropylacrylamide monomer (NIPAAm, 97%), N-methylene bisacrylamide (MBA, 99%), N,N,N′,N′Tetramethylethylenediamine (TEMED, 99%) and 5-Aminoisoquinoline (5-AIQ) and Phosphate buffer saline (PBS) were purchased from Sigma Aldrich. Caco-2 cell lines were purchased from the Cell Bank of Egyptian company for production of vaccine, sera and drugs (VACSERA) (Cairo, Egypt). (RPMI) medium, Methylthiazolyldiphenyl-tetrazolium bromide (MTT) and Dimethyl sulfoxide (DMSO) were obtained from Sigma-Aldrich, St. Louis, MO, USA. All used chemicals are analytical grade.

2.2.   Synthesis of superparamagnetic iron oxide nanoparticles SPIONs

SPIONs were prepared by the co-precipitation method. Briefly, 4.44 g of ferric chloride hexahydrate and 2.12 g of ferrous chloride tetra hydrate were dissolved in 150 ml of deionized water under magnetic stirring at 80 °C for 15 min; the pH of the solution was adjusted to 13 by addition of 10 M sodium hydroxide solution. After another 15 minutes of stirring at 80 °C, the black precipitate (iron oxide nanoparticles) was formed. The precipitate was separated by strong magnet and washed several times with distilled water. Finally, these nanoparticles were dried under vacuum at room temperature overnight. The obtained SPIONs powders were used for synthesis of magnetic thermoresponsive nanocomposite based on iron oxide and PNIPAAM (MTN).

2.3.   Synthesis of magnetic thermoresponsive nanocomposite (MTN)

N-isopropyacrylamide monomer was polymerized in the presence of SPIONs by free radical polymerization reaction. 66.4 ml solution of SPIONs (0.1 M) was added to 56.9 ml solution of NIPAAm monomer (0.28 M) and sonicated for 10 min. The mixture was transferred to a magnetic stirrer, during stirring, 4.74 ml of the crosslinker MBA solution (0.01 M) and 0.95 ml of the initiator APS (0.27 M) were added to the mixture. Afterwards, 1.8 ml TEMED was added to the final solution. Stirring was continued for 20 minutes and the solution was left without disturbance for 2 hours. The mixture was centrifuged at 13000 rpm to collect the magnetic thermoresponsive nanocomposites (MTN) and washed several times with deionized water. MTN was dried in vacuum at room temperature for 24 hours and subsequently used for drug loading and further characterization.

2.4.   Characterization

XRD pattern for SPIONs was obtained using an X-ray diffractometer (XRD, BRUKER Co. D8 ADVANCE-Germany) with CuKα radiation λ = 1.5418 Å. The crystallite size (T) of the sample was calculated by Scherrer equation (Equation 3) [24]; where β is the width of the peak at half maximum intensity for a specific plane with miller indices h, k, and l, whereas, C is the shape factor (taken as 0.9), λ is the wavelength of the incident X-ray and θ is the half angle between the incident and diffracted beams (2θ) in radians. The lattice parameter was calculated using Equation 4 [25]; where d _hkl is the interplanar spacing, and a is the lattice parameter.

FTIR spectra of SPIONs and magnetic thermoresponsive nanocomposite (MTN) samples, dispersed in KBr pellets, were obtained using FTIR (Nicolt 6700-USA) at 4 cm⁻¹ resolution. The morphology of magnetic thermoresponsive nanocomposites (MTN) was studied using high transmission electron microscope (HRTEM, JEM-2100, JEOL-Japan). The elemental composition of magnetic thermoresponsive nanocomposite (MTN) was determined using EDX spectroscopy (OXFORD INCA Penta FETX3- England).

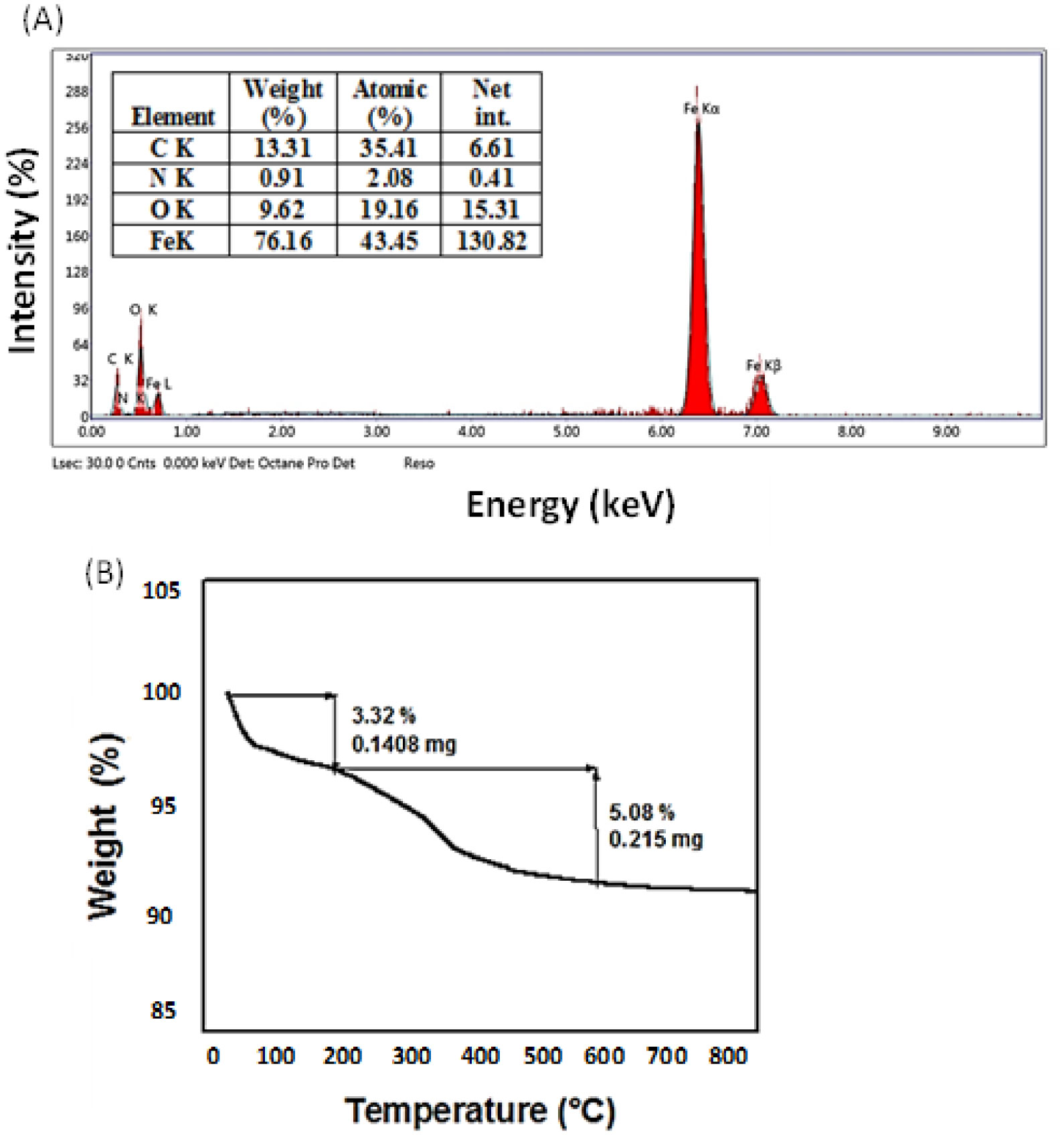
The polymer content in the magnetic thermoresponsive nanocomposite (MTN) was determined by thermogravimetric analyzer (TGA, SDT Q600 TA, USA) in the temperature range from room temperature to 850 °C at a heating rate of 10 °C min⁻¹ under nitrogen atmosphere.

The LCST of PNIPAAm and MTN.5-AIQ was estimated using differential scanning calorimeter (DSC, SDT Q600 TA, USA) in the temperature range from 25 to 70 °C at a heating rate of 5 °C min⁻¹ under nitrogen atmosphere. Whereas the turbidity test was performed on PNIPAAm solution with turbidimeter (HACH 2100N turbidimeter). Turbidity is measured in nephelometric turbidity unit (NTU) where, “nephelometric” describes an optical principle of instrumentation whereby turbidity is determined by measuring the amount of light scattered at some angle from the incident light path by particles suspended in the test solution. The scattered light by (0.625 mg/ml) PNIPAAm solution was measured for thermo-stated samples at various temperatures ranging from 25 to 50 °C.

The magnetization curves of magnetic nanoparticles (MNPs) and magnetic thermoresponsive nanocomposite (MTN) samples were obtained by applying the sample in powder form using a vibrating sample magnetometer (VSM; 9600-1 LDJ, USA) at room temperature. The operation of a VSM is based on magnetizing the sample using a direct magnetic field and simultaneously forcing it to vibrate in the vicinity of pickup coils. Such vibration induces a voltage which alternates at the same frequency with a magnitude determined by the magnetization of the sample.

The potential of the magnetic core to produce heat via relaxation losses is assessed via calculation of the SAR values using an induction heater (DW-UHF-10 kW, China) at 198 kHz, and 9.4 kA/m). A fixed volume of the ferrofluid (4 ml of 3 and 7mg/ml solution of magnetite in water) was placed in a glass vial that was inserted in a Styrofoam jacket -as an insulator- and the temperature was measured by an alcohol thermometer. SAR was calculated by using Equation 5 [26]; where c_i is the specific heat of water and glass vial that are 4.18 and 0.793 JK⁻¹g⁻¹ respectively, m_i is the mass of water and glass vial; taken as 4 and 5.2758 grams respectively, ΔTΔt is the initial slope of the time-dependent temperature curve and m_SPION is the mass of SPIONs in the solution in grams.

2.5.   Drug loading and release

MTN was allowed to swell in various concentrations of 5-AIQ, sonicated for 15 minutes, and transferred to a shaking water bath in dark for 23 hours at room temperature. Drug loaded MTN (MTN.5-AIQ) was separated from the solution by a strong magnet and the supernatant was analyzed by (HPLC, YOUNGLIN-9100, South Korea). Isocratic separation method was carried out according to the following conditions: RB₁₈ column; mobile phase: acetonitrile 0.8%: acetic acid (6: 4); flow rate:1.5 ml/min; and peaks were separated at λ = 260 nm. The drug concentration was calculated using a calibration curve. The drug uptake by MTN and drug loading efficiency were calculated by Equation 6 and Equation 7 [20], respectively.

Where, W_feed the weight of drug in which the MTN swelled and W_free, the weight of drug in the supernatant. To determine the temperature at which the maximum drug release occurred, MTN.5-AIQ sample was suspended in phosphate buffer saline (PH = 7.4) and incubated at different temperatures (35 up to 46 °C) for 30 min and the supernatant was analyzed by UV-visible spectrophotometer at a wavelength range from 200 to 250 nm. The released drug concentrations were determined by calculating the area under the peak from 200 to 232 nm.

2.6.   Biocompatibility and toxicological parameters

Male Swiss albino mice (weighing ~ 25–31 g) were kept at animal facility of Faculty of Science, Ain Shams University. The animals were housed in an air-conditioned facility with a 12-h light/dark cycle, allowed free access to food and water. Mice were humanely treated in accordance with the ARRIVE guidelines for animal care. All experimental procedures were approved by the Ain Shams University Research Ethics Committee.

Fifteen mice were randomly divided into three groups. The first group was intraperitoneally injected with saline and served as sham-operated control, the second one administered a single dose of cisplatin (15mg/kg) as a positive control (cisplatin-treated group). The last group administered a single intraperitoneal injection of (MTN.5-AIQ) (5mg/Kg). All mice were then euthanized, and blood samples were collected from the heart and sera form different groups were separated by centrifugation (1500/10 min) and kept at −20 °C until the time of analysis. The kidney and liver tissue samples were collected and fixed in 10% buffered neutral formalin for further histopathological studies.

2.6.1.   Kidney and liver functions

Renal functions were evaluated by measuring serum creatinine and uric acid according to manufacturer's instructions using commercial calorimetric kits (Bio-diagnostic Co., Cairo, Egypt). Hepatic functions were evaluated by measuring serum glutamic oxaloacetic transaminase (GOT) and glutamic pyruvic transaminase (GPT) according to manufacturer's instructions (Bio-diagnostic Co., Cairo, Egypt).

2.6.2.   Histological examinations

Kidney and liver samples obtained from different experimental groups were fixed in 10% buffered neutral formalin. The samples were then routinely dehydrated in graded series of ethanol, cleared in xylol and mounted in molten Paraplast at 58–62 °C. Paraffin sections of about 4 ± 5 µm were obtained, stained with H&E stain [27] and examined under light microscope (LICA, German, provided with HD camera).

2.7.   Cell culture and MTT assay

Cryopreserved Caco-2 cells were cultured in a humidified atmosphere (5% CO₂, 37 °C) with RPMI-1640 Medium supplemented with 2% fetal bovine serum (FBS) and 50 µg/mL gentamycin. Cells were passaged at 80–90% confluency after trypsinization with pre-warmed trypsin-EDTA solution. The cytotoxicity of 5-AIQ, MTN and MTN.5-AIQ.4 samples was investigated on Caco-2 cell lines by cell viability MTT assay. The experiment was conducted for determination of the IC50 (the concentration of the drug which causes 50% cell death). The selected samples were two-fold diluted in culture media. Cells were treated with 100 µl of each sample and incubated for further 24 hours. Then, 20 µl of MTT solution were added to each well and incubated for 1–5 hours. Finally, the produced formazan was dissolved in 200 µl DMSO and the mean absorbance of three replicates was measured at 570 nm.

2.8.   Statistical analysis

All values are presented as means ± SE. Statistical analysis of experimental data was performed using a one-way analysis of variance (ANOVA) followed by Donnett's multiple comparison test for comparing means from different treatment groups.

3.   Results and discussion

3.1.   Structure and morphology

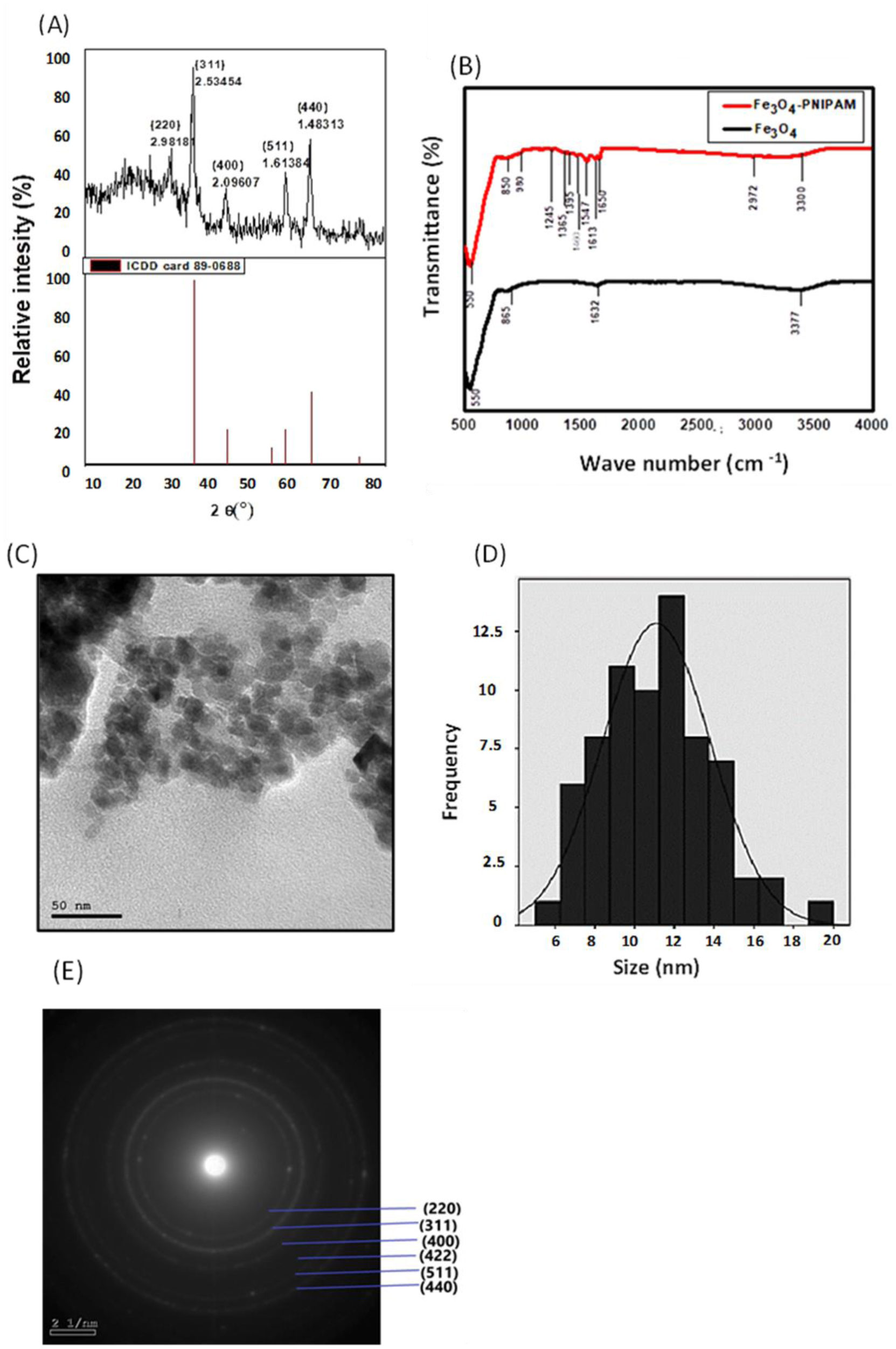
The X-ray diffraction (XRD) pattern of the iron oxide core is shown in Figure 1A. The obtained pattern shows a face centered cubic (FCC) structure, the peaks positioned at 2θ = 29.942 °, 35.386 °, 43.123 °, 57.019 ° and 62.581 ° correspond to reflections from the planes; (220), (311), (400), (511) and (440) respectively [28]. These positions and their relative intensities are consistent with ICDD 89 0688 card [28] which confirms that the synthesized particles are single phase magnetite or maghemite. The calculated average crystallite for the obtained SPIONs size is 12.7 nm and the average lattice parameter is 8.3992 Å.

The Fourier transform infrared spectroscopy (FTIR) spectrum of SPIONs is shown in Figure 1B (lower plot in black). The SPIONs sample exhibits one intense peak at 550 cm⁻¹ due to stretching vibration mode associated with the metal-oxygen absorption band (Fe–O bonds) in the Fe₃O₄ sample [29]. There are less intense peaks at 1632 and 865 cm⁻¹ resulting from the bending vibration of the O–H in plane and out of plane bonds of water respectively [30] in addition to a broad peak centered at 3377 cm⁻¹ due to the O-H bond stretching vibrations of water [31]. FTIR spectrum of SPION-PNIPAAm sample is also shown in Figure 1B (upper plot in red). The spectrum illustrates the characteristic peaks of Fe₃O₄ and PNIPAAm. The peak at 550 cm⁻¹ represents Fe-O bond with no observed shift because the SPION-PNIPAAm is prepared after the magnetite is synthesized (post synthesis polymerization). The characteristic peaks at 1545 cm⁻¹ and 1650 cm⁻¹ represent the amide II (N-H bending) and amide І (C=O stretching) vibrational mode found in PNIPAAm respectively, the peaks at 1365 and 1395 cm⁻¹ arise from bending vibration of isopropyl group -CH(CH₃)₂ found in PNIPAAm, the peak at 3300 cm⁻¹ corresponds to secondary N-H amide symmetric stretching vibration [32], the peaks at 2972 cm⁻¹ and 1460 cm⁻¹ correspond to (C-H) stretching and bending vibration respectively [31], the peak at 1245 cm⁻¹ corresponds to (C-N) bending vibration found in PNIPAAm [33].

High resolution transmission electron microscope (HRTEM) analysis shows the size and morphology of MTN. TEM micrograph of MTN in Figure 1C reveals the spherical shape of MTN with core shell structure. The MNPs appears as dark spots coated with PNIPAAm that constitutes the grayish layer as clarified by the arrows. The observed aggregation of the particles is a consequence of imaging under high vacuum conditions. The average diameter of SPIONs was estimated with automated size distribution analysis software (image J). The size distribution curve of SPIONs obtained from TEM micrographs is shown in Figure 1D. The SPIONs diameter was determined to be 11.03 nm, which is consistent with the size obtained from XRD data, suggesting each particle is a single crystal. Moreover, the statistical analysis of the particles reveals the narrow size distribution of the nanoparticles (5–20 nm). Selected area electron diffraction pattern is shown in Figure 1E. Peak indexing was performed using Equation 8 [34]; where d is the interplanar spacing, R_r is the ring radius, L_f is the camera focal length, λ is the wavelength of electron and V is 200 kV (Equation 9).

where,

For the (311) plane, the calculated d-value from SAED, XRD and standard d-values in literature [20] are 2.5340, 2.53454 and 2.53 (Å) respectively which confirms the face centered cubic structure of SPIONs.

Energy dispersive X-ray (EDX) spectrum of MTN is shown in Figure 2A. The major peaks of Fe at 0.7, 6.3, 7 keV correspond to the binding energy of Fe (Lα, Kα and Kβ respectively) [35]. The presence of nitrogen peaks confirms the coating of SPIONs with the Poly(N-isopropylacrylamide) [36].

The polymer content of magnetic thermoresponsive nanocomposite (MTN) was determined using TGA analysis. TGA thermogram estimates the weight loss occurring in the sample upon increasing the temperature from room temperature to 850 °C as shown in Figure 2B. The thermogram shows that weight loss occurred in two steps; one below 200 °C due to loss of water, the other occurred in the range from 200 to 600 °C. The latter loss was attributed to the degradation of the side chain functional group and back bone structure of the -PNIPAAm [22]. The results show that the amount of PNIPAAm in MTN is 5.08%.

3.2.   Thermal response

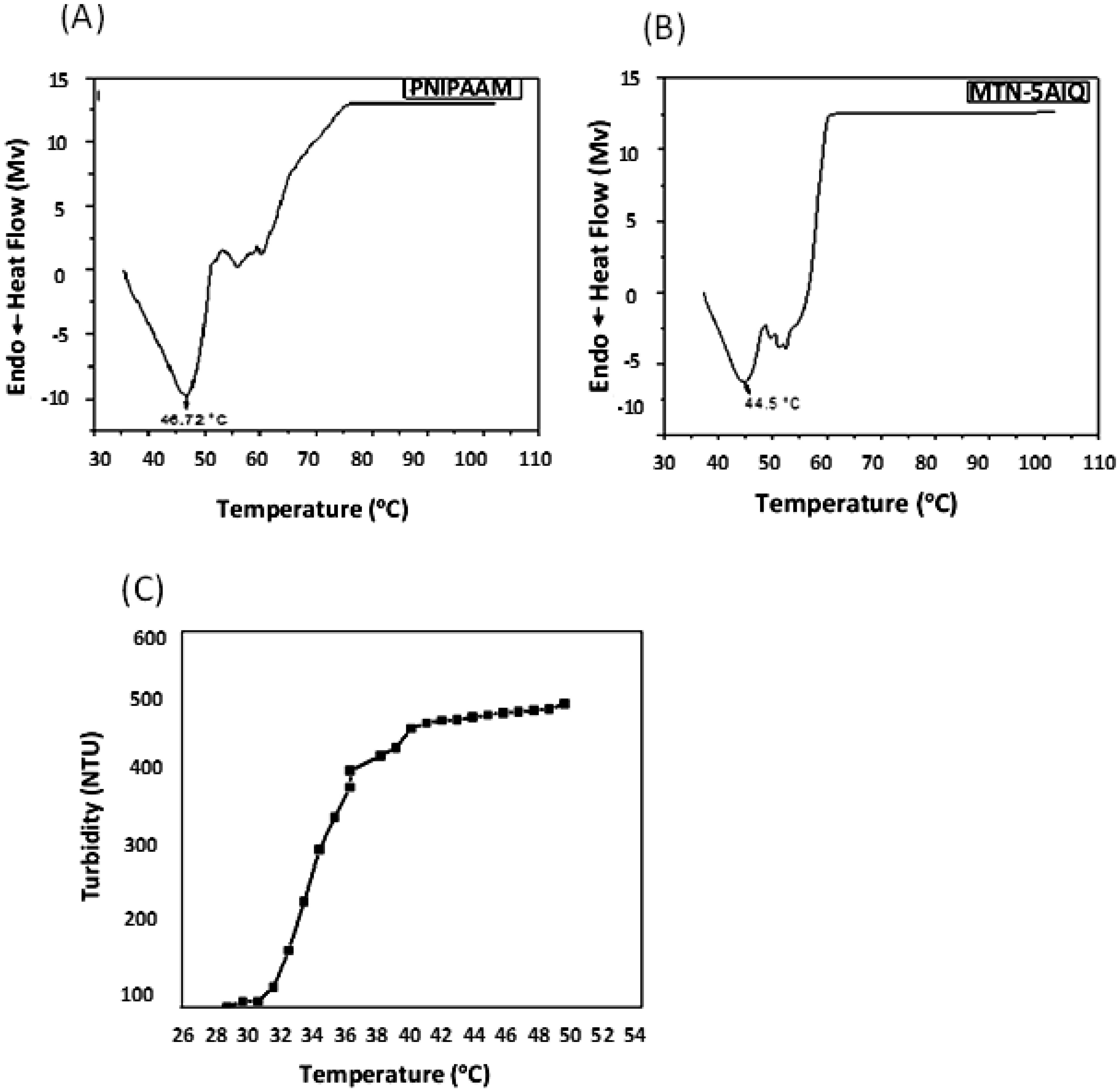
The coil to globule transition was assessed via two methods: DSC (a thermal method) and turbidimetry (an optical method). DSC was used to determine the LCST for the polymer alone and for MTN.5-AIQ and the thermograms are shown in Figure 3A, B. The LCST in each case can be determined in different ways; either from the tangent drawn at the onset of depression (44.5 °C for PNIPAAm and 43.5 °C for MTN.5AIQ) or the tangent along the curve (48 °C for PNIPAAm and 47 °C for MTN.5-AIQ, or the peak point (46.72 °C for PNIPAAMm or 44.5 °C for MTN.5-AIQ).

As for turbidimetry, the cloud point temperature (T_cp) indicates the collapse and aggregation of the soluble polymer leading to clouding of the solution. Figure 3C shows turbidity as a function of temperature for PNIPAAm. It is worth noting that, the turbidity test (based on light transmission) cannot be conducted for samples containing iron oxide as a major constituent. The results show that, as the temperature increases, the turbidity of PNIPAAm increases. As is the case for LCST data, there is no consent about the point on the curve at which T_cp is determined [37]. Therefore, T_cp is considered to lie in the range between 31 to 41 °C for PNIPAAM. The difference in the obtained values of LCST and T_cp for NIPAAM is physically accepted as the principles for obtaining them are different.

A wide range of transition temperature values have been reported in literature. The most common value was between 30–34 °C according to Priya James et al., 2014 [1], and Ward& Georgiou, 2011 [2]. Higher values have been also reported by (Xia et al., 2006). The study showed that T_cp for PNIPAAm decreased from 45.3 °C to 34.4 °C upon increasing the molecular weight with a sharper transition [38].

3.3.   Magnetic and specific absorption rate (SAR) measurements of magnetic core

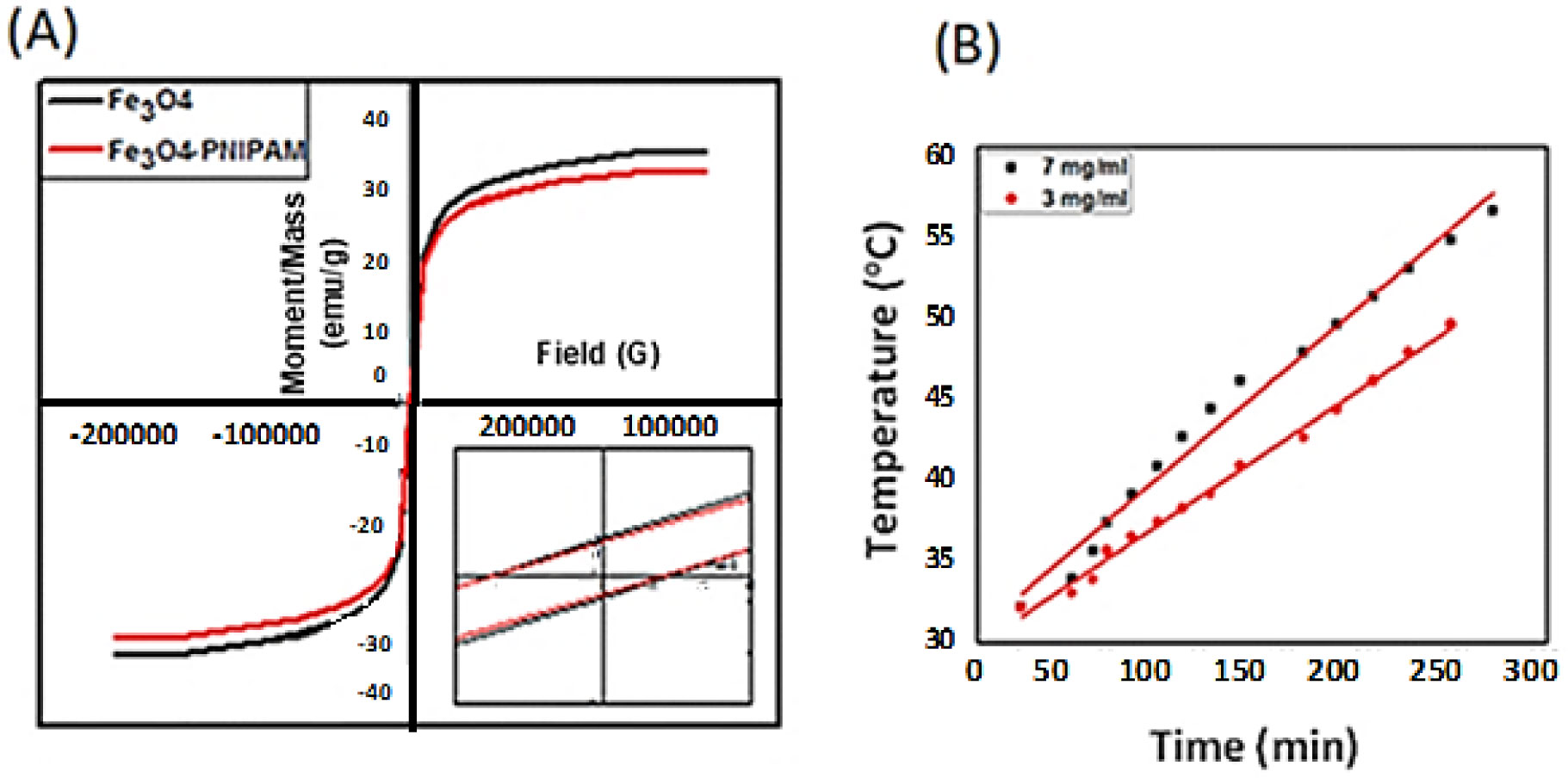
The magnetization curve of SPIONs is shown in Figure 4A. The curve reveals the superparamagnetic behavior of iron oxide nanoparticles at room temperature with inconspicuous value of remnant magnetization. The saturation magnetization of SPIONs is 35.412 emu/g which is less than the saturation magnetization of bulk magnetite (92 emu/gm) and (74–80 emu/gm) of maghemite [39]. The result is consistent with the fact that the saturation magnetization decreases with size. As the particle size decreases, the surface to volume ratio increases and in turn, the magnetically dead layer fraction increases because of the canted and disordered spins on the surface of the nanoparticles [40]. Likewise, the coercivity decreases with decreasing size below the critical size, which is consistent with previous theoretical estimations [41]. The low values of coercive field (36.3 G) and remanent magnetization (0.93694 emu/g) unveil that the sample is superparamagnetic at room temperature. Slightly lower value of saturation magnetization (32.74 emu/g) is obtained for MTN due to the non-magnetic polymer layer. It is worth noticing that the decrease in magnetization is consistent with the contribution of PNIPAAm in the MTN structure as obtained from the TGA analysis. Coercive field and remanent magnetization are 34.522 G and 0.83349 emu/g respectively; denoting a superparamagnetic behavior as well.

Assessment of specific absorption rate of SPIONs was performed by exposing the sample to alternating magnetic field (AMF) of strength equal to 9.4 kA/m and frequency of 198 kHz obtained by the induction heater. Figure 4B shows the temperature rise with time curve for two concentrations of SPIONs colloid (3 and 7 mg/ml) exposed to AMF. The field intensity and the operating frequency are within the acceptable range; ensuring compliance with the safety regulations for respective clinical application [26]. The calculated SAR values for the two-colloid concentrations (3 and 7 mg/ml) are 70.69 and 78.91 W/g respectively. This minor increase of SAR values upon increasing the concentration has been reported in literature [42] as being attributed to increasing the magnetic dipolar interactions between the particles. Even at the low concentration (3mg/ml), the therapeutic temperature (42 °C) was reached after only 4 minutes of exposure. The results proof the efficiency of the Magnetic thermoresponsive nanocomposite (MTN) as a MFH agent.

3.4.   Drug loading and release kinetics

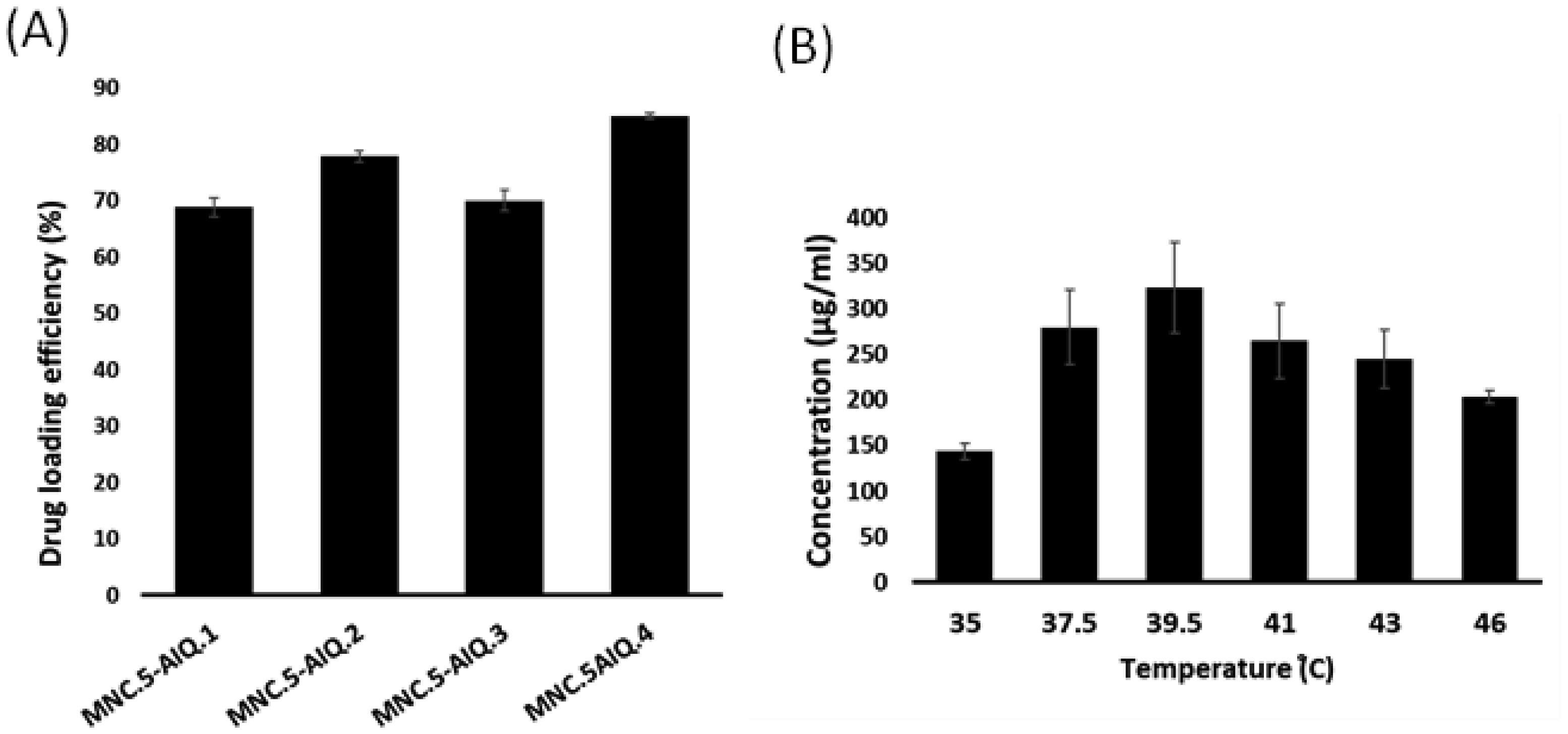
Magnetic thermoresponsive nanocomposite (MTN) sample was loaded with 5-aminoisoquinoline (5-AIQ) by resuspension of MTN in four different concentrations of the drug as listed in Table S1. MTN.5-AIQ samples were separated by a strong magnet then the residual concentration of 5-AIQ in the supernatants were quantified using HPLC analysis. The HPLC chromatogram of 5-AIQ is shown in Figure S1A. Table 1 illustrates the value of drug loading efficiency of the samples and Figure 5A illustrates the results. It was noticed that the drug loading efficiency increased as the concentration of feed drug increased and sample MTN.5-AIQ.4 has the highest drug loading capacity. Based on these results, the drug release kinetics were studied for sample, MTN.5-AIQ.4 only.

After incubation of MTN.5-AIQ.4 sample at temperatures of 35, 37.5, 39.5, 41, 43 and 46 °C for 30 minutes, the solution was separated by a strong magnet and the supernatant was analyzed by a UV-visible spectrophotometer. As shown in Figure 5B, the drug release was assessed at different temperatures and the maximum release of the 5-AIQ was at 39.5 °C. In addition, Figure S1B displays the drug release concentration at various temperatures analyzed by HPLC, which supports the findings obtained using UV-spectrophotometer and confirms that the maximum amount of drug is released at hyperthermia within the acceptable therapeutic range.

3.5.   Biocompatibility and toxicological parameters

3.5.1.   Kidney and liver functions

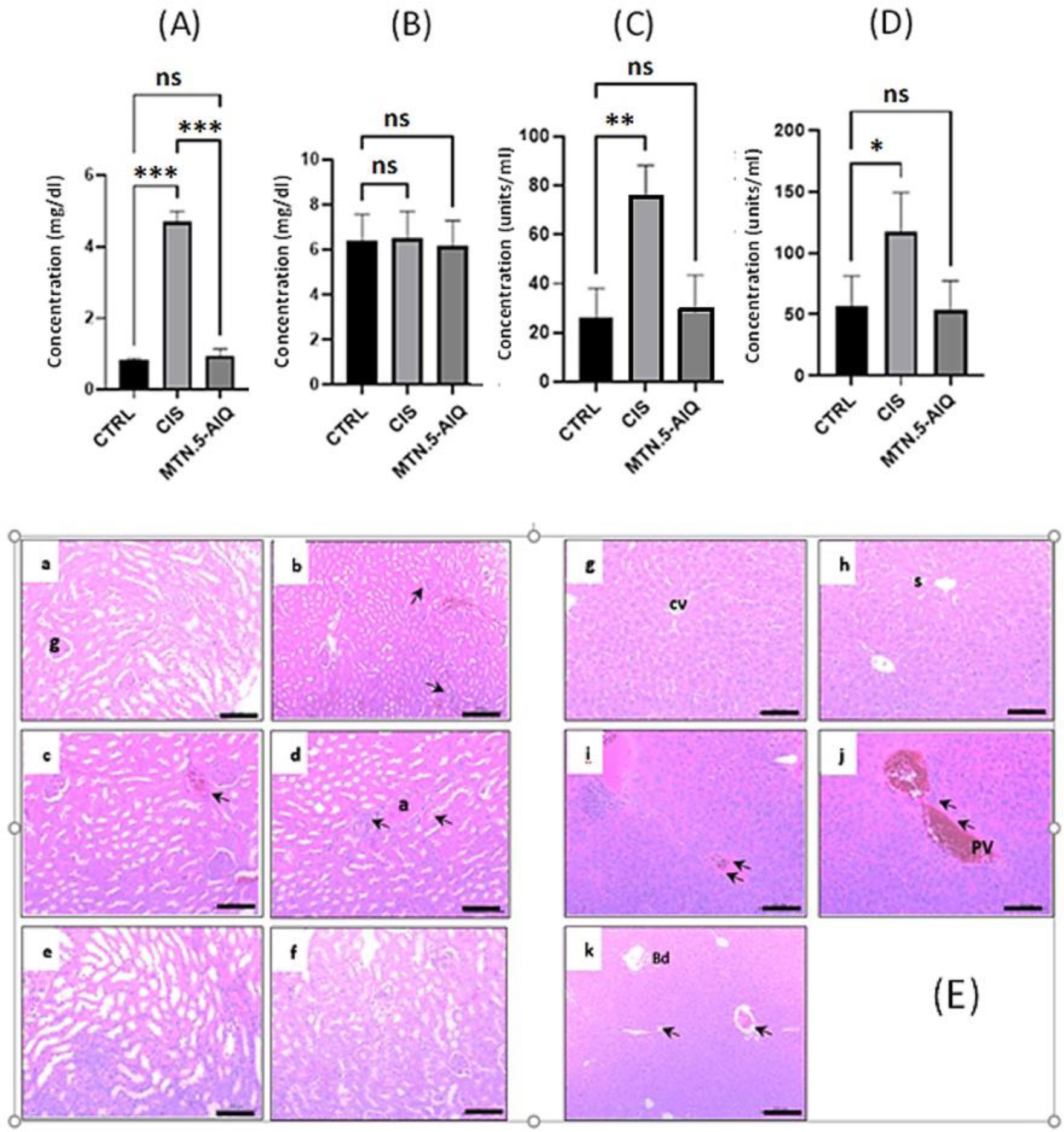
Serum levels of creatinine, uric acid, glutamic pyruvic transaminase (GPT) and glutamic oxaloacetic transaminase (GOT) were evaluated for the control, cisplatin-treated and MTN.5-AIQ-treated groups. Cisplatin impaired the renal function as is apparent from the significantly higher serum creatinine level (p < 0.05) compared with the control as shown in Figure 5A. the renal dysfunction induced by cisplatin was previously depicted in literature [43]. The serum creatinine and uric acid levels of the MTN.5-AIQ treated group, however, are not significantly different from those of the control group as illustrated in Figure 6A & B; proving the biocompatibility of MTN.5-AIQ. The significant elevation of serum level (P < 0.05) of GPT for the cisplatin group compared to control refers to the hepatotoxicity of cisplatin. On the other hand, the administration of MTN.5-AIQ did not produce any significant changes in liver function compared to the control as shown in Figure 6 C & D. This result proves the biocompatibility of MTN.5-AIQ.

3.5.2.   Histopathology examination

Upon cisplatin administration, a marked congestion and atrophy of glomeruli are observed in mice kidneys of cisplatin–treated group compared to normal, Figure 6E (a-c). Furthermore, liver histopathological abnormalities are detected, marked by swelling and vascular degeneration in hepatocytes, Figure 6E (i-j) comparable with normal control. These observations confirm the nephrotoxicity and hepatotoxicity of cisplatin [43]. In MTN.5-AIQ-treated group, normal renal and collecting tubules are shown in Figure 6E (e-f), only slight congestion can be detected in the interstitial blood vesicles. As for hepatotoxicity examination, the livers of MTN.5-AIQ-treated mice show normal histopathological pictures with slight congestion in portal veins with normal bile ductuli (Figure 6E. k). Such results supporting the biocompatibility of MTN.5-AIQ encouraged by undetectable toxicity of the examined organ applied for histological study.

3.6.   Cytotoxic effect of MTN.5-AIQ on colon adenocarcinoma

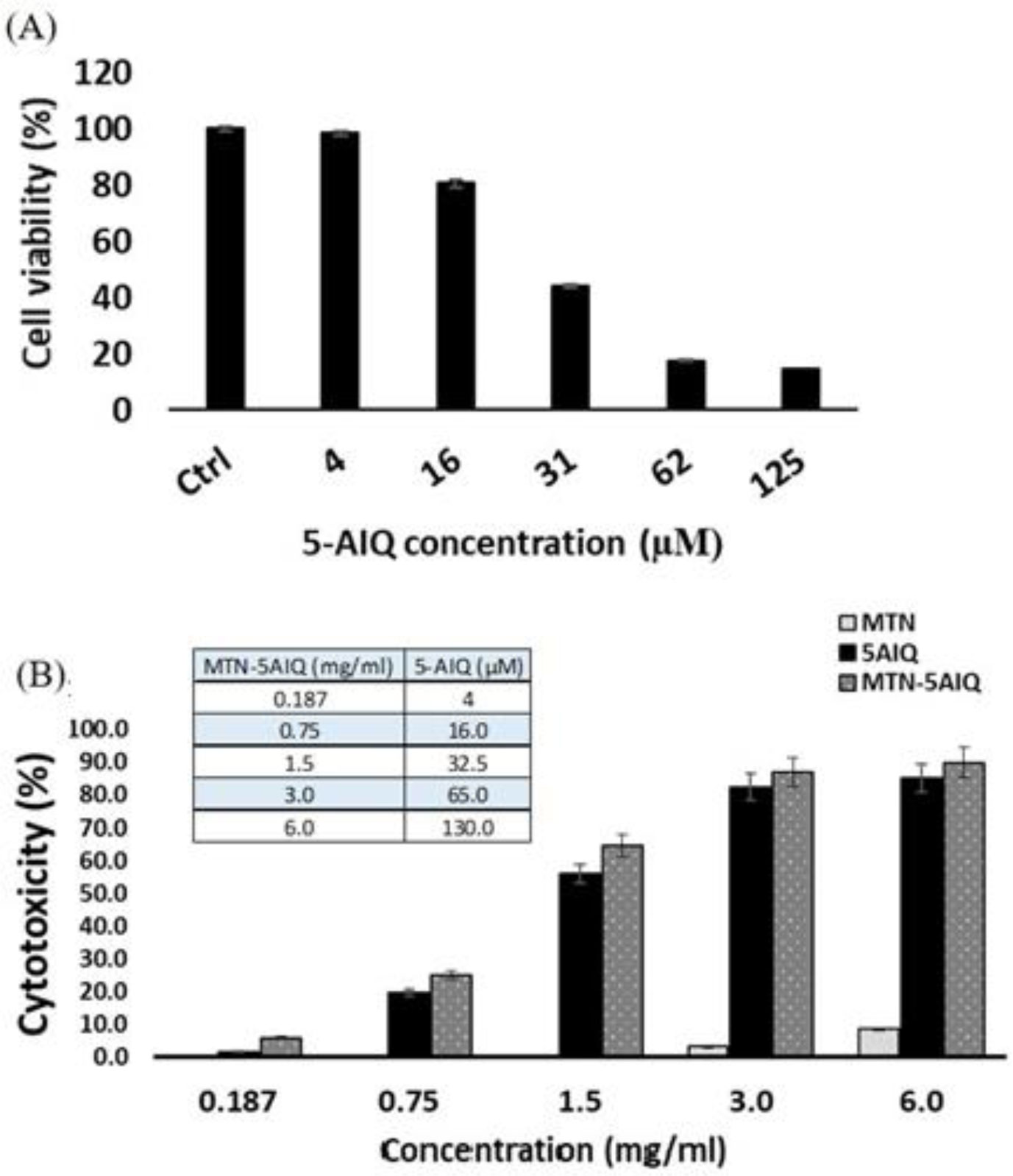
The effect of different 5-AIQ concentrations on Caco-2 cells is illustrated in Figure 7A. The cytotoxicity of MTN and MTN.5-AIQ was studied on Caco-2 cells as shown in Figure 7B. No significant cytotoxicity is induced by MTN on Caco-2 cells up to 6 mg/ml (stock solution). Upon further increasing the concentration of MTN, the cytotoxicity of MTN increased. Chang et al investigated the cytotoxicity of SPIONs nanoparticles on BHK-21 cells and concluded that, there was no cytotoxic effect of iron at a concentration up to 100 µg/mL incubated for 24 h [44]. It was accepted that below a concentration of 5 mg/ml concentration of PNIPAM polymer did not affect the cell survival. Such sublethal dose range was investigated by Vihola and his colleagues on two human cell lines; intestinal Caco-2 cell line and bronchial Calu-3 [45]. As shown in the present results, hyperthermia studies proved that low concentrations of SPIONs, around 3 mg/ml, can cause significant rise in temperature in a very short time; the phenomenon that trigger the 5-AIQ release (65 µM). These two factors; hyperthermia and thermally triggered-drug release are aimed to play synergistic effects in treatment of metastatic colon cancer without any aggravated response toward healthy tissues. In comparison to 5-AIQ alone, the MTN-5AIQ effectively increase the therapeutic levels of 5-AIQ inside the cells as indicated the elevated cytotoxicity.

4.   Conclusions

In this work, the smart nanocomposite (MTN.5-AIQ) was successfully prepared with superior properties. The high therapeutic temperature could be attained with considerably low concentration of SPIONs representing the magnetic core of the composite. Moreover, the polymeric shell showed high efficiency in drug uptake with convenient release kinetics at the therapeutic temperature range. Finally, MTN.5-AIQ showed good in vivo biocompatibility whereas, it caused antineoplastic effect for Caco-2 cell lines. The key mechanism beyond this synergy includes the blockage of PARylation-dependent DNA repair pathway as well as impairment of metabolic adaptation of cancer cell by virtue of PARP inhibition combined with hyperthermia. The uniqueness of MTN.5-AIQ over other anti-cancer approaches can be attributed to its selectivity.

These findings render the genuine loading of 5-AIQ on a thermoresponsive nanocomposite a promising candidate of magnetic-based hyperthermia-PARP inhibition dual therapy for colon adenocarcinoma. On limitation of our study was the design of an appropriate in vivo cancer model for further examination of MTN-5AIQ anti-cancer effects and further efforts are continued in the future. Upcoming work will focus on attempting to leverage the efficacy of magnetic thermoresponsive nanocomposites-loaded with different immunotherapies that are routinely used for treatment of resistance cancers.