1.
Introduction
Fire is a common natural disaster, which seriously endangers the safety of human life and property [1,2]. Traditional fire detection uses sensors such as smoke and temperature to monitor the changes of fire-related parameters in the environment [3,4,5]. However, due to the limitation of the detection range of sensors, the monitoring system can not cover a wide range of monitoring areas, and the traditional detection methods can not give valuable information of detected fires, such as fire scale and location information [6,7,8,9,10]. In recent years, with the popularization of intelligent monitoring equipment, the development of image processing technology, deep learning and intelligent optimization algorithms, the problem of fire monitoring based on video analysis has attracted more and more attention of researchers [11,12,13,14,15,16,17,18,19]. With the help of security monitoring, video-based fire detection is realized. It is a low-cost and high-efficiency fire detection scheme, which can greatly reduce casualties and property losses caused by fire.
Image-based fire detection technology is based on the characteristics of flame. CHEN et al. [20] studied flame irregularity detection in RGB and HSI color space. Fernandez et al. [21] proposed a method based on picture histogram to realize fire image recognition. Xu et al. [22] applied deep convolution neural network to fire image recognition, and achieved certain results. CELIK T and Demirel [23] designed classification rules based on the separation of chroma components and brightness in YCbCr space, but the rules have higher accuracy under larger flame sizes. Foggia et al. [24] combined flame color and dynamic characteristics to form a multi-dimensional flame recognition framework to realize fire detection. This method occupies a mainstream position in fire detection methods, but this method is still insufficient in the accuracy of fire recognition. Mueller et al. [2] studied the motion of rigid objects and the shape of flame, and proposed to extract the feature vector of flame through optical flow information and flame shape, so as to distinguish flame from other objects. With the continuous development of deep learning, Frizzi et al. [25] designed a fire identification algorithm based on convolutional neural network, which can classify fire and smoke. Fu et al. [26] used a 12-layer convolutional neural network to detect forest fires, and achieved good classification results, but it was not suitable for fire detection in real-time video because of its high computational complexity.
In daily life, most of the environmental information collected by safety monitoring equipment is non-fire environment, so most of the video streams transmitted by safety monitoring equipment are non-fire frames. If the non-fire frames and fire frames are not distinguished for detection, the time complexity of the algorithm will be greatly increased. To solve this problem, DeepFireNet proposed in this paper can filter the non-fire frames in the image preprocessing process with low time complexity, and transmit the images with possible fire to convolution network with slightly complicated calculation but high accuracy for fire detection. In this paper, based on the characteristics of fire, the video stream is pulled by OpenCV and a frame image in the current video stream is obtained. The frame image is Gaussian smoothed, and then combined with the static characteristics of fire color, a double color criterion based on RGB and HSI is established. The fire suspected area in the frame image is extracted by the color characteristics of fire. Then, it is further judged whether the extracted area is a fire area according to the dynamic characteristics of rapid growth of fire area. If the fire suspected area is detected, the suspected area is input into trained convolutional neural network for fire identification. If the suspected area is not detected, the next frame image is detected, and the convolution network is no longer called for secondary judgment, thus greatly reducing the computational complexity and maintaining high accuracy of fire identification. This method has a good performance in fire detection application in real-time video streaming environment.
2.
Materials and methods
2.1. Image preprocessing
2.1.1. Image smoothing filtering processing
In the process of image formation, transmission, reception and processing, due to the influence of the actual performance of equipment, there are inevitably external and internal interference, so various noises will be produced [27,28]. When a fire happens, it will also be affected by environmental noise such as weather and illumination, so the fire image should be smoothed and filtered before fire detection [29,30,31]. Commonly used methods include mean filtering [32,33], median filtering [34,35] and Gaussian filtering [36].
Mean filtering is simple in calculation and has a good effect on eliminating Gaussian noise, but it will destroy the edge details of the image in the process of eliminating noise. Median filtering performs well in eliminating random noise in images, while preserving the correlation of image texture. However, median filtering has high time complexity and is not suitable for image processing in real-time video. Gaussian filtering is a way of smoothing images by neighborhood averaging, in which pixels at different positions are given different weights. It is a classic way of smoothing images, and it is softer to process images. In order to solve the problem of smoothing a large number of images, this paper uses Gaussian smoothing filtering to realize image noise reduction. The effects of the three filtering processes are shown in Figure 1.
2.1.2. Fire area extraction
In the process of fire image recognition, it is necessary to extract the fire suspected areas to reduce the influence of complex background on fire recognition and improve the recognition accuracy. By judging the static and dynamic characteristics of fire, this paper realizes the accurate extraction of fire area [37,38].
(1) Fire static feature extraction
Color is the main static feature of fire. In this paper, the fire feature extraction based on color is realized by establishing RGB and HSI criterion models [39,40,41].
RGB model corresponds to three colors: red, green and blue. According to the principle of three primary colors, the amount of light is expressed in primary light units. In RGB color space, any color F can be expressed by adding and mixing different components of three primary colors R, G and B.
The HSI color model describes the color characteristics with three parameters: H, S and I, in which: H(Hue) indicates hue, which is used to indicate a certain range of colors, or to indicate the perception of different colors by human senses. S(Saturation), which indicates the purity of color, will become more vivid with the increase of saturation. Luminance I(Intensity), corresponding to imaging brightness and image gray scale. The establishment of HSI model is based on two important facts, one is that I component has nothing to do with the color information of the image, and the other is that H and S components are closely related to the way people feel the color. These characteristics make HSI model very suitable for color characteristic detection and analysis. RGB and HSI criteria are as follows.
In which R, G and B are color components in RGB color model, and S is color saturation in HSI model RT is the threshold of the R color component, GT is the threshold of the G color component, ST is the threshold of the S color component. According to many experiments, the value range of RT is between 115 and 135, the value range of GT is between 115 and 135, the value range of ST is between 55 and 65. The realization effect is shown in Figure 2.
It is inaccurate to detect the fire only according to the color characteristics of the fire, the interference sources such as candles, light sources and lighters in the room will also be mistaken for the fire because they have colors similar to the fire, thus causing interference to the identification process. As shown in Figure 3. To solve this problem, this paper proposes a method to extract the fire area by comprehensively using the static and dynamic features of fire. Firstly, the suspected areas close to the fire color are determined by the fire color features, and then the fire dynamic features of this area are identified, thus completing the extraction of the fire area.
(2) Fire dynamic feature extraction
The change of burning area during fire is one of the main manifestations of fire dynamic characteristics. In the initial stage of fire burning, the fire area increases rapidly, but the interference factors such as light source do not have the characteristics of rapid change of area. Therefore, in this paper, the dynamic features of fire are extracted by moving target monitoring technology [42,43].
At present, the commonly used moving target monitoring methods are optical flow field method, inter-frame difference method and background difference method. Optical flow field method [44] can be used in both moving and static scenes of cameras, but it is not suitable for real-time video processing because of its complicated calculation. Although the inter-frame difference method [45] is simple to implement, the extracted objects are easy to produce empty images. Compared with the inter-frame difference method, the complexity of the background difference method is slightly improved, but after many experiments, it is found that the algorithm meets the requirements of real-time video stream processing, and compared with the inter-frame difference method, it can obtain a more complete target image, which is beneficial to determine the fire area. Therefore, the background difference method is used to extract the dynamic characteristics of fire, as shown in Figure 4.
If only based on the dynamic characteristics of fire, the recognition effect will be affected by the movement of other objects in the monitoring environment. Therefore, in this paper, the static and dynamic characteristics of fire are comprehensively judged to complete the separation of fire area and background image, as shown in Figure 5.
2.2. Deep convolution neural network
Convolutional neural network (CNN) performs well in image recognition [46,47,48]. Through convolution network, the depth extraction of image features can be realized, and high-precision image recognition can be completed.
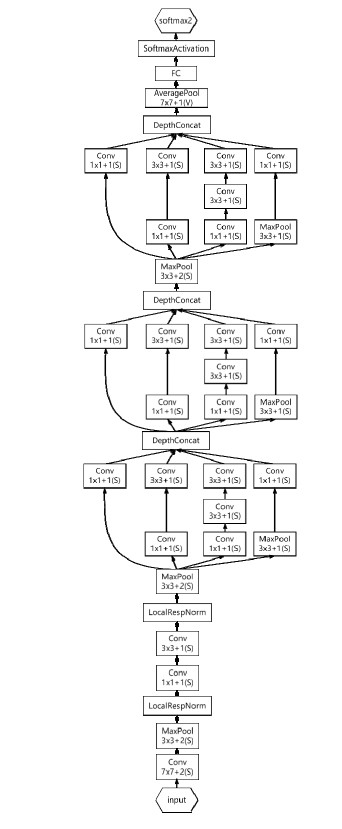
In this paper, Keras, a widely used deep learning framework, is used. CNN network initialization weight is based on the Inceptionv1-OnFire convolution network proposed by Andrew J. Dunnings et al. [49], Inceptionv1-OnFire provides a powerful initialization weight for the network to speed up convergence and avoid over-fitting on relatively small data sets. Compared with the nine linearly stacked inception modules in the InceptionV1 network [50], the network only uses three continuous inception modules, which greatly simplifies the complexity of the network architecture. Each Inception module uses the same convolution structure as InceptionV1, which consists of 1 × 1, 3 × 3, 5 × 5 convolution cores and 3 × 3 pooling layers. The front and back inputs and outputs of the three initiation modules adopt the same network architecture as that of the InceptionV1.
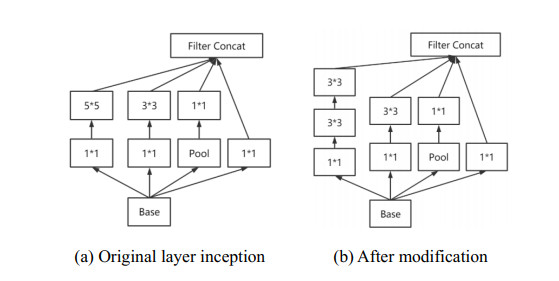
The main network architecture of this paper improves the inception module, and decomposes the convolution kernel of 5 × 5 into two 3 × 3. The receptive fields before and after decomposition are the same, and the representation ability of two 3 × 3 convolutions in series is stronger than that of a 5 × 5 convolution. The ratio of the parameters of two 3 × 3 convolutions and one 5 × 5 convolution is (9+9)/25, which reduces the parameters of the network by 28% and reduces the computation by 28% [51]. The network input image is a 3-channel fire image with a width and height of 224*224. The Layer inception correlation is shown in Figure 6 and the network structure is shown in Figure 7.
The VGG16 [52] network structure is used as the comparison network of the algorithm in this paper. The input image is a 3-channel fire image with a width and height of 224*224. The main network structure is VGG16, which stores the convolution layer and Max Pooling layer of VGG16 to realize feature extraction of input images. At the same time, two fully connected layers are added to receive the extracted features, thus realizing the classification and prediction of images. A Dropout layer is added between the last two fully connected layers to limit the number of participating neurons and reduce the occurrence of over-fitting. To solve the binary classification problem of fire identification, the optimizer uses RMSProp algorithm, the activation function uses sigmod, and the loss function uses Sigmod_cross_entropy_ with_logits to solve the logistic regression problem.
loss function:
In which, x represents the predicted value and z represents the label value.
3.
Evaluation
3.1. Experimental platform and data
The hardware platform of the algorithm is Intel(R) Core(TM) i5-7300HQ,A personal computer equipped with GTX 1060.
The training data set used in this paper comes from the public network fire picture data set and the public network video database, such as furg-fire-dataset (https://github.com/steffensbola/furg-fire-dataset), which used in [49]. About 10 500 fire pictures and 10 500 non-fire pictures are used in the experiment, mainly including fire and non-fire scenes in indoor and outdoor spaces such as offices, laboratories, kitchens, forests, streets, buildings and vehicles, so as to improve the generalization ability of convolution network. In the 21 000 pictures, 15 300 are used as training sets, 1 700 as verification sets and 10 videos (about 4 000 pictures) as test sets. After the training of the model, we use the model to verify in the user-defined dataset and furg-fire-dataset. The validation results are shown in Tables 1 and 2. Before the convolution network reads the picture, the fire area in the picture is extracted, and the extracted fire area is mirrored and reversed to expand the data set, and then the width and height of the picture are adjusted to 224*224 by cutting, classifying and normalizing, so as to make a fire data set.
3.2. Performance test index
Fire identification is a binary classification problem, so this paper uses ROC curve [53] and the total time needed to process the test video set as the performance index of the evaluation model.
True Positive Rate:
False Positive Rate:
Accuracy Rate:
In which, TP indicates the number of fire images correctly identified as fires, FP indicates the number of non-fire images incorrectly classified as fire images, TN indicates the number of non-fire images correctly identified as non-fire, and FN indicates the number of fire images incorrectly identified as non-fire images.
3.3. Analysis of experimental results
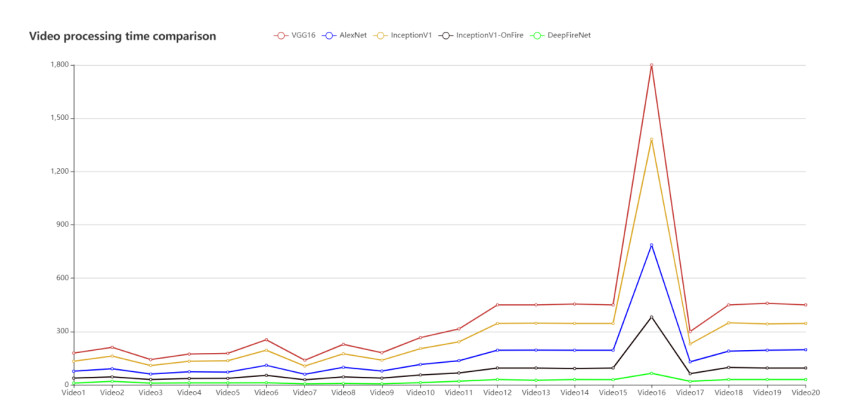
In the training process, this paper adopts the method of 10-fold cross validation to train. The training samples were divided into 10 samples, and 9 samples were randomly selected for model training and 1 sample was used for model verification, and 10 experiments were carried out in cross. At the same time, for 9 model training sets, 20 images were taken as a batch and randomly divided into 3 400 batches, with 17 000 iterative trainings. The loss value in the process of network training is recorded. With the increase of iteration times, the loss value decreases steadily, and the accuracy rate is stable at 0.967, which generally meets the training requirements and achieves the learning purpose. Save the trained network model in h5 format, load the video test set by using OpenCV, an open source image processing library widely used, and simulate the real-time video stream collected by the camera. The test data set results are shown in Table 1 below. Video1–10 is part of the user-defined dataset sample, and video11–20 is part of the sample video in furg-fire-dataset. The algorithm shows high accuracy in the test set. The comparison of the time spent by the five methods on each test video set is shown in Figure 8.
The test data set in Table 2 consists of user-defined dataset and furg-fire-dataset. The resulting frames per second (fps) is shown in Table 2. When the input image is not test by convolution network and only uses the dynamic and static characteristics of fire to judge, the fps of the algorithm is 55. When only using convolution network detection, fps is 25. Considering that most of the images collected by the monitoring equipment in daily environment are non-fire images, the algorithm can only detect the dynamic and static characteristics of fire, so the algorithm can detect 55 frames of images per second in the vast majority of time, only when the suspected fire image is detected, the convolution network is used to judge. At this time, the FPS will drop, but it will still be much higher than the FPS as compared algorithms. From the results presented in Table 2, we observe significant run-time performance gains for the reduced complexity DeepFireNet and InceptionV1-OnFire architectures compared to their parent architectures. Experimental statistics show that VGG16 network is not suitable for real-time video detection, and the algorithm implemented in this paper is superior to the Inceptionv1-OnFire network in fire detection accuracy and time complexity. Although there are still false detections, the accuracy of fire identification has reached over 96%. Especially when there are a large number of non-fire frames in the video, the time complexity of the proposed algorithm is significantly reduced compared with VGG16 network and InceptionV1-OnFire network.
For real-time video, the static and dynamic characteristics of fire are used for initial judgment, so that a large number of video frames without interference sources are filtered out. When the suspected fire is detected, the system calls convolution network to detect the fire in the suspected fire area of the frame image for the second time This method can improve the accuracy of fire detection and simplify the computational complexity, and has a good effect in the process of real-time video processing. Comprehensive comparison shows that the method implemented in this paper has a good effect.
4.
Conclusions
With the development of intelligent monitoring, it is of great significance to realize fire warning by monitoring equipment, so as to reduce casualties and property losses caused by fire. Compared with the traditional algorithm, this paper proposes a fire recognition algorithm with both recognition accuracy and low time complexity. The algorithm has a certain versatility and has a higher recognition rate for fires in different scenes.
According to the real-time requirement in the video stream processing process and the interference of other complex environments such as light sources and fast moving objects, In this paper, firstly, a fire static and dynamic feature detection algorithm with extremely low time complexity is used to extract the suspected fire area and filter a large number of non-fire images, and then input the detected fire suspected area into convolution network to complete the fire identification of this area.
The algorithm greatly reduces the time complexity by filtering a large number of non-fire images and improving the inception layer convolution network, and greatly reduces the interference of complex environment to the fire identification process by extracting the fire areas in the images, so that the convolution network only needs to focus on the identification of fire features, which effectively improves the accuracy of identification.
Because a large amount of smoke often appears when a fire occurs [54,55,56], in the following research, it is proposed to study the accurate detection of smoke generated when a fire occurs, so as to better ensure the timeliness of fire warning and the accuracy of fire warning in more complex environments.
Acknowledgments
This work is supported by the CERNET Innovation Project (No. NGII20190605), High Education Science and Technology Planning Program of Shandong Provincial Education Department (Grants No. J18KA340, J18KA385), Yantai Key Research and Development Program (Grants No. 2020YT06000970, 2019XDHZ081).
Conflict of interest
We have no conflict of interest in this paper.










 DownLoad:
DownLoad: