Poincaré inequalities and Neumann problems for the variable exponent setting

1.   Introduction

In biological systems, the continuous predator-prey model has been successfully investigated and many interesting results have been obtained (cf. ^{[1,2,3,4,5,6,7,8,9]} and the references therein). Moreover, based on the continuous predator-prey model, many human factors, such as time delay ^[10,11,12], impulsive effect ^{[13,14,15,16,17,18,19,20]}, Markov Switching ^[21], are considered. The existing researches mainly focus on stability, periodic solution, persistence, extinction and boundedness ^{[22,23,24,25,26,27,28]}.

In 2011, the authors ^[28] considered the system incorporating a modified version of Leslie-Gower functional response as well as that of the Holling-type Ⅲ:

With the diffusion of the species being also taken into account, the authors ^[28] studied a reaction-diffusion predator-prey model, and gave the stability of this model.

In model (1) $x$ represents a prey population, $y$ represents a predator with population, $a_{1}$ and $a_{2}$ represent the growth rate of prey $x$ and predator $y$ respectively, constant $b$ represents the strength of competition among individuals of prey $x$, $c_{1}$ measures the maximum value of the per capita reduction rate of prey $x$ due to predator $y$, $k_{1}$ and $k_{2}$ represent the extent to which environment provides protection to $x$ and to $y$ respectively, $c_{2}$ admits a same meaning as $c_{1}.$ All the constants $a_{1}, a_{2}, b, c_{1}, c_{2}, k_{1}, k_{2}$ are positive parameters.

However, provided with experimental and numerical researches, it has been obtained that bifurcation is a widespread phenomenon in biological systems, from simple enzyme reactions to complex ecosystems. In general, the bifurcation may put a population at a risk of extinction and thus hinder reproduction, so the bifurcation has always been regarded as a unfavorable phenomenon in biology ^[29]. This bifurcation phenomenon has attracted the attention of many mathematicians, so the research on bifurcation problem is more and more abundant ^{[30,31,32,33,34,35,36,37,38,39,40]}.

Although the continuous predator-prey model has been successfully applied in many ways, its disadvantages are also obvious. It requires that the species studied should have continuous and overlapping generations. In fact, we have noticed that many species do not have these characteristics, such as salmon, which have an annual spawning season and are born at the same time each year. For the population with non-overlapping generation characteristics, the discrete time model is more practical than the continuous model ^[38], and discrete models can generate richer and more complex dynamic properties than continuous time models ^[39]. In addition, since many continuous models cannot be solved by symbolic calculation, people usually use difference equations for approximation and then use numerical methods to solve the continuous model.

In view of the above discussion, the study of discrete system is paid more and more attention by mathematicians. Many latest research works have focused on flip bifurcation for different models, such as, discrete predator-prey model ^[41,42]; discrete reduced Lorenz system ^[43]; coupled thermoacoustic systems ^[44]; mathematical cardiac system ^[45]; chemostat model ^[46], etc.

For the above reasons, we will study from different perspectives in this paper, focusing on the discrete scheme of Eq (1).

In order to get a discrete form of Eq (1), we first let

and rewrite $u, v, \tau$ as $x, y, t,$ then (1) changes into:

where $\beta_{1} = \frac{b^{2}}{c_{1}a_{1}}, h_{1} = \frac{b^{2}k_{1}}{a_{1}^{2}}, \alpha = \frac{a_{2}}{c_{1}}, \beta_{2} = \frac{c_{2}b}{c_{1}a_{2}}, h_{2} = \frac{bk_{2}}{a_{1}}.$

Next, we use Euler approximation method, i.e., let

where $\bigtriangleup t$ denotes a time step, $x_{n}, y_{n}$ and $x_{n+1}, y_{n+1}$ represent consecutive points. Provided with Euler approximation method with the time step $\bigtriangleup t = 1$, (2) changes into a two-dimensional discrete dynamical system:

For the sake of analysis, we rewrite (3) in the following map form:

In this paper, we will consider the effect of the coefficients of map (4) on the dynamic behavior of the map (4). Our goal is to show how a flipped bifurcation of map (4) can appear under some certain conditions.

The remainder of the present paper is organized as follows. In section 2, we discuss the fixed points of map (4) including existence and stability. In section 3, we investigate the flip bifurcation at equilibria $E_{2}$ and $E^{\ast}.$ It has been proved that map (4) can undergo the flip bifurcation provided with that some values of parameters be given certain. In section 4, we give an example to support the theoretical results of the present paper. As the conclusion, we make a brief discussion in section 5.

2.   Existence and stability of fixed points

Obviously, $E_{1}(1, 0)$ and $E_{2}(0, \frac{h_{2}}{\beta_{2}})$ are fixed points of map (4). Given the biological significance of the system, we focus on the existence of an interior fixed point $E^{\ast}(x^{\ast}, y^{\ast}),$ where $x^{\ast} > 0, y^{\ast} > 0$ and satisfy

i.e., $x^{\ast}$ is the positive root of the following cubic equation:

Based on the relationship between the roots and the coefficients of Eq (5), we have

Lemma 2.1 Assume that $\beta_{1}h_{2}^{2}-\beta_{2}^{2}h_{1} < 0,$ then Eq (5) has least one positive root, and in particular

(ⅰ) a unique positive root, if $\beta_{1}\geq \beta_{2}^{2};$

(ⅱ) three positive roots, if $\beta_{1} < \beta_{2}^{2}.$

The proof of Lemma 2.1 is easy, and so it is omitted.

In order to study the stability of equilibria, we first give the Jacobian matrix $J(E)$ of map (4) at any a fixed point $E(x, y),$ which can be written as

For equilibria $E_{1},$ we have

The eigenvalues of $J(E_{1})$ are $\lambda_{1} = 0, \lambda_{2} = 1+\alpha$ with $\lambda_{2} > 1$ due to the constant $\alpha > 0,$ so $E_{1}(1, 0)$ is a saddle.

For equilibria $E_{2},$ note that

then the eigenvalues of $J(E_{2})$ are $\lambda_{1} = 2-\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}}, \lambda_{2} = 1-\alpha,$ and so we get

Lemma 2.2 The fixed point $E_{2}(0, \frac{h_{2}}{\beta_{2}})$ is

(ⅰ) a sink if $1 < \frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} < 3$ and $0 < \alpha < 2;$

(ⅱ) a source if $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} < 1$ or $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} > 3$ and $\alpha > 2;$

(ⅲ) a a saddle if $1 < \frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} < 3$ and $\alpha > 2,$ or, $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} < 1$ or $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} > 3$ and $0 < \alpha < 2;$

(ⅳ) non-hyperbolic if $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} = 1$ or $\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}} = 3$ or $\alpha = 2.$

3.   Flip bifurcation

In this section, we will use the relevant results of literature ^[38,39,40] to study the flip bifurcation at equilibria $E_{2}$ and $E^{\ast}.$

3.1.   Flip bifurcation at equilibria $E_{2}$

Based on (ⅲ) in Lemma 2.2, it is known that if $\alpha = 2$, the eigenvalues of $J(E_{2})$ are: $\lambda_{1} = 2-\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}}, \lambda_{2} = -1.$ Define

We conclude that a flip bifurcation at $E_{2}(0, \frac{h_{2}}{\beta_{2}})$ of map (4) can appear if the parameters vary in a small neighborhood of the set $Fl.$

To study the flip bifurcation, we take constant $\alpha$ as the bifurcation parameter, and transform $E_{2}(0, \frac{h_{2}}{\beta_{2}})$ into the origin. Let $e = 2-\frac{\beta_{1}h_{2}^{2}}{\beta_{2}^{2}h_{1}}, \alpha_{1} = \alpha-2,$ and

then map (4) can be turned into

Let

then by the following invertible transformation:

map (6) turns into

where

Provided with the center manifold theorem (Theorem 7 in ^[40]), it can be obtained that there will exist a center manifold $W^{c}(0, 0)$ for map (7), and the center manifold $W^{c}(0, 0)$ can be approximated as:

As the center manifold satisfies:

it can be obtained by comparing the coefficients of the above equality that $a = 0, b = 0, c = 0,$ so the center manifold of map (7) at $E_{2}(0, \frac{h_{2}}{\beta_{2}})$ is $s = 0.$ Then map (7) restricted to the center manifold turns into

Obviously,

so

Therefore, Theorem 4.3 in ^[38] guarantees that map (3) undergoes a flip bifurcation at $E_{2}(0, \frac{h_{2}}{\beta_{2}})$.

3.2.   Flip bifurcation at equilibria $E^{\ast}$

Note that

then the characteristic equation of Jacobian matrix $J(E^{\ast})$ of map (3) at $E^{\ast}(x^{\ast}, y^{\ast})$ is:

where

Firstly, we discuss the stability of the fixed point $E^{\ast}(x^{\ast}, y^{\ast}).$ The stability results can be described as the the following Lemma, which can be easily proved by the relations between roots and coefficients of the characteristic Eq (8), so the proof has been omitted.

Lemma 3.1 The fixed point $E^{\ast}(x^{\ast}, y^{\ast})$ is

(ⅰ) a sink if one of the following conditions holds.

(ⅰ.1) $0 < \alpha_{0}+\eta < 1,$ and $\frac{\alpha_{0}-1}{\alpha_{0}+\eta} < \alpha < \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅰ.2) $-1 < \alpha_{0}+\eta < 0,$ and $\alpha < \min \{\frac{\alpha_{0}-1}{\alpha_{0}+\eta}, \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta} \};$

(ⅰ.3) $\alpha_{0}+\eta < -1,$ and $\frac{\alpha_{0}-1}{\alpha_{0}+\eta} > \alpha > \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅱ) a source if one of the following conditions holds.

(ⅱ.1) $0 < \alpha_{0}+\eta < 1,$ and $\alpha < \min \{\frac{\alpha_{0}-1}{\alpha_{0}+\eta}, \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta} \};$

(ⅱ.2) $-1 < \alpha_{0}+\eta < 0,$ and $\frac{\alpha_{0}-1}{\alpha_{0}+\eta} < \alpha < \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅱ.3) $\alpha_{0}+\eta < -1,$ and $\alpha > \max \{\frac{\alpha_{0}-1}{\alpha_{0}+\eta}, \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta} \};$

(ⅲ) a saddle if one of the following conditions holds.

(ⅲ.1) $-1 < \alpha_{0}+\eta < 1,$ and $\alpha > \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅲ.2) $\alpha_{0}+\eta < -1,$ and $\alpha < \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅳ) non-hyperbolic if one of the following conditions holds.

(ⅳ.1) $\alpha_{0}+\eta = 1;$

(ⅳ.2) $\alpha_{0}+\eta\neq -1;$ and $\alpha = \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta};$

(ⅳ.3) $\alpha_{0}+\eta\neq 0, \alpha = \frac{\alpha_{0}-1}{\alpha_{0}+\eta}$ and $(1+\alpha_{0}-\alpha)^{2} < 4((1-\alpha)\alpha_{0}-\eta\alpha).$

Then based on (ⅳ.2) of Lemma 3.1 and $\alpha\neq 1+\alpha_{0}, 3+\alpha_{0},$ we get that one of the eigenvalues at $E^{\ast}(x^{\ast}, y^{\ast})$ is $-1$ and the other satisfies $|\lambda|\neq 1.$ For $\alpha, \beta_{1}, \beta_{2}, h_{1}, h_{2} > 0,$ let us define a set:

We assert that a flip bifurcation at $E^{\ast}(x^{\ast}, y^{\ast})$ of map (3) can appear if the parameters vary in a small neighborhood of the set $Fl.$

To discuss flip bifurcation at $E^{\ast}(x^{\ast}, y^{\ast})$ of map (3), we choose constant $\alpha$ as the bifurcation parameter and adopt the central manifold and bifurcation theory ^[38,39,40].

Let parameters $(\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2})\in Fl,$ and consider map (3) with $(\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2}),$ then map (3) can be described as

Obviously, map (9) has only a unique positive fixed point $E^{\ast}(x^{\ast}, y^{\ast}),$ and the eigenvalues are $\lambda_{1} = \; -\; 1, \lambda_{2} = 2+\alpha_{0}-\alpha,$ where $|\lambda_{2}|\neq1.$

Note that $(\alpha_{1}, \beta_{1}, \beta_{2}, h_{1}, h_{2})\in Fl,$ then $\alpha_{1} = \frac{2(1+\alpha_{0})}{1+\alpha_{0}+\eta}.$ Let $|\alpha^{\ast}|$ small enough, and consider the following perturbation of map (9) described by

with $\alpha^{\ast}$ be a perturbation parameter.

To transform $E^{\ast}(x^{\ast}, y^{\ast})$ into the origin, we let $u = x-x^{\ast}, v = y- y^{\ast},$ then map (10) changes into

where

$a_{1} = 2-2x^{\ast}-\beta_{1}(y^{\ast})^{2}f(0)-\beta_{1}x^{\ast}(y^{\ast})^{2}f'(0);$ $a_{2} = -2\beta_{1}x^{\ast}y^{\ast}f(0);$

$a_{3} = -1-\beta_{1}(y^{\ast})^{2}f'(0)-\frac{1}{2}\beta_{1}x^{\ast}(y^{\ast})^{2}f''(0);$ $a_{4} = -2\beta_{1}y^{\ast}f(0)-2\beta_{1}x^{\ast}y^{\ast}f'(0);$

$a_{5} = -\beta_{1}x^{\ast}f(0);$ $a_{6} = -\frac{1}{2}\beta_{1}(y^{\ast})^{2}f''(0)-\frac{1}{6}\beta_{1}x^{\ast}(y^{\ast})^{2}f'''(0);$

$a_{7} = -\beta_{1}x^{\ast}y^{\ast}f''(0)-2\beta_{1}y^{\ast}f'(0);$ $a_{8} = -\beta_{1}f(0)-\beta_{1}x^{\ast}f'(0), \; \; \; a_{9} = 0;$

$f(0) = \frac{1}{(x^{\ast})^{2}+h_{1}}, f'(0) = \frac{-2x^{\ast}}{[(x^{\ast})^{2}+h_{1}]^{2}}, f''(0) = \frac{6(x^{\ast})^{2}-2h_{1}}{[(x^{\ast})^{2}+h_{1}]^{3}}, f'''(0) = \frac{ 24x^{\ast} (h_{1}-(x^{\ast})^{2})}{[(x^{\ast})^{2}+h_{1}]^{4}}.$

$b_{1} = \frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{2} };$ $b_{2} = 1+\alpha_{1}-\frac{\alpha_{1}\beta_{2}y^{\ast} }{x^{\ast}+h_{2}};$ $b_{3} = -\frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{3} };$ $b_{4} = \frac{2\alpha_{1}\beta_{2}y^{\ast} }{ (x^{\ast}+h_{2})^{2} };$

$b_{5} = -\frac{\alpha_{1}\beta_{2} }{x^{\ast}+h_{2}};$ $c_{1} = \frac{\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{2} };$ $c_{2} = 1-\frac{\beta_{2}y^{\ast} }{x^{\ast}+h_{2}};$ $c_{3} = -\frac{\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{3} };$

$c_{4} = \frac{2\beta_{2}y^{\ast} }{(x^{\ast}+h_{2})^{2} };$ $c_{5} = -\frac{\beta_{2} }{x^{\ast}+h_{2} };$ $b_{6} = \frac{\alpha_{1}\beta_{2}(y^{\ast})^{2} }{(x^{\ast}+h_{2})^{4} };$ $b_{7} = -\frac{2\alpha_{1}\beta_{2}y^{\ast} }{ (x^{\ast}+h_{2})^{3} };$

Now let's construct an matrix

It's obvious that the matrix $T_{2}$ is invertible due to $\lambda_{2}\neq -1,$ and then we use the following invertible translation

map (11) can be described by

where

with

$u = a_{2}(s+w), v = (\lambda_{2}-a_{1})w-(a_{1}+1)s;$

$u^{2} = (a_{2}(s+w))^{2};$

$uv = (a_{2}(s+w))((\lambda_{2}-a_{1})w-(a_{1}+1)s);$

$v^{2} = ((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{2};$

$u^{3} = (a_{2}(s+w))^{3};$

$u^{2}v = (a_{2}(s+w))^{2}((\lambda_{2}-a_{1})w-(a_{1}+1)s);$

$uv^{2} = (a_{2}(s+w))((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{2};$

$v^{3} = ((\lambda_{2}-a_{1})w-(a_{1}+1)s)^{3}.$

In the following, we will study the center manifold of map (12) at fixed point (0, 0) in a small neighborhood of $\alpha^{\ast} = 0.$ The well-known center manifold theorem guarantee that a center manifold $W^{c}(0, 0)$ can exist, and it can be approximated as follows

which satisfies

By comparing the coefficients of the above equation, we have

So, restricted to the center manifold $W^{c}(0, 0),$ map (12) turns into

where

$e_{1} = A_{1}a_{2}^{2}-A_{2}a_{2}(a_{1}+1)+ A_{3}(a_{1}+1)^{2};$

$e_{2} = -A_{8}a_{2}+ A_{9}(a_{1}+1);$

$e_{3} = 2A_{1}d_{2}a_{2}^{2}+ A_{2}a_{2}d_{2}(\lambda_{2}-2a_{1}-1)-2A_{3}d_{2}(\lambda_{2}-a_{1})(a_{1}+1)-A_{8}a_{2}d_{1}$

$-A_{9}(\lambda_{2}-a_{1})d_{1}-A_{10}a_{2}^{2}+A_{11}a_{2}(a_{1}+1)-A_{12}(a_{1}+1)^{2};$

$e_{4} = -A_{8}a_{2}d_{2}-A_{9}(\lambda_{2}-a_{1})d_{2};$

$e_{5} = 2A_{1}a_{2}^{2}d_{1}+A_{2}a_{2}d_{1}(\lambda_{2}-2a_{1}-1)-2A_{3}d_{1}(\lambda_{2}-a_{1})(a_{1}+1)+A_{4}a_{2}^{3}$

$-A_{5}a_{2}^{2}(a_{1}+1)+A_{6}a_{2}(a_{1}+1)^{2}-A_{7}(a_{1}+1)^{3};$

with

$A_{1} = \frac{(\lambda_{2}-a_{1})a_{3}-a_{2} b_{3}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{2} = \frac{(\lambda_{2}-a_{1})a_{4}-a_{2} b_{4}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{3} = \frac{(\lambda_{2}-a_{1})a_{5}-a_{2} b_{5}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{4} = \frac{(\lambda_{2}-a_{1})a_{6}-a_{2} b_{6}}{ a_{2}(\lambda_{2}+1) };$

$A_{5} = \frac{(\lambda_{2}-a_{1})a_{7}-a_{2} b_{7}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{6} = \frac{(\lambda_{2}-1)a_{8}-a_{2} b_{8}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{7} = \frac{(\lambda_{2}-a_{1})a_{9}-a_{2} b_{9}}{ a_{2}(\lambda_{2}+1) }; \; \; A_{8} = \frac{a_{2}c_{1}}{a_{2}(\lambda_{2}+1)};$

$A_{9} = \frac{a_{2}c_{2}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{10} = \frac{a_{2}c_{3}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{11} = \frac{a_{2}c_{4}}{a_{2}(\lambda_{2}+1)}; \; \; \; \; \; \; \; \; A_{12} = \frac{a_{2}c_{5}}{a_{2}(\lambda_{2}+1)}.$

To study the flip bifurcation of map (13), we define the following two discriminatory quantities

and

which can be showed in ^[38]. Then provided with Theorem 3.1 in ^[38], the following result can be given as

Theorem 3.1. Assume that $\mu_{1}$ and $\mu_{2}$ are not zero, then a flip bifurcation can occur at $E^{\ast}(x^{\ast}, y^{\ast})$ of map (3) if the parameter $\alpha^{\ast}$ varies in a small neighborhood of origin. And that when $\mu_{2} > 0 (<0),$ the period-2 orbit bifurcated from $E^{\ast}(x^{\ast}, y^{\ast})$ of map (3) is stable (unstable).

4.   Example

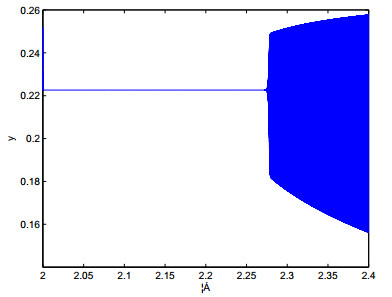
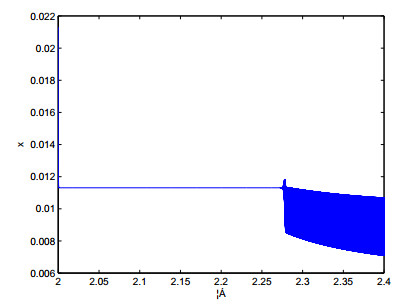
As application, we now give an example to support the theoretical results of this paper by using MATLAB. Let $\beta_{1} = 1, \beta_{2} = 0.5, h_{1} = 0.05, h_{2} = 0.1,$ then we get from (5) that map (3) has only one positive point $E^{\ast}(0.0113, 0.2226).$ And we further have $\mu_{1} = e_{2} = 0.1134 \neq 0, \mu_{2} = e_{5}+e_{1}^{2} = -4.4869 \neq 0,$ which implies that all conditions of Theorem 3.1 hold, a flip bifurcation comes from $E^{\ast}$ at the bifurcation parameter $\alpha = 2.2238$, so the flip bifurcation is supercritical, i.e., the period-2 orbit is unstable.

According to Figures 1 and 2, the positive point $E^{\ast}(0.0113, 0.2226)$ is stable for $2\leq \alpha \leq 2.4$ and loses its stability at the bifurcation parameter value $\alpha = 2.2238.$ Which implies that map (3) has complex dynamical properties.

5.   Conclusions

In this paper, a predator-prey model with modified Leslie-Gower and Holling-type Ⅲ schemes is considered from another aspect. The complex behavior of the corresponding discrete time dynamic system is investigated. we have obtained that the fixed point $E_{1}$ of map (4) is a saddle, and the fixed points $E_{2}$ and $E^{\ast}$ of map (4) can undergo flip bifurcation. Moreover, Theorem 3.1 tell us that the period-2 orbit bifurcated from $E^{\ast}(x^{\ast}, y^{\ast})$ of map (3) is stable under some sufficient conditions, which means that the predator and prey can coexist on the stable period-2 orbit. So, compared with previous studies ^[28] on the continuous predator-prey model, our discrete model shows more irregular and complex dynamic characteristics. The present research can be regarded as the continuation and development of the former studies in ^[28].

Acknowledgments

This work is supported by the National Natural Science Foundation of China (60672085), Natural Foundation of Shandong Province (ZR2016EEB07) and the Reform of Undergraduate Education in Shandong Province Research Projects (2015M139).

The authors would like to thank the referee for his/her valuable suggestions and comments which led to improvement of the manuscript.

Conflict of interest

The authors declare that they have no competing interests.

YYL carried out the proofs of main results in the manuscript. FXZ and XLZ participated in the design of the study and drafted the manuscripts. All the authors read and approved the final manuscripts.