1. Introduction
In recent years, virus dynamics attracts more and more attentions of researchers and plays a crucial role in many diseases research, including AIDS, hepatitis and influenza. Many mathematical models have provided insights into virus infection and dynamics, as well as on how an infection can be managed, reduced or even eradicated ([3], [4], [7], [15], [17], [27], [38], [43], [44]). Since the basic three-dimensional viral infection model was proposed by Nowak et al. [21], Perelson et al. [26], Perelson and Nelson [25], Nowak and May [20], many people have established different within-host infection model, which help us to better understand virus infection and various drug therapy strategies by mathematical analysis, numerical simulations and clinical data ([13], [19], [22], [28], [29]). Note that immune responses play a critical part in the process of viral infections. Concretely, cytotoxic T lymphocyte (CTL) cells can attack infected cells, and antibody cells can neutralize viruses. To better understand the role of the immune function during virus infection, Wodarz proposed the following model with both CTL and antibody immune responses [41],
|
{˙T(t)=λ−d1T(t)−βT(t)V(t),˙I(t)=βT(t)V(t)−d2I(t)−pI(t)C(t),˙V(t)=rd2I(t)−d3V(t)−qA(t)V(t),˙C(t)=k1I(t)C(t)−d4C(t),˙A(t)=k2A(t)V(t)−d5A(t),
|
(1)
|
where a dot denotes the differentiation with respect to time t, T(t),I(t),V(t),C(t) and A(t) are the concentrations of healthy cells, infected cells, free virus, CTL cells and antibody cells at time t, respectively. d1,d2,d3,d4,d5 are the death rates of healthy cell, infected cell, free virus, CTL cells and antibody cells, respectively. λ represents a constant production of the healthy cells. The term βTV represents the rate for the heathy T cells to be infected by virus. Furthermore, infected cells are killed by CTL cells at a rate pIC. Free virus are produced by infected cells at a rate rd2I, and are killed by antibody responses at a rate qAV. CTL immune responses are activated at a rate proportional to the abundance of CTL cells and infected cells, k1IC. Antibody responses are produced at a rate proportional to the abundance of antibodies and free virus, k2AV. Biologically, all parameters are positive.
After that, some researchers have taken into account the effect of immune responses including CTL responses or antibody responses ([24], [35], [36], [37], [39]). Some other researchers have incorporated the effect of CTL responses and intracellular delays ([11], [16], [18], [32], [45]). Concretely, the global dynamics of (1) with and without intracellular time delay is given in [24] and [42], respectively. Note that model (1) assumes that CTL and antibody responses are produced at bilinear rates. However, De Boer [5] pointed out that the bilinear rates cannot model several immune responses that are together controlling a chronic infection. In [5], De Boer has proposed an immune response function with the saturation. Incorporating the saturation effects of immune responses and the delay, [12] also obtained the global stability of the model, which is totally determined by the corresponding reproductive numbers. These results preclude the complicated behaviors such as the backward bifurcations and Hopf bifurcations which may be induced by saturation factors and time delay.
Note also that most of models assume CTL responses are activated by infected cells/antigenic stimulation, and antibody responses are activated by virus in these studies. However, as pointed out by Nowak and May [20], CTL responses have another function of self-regulating, i.e., the CTL responses are triggered by encountering foreign antigen and then adopts a constant level which is independent of the concentration of virions or infected cell. Bocharvor et al. have provided evidence the export of precursor CTL cells from the thymus [2]. Pang and Cui et al. have studied the export of specific precursor CTL cells from the thymus in [23], but they didn't considered intracellular time delay and antibody responses. Similarly, Wang and Wang have considered that neutralizing antibodies are produced at a constant rate after the injection [37], but they didn't take into account the effect of CTL responses and intracellular time delay.
Motivated by the above studies, we will formulate and analyze a virus dynamics model with the recruitment of immune responses, saturation effects of immune responses and an intracellular time delay, which can be described by the following functional differential equations:
|
{˙T(t)=λ−d1T(t)−βT(t)V(t),˙I(t)=βT(t−τ)V(t−τ)e−sτ−d2I(t)−pI(t)C(t),˙V(t)=rd2I(t)−d3V(t)−qA(t)V(t),˙C(t)=λ1+k1I(t)C(t)h1+C(t)−d4C(t),˙A(t)=λ2+k2A(t)V(t)h2+A(t)−d5A(t).
|
(2)
|
Here, we use λ1 to describe the export of specific precursor CTL cells from the thymus, λ2 to describe the recruitment rate of antibody responses. The production of infected cells is delayed in such a way that the production of new virus at time t depends on the population of virus and infected cells at a previous time t−τ, and only a fraction of e−sτ can survive after the interval τ, where 1/s is the average lifetime of infected cells without reproduction. h1,h2 are saturation constants. Other parameters are same as that in model (1).
The main aim of the present paper is to explore the effects of the recruitment of immune responses on virus infection. The organization of this paper is as follows. In the next section, some preliminary analyzes of the model (2) will be given. Stability of all equilibria are given in Section 3. In Section 4, some numerical simulations are given to explain the effects of λ1,λ2, i.e., the term of recruitment of immune responses. Lastly, some brief conclusions are given in Section 5.
2. Preliminary analyses of the model
In this section, we will first prove the positivity and boundedness of solutions, and then derive the expression of the basic reproduction number for model (2).
2.1. Positivity and boundedness of solutions
Let X:=C([−τ,0],R5) be the Banach space of continuous functions from [−τ,0] to R5. For ϕ=(ϕ1,ϕ2,ϕ3,ϕ4, ϕ5)∈X, define ∥ϕ∥=∑5i=1∥ϕi∥∞, in which ∥ϕi∥∞=maxθ∈[−τ,0]|ϕi(θ)|. The initial functions for model (2) are provided with ϕ∈X+=C([−τ,0],R5+).
Proposition 1. Under the above initial conditions, all solutions of model (2) are nonnegative. In particular, the solution (T(t),I(t),V(t),C(t),A(t)) of model (2) is positive for t>0 in its existence interval if T(0)>0,I(0)>0,V(0)>0,C(0)>0,A(0)>0.
Proof. We first verify that T(t) is positive in the existence interval of the solution. Suppose not. Then there is t1>0 such that T(t1)=0 and T(t)>0,t∈[0,t1). Indeed, if T(0)=0, we have ˙T(0)=λ>0. Thus, T(t)>0 for small positive t. Evidently, this remains valid if T(0)>0. As a result, the existence of t1 follows if the claim is not true. Note that ˙T(t1)=λ>0. Thus, there is a sufficiently small ε>0, such that T(t)<0 for all t∈(t1−ε,t1). We get a contradiction because T(t)>0,t∈[0,t1). Hence, T(t) is positive in the existence interval of the solution. In the same way, we obtain C(t) and A(t) are positive in the existence interval of the solution. Then, we verify that I(t) and V(t) are positive. In the same way, we assume that there is a first time t2 such that V(t2)=0, from the third equation of model (2) we have
By solving the second equation of model (2), we obtain
|
I(t2)=e∫t20−(d2+pC(ξ))dξ[I(0)+∫t20βT(θ−τ)V(θ−τ)e−sτe∫θ0(d2+pC(ξ))dξdθ]>0.
|
It follows that ˙V(t2)>0, hence V(t)>0. Furthermore,
|
I(t)=e∫t0−(d2+pC(ξ))dξ[I(0)+∫t0βT(θ−τ)V(θ−τ)e−sτe∫θ0(d2+pC(ξ))dξdθ].
|
From the above expression of I(t) solution, we get I(t)>0.
It follows easily that I(t)≥0,V(t)≥0 in the existence interval of the solution if the initial functions are in X+, and I(t)>0,V(t)>0,C(t)>0,A(t)>0 in the existence interval of the solution if I(0)>0,V(0)>0,C(0)>0,A(0)>0.
Proposition 2. All solutions of model (2) in X+ are ultimately bounded.
Proof. Set
|
L(t)=T(t)+I(t+τ)+13rV(t+τ)+d23k1C(t+τ)+d34k2rA(t+τ).
|
Calculating the derivative of L along the solution of (2), we get
|
˙L(t)=λ−d1T(t)−βT(t)V(t)+βT(t)V(t)−d2I(t+τ)−pI(t+τ)C(t+τ)+d23I(t+τ)−d33rV(t+τ)−q3rA(t+τ)V(t+τ)+d23k1λ1+d23I(t+τ)C(t+τ)h1+C(t+τ)−d23k1d4C(t+τ)+d34k2rλ2+d34rA(t+τ)V(t+τ)h2+A(t+τ)−d34k2rd5A(t+τ).
|
(3)
|
Since
|
C(t+τ)h1+C(t+τ)≤1,A(t+τ)h2+A(t+τ)≤1,
|
we obtain
|
˙L(t)≤λ−d1T(t)−d2I(t+τ)+d23I(t+τ)−d33rV(t+τ)+d23k1λ1+d23I(t+τ)−d23k1d4C(t+τ)+d34k2rλ2+d34rV(t+τ)−d34k2rd5A(t+τ)≤λ+d23k1λ1+d34k2rλ2−d1T(t)−d23I(t+τ)−d3413rV(t+τ)−d4d23k1C(t+τ)−d5d34k2rA(t+τ)≤λ+d23k1λ1+d34k2rλ2−mL(t),
|
where m=min{d1,d2/3,d3/4,d4,d5}. It follows that the nonnegative solutions of (2) exist on [0,∞) and are ultimately bounded. Moreover,
|
lim supt⟶∞L(t)≤λm+d2λ13k1m+d3λ24k2rm.
|
From the first equation of model (2), we get
It follows that
Set F(t)=T(t)+I(t+τ), then
|
˙F(t)=˙T(t)+˙I(t+τ)≤λ−nF(t),n=min{d1,d2},
|
thus
Then,
|
lim supt⟶∞(T(t)+I(t+τ))≤λn.
|
(4)
|
From the third equation of model (2) and (4), we have
Further, let
|
M=max{λd1,λn,rd2λd3n,λm+d2λ13k1m+d3λ24k2rm}.
|
The dynamics of model (2) can be analyzed in the following bounded feasible region
|
Γ={(T,I,V,C,A)∣0≤T≤M,0≤T+I≤M,0≤V≤M,0≤C≤M,0≤A≤M}.
|
2.2. The basic reproductive number
Based on the concept of the basic reproductive number for an epidemic disease presented in [6, 35], we know the basic reproductive number R0 of virus is the expected number of viruses that one virion gives rise to in an totally uninfected cell population during its lifetime.
From model (2), it is clear that healthy cells, CTL cells and antibody cells will stabilize to λ/d1,λ1/d4 and λ2/d5 if there is not infection, i.e., I(t)=V(t)=0. In this case, suppose that one virion is introduced, it can produce a maximum amount of P1(φ1)=βλd1e−sτφ1 infections during its mean lifetime of φ1=1/(d3+qλ2d5). In addition, an infected cell has an average lifetime of φ2=1/(d2+pλ1d4), and hence, it can averagely generate P2(φ2)=rd2φ2 virus. Therefore, the basic reproduction number of virus for model (2) can be defined as
|
R0=P1(φ1)P2(φ2)=βλd1rd2(d2+pλ1d4)1(d3+qλ2d5)e−sτ.
|
Based on the above expression, we know that there are inverse proportional relationship between the basic reproduction number of virus (R0) and the recruitment rate of immune responses (λ1 and λ2). Thus, R0 will decreases along with λ1,λ2 increasing, which means that ignoring the effects of recruitment rate of immune responses will overestimate the basic reproduction number of virus.
3. Stability of the equilibria
In this section, we first discuss the existence of infection-free equilibrium, and then analyze its stability. Besides, using the uniform persistence theory, we obtain the existence of an endemic equilibrium. After that, the stability of an endemic equilibrium was proved by constructing Lyapunov functional.
3.1. Infection-free equilibrium
Apparently, there is always an infection-free equilibrium in system (2): E0=(T0,0,0,C0,A0), where
Next, we discuss the stability of the infection-free equilibrium E0.
Theorem 3.1. When R0<1, the infection-free equilibrium E0 is globally asymptotically stable in region Γ.
Proof. First we define a Lyapunov functional L0 by
|
L0=∫T(t)T0(S−T0)SdS+esτI(t)+(1r+pC0rd2)esτV(t)+pesτk1∫C(t)C0(h1+S)(S−C0)SdS+(d2+pC0)rd2qesτk2∫A(t)A0(h2+S)(S−A0)SdS+∫0−τβT(t+θ)V(t+θ)dθ.
|
Calculating the time derivative of L0 along the solution of system (2), we obtain
|
˙L0=λ−d1T(t)−βT(t)V(t)−T0T(t)(λ−d1T(t)−βT(t)V(t))+βT(t−τ)V(t−τ)−d2I(t)esτ−pI(t)C(t)esτ+1r(rd2I(t)esτ−d3V(t)esτ−qA(t)V(t)esτ)+pC0rd2(rd2I(t)esτ−d3V(t)esτ−qA(t)V(t)esτ)+pesτk1(h1+C(t)){λ1−d4C(t)+k1I(t)C(t)h1+C(t)−C0C(t)(λ1+k1I(t)C(t)h1+C(t)−d4C(t))}+(d2+pC0)rd2qesτk2(h2+A(t)){λ2+k2A(t)V(t)h2+A(t)−d5A(t)−A0A(t)(λ2+k2A(t)V(t)h2+A(t)−d5A(t))}+βT(t)V(t)−βT(t−τ)V(t−τ).
|
Since λ=d1T0,λ1=d4C0,λ2=d5A0, it follows that
|
.L0=2d1T0−d1T(t)−T0T(t)d1T0+βT0V(t)−pI(t)C(t)esτ−d3rV(t)esτ−qrA(t)V(t)esτ+pI(t)C0esτ−pC0rd2d3V(t)esτ−pC0rd2qA(t)V(t)esτ+pesτk1λ1(h1+C(t))+pI(t)C(t)esτ−pesτk1d4C(t)(h1+C(t))−pesτk1λ1(h1+C(t))C0C(t)−pI(t)C0esτ+pesτk1d4C0(h1+C(t))+(d2+pC0)rd2qesτk2λ2(h2+A(t))+(d2+pC0)rd2esτqA(t)V(t)−(d2+pC0)rd2qesτk2d5A(t)(h2+A(t))−(d2+pC0)rd2qesτk2λ2A0A(t)(h2+A(t))−(d2+pC0)esτrd2qA0V(t)+(d2+pC0)rd2qk2esτd5A0(h2+A(t))=d1T0(2−T(t)T0−T0T(t))+(d2+pC0)(d3+qA0)esτrd2(R0−1)V(t)−pd4esτk1(C(t)−C0)2+pk1λ1h1esτ(2−C0C(t)−C(t)C0)
|
|
−(d2+pC0)qesτrd2k2d5(A(t)−A0)2+(d2+pC0)qesτrd2k2λ2h2(2−A0A(t)−A(t)A0).
|
Since the geometric mean is less than or equal to the arithmetical mean, it follows from R0<1 that ˙L0≤0. Let
|
D0={(T(t),I(t),V(t),C(t),A(t))|˙L0=0}.
|
It is easy to show that E0=(T0,0,0,C0,A0) is the largest invariant set in D0. By the Lyapunov-LaSalle invariance principle [8], E0 is globally asymptotically stable.
3.2. Uniform persistence
In order to obtain the the existence of an endemic equilibrium, in this subsection, we investigate the uniform persistence of (2). We first introduce a preliminary theory. Let X be a metric space and Φ be a semiflow on X. Suppose that X0 is an open set in X, X0⊂X,X0∩X0=∅, and X0∪X0=X. Define M∂={x∈X0:Φt(x)∈X0,t≥0}, which may be empty. A continuous p:X→[0,∞) satisfying condition: p(Φt(x))>0 for t>0 if either p(x)=0 and x∈X0 or if p(x)>0, will be called a generalized distance function for Φ.
Lemma 3.2. ([31], Theorem 3) Let p be a generalized distance function for semiflow Φ. Assume that
(H1) Φ has a global attractor ˜A.
(H2) There exists a finite sequence ˜M={M1,...,Mk} of pairwise disjoint, compact and isolated sets in X0 with the following properties:
(ⅰ) ⋃x∈˜M∂ω(x)⊂⋃ki=1Mi,
(ⅱ) no subset of ˜M forms a cycle in X0,
(ⅲ) Mi is isolated in X,
(ⅳ) Ws(Mi)⋂p−1(0,∞)=∅, i=1,...k.
Then there exists δ>0 such that for any compact chain transitive set L with L⊄Mi for i=1,..k, there holds minx∈Lp(x)>δ.
By applying Lemma 3.2 to (2), we can obtain the following result for the uniform persistence of (2).
Theorem 3.3. If R0>1, then system (2) is uniformly persistent, i.e., there exists ε>0 (independent of initial conditions), such that, lim inft→+∞T(t)≥ε,lim inft→+∞I(t)≥ε,lim inft→+∞V(t)≥ε,lim inft→+∞C(t)≥ε,lim inft→+∞A(t)≥ε, for all solutions of (2) with initial condition.
Proof. Let
|
X0={˜ϕ∈X+:˜ϕ2(θ)≡0,˜ϕ3(θ)≡0 for θ∈[−τ,0]},X0=X+∖X0,M∂={ψ∈X+:Φt(ψ)∈X0,t≥0}.
|
Basic analysis of (2) implies that X0 is a positive invariant set for (2). The positive invariance of X0 follows from Proposition 1. For any initial value condition ϕ0∈X+, define Φt(ϕ0) for t≥0 as Φt(ϕ0):=(Tt(θ),It(θ),Vt(θ),Ct(θ),At(θ)) for θ∈[−τ,0], where (Tt(θ),It(θ),Vt(θ),Ct(θ),At(θ)) is the solution of (2) with initial condition ϕ0. By Proposition 1 and Proposition 1 we have Φt(ϕ0) is dissipative in X+, and hence by Arzelˊa-Ascoli theorem, condition (H1) of Lemma 3.2 is satisfied.
Let ω(ψ) be the omega limit set of the orbit Φ(t) through ψ∈X+. Note that system (2) has an unique boundary equilibrium E0=(λ/d1,0,0,λ1/d4,λ2/d5). For any ψ∈M∂, i.e., Φt(ψ)∈X0, we have It(ψ)≡0,Vt(ψ)≡0 for all t≥0 and
|
{˙T(t)=λ−d1T(t),˙C(t)=λ1−d4C(t),˙A(t)=λ2−d5A(t).
|
(5)
|
It then follows from the result in [14] that (Tt(ψ),Ct(ψ),At(ψ))→(T0,C0,A0) as t→+∞. Thus, ⋃ψ∈M∂ω(ψ)=E0. Furthermore, by Theorem 3.1, E0 is unstable if R0>1. Then {E0} is isolated and acyclic covering and the conditions (ⅰ), (ⅱ) and (ⅲ) of Lemma 3.2 are satisfied.
Since
|
R0=βλd1rd2d2+pλ1d41d3+qλ2d5e−sτ>1,
|
we have
|
(d2+pλ1d4)(d3+qλ2d5)<βλd1rd2e−sτ.
|
(6)
|
Thus, there is sufficiently small σ such that
|
(d2+p(λ1d4+σ))(d3+q(λ2d5+σ))<β(λd1−σ)rd2e−sτ.
|
Suppose Ws(E0)∩X0≠∅. There exists a positive solution (T∗(t),I∗(t),V∗(t), C∗(t),A∗(t)) such that
|
(T∗(t),I∗(t),V∗(t),C∗(t),A∗(t))→(λ/d1,0,0,λ1/d4,λ2/d5) as t→+∞.
|
For sufficiently large t∗1, when t≥t∗1, we have
|
λd1−σ<T∗(t)<λd1+σ,λ1d4−σ<C∗(t)<λ1d4+σ,λ2d5−σ<A∗(t)<λ2d5+σ,
|
if t>t∗1+τ, it follows that
|
{˙I∗(t)≥−d2I∗(t)+βV∗(t)(λd1−σ)e−sτ−pI∗(t)(λ1d4+σ),˙V∗(t)≥−d3V∗(t)+rd2I∗(t)−q(λ2d5+σ)V∗(t).
|
(7)
|
Since
|
Aσ=(−d2−p(λ1d4+σ)β(λd1−σ)e−sτrd2−d3−q(λ2d5+σ)),
|
(8)
|
the non-diagonal elements of (8) are positive, and from (6), we obtain |Aσ|<0. By Perron-Frobrniuss Theorem, we can obtain the maximum eigenvalue α>0 of Aσ, and it has an eigenvector u=(u1,u2),u1>0,u2>0, then choose sufficiently small l such that I∗(t0)>lu1,V∗(t0)>lu2.
Now consider the following auxiliary system
|
{˙I∗(t)=−d2I∗(t)+βV∗(t)(λd1−σ)−pI∗(t)(λ1d4+σ),˙V∗(t)=−d3V∗(t)+rd2I∗(t)−q(λ2d5+σ)V∗(t).
|
(9)
|
Note I(t),V(t) are solutions of (9) with initial condition I(t0)=lu1,V(t0)=lu2. Since the model (9) is monotone, and Aσu>0, by [[30] Corollary 5.2.2], we have I(t)→+∞,V(t)→+∞ as t→+∞. Using the comparison theorem, we have I∗(t)→+∞,V∗(t)→+∞ for t→+∞, which is a contradiction. Hence, Ws(E0)∩X0=∅.
Define a continuous function p:X+→R+ by
|
p(¯ϕ)=min{¯ϕ2(0),¯ϕ3(0)},∀¯ϕ∈X+.
|
It is clear that p−1(0,∞)⊂X0 and if p(¯ϕ)>0 then p(Φt(¯ϕ))>0 for all t>0 (see e.g. [1]). Based on the above proof, and by Lemma 3.2, it then follows that there exists δ>0 such that lim inft→∞p(Φt(¯ϕ))≥δ for all ¯ϕ∈X0, which implies that there is a positive η0 such that lim inft→∞(I(t),V(t))≥(η0,η0) i.e., lim inft→∞I(t)≥η0, lim inft→∞V(t)≥η0.
Furthermore, from the first equation of (2), Proposition 1 and the above results, we have
|
˙T(t)=λ−d1T(t)−βT(t)V(t)>λ−d1T(t)−βMT(t)=λ−(d1+βM)T(t),
|
Thus,
From the fourth equation of (2),
|
˙C(t)=λ1+k1I(t)C(t)h1+C(t)−d4C(t)≥λ1−d4C(t),
|
we have
From the fifth equation of (2),
|
˙A(t)=λ2+k2A(t)V(t)h1+A(t)−d5A(t)≥λ2−d5A(t),
|
Therefore, taking ε=min{η0,λ1/d4,λ2/d5,λ/(d1+βM)}, we can conclude that
|
lim inft→+∞T(t)≥ε,lim inft→+∞I(t)≥ε,lim inft→+∞V(t)≥ε,lim inft→+∞C(t)≥ε,lim inft→+∞A(t)≥ε
|
are valid for any solution of system (2) with initial condition in X0. This completes the proof.
From the Theorem 3.1, we are easy to get that E0 is unstable if R0>1, and by Proposition 1 and the uniformly persistent of system (2), we can obtain that if R0>1, system (2) exists at least one endemic equilibrium E1=(T1,I1,V1,C1,A1).
3.3. The endemic equilibrium
Now, we discuss the stability of the endemic equilibrium E1.
Theorem 3.4. When R0>1, the endemic equilibrium E1 is globally asymptotically stable in region Γ.
Proof. Set
Define a Lyapunov functional L1 by
|
L1=∫T(t)T1(S−T1)SdS+esτ∫I(t)I1(S−I1)SdS+m1∫V(t)V1(S−V1)SdS+pesτk1∫C(t)C1(h1+C(t))(S−C1)SdS+m1qk2∫A(t)A1(h2+A(t))(S−A1)SdS+βT1V1∫0−τ(T(t+θ)V(t+θ)T1V1−1−lnT(t+θ)V(t+θ)T1V1)dθ.
|
Calculating the time derivative of L1 along the solution of system (2), we obtain
|
.L1=λ−d1T(t)−βT(t)V(t)−T1T(t)(λ−d1T(t)−βT(t)V(t))−pI(t)C(t)esτ+βT(t−τ)V(t−τ)−d2I(t)esτ−I1I(t)(βT(t−τ)V(t−τ)−d2I(t)esτ−pI(t)C(t)esτ)+m1(rd2I(t)−d3V(t)−qA(t)V(t))−m1V1V(t)(rd2I(t)−d3V(t)−qA(t)V(t))+pesτk1(h1+C(t)){λ1+k1I(t)C(t)h1+C(t)−d4C(t)−C1C(t)(λ1+k1I(t)C(t)h1+C(t)−d4C(t))}+qm1k2(h2+A(t)){λ2+k2A(t)V(t)h2+A(t)−d5A(t)−A1A(t)(λ2+k2A(t)V(t)h2+A(t)−d5A(t))}+βT(t)V(t)−βT(t−τ)V(t−τ)+βT1V1lnT(t−τ)V(t−τ)T(t)V(t).
|
Since
|
λ=d1T1+βT1V1, βT1V1=(d2I1+pI1C1)esτ, rd2I1=d3V1+qA1V1,λ1+k1I1C1h1+C1=d4C1, λ2+k2A1V1h2+A1=d5A1,
|
we have
|
˙L1=d1T1(2−T(t)T1−T1T(t))+βT1V1−βT1V1T1T(t)+βT1V(t)−I1I(t)βT(t−τ)V(t−τ)+d2I1esτ+pI1C(t)esτ−m1d3V(t)−m1qA(t)V(t)−βT1V1V1I(t)V(t)I1+m1d3V1+m1qA(t)V1+pesτk1λ1(h1+C(t))−pesτk1d4C(t)(h1+C(t))−pesτk1C1C(t)λ1(h1+C(t))+pesτk1d4C1(h1+C(t))+m1qk2λ2(h2+A(t))+m1qA(t)V(t)−m1qk2d5A(t)(h2+A(t))−m1qk2A1A(t)λ2(h2+A(t))−m1qA1V(t)+m1qk2d5A1(h2+A(t))+βT1V1lnT(t−τ)V(t−τ)T(t)V(t)=d1T1(2−T(t)T1−T1T(t))+βT1V1(1−T1T(t)+lnT1T(t))+βT1V1(1
|
|
−I1T(t−τ)V(t−τ)I(t)T1V1+lnI1T(t−τ)V(t−τ)I(t)T1V1)+βT1V1(1−V1I(t)I1V(t)+lnV1I(t)I1V(t))+pk1λ1h1esτ(2−C(t)C1−C1C(t))−pk1d4esτ(C(t)−C1)2+m1qk2λ2h2(2−A1A(t)−A(t)A1)−m1qk2d5(A(t)−A1)2.
|
Since the geometric mean is less than or equal to the arithmetical mean and 1−x+lnx≤0 for any x>0, it follows that ˙L1≤0. Let
|
D1={(T(t),I(t),V(t),C(t),A(t))|˙L1=0}.
|
It is easy to verify that ˙L1(t)=0 if and only if
|
T1T(t)=I1T(t−τ)V(t−τ)I(t)T1V1=V1I(t)I1V(t)=1.
|
Thus, T(t)=T1 and
As a result, we have V(t)=V1, and then I(t)=I1. From the second equation and the third equation of model (2), we have
|
{˙I(t)=βT1V1e−sτ−d2I1−pI1C1=0,˙V(t)=rd2I1−d3V1−qA1V1=0,
|
which implies C(t)=C1,A(t)=A1. Therefore, the largest invariant set in D1 is E1. Thus, when R0>1, all positive solutions converge to E1 by the LaSalle invariance principle [8].
4. Numerical simulations
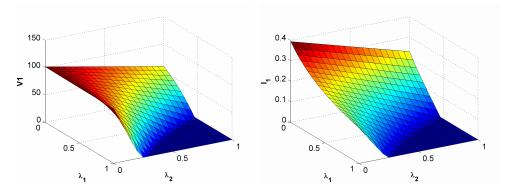
In this section, we implement numerical simulations to explore the effects of the recruitment of immune responses (λ1 and λ2) on the infected cells (I1) and virus load (V1) at the endemic equilibrium E1. The parameter values are chosen from literatures ([2], [26], [33], [32], [41], [38], [40], [46]). Especially, according to [9], we choose the range of λ1,λ2 from 0 to 1.
The all parameter values are shown in Table 1.
Table 1. Parameter definitions and values used in numerical simulations.
| Par. | Value | Description | Ref. |
| λ | 0-50 cells ml-day−1 | Recruitment rate of healthy cells | [33,38] |
| d1 | 0.007−0.1day −1 | Death rate of healthy cells | [38] |
| β | 5×10−7−0.5 ml virion-day−1 | Infection rate of target cells by virus | [33,38] |
| d2 | 0.2−0.8 day−1 | Death rate of infected cells | [41,46] |
| r | 10−2500 virions/cell | Burst size of virus | [38] |
| d3 | 2.4−3 day−1 | Clearance rate of free virus | [38] |
| p | 0.05−1 day−1 | Killing rate of CTL cells | [41,40] |
| q | 0.1−1 day−1 | Neutralizing rate of antibody | [41] |
| k1 | 0.1−0.12 day−1 | Proliferation rate of CTL response | [2,41] |
| k2 | 1.5 day−1 | Production rate of antibody response | [41] |
| d4 | 0.05−2 day−1 | Mortality rate of CTL response | [2,40] |
| d5 | 0.1 day−1 | Clearance rate of antibody | [41] |
| s | 0.001−1.4 | 1/s is the average time | [32,47] |
| τ | 0−2 days | Virus replication time | [38] |
| h1 | 1200 | Saturation constant | Assumed |
| h2 | 1500 | Saturation constant | Assumed |
| λ1 | Varied | Rate of CTL export from thymus | [9] |
| λ2 | Varied | Recruitment rate of antibody | [9] |
Figure 1 illustrates that I1,V1 decrease along with λ1,λ2 increasing in which implies that ignoring the recruitment of immune responses will overestimate the severity of the infection.
5. Conclusions
In this paper, the global dynamics of a within-host model with immune responses and intracellular time delay has been studied. By the method of Lyapunov functional and persistence theory, we obtain the global stability of the model (2) are completely determined by the values of the reproductive number. The results imply that the complicated behaviors such as backward bifurcations and Hopf bifurcations do not exist in the model with both immune responses and time delay.
Considering the basic reproductive number of virus
|
R0=R(τ)=λβrd2e−sτd1(d2+pλ1d4)(d3+qλ2d5)
|
as a function of τ, we can find that it is decreasing in τ and it tends to 0 if the time delay tends to ∞. Furthermore, comparing with the previous studies ([11], [12], [16], [23], [24], [39], [42], [45]), we find that the expression of R0 for model (2) is different, i.e., it includes the parameters λ1,λ2 which reflect the recruitment of immune responses. This implies that ignoring the recruitment of immune responses will result in overestimation of the reproductive number. Numerical simulations also show that the part of V1,I1 at steady state will decrease along with λ1,λ2 increasing (see Fig. 1), which mean that the recruitment of immune responses play a significant role in eradication of diseases. To sum up, we can conclude that ignoring the recruitment of immune responses will overestimate the infection degree and the severity of disease. These may provide a new insight for developing antiviral drug therapy strategies, which is to increase the recruitment rate of immune responses.
Acknowledgments
The authors are very grateful to the anonymous referees for their valuable comments and suggestions. This research is supported by the National Natural Science Fund of P. R. China (No. 11271369).









 DownLoad:
DownLoad: