1.
Introduction
The coronavirus disease (COVID-19) caused by a virus named "SARS-CoV-2" has created an unprecedented situation globally (WHO, 2020). The COVID-19 has also attracted Bangladesh, which was first confirmed on March 8, 2020, consequently, the country went into lockdown on March 26, 2020 (Alam and Khatun, 2021). A total lockdown has been imposed in many districts and upazilas of the country, one after another. All the government and non-government organizations, except emergency services, have been closed to prevent the transmission of the COVID-19 pandemic. But banks remained open amid the lockdown as an emergency service of financial need. Banks are operating with short hours through few branches and providing a limited range of services during this situation. Since fewer branches are working, customers of closed branches are facing problems in financial access for performing their day-to-day activity. Recently, the central bank has ordered all other banks across the country to scale down cash transactions and encourage customers to use cheques, mobile banking, online banking, or other banking instruments in order to reduce the spread of coronavirus (BB gazette and March 22, 2020 and Bangla Tribune Report, March 22, 2020). This has led to a sharp rise in the use of digital financial transactions during the pandemic. Amidst the pandemic, mobile financial services (MFS) witnessed overwhelming demands backed by the inability to make physical payments and the need for safe and secure financial access.
Terminologically, MFS are also recognized as mobile banking (m-banking) in Bangladesh (Azad, 2016). It is a financial service that is provided by a bank or a financial institution allowing people's financial transactions using a mobile device. It's an independent service that is not connected to any other account. By using a regular mobile phone, any customer can avail of this service. But a customer must need to open a mobile account first with his registered SIM, national ID card and picture from a particular agent's shop (Sultana, 2019). It is widely acknowledged that technology can play a key role in enhancing productivity and effectiveness through minimizing costs and improving customer services in the workplace. People are now more relined on using technology for advancing financial systems and improving life quality (Changchit and Chuchuen, 2016). In Bangladesh, many banks are offering a wide range of cost saving technology based channel services such as automated teller machines (ATM), telephone banking, internet banking and m-banking for which customers are encouraged to adopt (Tam and Oliveira, 2017; Hoehle et al., 2012; Sharma and Govindaluri, 2014; Sharma et al., 2015; Al-Somali et al., 2009).
Though mobile banking has many benefits, global use of mobile transactions or access to financial information is not expected level because of uncertainty and security along with lack of awareness (Dineshwar and Steven, 2013; Lin, 2011; Shaikh et al., 2015; Shih et al., 2010; Islam, 2014; Changchit et al., 2017). Research indicates that due to COVID-19, consumers are adopting digital activities significantly globally with a high willingness to continue in the future (Koslow et al., 2020). Consumers are also trying to avoid public space in response to COVID-19. A very recent survey (April, 2020) conducted by FIS on more than 1,000 American customers indicates that COVID-19 has enhanced digital banking, payments, and trade. The study also reveals that over 45% of customers changed their banking interactions permanently since COVID-19, about 45% of respondents used the platform of mobile payment in the past one month, about 31% of respondents will shift to online or mobile banking, and 40% of the respondents will shop online more than a store in the future (Marous, 2020). In Bangladesh, mobile banking transactions are mostly confined to the essential services such as cash-in, cash-out, P2P transfers, salary disbursement, and utility bill payments. In terms of monthly total transaction value, only 5% of transactions conducted for utility bill payments and salary disbursement, and almost 95% were accompanied by cash-in/cash-out and P2P transfers (BB, 2017).
In the period of pandemic, the results of this study can convey an important finding about the mobile banking adoption and its applicability, challenges and opportunities. Many previous studies have already shown the perception of mobile banking (Talwar et al., 2020), adoption behavior (Kaur et al., 2020; Talwar et al., 2020), demographic characteristics (Kaur et al., 2020), internet banking (Sudarsono et al., 2020), mobile payment (Zhao and Bacao, 2021; Khanra et al., 2021), and dimensions of mobile banking (Anysiadou et al., 2021). This study aims to explore the adoption, barriers and prospects of mobile banking as a digital financial transaction instrument in Bangladesh during COVID-19 pandemic and its aftermaths towards building a digital economy. The following research questions are set to achieve the objective: (i) What are the barriers of people's financial access? and (ii) How does mobile banking ease these barriers and amplify financial access by changing existing attitudes towards digital financial transaction platforms during COVID-19?
It is expected that the findings will help the policy-makers and banking industry to design an effective and fruitful platform for mobile banking services during and after the pandemic situation, which will further influence in making a digital Bangladesh.
2.
Methods
Secondary data were extensively used in this study to ascertain the desired objective. Data were collected from various internal and external documents such as newspaper articles, magazines, annual reports, website of the World Health Organization (WHO), Institute of Epidemiology, Disease Control and Research (IEDCR), Bangladesh Telecommunication Regulatory Commission (BTRC), Bangladesh Bank (BB) and different commercial banks in Bangladesh. Mainly documentation technique was followed to collect required data for this research. Documentation is one of the important data collection techniques of interpretive research (Bhattacherjee, 2012). Additionally, different national and international working papers, policy studies, and peer-reviewed journal articles were also reviewed for the study.
A well-structured data collection observation guide was developed by extensive desk research focusing on the key scenario of mobile financial services during the COVID-19 pandemic (2020 to 2021) that increases the people's financial access. To explore the linkage between mobile banking and digital financial access, at first, we have tried to find out the main barriers to people's financial access in Bangladesh by reviewing some grey literature and some national and international peer-reviewed journals. Then the adoption of mobile phones as a linkage of technology to the financial sector was measured by assessing the number of mobile phone subscribers with the passage of time (2012 to 2021). Similarly, the mobile banking inception and its progress as a sequential service to digital financial access were measured by considering the number of mobile banking customers over the years (2012 to 2021). After that, the people's financial access through mobile banking during and before the pandemic situation (2019 to 2020) as a linkage towards accelerated digital financial access was measured by calculating the existing and previous trend of registered mobile banking customer's number and transaction nature as well as using some government policies and initiatives regarding MFS during COVID-19 pandemic situation in Bangladesh.
3.
Results and discussion
3.1. Barriers to people's financial access
The financial system of Bangladesh is mainly consists of formal, semi-formal, and informal sectors, of which the former one dominates more. Until 1980s, the state-owned banks were controlled the financial system of the country (Batten et al., 2015). At present, the banking sector is encompassed of 6 state-owned commercial banks, 3 state-owned specialized banks mainly deal development financing, 42 private commercial banks, and 9 foreign commercial banks (Financial System: Banks and FIs, BB, 2020). A report by Akhtaruzzaman (2019) showed that the access to formal financial services is only 36 percent, and 43 percent to quasi-formal finance. Actually, a large number of people specially smallholder farmers and low earners in Bangladesh, do not have access to formal financial sources due to ignorance, collateral requirements, complex and lengthy loan sanctioning procedure (Khatun, 2019; Lowder et al., 2016; Chauke et al., 2013; Ololade and Olagunju, 2013; Khatun and Bashar, 2010). Besides, factors like financial illiteracy, lack of awareness, staff attitudes of banks, lack of physical access, high cost of products, inadequate initiatives of banks and financial institutions, and low level of technological infrastructure serve as barriers to access to financial services in Bangladesh (Akhtaruzzaman, 2019). The unavailability of financial access will continue to impede the investment into agriculture as well as business (Alam et al., 2018; Khatun et al., 2014). Hence, the provision of ATM, agent banking, online banking, and mobile banking may act as an excellent solution for some accessing financial hindrances and can play a pro-active role in people's smooth financial access in Bangladesh.
3.2. Mobile phone adoption
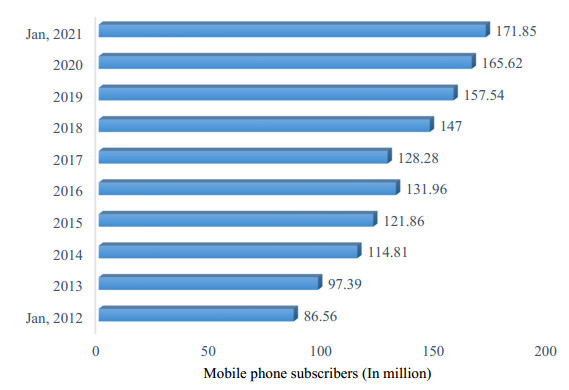
The mobile phone is an excellent information and communication technology (ICT) which is crucial to alleviate poverty and improve the quality of life by acquiring all kinds of information regarding livelihood, farming, education, medication as well as recreation easily (Alam et al., 2018; Aker, 2011). Bangladesh adopted cellular technology in 1993 when only one mobile company operated in the market. The adoption of mobile phones was only limited to wealthy people due to the higher cost of mobile phone connections (Alam et al., 2018). At present, five mobile phone operators, including one state-owned company, are functioning in Bangladesh. The number of mobile phone subscribers in Bangladesh reached 171.85 million in January 2021, about 91% more than the 86.56 million in January 2012 (Figure 1). Recently the population of Bangladesh is measured in March, 2021 as 165.904 million (Worldometer, 2021) which is lower than the mobile phone subscribers number. This evidence indicates that Bangladesh has adopted mobile phone technology at a faster pace.
Nowadays, almost every adult person owns a mobile phone irrespective of their income level (Alam et al., 2018). They usually use it to communicate with others but due to the availability of the internet and other technological innovations, mobile phone is being used for many different purposes such as business (Zhao et al., 2013). Now it is quite true that no one can think a single day without a mobile phone. Like other types of businesses, a mobile phone as a channel also provides enormous potential for banking activities (Lin, 2011).
3.3. Inception of mobile banking and its progress
Banks are providing financial services to both rural and unbanked people by digital ways like using mobile phones (Kikulwe et al., 2014). Mobile banking is a process to allow bank clients to access bank accounts products and services-related information through mobile devices. Previously only SMS services were provided by mobile banking, which was also known as SMS banking. European banks first started offering mobile banking services to the customer in 1999 due to the advent of smartphones with WAP (Wireless application protocol) support (Pandey, 2019).
Regarding Bangladesh, mobile banking is an incredible innovation in the banking sector that started on 31st March 2011. The following mobile banking services are currently offering in the country: (i) Disbursement of inward foreign remittances; (ii) Cash in/out using mobile account through agents/Bank branches/ATM's/Mobile Operator's outlets; (iii) Person to Business Payments (e.g. utility bills payment); (iv) Business to Person Payments (e.g. salary disbursement by corporate bodies/industries/offices etc); (v) Government to Person Payments (e.g. elderly allowances, freedom fighter allowances, subsidies, etc); (vi) Person to Government Payments e.g. tax, levy payments; (vii) Person to Person Payments (among registered account holders of the same bank) and (viii) Other payments like microfinance, overdrawn facility, insurance premium, DPS, etc (Sultana and Khan, 2016).
Generally, many private commercial banks run mobile banking activities all over the country at a faster pace. In contrast, a few state-owned commercial banks just started their journey in this direction. At the same time, specialized development banks and foreign commercial banks are not started mobile banking services to date. Dutch Bangla Bank Limited launched the first mobile banking service named "Rocket" in May 2011 in Bangladesh. Gradually, some other banks also started offering mobile banking facilities in the country which is summarized in Table 1.
Bangladesh has made good progress in financial inclusion through the delivery of affordable financial services to underprivileged and needy people by the introduction of some alternative delivery channels like mobile banking. In 2020, 48 percent of the adult population are under the umbrella of formal financial services, mainly due to the expansion of mobile banking services, which was only 20 percent in 2013 when there were limited MFS (Khan, 2020). In fact, mobile banking customer has increased gradually over the years in Bangladesh (Figure 2). Therefore, it is crucial to ensure that all mobile banking transactions are secured and confidential to attract potential customers and thus increase the financial access of the people.
3.4. Mobile banking during COVID-19 pandemic
The world is facing an unprecedented crisis due to the massive outbreak of COVID-19. This pandemic has changed the nature of work that people have done earlier, such as their working attitude, shopping style, mode of payments, transactions with bank etc. Conscious people are now trying to stay safe at any cost. For this, banks are now thinking about their banking services during COVID-19 and after the pandemic. Mobile banking is treated as a reasonable consideration in this regard to offer people's financial access easily and safely.
In Bangladesh, the number of customers registered for mobile banking increases rapidly after the country lockdown, which started on 26th March, 2020 in Bangladesh (Figure 3). In January 2020, the registered mobile banking clients were 80.92 million, which was risen sharply to 92.57 million in July. Within the next five consecutive months, the number gradually increased to 99.34 million in December 2020. This growth rate was higher than the preceding year 2019. In fact, the rate was started to increase sharply after June 2020 than the same time of the previous year due to declaration of the government and other originations to send/receive money through mobile banking. After the emergence of the COVID-19, the rate of increase of registered mobile banking clients from March to December 2020, was about 21 percent as against 16 percent during the same period of the previous year. Actually, due to the COVID-19 pandemic, people became afraid of transmission and preferred to pay their additional payments such as electricity, gas, and other utility bills through digital payment methods. For this, a large number of new mobile banking customers emerged during this pandemic situation. Now they are using their mobile banking platforms and feel comfortable doing such kinds of activities in this existing situation. Another important fact behind rising mobile banking customers that most of the readymade garment (RMG) owners ordered their workers to open own mobile banking account for receiving their salaries and other incentives which is a great initiative to allow the low earners into a digital financial access platform in Bangladesh. This also help to reduce the spread of COVID-19 in the country.
The nature of mobile money transactions on different products (Figure 4) reveals that cash-in, cash-out and P2P transactions were the prominent mobile banking transactions during the pandemic situation. In the mid of 2020, most mobile banking transactions reached the highest peak. Person to person (P2P) transaction increased to BDT 19146.25 crore in July, 2020 which was the highest mobile banking transaction during the COVID-19 pandemic situation in Bangladesh. Utility bill payment and salary disbursement (B2P) increased moderately up to BDT 992.94 and BDT 4586.97 crore during this pandemic situation due to various government initiatives and customers' concern on health awareness. Cash-in and the cash-out transaction had decreased from the month of February (before COVID-19) mainly due to the inconvenient operation environment of MFS agents. Still, they contributed 30% and 28% to the total transaction respectively in April, 2020 (strict country lockdown span). After that, these transactions have sharply increased for the next three months. After July, there was a fluctuation decreasing trend in cash-in, cash-out, and P2P transactions despite their highest transaction contribution. Therefore, it is expected that the mobile banking transaction on different products will increase rapidly in the future due to people's consciousness and hygiene issues to prevent the spread of coronavirus in Bangladesh.
"In Bangladesh, the necessity of traditional banking has already diminished as we have entered a digital era. The banks' cash counters will not be required soon due to the rapid expansion of digital banking and the strong base of the MFS. Banks hardly run their financial activities in rural backwaters, but the MFS providers have brought the underprivileged people of these territories to the formal financial sector. The coronavirus pandemic has given a strong message to all that there remains scope to embrace the digital financial tools to run the economy under any circumstances by easily financial access" said by Mustafa Jabbar, posts and telecommunication minister in Bangladesh, in a virtual dialogue on Digital Payment Solutions during COVID-19 Pandemic on 25th April, 2020.
3.5. Government initiatives to accelerate MFS
3.5.1. Mobile account for workers and simplifying payment systems
In order to stop the spread of COVID19, the Bangladesh Bank (BB) has issued an instruction on opening mobile banking account for every employee of export-oriented industries and factories within April 2020 to provide salaries and allowances from the governments' fiscal stimulus package of BDT5000 crore (which was announced at 25th March, 2020). To facilitate the mobile banking services, Bangladesh Bank has increased the P2P ceiling from BDT75,000 (USD883.56) to BDT200,000 (USD2356.16) per month, and cash-out charges have been kept free up to BDT1,000 (USD11.78). Moreover, the opening of a mobile banking account is charge-free. Bangladesh Bank has also advised commercial banks to take required steps to raise awareness and insisting people open mobile banking accounts, which ultimately increases the number of mobile banking account. Due to governments' instruction, about 1.92 million MFS accounts have been extended through various MFS providers since April 4 in the readymade garment (RMG) sector (BGMEA, 2020). As a major MFS provider, Bkash opened 0.97 million mobile banking accounts while 0.55 million by Rocket and 0.4 million by Nagad to facilitate the services (Imam, 2020).
3.5.2. Streamlining remittance
MFS has appeared as a swift transaction mode for migrants to send money in the country. From January to April 2020, bKash experienced a 144% increase in daily average remittance transactions, with BDT 1.38 billion transferred inward (Gomes, 2020).
3.5.3. Facilitating donation
The bKash, Nagad, Rocket, and Sure Cash are frequently using to transfer the donation. Many people are donating for organizations like Bidyanondo Foundation, Sajida Foundation, Obhizatrik Foundation, BRAC etc. using bKash, Nagad, Rocket and Sure Cash app. From mid-March to mid-April, 2020 more than BDT 50 million has been donated through bKash (Gomes, 2020). Moreover, people are sending money to poor people, relatives and friends easily and comfortably through bKash, Nagad, Rocket and Sure Cash during this pandemic situation.
3.5.4. Expediting safety net funds
Under the supervision of the Disaster Management and Relief Ministry, the government has started disbursing cash assistance to support 5 million families impacted by COVID-19 with the help of the four top MFS operators; bKash, Nagad, Rocket, and Sure Cash. The government has targeted to pay out BDT2500 per family amounting BDT1250 crore (USD147 million) through mobile banking (TBS report, May 10, 2020). The government is planning to adopt digital payment services for social security payments and government employee wages even after the COVID-19 pandemic. In 2020–2021 fiscal year, the government has allocated around BDT 74,367 crore (USD8.77 billion) for safety net programs which will be disbursed through MFS for hassle-free transactions.
3.5.5. Mobile recharge system
The use of mobile based internet data has enhanced by 15% to 20% due to lockdown in Bangladesh (BTRC, 2020). Mobile owners are increasingly using apps, such as bKash, Nagad, Rocket, and Sure Cash, to top up their mobile balance. The number of bKash users was approximately 45 million in April, 2020 but it was about 32 million before COVID-19, and about 40% increase of users during COVID-19 than before (TBS report, May 03, 2020). Customers of all local mobile operators can buy airtime or package with bKash, Nagad, Rocket, and Sure Cash. Different mobile banking such as bKash and Nagad are also providing some incentives such as instance cash back with a certain limit for mobile recharging when using their app.
"MFS is the most efficient way that can push the country to a full digital financial inclusion. I think the time has come to accept technology for the financial sector to enhance inclusion and bring transparency. There is no other effective way like MFS that can disburse cash assistance to the poor while maintaining social distancing to stop the spread of the deadly virus. Using this technology, the government can also think about disbursing other cash assistances, and even small agricultural loans and also repayment can be done" said by Zahid Hussain, a former lead economist of the World Bank's Dhaka Bangladesh office (The Daily Star, May 17, 2020).
4.
Conclusions and policy implications
Though digital technology such as mobile banking can accelerate people's financial access significantly in developing countries like Bangladesh but did not receive proper attention before COVID-19 pandemic. This study has explored the scenario of mobile banking services with relation to accelerate people's financial access in Bangladesh throughout the COVID-19 pandemic by using secondary data. Although mobile banking started its journey in 2011 in the country, its acceptance by the customer is gaining popularity in the recent COVID-19 pandemic era for obtaining financial access easily, promptly, and safely. People are now more hygienic concerned than before. In order to stop the spread of the COVID-19 pandemic, people are forced to open a mobile banking account on their own mobile devices. This resulted in a sharp increase in the number of registered mobile banking customers during the pandemic situation. Different mobile banking transactions such as cash in, cash out, and P2P transaction have sharply increased during COVID-19 pandemic due to people's changing habits towards digital transactions and different government initiatives. The importance of mobile banking has also amplified for mobile recharge, remittance transaction, donation delivery, safety net funds distribution, and so on.
The government should provide all supports to create a cashless society by offering a convenient financial access platform for fighting against the concurrent epidemic and making a digital Bangladesh. Steps should be taken to enhance the adoption of digital payment services for social security payments and government employee wages even after the COVID-19 pandemic. It is expected that these initiatives would help to accelerate mobile financial services in Bangladesh during and after the COVID-19 pandemic, which would ultimately increase the people's financial access to a greater extent in the upcoming days.
Limitations
This study has used only secondary data. Further study can be conducted on the customers' attitude, adoption pattern, and barriers of mobile payment during the COVID-19 pandemic using primary data.
Acknowledgement
This article is a preliminary output of a research project which was approved in 2020 for 2 years research grant from RMC (Research Management Committee) of BSMRAU (Bangabandhu Sheikh Mujibur Rahman Agricultural University) in Bangladesh, and grant number 11 (RMC/2020-23). The project title is "Financial inclusion of farmers through mobile banking: Empirical evidence from Mymensingh and Narsingdi district of Bangladesh".
Conflicts of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:






