Effects of magnetic field treated water on some growth parameters of corn (Zea mays) plants

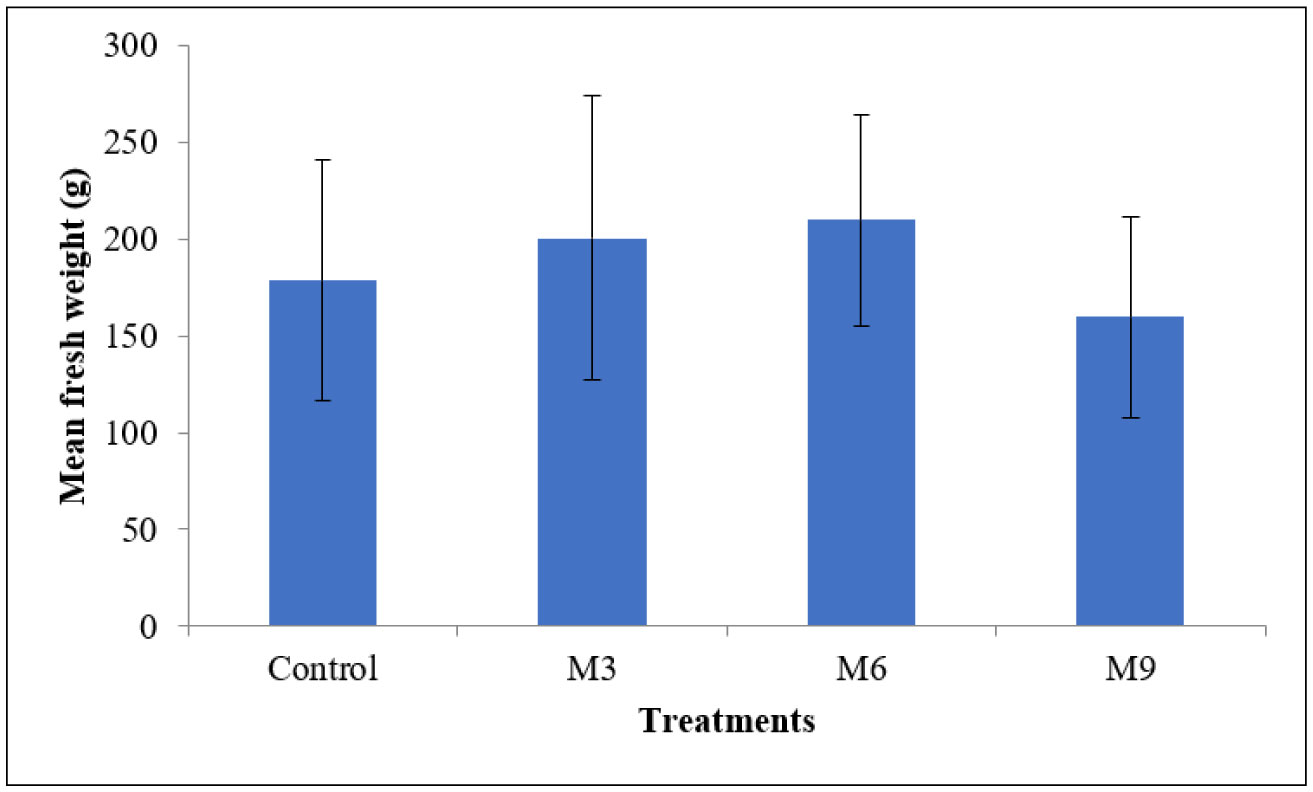
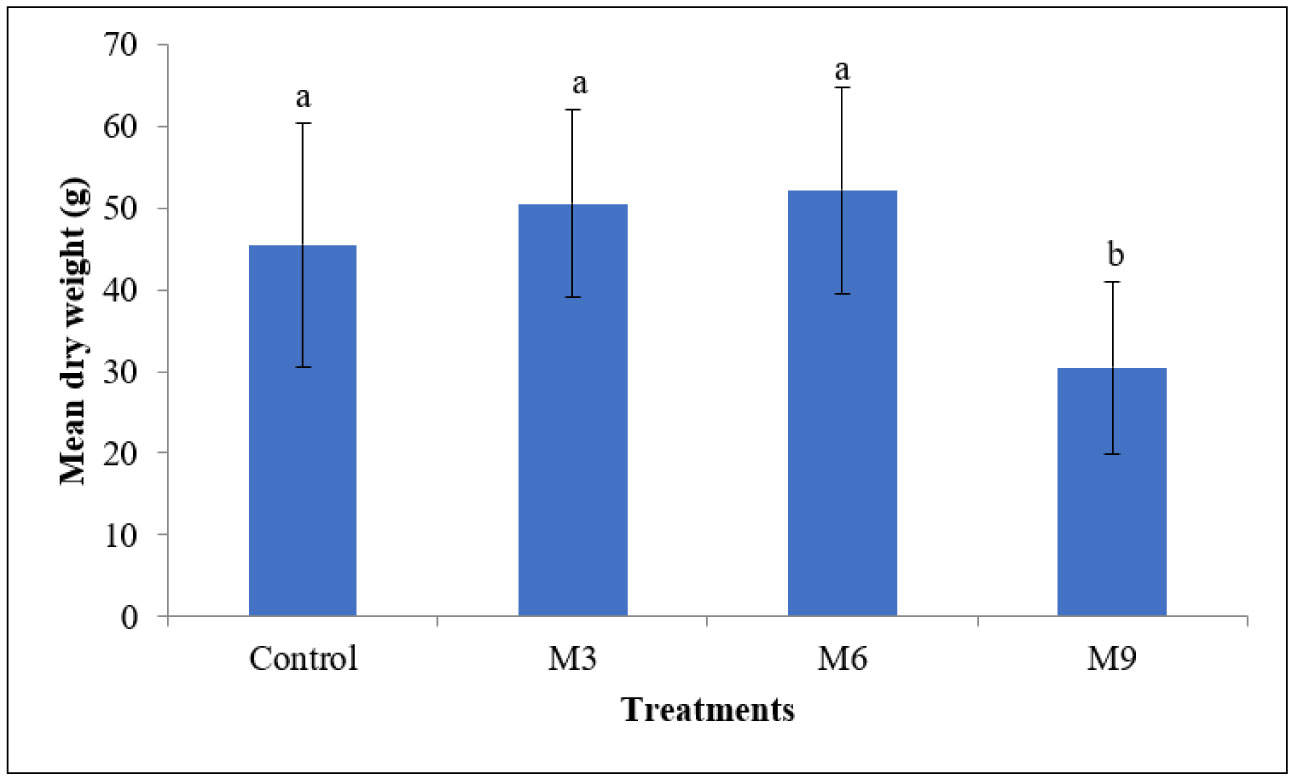
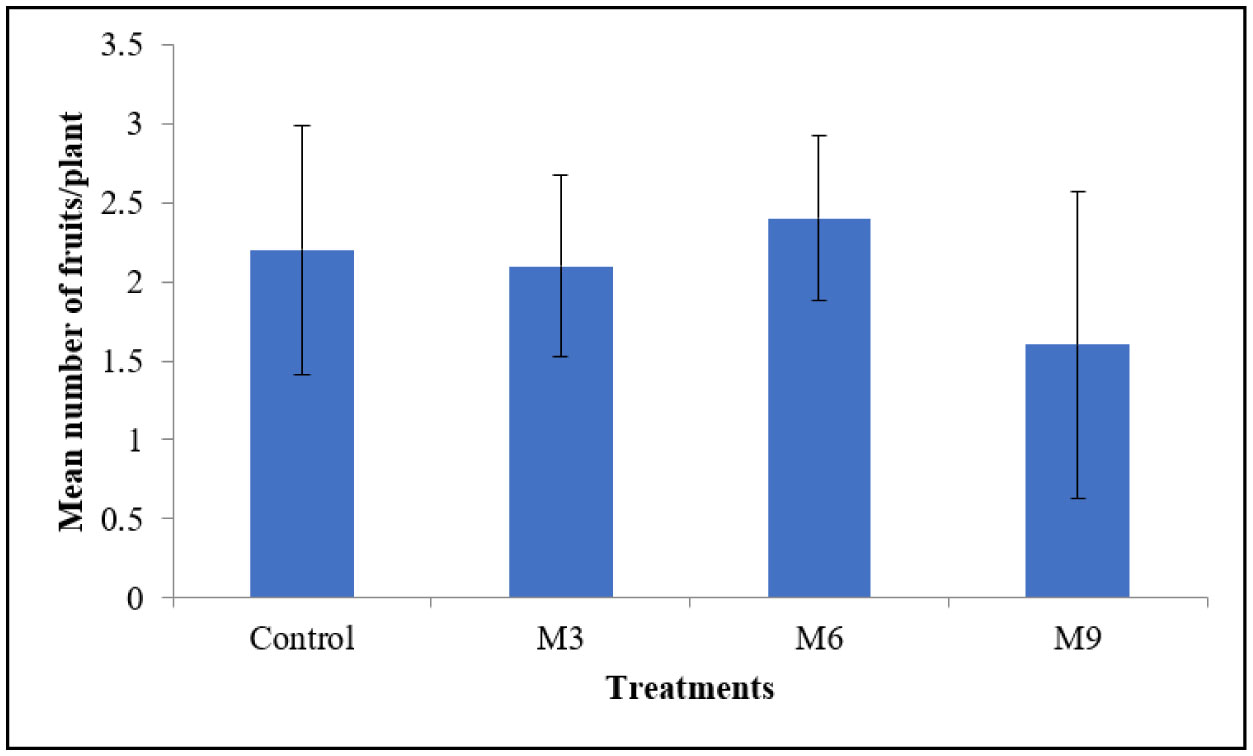
1.   Introduction

The research of nonlinear evolution equations, which describe the real features in a variety of applied science, technology and engineering areas, is booming. The findings of their exact solutions are helpful to understand a variety of qualitative and quantitative features of these nonlinear scientific phenomena, which are widely present in nature such as vibration and self reinforcing solitary waves ^[8,9,19,25]. Specially, the study of the calculation and evolution of traveling wave solution, a kind of analytical solution of nonlinear evolution equations about spatial translation invariance, is helpful to understand the change process of the wave phenomena described by models under the action of nonlinearity, and to explain the relevant natural phenomena. In last some decades, many useful methods have been proposed to obtain traveling wave solutions with different physical structures, such as Hirota's bilinear transformation ^[11], inverse scattering method ^[3], Bäcklund transformation ^[2], the auxiliary equation mapping method and its extended modified form ^[7,37], the modified extended direct algebraic method ^[4], the logarithmic transformation and symbolic computation ^[32], extended algebraic method ^[36].

Vakhnenko in 1992 first proposed a nonlinear evolution equation ^[38]

known as the Vakhnenko equation (VE), where $u = u(x, t)$ represents the pulse wave envelopes, variables $x$ and $t$ stand for normalized displacement and time, respectively. He pointed out that (1.1) exhibits hydrodynamics nonlinearity similar to the Korteweg-de-Vries (KdV) equation, which implies that it may at least partially possesses the significant properties inherent to the KdV equation, such as the existence of soliton solutions. A series of traveling wave solutions for (1.1) and its variants were obtained through the auxiliary equation method ^[29] and the traveling wave reduction combined with a smart variable transformation ^[28]. Li-Ma used the Hirota bilinear method to derive $N$-order solutions and discussed the interaction dynamics of hybrid solitons and breathers for a generalized VE in ^[23]. Moreover, Vakhnenko and Parkes found (1.1) possesses loop-like wave solutions ^[31,33,39]. Additionally, Li et al. calculated $N$-loop soliton solutions of a (2+1)-dimensional VE and observed the dynamical interactions among the $N$-solitons are elastic ^[24]. These loop-like waves describe a special physical phenomenon where waves may be compressed in the spatiotemporal domain, and have shown great application prospects in ultra-fast optics ^[10]. In fact, (1.1) is still an integrable system originally proposed to describe the propagation of high-frequency waves in relaxing media. Additionally, many studies have shown that photons have better performance when propagating in relaxed media than in traditional media ^[35,47], so (1.1) also has important applications in high-speed optical fibers ^[17,49].

Later in 1998, Vakhnenko and Parkes unintentionally evolved VE into another new equation ^[39]

namely, Vakhnenko-Parkes (VP) equation, by transforming the independent variables when they derived the exact two loop soliton solutions of (1.1). This transformation causes (1.2) to no longer have loop-like wave solutions, but the cusp-like wave solutions still exist. As a remarkable and important model to describe the propagation of gravity wave along the channel under the influence of Coriolis force, (1.2) has been proved to be integrable in sense of possessing multiple soliton-solutions ^[40,43]. Vakhnenko and Parkes found singular solutions of (1.2) with the inverse scattering method in ^[41] and the $N$-soliton solution with Hirota's method in ^[42]. The variable separation solutions with new coherent stuctures of (1.2), such as the soliton-type, instanton-type and rogue wave-type stuctures, were obtained in ^[48] by means of the variable separation approach based on the corresponding Bäcklund transformation. Moreover, there have been many profound achievements in the traveling wave solutions of (1.2), among which various methods have been developed including the (G'/G)-expansion method ^[1], the improved (G'/G)-expansion method ^[27], the simplest equation method ^[12], the exp-function and Exp(-$\phi(\xi)$)-expansion method ^[34] and the Hirota method ^[45]. Recently, Li proposed an extended Hirota bilinear method to construct the soliton, breather and multiple-wave soliton solutions of a generalized VP equation with time-dependent coefficients, and pointed out that the obtained soliton solutions can degenerate into existing single soliton solutions while the breather and multiple-wave soliton solutions are obtained for the first time ^[18].

In order to obtain more new and meaningful results, Majid et al. further extended (1.2) to family of the VP equation with power law nonlinearity ^[30]

where $a$, $b$ are nonzero real constants and $n\in\mathbb{Z}^{+}$ indicates the power law nonlinearity parameter. Using the ansatz method, they confirmed the existence of non-topological solitary waves for any exponent $n > 1/2$, topological solitary waves exist only in the case when $n = 3/2$ and closed form solitary wave solutions exist only for $a = -1$. And then the exact topological and non-topological solitary wave solutions of (1.3) were calculated in ^[30]. In ^[15], the Painlevé property of (1.3) was analysed by the Kruskal approach ^[13], its symmetry was derived with help of the Lie group formalism ^[6] and invariant solutions of (1.3) are obtained through Bäcklund transformation method. In 2020, Jyoti and Kumar proposed a modified Vakhnenko-Parkes (mVP) equation with power law nonlinearity in the following generalised form ^[14]

where $a$, $b$ are nonzero real constants and $n\neq1/3$ is a power law nonlinearity parameter. For $a = -1$, $b = 1$ and $n = 1$, (1.4) reduces to the modified form of (1.2), which was first introduced by Wazwaz in 2018 and is called the mVP equation. In the same year, Wazwaz proved the complete integrability of the mVP equation by applying the Painlevé analysis in ^[45] and introduced two complex forms of the simplified Hirota's method to determine its multiple traditional and complex soliton solutions in ^[46], respectively. Then, Jyotia and Kumar ^[14] used the Kruskal approach to perform the Painlevé analysis of the mVP equation. In ^[5], the sine-Gordon expansion method ^[44] was presented to obtain the mixed dark bright wave patterns and some exact solutions, which comprises the hyperbolic, trigonometric, rational and exponential function with few licentious parameter. Further, in order to understand the dynamic behavior of these analytical solutions with different physical structures, authors of ^[5] completed their graphical analysis by means of 2D, 3D and contour plots.

However, there are still few studies on the analytical solutions of (1.3) and (1.4), especially the traveling wave solutions. The purpose of this paper is to systematically discuss the traveling wave solutions of family of VP equation exhibiting power law nonlinearity. Using the sense of the generalized Korteweg-de Vries-modified Korteweg-de Vries (KdV-mKdV) equation with high-order nonlinear terms ^[26], we consider a generalized Vakhnenko-Parkes-modified Vakhnenko-Parkes (VP-mVP) equation with non-homogeneous power law nonlinearity

where $n\in Z^{+}$ is a power law nonlinearity parameter, and $\alpha, \beta, \gamma$ are nonzero real constants. It's not hard to see that when the parameters are taken as different values, the VP equation, the mVP equation and Eqs (1.3) and (1.4) can be derived from (1.5). Because a traveling wave solution of a nonlinear partial differential equation (NPDE) usually corresponds to a orbit of its traveling wave system in phase space, this correspondence just makes the bifurcation method of dynamical system become an effective way to study nonlinear evolution equations, and more detailed research ideas and usage techniques can be found in ^[16,22]. In recent years, Li and Liu et al. have utilized and developed this method to systematically analyze the existence laws of solitary waves, kink waves and periodic waves in the parameter space ^{[20,21,25,27]}. Based on these, we attempt to employ the bifurcation method of dynamical systems to investigate all possible bounded traveling wave solutions of (1.5). The topological phase portraits produced by the vector fields of the corresponding traveling wave system of (1.5) determine all possible traveling wave solutions $u(x, t) = \phi(\xi)$, $\xi = x-t$. If there is a finite real number $M$, such that $|\phi(\xi)| < M$ holds for any $\xi$, then $\phi(\xi)$ is called a bounded traveling wave solution, otherwise it is called an unbounded traveling wave solution.

The rest of the paper is organized as follows: in Section 2 we first study the traveling wave system corresponding to (1.5) to investigate the existence of all possible bounded traveling waves, including solitary wave, periodic wave, breaking wave, solitary cusp wave and periodic cusp wave. Then, we give all existence conditions of these waves in 4-dimensional parameter space of $\alpha, \beta, \gamma$ and an integral parameter. In Sections 3 and 4, we derive exact explicit expressions of solitary wave solution, periodic wave solution, breaking wave solution, solitary cusp wave solution and periodic cusp wave solution of (1.5), and analyze the evolutionary relationship between them. Finally, simulations of these traveling wave solutions and conclusions of this paper are given in Section 5.

2.   Analysis of traveling wave system of (1.5)

Substituting $u(x, t) = \phi(\xi)$ with $\xi = x-t$ into Eq (1.5) and integrating it once, we have the following ordinary differential equation

where $'$ denotes the derivative with respect to $\xi$, $G$ is an integral constant. When we let $\phi^{'} = y$, then (2.1) is transformed into

where $f(\phi): = -\beta\phi^{2n+1}/(2n+1)-\gamma\phi^{3n+1}/(3n+1)+G$. Since (2.2) is invariant under $(\alpha, \beta, \gamma, G)\rightarrow (-\alpha, -\beta, -\gamma, -G)$, we need only to consider $\beta > 0$. When $(\alpha-1)$ and $G$ are not $0$ at the same time, (2.2) is a singular traveling wave system of the first kind ^[22] with a singular straight line $\phi = 0$, which brings challenges to our study. Thus, we assume in (2.2) that

Further, we introduce the transformation $d\xi = \phi d\eta$, and then singular system (2.2) is reduced to the following regular system

Actually, (2.2) and (2.3) have the same first integral $H_{n}(\phi, y)$ of form

when $(\alpha-1)(\alpha+2n)(\alpha+3n)\ne0$, of form

when $\alpha = 1$, of form

when $\alpha = -2n$ and of form

when $\alpha = -3n$. This implies that (2.2) and (2.3) have the same topological phase portraits, except the singular line $\phi = 0$. Therefore, we can understand the phase portrait of (2.2) from that of (2.3).

2.1.   Bifurcation curves of equilibria of regular system (2.3)

It is not difficult to know that from the expression of (2.3) the equilibria of (2.3) only exist on the $\phi$-axis and the singular line $\phi = 0$, while the equilibria on the $\phi$-axis are the ones of (2.2). So, we first investigate the type and distribution of equilibria in (2.2), which requires us to determine the zeros of $f(\phi)$. Since the derivative function $f^{'}(\phi) = -\phi^{2n}\left(\beta+\gamma\phi^{n}\right)$ obviously has at most three zeros $0$ and $\phi^{\pm}_{n}: = \pm\sqrt[n]{-\beta/\gamma}$, and then we have at most three bifurcation curves

From $\left(G^{\pm}_{n}(\beta)\right)^{'} = \pm\sqrt[n]{-\beta/\gamma}\beta^{2}/\left((2n+1)\gamma^{2}\right)$, we can know that these three bifurcation curves do not intersect each other. Further, we conclude that when $n$ is odd, $f(\phi)$ has at most $2$ zeros which are denoted by $\phi^{i}_{n}(i = 1, 2)$ and satisfy $\phi^{1}_{n}\leqslant\phi^{2}_{n}$; when $n$ is even, $f(\phi)$ has at most $3$ zeros which are denoted by $\varphi^{j}_{n}(j = 1, 2, 3)$ and satisfy $\varphi^{1}_{n}\leqslant\varphi^{2}_{n}\leqslant\varphi^{3}_{n}$. Then, $\left(\phi^{i}_{n}, 0\right)(i = 1, 2)$ or $\left(\varphi^{j}_{n}, 0\right)(j = 1, 2, 3)$ is an equilibrium of (2.2) and has characteristic equation $\lambda^{2}-\phi_{0}f^{'}(\phi_{0}) = 0$, where $\phi_{0}$ is equal to $\phi^{i}_{n}$ or $\varphi^{j}_{n}$. This implies that the equilibria of (2.2) are distributed as follows:

(Ⅰ) Under $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, there exist the following facts.

(Ⅰ₁) If $G > G^{0}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $\phi^{1}_{n} < 0 < \phi^{2}_{n}$. And then (2.2) has exactly two equilibria $(\phi^{1}_{n}, 0)$ and $(\phi^{2}_{n}, 0)$, both of which are centers.

(Ⅰ₂) If $G = G^{0}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $\phi^{1}_{n} < \phi^{2}_{n} = 0$. And then (2.2) has only one equilibrium $(\phi^{1}_{n}, 0)$, which is a center.

(Ⅰ₃) If $G^{+}_{n}(\beta) < G < G^{0}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $\phi^{1}_{n} < \phi^{2}_{n} < 0$. And then (2.2) has exactly two equilibria $\left(\phi^{1}_{n}, 0\right)$ and $\left(\phi^{2}_{n}, 0\right)$, of which the former is a center and the latter is a saddle.

(Ⅰ₄) If $G = G^{+}_{n}(\beta)$, $f(\phi)$ has only one zero $\phi^{1}_{n}$, satisfying the inequality $\phi^{1}_{n} = \phi^{+}_{n} < 0$. And then (2.2) has only one equilibrium $\left(\phi^{1}_{n}, 0\right)$, which is a degenerated equilibrium.

(Ⅰ₅) If $G < G^{+}_{n}(\beta)$, $f(\phi)$ has no zeros, which means that (2.2) has no equilibria.

(Ⅱ) Under $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, there exist the following facts.

(Ⅱ₁) If $G > G^{+}_{n}(\beta)$, $f(\phi)$ has no zeros, which means that (2.2) has no equilibria.

(Ⅱ₂) If $G = G^{+}_{n}(\beta)$, $f(\phi)$ has only one zero $\phi^{1}_{n}$, satisfying the inequality $\phi^{1}_{n} = \phi^{+}_{n} > 0$. And then (2.2) has only one equilibrium $\left(\phi^{1}_{n}, 0\right)$, which is a degenerated equilibrium.

(Ⅱ₃) If $G^{0}(\beta) < G < G^{+}_{n}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $0 < \phi^{1}_{n} < \phi^{2}_{n}$. And then (2.2) has exactly two equilibria $\left(\phi^{1}_{n}, 0\right)$ and $\left(\phi^{2}_{n}, 0\right)$, of which the former is a center and the latter is a saddle.

(Ⅱ₄) If $G = G^{0}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $\phi^{1}_{n} = 0 < \phi^{2}_{n}$. And then (2.2) has only one equilibrium $(\phi^{2}_{n}, 0)$, which is a saddle.

(Ⅱ₅) If $G < G^{0}(\beta)$, $f(\phi)$ has two zeros $\phi^{1}_{n}$ and $\phi^{2}_{n}$, satisfying the inequality $\phi^{1}_{n} < 0 < \phi^{2}_{n}$. And then (2.2) has exactly two equilibria $(\phi^{1}_{n}, 0)$ and $(\phi^{2}_{n}, 0)$, both of which are saddles.

(Ⅲ) Under $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, there exist the following facts.

(Ⅲ₁) If $G > G^{0}(\beta)$, $f(\phi)$ has only one zero $\varphi^{1}_{n} > 0$. And then (2.2) has only one equilibrium $\left(\varphi^{1}_{n}, 0\right)$, which is a center.

(Ⅲ₂) If $G = G^{0}(\beta)$, $f(\phi)$ has only one zero $\varphi^{1}_{n} = 0$, which implies that (2.2) has no equilibria.

(Ⅲ₃) If $G < G^{0}(\beta)$, $f(\phi)$ has only one zero $\varphi^{1}_{n} < 0$. And then (2.2) has only one equilibrium $\left(\varphi^{1}_{n}, 0\right)$, which is a saddle.

(Ⅳ) Under $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, there exist the following facts.

(Ⅳ₁) If $G > G^{+}_{n}(\beta)$, $f(\phi)$ has only one zero $\varphi^{1}_{n} < 0$. And then (2.2) has only one equilibrium $\left(\varphi^{1}_{n}, 0\right)$, which is a center.

(Ⅳ₂) If $G = G^{+}_{n}(\beta)$, $f(\phi)$ has two zeros $\varphi^{1}_{n}$ and $\varphi^{2}_{n}$, satisfying the inequality $\varphi^{1}_{n} < 0 < \varphi^{2}_{n} = \phi^{+}_{n}$. And then (2.2) has exactly two equilibria $\left(\varphi^{1}_{n}, 0\right)$ and $\left(\varphi^{2}_{n}, 0\right)$, of which the former is a center and the latter is a degenerated equilibrium.

(Ⅳ₃) If $G^{0}(\beta) < G < G^{+}_{n}(\beta)$, $f(\phi)$ has three zeros $\varphi^{1}_{n}$, $\varphi^{2}_{n}$ and $\varphi^{3}_{n}$, satisfying the inequality $\varphi^{1}_{n} < 0 < \varphi^{2}_{n} < \varphi^{3}_{n}$. And then (2.2) has exactly three equilibria $\left(\varphi^{1}_{n}, 0\right)$, $\left(\varphi^{2}_{n}, 0\right)$ and $\left(\varphi^{3}_{n}, 0\right)$, of which the first two are centers and the last one is a saddle.

(Ⅳ₄) If $G = G^{0}(\beta)$, $f(\phi)$ has three zeros $\varphi^{1}_{n}$, $\varphi^{2}_{n}$ and $\varphi^{3}_{n}$, satisfying the inequality $\varphi^{1}_{n} < \varphi^{2}_{n} = 0 < \varphi^{3}_{n}$. And then (2.2) has exactly two equilibria $\left(\varphi^{1}_{n}, 0\right)$ and $\left(\varphi^{3}_{n}, 0\right)$, of which the former is a center and the latter is a saddle.

(Ⅳ₅) If $G^{-}_{n}(\beta) < G < G^{0}(\beta)$, $f(\phi)$ has three zeros $\varphi^{1}_{n}$, $\varphi^{2}_{n}$ and $\varphi^{3}_{n}$, satisfying the inequality $\varphi^{1}_{n} < \varphi^{2}_{n} <$$0$$< \varphi^{3}_{n}$. And then (2.2) has exactly three equilibria $\left(\varphi^{1}_{n}, 0\right)$, $\left(\varphi^{2}_{n}, 0\right)$ and $\left(\varphi^{3}_{n}, 0\right)$, of which the first one is a center and the last two are saddles.

(Ⅳ₆) If $G = G^{-}_{n}(\beta)$, $f(\phi)$ has two zeros $\varphi^{1}_{n}$ and $\varphi^{2}_{n}$, satisfying the inequality $\varphi^{1}_{n} = \phi^{-}_{n} < 0 < \varphi^{2}_{n}$. And then (2.2) has exactly two equilibria $\left(\varphi^{1}_{n}, 0\right)$ and $\left(\varphi^{2}_{n}, 0\right)$, of which the former is a degenerated equilibrium and the latter is a saddle.

(Ⅳ₇) If $G < G^{-}_{n}(\beta)$, $f(\phi)$ has only one zero $\varphi^{3}_{n} > 0$. And then (2.2) has only one equilibrium $\left(\varphi^{3}_{n}, 0\right)$, which is a saddle.

In addition, when $(\alpha-1)G > G^{0}(\beta)$, (2.3) also has two other equilibria $P_{\pm}\left(0, \pm\sqrt{2G/(\alpha-1)}\right)$ on the singular line $\phi = 0$. Their corresponding eigenvalues are

Thus, $P_{\pm}$ are two saddles for $\alpha > 1$ and are two nodes for $\alpha < 1$. When $G = G^{0}(\beta)$, (2.3) has only one equilibrium on the line $\phi = 0$, lying at $(0, 0)$. It is a high-order equilibrium because its Jacobian matrix is degenerate. When $(\alpha-1)G < G^{0}(\beta)$ or $\alpha = 1$, (2.3) has no equilibria on the line $\phi = 0$.

To sum up, all bifurcation curves of (2.3) with respect to the equilibria are given in (2.4).

2.2.   Bifurcation of phase portraits for regular system (2.3)

For a fixed integral constant $h\in\mathbb{R}$, $H_{n}(\phi, y) = h$ defines a set of invariant curves, which corresponds to a family of energy conservation orbits of (2.3). With the change of $h$, the dynamic behaviors of this family of orbits will change, which requires us to find out their topology in phase plan $(\phi, y)$.

Lemma 2.1. In the phase plane $(\phi, y)$ of (2.3), the intersection between $\phi$-axis and each family of energy conservation orbits with energy $h$ is given by $F_n(\phi) = h$, where

It is not difficult to find that the bifurcation curves of equilibria of (2.3) we have given in (2.4) are also bifurcation curves of its phase portraits. Moreover, from Lemma 2.1 we found another kind of bifurcation curves of phase portraits in the cases of $\alpha > 1$ and $\alpha < -3n$, on which the corresponding energy of the saddle of system (2.3) lying on $\phi$-axis is $0$. We denote this bifurcation curve as $G^{*}_{n}(\beta)$.

For $n = 1$, we can calculate the explicit expression of saddle of (2.3) lying on the $\phi$-axis through the Tianheng formula. Thus at the saddle making $H_{n}(\phi, y) = 0$, that is, when $\alpha > 1, \gamma < 0$ or $\alpha < -3, \gamma > 0$, the expression of the bifurcation curve $G^{*}_{1}(\beta) = G$ satisfies the following equation

where

For $n > 1$, since the explicit expression of saddle of (2.3) lying on $\phi$-axis is difficult to obtain, we only can draw the bifurcation curve $G^{*}_{n}(\beta)$ numerically. For example, let $n = 2$, $(\alpha-1)(\alpha+2n)(\alpha+3n)$$\ne0$ and expand the following equation

Comparing the coefficients of each order of $s$ on both sides of the above equation, we get the following equations

And then, we obtain the expression of $G^{*}_{2}(\beta)$ as

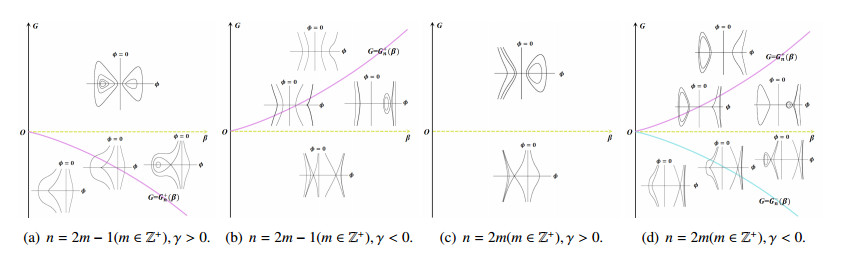
Similarly, we can apply this method to simulate bifurcation curves $G^{*}_{n}(\beta)$ when $n > 2$. Further, for given $\alpha, \beta$ and $\gamma$, we can get the value of $G^{*}_{n}(\beta)$ numerically, and obtain the bifurcation diagrams of (2.3) as shown in the Figures 1–4.

Based on the above analysis, (1.5) has solitary wave solutions, solitary cusp wave solutions, periodic wave solutions, periodic cusp wave solutions and breaking wave solutions, whose existence conditions are concluded in Lemmas 2.2–2.6.

Lemma 2.2. If and only if $\alpha > 1$, (1.5) has breaking wave solutions.

Lemma 2.3. When one of the following conditions holds, (1.5) has solitary wave solutions.

(Ⅰ) For the case of $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, one of the following conditions shall be met

(Ⅰ₁) $\alpha\geqslant-3n$ and $G^{+}_{n}(\beta) < G\leqslant G^{0}(\beta)$;

(Ⅰ₂) $-3n\leqslant\alpha\leqslant1$ and $G = G^{+}_{n}(\beta)$;

(Ⅰ₃) $\alpha < -3n$ is odd, and $G^{+}_{n}(\beta)\leqslant G < G^{*}_{n}(\beta)$ or $G = G^{0}(\beta)$;

(Ⅰ₄) $\alpha < -3n$ is even, and $G^{+}_{n}(\beta) < G < G^{*}_{n}(\beta)$ or $G^{*}_{n}(\beta) < G\leqslant G^{0}(\beta)$.

(Ⅱ) For the case of $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, one of the following conditions shall be met

(Ⅱ₁) $\alpha > 1$ and $G^{*}_{n}(\beta) < G < G^{+}_{n}(\beta)$;

(Ⅱ₂) $-3n\leqslant\alpha\leqslant1$ is odd or $\alpha < -3n$, and $G < G^{+}_{n}(\beta)$;

(Ⅱ₃) $-3n\leqslant\alpha\leqslant1$ is even, and $G^{0}(\beta)\leqslant G < G^{+}_{n}(\beta)$.

(Ⅲ) For the case of $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, one of the following conditions shall be met

(Ⅲ₁) $\alpha < -3n$ is odd, and $G = G^{0}(\beta)$;

(Ⅲ₂) $\alpha < -3n$ is even or $-3n\leqslant\alpha\leqslant1$, and $G\leqslant G^{0}(\beta)$.

(Ⅳ) For the case of $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, one of the following conditions shall be met

(Ⅳ₁) $\alpha > 1$ and $G^{*}_{n}(\beta) < G < G^{+}_{n}(\beta)$ or $G^{-}_{n}(\beta) < G\leqslant G^{0}(\beta)$;

(Ⅳ₂) $\alpha < -3n$ is odd, and $G^{-}_{n}(\beta)\leqslant G < G^{+}_{n}(\beta)$;

(Ⅳ₃) $\alpha < -3n$ is even or $-3n\leqslant\alpha\leqslant1$, and $G < G^{+}_{n}(\beta)$.

Lemma 2.4. When one of the following conditions holds, (1.5) has periodic wave solutions.

(Ⅰ) For the case of $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, one of the following conditions shall be met ${\rm (I_{1})}$ $\alpha < -3n$ is odd or $-3n\leqslant\alpha\leqslant1$;     ${\rm (I_{2})}$ $\alpha < -3n$ is even or $\alpha > 1$, and $G > G^{+}_{n}(\beta)$.

(Ⅱ) For the case of $n = 2m-1(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, one of the following conditions shall be met ${\rm (II_{1})}$ $G^{0}_{n}(\beta) < G < G^{+}_{n}(\beta)$;     ${\rm (II_{2})}$ $\alpha < -3n$ and $G < G^{0}(\beta)$.

(Ⅲ) For the case of $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma > 0$, one of the following conditions shall be met ${\rm (III_{1})}$ $\alpha > 1$ and $G > G^{0}(\beta)$;     ${\rm (III_{2})}$ $\alpha\leqslant1$ and $G\ne G^{0}(\beta)$.

(Ⅳ) For the case of $n = 2m(m\in\mathbb{Z}^{+})$ and $\gamma < 0$, one of the following conditions shall be met ${\rm (IV_{1})}$ $\alpha > 1$ and $G > G^{-}_{n}(\beta)$;     ${\rm (IV_{2})}$ $\alpha\leqslant1$.

Lemma 2.5. When $\alpha > 1, G = G^{*}_{n}(\beta)$ or $\alpha < 1, G = G^{0}(\beta)$, (1.5) with $\gamma < 0$ has a non-smooth solitary wave solution, also known as solitary cusp wave solution.

Lemma 2.6. When $\alpha > 1$ and one of the following conditions holds, (1.5) has a non-smooth periodic solitary wave solution, also known as periodic cusp wave solution.

(Ⅰ) $n = 2m(m\in\mathbb{Z}^{+})$ and $G > G^{0}(\beta)$;

(Ⅱ) $n = 2m-1(m\in\mathbb{Z}^{+})$, $\gamma > 0$ and $G > G^{0}(\beta)$;

(Ⅲ) $n = 2m-1(m\in\mathbb{Z}^{+})$, $\gamma < 0$ and $G^{0}(\beta) < G < G^{*}_{n}(\beta)$.

In fact, for a nonlinear evolution equation, a solitary wave solution (resp. a periodic wave solution) corresponds to a homoclinic orbit (resp. periodic closed orbit) in its traveling wave system. In particular, for a traveling wave system with singularity, when its homoclinic orbit (resp. periodic closed orbit) intersects its singular line at two different saddles, the smooth solitary wave solution (resp. smooth periodic wave solution) corresponding to the original NPDE will lose its smoothness and evolve into solitary cusp wave solution (resp. periodic cusp wave solution). From the above correspondence and the Figures 1–4, it is not difficult to prove Lemmas 2.2–2.6, so the detailed proof process is omitted here.

Moreover, by Lemmas 2.3–2.5 and [16,Theorems 2.3,2.4 and 2.6] we get that when $\alpha < 1$ and $G\leqslant G^{0}(\beta)$ (2.2) has the following four special properties.

Property A. There are two heteroclinic orbits connecting the saddle $\left(\phi^{2}_{n}, 0\right)$ (resp. $\left(\varphi^{3}_{n}, 0\right)$) and the degenerate equilibrium $\left(0, 0\right)$ when $n = 2m-1(m\in\mathbb{Z}^{+})$ (resp. $n = 2m(m\in\mathbb{Z}^{+})$), $\gamma < 0$ and $G = G^{0}(\beta)$, which gives rise to a solitary wave. And there are no equilibria inside the loop surrounded by these two heteroclinic orbits.

Property B. There are infinitely many periodic orbits passing through the singular line $\phi = 0$ and intersecting at two points $P_{\pm}$ when $G < G^{0}(\beta)$, which give rise to a family of periodic waves. And there are no equilibria inside this family of periodic orbits.

Property C. There are infinitely many homoclinic orbits intersecting to the singular line $\phi = 0$ at $(0, 0)$ when $G = G^{0}(\beta)$, which give rise to a family of smooth solitary waves. And there are no equilibria inside this family of homoclinic orbits.

Property D. There exists a homoclinic orbit passing through the singular line $\phi = 0$ and intersecting at two points $P_{\pm}$ in each of the following cases:

Case $D_{a}$. $n = 2m-1(m\in\mathbb{Z}^{+})$ and one of the following five conditions holds

($D_{a1}$) $-3n\leqslant\alpha < 1$, $\gamma > 0$ and $G^{+}_{n}(\beta)\leqslant G < G^{0}(\beta)$;

($D_{a2}$) $\alpha < -3n$ is odd, $\gamma > 0$ and $G^{+}_{n}(\beta)\leqslant G < G^{*}_{n}(\beta)$;

($D_{a3}$) $\alpha < -3n$ is even, $\gamma > 0$ and $G^{*}_{n}(\beta) < G < G^{0}(\beta)$;

($D_{a4}$) $-3n\leqslant\alpha < 1$ is odd, $\gamma < 0$ and $G < G^{0}(\beta)$;

($D_{a5}$) $\alpha < -3n$, $\gamma < 0$ and $G < G^{0}(\beta)$.

Case $D_{b}$. $n = 2m(m\in\mathbb{Z}^{+})$ and one of the following conditions holds

($D_{b1}$) $-3n\leqslant\alpha < 1$, $\gamma > 0$ and $G < G^{0}(\beta)$;

($D_{b2}$) $\alpha < -3n$ is even, $\gamma > 0$ and $G < G^{0}(\beta)$;

($D_{b3}$) $\alpha < -3n$, $\gamma < 0$ and $G^{-}_{n}(\beta)\leqslant G < G^{0}(\beta)$;

($D_{b4}$) $-3n\leqslant\alpha < 1$, $\gamma < 0$ and $G < G^{0}(\beta)$.

There are no equilibria inside this family of homoclinic orbits, and they give rise to a family of smooth solitary waves.

3.   Expressions of smooth wave solutions of (1.5)$_{n=1}$

In this section, combined with the existence conditions of solitary wave solutions and periodic wave solutions given by Lemmas 2.3 and 2.4, we calculate the explicit expressions of these two kinds of solutions of (1.5) for the case of $n = 1$ and $\alpha = -1$.

Theorem 3.1. For $\gamma < 0$, (1.5)$_{n = 1}$ holds the following conclusions:

(1) when $G^{0}(\beta) < G < G^{+}_{1}(\beta)$, there are a valley-solitary wave solution

and a family of periodic wave solutions with expression

(2) when $G = G^{0}(\beta)$, there are infinitely many peak-solitary wave solutions

where $s_{1} = \left(4\beta-2\sqrt{4\beta^{2}+9\gamma\tilde{h}}\right)/(-3\gamma)$, $s_{2} = \left(4\beta+2\sqrt{4\beta^{2}+9\gamma\tilde{h}}\right)/(-3\gamma)$, $\tilde{h}\in\left(0, 4\beta^{2}/(-9\gamma)\right)$. Moreover, $r_{i}(i = 1, 2, \cdots, 6)$ satisfy inequalities $r_{1} < r_{2}$, $r_{3} < r_{4} < r_{5} < r_{6}$ and equations $H_{1}(r_{1}, 0) = H_{1}(r_{2}, 0) = H_{1}(\phi^{2}_{1}, 0)$, $H_{1}(r_{3}, 0) = H_{1}(r_{4}, 0) = H_{1}(r_{5}, 0) = H_{1}(r_{6}, 0) = h$, $h\in\left(H_{1}(\phi^{1}_{1}, 0), H_{1}(\phi^{2}_{1}, 0)\right)$, where $(\phi^{1}_{1}, 0)$ and $(\phi^{2}_{1}, 0)$ are the center and the saddle of (2.2) respectively. It is worth noting that when $h\rightarrow H_{1}(\phi^{2}_{1}, 0)-0$, we have

which means that the solitary wave solution $\phi_{1}(\xi)$ is the limit solution of this family of periodic wave solutions $\phi_{2}(\xi, h)$.

Theorem 3.2. For $\gamma > 0$, (1.5)$_{n = 1}$ holds the following conclusions:

(1) when $G = G^{0}(\beta)$, there are a family of periodic wave solutions with expression

a family of valley-solitary wave solutions with expression

and a family of peak-solitary wave solutions with expression

(2) when $G^{+}_{1}(\beta) < G < G^{0}(\beta)$, there are a valley-solitary wave solution

and a peak-solitary wave solution with expression

(3) when $G = G^{+}_{1}(\beta)$, there are a peak-solitary wave solution with expression

and a family of periodic wave solutions with expression

Here, $\phi^{1}_{1}$ and $\phi^{2}_{1}$ are the abscissa values of the center and the saddle point of (2.2) respectively, $r_{7} = -(4\beta+\sqrt{16\beta^{2}+144\gamma h_{1}})/(3\gamma)$, $r_{8} = -(4\beta-\sqrt{16\beta^{2}+144\gamma h_{1}})/(3\gamma)$, $r_{9} = -(4\beta+\sqrt{16\beta^{2}+144\gamma h_{2}})/(3\gamma)$, $r_{10} = -(4\beta-\sqrt{16\beta^{2}+144\gamma h_{2}})/(3\gamma),$ $A^{2} = (8\beta(r_{13}+2r_{14})+3\gamma(r_{13}^{2}+2r_{13}r_{14}+3r_{14}^{2})-12h_{3})/(3\gamma),$ $B^{2} = (8\beta(2r_{13}+r_{14})+3\gamma(3r_{13}^{2}+2r_{13}r_{14}+r_{14}^{2})-12h_{3})/(3\gamma),$ $h_{1}\in(H_{1}(\phi^{1}_{1}, 0), 0)$, $h_{2}\in(0, +\infty)$, $h_{3}\in\mathbb{R}\backslash\{-\beta^{2}/(2\gamma)\}$, and parameters $r_{i}(i = 11, 12, 13, 14)$ satisfy $r_{11} < r_{12}$, $r_{13} < r_{14}$, $H_{1}(r_{11}, 0) = H_{1}(r_{12}, 0) = H_{1}(\phi^{2}_{1}, 0)$ and $H_{1}(r_{13}, 0) = H_{1}(r_{14}, 0) = h_{3}$. Moreover, when $G\rightarrow G^{0}(\beta)-0$, we have

when $G\rightarrow G^{+}_{1}(\beta)+0$, we have

which reveals the process that the solitary wave solutions of (1.5)$_{n = 1}$ changes with the change of $G$ in the case of $\alpha = -1$ and $\gamma > 0$.

Detailed proofs of the above two theorems are given below.

Proof of Theorem 3.1. Assume that $\alpha = -1$ and $\gamma < 0$ (see Figure 3(b)). The proof is divided into the following two cases.

Case 1. $G^{0}(\beta) < G < G^{+}_{1}(\beta)$. Clearly, $H_{1}(\phi, y) = H_{1}\left(\phi^{2}_{1}, 0\right)$ defines a homoclinic orbit of (2.3)$_{n = 1}$. It possesses the expression

Substituting the above formula into the first equation of (2.2) and integrating it along the homoclinic orbit, we have

Letting $x = \sqrt{(\phi-r_{2})/(\phi-r_{1})}$, we get

and express the solitary wave solution $\phi_{1}(\xi)$.

Moreover, $H_{1}(\phi, y) = h, h\in\left(H_{1}(\phi^{1}_{1}, 0), H_{1}(\phi^{2}_{1}, 0)\right)$, defines a periodic closed orbits with expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding periodic closed orbit, we have

According to the elliptic integral formula,

Thus, we can express the periodic wave solutions $\phi_{2}(\xi, h)$. In particular, as $h\rightarrow H_{1}\left(\phi^{2}_{1}, 0\right)-0$, it follows that $r_{3}\rightarrow r_{1}$, $r_{4}\rightarrow r_{2}$ and $r_{5, 6}\rightarrow \phi^{2}_{1}$. Then we have

Case 2. $G = G^{0}(\beta)$. Clearly, when $\tilde{h}\in\left(0, 4\beta^{2}/(-9\gamma)\right)$, $H_{1}(\phi, y) = \tilde{h}$ defines a homoclinic orbit of (2.3)$_{n = 1}$. It possesses the expression

Substituting the above formula into the first equation of (2.2) and integrating it along the homoclinic orbit, we have

Letting $x = \sqrt{(s_{1}-\phi)/(s_{2}-\phi)}$, we get

and express the solitary wave solution $\phi_{3}\left(\xi, \tilde{h}\right)$. Furthermore, it confirms the validity of Property C mentioned in Section 2. □

Proof of Theorem 3.2. Assume that $\alpha = -1$ and $\gamma > 0$ (see Figure 3(a)). The proof is divided into the following three cases.

Case 1. $G = G^{0}(\beta)$. Clearly, for given $h_{1}\in\left(H_{1}\left(\phi^{1}_{1}, 0\right), 0\right)$, $H_{1}(\phi, y) = h_{1}$ defines a periodic closed orbit of (2.3). It possesses the expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding periodic closed orbit, we have

Letting $x = \sqrt{(\phi-r_{7})/(r_{8}-\phi)}$, we get

and then express the solitary wave solution $\phi_{4}(\xi)$.

Moreover, for any $h_{2}\in\left(0, +\infty\right)$, $H_{1}(\phi, y) = h_{2}$ defines two homoclinic orbits with expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding homoclinic orbit, we have

and

respectively. Letting $x = \sqrt{(\phi-r_{9})/(r_{10}-\phi)}$ and $z = \sqrt{(r_{10}-\phi)/(\phi-r_{9})}$, we get

and

respectively. Therefore, we can express the solitary wave solutions $\phi_{5}(\xi)$ and $\phi_{6}(\xi)$. Furthermore, it confirms the validity of Property C mentioned in Section 2.

Case 2. $G^{+}_{1}(\beta) < G < G^{0}(\beta)$. Clearly, $H_{1}(\phi, y) = H_{1}\left(\phi^{2}_{1}, 0\right)$ defines two homoclinic orbits with a same expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding homoclinic orbit, we have

and

respectively. Letting $x = \sqrt{(\phi-r_{11})/(r_{12}-\phi)}$ and $z = \sqrt{(r_{12}-\phi)/(\phi-r_{11})}$, we get

and

respectively. Therefore, we can express the solitary wave solutions $\phi_{7}(\xi, G)$ and $\phi_{8}(\xi, G)$. Furthermore, it confirms the validity of Property D mentioned in Section 2.

Case 3. $G = G^{+}_{1}(\beta)$. Clearly, $H_{1}(\phi, y) = -\beta^{4}/\left(2\gamma^{3}\right)$ defines a homoclinic orbit with expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding homoclinic orbit, we have

and then express the peak-solitary wave solution $\phi_{9}(\xi)$. Furthermore, it confirms the validity of Property D mentioned in Section 2.

Moreover, for any $h_{3}\in\mathbb{R}\backslash\left\{-\beta^{4}/\left(2\gamma^{3}\right)\right\}$, $H_{1}(\phi, y) = h_{3}$ defines a periodic closed orbit with expression

for $r_{13}\leqslant\phi\leqslant r_{14}$. Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding closed orbit, we have

According to the elliptic integral formula, we can express the periodic wave solution $\phi_{10}(\xi)$, which confirms the validity of Property B mentioned in Section 2.

Finally, from the expressions of $\phi_{i}(\xi)(i = 5, 6, 9)$ and $\phi_{j}(\xi, G)(i = 7, 8)$ we further obtain the following relationship of these solitary waves. As $G\rightarrow G^{0}(\beta)-0$, it follows that $\phi^{2}_{1}\rightarrow0$, $r_{11}\rightarrow r_{9}$ and $r_{12}\rightarrow r_{10}$. Then it is not difficult to deduce

As $G\rightarrow G^{+}_{1}(\beta)+0$, it follows that $\phi^{2}_{1}\rightarrow -\beta/\gamma$, $r_{11}\rightarrow -\beta/\gamma$, $r_{12}\rightarrow \beta/(3\gamma)$ and

Then it is not difficult to deduce $\lim_{G\rightarrow G^{+}_{1}(\beta)+0}\phi_{7}(\xi, G) = -\beta/\gamma$ and

□

4.   Expressions of non-smooth wave solutions of (1.5)$_{n=1}$

From Lemmas 2.5 and 2.6, (1.5) may have non-smooth traveling wave solutions. In this section we give explicit expressions of solitary cusp wave solution and periodic cusp wave solution of (1.5) for the case of $n = 1$.

Theorem 4.1. For $\alpha > 1$, $\gamma > 0$ and $G > G^{0}(\beta)$, (1.5)$_{n = 1}$ has a peak-periodic cusp wave solution with expression

and a valley-periodic cusp wave solution with expression

Here, $k = \sqrt{((r_{16}-r_{15})^{2}-(C-D)^{2})/(4CD)}$, $C^{2} = 4\beta(\alpha+3)(r_{15}+2r_{16})/(3\gamma(\alpha+2))+r_{15}^{2} +2r_{15}r_{16}+3r_{16}^{2}$, $D^{2} = 4\beta(\alpha+3)(2r_{15}+r_{16})/(3\gamma(\alpha+2))+3r_{15}^{2} +2r_{15}r_{16}+r_{16}^{2}$, and parameters $r_{15, 16}$ satisfy $r_{15} < r_{16}$ and are determined by equations

Theorem 4.2. For $\alpha > 1$, $\gamma < 0$ and $G = G^{*}_{1}(\beta)$, (1.5)$_{n = 1}$ has a valley-solitary cusp wave solution with expression

Theorem 4.3. For $\alpha = -1$, $\gamma < 0$ and $G = G^{0}(\beta)$, (1.5)$_{n = 1}$ has a valley-solitary cusp wave solution

Detailed proofs of the above three theorems are given below.

Proof of Theorem 4.1. For the case of $\alpha > 1$, $\gamma > 0$ and $G > G^{0}(\beta)$ (see Figure 2(a)), $H_{1}(\phi, y) = 0$ defines two heteroclinic orbits of (2.3), which possess the same expression

for $r_{15}\leqslant\phi < 0$ or $0 < \phi\leqslant r_{16}$. Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding orbit, we have

and

respectively. According to the elliptic integral formula,

and

Thus, we can express the peak-periodic cusp wave solution $\phi_{11}(\xi)$ and the valley-periodic cusp wave solution $\phi_{12}(\xi)$. □

Proof of Theorem 4.2. For the case of $\alpha > 1$, $\gamma < 0$ and $G = G^{*}_{1}(\beta)$, $H_{1}(\phi, y) = 0$ defines three heteroclinic orbits of (2.3) connecting the saddles $P_{\pm}$ and $\left(-\beta(\alpha+3)/(\gamma(\alpha+2)), 0\right)$ with expression

for $0 < \phi < -\frac{\beta(\alpha+3)}{\gamma(\alpha+2)}.$ Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding orbit, we have

Letting $\tan(\theta) = \sqrt{2}/2-3\gamma(\alpha+2)\phi/\left(\sqrt{2}\beta(\alpha+3)\right)$, we calculate

where $r_{0} = -\beta(\alpha+3)/\left(\gamma(\alpha+2)\right)$. Thus, we express the valley-solitary cusp wave solution $\phi_{13}(\xi)$. □

Proof of Theorem 4.3. For the case of $\alpha = -1$, $\gamma < 0$ and $G = G^{0}(\beta)$, $H_{1}(\phi, y) = -4\beta^{2}/(9\gamma)$ defines two heteroclinic orbits of (2.3) connecting the saddles $(0, 0)$ and $\left(-4\beta/(3\gamma), 0\right)$, which possess the following expression

Substituting the above formula into the first equation of (2.2) and integrating it along the corresponding orbits, we have

By direct calculation, we have

Thus, we express the valley-solitary cusp wave solution $\phi_{14}(\xi)$. Furthermore, it confirms the validity of Property A mentioned in Section 2. □

5.   Conclusions and simulations

In this paper, we apply the dynamical system methods to investigate the traveling wave system (2.3) corresponding to a generalized VP-mVP equation with non-homogeneous power law nonlinearity (1.5) in the case of $(\alpha, \beta, \gamma, G)\in\Omega$. This method allows detailed analysis on phase space geometry of (2.3) to obtain parameter bifurcation sets so that all possible traveling waves of (1.5) and corresponding existence conditions can be identified clearly. All types of traveling waves and bifurcation diagrams of (2.3) have been obtained. 14 exact explicit expressions of traveling wave solutions, including smooth and non-smooth ones, are derived.

Notice that $\alpha$ is an important parameter in (1.5). Depending on $\alpha > 1$, $\alpha = 1$ or $\alpha < 1$, system (2.3) has different dynamics. When $\alpha > 1$, (1.5) has non-smooth traveling wave solutions, including solitary cusp wave solutions and periodic cusp wave solutions. When $\alpha = 1$, (1.5) has only smooth traveling wave solutions, including solitary wave solutions and periodic wave solutions, whose phase orbits do not intersect the singular line $\phi = 0$. When $\alpha < 1$, there is a special class of homoclinic orbits (resp. periodic closed orbits), that intersects with the singular line $\phi = 0$ and there are no equilibria inside them. Then, these orbits give rise to a family of smooth solitary wave solutions (resp. smooth periodic wave solutions).

Finally, by (2.1) we give two examples of numerical simulation to visualize each kind of traveling wave solution of (1.5).

Example 1. For the case of $n = \alpha = \beta = 2$, $\gamma = -1$ and $G = 256\sqrt{6}/2835$, when taking initial values $(\tilde{\varphi}_{1}-0.1, 0)$, $(\tilde{\varphi}_{1}-0.3, 0)$, $(\tilde{\varphi}_{1}-0.5, 0)$ and $(\tilde{\varphi}_{1}-0.7, 0)$ respectively, we get the numerical simulation results as shown in Figure 5(a). When taking initial values $(\tilde{\varphi}_{1}, 0)$, $(\tilde{\varphi}_{1}+0.02, 0)$, $(\tilde{\varphi}_{1}+0.04, 0)$ and $(\tilde{\varphi}_{1}+0.07, 0)$ respectively, we get the numerical simulation results as shown in Figure 5(b). When taking initial values $(\tilde{\varphi}_{2}, 0)$, $(\tilde{\varphi}_{2}+0.1, 0)$, $(\tilde{\varphi}_{2}+0.2, 0)$ and $(\tilde{\varphi}_{2}+0.5, 0)$ respectively, we get the numerical simulation results as shown in Figure 5(c). Here, $\tilde{\varphi}_{1} = -2.024285$ and $\tilde{\varphi}_{2} = 0.000001$.

From Figure 5(a), it is seen that when the initial value $\left(\phi(0), \phi^{'}(0)\right)$ meets $\phi(0)\in\left(-\infty, \tilde{\varphi}_{1}\right)$ and $\phi^{'}(0) = 0$, the graph of $\phi(\xi)$ satisfying (2.1) is fully close to the line $\phi = 0$ within a limited time. This implies that, for an orbit of (2.2) with initial value being on the left of the point $(\tilde{\varphi}_{1}, 0)$, there is a finite value $\xi = \tilde{\xi}$, such that $\lim_{\xi\rightarrow \pm\tilde{\xi}}\phi(\xi) = 0$. By [16,Theorem 2.4], these orbits give rise to uncountably infinitely many bounded breaking wave solutions (i.e., Compactons). From Figure 5(b), we see that if $(\phi(0), \phi^{'}(0))$ meets $\phi(0)\in\left(\tilde{\varphi}_{1}, 0\right)$ and $\phi^{'}(0) = 0$, the graph of $\phi(\xi)$ satisfying (2.1) is a periodic curve, which gives rise to a periodic wave solution. Especially when $\phi(0)\rightarrow \tilde{\varphi}_{1}$, this curve is fully close to the boundary curves consisting of a segment $P_{+}P_{-}$ and an arc $\widehat{P_{+}P_{-}}$ defined by $H_{2}(\phi, y) = 0$, in which by [16,Theorems 2.3 and 2.4] the arc $\widehat{P_{+}P_{-}}$ gives rise to a periodic cusp wave solution. From Figure 5(c), we see that if $(\phi(0), \phi^{'}(0))$ meets $\phi(0)\in\left(0, 1.632993\right)$ and $\phi^{'}(0) = 0$, the graph of $\phi(\xi)$ satisfying (2.1) is a periodic curve, which gives rise to a periodic wave solution of (1.5). Especially when $\phi(0)\rightarrow0$ or $\phi(0)\rightarrow1.632993$, this curve gradually loses its smoothness and periodicity, which implies that this periodic wave solution gradually evolve into a solitary cusp wave solution.

Example 2. For the case of $n = \beta = 1$, $\alpha = \gamma = -4$ and $G = 0$, when taking initial values $(0.1, 0)$, $(0.2, 0)$, $(0.3, 0)$ and $(0.333333, 0)$ respectively, we get the numerical simulation results as shown in Figure 6(a). For the case of $n = \beta = 1$, $\alpha = \gamma = -4$ and $G = -4$, when taking initial values $(0.872629, 0)$ and $(-0.992475, 0)$ respectively, we get the numerical simulation results as shown in Figure 6(b); when taking initial values $(-1.2, 0)$, $(-1.1, 0)$ and $(-1, 0)$ respectively, we get the numerical simulation results as shown in Figure 6(c).

From Figure 6(a), it is seen that the graphs of $\phi(\xi)$ is a family of Gaussian curves when initial values $\left(\phi(0), \phi^{'}(0)\right)$ meet $\phi(0)\in(0, 1/3)$ and $\phi^{'}(0) = 0$, which giving rise to uncountably infinitely many solitary wave solutions. From Figure 6(b), it is seen that the graphs of $\phi(\xi)$ are two Gaussian curves when initial values are $(0.872629, 0)$ and $(-0.992475, 0)$ respectively and pass through the line $\phi = 0$. This phenomenon implies that two homoclinic orbits of (2.2) pass through the singular line $\phi = 0$. From Figure 6(c), we see that when $(\phi(0), \phi^{'}(0))$ meets $\phi(0)\in\left(-1.337699, -0.992475\right)$ and $\phi^{'}(0) = 0$, the graph of $\phi(\xi)$ satisfying (2.1) passes through the line $\phi = 0$ periodically. This phenomenon implies that infinitely many periodic orbits of (2.2) pass through the singular line $\phi = 0$.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Fundamental Research Funds for the Central Universities (No. PHD2023-053) and the Natural Science Foundation of China (No. 12271378).

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.