Decay rate for systems of $m$-nonlinear wave equations with new viscoelastic structures

1.   Introduction

This paper proposes an explicit finite volume scheme for first-order scalar conservation laws on a network having a single junction. The algorithm and analysis extend readily to networks with multiple junctions, due to the finite speed of propagation of the solutions of conservation laws. For the sake of concreteness, we view the setup as a model of traffic flow, with the vector of unknowns representing the vehicle density on each road. A number of such scalar models have been proposed, mostly differing in how the junction is modeled. An incomplete list of such models can be found in [4,5,6,7,8,11,12,13,14,15,16,18,19]. In this paper we focus on the so-called vanishing viscosity solution proposed and analyzed in [7] and [2]. The junction has $m$ incoming and $n$ outgoing roads. With $u_h$ denoting the density of vehicles on road $h$, and $f_h(\cdot)$ denoting the flux on road $h$, on each road traffic evolves according to the Lighthill-Witham-Richards model

Incoming roads are indexed by $i\in \{1, \ldots, m\}$, and outgoing roads by $j \in \{m+1, \ldots m+n \}$. Each road has a spatial domain denoted by $\Omega_h$, where $\Omega_i = (-\infty, 0)$ for $i\in \{1, \ldots, m\}$ and $\Omega_j = (0, \infty)$ for $j \in \{m+1, \ldots m+n \}$. The symbol $\Gamma$ is used to denote the spatial domain defined by the network of roads, and $L^{\infty}(\Gamma \times \mathbb{R}_+;[0, R]^{m+n})$ denotes the set of vectors $\vec{u} = (u_1, \ldots, u_{m+n})$ of functions satisfying

Following [2] we make the following assumptions concerning the fluxes $f_h$.

$(\bf{A.1)}$ For each $h \in \{1, \ldots, m+n\}$, $f_h \in \mathrm{Lip}([0, R]; \mathbb{R}_+)$, and $\left\|{f'_h}\right\|_{\infty} \le L_h$. Each $f_h$ satisfies $f_h(0) = f_h(R) = 0$ and is unimodal (bell-shaped), meaning that for some $\bar{u}_h \in (0, R)$ $f'_h(u)(\bar{u}_h-u)>0$ for a.e. $u \in [0, R]$.

$\bf{(A.2)}$ For each $h \in \{1, \ldots, m+n\}$, $f_h$ is not linearly degenerate, meaning that $f'_h$ is not constant on any nontrivial subinterval of $[0, R]$.

The study of vanishing viscosity solutions on a network was initiated by Coclite and Garavello [7], who proved that vanishing viscosity solutions converge to weak solutions if $n = m$ and all of the fluxes $f_h$ are the same. Andreianov, Coclite and Donadello [2] proved well-posedness of the more general problem discussed in this paper, relying upon a generalization of recent results concerning conservation laws with discontinuous flux [1,3].

For the convenience of the reader, and to establish notation, we review some relevant portions of the theory of network vanishing viscosity solutions, as described in [2], where we refer the reader for a more complete development. Let $G_h(\cdot, \cdot)$ denote the Godunov flux associated with $f_h(\cdot)$:

(Compared to [2], we list the arguments $\alpha$, $\beta$ of $G_h$ in reversed order.) Note that $G_h$ is consistent, i.e., $G_h(\alpha, \alpha) = f_h(\alpha)$. Also, $G_h(\cdot, \cdot)$ is a nonincreasing (nondecreasing) function of its first (second) argument, is Lipschitz continuous with respect to each argument, i.e., for $\alpha, \beta \in [0, R]$ there exists $L_h >0$ such that

Definition 1.1 (Vanishing viscosity germ [2]). The vanishing viscosity germ $\mathcal{G}_{VV}$ is the subset of $[0, R]^{m+n}$ consisting of vectors $\vec{u} = (u_1, \ldots, u_{m+n})$ such that for some $p_{ \vec{u}} \in [0, R]$ there holds

The definition of entropy solution requires one-sided traces along the half-line $x = 0$ in $\mathbb{R} \times \mathbb{R}_+$. Thanks to Assumption A.2, the existence of strong traces at $x = 0$ in the $L^1_{ \text{loc}}$ sense is guaranteed [20]. The traces are denoted

Definition 1.2 ($\mathcal{G}_{VV}$-entropy solution [2]). Define $q_h: [0, R]^2 \rightarrow \mathbb{R}$:

Given an initial condition $\vec{u}_0 \in L^{\infty}(\Gamma; [0, R]^{m+n})$, a vector $\vec{u} = (u_1, \ldots, u_{m+n})$ in $L^{\infty}(\Gamma \times \mathbb{R}_+; [0, R]^{m+n})$ is a $\mathcal{G}_{VV}$ entropy solution associated with $\vec{u}_0$ if it satisfies the following conditions:

● For each $h \in \{1, \ldots, m+n\}$, each $c \in [0, R]$, and any test function $\xi \in \mathcal{D}(\Omega_h \times \mathbb{R}; \mathbb{R}_+)$,

● For a.e. $t \in \mathbb{R}_+$, the vector of traces at the junction

$\gamma \vec{u}(t): = (\gamma_1u_1(t), \ldots, \gamma_{m+n} u_{m+n}(t))$ belongs to $\mathcal{G}_{VV}$.

Associated with each $\vec{k} \in \mathcal{G}_{VV}$, and allowing for a slight abuse of notation, one defines a road-wise constant stationary solution $\vec{k}(x)$ via

It is readily verified that viewed in this way, $k_h$ is a $\mathcal{G}_{VV}$-entropy solution. In fact all road-wise constant stationary solutions that are $\mathcal{G}_{VV}$-entropy solutions are associated with a $\vec{k} \in \mathcal{G}_{VV}$ in this manner.

Definition 1.2 reveals the relationship between the set $\mathcal{G}_{VV}$ and $\mathcal{G}_{VV}$-entropy solutions, and is well-suited to proving uniqueness of solutions. On the other hand, Definition 1.3 below is equivalent (Theorem 2.11 of [2]), and is better suited to proving that the limit of finite volume approximations is a $\mathcal{G}_{VV}$-entropy solution.

Definition 1.3 ($\mathcal{G}_{VV}$-entropy solution [2]). Given an initial condition $\vec{u}_0 \in L^{\infty}(\Gamma; [0, R]^{m+n})$, a vector $\vec{u} = (u_1, \ldots, u_{m+n})$ in $L^{\infty}(\Gamma \times \mathbb{R}_+; [0, R]^{m+n})$ is a $\mathcal{G}_{VV}$ entropy solution associated with $u_0$ if it satisfies the following conditions:

● The first item of Definition 1.2 holds.

● For any $\vec{k} \in \mathcal{G}_{VV}$, $\vec{u}$ satisfies the following Kružkov-type entropy inequality:

for any nonnegative test function $\xi \in \mathcal{D}( \mathbb{R} \times (0, \infty))$.

Theorem 1.4 (Well posedness [2]). Given any initial datum

there exists one and only one $\mathcal{G}_{VV}$-entropy solution $\vec{u} \in L^{\infty}(\Gamma\times \mathbb{R}_+;[0, R]^{m+n})$ in the sense of Definition 1.2.

In addition to the results above, reference [2] also includes a proof of existence of the associated Riemann problem. Based on the resulting Riemann solver, a Godunov finite volume algorithm is constructed in [2], which handles the interface in an implicit manner. This requires the solution of a single nonlinear equation at each time step. The resulting finite volume scheme generates approximations that are shown to converge to the unique $\mathcal{G}_{VV}$-entropy solution. Reference [21] validates the algorithm by comparing finite volume approximations with exact solutions of a collection of Riemann problems.

The main contribution of the present paper is an explicit version of the finite volume scheme of [2]. It differs only in the processing of the junction. We place an artificial grid point at the junction, which is assigned an artificial density. The artificial density is evolved from one time level to the next in an explicit manner. Thus a nonlinear equation solver is not required. (However, we found that in certain cases accuracy can be improved by processing the junction implicitly on the first time step.) Like the finite volume scheme of [2], the new algorithm has the order preservation property and is well-balanced. This makes it possible to employ the analytical framework of [2], resulting in a proof that the approximations converge to the unique entropy solution of the associated Cauchy problem.

In Section 2 we present our explicit finite volume scheme and prove convergence to a $\mathcal{G}_{VV}$-entropy solution. In Section 3 we discuss numerical experience with the new scheme, including one example. Appendix A contains a proof that a fixed point algorithm introduced in Section 2 converges.

2.   The explicit finite volume scheme

For a fixed spatial mesh size ${\Delta} x$, define the grid points $x_0 = 0$ and

Each road $\Omega_h$ is discretized according to

Our discretization of the spatial domain $\Gamma$ is identical to that of [2], but differs slightly in appearance since we prefer to use whole number indices for cell centers and fractional indices for cell boundaries. We use the following notation for the finite volume approximations:

We are somewhat artificially assigning a density, namely $P^s$, to the single grid point $x_0 = 0$ where the junction is located. We view the junction as a grid cell with width zero. We advance $P^s$ from one time level to the next in an explicit manner, without requiring a nonlinear equation solver. This is the novel aspect of our finite volume scheme.

Remark 1. We make the association $P^s \approx p_{\gamma \vec{u}(t^s)}$ because it is conceptually helpful. In fact, it is justified in the special case of a stationary solution of the scheme associated with $\vec{k} \in \mathcal{G}_{VV}$; see the proof of Lemma 2.3. However, we do not attempt to prove that $P^s \rightarrow p_{\gamma \vec{u}(t^s)}$ when ${\Delta} \rightarrow 0$. Fortunately, the convergence proof does not rely on pointwise convergence of $P^s$ as ${\Delta} \rightarrow 0$.

The initial data are initialized via

Note that $P^0$ can be any conveniently chosen value lying in $[0, R]$ (but see Remark 3 and Section 3). Recall that (2.3) introduced $U_{\ell}^{h, s}$ only for $\ell \in \mathbb{Z} \setminus \{0\}$. We can simplify some of the formulas that follow by defining $U_0^{h, s} = P^s$ for each $h\in \{1, \dots, m+n\}$. The finite volume scheme then advances the approximations from time level $s$ to time level $s+1$ according to

Define $\lambda = {\Delta} t /{\Delta} x$. When taking the limit ${\Delta} : = ({\Delta} x, {\Delta} t) \rightarrow 0$, we assume that $\lambda$ is fixed. Let $L = \max\{L_h | h \in \{1, \ldots, m+n \} \}$. In what follows we assume that the following CFL condition is satisfied:

If all of the $f_h$ are the same, i.e., $f_h(\cdot) = f(\cdot)$ for all $h \in \{1, \ldots, m+n\}$, then (2.6) can be replaced by the following less restrictive condition (see Remark 6):

Remark 2. The algorithm (2.5) is an explicit version of the scheme of [2]. To recover the scheme of [2] from (2.5), one proceeds as follows:

● first substitute $P^s$ for $P^{s+1}$ in the first equation of (2.5), and solve the resulting equation for $P^s$ (the implicit part of the algorithm of [2]),

● then advance each $U^{h, s}$ to the next time level using the second and third equations of (2.5) (recalling the notational convention $U^{h, s}_0 = P^s$).

The equation mentioned above (after substituting $P^s$ for $P^{s+1}$) is clearly equivalent to

The implicit portion of the scheme of [2] consists of solving (2.8) for the unknown $P^s$. Lemma 2.3 of [2] guarantees that this equation has a solution, which can be found using, e.g., regula falsi.

Remark 3. The convergence of the scheme (2.5) is unaffected by the choice of $P^0$, as long as it lies in $[0, R]$. However the choice of $P^0$ does affect accuracy, see Section 3. We found that accurate results are obtained when $P^0$ is a solution to the $s = 0$ version of (2.8). We also found this solution can be conveniently approximated by iterating the first equation of (2.5), i.e.,

Moreover, we found that this same fixed point iteration approach is a convenient way to solve (2.8) when implementing the implicit scheme of [2]. From this point of view the algorithm of this paper and the algorithm of [2] only differ in whether the first equation of (2.5) is iterated once, or iterated to (approximate) convergence. See Appendix A for a proof that the iterative scheme (2.9) converges to a solution of (2.8).

Remark 4. The CFL condition associated with the finite volume scheme of [2] is

As soon as there are more than a few roads impinging on the junction, our CFL condition (2.6) imposes a more severe restriction on the allowable time step, which becomes increasingly restrictive as more roads are included. One could view this as the price to be paid for the simplified processing of the junction. On the other hand, most of the specific examples discussed in the literature are limited to $\max(m, n) = 2$. In that case, if also all of the $f_h$ are the same, then (2.7) and (2.10) are equivalent. Finally, at the cost of some additional complexity, one could use a larger spatial mesh adjacent to the junction, which would allow for larger time steps. We do not pursue that here.

Let $\chi_{\ell}(x)$ denote the characteristic function of the spatial interval $I_{\ell}$, and let $\chi^s(t)$ denote the characteristic function of the temporal interval $[s {\Delta} t, (s+1){\Delta} t)$. We extend the grid functions to functions defined on $\Omega_{\ell} \times \mathbb{R}_+$ via

The discrete solution operator is denoted by $\mathcal{S}^{\Delta}$, which operates according to

The symbol $\Gamma_{ \text{discr}}$ is used to denote the spatial grid (excluding the artificial grid point associated with $\ell = 0$):

and with the notation

$(U^s, P^s)$ denotes the grid function generated by the scheme at time step $s$.

Remark 5. In the case where $m = n = 1$, i.e., a one-to-one junction, and $f_1 \neq f_2$, we have the special case of a conservation law with a spatially discontinuous flux at $x = 0$. If we redefine the grid so that $x_j = j {\Delta} x$, and set $U_0^s = P^s$, the explicit finite volume scheme proposed here reduces to the Godunov scheme first proposed in [10]. In reference [17] it was proven that (for $m = n = 1$) the scheme converges to the vanishing viscosity solution under more general assumptions about the flux than the unimodality condition imposed here.

Lemma 2.1. Fix a time level $s$. Assume that $P^s \in [0, R]$ and $U_{\ell}^{h, s} \in [0, R]$ for each $h \in \{1, \ldots m+n\}$. Then each $U_{\ell}^{h, s+1}$ is a nondecreasing function of each of its three arguments. Likewise, $P^{s+1}$ is a nondecreasing function of each of its $m+n+1$ arguments.

Proof. For $h\in \{1, \ldots, m \}$ and $\ell<-1$, or $h \in \{m+1, \ldots, m+n \}$ and $\ell>1$, the assertion about $U_{\ell}^{h, s+1}$ is a standard fact about three-point monotone schemes for scalar conservation laws [9]. For the remaining cases, we show that the relevant partial derivatives are nonnegative.

Fix $i \in \{1, \ldots, m \}$, let $\ell = -1$. The partial derivatives of $\partial U^{i, s+1}_{-1}$ are

That partial derivatives in the first two lines are nonnegative is a well-known property of the Godunov numerical flux. The partial derivative on the third line is nonnegative due to (1.4) and the CFL condition (2.6).

A similar calculation shows that the partial derivatives of $U^{j, s+1}_{1}$ are nonnegative, for each $j \in \{m+1, \ldots, m+n \}$.

It remains to show that the partial derivatives of $P^{s+1}$ are all nonnegative. Note that $P^{s+1}$ is a function of $P^s$, along with $U^{i, s}_{-1}$ for $i \in \{1, \ldots, m \}$, and $U^{j, s}_{1}$ for $j \in \{m+1, \ldots, m+n \}$. The partial derivatives of $P^{s+1}$ are

The first two partial derivatives are clearly nonnegative. For the third partial derivative we have used the following readily verified fact about the Godunov flux:

and thus the third partial derivative is nonnegative due to (1.4) and the CFL condition (2.6).

Remark 6. If all of the fluxes $f_h = f$ are the same, then the bound above for $\partial P^{s+1}/\partial P^s$ simplifies to

from which it is clear that $\partial P^{s+1}/\partial P^s \ge 0$ under the less restrictive CFL condition (2.7).

Lemma 2.2. Assuming that the initial data satisfies $\vec{u}_0 \in L^{\infty}(\Gamma; [0, R]^{m+n})$, the finite volume approximations satisfy $U^{h, s}_{\ell} \in [0, R]$, $P^s \in [0, R]$ for $s\ge 0$.

Proof. The assertion is true for $s = 0$, due to our method of discretizing the initial data. Define a pair of grid functions $(\tilde{U}, \tilde{P})$ and $(\hat{U}, \hat{P})$:

It is readily verified that $(\tilde{U}, \tilde{P})$ and $(\hat{U}, \hat{P})$ are stationary solutions of the finite volume scheme, and we have

After an application of a single step of the finite volume scheme, these ordering relationships are preserved, as a result of Lemma 2.1. Since $(\tilde{U}, \tilde{P})$ and $(\hat{U}, \hat{P})$ remain unchanged after applying the finite volume scheme, we have

This proves the assertion for $s = 1$, and makes it clear that the proof can be completed by continuing this way by induction on $s$.

Given $\vec{k} \in \mathcal{G}_{VV}$, we define a discretized version $(K, P)$ with $K = \left(K_{\ell}^{h} \right)_{(h, l)\in \Gamma_{ \text{discr}}}$ where

and $P = p_{ \vec{k}}$. Here $p_{ \vec{k}}$ denotes the value of $p$ associated with $\vec{k}$ whose existence is stated in Definition 1.1.

Lemma 2.3. The finite volume scheme of Section 2 is well-balanced in the sense that each $(K, P)$ associated with $\vec{k} \in \mathcal{G}_{VV}$ as above is a stationary solution of the finite volume scheme.

Proof. For each fixed $h$, and $\left|{\ell}\right| >1$, the scheme reduces to the classical Godunov scheme without any involvement of the junction, and thus $\{K^h_{\ell} \}_{\left|{\ell}\right|>1}$ is clearly unchanged by application of the scheme in this case.

Fix $i \in \{1, \ldots, m \}$, and take $\ell = -1$. When the scheme is applied in order to advance $K^i_{-1} = k^i$ to the next time level, the result is

Here we have used the definition of $p_{ \vec{k}}$, along with the consistency of the Godunov flux, $G_i(\alpha, \alpha) = f_i(\alpha)$. Similarly, when $j \in \{m+1, \ldots, m+n \}$ is fixed, and the scheme is applied at $\ell = 1$, the result is $k^j$. It remains to show that the scheme leaves $P$ unchanged. The quantity $P = p_{ \vec{k}}$ is advanced to the next time level according to

where we have applied the first equation of (1.5).

With the notation $a\vee b = \max(a, b)$ and $a \wedge b = \min(a, b)$, define

Lemma 2.4. Let $0\le \xi \in \mathcal{D}( \mathbb{R} \times (0, \infty))$, and define $\xi^s_{\ell} = \xi(x_{\ell}, t^s)$. Given any initial conditions $\vec{u}_0, \hat{ \vec{u}}_0 \in L^{\infty}(\Gamma; [0, R]^{m+n})$, the associated finite volume approximations satisfy the following discrete Kato inequality:

Proof. From the monotonicity property (Lemma 2.1), a standard calculation [9] yields

We first multiply each of the first and second set of inequalities indexed by $- \Delta x \xi^s_{\ell}$. Likewise, we multiply each of the last set of inequalities by $-{\Delta} x \xi_0^s$. Next we sum the inequalities indexed by $i$ over $i \in \{1, \ldots, m \}$, $s \ge 0$, $\ell \le -1$, and then sum by parts in $s$ and $\ell$. Similarly, we sum the inequalities indexed by $j$ over $j \in \{m+1, \ldots, m+n \}$, $s \ge 0$, $\ell \ge 1$, and then sum by parts in $s$ and $\ell$. For the last set of inequalities we sum over $s\ge 0$, and then sum by parts in $s$. When all of the sums are combined the result is (2.26).

Lemma 2.5. Suppose that $\vec{u}$ is a subsequential limit of the finite volume approximations $\mathcal{S}^{{\Delta}} \vec{u}_0$ generated by the scheme of Section 2. Then $\vec{u}$ is a $\mathcal{G}_{VV}$ entropy solution.

Proof. The proof that the first condition of Definition 1.2 holds is a slight adaptation of a standard fact about monotone schemes for scalar conservation laws [9].

The proof is completed by verifying the second condition of Definition 1.2. Let $\vec{k} \in \mathcal{G}_{VV}$, with $\vec{k}$ also denoting (by a slight abuse of notation) the associated road-wise constant $\mathcal{G}_{VV}$ solution. Following [2], we invoke Lemma 2.4, with $\hat{ \vec{u}} = \vec{k}$, and rely on the fact that $\mathcal{S}^{{\Delta}} \vec{k}$ is a stationary solution of the finite volume scheme (Lemma 2.3). When ${\Delta} \rightarrow 0$ in the resulting version of (2.26), the result is the desired Kružkov-type entropy inequality (1.10). The crucial observation here is that the last sum on the left side of (2.26) vanishes in the limit.

With Lemmas 2.1 through 2.5 in hand it is possible to repeat the proof of Theorem 3.3 of [2], which yields Theorem 2.6 below.

Theorem 2.6. For a given initial datum $\vec{u}_0 \in L^{\infty}(\Gamma;[0, R^{m+n}])$, the finite volume scheme of Section 2 converges to the unique $\mathcal{G}_{VV}$-entropy solution $\vec{u}$, i.e., $\mathcal{S}^{{\Delta}} \vec{u}_0 \rightarrow \vec{u}$ as ${\Delta} \rightarrow 0$.

3.   Numerical experience

We found that if $P^0$ is initialized carefully the approximations generated by the explicit scheme of Section 2 differ only slightly from those generated by the implicit scheme of [2]. This conclusion is based on testing on the Riemann problems of [21], among others. Thus we limit our discussion to the initialization of $P^0$, including one numerical example that illustrates the difference between a bad choice for $P^0$ and a good one.

Initialization of $P^0$. As mentioned previously, convergence is guaranteed as long as $P^0 \in [0, R]$, but the choice of $P^0$ can affect accuracy. A bad choice of $P^0$ can result in spurious numerical artifacts, more specifically "bumps" that travel away from $x = 0$. These bumps have been noticed before in the case of a one-to-one junction, see Example 2 of [17]. We have found two approaches that are effective in initializing $P^0$:

● Initialize $P^0$ by solving the nonlinear equation (2.8) (with $s = 0$). In other words, the scheme is implicit on the first time step, and explicit on all subsequent time steps. No spurious artifacts were observed with this method of initialization. For our numerical tests, we solved (2.8) via the iteration (2.9) purely as a matter of convenience, but regula falsi, as suggested in [2], may be more efficient.

● Initialize $P^0$ by choosing $P^0 = U^{i, 0}_{-1}$ for some $i \in \{1, \ldots, m \}$ or $P^0 = U^{j, 0}_{1}$ for some $j \in \{m+1, \ldots, m+n \}$. If a spurious bump is observed, try a different choice from the same finite set. Obviously, this is a trial and error method, and may require re-running a simulation. Based on a substantial amount of experience with one-to-one junctions (discontinuous flux problems), there seems to always be a choice for which no spurious bump appears. This approach also seems to work for more general junctions (up to and including two-by-two), but our experience here is more limited.

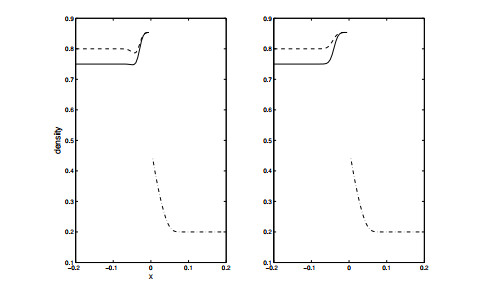
Example 1. This example demonstrates the appearance of a spurious bump when $P^0$ is initialized with a "bad" value. We emphasize that convergence is not affected, only accuracy. This is a Riemann problem featuring a two-to-one merge junction. The initial data is $(u_{1, 0}, u_{2, 0}, u_{3, 0}) = (3/4, 4/5, 1/5)$. See Figure 1. We used $({\Delta} x, {\Delta} t) = (.005, .0025)$, $\lambda = 1/2$, for 25 time steps. In the left panel, we used $P^0 = 1/5$. In the right panel, we computed $P^0$ by the fixed point iteration (2.9), stopping when the difference was $\left|{P^0_{k+1}-P^0_k}\right|< 10^{-6}$. In the left panel, a spurious bump in the graph of $u_2$ left is visible. This numerical artifact is not visible in the right panel.

One can also get rid of the spurious bump by choosing $P^0 = 4/5$. With this choice we got results that are visually indistinguishable from those obtained when using (2.9) for $P^0$.

Acknowledgments

I thank two anonymous referees for their comments and suggestions.

Appendix A.   Convergence of the iterative scheme (2.9)

In this appendix we prove that the fixed point iterations (2.9) converge to a solution of the equation (2.8). Let $p = P^s$, and define the vector $\vec{u} = (u_1, \ldots, u_{m+n})$ by

Then (2.8) takes the form

where

This notation agrees with that of [2], where it was shown that $\Phi_{\vec{u}}^{ \text{in}}(\cdot)- \Phi_{{\vec u}}^{ \text{out}}(\cdot)$ changes from nonnegative to nonpositive over the interval $[0, R]$, and thus the intermediate value theorem guarantees at least one solution of (A.2). Reference [2] suggested regula falsi as a method of locating such a solution. As an alternative we proposed the iterative method (2.9) because it clarifies the relationship between the finite volume algorithm of this paper and that of [2]. Moreover we found that our explicit finite volume scheme can be improved by using a hybrid method, where the implicit scheme of [2] is employed on the first time step and our explicit method is used on all later time steps. In that situation the iterative algorithm (2.9) was found to be a convenient way to implement the nonlinear equation solver that is required on the first time step.

With the simplified notation introduced above, the iterative scheme (2.9) becomes

Proposition 1. The sequence $\{p_{\nu} \}$ produced by the iterative scheme (A.4) converges to a solution of (A.2).

Proof. Note that $p \mapsto G_i(p, u_i)$ is nonincreasing on $[0, R]$, $p \mapsto G_j(u_j, p)$ is nondecreasing on $[0, R]$, and

Thus, $p \mapsto \Phi_{\vec{u}}^{ \text{in}}(p)$ is nonincreasing on $[0, R]$, $p \mapsto \Phi_{{\vec u}}^{ \text{out}}(p)$ is nondecreasing on $[0, R]$, and

Define $\Psi_{ \vec{u}}$ according to

and observe that $\Psi_{ \vec{u}}$ is Lipschitz continuous on $[0, R]$ with Lipschitz constant bounded by $(m+n)L$. Also note that $\Psi_{ \vec{u}}$ is nondecreasing on $[0, R]$, and

Define

$\Pi$ is Lipschitz continuous and

Thanks to (A.10) and the CFL condition (2.6), it is clear that $\Pi$ is nondecreasing on $[0, R]$, and recalling (A.8) we have

Thus $\Pi$ maps $[0, R]$ continuously into $[0, R]$. In terms of $\Pi$, the iterative scheme (A.4) is

We can now prove convergence of the sequence $\{p_{\nu} \}$. First take the case where $p_{\nu_0 +1} = p_{\nu_0}$ for some $\nu_0$. Then $p_{\nu} = p_{\nu_0}$ for $\nu \ge \nu_0$, so $p_{\nu} \rightarrow p_{\nu_0}$. Also $p_{\nu_0 +1} = p_{\nu_0}$ implies that $\Psi_{ \vec{u}}(p_{\nu_0}) = 0$, and thus $p_{\nu_0}$ is a solution of (A.3).

Now consider the case where $p_{\nu +1} \neq p_{\nu}$ for all $\nu \ge 0$. Then

Since $\Pi$ is nondecreasing and $p_{\nu} - p_{\nu-1} \neq 0$, $p_{\nu+1} - p_{\nu} \neq 0$, (A.13) implies that

In other words, the sequence $\{p_{\nu} \}$ is monotonic. Since we also have $\{p_{\nu}\} \subseteq [0, R]$, $p_{\nu}$ converges to some $p \in [0, R]$, and it follows from continuity of $\Psi_{ \vec{u}}$ that the limit $p$ is a solution of (A.3).