1. Introduction
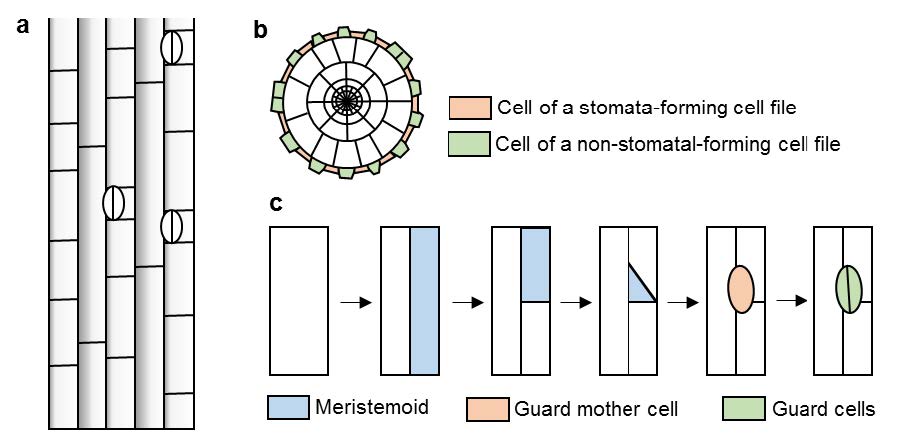
The Arabidopsis epidermis has attracted widespread attention as an excellent model system for studying the molecular mechanisms underlying cell fate determination and pattern formation in plants. Factors such as the rapid growth of the hypocotyl, which completes its development within 1 week after germination, as well its simplicity, have encouraged researchers to delve into the development of this embryonic organ. The hypocotyl epidermis is composed of only two types of cell columns, which run parallel to its longitudinal axis (Figure 1a and b) [1,2]: (1) files overlying two cortical cell files, consisting of narrower, shorter cells, and (2) cell columns that overlap with a single cortical cell file, containing protruding, longer cells.
Stomata only develop in the files overlying two cortical cell files [2,3]. Therefore, stomata-forming cell files alternate with non-stomatal-forming ones. Several asymmetric divisions occur in an inward-spiral pattern before stomata formation, which tend to cause the immediate stomatal precursor to be located at the center of the clonal structure (Figure 1c) [3]. The first asymmetric division takes place along the longitudinal axis of the cell, which is parallel to the longitudinal axis of the organ and produces a rectangular o triangular cell named meristemoid. Meristemoids divide to give rise to more meristemoids, perpetuating their production throughout hypocotyl development. The meristemoids then assume guard mother cell identity and divide symmetrically to differentiate into the two guard cells that integrate the stomata.
During the past several years, our understanding of the molecular mechanism that guides stomatal cell fate specification and patterning has advanced due to the identification of a number of hormones and genetic networks involved in these processes. Here, I review current insights into the role played by these hormonal signaling pathways and genetic networks and the possible crosstalk among them. The emerging picture reveals that brassinosteroids and gibberellins, which positively regulate the initiation of stomatal development in the embryonic stem [4-6], might perform this function through the convergence of their signaling pathways. In addition, brassinosteroids act upstream of the TTG-BHLH-MYB-GL2 transcriptional network in regulating stomatal patterning specification [5]. The leucine-rich repeat-containing receptor-like protein TOO MANY MOUTHS (TMM) functions later than these genes and hormones, promoting progression from meristemoids to stomata [7]. It also appears to promote the initiation of stomatal development in response to brassinosteroids [5].
2. The role of the TTG-BHLH-MYB-GL2 network
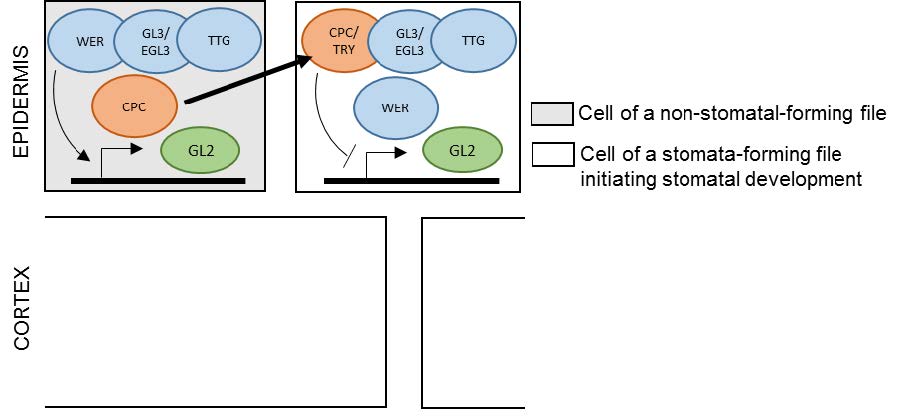
A number of genes that play in the same transcriptional network, and whose function was primarily deduced by studying root hair patterning, regulate stomatal formation in the hypocotyl. Mutations in TRANSPARENT TESTA GLABRA (TTG), WEREWOLF (WER), or GLABRA3 (GL3) and ENHANCER OF GLABRA3 (EGL3) increase the number of stomata and disrupt their patterning, enabling the formation of stomata in the files overlying a single cortical cell file [2,3,8,9]. These genes encode transcription factors that assemble into a multimeric complex. TTG encodes a WD40 repeat protein that interacts with GL3 and EGL3 [10,11,12], both of which encode basic helix-loop-helix (BHLH) proteins [11,12]. These BHLH proteins mediate homo-and heterodimeric interactions [11,12]. WER also physically associates with both GL3 and EGL3 [13]. This multimeric complex represses stomata formation in the files overlying a single cortical cell file [14,15,16,17], which depends on its ability to induce the transcription of GLABRA2 (GL2) in the cells of these files [14,15,16,17] (Figure 2). GL2 encodes a homeodomain-leucine zipper protein [18,19], and disruption of this gene also breaks down stomatal patterning, producing stomata in both the files above a single cortical cell file and the files overlapping two cortical cell files [2,3].
How is GL2 expression blocked to allow stomatal production? This process depends on the sequestration of GL3 and EGL3 by the R3MYB protein CAPRICE (CPC) and/or TRIPTYCHON (TRY), promoting the formation of a complex consisting of CPC (and/or TRY), TTG, GL3, and EGL3 in stomatal-forming cell files [20]. GL3 and EGL3 can physically interact with either WER or CPC and TRY [11,12,13] (Figure 2). Interestingly, three-hybrid analysis in yeast showed that TRY prevents the interaction between GL3 and the R2R3 MYB GL1 [21], suggesting that, given that WER and GL1 share high amino acid identity, TRY also competes with WER in BHLH protein binding. To form the complex consisting of TTG, GL3, and/or EGL3 and CPC or TRY, CPC (and probably TRY), whose gene is expressed in files characterized by the absence of stomata [20,22], moves to the stomatal-forming cell files where it competes with WER in BHLH protein binding[20]. In agreement with this model, the cpc try double mutant does not form stomata [5].
3. Brassinosteroids and gibberellins promote stomatal development
Brassinosteroids positively regulate stomatal formation in the embryonic stem [5,6]. Indeed, plants grown on medium supplemented with brassinolide, the most active natural brassinosteroid, exhibit increased numbers of stomata without affecting stomatal patterning, whereas brassinazole and triadimefon, which inhibit brassinosteroid biosynthesis, reduce stomatal production [5,6]. Supporting these findings, plants with enhanced responses to brassinosteroids (plants overexpressing either DWARF4 or BRASSINOSTEROID INSENSITIVE1 [BRI1] and the mutants brassinosteroid insensitive2-3 [bin2-3] and bin2-3 bil1 bil2) produce more stomata than wild-type plants, and those unable to synthesize brassinosteroids (constitutive photomorphogenesis and dwarfism [cpd], deetiolated2-1 [det2-1]) or with reduced sensitivity to these regulators (bri1-1, bri1-4, bri1-116, and the dominant mutant bin2-1) display the opposite phenotype [5,6]. Mutant plants also respond to these hormonal treatments as expected: those with disruptions in brassinosteroid perception (bri1-1 and bri1-4) exhibit absolute insensitivity to brassinolide, while those that fail in brassinosteroid biosynthesis (det2-1) develop more stomata when they are grown in the presence of this plant growth regulator [5]. Interestingly, the stomatal production of the gain-of-function mutants bri1-ems-suppressor1 (bes1-d) and brassinazole resistant1 (bzr1-d) is similar to that of wild-type plants [6]. This finding indicates that the GLYCOGEN SYNTHASE KINASE3-like BIN2 represses stomatal development in the hypocotyl independently of its direct targets BZR1 and BES1 transcription factors [6].
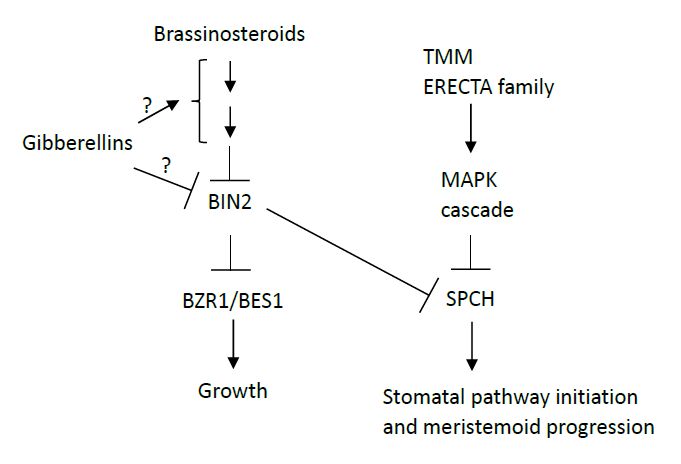
Gudesblat et al. [6] took a step forward by analyzing the possible interactions between brassinosteroid signaling and genes that function in the stomatal pathway. The authors found that brassinolide increases stomatal production in the hypocotyls of epidermal patterning factor1 (epf1), epf2, erecta105 (er-105), erecta-like1-2 (erl1-2), erl2-1, and yoda5 (yda-5), but it has no effect on speechless-3 (spch-3), strongly suggesting that SPCH acts as a downstream regulator of brassinosteroid signaling, promoting stomatal lineage initiation. A plausible scenario is that BIN2 represses SPCH via phosphorylation. Indeed, in vitro phosphorylation assays showed that BIN2 phosphorylates two residues of SPCH located within the mitogen-activated protein kinase (MAPK) target domain and one residue located at the N-terminus of this protein [6]. In addition, brassinolide reduces the phosphorylation of two of the three SPCH residues that are phosphorylated by BIN2 [6]. It is likely that brassinosteroids promote SPCH activity, and thus stomatal development in the stomatal-forming cell files of the hypocotyl, by inhibiting the phosphorylation of these two BIN2 target residues (Figure 3). Such inhibition would lead to an increase in SPCH levels, most likely by preventing SPCH degradation [6].
Gibberellins also positively regulate stomatal formation in the embryonic stem [4]. The growth of seedlings on medium supplemented with paclobutrazol, an inhibitor of gibberellin biosynthesis [23], blocks stomatal formation [4]. This inhibition of stomatal development is counteracted by the addition of gibberellins, which indicates that the effect of paclobutrazol is due to the inhibition of gibberellin biosynthesis [4]. Supporting the role of gibberellins in stomatal production, the absence of stomata in the gibberellin-deficient mutant ga1-3 is recovered by the addition of gibberellins to the growth medium [4]. Do gibberellins control stomatal formation through the regulation of SPCH? The recent identification of LLM-domain B-GATA factors as positive regulators of stomatal development in the hypocotyl indicates that this may indeed be the case: LLM-domain B-GATA transcription factors are regulated by gibberellins [24] and control stomatal formation upstream of SPCH [25]. A possible scenario is that this plant hormone regulates SPCH through the regulation of brassinosteroid signaling. Indeed, BZR1 and gibberellic acid-inactivated DELLA transcriptional regulators physically interact [26,27,28].However, the finding that brassinosteroids control stomatal production in the hypocotyl in a BZR1-independent manner [6] indicates that, if the gibberellin signaling pathway interacts with the brassinosteroid signaling pathway, it must do so upstream of, and/or directly with, BIN2 (Figure 3). If the gibberellin signaling pathway converges with the brassinosteroid signaling pathway at the level of BIN2, it should repress this kinase to prevent SPCH inactivation. By contrast, if the gibberellin signaling pathway interacts with proteins upstream of BIN2, it should activate such proteins so that they can repress BIN2. The repression of BIN2 would prevent SPCH inactivation, triggering stomatal development. SPCH would not be inactivated by the MAPK cascade that functions upstream, because it is assumed that low levels of the components of this cascade are present in the embryonic stem [29].
Interestingly, low levels of brassinosteroids or gibberellins do not appear to repress stomatal formation in cotyledons [4,6,30]. Moreover, high levels of phytohormones, at least of brassinosteroids [30], repress stomatal formation in these plant organs [30]. BIN2 not only represses SPCH activity [6], it also negatively regulates two members of the MAPK module via phosphorylation [30,31]. Organ type may affect the levels of the components of the MAPK module [29]: high levels of the MAPK components in cotyledon cells could enable BIN2-mediated their repression promoting stomatal formation, whereas low MAPK levels in hypocotyl cells could enable BIN2 regulation of SPCH to repress stomatal development.
Auxin controls stomatal development and patterning in the cotyledons of dark-grown seedlings via Aux/IAA proteins [32,33]. Auxin is also thought to control stomatal development and/or patterning in the embryonic stem, although this notion is based on limited data [32]: the hypocotyls of dark-grown aux/iaa mutants, like their cotyledons, also exhibit an increased number of stomata compared to wild-type seedlings. More data are needed to confirm the involvement of this plant growth regulator in the production of stomata on the hypocotyl and to prove its hypothetical interaction with hormonal signaling pathways and other genetic networks regulating stomatal production.
4. Crosstalk between the TTG-BHLH-MYB-GL2 network and phytohormone signaling
Does the TTG-BHLH-MYB-GL2 network interact with the brassinosteroid and/or gibberellin signaling pathway? Although the cpc mutant shows increased stomatal production in response to brassinolide treatment, the try cpc mutant exhibits absolute insensitivity to this plant growth regulator [5]. These findings strongly suggest that brassinosteroids positively regulate stomatal development upstream of CPC and TRY and that cpc responds to this phytohormone due to genetic redundancy [5]. Supporting this interpretation, brassinolide treatment partially rescues stomatal number in det2-1, but not in try cpc det2-1 [5]. Interestingly, triadimefontreatment reduces the level of CPC promoter activity [5]. The effect of triadimefon on CPC promoter activity also explains the absence of a response of the cpc mutant to this inhibitor [5]: stomatal production in the cpc mutant grown in medium supplemented with triadimefon is indistinguishable from that in medium devoid of this inhibitor.
Treatment with triadimefon also alters the pattern of GL2 promoter induction, triggering random induction of this promoter [5]. However, the response of gl2-1 to both brassinolideand triadimefon is similar to that of wild-type plants [5]. This finding suggests that other unidentified genes might perform the function of GL2 in the gl2-1 mutant [5]. The data also suggest that brassinosteroids regulate stomatal cell fate and patterning in the hypocotyl by regulating expression of at least two members of the TTG-BHLH-MYB-GL2 network [5]: CPC and GL2. The effect of this plant growth regulator on the expression of CPC and GL2 mirrors that taking place in the root: the loss of brassinosteroid signaling in the root also results in a strong reduction in CPC expression as well as random patterning of GL2 expression [34].
Although no data are available on the possible interaction between the TTG-BHLH-MYB-GL2 network and the gibberellin signaling pathway, it has been proposed that gibberellins regulate the WER homologous genes GLABRA1 and TTG during trichome formation in Arabidopsis [35]. This notion suggests that gibberellins might also regulate the expression of genes in the TTG-BHLH-MYB-GL2 network during stomatal development, either directly or indirectly, through the interaction of its signaling pathway with the brassinosteroid signaling pathway.
5. Genes functioning later in stomatal development: the role of TMM
TMM encodes a leucine-rich repeat receptor-like protein without a cytoplasmic domain [36]. Plants with mutations in this gene do not form stomata, but they develop arrested meristemoids [7], indicating that TMM promotes stomatal formation from their immediate precursors, the meristemoids [7]. This finding indicates that TMM regulates a later stage in the stomatal development pathway than that regulated by the brassinosteroid and/or gibberellin pathways.
In agreement with the finding that brassinosteroids control stages that take place earlier than that regulated by TMM, treatment with brassinolide fails to reverse the lack of stomata in the tmm-1 hypocotyl [5,6]. Supporting this interpretation, bri1-1, bri1-4, and det2-1 mutants, as well as wild-type plants treated with triadimefon, do not display arrested meristemoids [5]. Interestingly, under brassinolide treatment, the production of stomata in wild-type plants is higher than the production of meristemoids in tmm-1 [5], suggesting that TMM, in addition to positively regulating the progression from meristemoids toward stomata, also controls the initiation of the stomatal pathway.
How could TMM regulate both of these steps? A plausible scenario is that the action of TMM may reduce MAPK activity in the hypocotyl. High levels of brassinosteroids would inactivate BIN2, thereby repressing SPCH inactivation [29]. In agreement with this interpretation, a component of the MAPK module (YDA) is not required for the stomatal development-promoting function of brassinosteroids [37]. Given that SPCH controls both the initiation of the stomatal pathway [38,39] and the maintenance of the self-renewing activity of meristemoids in leaves [40], it appears logical that TMM, which functions in the same signaling pathway, also regulates such functions.
6. Conclusions
The findings discussed in this review indicate that brassinosteroids negatively regulate the signaling pathway that inactivates SPCH, allowing stomatal cell fate determination to take place. These plant growth regulators also control stomatal patterning specification through the regulation of genes that function in the TTG/BHLHs/MYBs/GL2 network. Although much less is known about the role of gibberellins in stomatal formation, these phytohormones, like brassinosteroids, also positively regulate stomatal formation. This finding opens up the possibility that these phytohormones may function in the same pathway. The observation that LLM-domain B-GATA factors, which act downstream of gibberellins [24], positively regulate stomatal development in the hypocotyl upstream of SPCH [25] suggests that the brassinosteroid and gibberellin signaling pathways converge to control stomatal cell fate specification. Future research should focus on detecting and defining the precise convergence point. More work is also needed to determine if gibberellins control stomatal pattern formation and, if so, how the underlying mechanism operates.
Acknowledgement
This work was supported by the Communities Council of Castilla-La Mancha (grant n PEII-2014-016-A).
Conflict of interest
The author declares no conflicts of interest.









 DownLoad:
DownLoad: