On regularization of charge singularities in solving the Poisson-Boltzmann equation with a smooth solute-solvent boundary

Siwen Wang; Emil Alexov; Shan Zhao; Siwen Wang; Emil Alexov; Shan Zhao

doi:10.3934/mbe.2021072

Mathematical Biosciences and Engineering

2021, Volume 18, Issue 2: 1370-1405. doi: 10.3934/mbe.2021072

Previous Article Next Article

Research article Special Issues

On regularization of charge singularities in solving the Poisson-Boltzmann equation with a smooth solute-solvent boundary

1.
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
2.
Department of Physics and Astronomy, Clemson University, Clemson, SC 29634, USA

Received: 25 October 2020 Accepted: 12 January 2021 Published: 21 January 2021

Numerical treatment of singular charges is a grand challenge in solving the Poisson-Boltzmann (PB) equation for analyzing electrostatic interactions between the solute biomolecules and the surrounding solvent with ions. For diffuse interface PB models in which solute and solvent are separated by a smooth boundary, no effective algorithm for singular charges has been developed, because the fundamental solution with a space dependent dielectric function is intractable. In this work, a novel regularization formulation is proposed to capture the singularity analytically, which is the first of its kind for diffuse interface PB models. The success lies in a dual decomposition – besides decomposing the potential into Coulomb and reaction field components, the dielectric function is also split into a constant base plus space changing part. Using the constant dielectric base, the Coulomb potential is represented analytically via Green's functions. After removing the singularity, the reaction field potential satisfies a regularized PB equation with a smooth source. To validate the proposed regularization, a Gaussian convolution surface (GCS) is also introduced, which efficiently generates a diffuse interface for three-dimensional realistic biomolecules. The performance of the proposed regularization is examined by considering both analytical and GCS diffuse interfaces, and compared with the trilinear method. Moreover, the proposed GCS-regularization algorithm is validated by calculating electrostatic free energies for a set of proteins and by estimating salt affinities for seven protein complexes. The results are consistent with experimental data and estimates of sharp interface PB models.

Keywords:

Citation: Siwen Wang, Emil Alexov, Shan Zhao. On regularization of charge singularities in solving the Poisson-Boltzmann equation with a smooth solute-solvent boundary[J]. Mathematical Biosciences and Engineering, 2021, 18(2): 1370-1405. doi: 10.3934/mbe.2021072

Related Papers:

[1]	Jin Li, Yongling Cheng . Barycentric rational interpolation method for solving time-dependent fractional convection-diffusion equation. Electronic Research Archive, 2023, 31(7): 4034-4056. doi: 10.3934/era.2023205
[2]	Jin Li, Yongling Cheng . Barycentric rational interpolation method for solving KPP equation. Electronic Research Archive, 2023, 31(5): 3014-3029. doi: 10.3934/era.2023152
[3]	Xiumin Lyu, Jin Li, Wanjun Song . Numerical solution of a coupled Burgers' equation via barycentric interpolation collocation method. Electronic Research Archive, 2025, 33(3): 1490-1509. doi: 10.3934/era.2025070
[4]	Waleed Mohamed Abd-Elhameed, Omar Mazen Alqubori, Abdulrahman Khalid Al-Harbi, Mohammed H. Alharbi, Ahmed Gamal Atta . Generalized third-kind Chebyshev tau approach for treating the time fractional cable problem. Electronic Research Archive, 2024, 32(11): 6200-6224. doi: 10.3934/era.2024288
[5]	Li Tian, Ziqiang Wang, Junying Cao . A high-order numerical scheme for right Caputo fractional differential equations with uniform accuracy. Electronic Research Archive, 2022, 30(10): 3825-3854. doi: 10.3934/era.2022195
[6]	Sahar Albosaily, Wael Mohammed, Mahmoud El-Morshedy . The exact solutions of the fractional-stochastic Fokas-Lenells equation in optical fiber communication. Electronic Research Archive, 2023, 31(6): 3552-3567. doi: 10.3934/era.2023180
[7]	Ziqing Yang, Ruiping Niu, Miaomiao Chen, Hongen Jia, Shengli Li . Adaptive fractional physical information neural network based on PQI scheme for solving time-fractional partial differential equations. Electronic Research Archive, 2024, 32(4): 2699-2727. doi: 10.3934/era.2024122
[8]	Nelson Vieira, M. Manuela Rodrigues, Milton Ferreira . Time-fractional telegraph equation of distributed order in higher dimensions with Hilfer fractional derivatives. Electronic Research Archive, 2022, 30(10): 3595-3631. doi: 10.3934/era.2022184
[9]	Ping Zhou, Hossein Jafari, Roghayeh M. Ganji, Sonali M. Narsale . Numerical study for a class of time fractional diffusion equations using operational matrices based on Hosoya polynomial. Electronic Research Archive, 2023, 31(8): 4530-4548. doi: 10.3934/era.2023231
[10]	Yin Yang, Sujuan Kang, Vasiliy I. Vasil'ev . The Jacobi spectral collocation method for fractional integro-differential equations with non-smooth solutions. Electronic Research Archive, 2020, 28(3): 1161-1189. doi: 10.3934/era.2020064

Abstract

1. Introduction

Lots of physical phenomena can be expressed by the FC equation, including, inter alia, dissipative and dispersive partial differential equations (PDEs). In this paper, we consider the FC equation

$\begin{eqnarray} \frac{\partial \phi(t,s)}{\partial t} = -\mu_{0}\ _{0}C_{t}^{1-\alpha_{1}}\phi(t,s)+\ _{0}C_{t}^{1-\alpha_{2}}\frac{\partial^2 \phi(t,s)}{\partial s^2} +f(t,s) ,0 \le s\le 1,0 \le t \le T, \end{eqnarray}$

(1.1)

$\begin{eqnarray} \phi(0,s) = 0, \phi(1,s) = 0, s\in [0,T], \end{eqnarray}$

(1.2)

$\begin{eqnarray} \phi(t,0) = \varphi(t), t\in [0,1] \end{eqnarray}$

(1.3)

where $\mu_{0}\in R, 0 \ < \alpha_{1}, \alpha_{2} < 1$ are constants. There are some definitions of fractional derivatives, such as the Caputo type, Riemann-Liouville type and so on. In the following, we adopt the Caputo type time fractional-order partial derivative as

$\begin{eqnarray} _{0}C_{t}^{\alpha}\phi(t) = \frac{1}{\Gamma(1-\alpha)}\int_{0}^{t}\frac{\phi'(t)}{(t-\tau)^{\alpha}}d\tau, \end{eqnarray}$

(1.4)

and $\Gamma(\alpha)$ is the $\Gamma$ function.

In ^[1], a scheme combining the finite difference method in the time direction and a spectral method in the space direction was proposed. In ^[2], two implicit compact difference schemes for the FC equation were studied, this scheme was proved to be stable, and the convergence order $O(\tau+h^4)$ was given. In ^[3], a two-dimensional FC equation was solved by orthogonal spline collocation (OSC) methods for space discretization and finite difference method for time, which was proved to be unconditionally stable. In^[4], the FC equation with two time Riemann-Liouville derivatives was solved by an explicit numerical method; and the accuracy, stability and convergence of this method were studied. In ^[5], FC equation with two fractional time derivatives were considered, and two new implicit numerical methods for the FC equation were proposed, respectively. The stability and convergence of these methods were also investigated. In ^[6], nonlinear FC equation was solved by a two-grid algorithm with the finite element (FE) method. A time second-order fully discrete two-grid FE scheme and the space direction were approximated. In ^[7], the discrete Crank-Nicolson (CN) finite element method was obtained by the finite difference in time and the finite element in space to approximate the FC equation, the stability and error estimate were analyzed in detail and the optimal convergence rate was obtained. In ^[8], the FC equation involving two integro-differential operators was solved by semi-discrete finite difference approximation, and the scheme was proved unconditionally stable. In reference ^[9], numerical integration with the reproducing kernel gradient smoothing integration are constructed. In reference ^[10], recursive moving least squares (MLS) approximation was constructed.

Like the above methods to solve the FC equation by finite difference approach or finite element method, the time direction and space direction were solved separatively. In the following, we presented the BRIM to solve the time direction and space direction of FC equation at the same time. Lagrange interpolation has been presented by mathematician Lagrange to fitting data to be a certain function. When the number $n$ increases, there are Runge phenomenon that the interpolation result deviates from the original function. In order to avoid the Runge phenomenon, among them, barycentric interpolation was developed in 1960s to overcome it. In recent years, linear rational interpolation (LRI) was proposed by Floater ^[14,15,16] and error of linear rational interpolation ^[11,12,13] is also proved. The barycentric interpolation collocation method (BICM) has developed by Wang et al.^[25,26] and the algorithm of BICM has used for linear/non-linear problems ^[27,28]. In recent research, Volterra integro-differential equation (VIDE) ^[17,21], heat equation (HE) ^[18], biharmonic equation (BE) ^[19], telegraph equation (TE) ^[20], generalized Poisson equations ^[22], fractional reaction-diffusion equation ^[23] and KPP equation ^[24] have been studied by the linear barycentric rational interpolation method (LBRIM) and their convergence rate are also proved.

In this paper, BRIM has been used to solve the FC equation. As the fractional derivative is the nonlocal operator, the spectral method is developed to solve the FC equation and the coefficient matrix is the full matrix. The fractional derivative of the FC equation is changed to nonsingular integral by the order of density function plus one. New Gauss formula is constructed to compute it simply and matrix equation of discrete FC equation is obtained by the unknown function replaced by barycentric rational interpolation basis function. Then, the convergence rate of BRIM is proved.

2. Matrix equation of FC equation

As there is singularity in Eq (1.1), the numerical methods cannot get high accuracy, by fractional integration to second part of (1.1) to overcome the difficulty of singularity. We get

$\begin{align} & _{0}C_{t}^{\alpha}\phi(t,s) \\ & = \frac{1}{\Gamma(\xi-\alpha)}\int_{0}^{t}\frac{\partial^{\xi} \phi(\tau,s)}{\partial \tau^{\xi}}\frac{d\tau}{(\tau-t)^{\alpha+1-\xi}} \\ & = \frac{1}{(\xi-\alpha)\Gamma(\xi-\alpha)}\left[\frac{\partial^{\xi} \phi(0,s)}{\partial t^{\xi}}t^{\xi-\alpha}+\int_{0}^{t}\frac{\partial^{\xi+1} \phi(\tau,s)}{\partial \tau^{\xi+1}}\frac{d\tau}{(t-\tau)^{\alpha-\xi}}\right] \\ & = \Gamma_{\alpha}^{\xi}\left[\frac{\partial^{\xi} \phi(0,s)}{\partial t^{\xi}}t^{\xi-\alpha}+\int_{0}^{t}\frac{\partial^{\xi+1} \phi(\tau,s)}{\partial \tau^{\xi+1}}\frac{d\tau}{(t-\tau)^{\alpha-\xi}}\right], \end{align}$

(2.1)

where $\Gamma_{\alpha}^{\xi} = \frac{1}{(\xi-\alpha)\Gamma(\xi-\alpha)}$ .

Combining (2.1) and (1.1), we have

$\begin{eqnarray} & \frac{\partial \phi}{\partial t}+\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\left[\frac{\partial^{\xi} \phi(0,s)}{\partial t^{\xi}}t^{\xi-\alpha_{1}}+\int_{0}^{t}\frac{\partial^{\xi+1} \phi(\tau,s)}{\partial \tau^{\xi+1}}\frac{d\tau}{(t-\tau)^{\alpha_{1}-\xi}}\right] \\& = \Gamma_{\alpha_{2}}^{\xi}\left[\frac{\partial^{\xi+2} \phi(0,s)}{\partial t^{\xi}\partial s^2 }s^{\xi-\alpha_{2}}+\int_{0}^{t}\frac{\partial^{\xi+3} \phi(\tau,s)}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(s-\tau)^{\alpha_{2}-\xi}}\right]+f(t,s). \end{eqnarray}$

(2.2)

In the following, we give the discrete formula of FC equation and to get the matrix equation from BRIM.

Let

$\begin{eqnarray} \phi(t,s) = \sum\limits_{j = 1}^{m}R_{j}(t)\phi_{j}(s) \end{eqnarray}$

(2.3)

where

$\phi(t_{i},s) = \phi_{i}(s),i = 1,2,\cdots,m$

and

$\begin{equation} R_{j}(t) = \frac{ \frac{\lambda_{j}}{t-t_{j}}}{ \sum\limits_{k = 1}^{n} \frac{\lambda_{k}}{t-t_{k}}} \end{equation}$

(2.4)

where

$\lambda_{k} = \sum\limits_{j\in J_{k}}(-1)^j\prod\limits_{i = j,j \neq k}^{j+d_{t}}\frac{1}{t_{k}-t_{i}},\ \ \ J_{k} = \{j\in \{ 0,1,\cdots, l-d_{t}\}:k-d_{t}\leq j \leq k\}$

is the basis function ^[18]. Taking (2.3) into Eq (2.2),

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}R'_{j}(t)\phi_{j}(s) +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi_{j}(s)t^{\xi-\alpha_{1}}+\int_{0}^{t} \phi_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t-\tau)^{\alpha_{1}-\xi}}\right] \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi^{(2)}_{j}(s)t^{\xi-\alpha_{2}} +\int_{0}^{t} \phi^{(2)}_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t-\tau)^{\alpha_{2}-\xi}}\right]+f(t,s). \end{eqnarray}$

(2.5)

By taking $0 = t_{1} < t_{2} < \cdots < t_{m} = T, a = s_{1} < s_{2} < \cdots < s_{n} = b$ with $h_{t} = T/m, h_{s} = (b-s)/n$ or uninform as Chebychev point $s = \cos((0:m)'\pi/m), t = \cos((0:n)'\pi/n)$ , we get

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}R'_{j}(t_{i})\phi_{j}(s) +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi_{j}(s)t_{i}^{\xi-\alpha_{1}}+\int_{0}^{t_{i}} \phi_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}}\right] \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi^{(2)}_{j}(s)t_{i}^{\xi-\alpha_{2}} +\int_{0}^{t_{i}} \phi^{(2)}_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}}\right]+f(t_{i},s), \end{eqnarray}$

(2.6)

by noting the notation, $R_{j}(t_{i}) = \delta_{ij}, R'_{j}(t_{i}) = R_{ij}^{(1, 0)}$ , where $R_{ij}^{(1, 0)}$ is the first order derivative of barycentric matrix. Equation (2.6) can be written as

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}R_{ij}^{(1,0)}\phi_{j}(s) +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi_{j}(s)t_{i}^{\xi-\alpha_{1}}+\int_{0}^{t_{i}} \phi_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}}\right] \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\left[R^{(\xi)}_{j}(0) \phi^{(2)}_{j}(s)t_{i}^{\xi-\alpha_{2}} +\int_{0}^{t_{i}} \phi^{(2)}_{j}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}}\right]+f(t_{i},s). \end{eqnarray}$

(2.7)

Similarly as the discrete $t$ for $s$ , we get

$\begin{eqnarray} \phi_{j}(s) = \sum\limits_{k = 1}^{n}R_{k}(s)\phi_{ik} \end{eqnarray}$

(2.8)

where $\phi_{i}(s_{j}) = \phi(t_{i}, s_{j}) = \phi_{ij}, i = 1, \cdots, m; j = 1, \cdots, n$ and

$\begin{equation} R_{i}(s) = \frac{ \frac{w_{i}}{s-s_{i}}}{ \sum\limits_{k = 1}^{m} \frac{w_{k}}{s-s_{k}}} \end{equation}$

(2.9)

where

$w_{i} = \sum\limits_{j\in J_{i}}(-1)^j\prod\limits_{k = j,j \neq i}^{j+d_{s}}\frac{1}{s_{i}-s_{k}},\ J_{i} = \{j\in \{ 0,1,\cdots, m-d_{s}\}:i-d_{s}\leq j \leq i\},$

is the basis function ^[18].

Taking (2.8) into Eq (2.7), we get

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}R_{ij}^{(1,0)}R_{k}(s)\phi_{ik} +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{k}(s)t_{i}^{\xi-\alpha_{1}}+\int_{0}^{t_{i}} R_{k}(s)\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}}\right]\phi_{ik} \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{k}^{(2)}(s)t_{i}^{\xi-\alpha_{2}} +\int_{0}^{t_{i}} R^{(2)}_{k}(s) \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}}\right]\phi_{ik}+f(t_{i},s). \end{eqnarray}$

(2.10)

By taking $s_{1}, s_{2}, \cdots, s_{n}$ at the mesh-point, we get

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}R_{ij}^{(1,0)}R_{k}(s_{l})\phi_{ik} +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{k}(s_{l})t_{i}^{\xi-\alpha_{1}}+\int_{0}^{t_{i}} R_{k}(s_{l})\frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}}\right]\phi_{ik} \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{k}^{(2)}(s_{l})t_{i}^{\xi-\alpha_{2}} +\int_{0}^{t_{i}} R^{(2)}_{k}(s_{l}) \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}}\right]\phi_{ik}+f(t_{i},s_{l}). \end{eqnarray}$

(2.11)

By noting the notation, $R_{k}(s_{l}) = \delta_{kl}, R''_{k}(s_{l}) = R_{ij}^{(0, 2)}$ , where $R_{ij}^{(0, 2)}$ is the second order derivative of barycentrix matrix.

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}R_{ij}^{(1,0)}\delta_{kl}\phi_{ik} +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) \delta_{kl}t_{i}^{\xi-\alpha_{1}}+\delta_{kl}\int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau) d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}}\right]\phi_{ik} \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{ij}^{(0,2)}t_{i}^{\xi-\alpha_{2}} +R_{ij}^{(0,2)}\int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}}\right]\phi_{ik}+f(t_{i},s_{l}), \end{eqnarray}$

(2.12)

where

$\begin{array}{ll}{ R_{k}(\tau) = \frac{ \frac{\lambda_{k}}{\tau-\tau_{k}}}{ \sum\limits_{k = 0}^{n} \frac{\lambda_{k}}{\tau-\tau_{k}}}} \end{array}$

and

$\left\{ \begin{aligned} R_{i}^{'}(\tau)& = R_{i}(\tau)\left[- \frac{1}{\tau-\tau_{k}}+ \frac{\sum\limits_{s = 0}^{l} \frac{\lambda_{k}}{(\tau-\tau_{k})^{2}}}{\sum\limits_{s = 0}^{l} \frac{\lambda_{k}}{\tau-\tau_{k}}}\right], \\{\vdots}\\ R_{i}^{(\xi+1)}(\tau)& = [R_{i}^{(\xi)}(\tau)]^{'},\xi\in\mathbf{N^{+}}. \end{aligned}\right.$

The integral term of (2.12) can be written as

$\begin{equation} \int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}} = Q_{j}^{\alpha_{1}}(t_{i}) = Q^{\alpha_{1}}_{ji}, \end{equation}$

(2.13)

$\begin{equation} \int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}} = Q_{j}^{\alpha_{2}}(t_{i}) = Q^{\alpha_{2}}_{ji}, \end{equation}$

(2.14)

then we get

$\begin{eqnarray} & \sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}R_{ij}^{(1,0)}\delta_{kl}\phi_{ik} +\mu_{0}\Gamma_{\alpha_{1}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) \delta_{kl}t_{i}^{\xi-\alpha_{1}}+\delta_{kl}Q_{j}^{\alpha_{2}}(t_{i})\right]\phi_{ik} \\& = \Gamma_{\alpha_{2}}^{\xi}\sum\limits_{j = 1}^{m}\sum\limits_{k = 1}^{n}\left[R^{(\xi)}_{j}(0) R_{ij}^{(0,2)}t_{i}^{\xi-\alpha_{2}} +R_{ij}^{(0,2)}Q_{j}^{\alpha_{1}}(t_{i})\right]\phi_{ik}+f(t_{i},s_{l}). \end{eqnarray}$

(2.15)

The integral (2.12) is calculated by

$\begin{eqnarray} Q_{j}^{\alpha_{1}}(t_{i}) = \int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{1}-\xi}} : = \sum\limits_{i = 1}^{g}R^{(\xi+1)}_{i}(\tau_{i}^{\theta,\alpha_{1}})G_{i}^{\theta,\alpha_{1}}, \end{eqnarray}$

(2.16)

and

$\begin{eqnarray} Q_{j}^{\alpha_{2}}(t_{i}) = \int_{0}^{t_{i}} \frac{R^{(\xi+1)}_{j}(\tau)d\tau}{(t_{i}-\tau)^{\alpha_{2}-\xi}} : = \sum\limits_{i = 1}^{g}R^{(\xi+1)}_{i}(\tau_{i}^{\theta,\alpha_{2}})G_{i}^{\theta,\alpha_{2}}, \end{eqnarray}$

(2.17)

where $G_{i}^{\theta, \alpha_{1}}, G_{i}^{\theta, \alpha_{2}}$ are Gauss weights and $\tau_{i}^{\theta, \alpha_{1}}, \tau_{i}^{\theta, \alpha_{2}}$ are Gauss points with weights $(t_{i}-\tau)^{\xi-\alpha_{1}}, (t_{i}-\tau)^{\xi-\alpha_{2}}$ , see reference ^[22].

Equation systems (2.15) can be written as

$\begin{eqnarray} & \left[{R}^{(01)}\otimes{I}_{n}+\Gamma_{\alpha_{2}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{2}}}\right)\right]\left[\begin{array}{cc}{{\phi}_{11}}\\ {\vdots}\\ {{\phi}_{1n} } \\ {{\phi}_{n1}} \\{\vdots} \\{{\phi}_{mn}}\end{array}\right] \\& - \left[\mu_{0}\Gamma_{\alpha_{1}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{1}}}\right)\right]\left[\begin{array}{cc}{{\phi}_{11}}\\ {\vdots}\\ {{\phi}_{1n} } \\ {{\phi}_{n1}} \\{\vdots} \\{{\phi}_{mn}}\end{array}\right] = \left[\begin{array}{cc}{{f}_{11}}\\ {\vdots}\\ {{f}_{1n}} \\ {{f}_{n1}} \\{\vdots} \\{{f}_{mn}}\end{array}\right], \end{eqnarray}$

(2.18)

$I_{m}$ and $I_{n}$ are identity matrices, $\otimes$ is Kronecker product.

Then Eq (2.18) can be noted as

$\begin{equation} \left[{R}^{(01)}\otimes{I}_{n}+\Gamma_{\alpha_{2}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{2}}}\right)-\mu_{0}\Gamma_{\alpha_{1}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{1}}}\right)\right]\Phi = F \end{equation}$

(2.19)

and

$\begin{equation} R\Phi = F, \end{equation}$

(2.20)

with $R = {R}^{(01)}\otimes{I}_{n}+\Gamma_{\alpha_{2}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{2}}}\right)-\mu_{0}\Gamma_{\alpha_{1}}^{\xi} \left({M}_{1}^{(\xi0)}\otimes {I}_{n}+ {I}_{m}\otimes {Q^{\alpha_{1}}}\right)$ and $\Phi = [{{\phi}_{11}} {\dots} {{\phi}_{1n} } {\dots} {{\phi}_{n1}} {\dots} {{\phi}_{mn}}]^{T}, F = [{{f}_{11}} {\dots} {{f}_{1n} } {\dots} {{f}_{n1}} {\dots} {{f}_{mn}}]^{T}$ .

The boundary condition can be solved by substitution method, additional method or elimination method, see ^[26]. We adopt substitution method and additional method to deal with boundary condition.

3. Convergence rate of FC equation

In this part, error estimate of the FC equation is given with $r_n(s) = \sum\limits_{i = 1}^{n} r_{i}(s) \phi_{i}$ to replace $\phi(s)$ , where $r_{i}(s)$ is defined as (2.9) and $\phi_{i} = \phi(s_{i})$ . We also define

$\begin{eqnarray} e(s): = \phi(s)-r_n(s) = (s-s_{i}) \cdots(s-s_{i+d})\phi\left[s_{i}, s_{i+1}, \ldots, s_{i+d}, s\right], \end{eqnarray}$

(3.1)

see reference ^[18].

Then we have

Lemma 1. For $e(s)$ be defined by (3.1) and $\phi(s)\in C^{d+2}[a, b], d = 1, 2, \cdots$ , there

$\begin{equation} \left|e^{(k)}(s)\right| \leq C h^{d-k+1},k = 0,1,\cdots. \end{equation}$

(3.2)

For the FC equation, rational interpolation function of $\phi(t, s)$ is defined as $r_{mn}(t, s)$

$\begin{equation} r_{mn}(t,s) = \frac{ \sum\limits_{i = 1}^{m+d_{s}} \sum\limits_{j = 1}^{n+d_{t}} \frac{w_{i, j}}{\left(s-s_{i}\right)\left(t-t_{j}\right)} {\phi}_{i, j}}{ \sum\limits_{i = 1}^{m+d_{s}} \sum\limits_{j = 1}^{n+d_{t}} \frac{w_{i, j}}{\left(s-s_{i}\right)\left(t-t_{j}\right)}} \end{equation}$

(3.3)

where

$\begin{equation} w_{i, j} = (-1)^{i-d_{s}+j-d_{t}} \sum\limits_{k_{1} \in J_{i}}\prod\limits_{h_{1} = k_{1}, h_{1} \neq j}^{k_{1}+d_{s}}\frac{1}{\left|s_{i}-s_{h_{1}}\right|} \sum\limits_{k_{2} \in J_{i}} \prod\limits_{h_{2} = k_{2}, h_{2} \neq j}^{k_{2}+d_{t}} \frac{1}{\left|t_{j}-t_{h_{2}}\right|}. \end{equation}$

(3.4)

We define $e(t, s)$ be the error of $\phi(t, s)$ as

$\begin{eqnarray} e(t,s) :& = & \phi(t,s)-r_{mn}(t,s) \\ & = & \left(s-s_{i}\right) \cdots\left(s-s_{i+d_{s}}\right)\phi\left[s_{i}, s_{i+1}, \ldots, s_{i+d_1}, s;t\right] \\ &+&\left(t-t_{j}\right) \cdots\left(t-t_{j+d_{t}}\right)\phi\left[s; t_{j}, t_{j+1}, \ldots, t_{j+d_2}, t\right] \\ &-&\left(s-s_{i}\right) \cdots\left(s-s_{i+d_{s}}\right)\left(t-t_{j}\right) \cdots\left(t-t_{j+d_{t}}\right)\phi\left[s_{i}, s_{i+1}, \ldots, s_{i+d_1}, s; t_{j}, t_{j+1}, \ldots, t_{j+d_2}, t\right]. \end{eqnarray}$

(3.5)

With similar analysis of Lemma 1, we have

Theorem 1. For $e(t, s)$ defined as (3.5) and $\phi(t, s) \in C^{d_{s}+2}[a, b]\times C^{d_{t}+2}[0, T]$ , then we have

$\begin{equation} \left|e^{(k_{1},k_{2})}\left(s,t\right)\right| \leq C (h_{s}^{d_{s}-k_{1}+1}+h_{t}^{d_{t}-k_{2}+1}), k_{1},k_{2} = 0,1,\cdots. \end{equation}$

(3.6)

Let $\phi(s_{m}, t_{n})$ be the approximate function of $\phi(t, s)$ and $L$ to be bounded operator, there holds

$\begin{eqnarray} L \phi(t_{m},s_{n}) = f(t_{m},s_{n}) \end{eqnarray}$

(3.7)

and

$\begin{eqnarray} \lim\limits_{m,n\rightarrow \infty}L \phi(t_{m},s_{n}) = \phi(t,s). \end{eqnarray}$

(3.8)

Then we get

Theorem 2. For $\phi(t_{m}, s_{n}):L\phi(t_{m}, s_{n}) = \phi(t, s)$ and $L$ defined as (3.7), there

$|\phi(t,s)-\phi(t_{m},s_{n})|\le C(h^{d_{s}-1}+\tau^{d_{t}-1}).$

Proof. By

$\begin{eqnarray} \begin{array}{ll} &L\phi(t,s)-L\phi(t_{m},s_{n}) \\& = \frac{\partial \phi(t,s)}{\partial t}- \ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi(t,s)}{\partial s^2} +\mu_{0}\ _{0}C_{t}^{1-\alpha_{2}}\phi(t,s)-f(t,s) \\&- \left[\frac{\partial \phi(t_{m},s_{n})}{\partial t}-\ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi(t_{m},s_{n})}{\partial s^2} +\mu_{0}\ _{0}C_{t}^{1-\alpha_{2}}\phi(t_{m},s_{n})-f(t_{m},s_{n}) \right] \\& = \frac{\partial \phi}{\partial t}-\frac{\partial \phi}{\partial t}(t_{m},s_{n}) -\left[_{0}C_{t}^{1-\alpha_{1}} \frac{\partial^2 \phi}{\partial s^2}-\ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi}{\partial s^2}(s_{m},t_{n})\right] \\&+\mu_{0} \left[_{0}C_{t}^{1-\alpha_{2}}\phi(t,s)-\ _{0}C_{t}^{1-\alpha_{2}}(t_{m},s_{n})) \right] \\&-[f(t,s)-f(t_{m},s_{n})] \\&: = E_{1}(t,s)+E_{2}(t,s)+E_{3}(t,s)+E_{4}(t,s), \end{array} \end{eqnarray}$

(3.9)

here

$E_{1}(t,s) = \frac{\partial \phi}{\partial t}-\frac{\partial \phi}{\partial t}(t_{m},s_{n}),$

$E_{2}(t,s) = _{0}C_{t}^{1-\alpha_{1}} \frac{\partial^2 \phi}{\partial s^2}-\ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi}{\partial s^2}(t_{m},s_{n}),$

$E_{3}(t,s) = \mu_{0} \left[_{0}C_{t}^{1-\alpha_{2}}\phi(t,s)-\ _{0}C_{t}^{1-\alpha_{2}}(t_{m},s_{n})) \right],$

$E_{4}(t,s) = f(t,s)-f(t_{m},s_{n}).$

As for $E_{1}(t, s)$ , we get

$\begin{equation} \begin{array}{ll} E_{1}(t,s) = \left|\frac{\partial \phi}{\partial t}(t,s)-\frac{\partial \phi }{\partial t}(t_{m},s_{n})\right| \\ = \left|\frac{\partial \phi }{\partial t}(t,s)-\frac{\partial \phi }{\partial t}(t_{m},s)+\frac{\partial \phi }{\partial t}(t_{m},s)-\frac{\partial \phi }{\partial t}(t_{m},s_{n})\right| \\ \le \left|\frac{\partial \phi }{\partial t}(t,s)-\frac{\partial \phi }{\partial t}(t_{m},s)\right|+\left|\frac{\partial \phi }{\partial t}(t_{m},s)-\frac{\partial \phi }{\partial t}(t_{m},s_{n})\right| \\ \\ = \left| \frac{ \sum\limits_{i = 1}^{m-d_{s}} (-1)^{i}\frac{\partial \phi }{\partial t}[s_{i}, s_{i+1}, \ldots, s_{i+d_1}, s_{n},t]} { \sum\limits_{i = 1}^{m-d_{s}} \lambda_{i}(s)}\right| \\\\ \nonumber+ \left|\frac{ \sum\limits_{j = 1}^{n-d_{t}}(-1)^{j}\frac{\partial \phi }{\partial t}[ t_{j}, t_{j+1}, \ldots, t_{j+d_2}, s_{n},t_{m}]} { \sum\limits_{j = 1}^{n-d_{t}}\lambda_{j}(t)}\right| \\\\ = \left|\frac{\partial e }{\partial t}(t_{m},s)\right|+\left|\frac{\partial e}{\partial t}(t_{m},s_{n})\right|, \end{array} \end{equation}$

we get

$\begin{equation} |E_{1}(t,s)| \le C (h^{d_{s}}+\tau^{d_{t}}). \end{equation}$

(3.10)

As $E_{2}(t, s)$ , we have

$\begin{equation} \begin{array}{ll} E_{2}(t,s) = _{0}C_{t}^{1-\alpha_{1}} \frac{\partial^2 \phi}{\partial s^2}- \ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi}{\partial s^2}(t_{m},s_{n}) \\ = \Gamma_{\alpha_{2}}^{\xi}\left[\frac{\partial^{\xi+2} \phi(0,s)}{\partial t^{\xi}\partial s^2 }s^{\xi-\alpha_{2}}+\int_{0}^{t}\frac{\partial^{\xi+3} \phi(\tau,s)}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t-\tau)^{\alpha_{2}-\xi}}\right] \\ - \Gamma_{\alpha_{2}}^{\xi}\left[\frac{\partial^{\xi+2} \phi(0,s_{n})}{\partial t^{\xi}\partial s^2 }s_{n}^{\xi-\alpha_{2}}+\int_{0}^{t_{m}}\frac{\partial^{\xi+3}\phi(\tau,s_{n})}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t_{m}-\tau)^{\alpha_{2}-\xi}}\right] \\ = \Gamma_{\alpha_{2}}^{\xi}\left[\frac{\partial^{\xi+2} \phi(0,s)}{\partial t^{\xi}\partial s^2 }s^{\xi-\alpha_{2}}-\frac{\partial^{\xi+2} \phi(0,s_{n})}{\partial t^{\xi}\partial s^2 }s_{n}^{\xi-\alpha_{2}}\right] \\ + \Gamma_{\alpha_{2}}^{\xi}\left[\int_{0}^{t}\frac{\partial^{\xi+3} \phi(\tau,s)}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t-\tau)^{\alpha_{2}-\xi}}-\int_{0}^{t_{m}}\frac{\partial^{\xi+3}\phi(\tau,s_{n})}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t_{m}-\tau)^{\alpha_{2}-\xi}}\right] \end{array} \end{equation}$

(3.11)

and

$\begin{equation} \begin{array}{ll} |E_{2}(t,s)| \\ \le \left|\Gamma_{\alpha_{2}}^{\xi}\left[\frac{\partial^{\xi+2} \phi(0,s)}{\partial t^{\xi}\partial s^2 }s^{\xi-\alpha_{2}}-\frac{\partial^{\xi+2} \phi(0,s_{n})}{\partial t^{\xi}\partial s^2 }s_{n}^{\xi-\alpha_{2}}\right]\right| \\ + \left|\Gamma_{\alpha_{2}}^{\xi}\left[\int_{0}^{t}\frac{\partial^{\xi+3} \phi(\tau,s)}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t-\tau)^{\alpha_{2}-\xi}}-\int_{0}^{t_{m}}\frac{\partial^{\xi+3}\phi(\tau,s_{n})}{\partial \tau^{\xi+1} \partial s^{2}}\frac{d\tau}{(t_{m}-\tau)^{\alpha_{2}-\xi}}\right]\right| \\ \le |\Gamma_{\alpha_{2}}^{\xi}| \left|\frac{\partial^{\xi+2} \phi}{\partial t^{\xi} \partial s^{2}}(0,s)-\frac{\partial^{\xi+2} \phi }{\partial t^{\xi} \partial s^{2}}(0,s_{n})\right|+ |\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t,s)-\frac{\partial^{\xi+3} \phi }{\partial t^{\xi+1} \partial s^{2}}(t_{m},s_{n})\right| \\ : = E_{21}(t,s)+E_{22}(t,s) \end{array} \end{equation}$

(3.12)

where

$\begin{equation} \begin{array}{ll} E_{21}(t,s) = |\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+2} \phi}{\partial t^{\xi} \partial s^{2}}(0,s)-\frac{\partial^{\xi+2} \phi }{\partial t^{\xi} \partial s^{2}}(0,s_{n})\right|, \\ E_{22}(t,s) = |\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t,s)-\frac{\partial^{\xi+3} \phi }{\partial t^{\xi+1} \partial s^{2}}(t_{m},s_{n})\right|. \end{array} \end{equation}$

(3.13)

Now we estimate $E_{21}(t, s)$ and $E_{22}(t, s)$ part by part, for the second part we have

$\begin{equation} \begin{array}{ll} E_{22}(t,s) = |\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t,s)-\frac{\partial^{\xi+3} \phi }{\partial t^{\xi+1} \partial s^{2}}(t_{m},s_{n})\right| \\ = |\Gamma_{\alpha_{2}}^{\xi}| \left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t,s)-\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t_{m},s)+\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t_{m},s)-\frac{\partial^{\xi+3} \phi }{\partial t^{\xi+1} \partial s^{2}}(t_{m},s_{n})\right| \\ \le |\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t,s)-\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t_{m},s)\right|+|\Gamma_{\alpha_{2}}^{\xi}|\left|\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1} \partial s^{2}}(t_{m},s)-\frac{\partial^{\xi+3} \phi }{\partial t^{\xi+1} \partial s^{2}}(t_{m},s_{n})\right| \\ \\ = |\Gamma_{\alpha_{2}}^{\xi}| \left| \frac{ \sum\limits_{i = 1}^{m-d_{s}} (-1)^{i}\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1}\partial s^2}[s_{i}, s_{i+1}, \ldots, s_{i+d_1}, s_{n},t]} { \sum\limits_{i = 1}^{m-d_{s}} \lambda_{i}(s)}\right| \\\\ \nonumber+ |\Gamma_{\alpha_{2}}^{\xi}| \left|\frac{ \sum\limits_{j = 1}^{n-d_{t}}(-1)^{j}\frac{\partial^{\xi+3} \phi}{\partial t^{\xi+1}\partial s^2}[ t_{j}, t_{j+1}, \ldots, t_{j+d_2}, s_{n},t_{m}]} { \sum\limits_{j = 1}^{n-d_{t}}\lambda_{j}(t)}\right| \\\\ = |\Gamma_{\alpha_{2}}^{\xi}| \left|\frac{\partial^{\xi+3} e}{\partial t^{\xi+1}\partial s^2}(t_{m},s)\right|+ |\Gamma_{\alpha_{2}}^{\xi}| \left|\frac{\partial^{\xi+3} e}{\partial t^{\xi+1}\partial s^2}(t_{m},s_{n})\right|, \end{array} \end{equation}$

then we have

$\begin{equation} |E_{22}(t,s)|\le \left|\frac{\partial^{\xi+3} e}{\partial t^{\xi+1}\partial s^2}(t_{m},s)\right|+\left|\frac{\partial^{\xi+3} e}{\partial t^{\xi+1}\partial s^2}(t_{m},s_{n})\right|\le C (h^{d_{s}-\xi}+\tau^{d_{t}-1}). \end{equation}$

(3.14)

For $E_{21}(t, s)$ , we get

$\begin{equation} |E_{21}(t,s)|\le C (h^{d_{s}+1-\xi}+\tau^{d_{t}-1}). \end{equation}$

(3.15)

Similarly as $E_{2}(t, s)$ , for $E_{3}(t, s)$ we have

$\begin{equation} |E_{3}(t,s)| \le C (h^{d_{s}}+\tau^{d_{t}}). \end{equation}$

(3.16)

Combining (3.9), (3.14), (3.16) together, proof of Theorem 2 is completed.

4. Numerical examples

In this part, one example is presented to test the theorem. The nonuniform partition in this experiment defined as second kind of Chybechev point $s = \cos((0:m)'\pi/m), t = \cos((0:n)'\pi/n)$ .

Example 1. Consider the FC equation

$\frac{\partial \phi}{\partial t} = \ _{0}C_{t}^{1-\alpha_{1}}\frac{\partial^2 \phi}{\partial s^2}\phi(t,s) -\mu_{0}\ _{0}C_{t}^{1-\alpha_{2}}\phi(t,s)+f(t,s) ,0 \le s\le 1,0 \le t \le T,$

with the analysis solutions is

$\phi(t,s) = t^2\sin(\pi s),$

with the initial condition

$\phi(s, 0) = 0,$

and boundary condition

$\phi(0, t) = \phi(1, t) = 0,$

and

$f(t,s) = 2\left(t+\frac{\pi^2 t^{1+\alpha_{1}}}{\Gamma(2+\alpha_{1})} +\frac{ t^{1+\alpha_{2}}}{\Gamma(2+\alpha_{2})}\right)\sin(\pi s).$

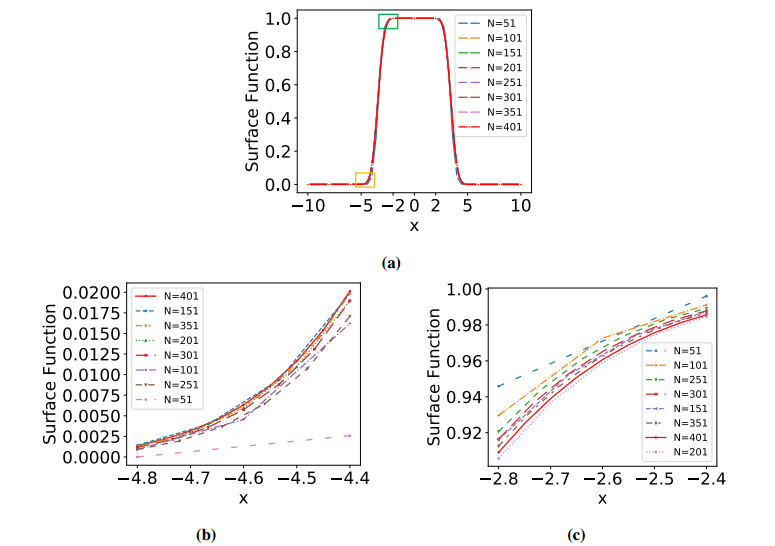
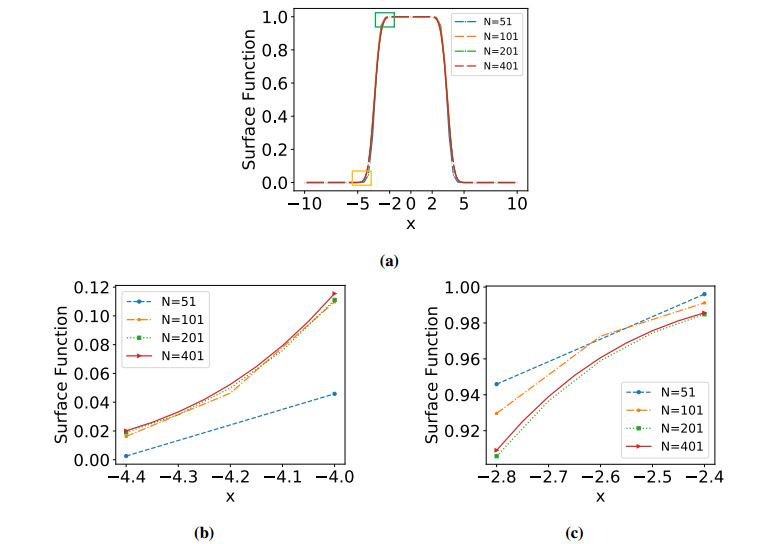
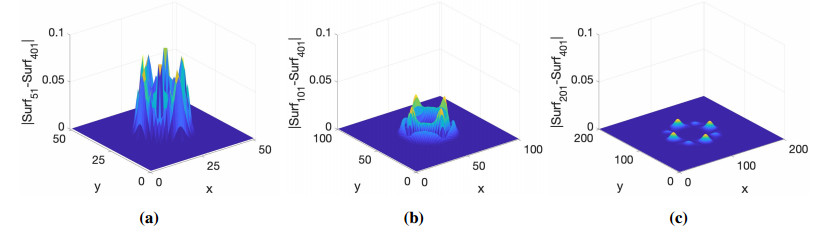
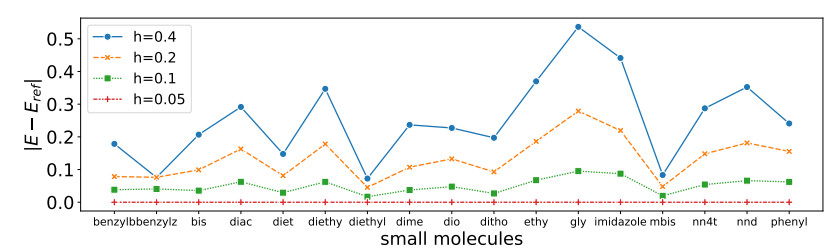
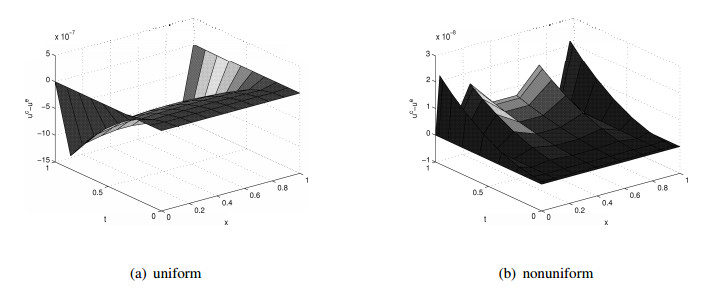
In and , errors of $m = n = 10$ , $[a, b] = [0, 1]$ and $m = n = 10, d_{t} = d_{s} = 7$ , $[a, b] = [0, 1]$ in Example 1. (a) uniform; (b) nonuniform for FC equation by rational interpolation collocation methods are presented, respectively. From the figure, we know that the precision can reach to $10^{-6}$ for both uniform and nonuniform partition.

Figure 1. Errors of

$m = n = 10$ ,

$[a, b] = [0, 1]$ in Example 1 (a) uniform; (b) nonuniform.

DownLoad: Full-Size Img PowerPoint

Figure 2. Errors of

$m = n = 10, d_{t} = d_{s} = 7$ ,

$[a, b] = [0, 1]$ in Example 1 (a) uniform; (b) nonuniform.

DownLoad: Full-Size Img PowerPoint

In , errors of the FC equation with $m = n = 10, \alpha_1 = \alpha_2 = 0.2$ for substitution methods and additional methods are presented, there are nearly no difference for the two methods. Additional method is more simple than substitution methods to add the boundary condition. In the following, we choosing the substitution method to deal with the boundary condition.

Table 1. Errors of FC equation with

$m = n = 10, \alpha_1 = \alpha_2 = 0.2$ .

	method of substitution		method of additional
	uniform	nonuniform	uniform	nonuniform
Larange	1.4662e-06	2.1919e-08	2.7900e-07	1.4310e-07
Rational	1.3038e-05	2.4541e-07	4.9788e-06	1.4310e-07

| Show Table

DownLoad: CSV

Errors of the FC equation for $\alpha_1 = 0.4, \alpha_{2} = 0.6, d_{t} = d_{s} = 5$ with $t = 0.1, 0.9, 1, 5, 10, 15$ are presented under the uniform and nonuniform in . As the time variable become from $0.5$ to $15$ , there are high accuracy for our methods. We can improve the accuracy by increasing $m, n$ or choosing the parameter $d_{t}, d_{s}$ approximately which means our methods is useful.

Table 2. Errors of FC equation for

$\alpha_1 = 0.4, \alpha_{2} = 0.6, d_{t} = d_{s} = 5$ .

	uniform	nonuniform	uniform	nonuniform
$t$	$(12, 12)$	$(12, 12)$	$(12, 12) d_{t}=d_{s}=5$	$(12, 12) d_{t}=d_{s}=5$
0.5	2.1021e-11	3.8250e-09	6.8506e-06	1.6436e-06
1	9.0394e-13	4.4206e-10	4.6667e-06	7.8141e-07
5	6.1833e-12	5.6655e-08	2.3777e-04	4.2230e-05
10	1.0094e-12	8.5622e-07	1.9813e-04	1.5634e-05
15	3.5397e-12	1.8827e-05	8.5498e-04	8.2551e-05

| Show Table

DownLoad: CSV

In , errors of $\alpha_1 = 0.01, 0.1, 0.3, 0.5, 0.9, 0.99$ under uniform with $m = n = 10, d_{t} = 5, d_{s} = 5$ with $\alpha_2 = 0.1, 0.4, 0.6, 0.8, 0.99$ are presented under the uniform partition. From the table, we know that for different $\alpha_1, \alpha_2$ our methods have high accuracy with little number $m$ and $n$ . In the following table, numerical results are presented to test our theorem. From and , error of uniform for $\alpha_1 = \alpha_2 = 0.2, d_{s} = 5$ with different $d_{t}$ are given, the convergence rate is $O(h^{d_{t}})$ . From , with space variable uniform for $\alpha_1 = \alpha_2 = 0.2, d_{t} = 5$ , the convergence rate is $O(h^{7})$ , we will investigate in future paper. For and , the errors of Chebyshev partition for $s$ and $t$ are presented. For $d_{t} = 5$ , the convergence rate is $O(h^{d_{s}})$ in , while in , the convergence rate is $O(h^{d_{t}})$ which agrees with our theorem.

Table 3. Errors of

$\alpha_1$ under uniform with

$m = n = 10, d_{t} = 5, d_{s} = 5$ .

$\alpha_1$	$\alpha_2=0.1$	$\alpha_2=0.4$	$\alpha_2=0.6$	$\alpha_2=0.8$	$\alpha_2=0.99$
0.01	1.0153e-04	1.0246e-04	1.0300e-04	1.0346e-04	1.0384e-04
0.1	1.2753e-05	1.2865e-05	1.2930e-05	1.2987e-05	1.3033e-05
0.3	2.7464e-05	2.7704e-05	2.7845e-05	2.7971e-05	2.8074e-05
0.5	4.5746e-06	4.6152e-06	4.6399e-06	4.6609e-06	4.6794e-06
0.9	9.0295e-06	9.1193e-06	9.1240e-06	9.2142e-06	9.2479e-06
0.99	1.8981e-06	1.8247e-06	1.5293e-06	1.9193e-06	2.0670e-06

| Show Table

DownLoad: CSV

Table 4. Errors of uniform for

$\alpha_1 = \alpha_2 = 0.2, d_{s} = 5$ .

$m, n$	$d_{t}=2$		$d_{t}=3$		$d_{t}=4$		$d_{t}=5$
8	1.3626e-02		6.9619e-03		2.0708e-03		9.8232e-04
10	9.6780e-03	1.5332	3.4354e-03	3.1653	6.9542e-04	4.8900	3.2829e-04	4.9117
12	7.0485e-03	1.7389	1.9408e-03	3.1320	2.9186e-04	4.7621	1.3132e-04	5.0255
14	5.4466e-03	1.6725	1.2017e-03	3.1097	1.4211e-04	4.6686	6.0148e-05	5.0654

| Show Table

DownLoad: CSV

Table 5. Errors of uniform for

$\alpha_1 = \alpha_2 = 0.2, d_{t} = 5$ .

$m, n$	$d_{s}=2$		$d_{s}=3$		$d_{s}=4$
8	4.9495e-04		4.9492e-04		4.9486e-04
10	1.0051e-04	7.1443	1.0053e-04	7.1431	1.0053e-04	7.1426
12	2.7700e-05	7.0690	2.7711e-05	7.0679	2.7714e-05	7.0673
14	9.4272e-06	6.9921	9.4315e-06	6.9917	9.4314e-06	6.9925

| Show Table

DownLoad: CSV

Table 6. Errors of non-uniform partition with

$\alpha_1 = \alpha_2 = 0.2, d_{t} = 5$ .

$m, n$	$d_{s}=2$		$d_{s}=3$		$d_{s}=4$
8	2.8113e-05		2.8110e-05		2.8108e-05
10	2.1197e-05	1.2654	2.1196e-05	1.2652	2.1195e-05	1.2651
12	6.6990e-06	6.3180	6.6989e-06	6.3178	6.6988e-06	6.3176
14	1.6712e-06	9.0069	1.6712e-06	9.0068	1.6712e-06	9.0067

| Show Table

DownLoad: CSV

Table 7. Errors of non-uniform partition

$\alpha_1 = \alpha_2 = 0.2, d_{s} = 5$ .

$m, n$	$d_{t}=2$		$d_{t}=3$		$d_{t}=4$		$d_{t}=5$
8	3.1539e-02		8.7995e-03		2.1930e-03		3.3004e-04
10	2.4329e-02	1.1632	4.0288e-03	3.5010	2.7133e-04	9.3648	2.2278e-04	1.7613
12	1.5223e-02	2.5716	1.9127e-03	4.0859	9.5194e-05	5.7449	5.1702e-05	8.0116
14	1.1407e-02	1.8721	1.1143e-03	3.5049	3.5772e-05	6.3493	1.1369e-05	9.8255

| Show Table

DownLoad: CSV

In the following table, $\alpha_{1} = 0.4, \alpha_{2} = 0.6$ is chosen to present numerical results. From and , error of uniform partition $d_{t} = 5$ with different $d_{s}$ are given, the convergence rate is $O(h^{7})$ . From , with space variable $s, d_{s} = 5$ , the convergence rate is $O(h^{d_{t}})$ which agrees with our theorem.

Table 8. Errors of uniform with

$\alpha_{1} = 0.4, \alpha_{2} = 0.6, d_{t} = 5$ .

$m, n$	$d_{s}=2$		$d_{s}=3$		$d_{s}=4$
8	4.9427e-04		4.9426e-04		4.9414e-04
10	1.0035e-04	7.1455	1.0041e-04	7.1427	1.0041e-04	7.1413
12	2.7639e-05	7.0720	2.7674e-05	7.0684	2.7684e-05	7.0669
14	9.3984e-06	6.9977	9.4153e-06	6.9942	9.4254e-06	6.9895

| Show Table

DownLoad: CSV

Table 9. Errors of uniform with

$\alpha_{1} = 0.4, \alpha_{2} = 0.6, d_{s} = 5$ .

$m, n$	$d_{t}=1$		$d_{t}=2$		$d_{t}=3$		$d_{t}=4$
8	1.3587e-02		6.9513e-03		2.0677e-03		9.8084e-04
10	9.6497e-03	1.5334	3.4314e-03	3.1637	6.9462e-04	4.8884	3.2791e-04	4.9102
12	7.0259e-03	1.7404	1.9389e-03	3.1311	2.9157e-04	4.7613	1.3118e-04	5.0249
14	5.4269e-03	1.6752	1.2005e-03	3.1096	1.4198e-04	4.6682	6.0090e-05	5.0648

| Show Table

DownLoad: CSV

For and , the errors of Chebyshev partition for non-uniform with $\alpha_{1} = 0.4, \alpha_{2} = 0.6$ are presented. For $d_{t} = 5$ , the convergence rate is $O(h^{7})$ in , while in , the convergence rate is $O(h^{d_{t}})$ which agrees with our theorem.

Table 10. Errors of non-uniform with

$\alpha_{1} = 0.4, \alpha_{2} = 0.6, d_{s} = 5$ .

$m, n$	$d_{t}=1$		$d_{t}=2$		$d_{t}=3$		$d_{t}=4$
8	3.1481e-02		8.7825e-03		2.1876e-03		3.2930e-04
10	2.4263e-02	1.1671	4.0219e-03	3.5000	2.7124e-04	9.3553	2.2231e-04	1.7606
12	1.5185e-02	2.5704	1.9076e-03	4.0912	9.5106e-05	5.7481	5.1649e-05	8.0057
14	1.1373e-02	1.8751	1.1117e-03	3.5026	3.5733e-05	6.3504	1.1365e-05	9.8211

| Show Table

DownLoad: CSV

Table 11. Errors of non-uniform with

$\alpha_{1} = 0.4, \alpha_{2} = 0.6, d_{t} = 5$ .

$m, n$	$d_{s}=2$		$d_{s}=3$		$d_{s}=4$
8	2.8065e-05		2.8059e-05		2.8056e-05
10	2.1156e-05	1.2665	2.1154e-05	1.2660	2.1153e-05	1.2656
12	6.6875e-06	6.3168	6.6874e-06	6.3164	6.6873e-06	6.3161
14	1.6693e-06	9.0033	1.6693e-06	9.0031	1.6693e-06	9.0030

| Show Table

DownLoad: CSV

5. Concluding remarks

In this paper, BRIM was used to solve the (1+1) dimensional FC equation that is presented. For fractional-order PDEs, the convergence order is seriously affected by the orders of fractional derivatives. By fractional integration, the singularity of the fractional derivative of the FC equation can be changed to nonsingular integral, with adding one order to the derivatives of density function. So there are no effects on the orders of fractional derivatives. The singularity of fractional derivative is overcome by the integral to density function from the singular kernel. For the arbitrary fractional derivative, the new Gauss formula is constructed to calculated it simply. For the Diriclet boundary condition, the FC equation is changed to the discrete FC equation and the matrix equation of it is given. In the future, the FC equation with Nuemann condition can be solved by BRIM, and high dimensional FC equation can also be studied by our methods.

Acknowledgments

The work of Jin Li was supported by Natural Science Foundation of Shandong Province (Grant No. ZR2022MA003).

Conflicts of interest

The authors declare that they have no conflicts of interest.

References

[1]	N. A. Baker, D. Sept, S. Joseph, M. J. Holst, J. A. McCammon, Electrostatics of nanosystems: application to microtubules and the ribosome, Proc. Natl. Acad. Sci., 98 (2001), 10037–10041. doi: 10.1073/pnas.181342398
[2]	B. Honig, A. Nicholls, Classical electrostatics in biology and chemistry, Science, 268 (1995), 1144–1149. doi: 10.1126/science.7761829
[3]	A. Nicholls, B. Honig, A rapid finite difference algorithm, utilizing successive over-relaxation to solve the Poisson-Boltzmann equation, J. Comput. Chem., 12 (1991), 435–445. doi: 10.1002/jcc.540120405
[4]	B. Lee, F. M. Richards, Interpretation of protein structure: estimation of static accessibility, J. Molecular Bio., 55 (1973), 379–400.
[5]	F. M. Richards, Areas, volumes, packing and protein structure, Ann. Rev. Biophys. Bioeng., 6 (1977), 151–176.
[6]	J. A. Grant, B. Pickup, A Gaussian description of molecular shape, J. Phys. Chem., 99 (1995), 3503–3510. doi: 10.1021/j100011a016
[7]	S. Ahmed-Ullah, S. Zhao, Pseudo-transient ghost fluid methods for the Poisson-Boltzmann equation with a two-component regularization, Appl. Math. Comput., 380 (2020), 125267.
[8]	W. Geng, S. Zhao, A two-component matched interface and boundary (MIB) regularization for charge singularity in implicit solvent, J. Comput. Phys., 351 (2017), 25–39. doi: 10.1016/j.jcp.2017.09.026
[9]	P. Bates, G.W. Wei, S. Zhao, Minimal molecular surfaces and their applications, J. Comput. Chem., 29 (2008), 380–391. doi: 10.1002/jcc.20796
[10]	P. Bates, Z. Chen, Y. H. Sun, G. W. Wei, S. Zhao, Geometric and potential driving formation and evolution of biomolecular surfaces, J. Math. Biol., 59 (2009), 193–231. doi: 10.1007/s00285-008-0226-7
[11]	C. Arghya, Z. Jia, L. Li, S. Zhao, E. Alexov, Reproducing the ensemble average polar solvation energy of a protein from a singlestructure: Gaussian-based smooth dielectric function for macromolecular modeling, J. Chem. Theor. Comput., 14 (2018), 1020–1032. doi: 10.1021/acs.jctc.7b00756
[12]	T. Hazra, S. Ahmed-Ullah, S. Wang, E. Alexov, S. Zhao, A super-Gaussian Poisson-Boltzmann model for electrostatic solvation free energy calculation: smooth dielectric distribution for protein cavities and in both water and vacuum states, J. Math. Bio., 79 (2019), 631–672. doi: 10.1007/s00285-019-01372-1
[13]	L. Li, C. Li, Z. Zhang, E. Alexov, On the dielectric "constant" of proteins: smooth dielectric function formacromolecular modeling and its implementation in DelPhi, J. Chem. Theory Comput., 9 (2013), 2126–2136. doi: 10.1021/ct400065j
[14]	A. Chakravorty, S. Pandey, S. Pahari, S. Zhao, E. Alexov, Capturing the effects of explicit waters in implicit electrostatics modeling: Qualitative justification of Gaussian-based dielectric models in DelPhi, J. Chem. Inf. Modeling, 60 (2020), 2229–2246. doi: 10.1021/acs.jcim.0c00151
[15]	A. Abrashkin, D. Andelman, H. Orland, Dipolar Poisson-Boltzmann equation: ions and dipoles close to charge interfaces, Phy. Rev. Lett., 99 (2007), 077801. doi: 10.1103/PhysRevLett.99.077801
[16]	L. T. Cheng, J. Dzubiella, J. A. McCammon, B. Li, Application of the level-set method to the solvation of nonpolar molecules, J. Chem. Phys., 127 (2007), 084503. doi: 10.1063/1.2757169
[17]	S. Dai, B. Li, J. Liu, Convergence of phase-field free energy and boundary force for molecular solvation, Arch. Ration. Mech. Anal., 227 (2018), 105–147. doi: 10.1007/s00205-017-1158-4
[18]	Y. Zhao, Y. Y. Kwan, J. Che, B. Li, J. A. McCammon, Phase-field approach to implicit solvation of biomolecules with Coulomb-field approximation, J. Chem. Phys., 139 (2013), 024111. doi: 10.1063/1.4812839
[19]	L. Chen, M. J. Holst, J. Xu, The finite element approximation of the nonlinear Poisson-Boltzmann equation, SIAM J. Numer. Anal., 45 (2007), 2298–2320. doi: 10.1137/060675514
[20]	W. Deng, J. Xu, S. Zhao, On developing stable finite element methods for pseudo-time simulation of biomolecular electrostatics, J. Comput. Appl. Math., 330 (2018), 456–474. doi: 10.1016/j.cam.2017.09.004
[21]	J. A. Grant, B. Pickup, A. Nicholls, A smooth permittivity function for Poisson-Boltzmann solvation methods, J. Comput. Chem., 22 (2001), 608–640. doi: 10.1002/jcc.1032
[22]	M. J. Schnieders, N. A. Baker, P. Ren, J. W. Ponder, Polarizable atomic multipole solutes in a Poisson-Boltzmann continuum, J. Chem. Phys., 126 (2002), 124114.
[23]	R. Egan, F. Gibou, Geometric discretization of the multidimensional Dirac delta distribution - Application to the Poisson equationwith singular source terms, J. Comput. Phys., 346 (2017), 71–90. doi: 10.1016/j.jcp.2017.06.003
[24]	W. Rocchia, E. Alexov, B. Honig, Extending the applicability of the nonlinear Poisson-Boltzmann equation: Multiple dielectric constants and multivalent ions, J. Phys. Chem. B, 105 (2001), 6507–6514.
[25]	W. Rocchia, S. Sridharan, A. Nicholls, E. Alexov, A. Chiabrera, B. Honig, Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: applications to the molecular systems and geometric objects, J. Comput. Chem., 23 (2002), 128–137.
[26]	P. Benner, V. Khoromskaia, B. Khoromskij, C. Kweyu, M. Stein, Computing electrostatic potentials using regularization based on the range-separated tensor format, preprint, arXiv: 1901.09864v1.
[27]	Q. Cai, J. Wang, H. K. Zhao, R. Luo, On removal of charge singularity in Poisson-Boltzmann equation, J. Chem. Phys., 130 (2009), 145101. doi: 10.1063/1.3099708
[28]	I. L. Chern, J. G. Liu, W. C. Wang, Accurate evaluation of electrostatics for macromolecules in solution, Methods Appl. Anal., 10 (2003), 309–328.
[29]	W. Geng, S. Yu, G. W. Wei, Treatment of charge singularities in implicit solvent models, J. Chem. Phys., 127 (2007), 114106. doi: 10.1063/1.2768064
[30]	M. Holst, J. A. McCammon, Z. Yu, Y. C. Zhou, Y. Zhu, Adaptive finite element modeling techniques for the Poisson-Boltzmann equation I, Commun. Comput. Phys., 11 (2012), 179–214. doi: 10.4208/cicp.081009.130611a
[31]	B. Khoromskij, Range-separated tensor decomposition of the discretized Dirac delta and elliptic operator inverse, J. Comput. Phys., 401 (2020), 108998. doi: 10.1016/j.jcp.2019.108998
[32]	D. Xie, New solution decomposition and minimization schemes for Poisson-Boltzmann equation in calculation of biomolecular electrostatics, J. Comput. Phys., 275 (2014), 294–309. doi: 10.1016/j.jcp.2014.07.012
[33]	Z. Zhou, P. Payne, M. Vasquez, N. Kuhn, M. Levitt, Finite-difference solution of the Poisson-Boltzmann equation: complete elimination of self-energy, J. Comput. Chem., 11 (1996), 1344–1351.
[34]	A. Lee, W. Geng, S. Zhao, Regularization methods for the Poisson-Boltzmann equation: comparison and accuracy recovery, J. Comput. Phys., in press, 2021.
[35]	C. Xue, S. Deng, Unified construction of Green's functions for Poisson's equation in inhomogeneous media with diffuse interfaces, J. Comput. Appl. Math., 326 (2017), 296–319. doi: 10.1016/j.cam.2017.06.007
[36]	S. Wang, A. Lee, E. Alexov, S. Zhao, A regularization approach for solving Poisson's equation with singular charge sources and diffuse interfaces, Appl. Math. Lett., 102 (2020), 106144. doi: 10.1016/j.aml.2019.106144
[37]	M. Holst, The Poisson–Boltzmann Equation: Analysis and Multilevel Numerical Solution, Ph.D thesis, UIUC, 1994.
[38]	W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P. Flannery, Numerical Recipes in Fortran: The Art of Scientific Computing, 2nd edition, Cambridge University Press, 1992.
[39]	A. Nicholls, D. L. Mobley, P. J. Guthrie, J. D. Chodera, V. S. Pande, Predicting small-molecule solvation free energies: An informal blind test for computational chemistry, J. Med. Chem. 51 (2008), 769–-779.
[40]	S. Zhao, Operator splitting ADI schemes for pseudo-time coupled nonlinear solvation simulations, J. Comput. Phys., 257 (2014), 1000–1021. doi: 10.1016/j.jcp.2013.09.043
[41]	C. Bertonati, B. Honig, E. Alexov, Poisson-Boltzmann calculations of nonspecific salt effects on protein-protein binding free energies, Biophy. J., 92 (2007), 1891–1899. doi: 10.1529/biophysj.106.092122
[42]	J. Zha, L. Li, A. Chakravorty, and E. Alexov, Treating ion distribution with Gaussian-based smooth dielectric function in DelPhi, J. Comput. Chem., 38, 1974-1979, (2017).

This article has been cited by:

1.	Jin Li, Yongling Cheng, Barycentric rational interpolation method for solving 3 dimensional convection–diffusion equation, 2024, 304, 00219045, 106106, 10.1016/j.jat.2024.106106
2.	Jin Li, Yongling Cheng, Spectral collocation method for convection-diffusion equation, 2024, 57, 2391-4661, 10.1515/dema-2023-0110

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)