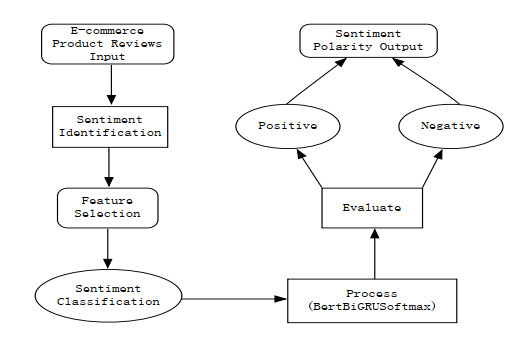
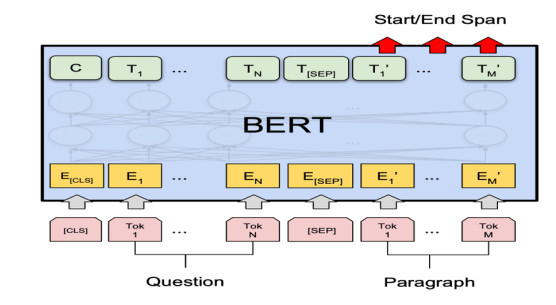
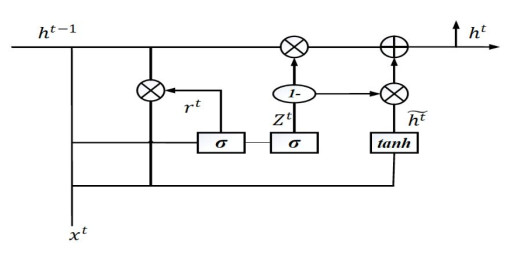
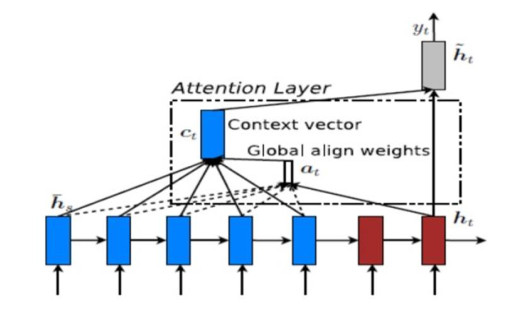
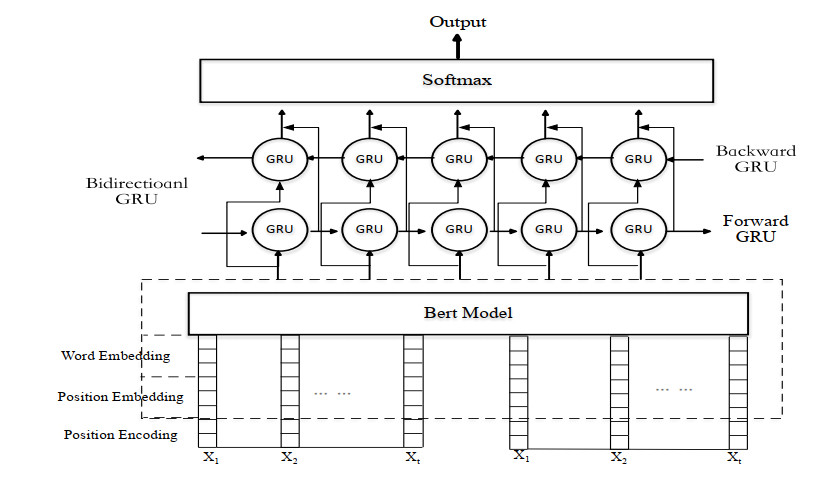
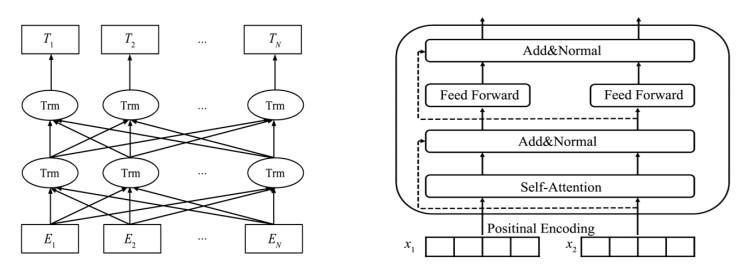
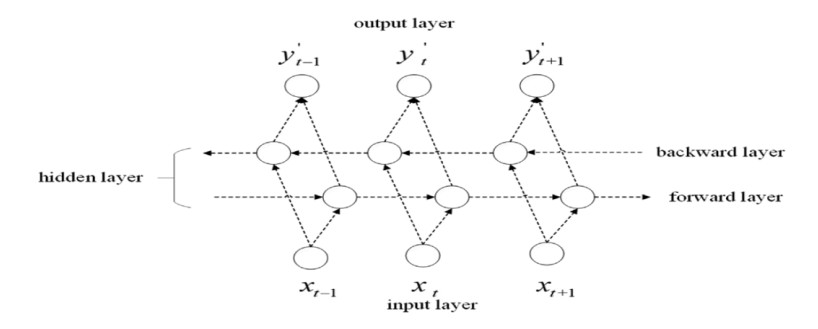
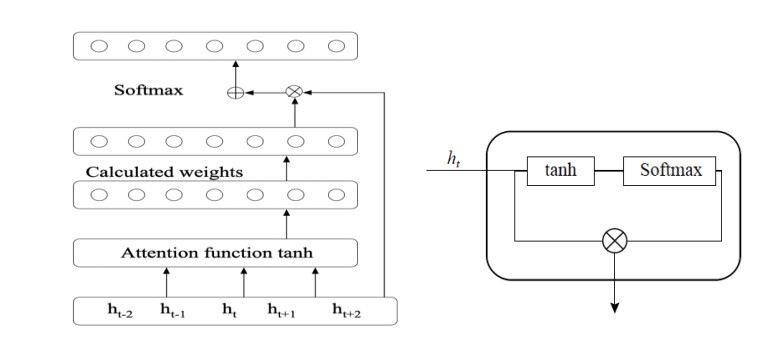
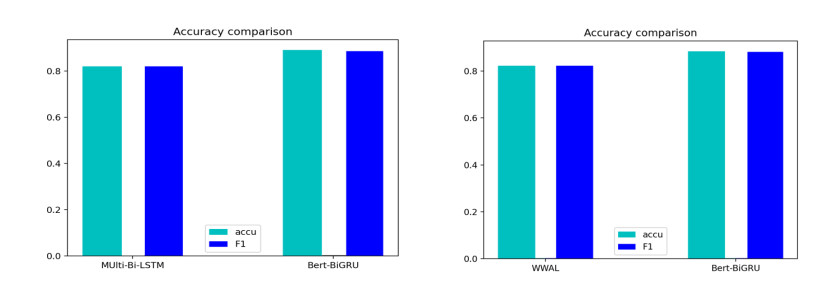
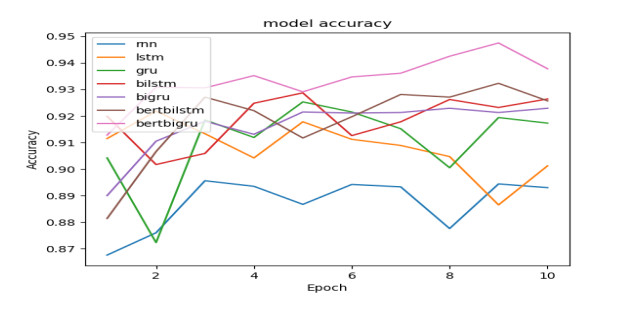
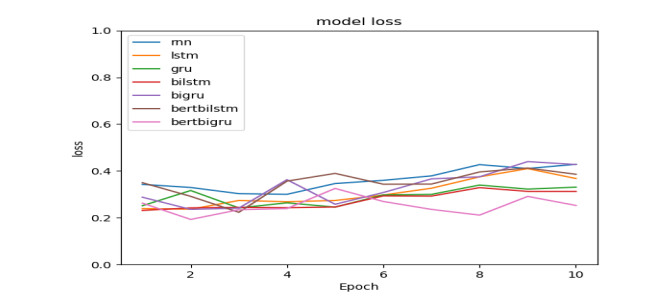
Sentiment analysis for e-commerce product reviews by deep learning model of Bert-BiGRU-Softmax

1.   Introduction and definitions

The function class $\mathcal{H}\left(E\right)$ is a collection of the function $f$ which are holomorphic in the open unit disc

Let $\mathcal{A}_{p}$ denote the class of all functions $f$ which are analytic and $p$-valent in the open unit disk $E$ and has the Taylor series expansion of the form

For briefly, we write as:

Moreover, $\mathcal{S}$ represents the subclass of $\mathcal{A}$ which is univalent in open unit disk $E$. Further in area of Geometric Function Theory, numerous researchers offered their studies for the class of analytic function and its subclasses as well. The role of geometric properties is remarkable in the study of analytic functions, for instance convexity, starlikeness, close-to-convexity. A function $f\in \mathcal{A}_{p}$ is known as $p$-valently starlike $\left(\mathcal{S}_{p}^{\ast }\right)$ and convex $\left(\mathcal{K}_{p}\right),$ whenever it satisfies the inequality

and

Moreover, a function $f(z)\in \mathcal{A}_{p}$, is said to be $p$-valently starlike function of order $\alpha,$ written as $f(z)\in \mathcal{S} _{p}^{\ast }\left(\alpha \right),$ if and only if

Similarly, a function $f(z)\in \mathcal{A}_{p}$, is said to be $p$-valently convex functions of order $\alpha,$ written as $f(z)\in$ $\mathcal{K} _{p}(\alpha)$, if and only if

for some $0\leq \alpha < p.$ In particular, we have

and

The convolution (Hadamard product) of $f(z)$ and $g(z)$ is defined as:

where

Let $\mathcal{P}$ denote the well-known Carathéodory class of functions $m$, analytic in the open unit disk $E$ of the form

and satisfy

The quantum (or $q$-) calculus has a great important because of its applications in several fields of mathematics, physics and some related areas. The importance of $q$-derivative operator ($D_{q})$ is pretty recongnizable by its applications in the study of numerous subclasses of analytic functions. Initially in 1908, Jackson ^[14] defined the $q$ -analogue of derivative and integral operator as well as provided some of their applications. Further in ^[11] Ismail et al. gave the idea of $q$ -extension of class of $q$-starlike functions after that Srivastava ^[37] studied $q$-calculus in the context of univalent functions theory, also numerous mathematician studied $q$-calculus in the context of geometric functions theory$.$ Kanas and Raducanu ^[17] introduced the $q$ -analogue of Ruscheweyh differential operator and Arif et al. ^[3,4] discussed some of its applications for multivalent functions while Zhang et al. in ^[50] studied $q$-starlike functions related with generalized conic domain $\Omega _{k, \alpha }.$ By using the concept of convolution Srivastava et al. ^[40] introduced $q$-Noor integral operator and studied some of its applications, also Srivastava et al. published set of articles in which they concentrated class of $q$-starlike functions from different aspects (see ^{[24,41,42,44,46,47]}). Additionally, a recently published survey-cum-expository review article by Srivastava ^[38] is potentially useful for researchers and scholars working on these topics. For some more recent investigation about $q$ -calculus we may refer to ^{[1,18,19,20,21,22,23,25,31,32,33,34,38,39,45]}.

For better understanding of the article we recall some concept details and definitions of the $q$-difference calculus. Throughout the article we presume that

Definition 1. (^[10]) The $q$-number $[t]_{q}$ for $q\in (0, 1)$ is defined as:

Definition 2. The $q$-factorial $[n]_{q}!$ for $q\in (0, 1)$ is defined as:

Definition 3. The $q$-generalized Pochhammer symbol $[t]_{n, q}$, $t\in \mathbb{C},$ is defined as:

And the $q$-Gamma function be defined as:

Definition 4. The $q$-integral of any function $f(z)$ was defined be Jackson ^[15] as follows:

provided that the series on right hand side converges absolutely.

Definition 5. (^[14]) For given $q\in \left(0, 1\right),$ the $q$-derivative operator or $q$-difference operator of $f$ is defined by:

Now we extend the idea of $q$-difference operator to a function $f$ given by (1.1) from the class $\mathcal{A}_{p}$ as:

Definition 6. For $f\in \mathcal{A}_{p},$ let the $q$-derivative operator (or $q$ -difference operator) be defined as:

We can observe that for $p = 1,$ and $q\rightarrow 1-$ in (1.4) we have

Definition 7. An analytic function $f(z)\in \mathcal{S}_{p}^{\ast }\left(\alpha, q\right)$ of $p$-valent $q$-starlike functions of order $\alpha$ in $E,$ if $f(z)\in \mathcal{A}_{p}$, satisfies the condition

for some $0\leq \alpha < p.$

Definition 8. An analytic function $f(z)\in \mathcal{K}_{p}(\alpha, q)$ of $p$-valent $q$ -convex functions of order $\alpha$ in $E,$ if $f(z)\in \mathcal{A}_{p}$, satisfies the condition

for some $0\leq \alpha < p.$

Remark 1. Let $f(z)\in \mathcal{A}_{p},$ it follows that

and

Remark 2. By putting value of parameters $\alpha$ and $p$ we can get some new subclasses of analytic functions:

Remark 3. By taking $q\rightarrow 1-,$ then we obtain two known subclasses $\mathcal{S} _{p}^{\ast }\left(\alpha \right)$ and $\mathcal{K}_{p}(\alpha)$ of $p$ -valently starlike and convex functions of order $\alpha,$ introduced by Hayami and Owa in ^[12].

Let $n\in \mathbb{N}_{0}$ and $j\in \mathbb{N}$. The $j$th Hankel determinant was introduced and studied in ^[29]:

where $a_{1} = 1$. The Hankel determinant $H_{2}(1)$ represents a Fekete-Szeg ö functional $\left \vert a_{3}-a_{2}^{2}\right \vert$. This functional has been further generalized as $\left \vert a_{3}-\mu a_{2}^{2}\right \vert$ for some real or complex number $\mu$ and also the functional $\left \vert a_{2}a_{4}-a_{3}^{2}\right \vert$ is equivalent to $H_{2}(2)$ (see ^[16]). Babalola ^[5] studied the Hankel determinant $H_{3}(1)$ (see also ^[43]). The symmetric Toeplitz determinant $T_{j}(n)$ is defined as follows:

so that

and so on. The problem of finding the best possible bounds for $\left \vert \left \vert a_{n+1}\right \vert -\left \vert a_{n}\right \vert \right \vert$ has a long history (see ^[8]). In particular, several authors ^[13,44] have studied $T_{j}(n)$ for several classes.

For our simplicity, we replace $n = n+p-1,$ into $(1.5),$ then the symmetric Toeplitz determinant $T_{j}(n)$ can be written as:

so that

Hankel determinants generated by perturbed Gaussian, Laguerre and Jacobi weights play an important role in Random Matrix Theory, since they represent the partition functions for the perturbed Gaussian, Laguerre and Jacobi unitary ensembles, see for example ^{[7,26,27,28,49]}.

2.   A set of Lemmas

In order to discuss our problems, we need some lemmas.

Lemma 1. (see ^[8]). If a function $m(z) = 1+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}\in \mathcal{P}$, then

The inequality is sharp for

Lemma 2. If a function $m(z) = [p]_{q}+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}$ satisfies the following inequality

for some $\alpha,$ $\left(0\leq \alpha < p\right)$, then

The result is sharp for

Proof. Let

Noting that $l(z)\in \mathcal{P}$ and using Lemma 1, we see that

which implies

Remark 4. When $q\rightarrow 1-$, then Lemma 2, reduces to the lemma which was introduced by Hayami et al. ^[12].

Lemma 3. (^[36]) If $m$ is analytic in $E$ and of the form (1.2), then

and

for some $x,$ $z\in \mathbb{C}$, with $\left \vert z\right \vert \leq 1,$ and $\left \vert x\right \vert \leq 1.$

By virtue of Lemma 3, we have

Lemma 4. If $m(z) = [p]_{q}+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}$ satisfy $\Re(m(z) > \alpha$, for some $\alpha$ $(0\leq \alpha < p),$ then

and

for some $x,$ $z\in \mathbb{C}$, with $\left \vert z\right \vert \leq 1,$ and $\left \vert x\right \vert \leq 1.$

Proof. Since $l(z) = \frac{m(z)-\alpha }{[p]_{q}-\alpha } = 1+\sum \limits_{n = 1}^{\infty }\frac{c_{n}}{[p]_{q}-\alpha }z^{n}\in \mathcal{P}$, replacing $c_{2}$ and $c_{3}$ by $\frac{c_{2}}{[p]_{q}-\alpha }$and $\frac{ c_{3}}{[p]_{q}-\alpha }$ in Lemma 3, respectively, we immediately have the relations of Lemma 4.

Remark 5. When $q\rightarrow 1-$, then Lemma 4, reduces to the lemma which was introduced by Hayami et al. ^[12].

Lemma 5. (^[9]) Let the function $m(z)$ given by (1.2) having positive real part in $E$. Also let $\mu \in \mathbb{C},$ then

3.   Main results

Theorem 1. Let the function $f$ given by (1.1) belong to the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, then

where $\Lambda _{2}$ is given by (3.6).

Proof. Let $\ f\in \mathcal{S}^{\ast }(\alpha, q),$ then their exist a function $\mathcal{P}(z) = [p]_{q}+\sum \limits_{n = 1}^{\infty }c_{n}z^{n}$ such that $\Re (m(z)) > \alpha$ and

which implies that

Therefore, we have

where $n\geq p+1, a_{p} = 1,$ $c_{0} = \left[p\right] _{q}.$ From (3.1), we have

where

By using Lemma 2, we obtain the required result.

Theorem 2. Let an analytic function $f$ given by (1.1) be in the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, then

where

Proof. A detailed calculation of $T_{3}(p+1)$ is in order.

where $a_{p+1},$ $a_{p+2},$ and $a_{p+3 }$ is given by (3.2), (3.3) and (3.4).

Now if $f\in \mathcal{S}^{\ast }(\alpha, q),$ then we have

where $\Omega _{1},$ $\Omega _{2},$ $\Omega _{3},$ is given by (3.9), (3.10) and (3.11).

We need to maximize $\left \vert a_{p+1}^{2}-2a_{p+2}^{2}+a_{p+1}a_{p+3}\right \vert$ for $f\in \mathcal{S} ^{\ast }(\alpha, q),$ so by writing $a_{p+1},$ $a_{p+2},$ $a_{p+3}$ in terms of $c_{1}, c_{2}, c_{3},$ with the help of (3.2), (3.3) and (3.4), we get

Finally applying Lemmas 2 and 5 along with (3.14) and (3.15), we obtained the required result.

For $q\rightarrow 1-,$ $p = 1$ and $\alpha = 0,$ we have following known corollary.

Corollary 1. (^[2]). Let an analytic function $f$ be in the class $\mathcal{S} ^{\ast }$, then

Theorem 3. If an analytic function $f$ given by (1.1) belongs to the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, then

Proof. Making use of (3.2), (3.3) and (3.4), we have

where

By using Lemma 3 and we take $\Upsilon = 4\left(\left[p\right] _{q}-\alpha \right) ^{2}-c_{1}^{2}$ and $\mathcal{Z} = \left(1-\left \vert x\right \vert ^{2}\right) z$. Without loss of generality we assume that $c = c_{1}$, $\left(0\leq c\leq 2\left(\left[p\right] _{q}-\alpha \right) \right),$ so that

where

Taking the modulus on (3.16) and using triangle inequality, we find that

Now, trivially we have

on $[0, 1]$, which shows that $\mathcal{G}(c, \left \vert x\right \vert)$ is an increasing function in an interval $[0, 1],$ therefore maximum value occurs at $x = 1$ and Max $\mathcal{G}(c, \left \vert 1\right \vert) = \mathcal{G }(c).$

and

Hence, by putting $\Upsilon = 4-c_{1}^{2}$ and after some simplification, we have

We consider $\mathcal{G}^{^{\prime }}(c) = 0$, for optimum value of $\mathcal{G }(c)$, which implies that $c = 0$. So $\mathcal{G}(c)$ has a maximum value at $c = 0$. Hence the maximum value of $\mathcal{G}(c)$ is given by

Which occurs at $c = 0$ or

Hence, by putting $\lambda _{4} = \frac{\mathcal{D}}{4(\left[p\right] _{q}-\alpha)^{2}}$ and $\mathcal{D} = \frac{1}{\left(\left[p+2\right] _{q}- \left[p\right] _{q}\right) ^{2}}$ in (3.17) and after some simplification, we obtained the desired result.

For $q\rightarrow 1-,$ $p = 1$ and $\alpha = 0,$ we have following known corollary.

Corollary 2. (^[16]). If an analytic function $f$ belongs to the class $\mathcal{S} ^{\ast }$, then

3.1.   Fekete–Szegö problem

Theorem 4. Let $f$ be the function given by (1.1) belongs to the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, $0\leq \alpha < p,$ then

where

Proof. From (3.2) and (3.3) and we can suppose that $c_{1} = c$ $\left(0\leq c\leq 2(\left[p\right] _{q}-\alpha)\right),$ without loss of generality we derive

where

Applying the triangle inequality, we deduce

where

If $q\rightarrow 1-$ in Theorem 4, we thus obtain the following known result.

Corollary 3. (^[12]). Let $f$ be the function given by (1.1) belongs to the class $\mathcal{S}_{p}^{\ast }(\alpha)$, $0\leq \alpha < p,$ then

3.2.   Applications of our main results

In this section, firstly we recall that the $q$-Bernardi integral operator for multivalent functions $\mathcal{L(}f\mathcal{) = B}_{p, \beta }^{q}$ given in ^[35] as:

Let $f\in \mathcal{A}_{p},$ then $\mathcal{L}$:$\mathcal{A}_{p}\rightarrow \mathcal{A}_{p}$ is called the $q$-analogue of Benardi integral operator for multivalent functions defined by $\mathcal{L(}f\mathcal{) = B}_{q, \beta }^{q}$ with $\beta > -p,$ where, $\mathcal{B}_{q, \beta }^{q}$ is given by

The series given in (3.19) converges absolutely in $E$.

Remark 6. For $q\rightarrow 1-$, then the operator $\mathcal{B}_{p, \beta }^{q}$ reduces to the integral operator studied in ^[48].

Remark 7. For $p = 1$, we obtain the $q$-Bernardi integral operator introduced in ^[30].

Remark 8. If $q\rightarrow 1-$ and $p = 1$, we obtain the familiar Bernardi integral operator studied in ^[6].

Theorem 5. If $f$ is of the form (1.1), belongs to the class $\mathcal{S} _{p}^{\ast }(\alpha, q)$, and

where $\mathcal{B}_{p, \beta }^{q}$ is the integral operator given by (3.18), then

where

Proof. The proof follows easily by using (3.19) and Theorem 1.

Theorem 6. Let an analytic function $f$ given by (1.1) be in the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, in addition $\mathcal{B}_{p, \beta }^{q}$ is the integral operator defined by (3.18) and is of the form (3.19), then

where

Proof. The proof follows easily by using (3.19) and Theorem 2.

Theorem 3. If an analytic function $f$ given by (1.1) belongs to the class $\mathcal{S}_{p}^{\ast }(\alpha, q)$, in addition $\mathcal{B}_{p, \beta }^{q}$ is the integral operator is defined by (3.18) and is of the form (3.19), then

Theorem 8. Let $f$ be the function given by (1.1) belongs to the class $\mathcal{ S}_{p}^{\ast }(\alpha, q)$, in addition $\mathcal{B}_{p, \beta }^{q}$ is the integral operator defined by (3.18) and is of the form (3.19), then

where

and $\Lambda _{2}$ is given by (3.6).

4.   Conclusions

Motivated by a number of recent works, we have made use of the quantum (or $q$-) calculus to define and investigate new subclass of multivalent $q$ -starlike functions in open unit disk $E$. We have studied about Hankel determinant, Toeplitz matrices, Fekete–Szegö inequalities. Furthermore we discussed applications of our main results by using $q$-Bernardi integral operator for multivalent functions. All the results that have discussed in this paper can easily investigate for the subclass of meromorphic $q$-convex functions $(\mathcal{K}_{p}(\alpha, q))$ of order $\alpha$ in $E$, respectively.

Basic (or $q$-) series and basic (or $q$-) polynomials, especially the basic (or $q$-) hypergeometric functions and basic (or $q$-) hypergeometric polynomials, are applicable particularly in several diverse areas (see ^[38], p328). Moreover, in this recently-published survey-cum expository review article by Srivastava ^[38], the so called $(p, q)$-calculus was exposed to be a rather trivial and inconsequential variation of the classical $q$-calculus $($see for details ^[38], p340$).$

By this observation of Srivastava in ^[38], we can make clear link between the $q$-analysis and $(p, q)$-analysis and the results for $q$ -analogues which we have included in this paper for $0 < q < 1,$ can be easily transformed into the related results for the $(p, q)$-analogues with $(0 < q < p\leq 1)$.

Acknowledgements

This work is supported by the program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region under the Grant NJYT-18-A14, the Natural Science Foundation of Inner Mongoliaof the people's Republic of China under Grant 2018MS01026, the Natural Science Foundation of the people's Republic of China under Grant 11561001.

Conflict of interest

The authors declare that they have no competing interests.