In the ecological literature, mutual interference (self-interference) or competition among predators (CAP) to effect the harvesting of their prey has been modeled through different mathematical formulations. In this work, the dynamical properties of a Leslie-Gower type predation model is analyzed, incorporating one of these forms, which is described by the function g(y)=yβ, with 0<β<1. This function g is not differentiable for y=0, and neither the Jacobian matrix of the system is not defined in the equilibrium points over the horizontal axis (x−axis). To determine the nature of these points, we had to use a non-standard methodology. Previously, we have shown the fundamental properties of the Leslie-Gower type model with generalist predators, to carry out an adequate comparative analysis with the model where the competition among predators (CAP) is incorporated.
The main obtained outcomes in both systems are:
(ⅰ) The unique positive equilibrium point, when exists, is globally asymptotically stable (g.a.s), which is proven using a suitable Lyapunov function.
(ⅱ) There not exist periodic orbits, which was proved constructing an adequate Dulac function.
1.
Introduction
The dynamic relationship between predators and their prey has been and will continue to be one of the dominant themes in Theoretical Ecology (Mathematical Ecology) and particularly in Population Dynamics. This is due to its universal existence [1] and because the more exhaustive knowledge of this interaction allows a better understanding of the behavior of food chains or trophic webs [2,3].
It is well known that the first predator-prey model was proposed by the Italian mathematician Vito Volterra [4,5] in a well-known monograph published in 1926 [6], being described by an autonomous nonlinear ordinary differential equation system (ODEs). This model coincided with a two-dimensional model for biochemical interactions previously proposed by the American mathematician-physicist Alfred J. Lotka; for this, the ODE system is known by the name of Lotka-Volterra model [2,3,5,7].
The main dynamic characteristic of this first predation model is that the only point of positive equilibrium is a center [8,9], that is, all the paths are concentric closed orbits around that point [2,3,5,7]. This implies that the population sizes of predators and their prey would permanently oscillate around that point for any initial condition [3,7]. This behavior of the system solutions was strongly questioned after its formulation because in nature no predator-prey interactions with these characteristics are found [2,3].
Based on Volterra's work, different proposals came up to face and resolve the various objections made [10]. One of the first proposals to solve some of the objections to the Lotka-Volterra model was raised by the Russian biologist Georgii F. Gause (1910–1986). In 1934 he proposed a model that takes into account the intraspecific competition on the prey population [11], replacing the Malthusian prey growth incorporated in the Lotka-Volterra model, by the logistic growth function (also called the Verhulst-Pearl equation [4]).
Another important subsequent result is the Theorem proposed by the Russian mathematician Andrei N. Kolmogorov in 1936 [2,5]. In this, conditions for a general ODE system describing a predator-prey interaction are established, to ensure the existence of a single stable periodic solution [12] (mathematically, an attractor limit cycle [8,9]). For the phenomenon of oscillations of population sizes of prey and predators, there is sufficient evidence in nature, which are called ecologically stable cycles [12].
A different alternative is presented in the model formulated by the British ecologist Patrick Holt Leslie in 1948 [13], which does not fit the Lotka-Volterra model scheme [3]. Unlike the Gause-type compartmentalized models [3,14], based on a principle of mass or energy transfer [1], the Leslie model characterizes because the predator growth equation is of the logistic type, just like the prey growth equation [3,4].
Leslie assumed that the conventional environmental carrying capacity of the predators Ky is proportional to the abundance of prey x [2], i.e., it is assumed that Ky=K(x)=nx [2,3,15,16,17].
However, when the predator is a generalist [3] and there is no favorite prey available, predators can switch to a different food source. In this case, the predator environmental carrying capacity can be expressed as K(x)=nx+c, where the parameter c>0 indicates the amount of alternative food available to predators [18,19]. Thus, a modified Leslie-Gower or a Leslie-Gower scheme is obtained [20,21].
On the other hand, it is known that the action of predators in the interaction is called the functional response of predators or consumption function [14]; it refers to the change in prey density attacked per unit time per predator, when prey density changes [14]. They are classified into various types, depending on the size of the prey population or the size of both populations, and there are various mathematical ways to describe them.
Based on laboratory experiments, the Canadian ecologist Crawford S. Holling (1930–2019) in 1959 [22] described three types of saturated functions, which he considered only dependent on the size of the prey population (prey-dependent functional response).
Later, in 1984, Robert J. Taylor [23], proposed the non-monotonic functional response, usually used to describe the ecological phenomenon called group defense formation [23] and others, as the agammaegation and inhibition for microorganism interactions. Prey-dependent functional responses are classified as Holling-type, Ⅰ, Ⅱ, Ⅲ, and Ⅳ, and there are various mathematical ways to describe each type [2,3]. For example, in the so-called May-Holling-Tanner model [2,3,17,20,24,25], which is derived from the Leslie model, the hyperbolic functional response is considered [18,25]. Functional responses, depending on both populations have also been proposed, such as the Beddington-DeAngelis [26,27], the ratio-dependent [3], etc.
In the Leslie model, the functional response of the predator is expressed by the linear function h(x)= qx, also used in the classic Lotka-Volterra model [2,3]. Nevertheless, this functional response does not correspond to any of the types proposed by Holling, since it is not bounded.
In this work, the ecological phenomenon called interference or competition among predators (CAP) is incorporated in the Leslie model, which means that two or more predators are bothered when capturing prey and therefore the prey can avoid predation [28].
A similar situation can be assumed in open access bioeconomic models when fishermen go to the same place with their boats to harvesting fish [29,30]; the boats can collide with each other and even cause agammaessions between the crews (making shots, breaking fishing implements, etc.), as has happened in various places on the planet [29,30].
There are three ways to mathematically represent CAP. In this work we will assume the expression formulated by the Canadian mathematician Herbert I. Freedman in 1979 [31], modifying the assumption of the usual models to express the functional response. Freedman formulated a change in the predation function in Gause-type models, proposing the expression:
power function, where β is the constant of mutual interference, and h(x) is the functional response of the predator dependent only on the prey population. He also included a second mathematical form for the CAP in the Gause type models by adding the negative term m(y)=−ey2 in the equation that describes the growth of predators [5].
The power function appears also proposed in the bioeconomic literature [29] as a particular case of a more general function called Cobb-Douglas type production function [30,32,33], described by G(x,y)=qxαyβ, with 0<α,β<1 and q>0.
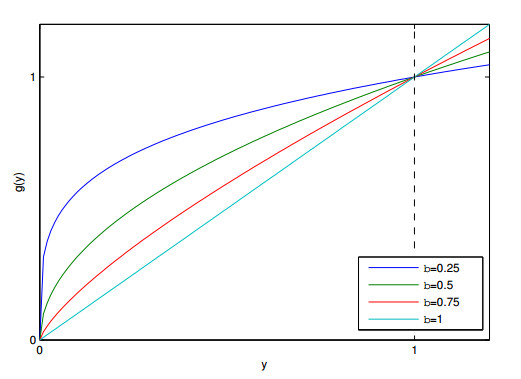
In Figure 1, we see the behavior of the function g(y)=yβ, with 0<β<1, for different values of β.
It can observe that if β →0, the graphic of the function grows more abruptly. This means that the competition among predators is more intense, whereas for large values of β (β →1) the competition decreases. When β=1, we have the well-known Leslie-Gower model [34].
As we will show, the function g(x,y) has no strong implication on the dynamics of the system, such as happens when is incorporated in the Volterra model [31].
Other alternative mathematical ways to model CAP are: the Beddington-DeAngelis functional response [3,26,27], dependent on both population sizes, and the addition of a quadratic term in the growth equation of predators, which is incorparated mainly in Gause-type models [5,28,31]. Nonetheless, according to our knowledge, the modified Leslie-Gower type model presented here considering a power function describing CAP has not been previously analyzed.
This work is focused on the analysis of two models derived from the Leslie-Gower model, assuming both have an alternative food, but in one of them, we consider a predator compete with each other; the differences with the models in which other ways to describe CAP are considered will be show.
The rest of the article is organized as follows: In Section 2 we will present the modified Leslie-Gower type model considering alternative food and its basic properties. In Section 3 we will show the main properties of the model assuming CAP and an alternative supply to this species and in Section 4 we will discuss the consequences of CAP on the modified Leslie-Gower type model.
2.
The Leslie model with generalist predators
The Leslie-Gower model considering a generalist or alternating food for predators is described by the following Kolmogorov-type system [14,36]:
where x=x(t) and y=y(t) indicate the population sizes of prey and predator, respectively, at any time t≥0, subject to x(0)>0 and y(0)>0, measured in number of individuals, biomass or density per unit area or volume, with σ=(r,k,q,s,n,c)∈R6+. The parameters have the ecological meanings described in the following Table 1:
The parameter c>0 characterizes to generalist predators [20,21], because in the absence of his favorite prey (when x=0), it searches for an alternative food source [3,19]. If c=0, the original model formulated by Leslie in 1948 is obtained [13,34] and the predator is said to be a specialist [3]
According to Turchin [3], when the favorite prey population size is low, generalist predators should focus on other prey species. When the favorite prey population size is high, predators will switch to hunting it, because it becomes profitable for them to do so [3].
In some articles, the parameter c>0 is assumed to measure the extent to which the environment provides protection to predators, but we prefer the annotated meaning in Table 1.
Another form to describe the behavior of generalist predators is using a Holling Ⅲ functional response [5,2,3]. In [35] a Gause type predator-prey model was studied, considering a sigmoid functional response and complex dynamics were obtained as bi-stability, limit-cycles, and bifurcations.
It should be noted that in model (1),
(ⅰ) In the absence of favorite prey, when x=0, the growth of the predator population is assured.
(ⅱ) If y> rq(1−xK), then dxdt<0 and the prey population becomes extinct.
(ⅲ) If y>nx+c, then dydt<0 and the predator population goes to extinction.
The domain of the system (1) or vector field Gσ(x,y) is the set
Unlike the original Leslie-Gower model, system (1) is defined at x=0 and has four equilibrium points or singularities. They are: (0,0), (K,0), (0,c) and (xe,nxe+c) with xe=(r−cq)Kr+nqK.
Formally for this last equilibrium point, we have the following lemma
Lemma 1. The equilibrium point (xe,nxe+c)
i) belongs to the interior of the first quadrant and is unique, if and only if, c<rq,
ii) coincides with the equilibrium point (0,c), if and only if, c=rq,
iii) is outside of the first quadrant, if and only if, c>rq.
Proof. The equilibrium point (xe,nxe+c) is at the intersection of the isoclines and the abscissa xe satisfies the equations
Both are straight lines.
f1 is a decreasing function and passes through the points (0,rq) and (K,0),
f2 is an increasing function that passes through the point (0,c).
Thus, the graphs of f1(x) and f2(x) intersect inside the first quadrant Int(R+0)2, if and only if, c<rq
Clearly, if c=rq, the equilibrium point (xe,nxe+c) coincides with the point (0,c), and is outside the first quadrant, if and only if, c>rq.
To determine the nature of the hyperbolic equilibrium points we require the Jacobian matrix, which is
Thus, it is defined for every point (x,y)∈Ω.
2.1. Main properties of the system (1)
The main properties of the modified Leslie-Gower model described by the system (1) or vector field Gσ(x,y) are shown below.
Lemma 2. The set
is a positively invariant region.
Proof. Clearly, the coordinate axes are invariant sets
Let's consider x=K; then, we get that
Thus, dxdt<0. Then, the orbits with an initial condition outside the set Γ will enter into it; the trajectories with initial conditions within the set Γ cannot leave it, whatever the sign of dydt.
Remark 3. We note that the subregion
is also a positively invariant region for system (1).
Lemma 4. The solutions are uniformly bounded.
Proof. We will use the comparison theorem for differential inequalities [41].
From the first equation we have
We also know that
Let L=max{x(0),K}; thus x(t)≤L, for all t≥0.
Also, 0<y<nx+c.
Let's consider the variable w(x,y)= x+1sy. Clearly, w(x,y)>0, for all t≥0.
Then,
Now consider the sum of dwdt and σw, with σ>0, obtaining
Thus,
Let M= rK4+σ x+(σs+1)y; hence
which is a first order differential inequality.
Applying the comparison theorem for differential inequalities (Page 30 in [41]), we get that
For t=0, we obtain that w(0)≤M+H; that is, H≥ w(0)−M.
Then, there is m∈N such that H≤m (w(0)−M);
therefore, w(t)et≤Met+m(w(0)−M), i.e., w(t)≤M+m(w(0)−M)e−t
Therefore, when t→∞ then w(t)≤M.
Thus, the solutions are bounded.
Remark 5. The previous result ensures that there is a set
which is the region where all the solutions of the system (1) with initial conditions in Ω are confined [36].
This property ensures that the model is well-posed [1].
Therefore, many predators and a small prey population size may coexist; but this would be a contradictory situation if the predators are specialists.
Lemma 6. The equilibrium point (0,0) is a hyperbolic repeller for all parameter values.
Proof. The Jacobian matrix evaluated at point (0,0) is
Thus,
Applying the trace and determinant theorem [7,37], the thesis is held.
Lemma 7. The singularity (K,0) is hyperbolic saddle point for any set of parameters.
Proof. The Jacobian matrix evaluated at point (K,0) is
and detDGσ(K,0)=−rs(c+nK)<0.
According to the trace and determinant theorem [7,37] the thesis is obtained.
Theorem 8. The equilibrium point (0,c) is
(ⅰ) a hyperbolic saddle point, if and only if, c<rq.
(ⅱ) a non-hyperbolic saddle point, if and only if, c=rq.
(ⅲ) a hyperbolic attractor, if and only if, c>rq.
Proof. The Jacobian matrix evaluated at point (0,c) is
Thus, detDGσ(0,0)=−s(r−cq), whose sign depends on the factor b=r−cq.
(ⅰ) r−cq>0 implies that (0,c) is a hyperbolic saddle point.
(ⅱ) r−cq=0 implies that (0,c) is a non-hyperbolic saddle point.
(ⅲ) r−cq<0 it has that (0,c) is a hyperbolic attractor.
Theorem 9. When the equilibrium point or singularity (xe,nxe+c)
(i) belongs to the first quadrant, then is locally asymptotically stable (l.a.s).
(ii) coincides with the point (0,c) is a non-hyperbolic attractor.
Proof. The Jacobian matrix evaluated at point (x,nx+c) is
Then,
Replacing x by xe=(r−cq)Kr+nqK it has
which can be positive, negative or zero.
Besides, trDGσ(x,nx+c)= Kr−Ks−2rx−Kcq−KnqxK.
It has that, trDGσ(xe,nxe+c)=−rs+r2−cqr+Knqsr+Knq<0, if and only if, c<rq.
Hence, (xe,nxe+c) is locally asymptotically stable, for c<rq.
If r−cq=0 implies that (xe,nxe+c) conincides with (0,c) is a non-hyperbolic attractor.
Remark 10. Considering the Poincaré-Bendixson Theorem [8,39], if the equilibrium point (xe,nxe+c) is locally asymptotically stable (l.a.s.) in the bidimensional system (1), then it is globally asymptotically stable (g.a.s.). This result is reinforced by building a suitable Lyapunov function [36,40] and also proving that there are no cycles [12], which is shown in the following theorems.
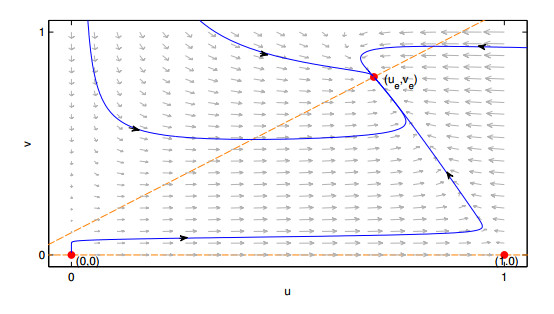
Theorem 11. The equilibrium point (xe,nxe+c) is globally asymptotically stable (g.a.s.).
Proof. Because (1) is a system of Kolmogorov type describing a continuous-time predator-prey model, we will consider the Lyapunov function [38] described by
which is similar to a proposal in [36] and in [40], with c1 and c2>0, to be determined.
Clearly V(x,y)>0, for all (x,y) ∈Int(R+0) and x≠xe e y≠ye [36].
Deriving the function V with respect to t, we have:
Factoring for the respective derivatives, we get:
Replacing it has
or else,
Remembering that(xe,ye) satisfies the equations of both isoclines we have
Reordered we become
Expanding the products we have
Choosing c2=Kqsnc1, finally it is obtained that
Thus V(x,y) is a suitable Lyapunov function [36,38,40], since it is defined negative.
Then the equilibrium point (xe,nxe+c) is g.a.s, by Lyapunov's stability Theorem [38].
Theorem 12. There are not periodic solutions.
Proof. We will use the Bendixson-Dulac criterion [29] considering the function g(x,y)=1xy>0 for all (x,y) at inside the first quadrant, Int(R+0)2.
Considering the sum
where M(x,y)=(r(1−xK)−qy)x and N(x,y)=s(1−ynx+c)y,
it gets that
Then, S(x,y)<0 for all (x,y) at inside the first quadrant.
Therefore, by the Bendixson-Dulac criterion [8,29,39], there are nonconstant periodic solutions (or limit cycles) within the first quadrant.
3.
Model with CAP and generalist predator
The second model to study is described by the Kolmogorov-type system [14,36]:
where x=x(t), y=y(t), are the population sizes. The parameter 0<β<1, indicates the level of interference between predators and the other parameters have the same meanings given above in Table 1. Therefore, λ= (r,K,q,s,n,c,β)∈R6+×]0,1[.
The equilibrium points are (0,0), (K,0), (0,c) and (xe,nxe+c), where xe satisfies the isoclines equation
The graphic of g1 represents a decreasing curve that passes through the points (0,(rq)1β) and (K,0).
The graph of g2 represents an increasing straight line through the point (0,c).
Then the isoclines intersect, if and only if, c<(rq)1β.
To determine the nature of the hyperbolic equilibrium points we require the Jacobian matrix, which is
but it is not defined for points on the x−axis, i.e., when y=0. Therefore, we must use an alternative method to obtain the type of stability of the points (0,0) and (K,0).
In order to simplify the calculations, it is convenient to reduce system (2) to a normal form; we will follow the methodology used in [15,17,42,43] making a change of variable and a time rescaling, obtaining the following:
Theorem 13. System (2) is topologically equivalent to the Kolmogorov-type system [14,36]:
where η=(Q,S,C,β)∈R3+×]0,1[. Its domain is
with Q=q(nK)βr, S=sr y C=cnK.
Proof. Let us x=Ku and y=nKv; hence dxdt=Kdudt and dydt=nKdvdt.
Replacing and factoring in system (2) we have:
Making a time rescaling (independent variable), given by τ=rut; by the chain rule we get
Replacing in the vector fieldVλ(x,y) it has
Defining Q=q(nK)βr, S=sr and C=cnK, we get the system (3).
Remark 14. We have built the function φ:¯Ω×R⟶Ω×R given by
The Jacobian matrix of transformation φ is
and detDφ(u,v,τ)=nK2r(u+cnK)>0.
Then, φ is a diffeomorphism [8,9] preserving the time orientation, whereby the vector field Xλ is topologically equivalent to the vector field Uη(u,v)=φ∘Xλ(x,y).
In this way, system (3) is a continuous extension of system (2).
The equilibrium points of the system (3) are (0,0), (1,0), (0,C) and (ue,ue+C), with ue determined by the intersection of the isoclines
The Jacobian matrix of system (3) is
with,
according to the derivative of the triple product. We note that DUη(u,v) is not defined at the points (0,0) and (1,0), due to the entry DUη(u,v)12=−Qβuvβ−1(u+C) is not defined for v=0.
3.1. Main results
The main properties of the system (3) or vector field Uη(u,v) and therefore of the modified Leslie-Gower model described by the system (2) are:
Lemma 15. The set
is a positively invariant region.
Proof. Clearly, coordinate axes are invariant sets
Considering u=1, we obtain that dxdt=−Q(1+C)vβ.
Therefore, solutions with an initial condition outside the set ˉΓ will enter to the set ˉΓ and the solutions within the set will not leave it, whatever the sign of the equation dvdτ=S(1+C−v)v.
Remark 16. The set Γ={(x,y)∈R2:0≤x≤K, y≥0} is a positively invariant region (2).
The subregion
is also a positively invariant region for the system (3).
Lemma 17. The solutions are bounded.
Proof. Using the Poincaré compactification [39].
Let us X=uv and Y=1v; clearly, if v→∞, the point (0,∞) is associated with the point (0,0).
Thus, u=XY and v=1Y, obtaining
Replacing, it get
Factoring by 1Y in each equation becomes
The latter system is not defined for Y=0. To solve this difficulty, a rescaling of the time given by T=1Y2τ is considered. So by chain rule, it has
Applying these relationships to the vector field ˉUη(X,Y) we obtain
Clearly, the Jacobian matrix evaluated at point (0,0) is not defined since the derivative of the term QXY1−β respect to Y is ddY(QXY1−β)=QXYβ(1−β).
To overcome this difficulty, we will use the method of the blowing-up directional with the change of variables X=pq2, Y=q. Hence, dXdT=q2dpdT+2pqdqdT, dYdT=dqdT; thus, dpdT=1q2(dXdT−2pqdqdT).
By replacing and factoring the new system is obtained
whose Jacobian matrix evaluated at point (0,0) is the null matrix.
Rescaling now by changing κ=qT, we get
The Jacobian matrix of the vector field ˇUη(p,q) is
with
and
Then, DˇUη(0,0)=(−S 00 S).
Therefore, the point (0,0) of the vector field ˇUη(p,q) is a hyperbolic saddle, attractor by the x−axis and repeller by the y−axis. Then there is a non-hyperbolic chair of the vector fields ˆUη(p,q) and ˉUη(X,Y).
So the point (0,∞) is a non-hyperbolic saddle of the compacted vector field of Uη(u,v).
Thus, the trajectories are bounded.
Remark 18. As in the previous model, this property ensures that the model is well-posed.
[1].
As in the model without CAP, for the existence of the equilibrium point (ue,ue+C) we have:
Lemma 19. The equilibrium point (ue,ue+C)
(i) belongs to the first quadrant Int(R+0) and is unique, if and only if, CQβ<1,
(ii) coincides with the point (0,C), if and only if, CQβ=1,
(iii) is outside the first quadrant, if and only if, CQβ>1.
Proof. The equilibrium point (ue,ue+C) is at the intersection of the isoclines and the abscissa xe satisfies the equations
We have that:
g1 is a decreasing function and passes through the points (0,(1Q)β) y (1,0),
g2 is an increasing linear function that passes through the point (0,C).
Therefore, the graphics of g1(u) and g2(u) intersect inside the first quadrant Int(R+0)2, if and only if, C<(1Q)β.
Since the Jacobian matrix is not defined when v=0, it considers the change of variable given by w=vβ.
Thus, dvdτ= 1βw1β−1dwdτ. Replacing the second equation of the system (2) we obtain the new system
with η=(Q,S,C,β)∈R3+×]0,1[. The equilibrium points are (0,0), (1,0), (0,Cβ) and (u∗e,(u∗e+C)β) with ue determined by the intersection of the isoclines
or else, ue satisfies the equation
The isocline h2(u) is a straight line that passes through the points (0,1Q) and (1.0), while the isocline h1(u) is an increasing curve concave downwards, passing through the point (0,Cβ). See Figure 2.
Clearly, there is an intersection between both curves, if and only if, Cβ<1Q, i.e., if and only if, QCβ<1.
The Jacobian matrix of system (4) is:
with DWσ(u,w)11=u(u+C)(−1)+(1−u−Qw)(u+C)+(1−u−Qw)u.
Lemma 20. The equilibrium point (0,0) is a repeller.
Proof. The Jacobian matrix evaluated in (0,0) is:
Then, detDWη(0,0)=βC2S>0 and trDWη(0,0)=C(1+βS)>0.
Therefore, keeping in mind the trace and the determinant Theorem [7,37], the equilibrium point (0,0) is repeller.
Lemma 21. The equilibrium point (1,0) is a hyperbolic saddle.
Proof. The Jacobian matrix evaluated in (1,0) is:
hence, detDWη(1,0)=−β(1+C)2S<0.
Then, considering the trace and the determinant Theorem [7,37], the equilibrium point (1,0) is a hyperbolic saddle.
Remark 22. With the two previous lemmas and bearing in mind the change of variable made to obtain the system (4) or vector field Wη(u,w), the equilibrium points (0,0) and (1,0), of the system (3) or vector field Uη(u,v), are non-hyperbolic repeller and non-hyperbolic saddle, respectively. Therefore, the equilibrium points (0,0) and (K,0) of the system (2) are also non-hyperbolic repeller and non-hyperbolic saddle, respectively.
To determine the nature of the equilibrium points (0,C) and (ue,ue+C) we will again consider the system (3).
Lemma 23. The equilibrium point (0,C) is:
i) a hyperbolic saddle, if and only if, QCβ<1,
ii) a non-hyperbolic saddle, if and only if, QCβ=1,
iii) an attractor node, if and only if, QCβ>1,
Proof. The Jacobian matrix evaluated in (0,C) is:
As detDWη(0,C)=−SC2(1−QCβ) we have that
(ⅰ) if QCβ<1, the equilibrium point (0,C) is saddle,
(ⅱ) if QCβ=1, the equilibrium point (0,C) is non-hyperbolic saddle,
(ⅲ) If QCβ>1, thus
So (0,C) is an attractor node.
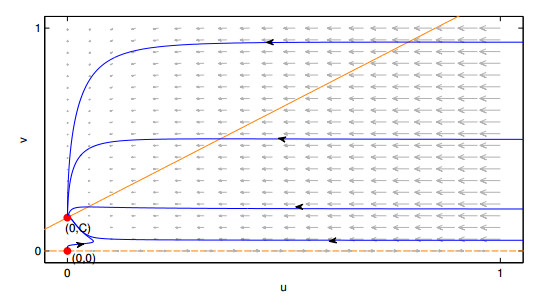
Remembering that If QCβ>1, the positive equilibrium is out of the first quadrant, by the Poincaré-Bendixson Theorem, the point (0,C) is globally asymptotically stable (g.a.s.).
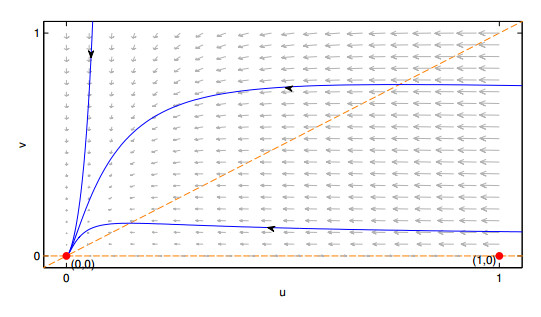
Remark 24. When C=0, the equilibria (0,C) and (0,0) collapse. Then, for certain conditions on the parameter values, the point is a non-hyperbolic attractor. So, there exist trajectories in the system (1), with the point (0,0) as their ω−limit (See Figure 3).
Theorem 25. When the equilibrium point (ue,ue+C) belongs to Int(R20), is a hyperbolic node locally asymptotically stable (l.a.e.).
Proof. The Jacobian matrix of system (3) evaluated in (u,u+C) is:
Then,
and
Remark 26. As the unique positive equilibrium point (ue,ue+C)∈Int(R20) is l.a.e., if and only if, QCβ<1, Considering the Poincaré-Bendixson Theorem, we have that it is globally asymptotically stable (g.a.s.). This result is reinforced by the following theorems.
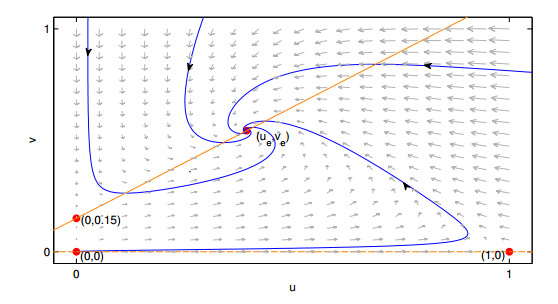
Theorem 27. The equilibrium point (ue,ue+C) is globally asymptotically stable (g.a.s).
Proof. Consider the function described by
with c1 and c2>0, to be determined.
Clearly V(u,v)>0, for all (u,v) ∈Int(R+0)2 and u≠ue, v≠ve [36].
Deriving the function V with respect to τ, it has:
Replacing 1ududτ and 1vdvdτ is obtained
i.e.,
As (ue,ue+C) satisfies the equations of both isoclines we have
Reordering it becomes
Expanding the products we have
Choosing, c2=QβSc1 we obtain that
but,
with p(v,ve) a positive function.
Then,
Therefore, V(u,v) is a suitable Lyapunov function [36,38,40], since it is defined negative.
Then the point (ue,ue+C) is g.a.s, by the Lyapunov stability Theorem [36,38].
Theorem 28. There are no cycles.
Proof. Using the Bendixson-Dulac criterion with the function g(u,v)=1u(u+C)v>0, for all (u,v) inside the first quadrant, Int(R+0).
Considering the sum
where M(u,v)=(1−u−Qvβ)u(u+C) y N(u,v)=S(u+C−v)v,
it is obtained that
namely
Hence S(u,v)<0 for all (u,v) inside the first quadrant.
Therefore, by the Bendixson-Dulac criterion [8,39], there are no cycles (or limit cycles) within the first quadrant.
4.
Some numerical simulations
In Figure 3, considering values for system (3), we can see that the point (0,0) of system (1) is a global attractor for the trajectories.
The following three figures show the global stability of the positive equilibrium point (Figures 4, 5 and 6), when exists at interior of the first quadrant Int(R+0) and the global stability of the equilibrium point (0,C).
5.
Conclusion
In this work, the study of the dynamics of a predator model prey of the Leslie-Gower type was carried out considering the competition (or interference) among predators, CAP, described by the system (1).
We have also detailed the main properties of the modified Leslie-Gower model considering a generalist predator in order to carry out a comparative study of the influence that the CAP has on the original model.
To simplify the calculations in the second model, a reparameterization and a time rescaling were carried out and the system (3) topologically equivalent to (2) was obtained.
The main features of the modified Leslie-Gower type models with CAP are:
● There is a region of positive invariance
● The solutions are bounded, that is, the system is well-posed [1].
● The model with CAP is not defined in (0,0) and neither the Jacobian matrix of the topologically equivalent system (2) is defined for y=0. The nature of the equilibrium points on the x−axis was determined using system (3), topologically equivalent to system (2).
● The equilibrium point (K,0) is a non-hyperbolic saddle.
● The equilibrium point (0,0) is a non-hyperbolic repeller.
● There are no cycles (or limit cycles) inside the first quadrant Int(R+0)2.
Therefore, both models, with or without CAP, have similar dynamics, since in both the common equilibrium points have the same characteristics (nature), except for the hyperbolicity of the equilibrium points (0,0) and (K,0) in each of the models.
The main difference for the model with generalist predators is the existence of the equilibrium (0,C) over the vertical axis. Then, there are conditions ensuring that this point is globally asymptotically stable (g.a.s.). This fact is obtained for CQβ>1, with (Q,S,C,β)∈R2+×]0,1[, implying that the CAP can produce the extinction of the prey population and the permanence of the predator populations in its maximum environmental carrying capacity.
Both in system (2) and in the Leslie-Gower model without interference among predators described by system (1), there is a unique point of coexistence of species, which is globally asymptotically stable (gas) when it exists.
This means that whatever the initial size of each of the populations, as time passes, the population sizes stabilize at that point of equilibrium. This property of both models is highly desirable by some ecologists or managers of exploitation of renewable resources. For example, if we consider that a fish population is caught by many stakeholders (artisanal or industrial fishing, that is, humans acting as predators.
These conclusions are deduced in our analysis, assuming the CAP described by the function B(x,y)=qxyβ, with 0<β<1, but other outcomes would be obtained considering distinct prey-dependent functional response, i.e., assuming B(x,y)=h(x)yβ, with 0<β<1 and h(x) a Holling type functional response.
Although similar results have been obtained for the Leslie-Gower model with or without CAP [19], we cannot conclude that CAP induces the stability of the predator-prey interaction. We know that in many of the real-world interactions, there are extinctions of one or both populations [30], or there exist periodic oscillations of the population sizes, which can be explained by the existence of limit cycles [12,15,43].
These different situations are obtained as possible dynamics appearing in models that consider the CAP described by other mathematical forms. Such cases are obtained, for example, by assuming a Beddington-DeAngelis functional response [3,26] in the Leslie-Gower model [27] or else, assuming the addition of a quadratic term in the predator growth equation [5,28], although this second form is mainly included in Gause type predation models [5,28].
In the model studied in [27], the positive equilibrium point is not necessarily g.a.s., when it exists, and there are also limit cycles around a positive equilibrium point, which implies oscillations of population sizes [27]. For the same set of parameters, different dynamic behaviors coexist, due to the appearance of a separatrix curve in the phase plane [27]. Therefore, the trajectories or solutions of the system are highly sensitive to the initial conditions, since there exist trajectories with very near initial conditions, but to distinct side of that separatrix curve having far ω−limit.
In this way, an important dilemma arises, which is: What is the most efficient model to represent a certain interaction of predation in nature?. We believe that the same interaction can be represented by a given model (whatever its mathematical nature) at a defining moment or time, but its validity will depend strongly on the underlying hypotheses, which are usually not declared.
Bearing in mind that the dynamic complexity of an ODE system does not imply the ecological complexity of the model described by that system, we could not reliably affirm that one model is better than another. However, more complex ecological situations (for example, considering gestation time, non-homogeneous distribution of populations or classified by age and sex, etc.) require the use of more sophisticated mathematical tools than ODEs.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: