Fuzzy logic controller and game theory based distributed energy resources allocation

1.   Introduction

Energy consumption is increasing and it is challenging to meet the demand with limited available resources. Conventional electrical systems are unidirectional, electricity is generated by centralized generation sources and distributed to consumers through large transmission networks ^[1]. Advancement in the applications of sensors, communication networks, real-time monitoring, intelligent appliances etc. are important technologies for transformation of the conventional grid into an intelligent grid. Intelligent grid will generate a huge amount of energy through DERs, and store bulk power as a backup energy resource to supply during peak hours ^[2]. An intelligent power grid includes the basic structure of conventional power grid and smart components (i.e., electric vehicles, solar photovoltaic, wind generators, mini/micro hydro, energy storage devices, smart meters etc.) at low voltage distribution networks. DERs are the small scale energy sources connected near load centers to manage the demand and to maintain the peak of energy consumption ^[3]. A Conventional electric power system with centralized generation is facing the following challenges to manage the demand of the consumers:

■ According to World Energy Scenario 2019 ^[4], the demand for electricity grows at its fastest rate and increase 40 to 60% from 2020 to 2040. To meet with the required demand through fossil fuels, carbon emission will increase by 59% will show the worst effect on the environment.

■ The most challenging task is to provide electricity to all available consumers all the time.

■ Participation of consumers in grid operations.

■ Enhancement in electric vehicles penetration will introduce an extra burden on the electric grid.

■ Reform the structure of the distribution network with the integration of DERs.

■ Optimal allocation of DERs to maintain the voltage profile and reduction in power losses ^[5].

The optimal integration of DERs is important to reduce active and reactive power losses, improving the voltage profile, network reliability etc. in the distribution network. Authors of ^{[6,7,8,9,10,11]} are discussed the challenges associated with the integration of DERs. Proper allocation of DERs are essential for multiple advantages i.e., minimize of real and reactive power losses, line loading, carbon emission, initial cost, tariff structuring, cost of energy generation, utility cost, etc. and improve the voltage profile of the distribution network. Sever methodologies of DERs integration are available in literature i.e., novel method, power loss sensitivity method, voltage indexing, voltage sensitivity analysis, etc. and optimized by different tools i.e., fuzzy logic controllers, genetic algorithms, practical swarm optimizations, neural networks, machine learning etc. The novel method of DERs optimization based on active power loss of the system for unity power factor and further it is modified for lagging and leading power factor cases to integrate DERs ^[12,13]. Power loss sensitivity method calculates the loss sensitivity of the network by load flow analysis. The node where the loss sensitivity is maximum is selected for DERs integration. The capacity of DERs is obtained by connecting different capacity DERs at define node and where the active power losses are minimum use for integration ^[14,15]. Voltage sensitivity analysis calculates the sensitivity of voltage at each bus and the minimum voltage sensitive bus is identified for DERs integration and capacity of DERs is calculated with the same method used in the power loss sensitivity analysis ^[16].

In this paper, existing DERs optimization methodologies are compared with the proposed methodology of DERs integration using the fuzzy logic controller and game theory. The fuzzy logic controller is a mathematical system based on the predefined set of rules to optimize the non-linear equations. The proposed methodology calculates the capacity of DERs to integrate with radial distribution network by FLC. Game theory is a mathematical tool mostly used for sharing the profits between players. The game theory methodology calculates the payoff functions for different players and obtains the solutions for conflicts between the players ^[17]. Characteristically game theory is classified into two categories cooperative and non-cooperative game theory. When players communicate with each other and share their strategies to other players to maximize the payoffs as a group are known as cooperative game theory and when consumers don’t share their strategies or actions to other players to maximize their payoffs are known as non-cooperative game theory ^[18,19,20]. In this work, cooperative game theory is used to optimize the location of DERs integration based on a predefined set of rules. This paper compares the modified novel method, power loss sensitivity, voltage sensitivity analysis of DERs integration with the proposed methodology using a fuzzy logic controller and game theory for IEEE 33 bus radial distribution network. Major contributions of the paper with the proposed methodology for the integration of DERs are:

■ Integration of the DERs with IEEE 33 bus system using different methodologies.

■ Two case studies are identified for DERs integration at unity and 0.9 power factor in a radial distribution network.

■ The fuzzy logic controller is used to optimize the DERs capacity at different buses.

■ Game theory methodology is used to optimize the location of DERs to integrate with a radial distribution network.

■ Compared the different DERs integration methodologies with the proposed approach.

The rest of the paper is organized as follows, section-2 defines the modified novel method, section-3 defines the power loss sensitivity method, section-4 defines the voltage sensitivity analysis method and section-5 defines the proposed method using the fuzzy logic controller and cooperative game theory for the integration of DERs. Results of two different cases for IEEE 33 bus system are explicating in section-6. Section-7 compares the results obtained by various methods. Finally, section 8 concludes the paper with the advantages of the proposed methodology.

2.   DERs integration using modified novel method

DERs integration at unity power factor was proposed by novel method without the calculation of Y_bus & Z_bus. Further, the methodology is updated for lagging power factor and denoted as a modified novel method. According to modified novel method DERs are integrate with distribution network where the active power losses are minimum ^[21]. DERs are generating active as well as reactive power. For calculation of degenerating current from DERs include active and reactive current and the total power generated by DERs. Total number of nodes are denoted as n and total branches are denoted as b. Total active power losses P_T in the system is calculated by (1):

where, I_i is the current in branch R_i. Total current on i^th node I_i includes the active component of current (I_{a, i}) and reactive components of current (I_{r, i}).

Put the current component from (2) to (1)

DERs are integrated at bus m, an active component of current generated by DERs at bus m is I_{aDG, m} and total active power losses including DERs at bus m is P_{T, DG} by (4)

Subtract (3) from (4):

For maximum loss saving:

Optimal size of DERs at bus m is calculated by multiplying (7) with voltage at node m denoted as V_{DG, m} and defined power factor by (8):

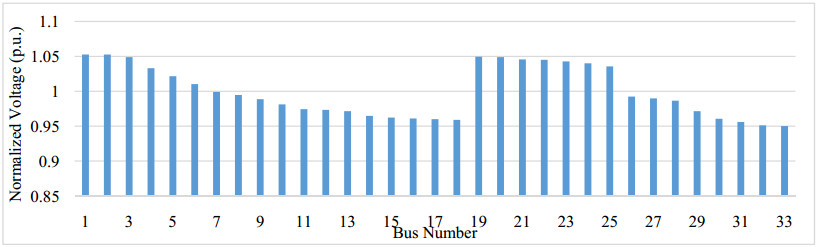
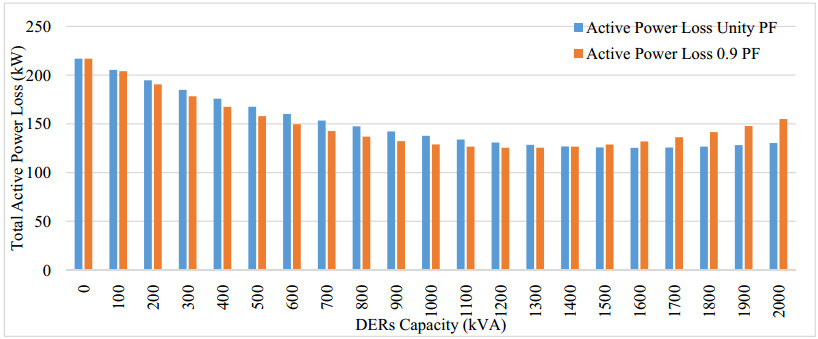
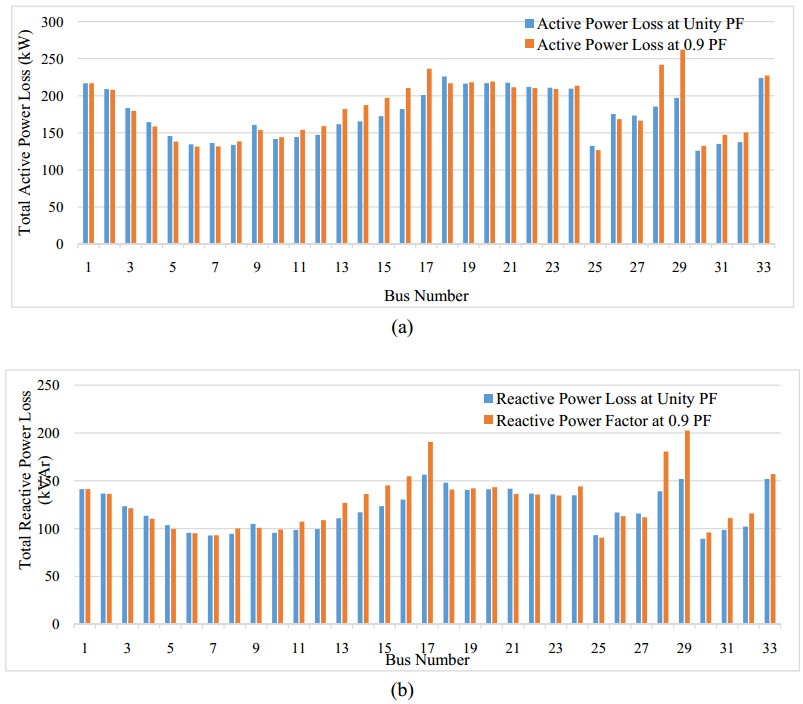
The optimal size of DERs to integrate at different buses at unity and 0.9 power factor for IEEE 33 bus system using the modified novel method is calculated by (8) and shown in Figure 1.

Figure 1.  Optimal DERs capacity using Modified Novel Method.

DownLoad: Full-Size Img PowerPoint

3.   DERs integration using power loss sensitivity method

Power loss sensitivity factor is calculated for defining the proper size and location of DERs to integrate with radial distribution network. DERs integration is affecting by active as well as reactive power losses therefore, loss sensitivity factor is depending upon the active and reactive power loss components ^[22]. Loss sensitivity factor concerning active power is calculated by (9) and loss compassion factor concerning reactive power is calculated by (10):

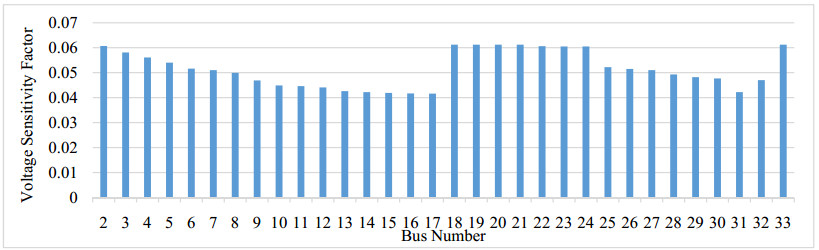
where, S_i is the apparent power losses at i^th bus (I = 1, 2, ….., n), P_i is the active power losses at i^th bus, Q_i is the reactive power losses at i^th bus, P_{l, i} is the active power load connected at i^th bus and Q_{l, i} is the reactive power load connected at i^th bus. The loss sensitivity factor is calculated by forward-backward load flow analysis as Shown in Figure 2 for IEEE 33 bus system.

Figure 2.  Power loss sensitivity for IEEE 33 bus system.

DownLoad: Full-Size Img PowerPoint

Normalized voltage V_n is calculate to maintain the voltage profile near unity PF after integration of DERs by (11).

where, V_i is the voltage at i^th node. DERs are integrate at a particular bus, where the active power losses sensitivity is maximum and normalized voltage shown in Figure 3 is less than 1.01 p.u.. Figure 2 shows the maximum power loss sensitivity for IEEE 33 bus system. Power loss sensitivity is maximum for buses 3, 4, 5 & 18 are respectively 0.208, 0.1455, 0.138 & 0.1124 but at these busses normalized voltage is more than 1.01 p.u.. Therefore these busses are not consider for the integration of DERs with the proposed system. After this bus 28 have maximum loss sensitivity 0.0623 have normalized voltage 0.9865 p.u. is selected for the integration of DERs.

Figure 3.  Normalized voltage profile for IEEE 33 bus system.

DownLoad: Full-Size Img PowerPoint

4.   DERs integration using voltage sensitivity analysis metho

Voltage Sensitivity Analysis method (VSA) is defining the best position at which the system is stable. In this method voltage profile is used to optimize the location of DERs. VSA defines the utility operator that the system is close to collapse and required to improve voltage profile. VSA is calculating by connecting DERs with a capacity of 20% of the total connected active load at each node. VSA is calculated by (12) and the point where VSA is minimum is selected for the integration of DERs ^[23,24].

where, V_m is the voltage at m^th bus and n is the total number of busses. Figure 4 shows the VSA profile of the IEEE 33 by connecting 20% capacity of DERs of total load capacity 3710 kW.

Figure 4.  Voltage sensitivity factor for IEEE 33 bus system.

DownLoad: Full-Size Img PowerPoint

It shows that VSA is minimum at bus 17, therefore this bus is selected for DERs integration. DERs capacity is calculating by connecting different capacities of DERs at bus 17 and at a particular capacity where active power losses are minimum is selected for the integration.

5.   Proposed methodology

5.1.   DERs capacity for integration using Fuzzy Logic Controller

Fuzzy system is an extension of integer numbers and used to transmute the verbal rules into mathematical modelling. In this work, the capacity of DERs to integrate with proposed system is calculate by the fuzzy logic controller by applying three input sets in the form of triangular function, voltage profile, active power losses, and reactive power losses. Further, every input is subdivided into three subsets of lower, medium and the higher range shown in Table 1 ^[25]. The output of fuzzy logic controller is the capacity of DERs to integrate with proposed system for unity and 0.9 PF are shown in Figure 5.

Table 1.  Membership functions of Fuzzy Logic Controller.

Input’s/Output’s	Range Criteria	Range of Triangular function [min. Peak Max.]
Voltage (pu)	Low	[0.9, 0.92, 0.94]
	Medium	[0.93, 0.95, 0.96]
	High	[0.95, 0.98, 1]
Active Power Loss (kW)	Low	[0, 5, 10]
	Medium	[10, 20, 30]
	High	[30, 50, 100]
Reactive Power Loss (kVAr)	Low	[0, 5, 10]
	Medium	[10, 20, 30]
	High	[30, 40, 50]
DG Capacity (MVA)	Low	[0, 1, 1.5]
	Medium	[1.5, 2.25, 2.5]
	High	[2.5, 4.0, 5.0]

---

 | Show Table

DownLoad: CSV

Figure 5.  Energy generation capacity from DERs using Fuzzy Logic Controller.

DownLoad: Full-Size Img PowerPoint

5.2.   DERs location of Integration using game theory

Game theory is a tool of mathematical expressions to identify the best suitable combination for the participants among the rules designed to get maximum benefits. Cooperative game theory is used in the proposed methodology to identify the location to integrate the DERs with maximum benefits. Cooperative game theory allowed the players to communicate with each other and find the nash equilibrium by their mutual concerns. Cooperative game theory games are categorized as static and dynamic games. When each consumer select their best response only once are known as static games. When consumers update their best responses after considering the responses of other players are known as dynamic games. Dynamic games allowed the consumers to modify the action more than one to increase the payoffs. Dynamic game with cooperative game theory is designed for optimization of DERs integration location. The capacity of all the DERs to integrate at different buses are calculated by FLC and active & reactive power losses by the integration of these DERs are determined by load flow analysis. Two inputs for the cooperative game is considered as active & reactive power losses and voltage profile. Some rules are design before identify the suitable location for the integration of DERs.

Rule-Ⅰ: The maximum capacity of DERs to integrate into the system at different busses are always less than and equal to the maximum power handling capacity of the system.

Rule-Ⅱ: One branch includes several buses will consider for the integration of DERs at any one bus.

Rule-Ⅲ: A maximum of three DERs are integrate with a particular system at three different locations.

Rule-Ⅳ: DERs are integrating where active and reactive power losses after the integration of proper size of DERs, calculate by fuzzy logic controller are minimum and voltage profile before integration is minimum.

As per the defined rules, a game is played between busses to integrate DERs. The capacity of DERs is obtaining by two sets of input strategies are I = { I₁, I₂, ………I_k} the strategy of finding the buses to integrate DERs and J = {J₁, J₂, ………, J_k} strategy of DERs capacity to connect ^[20]. Payoff function for strategy set I with strategy set J is in (13).

Strategy set J with set I is in (14)

where, I_i and J_i are the proportion of effort for payoff function of U_i and U_j respectively are the real numbers between zero to one and having the possibilities of infinite set actions so not required to prepare game table. Maximum payoffs are calculated by differentiating (13) and (14) with respect to I_i and J_i respectively in (15) and (16) to find the best response ${U_i}{({I_{i}}, {J_i})^*}$ and ${\rm{}}{U_j}{({J_{i}}, {I_i})^*}$.

The Nash equilibrium of the two payoff functions is calculated where the two best responses intersect. Best response of each player are intersected with another player’s best response in (17) and (18) respectively:

Nash equilibrium for both these equations are shown in (19):

6.   Simulation results

IEEE 33 bus radial distribution system is used to optimize the integration problem of DERs to the system with the load capacity of 3710 kW & 2300 kVAr.

6.1.   Modified novel method

IEEE standard 33 bus system is used to integrate the DERs of different capacities at different busses as shown in Figure 1. Without installation of DERs, active and reactive power losses at IEEE 33 bus system are 216.84 kW, 141.3417 kVAr respectively. As per the modified novel method, the bus where active power losses are minimum is specified to integrate the DERs. DERs at bus 6 with a capacity of 2093.5 kVA and 2306.86 kVA respectively for unity and 0.9 power factor are integrated. Active and reactive power losses after integration of DERs at unity power factor are 133.098 kW & 109.3978 kVAr respectively and at 0.9 power factor 129.99 kW & 107.2327 kVAr respectively as shown in Figure 6 and Table 2.

Figure 6.  Total active power losses by integration of DERs using modified novel method.

DownLoad: Full-Size Img PowerPoint

Table 2.  33 bus system results using modified novel method.

	Without DERs	DERs at Unity PF	DERs at 0.9 PF
DERs Size	-	2093.5 kVA	2306.86 kVA
DERs Integration Location (bus)	-	6	6
Total Active Power Losses	216.84 kW	133.098 kW	129.99 kW
Total Reactive Power Losses	141.3417 kVAr	109.3978 kVAr	107.2327 kVAr
Min. Bus Voltage	0.9025 pu	0.9133 pu	0.9143 pu

---

 | Show Table

DownLoad: CSV

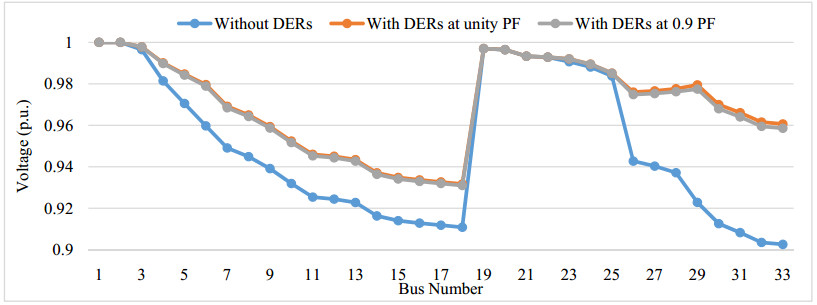
The integration of DERs are improving the voltage profile of the system. Figure 7 shows the voltage profile in three cases, without the integration of DERs, integration of DERs at unity power factor and integration of DERs at 0.9 power factor for IEEE 33 bus system. It shows that the minimum voltage after integration of DERs is improving at unity power factor is 0.913291 p.u. and at 0.9 power factor 0.91435 p.u. from 0.9025 p.u. the without integration of DERs.

Figure 7.  Voltage Profile at IEEE 33 Bus System using Modified Novel Method for DERs Integration.

DownLoad: Full-Size Img PowerPoint

6.2.   Power loss sensitivity method

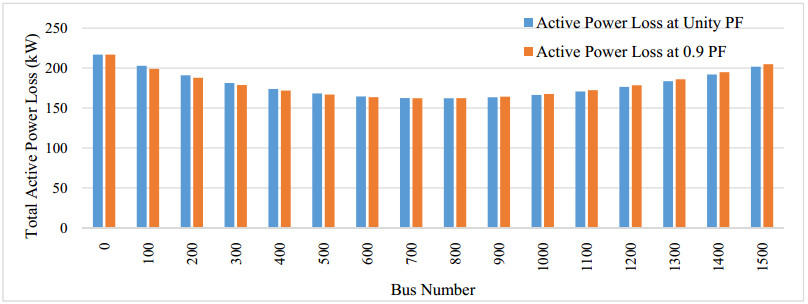
The power loss sensitivity method allowed the grid to integrate the DERs where power loss sensitivity is highest and normalized voltage is less than 1.01. DERs capacity optimize by integrating different capacity of DERs to defined bus and calculate the active & reactive power losses and voltage profile. Before installation of DERs, active and reactive power losses of IEEE 33 bus system are 216.84 kW, 141.3417 kVAr respectively. As per power loss sensitivity method, DERs are connected at bus 28. Different capacity of DERs are integrated from 0 kVA capacity to 2000 kVA capacity and the DERs capacity where the active power losses are minimum are used to integrate the DERs. DERs at bus 28 with a capacity of 1600 kVA and 1200 kVA respectively for unity and 0.9 power factor are integrate as shown in Fig. 8 have minimum power losses respectively for unity and 0.9 PF.

Figure 8.  Total power losses with different capacity DERs at bus 28 using power loss sensitivity method.

DownLoad: Full-Size Img PowerPoint

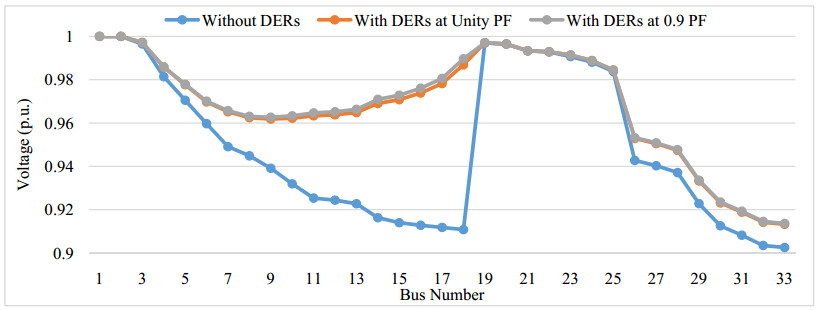
The integration of DERs are improving the voltage profile of the system. Figure 9 shows the voltage profile without integration of DERs, integration of DERs at unity power factor and integration of DERs at 0.9 power factor for IEEE 33 bus system. It shows that the minimum voltage is improved from integration of DERs at unity power factor is 0.9317 p.u. and at 0.9 power factor 0.9309 p.u. from 0.9025 p.u. without integration of DERs. Active and reactive power losses after integration of DERs at unity power factor are 125.3946 kW & 89.7300 kVAr respectively and at 0.9 power factor 125.5273 kW & 89.4465 kVAr respectively are shown in Table 3.

Figure 9.  Voltage profile at IEEE 33 bus system using power loss sensitivity method for DERs integration.

DownLoad: Full-Size Img PowerPoint

Table 3.  33 bus system results using power loss sensitivity method.

	Without DERs	DERs at Unity PF	DERs at 0.9 PF
DERs Size	-	1600 kVA	1200 kVA
DERs Integration Location (bus)	-	28	28
Total Active Power Losses	216.84 kW	125.3946 kW	125.5273 kW
Total Reactive Power Losses	141.3417 kVar	89.7300 kVar	89.4465 kVar
Min. Bus Voltage	0.9025 pu	0.9317 pu	0.9309 pu

---

 | Show Table

DownLoad: CSV

6.3.   Voltage sensitivity analysis

Without DERs, active and reactive power losses of IEEE 33 bus system are 216.84 kW, 141.3417 kVAr respectively. As per voltage sensitivity analysis method, DERs are connected at bus 17 as shown in Figure 4. DERs at bus 17 with a capacity of 800 kVA for unity and 0.9 power factor are integrate as shown in Figure 10 as they have minimum active power losses.

Figure 10.  Total power losses with different capacity DERs at bus 17 using voltage sensitivity analysis method.

DownLoad: Full-Size Img PowerPoint

The integration of DERs are improving the voltage profile of the system. Figure 11 shows the voltage profile without integration of DERs, integration of DERs at unity power factor and integration of DERs at 0.9 power factor for IEEE 33 bus system. It shows that the minimum voltage is improve after integration of DERs at unity power factor is 0.9132 p.u. and at 0.9 power factor 0.9136 p.u. from 0.9025 p.u. without integration of DERs. Active and reactive power losses after integration of DERs at unity power factor are 161.1102 kW & 111.7854 kVAr respectively and at 0.9 power factor 162.3449 kW & 112.5487 kVAr respectively are shown in Table 4.

Figure 11.  Voltage profile using voltage sensitivity analysis method for DERs integration.

DownLoad: Full-Size Img PowerPoint

Table 4.  33 bus system results using voltage sensitivity analysis method.

	Without DERs	DERs at Unity PF	DERs at 0.9 PF
DERs Size	-	800 kVA	800
DERs Integration Location (bus)	-	17	17
Total Active Power Losses	216.84 kW	162.1102 kW	162.3449 kW
Total Reactive Power Losses	141.3417 kVar	111.7854 kVar	112.5487 kVar
Min. Bus Voltage	0.9025 pu	0.9132 pu	0.9136 pu

---

 | Show Table

DownLoad: CSV

6.4.   Proposed Methodology

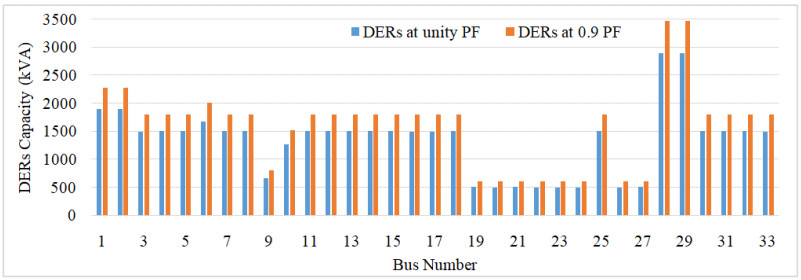
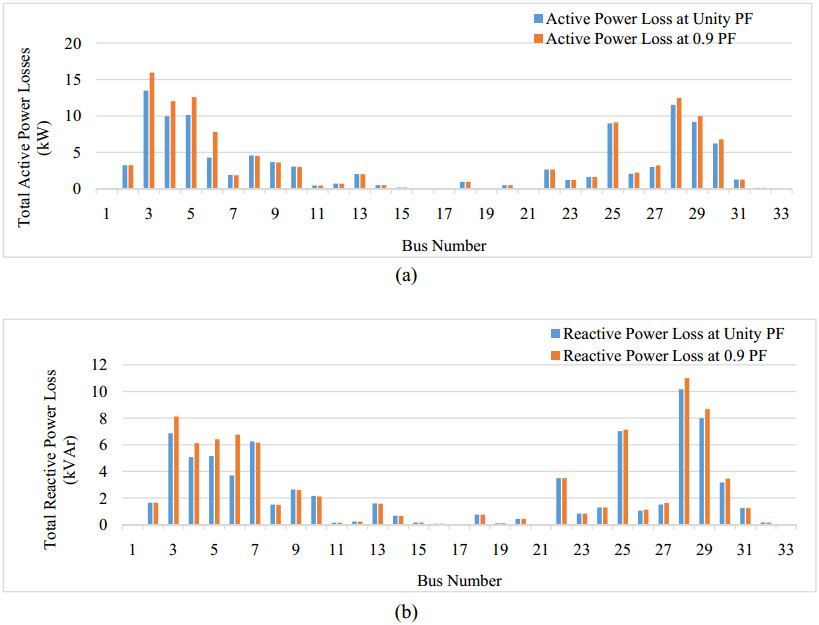
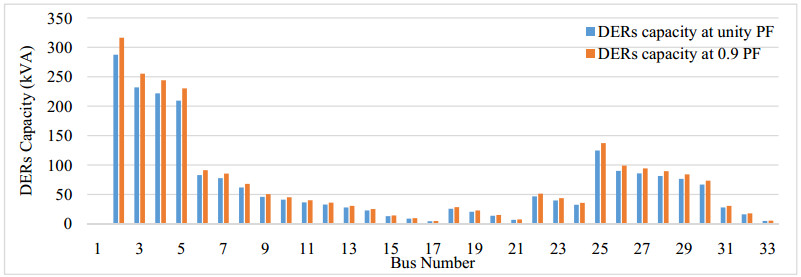
Before integration of DERs minimum bus voltage is identified at bus 6, bus 22, bus 25, and bus 30. Maximum of 3 DERs are integrated at three different branches, therefore select bus 6, 25, 30 for integration of DERs with capacities of 1671.50 kVA, 1499.70 kVA & 1499.95 kVA respectively for unity power factor and 1856.80 kVA, 1799.65 kVA, 1699.94 kVA for 0.9 PF respectively. Total capacity at DERs connected at three buses are more than total system load, therefore bus 25 is not selected for DERs integration as it have maximum power loss among remaining system. Figure 12 shows the total active and reactive power losses by the integrating of DERs of different capacity at different buses.

Figure 12.  Total power losses at unity and 0.9 PF (a) Active Power Losses (b) Reactive Power Losses.

DownLoad: Full-Size Img PowerPoint

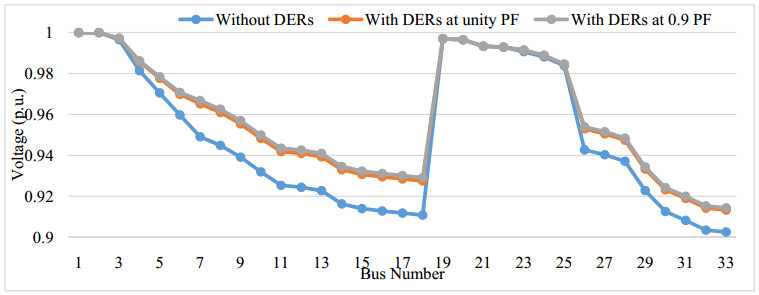
Nash equilibrium is obtained to integrate the DERs at bus 6 & 30 with a total capacity of 3171.45 kVA for unity power factor and 3556.74 kVA for 0.9 power factor lagging. The nash equilibrium is the win-win situation among all the buses to integrate the DERs. DERs power handling capacity is variable in a day and the location to integrate is calculate by using base line load. Results of Figure 13 shows the active and reactive power losses after integration of DERs at bus 6 and 30 shown that the total active power losses are reduced from 216.84 kW to 107.8397 kW for unity PF and 120.8873 for 0.9 PF. Total reactive power losses are reduced from 141.3417 kVAr to 77.332 kVAr and 85.7890 kVAr respectively for unity and 0.9 PF. Figure 14 shows the voltage profile without integration of DERs, integration of DERs at unity power factor and integration of DERs at 0.9 power factor for IEEE 33 bus system. It shows that the minimum voltage is improve after integration of DERs at unity power factor is 0.9630 p.u. and at 0.9 power factor 0.9704 p.u. from 0.9025 p.u. without integration of DERs shown in Table 5.

Figure 13.  Power loss after integration of DERs at bus 6 and 30 (a) Active Power Loss (b) Reactive Power Loss.

DownLoad: Full-Size Img PowerPoint

Figure 14.  Voltage profile after integration of DERs at bus 6 and 30.

DownLoad: Full-Size Img PowerPoint

Table 5.  33 bus system results using proposed method includes FLC and game theory.

	Without DERs	DERs at Unity PF	DERs at 0.9 PF
DERs Size	-	3171.45 kVA	3556.74
DERs Integration Location (bus)	-	6 & 30	6 & 30
Total Active Power Losses	216.84 kW	107.8397 kW	120.8873 kW
Total Reactive Power Losses	141.3417 kVAr	77.3332 kVAr	85.7890 kVAr
Min. Bus Voltage	0.9025 pu	0.9630 pu	0.9704 pu

---

 | Show Table

DownLoad: CSV

7.   Results comparison

Proposed method of DERs integration using FLC and game theory is compared with conventional method i.e., novel modified method, power loss sensitivity method, voltage sensitivity analysis method for IEEE 33 bus radial distribution network. The results are compared based on three constraints active power losses, reactive power losses and voltage profile. The method is useful which have maximum voltage improvement and minimum active and reactive power losses. DERs are integrate at different locations from different methods and their capacity is also different. Tables 6 and 7 the results of different DERs integration at unity and 0.9 PF respectively shows that the active power losses, reactive power losses are minimum in proposed methodology and minimum voltage is maximum in proposed methodology using FLC and game theory. The results comparison of different methodologies to integrate DERs define the proposed methodology is best suitable in terms of voltage profile management and active and reactive power loss management. As per IEEE standards voltage profile more than 0.95 p.u. increase reliability of the system and the results of proposed methodology maintain the voltage between 0.9630 p.u. to 1.00157 p.u. and between 0.970385 p.u. to 1.00157 p.u. for unity and 0.9 PF respectively.

Table 6.  Compression of results of 33 bus system at unity PF.

	Without DERs	With DERs
		Modified Novel Method	Power Loss Sensitivity Method	Voltage Sensitivity Analysis Method	Proposed Method
DERs Location	-	6	28	17	6 & 30
DERs Capacity (kVA)	-	2093.5	1600	800	3171.45
Total Active Power Losses (kW)	216.84	133.098	125.3946	162.1102	107.8397
Total Reactive Power Losses (kVAr)	141.3417	109.3978	89.7300	111.7854	77.3332
Minimum Voltage (pu)	0.9025	0.9133	0.9317	0.9132	0.9630

---

 | Show Table

DownLoad: CSV

Table 7.  Compression of results of 33 bus system at 0.9 PF lagging.

	Without DERs	With DERs
		Modified Novel Method	Power Loss Sensitivity Method	Voltage Sensitivity Analysis Method	Proposed Method
DERs Location	-	6	28	17	6 & 30
DERs Capacity (kVA)	-	2306.86	1200	800	3556.74
Total Active Power Losses (kW)	216.84	129.99	125.5273	162.3449	120.8873
Total Reactive Power Losses (kVAr)	141.3417	107.2327	89.4465	112.5487r	85.7890
Minimum Voltage (pu)	0.9025	0.9143	0.9309	0.9136	0.9704

---

 | Show Table

DownLoad: CSV

8.   Conclusions

Distributed energy resources are integrated with distribution networks near load centers to minimize the losses and to maintain the voltage profile. A Novel approach based on fuzzy logic controller and game theory is proposed in this paper. The capacity and the proper location for the integration of DERs are essential to maintain the reliability of the system. Fuzzy logic controller is used to optimizing the capacity of DERs to integrate with distribution network and game theory obtain the location of integration. The proposed methodology obtains the results of active power losses, reactive power losses and voltage profile with and without DERs. To authenticate the results obtained from the proposed system are compared with conventional methods i.e. modified novel method, power loss sensitivity method and voltage sensitivity analysis method for IEEE 33 bus system for unity and 0.9 power factor. The results show the voltage profile is improved respectively for unity and 0.9 PF is 1.2% & 1.3% using modified novel method, 3.23% and 3.14% using power loss sensitivity analysis, 1.18% & 1.22% using voltage sensitivity analysis, and 6.70% & 7.52% using the proposed methodology. The results of active & reactive power losses are reduced 38.42% & 22.62%, 42.17% & 36.51%, 25.29% & 20.91% and 50.27% & 45.28% respectively for modified novel method, power loss sensitivity method, voltage sensitivity analysis method and the proposed method for unity power factor. The results of active & reactive power losses are reduced 40.05% & 24.13%, 42.11% & 36.71%, 25.13% & 20.37% and 44.25% & 39.30% respectively for modified novel method, power loss sensitivity method, voltage sensitivity analysis method and the proposed method for 0.9 power factor. The proposed methodology is useful for practical implementation of the integration of DERs as maximize the voltage profile and minimize the active and reactive power losses.

Conflict of interest

No conflict of interest.