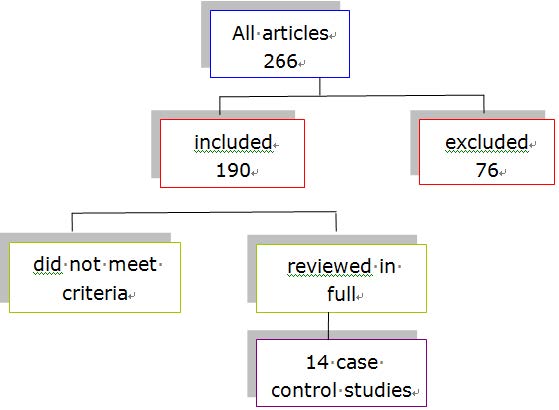
Background: Brain Derived Neurotrophic Factor (BDNF) is one of the neuromodulators crucial for the survival, development and function of neurones in the brain and nervous system. Several authors linked its changes in production and concentration to Schizophrenia syndromes. Aim: This systematic review examined the available evidence to clarify the association between plasma BDNF levels and Schizophrenia. Method: Initial searches revealed 266 records. After screening of abstracts, 20 studies were selected. Following a preliminary review, 14 studies were included in this systematic review and meta-analysis. Results: Of the 14 studies (910 patients, 717 controls) 8 reported decreased BDNF levels in patients with schizophrenia as compared to controls; 3 studies (274/128) found increased BDNF levels; while 3 (62/62) reported no group differences. Meta-analysis of all pooled studies confirmed reduced BDNF levels in schizophrenia versus controls (medium effect size); however, the group difference was not significant when studies using unmedicated cases were considered. Conclusion: The cumulative evidence indicates reduced BDNF levels existing in schizophrenia. However, findings are less clear in unmedicated cases, suggesting that reduced BDNF levels in schizophrenia may be associated with symptom chronicity and/or chronic effects of antipsychotic medication.
1.
Introduction
With the worsening of the global energy crisis, wind power, as an important part of renewable energy, is gradually becoming an important support for the power system. However, the random volatility of wind power output and the uncertainty of load demand make it difficult for traditional deterministic optimization methods to meet the scheduling requirements. At present, the prevailing methods encompass probabilistic constraints and fuzzy optimization. However, the majority of these methodologies exclusively consider unilateral uncertainty, thereby hindering their capacity to account for the prediction error of wind power output and the volatility of demand response [1,2]. In addition, in power system dispatch, wind power output has a stochastic nature; on the other hand, load response, especially demand response, has a fuzzy nature, and traditional optimization methods show difficulty in dealing with these two uncertainties simultaneously. In contrast, this study uses fuzzy stochastic constraints to construct a day-ahead dispatch optimization model, which enables the dispatch scheme to consider the economy and reliability under different confidence levels. Compared with probabilistic constraints, this method is able to deal with stochasticity and ambiguity at the same time by introducing confidence and affiliation functions; meanwhile, the degree of uncertainty of the system is more accurately described by the membership function, which enhances the robustness and adaptability of the scheduling strategy [3,4]. The core scientific problem of the study is how to accurately represent the uncertainty of wind power output forecast error and load response and optimize the scheduling scheme of the wind power system. In order to achieve the above objectives, this study uses a kernel density estimation method to model the wind power prediction error starting from the dual uncertainty of the source side and the load side. Compared with traditional parametric distribution fitting methods, such as normal, Student's t, and beta distributions, kernel density estimation is a nonparametric modeling method that does not require preset distribution types and can more flexibly fit the actual error distribution of wind power output. Utilizing the triangular subordinate function to represent the uncertainty of the load response enhances the adaptability of the dispatch scheme.
With respect to the economic and environmental objectives of power system operation, this study introduces multi-objective optimization to ensure that the dispatch scheme can achieve an optimal balance between cost and carbon emissions. The core of multi-objective optimization is to find the optimal balance between mutually constraining objectives, rather than ultimately optimizing for a single objective, which can focus on minimizing or maximizing a specific objective compared to single-objective optimization.
The innovation of this study is evident in three aspects. First, the incorporation of fuzzy random chance constraints enables the consideration of wind power output uncertainty and demand response ambiguity. This approach facilitates a more precise depiction of random fluctuations and ambiguous information, thereby enhancing the robustness of the scheduling scheme in comparison to traditional probability constraints. Second, the kernel density estimation is used to optimize the modeling of the wind power prediction error and is combined with the triangular subordinate function to construct the load response uncertainty model, thus improving the adaptability of the dispatch model. Finally, the multi-objective optimization method is combined to seek a reasonable trade-off between economy and environmental protection, so as to make the scheduling scheme more in line with the demand of the actual power system. A comparison of the studied model with existing methods reveals its ability to comprehensively consider the uncertainty characteristics of wind power systems. The model's integration of the main objective method and the maximum affiliation method in its optimization solution, employing the CPLEX optimizer, is a significant advancement that enhances computational efficiency and solution quality. The study proposes a day-ahead scheduling optimization framework applicable to environments characterized by a high penetration rate of wind power from both the source and load sides. This framework offers a novel optimization approach aimed at enhancing the stability of wind power grid integration and the comprehensive benefits of grid scheduling.
2.
Related work
Promoting the development of renewable energy and studying the optimization of wind power systems has become an important topic, and many excellent researchers have conducted in-depth research on the subject [5]. Wang C. et al. proposed a wind speed prediction model that combined time series decomposition algorithm, adaptive noise experience, and wavelet decomposition to improve the accuracy of short-term wind speed prediction. Although the method achieved better results in short-term forecasting, its adaptability to long-term fluctuations in wind power was still limited, and it did not sufficiently consider the impact of forecast errors on grid dispatch [6]. Huang C. et al. investigated the optimization of the economic efficiency of the grid system and proposed an omnidirectional optimization of the smart grid system. Although the method improved economic efficiency, it modeled the uncertainty of wind power in a coarse way and did not consider the robustness of dispatch [7]. Fernández-Guillamón A. et al. focused on the impact of wind power integration on power system stability and proposed a method to evaluate the frequency deviation of high wind power penetration. Although this method effectively analyzed the impact of wind power penetration on grid stability, their study focused on system security and did not provide a systematic solution in terms of optimal dispatch [8]. In addition, optimal dispatch methods for wind power systems were widely investigated in various studies. Griche I. et al. used fuzzy logic and honey algorithms for voltage regulation of PI controllers to optimize the steady-state performance in power systems. However, this method was mainly applied to voltage regulation and lacked direct applicability to global dispatch optimization of wind power systems [9]. Liu Y. et al. investigated the impact of wind power fluctuations on grid stability and proposed a multi-temporal wind power fluctuation evaluation method. Although the method performed well in predicting wind power fluctuations, it lacked a mechanism to jointly optimize the uncertainty of wind power and the uncertainty of load response [10]. Mummey J. et al. optimized wind farm scheduling by the stochastic optimization method to improve the ability of wind power resource allocation. However, the robustness of their method was still affected by the wind power shortage period, and it was difficult to adapt to the complex scheduling needs [11]. Yuan C. et al. proposed a wind power dispatch optimization method based on dynamic VAR allocation to improve voltage stability. However, the method only optimized the grid voltage stability and did not give enough consideration to the overall optimization of the dispatch strategy [12]. Touqeer M. et al. investigated the advantages of Pythagorean fuzzy sets in uncertainty handling and proposed a linear programming method based on random constraints for shortest path and minimum spanning tree problems. However, the method mainly focused on static optimization problems and lacked applicability analysis for dynamic uncertain systems such as wind power scheduling [13]. Zolfaghari S. et al. used mixed integer programming to model portfolio scheduling and introduced triangular interval-valued fuzzy stochastic variables to improve the adaptability of the model in uncertain environments. However, their approach relied too much on a specific way of describing uncertainty. It was difficult to generalize to complex wind power scheduling problems, especially with limitations in modeling bilateral source-load uncertainty [14]. Zhang X. et al. proposed a two-stage stochastic robust optimal scheduling method considering source-load side uncertainties for the optimal scheduling problem of a virtual power plant with multiple source-load side uncertainties. The results showed that the method could generate a certain robust and stochastic optimal scheduling scheme, but its operation in complex environments needed to be improved [15]. Li J. et al. proposed a two-layer optimization model to improve the system scheduling capability while considering the impact of the unpredictability of wind power. The results showed that both the upper and lower layers of the model could successfully reduce the wind abandonment rate, reduce the system operation cost, and improve the accuracy of day-ahead scheduling. However, unfortunately, the final scheduling error was not low and needs to be subsequently optimized [16].
A review of the existing research reveals a predominant focus on the direction of wind power forecast optimization, economic dispatch optimization, the impact of wind power integration on the power grid, and dispatch methods based on intelligent optimization algorithms. However, three issues remain to be addressed. First, there are still limitations in the uncertainty modeling of wind power dispatch. Most of the studies focus on optimizing the uncertainty of wind power output or load unilaterally, ignoring the synergistic effect of the uncertainty of the source and load sides. Second, it is difficult for traditional optimization methods to balance economic and environmental concerns. Most of the existing multi-objective optimization methods lack effective constraint modeling, which makes it difficult to provide both economically efficient and environmentally friendly scheduling solutions under complex uncertainty environments. Third, the solution method of scheduling optimization requires higher computational efficiency. Although some studies have introduced intelligent optimization algorithms, they have not effectively improved solution efficiency. This makes it difficult to meet the real-time scheduling requirements of large-scale wind power systems.
In light of the aforementioned issues, this study examines the source and load sides and devises a day-ahead scheduling model for wind power systems based on fuzzy random chance constraints. It encourages the study of wind power system scheduling and proposes a novel approach for the comprehensive study of the stochasticity of wind power output and the fuzzy nature of load response. Fuzzy stochastic chance-constrained optimization is a novel optimization method that quantifies ambiguity by introducing an affiliation function and handles stochasticity in combination with chance constraints, which can ensure that the system satisfies the constraints with a high confidence level. In comparison with the classical probabilistic constraint approach, the fuzzy random chance constraint approach not only considers the statistical properties of random variables but also describes the ambiguity of load demand with greater accuracy by means of the affiliation function. This enhancement of the adaptability and robustness of the scheduling model is a significant contribution of this approach. Compared with the traditional fuzzy constraint approach, the fuzzy random chance constraint can ensure the system's feasibility at a higher confidence level, especially when facing the double uncertainty of wind power output and load response, which shows better performance. Specifically, the affiliation function defines the degree of affiliation of each element in a fuzzy set, and this degree of affiliation indicates the degree to which a variable belongs to a certain fuzzy set. In the context of wind power system dispatch optimization, the imprecise nature of load demand, exemplified by the nonlinear behavior of user response, can be effectively quantified through the judicious design of the affiliation function. In this way, the fuzzy stochastic chance-constrained optimization model is able to maintain higher system stability and optimization effect in the face of uncertain environments.
3.
Research on day-ahead scheduling model of wind power system considering source load uncertainty
3.1. Wind power forecasting error uncertainty model and demand uncertainty model
Wind power forecasting is the basic module of wind power grid systems. With the increasing demand for wind energy, wind power capacity continues to expand. Therefore, evaluating how forecasting accuracy impacts the stability of wind power systems is increasingly relevant [17,18,19,20]. Wind power prediction error fitting methods are generally classified as either parametric or nonparametric. Parametric methods typically involve classical distribution fitting, such as the normal distribution, Student's t-square, and beta distribution. Normal distribution is an important fitting method with important applications in basic science and engineering practices. According to the law of large numbers, only normal distribution can be used when the amount of sample data to be processed reaches a certain level. Beta distribution is defined in the (0, 1) interval and is widely used in real life to model market occupancy and product disqualification rates, among others. The Student's t-distribution, called t-distribution for short, is often used with small sample sizes to approximate a normally distributed population.
Although classical distribution fitting models are widely used in daily life, they present challenges with accurately depicting the peakedness and thick-tail characteristics of wind power forecast errors [21,22,23]. Therefore, a nonparametric kernel density function is introduced for modeling wind power output [24,25]. Kernel density estimation is a nonparametric approach that does not require assuming a specific type of distribution; instead, it constructs a probability density function based on the sample data. This allows it to more accurately represent the spike and long-tail characteristics of wind power forecast errors.
Furthermore, density estimation has been identified as a particularly suitable approach for wind power output modeling. This is primarily due to the fact that wind power output is significantly influenced by meteorological factors, including wind speed, wind direction, and temperature. Consequently, prediction errors often exhibit complex distribution characteristics, such as long-tailed, spiky, and other irregular forms. The conventional parametric method typically assumes that data follows a specific distribution, which hinders the ability to accurately depict the asymmetric and kurtosis characteristics of the actual distribution of the error. The function $ Z\left(u \right) $ is shown in Eq (1) [26].
There exists an overall sample $ X $, when the sample point $ {x_i} $ is in the domain centered at $ x $ with radius $ \frac{h}{2} $, $ Z\left({\frac{{x - {x_i}}}{h}} \right) $ is 1, otherwise it is 0. At this time, the total number of samples in the neighborhood is $ \sum\limits_{i = 1}^n {Z\left({\frac{{x - {x_i}}}{h}} \right)} $, and the density valuation at $ x $ is calculated as shown in Eq (2) [27].
where $ h $ denotes the interval of the sample, $ {f_h}(x) $ denotes the density valuation, and $ n $ denotes the total number of samples. This is the kernel density estimation method, Parzen window density estimation, which is the basis in the nonparametric fitting. In this method, there is a problem of correlation between distance and contribution values. Therefore, in practice, in order to obtain a function with higher generalizability, it needs to be optimized again. For a set of continuous samples $ {X_1}, {X_2}, ..., {X_n} $, the kernel density method is defined for the overall density of the point $ x $, as shown in Eq (3) [28].
In Eq (3), $ K(\cdot) $ denotes the kernel function and $ K(x) \geqslant 0, \int_{ - \infty }^{ + \infty } {K(x)dx = 1} $. To better fit the wind power prediction error characteristics, the Gaussian kernel function is chosen for the study. Its expression is shown in Eq (4) [29].
The accuracy of source-side forecasting can be effectively increased through kernel parameter fitting analysis. As the development of smart grids accelerates, demand response plays an increasingly critical role in grid dispatch. Due to the different forms of demand response, both price-sensitive demand response (PSDR) and incentive-based demand response (IBDR) need to be analyzed [30].
Residential electricity consumption varies according to the fluctuation of electricity prices; such behavior is modeled by the PSDR approach. The analysis of this model relies on the price elasticity matrix model and the consumer psychology model. On the other hand, the IBDR model refers to the agreement between the consumer and the grid, including consumption, reward and punishment compensation measures, etc. This model belongs to the grid dispatch users, using compensation strategies to achieve peak shaving and valley filling for enhanced grid regulation. To analyze the uncertainty in both PSDR and IBDR, a triangular affiliation function is employed. This function is used to represent the uncertainty of the load response mainly due to its ease of calculation, adaptability, and high interpretability. Load response is affected by multiple factors, such as electricity price, customer behavior, environmental changes, etc., and is characterized by significant fuzziness and nonlinearity. Compared with traditional probabilistic methods, the triangular conditional function can represent uncertainty without a large amount of historical data, which is suitable for limited data or unknown distributions. In comparison with higher-order fuzzy functions, the triangular dependency function has a simple structure and provides high computational efficiency, facilitating the optimization of solutions while maintaining a more precise description of uncertainty in load responses. In addition, the delta-affine function can flexibly adjust its shape to fit different load characteristics, making the scheduling model more robust and adaptable under a variety of operating conditions. Let the load response rate be $ {\lambda _t} $, $ {\lambda _t} = ({r_1}, {r_2}, {r_3}) $, where $ {r_1} $, $ {r_2} $, and $ {r_3} $ denote the lower, peak, and upper values of the triangular fuzzy number, respectively. The relationship between load response rate and affiliation degree at this time is shown in Eq (5).
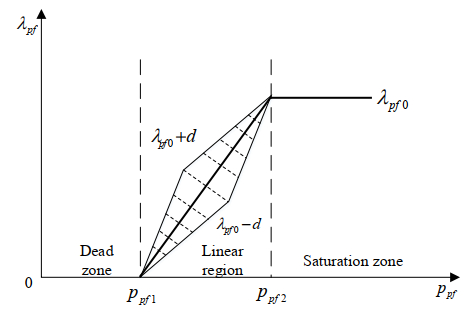
Based on the modified improvement of the consumer psychology model, when the tariff difference is in a small range, the customer's willingness to transfer electricity has a value of 0, i.e., uncertainty is not considered. When it is in the linear region, within a certain range, the tariff difference increases, the load response rate also increases, and the uncertainty increases. Beyond the range, the user bears the expectation above the limit, i.e., the maximum response rate is reached, and the price no longer stimulates uncertainty. When the price difference reaches the user's maximum expectation, the response is determined at that point. The corrected peak and valley tariff load changes are shown in Figure 1.
In Figure 1, $ \Delta {p_{pf}} $ is the peak-to-peak tariff difference, $ \Delta {p_{pf1}} $ is the linear region of the customer tariff difference, and $ \Delta {p_{pf2}} $ is the saturation of the customer tariff difference. $ {\lambda _{pf}} $ is the actual peak-to-peak response rate of the customer, and $ {\lambda _{pf0}} $ is the theoretical peak-to-peak response rate. $ {\lambda _{pf0}} + d $ and $ {\lambda _{pf0}} - d $ represent the extreme small values of the fuzzy affiliation parameters under uncertainty, respectively. In the linear interval, the load response rate fuzzy parameters $ {r_1} $ and $ {r_3} $ are the variables, and the fuzzy affiliation parameters of the load response rate in the peak-level linear interval segment are modeled with the results shown in Eq (6).
In Eq (6), $ d $ is the deviation quantity, which is related to the theoretical response rate of the load. The range of fuzzy parameters at this point is shown in Figure 2.
As shown in Figure 2, the value of $ d $ increases with the increase of $ {\lambda _{pf0}} $ when it is within the interval of $ [0, {\lambda _{pf\max }}/2] $, and the value of $ d $ decreases with the increase of $ {\lambda _{pf0}} $ when it is within the interval of $ [{\lambda _{pf\max }}/2, {\lambda _{pf\max }}] $. The values $ d $ are calculated as shown in Eq (7).
In Eq (7), $ {\lambda _{pf0}} $ represents the theoretical value of the peak-to-peak response rate, and $ {d_{pf\max }} $ represents the maximum deviation of the load response rate. At this point, the peak-valley tariff load amount considering uncertainty is shown in Eq (8).
In Eq (8), $ L_{i0}^t $ represents the PSDR baseline load when the incentive price is not implemented. $ {\lambda _{pf}} $, $ {\lambda _{pv}} $, and $ {\lambda _{fv}} $ denote the flat period response rate, trough response rate, and peak response rate, respectively. $ t $ represents the time period.
3.2. Multi-objective optimal scheduling model for power systems containing wind power based on fuzzy stochastic chance constraints
Existing methods usually use probabilistic constraints or fuzzy optimization in wind power dispatch optimization to deal with the uncertainty of wind power output or load demand. However, these methods have limitations. First, probabilistic constraint methods only model the stochastic nature of wind power output based on historical statistics, ignoring the fuzzy response of the load side, which makes it difficult to accurately represent the uncertainty of the power system supply and demand. Second, although the fuzzy optimization method can deal with the fuzziness of the load response, it cannot describe the probability distribution characteristics of the wind power output. It leads to insufficient adaptability of the scheduling scheme in practical applications. To alleviate the stability problem brought by wind power grid connection to power dispatch, a multi-objective optimal dispatching model needs to be established by considering the uncertainty of both sides of wind power load at the same time [31,32]. Starting from the lowest economic cost of the system $ {F_1} $, the objective function model is established as shown in Eq (9) [33].
In Eq (9), the former term represents the startup and shutdown costs and coal consumption cost of conventional units, and the latter term represents the compensation cost of IBDR. $ {\Omega _T} $ is the combined time period of the unit, and $ {\Omega _G} $ is the number of conventional units. $ p_i^t $ denotes the unit $ i $ output in $ t $ time period. $ {C_i}(p_i^t) $ indicates the cost of generation. $ u_{i, up}^t{s_{i, up}} $ and $ u_{i, down}^t{s_{i, down}} $ indicate the start-stop state volume. $ C_{Idr}^ + $ and $ C_{Idr}^ - $ indicate the incentive demand response compensation cost per unit plus or minus. $ \lambda _{Idr}^t $ denotes the response rate of incentive demand response. $ L_{i, Idr}^{t, + } $ and $ L_{i, Idr}^{t, - } $ denote the theoretically desired increase and decrease in the incentive demand response of the grid. The model is constructed based on the fuzzy stochastic chance constraint, starting from the power balance constraint, and using fuzzy variables in the network balance constraint to substitute the desired values as shown in Eq (10) [34].
In Eq (10), $ WT_i^t $ and $ \Delta WT_i^t $ represent the predicted output and prediction error of the wind turbine at $ i $ and $ t $. $ E(\Delta WT_i^t) $ is the expectation of forecast error, $ {\Omega _{WT}} $ is the set of wind farms, $ {\Omega _N} $ is the set of nodes, and $ L_i^t $ is the total load of node at the time $ i $ and $ t $. $ L_{i, Pdr}^t $ is the actual response of the price-demand response load. It considers the wind out point uncertainty and load response uncertainty, sets the confidence level of the positive and negative standby constraints to $ 1 - \frac{\alpha }{2} $ and $ 1 - \frac{\gamma }{2} $, and gets the constraints, as shown in Eq (11).
In Eq (11), $ A(t) = \sum\limits_{i \in {\Omega _G}} {I_i^t\min ({{\overline P }_i}, p_i^t + {r_{iup}}) + \sum\limits_{i \in {\Omega _{WT}}} {WT_i^t} } $ and $ B(t) = \sum\limits_{i \in {\Omega _G}} {I_i^t\max ({{\underline P }_i}, p_i^t + {r_{idown}}) + \sum\limits_{i \in {\Omega _{WT}}} {WT_i^t} } $. $ Ch $$ {\overline P _i} $ indicates the maximum output of the conventional unit, $ {\underline P _i} $ means the minimum output of the conventional unit, and $ {r_{iup}} $ and $ {r_{idown}} $ are the up and down climbing rates of the conventional unit $ i $, respectively. $ I_i^t $ is the state of the conventional unit $ i $ at the time of $ t $ indicated; a value of 1 indicates the on-state, and a value of 0 indicates the off-state. Considering the deterministic constraint, the upper and lower limits of the output of the conventional unit are constrained as shown in Eq (12).
The start-stop state constraint of the conventional unit is shown in Eq (13).
The climbing constraint of the conventional unit is shown in Eq (14).
The minimum continuous on-time constraint is shown in Eq (15).
The PSDR load constraint is shown in Eq (16).
The IBDR load constraint is shown in Eq (17).
From the above, it can be concluded that the fuzzy stochastic chance constraint combines stochasticity (e.g., wind power output is affected by meteorological variations) and fuzziness (e.g., non-determinism of load response to tariff variations) to characterize the bilateral uncertainty in wind power systems. In comparison with conventional probabilistic constraint and deterministic optimization methods, this study employs fuzzy stochastic chance constraints to construct a day-ahead scheduling optimization model. This approach enables the simultaneous consideration of the stochastic nature of wind power generation and the fuzzy nature of load demand. The conventional probabilistic constraint method primarily constructs a probabilistic model based on historical statistical data. However, it is incapable of effectively addressing the dynamic characteristics of wind power prediction error. Conversely, the deterministic optimization method faces challenges in adapting to changes in wind power and load demand.
Specifically, the fuzzy stochastic chance constraint method combines the advantages of probabilistic constraints and fuzzy optimization, which can deal with both random variables (fluctuations in wind power output) and fuzzy variables (uncertainty in load response). Also, the traditional probabilistic constraint approach is limited in its ability to describe the statistical characteristics of random variables. It cannot portray the subjective ambiguity of load response. Conversely, the fuzzy optimization approach is adept at dealing with expert experience and uncertainty. However, it is difficult to combine this approach with probabilistic constraints to ensure system robustness. The fuzzy stochastic chance constraint delineates the uncertainty at the load side through the affiliation function, and concomitantly, the chance constraint method is employed to ensure that the power system meets the operational requirements at a high level of confidence. This ensures the feasibility of the dispatch scheme while enhancing the system's economy and robustness. The model is solved using the multi-objective optimization problem characteristics. Commonly used multi-objective optimization methods are the Pareto optimal solution, weak Pareto optimal solution, and absolute optimal solution [35]. When there is no absolute optimal solution for subobjective contradiction, finding the Pareto optimal solution is the best choice. Then, the model is solved using the CPLEX solver, and multi-objective transformation and single-objective optimization methods such as the main objective and the maximum subordination methods are used [36]. Fuzzy random chance constraint rules are introduced to limit the uncertainty at the power and load side of the wind power system. The solved model is equivalently transformed with fuzzy random chance constraints. Among the positive and negative alternate constraints, the usual segment alternate constraints are transformed as shown in Eq (18).
The valley time standby constraint transformation is shown in Eq (19).
In summary, a multi-objective optimization scheduling model for wind power systems based on fuzzy random chance constraints is established to address the randomness and uncertainty issues of the load source dual side rough existence in wind power systems. Then, an equivalent class method with fuzzy random chance constraints is proposed for the fuzzy random variables in the model. The optimization model constructed by the research takes into account both the lowest system operating cost and the lowest carbon dioxide emissions. It can provide new ideas for the study of the randomness of wind power output on the source side and the uncertainty of load response on the load side.
4.
Simulation experiments and analysis of day-ahead dispatching models for power systems containing wind power
4.1. Simulation experiment analysis of parameter fitting distribution
The wind power output data of an energy laboratory is used to analyze the parameter fitting distribution effect. MATLAB R2021b is used to verify the fitting effect. The wind power prediction error data are all normalized, as shown in Figure 3.
Figure 3(a) shows the curve of wind farm output prediction error at time 1. Figure 3(b) shows the curve of wind farm output prediction error at time 22. In Figure 3, the frequency histograms at different times are almost the same, showing a state of almost zero skewness and thick-tailed peaks. The three classical fitted distributions indicate that the beta distribution is generally stable, and the fit is significantly worse. Both the normal and t-distributions can show peak characteristics to a certain extent. On the whole, the three classical fitting predictions are not accurate enough to accurately depict the characteristics of wind farm prediction errors. The experimental results are in line with expectations and confirm the correctness of using nonparametric fitting in the study. By continuing to use MATLAB to verify the effect of kernel parameter fitting, results are shown in Figure 4.
Figure 4(a) shows the kernel density estimation of wind farm output prediction error at time 1, and Figure 4(b) shows the kernel density estimation of wind farm output prediction error at time 22. Compared with the t-distribution, the kernel density function can better fit the probability density distribution of prediction error, showing a spike and a thick tail. Therefore, the kernel density function has high accuracy, superior to the use of parameter fitting modeling.
4.2. Simulation experiment and analysis of day-ahead scheduling model
The study uses the optimized IEEE 6-node three-unit model for simulation experiments. The parameter configuration of the conventional unit is shown in Table 1.
The system line parameter configuration is shown in Table 2.
Among the nodes, nodes 3, 4, and 5 belong to the load nodes. Moreover, the 24-h load of the three nodes is set to be the same, as shown in Table 3
PSDR-related parameters are set as follows: 1:00 to 6:00 and 22:00 to 24:00 are set as valley hours, 7:00 to 8:00 and 14:00 to 18:00 are set as normal hours, and 9:00 to 13:00 and 19:00 to 21:00 are set as peak hours. The entry tariff difference for peak and flat response rate curves is $50, and the saturation tariff difference is $400. The entry tariff difference for peak and valley response rate curves is $100, and the saturation tariff difference is $700. The entry tariff difference for flat and valley response rate curves is $50, and the saturation tariff difference is $400. The tariff for weekdays is $500. The tariff for peaks is $500–800, and the tariff for valleys is $200–500. IBDR-related parameters are set as follows: $ C_{Idr}^ + $ is $100, $ C_{Idr}^ - $ is $200, and the total duration of dispatch does not exceed 12 hours. The wind power output data is based on the Wind Power Prediction dataset provided by the Aliyun Tianchi platform (https://tianchi.aliyun.com/dataset/159885?utm_source=chatgpt.com), which contains measured data from wind farms and is used for wind power prediction research. Second, the topology and parameters of the power system are based on the IEEE 6-node system model, which is widely used in power system research and simulation (https://blog.csdn.net/2301_76674985/article/details/129199427?utm_source=chatgpt.com). Before conducting simulation experiments on the scheduling of the integrated wind power system, all the experimental data are pre-processed to ensure the completeness and accuracy of the data. The wind power output data is derived from measured data from an energy laboratory, and outlier detection is performed to remove extreme outliers. The kernel density estimation method is used to model the wind power forecast error. The load data is based on historical records, using interpolation to fill in missing values and normalization to ensure a reasonable data distribution.
Environment 1 is set to the objective of considering only the minimum economic cost. Environment 2 is set to consider only the minimum carbon emission. The remaining parameters of the two sets of environments are the same, and the single-objective optimization effect of the decision model is compared. Table 4 represents the optimization outcomes.
The output of each unit in the two environments is shown in Figure 5.
In Environment 1, the total cost is the lowest ($8.84 × 104), but the carbon emission is higher (5.54 × 104 kg). In Environment 2, the carbon emission decreases to 2.31 × 104 kg, but the total cost increases to $12.35 × 104. This indicates a significant change in the focus of the scheduling strategy under different optimization objectives. As shown in Figure 5, the unit power curves in Environment 1 indicate that the low-cost unit G1 operates at high load most of the time, mainly due to the lower operating cost and high economics of unit G1. During the dispatch optimization process, the system prioritizes the dispatch of unit G1 to reduce the overall generation cost. Meanwhile, unit G2 has a lower output most of the time due to its higher operating cost and tends to be shut down when load demand is low. Unit G2 is only activated when the system load demand is high. In addition, the output of the G3 unit fluctuates more during dispatch, mainly due to the fact that the unit G3 is used as an auxiliary unit responsible for providing regulation capability during periods of high demand fluctuation, despite its shorter overall operating time. Considering the effect of creep rate, unit G3 needs to regulate its output quickly during load fluctuations, which may lead to frequent startups and shutdowns, and higher startup and shutdown costs. The dispatch model prioritizes reducing the run time of the high-cost unit G2 and starting unit G3 for fast regulation during peak load demand to optimize economics, a strategy that helps reduce overall operating costs, although it may also increase startup and shutdown costs. On the contrary, in Environment 2 (carbon minimization), the output of unit G1 is significantly reduced, and the output of units G2 and G3 is significantly increased; the output of unit G3 is particularly increased. This indicates that the system gives priority to dispatching low-carbon units under the carbon minimization objective, even though it increases the total cost. Under this strategy, the low-carbon advantage of unit G1 is reduced, resulting in an increase in the number of starts and stops and a greater role for units with higher creep rates (e.g., G3). In this scenario, carbon emissions are reduced by 58.3%, but costs increase by 39.7%, indicating the need to weigh the relationship between economic costs and carbon emissions when implementing a carbon optimization strategy.
In Environment 3, scheduling optimization considering both total cost and carbon emissions is shown in Table 4. The ideal value of cost optimization F1 is set to $8.84 × 104, the ideal value of carbon emission optimization F2 is set to 2.31 × 104 kg, and the remaining settings are kept consistent with Environment 1 and Environment 2. The multi-objective optimization outcomes of the scheduling model are denoted in Table 5.
The total cost of system operation in multi-objective optimal scheduling is $10.36 × 104, carbon emissions are 2.66 × 104, and global optimization satisfaction is 0.713. Compared with Environment 1, the system cost increases by 17.19% and carbon emission decreases by 51.99%, increasing economic cost but improving environmental protection substantially. Compared with Environment 2, the system cost decreases by 16.11% and carbon emission increases by 15.15%, which reduces economic cost and takes into account certain environmental protection measures. The output of each unit of Environment 3 is shown in Figure 6.
Table 5 shows the scheduling results under Environment 3 (multi-objective optimization), which achieves a better balance between economics and environmental friendliness compared to single-objective optimization. In this case, the total cost is $10.36 × 104 and the carbon emission is 2.66 × 104 kg, which is an increase of 17.19% in cost but a decrease of 51.99% in carbon emission compared to Environment 1, and a decrease of 16.11% in cost and an increase of 15.15% in carbon emission compared to Environment 2. Figure 6 illustrates the results of scheduling optimization for unit output. Compared to Environment 1, the output of unit G1 is reduced, and the output of unit G3 is increased, reflecting that the multi-objective optimization strategy optimizes the overall scheduling of the unit while reducing carbon emissions. In this process, the dispatch model not only focuses on economics and carbon emissions but also needs to consider the unit's ramping capability and startup/shutdown costs. Compared to Environment 2, unit G1 remains partially operational, but units G2 and G3 have fewer starts and stops. This scheduling strategy of reducing the frequency of starts and stops not only helps to reduce startup/shutdown costs but also reduces the equipment maintenance costs associated with frequent starts and stops, thus improving the operating efficiency of the equipment. The sensitivity analysis demonstrates that this multi-objective optimization approach effectively balances the economic and environmental protection needs in the scheduling of wind power systems. However, the adjustment of the weights of the different objectives affects the allocation of unit output. In the context of high wind penetration, this strategy not only optimizes unit scheduling but also provides an effective solution for reducing maintenance costs and improving system stability. The incorporation of factors such as startup and shutdown costs, as well as creep rate, facilitates a more comprehensive understanding of the impact of the scheduling strategy on the fluctuation of unit output. This, in turn, contributes to the enhancement of the realistic adaptability of the scheduling model, particularly within the context of high penetration wind power.
5.
Discussion
With the integration of renewable energy sources into the grid and the large-scale application of demand-side response in actual power grids, uncertainty remains on both the source and load sides, which poses a serious challenge to the actual operation and scheduling of the power grid. Hao LX. et al. addressed the issue of randomness and uncertainty in renewable energy generation by modeling the uncertainty of renewable energy generation using probability constraints. Based on this, they proposed a practical multi-objective optimization scheduling model grounded on chance constrained programming, with the aim of minimizing operating costs [37]. Lee CY. et al. proposed a method using a modified particle swarm optimization algorithm with inertia weights to address the uncertainty issues in wind and solar photovoltaic power operations in microgrids. This approach addressed unexpected prediction errors caused by the uncertainty of renewable distributed generation and loads in the microgrid market, optimized the scheduling problem of the microgrid, and achieved the lowest operating cost [38]. Li Y. et al. proposed an interval method to quantify the uncertainty brought by the uncertainty of renewable energy resources and energy demand to the optimal operation of integrated energy systems. In the proposed model, the daily total cost was optimized, and the system operation constraints were fully considered and finally solved by the CPLEX optimizer [39].
According to the most recent studies, when confronted with the uncertainty inherent to the process of renewable energy generation, the prevailing approach entails the formulation of an optimization scheduling model for renewable energy distribution systems. The overarching objective of this model is to minimize the operational expenses of the entire system. This objective is pursued by employing diverse algorithms to identify the optimal solution. The research considers the uncertainty of wind power output and load response. It proposes a multi-objective optimization scheduling model for power systems based on fuzzy stochastic chance constraints. The goal of this model is to minimize economic operating costs and carbon emissions. At the same time, an equivalent class of fuzzy random constraints is proposed for the fuzzy random variables in the model, transforming the problem into a deterministic problem. The results show that this optimization method can ensure low operating costs of the power system while protecting the environment.
6.
Conclusions
In this study, a day-ahead scheduling optimization model for wind power systems based on fuzzy random chance constraints was proposed for the uncertainty problem of wind power output and load demand. In-depth research was carried out for source and load bilateral uncertainty modeling, multi-objective optimization, and scheduling scheme stability. The experimental results showed that the model could achieve the lowest operating cost and the lowest carbon emissions under single-objective optimization, striking a reasonable balance between the two with multi-objective optimization. Compared with the single-objective optimization, the multi-objective optimization increased the system cost by 17.19% and reduced the carbon emission by 51.99%. Compared with the minimum carbon emission optimization objective, system costs were reduced by 16.11% and carbon emissions increased by 15.15%, which indicates that the method could provide reasonable scheduling solutions under different optimization objectives and achieve a better trade-off between economy and environmental protection. To verify the effectiveness of the model, the experiments were compared with the single-objective optimization scheme, and the optimization capability was evaluated from both cost and carbon emission dimensions. The core contribution of this study is that it systematically constructs, for the first time, a collaborative modeling framework that simultaneously considers the stochasticity of wind power output and the ambiguity of load response. This effectively fills the research gap of coupling source-load uncertainty in the dispatch optimization of wind power systems. Traditional research focuses on unilateral uncertainty modeling, which proves difficult to comprehensively reflect the complexity of bidirectional fluctuations of supply and demand in the actual power system. This study integrates the kernel density estimation method with the fuzzy subordinate function modeling technique and establishes a wind power scheduling model that is closer to the actual operation scenario. This significantly improves the robustness and adaptability of the system. In addition, the study also provides operable optimization ideas and reference paths for actual wind power system scheduling. In the context of high wind power penetration, low-carbon grid transition, and rapid development of demand response mechanisms, this method provides a systematic optimization strategy for power systems to achieve cost control and carbon emission management at the same time. In the future, the method can be further expanded to real-time scheduling, multi-energy system optimization, and other application scenarios; combined with deep learning and reinforcement learning techniques, it can promote the intelligence and dynamic response capability of the scheduling model, so as to better serve the construction and operation of a new type of power systems.
7.
Future work
Despite the efficacy of the method in optimizing scheduling, there are still some limitations. First, the modeling of wind power prediction error has room for improvement. The current study adopts the kernel density estimation method to portray the uncertainty of wind power output. This can be combined with the deep learning method or the dynamic probability distribution adjustment to further improve the prediction accuracy and reduce the scheduling error in the future. Second, the current study's approach to uncertainty modeling of demand response is relatively simplistic. The study primarily describes the uncertainty of load response based on the triangular affiliation function. In the future, the introduction of user behavior analysis and dynamic tariff response mechanisms could improve the accuracy of load modeling. Furthermore, the implementation of alternative existing scheduling optimization methods (e.g., robust optimization, opportunity constrained planning, and reinforcement learning-based optimal scheduling) can be pursued to enhance the quantification of the scheduling performances of different methods. This approach will validate the advantages of the model proposed in this study under various operating conditions. Comprehensively, the scheduling methods proposed in this study achieve an effective balance between economy and environmental protection. In addition, the methods provide new optimization ideas and practical guidance for wind power scheduling optimization, grid economic operation, and clean energy promotion. In terms of practical application, the optimization method proposed in this study offers a more economical and low-carbon scheduling strategy for high-penetration wind power systems, particularly in scenarios such as new energy grid-connected scheduling and smart grid optimization. Future research endeavors should explore the potential of integrating the model with real-time dispatch systems. This integration would enable the model to be utilized not only for day-ahead dispatch but also for short-term load forecasting and real-time dispatch optimization.
Use of AI tools declaration
The author declare that he has not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The author declares that there is no conflict of interest in this article.









 DownLoad:
DownLoad: