This article aims to prove the existence and uniqueness of solutions to a nonlinear boundary value problem of fractional differential equations involving the Caputo-Hadamard fractional derivative with nonlocal fractional integro-differential boundary conditions. The concerned results are obtained employing topological degree for condensing maps via a priori estimate method and the Banach contraction principle fixed point theorem. Besides, two illustrative examples are presented.
1.
Introduction
With the advent of technologies allowing for large-scale, high throughput data, a much clearer understanding of the genomic mechanisms behind gene regulation have been gained. The scientists found that there are unexpected far more noncoding RNAs comparing with protein-coding genes and, and these noncoding regions play important roles in determining the complexity observed in the human genome [1,2]. Within these noncoding regions, long noncoding RNAs (lncRNAs), which are functionally defined as noncoding regions of RNA that are at least 200 base-pairs in length, have attracted lots of attention. Certain lncRNAs appear to act locally, while others have more distal regulatory effects, even acting across multiple chromosomes [3]. Many studies have identified specific functions of particular lncRNAs, including embryonic mechanisms, cell cycle functions, innate immunity, and disease processes. However, there are still thousands of lncRNAs have no identified functions [1,3,4,5,6]. Some studies have been performed that produce relatively few numbers of lncRNA functions [7], and have shown that the function of lncRNAs is highly cell-type-specific: one lncRNA may inhibit particular genes in one type of cell while promoting the same gene in another. This phenomenon makes it even more difficult to identify lncRNA functions on a large scale. Due to this specificity, researchers propose that future lncRNA studies should be performed on specific cell types to identify particular regulatory mechanisms.
One of the most prominent and intriguing applications of lncRNA regulatory investigation comes from cancer studies [8,9]. It has been shown that lncRNAs appear to have high connectivity with numerous diseases, especially cancer. Because of the highly cell type-specific nature of lncRNA regulatory functions and the irregularity of cancer cell genetic information, studying lncRNA regulation in specific cancer types may provide promising insight into specific genomic regulations of common cancer cells. In a few documented cases, specific lncRNAs have been shown to be significantly differentially expressed in specific cancer types, such as prostate cancer and breast cancer [1]. For these reasons, it seems appropriate to further investigate lncRNA-gene interactions in particular cancer cells.
The wealth of gene expression datasets available provides an opportunity to computationally identify co-expressed gene modules(CEMs), each of which is defined as a highly structured expression pattern on a specific gene set [10,11]. These CEMs tend to be functionally related or co-regulated by the same transcriptional regulatory signals (e.g., transcription factors, lncRNA and so on) under a specific condition or in a particular disease cell type. Overall, successful derivation of the CEMs may grant a higher-level interpretation of large-scale gene expression data, improve functional annotation of condition-specific gene activities, facilitate inference of gene regulatory relationships, hence, provide a better mechanism level understanding of complex diseases.
The computational identification of CEMs can be solved by a biclustering approach [12], which is a two-dimensional data mining technique that simultaneously identifies co-expressed genes under a subset of conditions. a high proportion of enriched biclusters on real datasets. Within this study, we try to identify new lncRNA-gene interactions and transcription factor-lncRNA partnerships from cancer RNA-seq data using a biclustering approach. The biclustering method will allow for the identification of particular expression patterns across multiple datasets, indicating networks of lncRNA and gene interactions. This developed method will also provide a framework for future lncRNA interaction studies. We applied this method on two sets of TCGA breast cancer RNA-seq data to generated CEMs based on known lncRNA-gene interactions. Then, the predicted CEMs are linked to lncRNA by a statistic p-value and the new lncRNA-gene relationship are generated. The evaluation on the predicted results showed that the pipeline can find some target genes for given lncRNA, and meanwhile the performance still has some space to be improved. We further conducted a TF motif analysis on the predicted CEMs and provide potential regulation cooperation between TFs and lncRNAs. The related original data with codes, results and supplementary data can be downloaded on https://github.com/IvesG/sGavin.git.
2.
Materials and method
2.1. Data collection
Two sets of TCGA (The Cancer Genome Atlas) breast cancer RNA-seq data, one from the normal cell (referred as normal data) and the other from tumor cell (referred as tumor data) were downloaded from https://portal.gdc.cancer.gov/. The normal and tumor data consist of 113 and 1091 samples, respectively. And of the 113 normal samples, 112 of them are from the same patient among the tumors. Both datasets contain 60,483 genes, among which there are 19,824 protein-coding genes and 7,399 long intergenic noncoding RNAs (lincRNAs) genes. The RNA-seq data are all Upper Quartile normalized FPKM (UQ-FPKM) values.
A total of 1,081 experimentally validated lncRNA-associated regulatory entries were downloaded from LncReg [13], describing the comprehensive regulatory relationships among 258 lncRNAs and 571 genes. All these relationships were manually collected from PubMed with focus on the data generated by laboratory methods, and can be categorized into up/down/active/inactive based on regulatory relationships or transcription/post-transcription/translation/post-translation based on regulatory mechanisms.
2.2. Extract expression of target genes from RNA-seq dataset
As we focus on lncRNA-gene interactions, the relationships downloaded from LncReg were filtered to retain only relationships describing genes regulated by lncRNAs with specified species information (constrained to Homo sapiens and Mus musculus), resulting 925 relationships in total for the downstream analysis, covering interactions between 309 unique human genes and 103 human lncRNAs, as well as between 199 mouse genes and 100 mouse lncRNAs. It is noteworthy that these 925 relationships include 28 post-transcriptional regulations, 41 post-translational regulations, 714 transcriptional regulations, 23 translational regulations, 1 transcriptional & translational regulation and 118 unspecified relationships.
As the table from LncReg [13] only provides gene symbols, while the RNA-seq dataset uses Ensembl ID as gene's identifiers, we use Ensembl BioMart [14] to match gene symbols with Ensembl IDs for all the genes and lncRNAs. Then we got orthologous genes between mouse and human also using BioMart; we found orthologous human genes for all 199 mouse genes, and 38 overlapped with original human genes. For convenience, we recorded human genes, mouse genes that don't overlap with human genes, human lncRNAs and mouse lncRNAs that don't overlap with human lncRNAs as HG, MG, HL, and ML, respectively.
We combined the normal and tumor RNA-seq dataset together, then extracted expression values for all the HG, MG, HL, ML, protein-coding genes (PC, the remaining protein-coding genes except HG and MG) and lincRNAs (linc, the remaining lincRNA except HL and ML). Taking the genes as rows and the conditions as columns, we obtained the RNA-seq expression matrix on which biclustering will be performed to detect CEMs.
2.3. Bi-clustering analysis
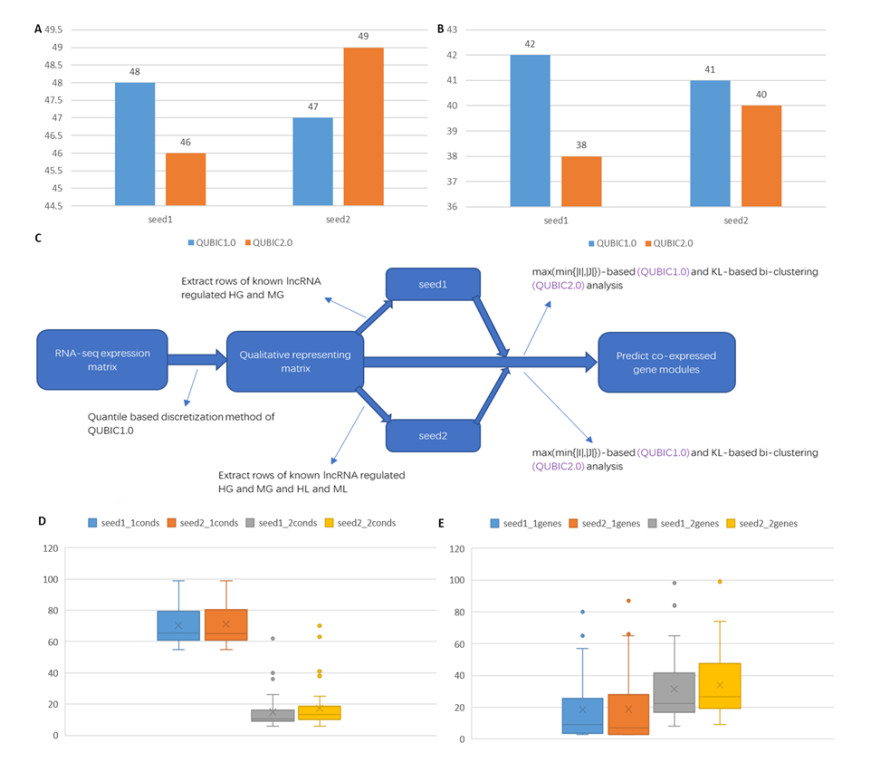
QUBIC is a biclustering analysis tool designed for co-expression analyses of genes based on their gene-expression patterns under multiple conditions. The software can generally identify all statistically significant groups, or biclusters, of genes with similar expression patterns under at least a specific number of experimental conditions, which tend to be more sensitive and more specific than other biclustering tools [15]. We use a quantile-based discretization method of QUBIC to generate a qualitative representing matrix for the RNA-seq expression matrix. Then we extracted the rows of known lncRNA regulated HG and MG from this representing matrix as seed 1 and HG, MG, HL, and ML rows as seed 2. Next bi-clustering analysis was performed on these two seeds to predict co-expressed gene modules (CEMs) in the qualitative representing matrix, respectively.
2.4. Predict the potential lncRNA-gene interactions
For an identified CEMs, we calculated the P-value of a bicluster enriched with genes regulated by a lncRNA using the hypergeometric function [16],
where r is the number of genes in a CEMs (with size n) that regulated by certain lncRNA, N is the total number of known lncRNA regulated genes in the whole genome, K is the number of genes regulated by that lncRNA in the whole genome.
We assumed that, if the known target genes of a given lncRNA are highly covered by a CEM with a significant p-value, the other genes in this CEM have high possibilities regulated by the given lncRNA. Thus, we used the smallest P-value for all possible lncRNAs as the p-value of the current bicluster and the relationships between lncRNA and genes in the bicluster are predicted.
2.5. Validation of the prediction
To evaluate the performance of the new methods on the prediction of new relationships between lncRNA and genes, we randomly separate seed2 into two parts with equal size named seedpart1 and seedpart2, for multiple times. Then bi-clustering analysis will be performed on seedpart2 to predict co-expressed gene modules (CEMs). For seedpart1 we find its part which is covered by co-expressed gene modules (CEMs) from seedpart2. We calculate the cover ratios by the size of seedpart1 to be divided by the size of the covered part by CEMs generated from seedpart2. Also, we calculate the p-values for the coverage rates to present the statistical significance of them.
2.6. Motif analysis on predicted CEMs
We choose several significant CEMs with sizes or conditions below 100, to conducted TF motif analysis. The promoter regions of the corresponding genes are inputted into the sub-routine findMotifs.pl of Homer [17], respectively. The script findMotifs.pl can firstly search for the upstream promoter sequences of a certain length automatically, and then perform motif finding on the promoters. For each run of findMotifs.pl on the datasets, we let the program output at most 5 top-ranking motifs, i.e. there will be up to 5 motifs discovered by findMotifs.pl for each CEMs. To evaluate the validity of the discovered motifs, findMotifs.pl automatically compares the similarity between the discovered motif profiles and the motif profiles archived in JASPAR [18] v2018 (http://jaspar.genereg.net/) under its default parameter setting. For each discovered motif having similarity with at least one motif archived in JASPAR, we present its motif logo as well as the information of its most similar motif in JASPAR.
3.
Results
3.1. The known interactions of genes and lncRNAs
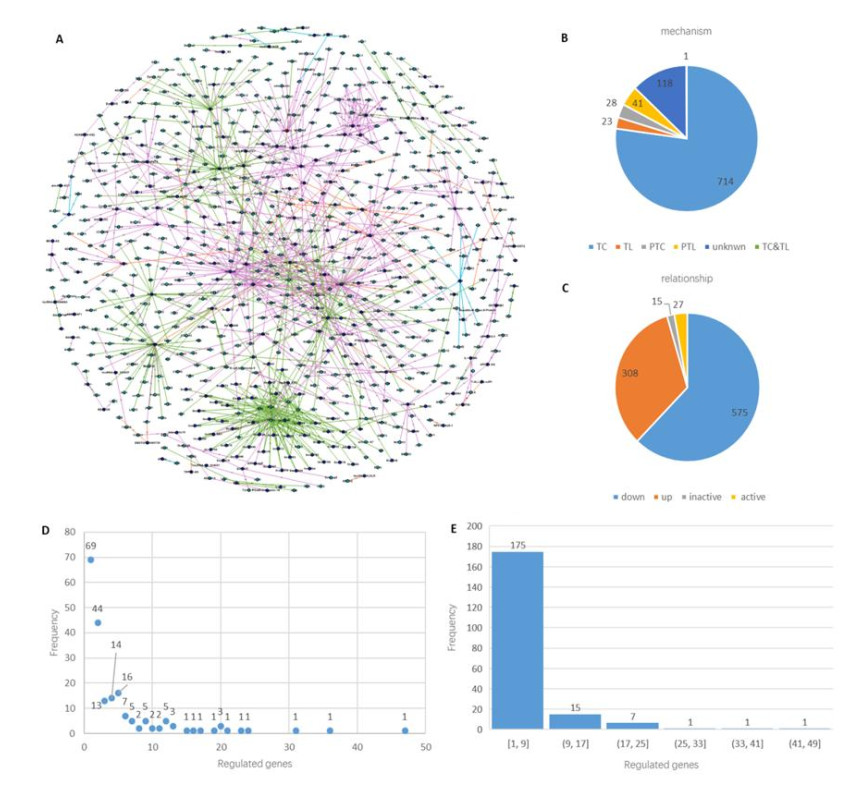
All the known interactions between lncRNAs and genes are showcased in Figure 1A. The related data can be download from https://github.com/IvesG/sGavin.git data/LncReg0419 and more details are written in data/readme.txt. In figure 1A, dark-blue nodes represent LncRNAs, light-blue nodes represent proteins, pink edges represent interactions documented in Homo, green edges represent interactions documented in Mus, orange edges represent interactions documented in both Homo and Mus. Meanwhile, there are some labels on the edges, categorized based on regulatory mechanisms including PTL (post-translational regulation), TC (transcriptional regulation), PTC (post-transcriptional regulation), TL (translational regulation), and NS (not sure). The distribution above is displayed in Figure 1B and nearly three fourth (714/925) of them are identified at the transcriptional level. Other labels on the edges are categorized based on regulatory relationships including down, up, active and inactive. The distribution above is displayed in Figure 1C. The down relationships (575) are more than up relationships (308), and the proportion of active/inactive is scarce (4.5%).
Figure 1E showed the distribution of a number of genes regulated by each lncRNA. It can be found that most lncRNA (~78%) regulate less than 5 genes. To show the specific details of the number of genes regulated by each lncRNA, Figure 1D is made, each point in the Figure 1D reflect the number of lncRNA (horizontal coordinate) that regulate certain number of genes (longitudinal coordinates) e.g. the point with coordinate (4, 14) in Figure 1D indicate that there are 14 lncRNA and each of them regulate 4 genes. The lncRNA that regulate more genes in Figure 1D belongs to the more concentrated parts in Figure 1(A).
3.2. The predicted co-expressed gene modules (CEMs)
With the quantile-based discretization method and biclustering analysis, there are some co-expressed gene modules (CEMs) are found. The details of the way we identify CEMs are showcased in Figure 2C. Figure 2A shows the number of co-expressed gene modules(CEMs) we have got from seed1 and seed2 processed by max(min [19])-based (QUBIC1.0, [15,20]) and KL-based bi-clustering analysis (QUBIC2.0 [21]) respectively. And the distributions of numbers of genes and conditions for each CEM can be found in Figure 2D and Figure 2E. For instance, label seed1_1genes represent that Qubic1.0 is performed on seed1. To better illustrate the distributions, we have constrained the number of each gene and the number of each condition below 100 (in Figure 2B). It is found that the KL-based biclustering method tends to generate CEMs that contain fewer genes while more conditions than max(min [22])-based biclustering method from Figure 2D and Figure 2E. The difference between the results (whether the distribution of genes sizes and condition sizes or the number of CEMs that we have predicted) we get from seed1 and seed2 is subtle.
3.3. Predicting potential interaction between lncRNAs and genes
The proportion of CEMs that have significant P-values (below a pre-selected P-value cutoff) as well as proportions of the number of unique enriched lncRNA in each bicluster that belong to certain categories (i.e., number of lncRNA = 2, 3 or > 3) are calculated and shown in Figure 3A and Figure 3B. In the figures, Seed1_qubic1 represent the proportions from the results obtained using quantile discretization and using max(min [23])-based biclustering on seed 1, seed1_qubic2 represent using quantile discretization and using KL-based biclustering on seed1. In Figure 3A, it can be found that most CEMs have P-value more than 0.001 and seed1_qubic1 seems to have more significant P-value. Constrain P-value below 0.00001 and there is barely CEMs remained (less than 7%). In Figure 3B the majority of (more than70%) CEMs are with enriched lncRNA more than 3 and especially most (around 85%) of CEMs from seed1_qubic1.
3.4. Performance evaluation of the pipeline
For validation, we separated the HG + MG genes into two parts randomly and equally for 10 times and obtained 10 cover ratios correspondingly to check the accuracy of the previously predicted genes. The results of our validation are calculated and shown in Table 1. From Table 1 it can be found that all of the cover ratios are under 25% and the average ratio is 16.25%. We further calculated the p-value of the coverage rates. The results indicated that even the coverage date has a lot of space to be improved, the statistical significance of them are acceptable.
3.5. TF motif analysis on CEMs
Since lncRNA plays an important role in regulation, they should have cooperation with transcription factor [23,24]. Thus we conduct the analysis about the DNA binding sites of related to CEMs [19,22,25]. As described in the Method section, we choose five CEMs to conducted TF motif analysis. The corresponding gene list files each containing 3, 6, 14, 20 and 21 genes. The predicted motifs and the comparison between them and JASPAR motifs are listed in Table 2, along with the function of the target TFs. In Table 2, the second column has the name of lncRNA related with this CEMs and the p-value of their correlations; The third column contains the motif consensus by Homer; The fourth column provides TF names of the most similar motifs in JASPAR, along with the similarity scores in the fifth column. These TFs may have cooperation with corresponding lncRNAs. In the first column, all the P-value of the LncRNA from the CEM is below 0.01 and the least P-value is from LncRNA HOTAIR. The supplementary table S1 with more details, including and the logo of discovered motifs and the functions of corresponding TFs, can be downloaded by visiting the GitHub link.
3.6. Gene ontology terms and KEGG pathway information of selected CEMs
In order to further evaluate the biological significance of the identified CEMs, we tested the enrichment of the genes in each CEM in Gene ontology terms and KEGG pathways using clusterProfiler package of R project BioConductor under q-value cutoff 0.05, of which the description of the GO terms and KEGG pathways that the CEMs are enriched in are presented in Table 3 and Table 4 respectively. And the supplementary table S2 with more details, including original and adjusted P-value, proportion of the matched genes, gene's ID, etc., can be downloaded on GitHub link.
4.
Discussion
Within this study, we have developed a method for elucidating lncRNA-gene and transcription factor-lncRNA interactions using a biclustering approach. The method was performed on 2 breast cancer RNA-seq datasets from TCGA. The bicluster method allows for the identification of particular expression patterns across multiple datasets, indicating networks of lncRNA and gene interactions. The developed method will also provide a way for future lncRNA interaction studies. Certainly, the predict performance still far from satisfactory, which is not unexpected since we only used RNA-Seq data. Actually, the interaction mechanism between lncRNA and genes are far more complex, and more data should be involved if we want to capture the whole picture of them. We are planning to include some other data, like proteomics and chromatin accessibility information, to improve the prediction. Besides, the evaluation on the relationship between lncRNA and predicted CEMs also has the potential to be improved, e.g. calculating the adjusted P-value or overall P-value in place of the original P-values used in this study. In view of the application, we will work on more specific examples of the regulatory functions of some particular lncRNAs and identify some hypothesized mechanisms of these regulatory functions. Also, the further analysis of the difference of lncRNA related genes between tumor and normal samples could provide more information for studying the process and mechanism of cancer occurrence and development, e.g. determination of the stage of developed tumors, which will be our concern in the future research.
Acknowledgments
This work was supported by the National Nature Science Foundation of China (NSFC) [61772313 and 61432010], Young Scholars Program of Shandong University [YSPSDU, 2015WLJH19], the Innovation Method Fund of China (2018IM020200), and Shanghai Municipal Science and Technology Major Project (2018SHZDZX01) and ZHANGJIANGLAB. Qin Ma's work was supported by an R01 Award from the National Institute of General Medical Sciences of the National Institutes of Health [GM131399-01]. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation [ACI-1548562]. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health and the National Science Foundation.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: