Relation theoretic metrical fixed point results for Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction with an application

1.   Introduction

In 1922, Banach ^[1] proved his noted contraction mapping theorem which is now popularly referred to as Banach contraction principle (in short BCP) which asserts that, every contraction mapping on a complete metric space admits a unique fixed point. Due to the enormous utility and applications of this classical result, BCP has further been extended and generalized in various directions ^{[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]}. In 1986, Turinici ^[17] was the first mathematician who initiated the idea of an order-theoretic fixed point result. In 2004, Ran and Reurings ^[18] established a relatively more natural order-theoretic version of BCP besides presenting an application of their result to matrix equations. Thereafter, Samet and Turinici ^[19] obtained fixed point results under symmetric closure of an amorphous binary relation for nonlinear contractions. Recently, Alam and Imdad ^[20] obtained a relation-theoretic analogue of BCP employing an arbitrary binary relation which unify several well-known relevant order-theoretic results. In 2015, Khojasteh et al.^[21] introduced the notion of $\mathcal{Z}$-contraction using a family of control functions known as simulation functions and unified several types of linear as well as nonlinear contractions of the existing literature. Recently, Sawangsup and Sintunavarat ^[22] have combined these two ideas to define the notion of $\mathcal{Z}_\mathcal{R}$-contraction and utilized the same to prove some fixed point results in complete metric spaces equipped with a transitive binary relation.

In 2009, Suzuki ^[23] introduced yet another new contraction often referred as Suzuki contraction which enunciates that a self-mapping $S$ on a metric space $(M, d)$ is called a Suzuki contraction if for all $r, s\in M$ with $r\not = s$ and $\frac{1}{2}d(r, Sr) < d(r, s)\ \text{implies}\ d(Sr, Ss) < d(r, s)$ and utilized this contraction to prove fixed point result which remains yet another substantial generalization of BCP. In recent past, Kumam et al. ^[24] introduced the idea of Suzuki type $\mathcal{Z}$-contraction and utilized the same to prove a fixed point theorem.

In this article, we define the notion of Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction, where $\mathcal{R}$ is an amorphous binary relation and also provide some examples to exhibit the genuineness of our newly introduced contraction over $\mathcal{Z}$-contraction, Suzuki type $\mathcal{Z}$-contraction and $\mathcal{Z_\mathcal{R}}$-contraction. We prove an existence and corresponding uniqueness fixed point results for Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction employing an amorphous binary relation on metric spaces without completeness which in turn generalizes many well-known results of the existing literature. An example is adopted to demonstrate the utility of our newly proved results over earlier ones especially due to Sawangsup and Sintunavarat ^[22] and Kumam et al. ^[24]. Finally, we utilize our main results to discuss the existence and uniqueness of solutions of a family of nonlinear matrix equations.

2.   Preliminaries

To make our paper self-contained, we recall the following terminological and notational conventions. In what follows $\mathbb{N}$, $\mathbb{Q}$ and $\mathbb{R}$ respectively denote the sets of natural numbers, rational numbers and real numbers wherein $\mathbb{N}_0 = \mathbb{N}\cup\{0\}$.

In 2015, Khojasteh et al.^[21] initiated the idea of simulation functions as follows:

Definition 2.1. A mapping $\zeta:[0, \infty)\times[0, \infty)\rightarrow\mathbb{R}$ is said to be a simulation function if the following conditions are satisfied:

($\zeta_1$) $\zeta(0, 0) = 0$;

($\zeta_2$) $\zeta(x, y) < y-x$ for all $x, y > 0$;

($\zeta_3$) if $\{x_n\}, \{y_n\}$ are sequences in $(0, \infty)$ such that $\lim\limits_{n\to\infty}x_n = \lim\limits_{n\to\infty}y_n > 0$, then $\limsup\limits_{n\to\infty}\zeta(x_n, y_n) < 0.$

From now on, the family of all simulation functions will be denoted by $\mathcal{Z}$. Some well-known examples of simulation functions available in the existing literature are as follows:

Example 2.1. ^{[21,25,26,27]} We define the mappings $\zeta_i:[0, \infty)\times[0, \infty)\rightarrow\mathbb{R}$ for $i = 1, 2, 3, 4, 5$, as follows:

● $\zeta_1(x, y) = \Psi(y)-\Phi(x)$ for all $x, y\in[0, \infty)$, where $\Phi, \Psi:[0, \infty)\rightarrow[0, \infty)$ are two continuous functions such that $\Psi(x) = \Phi(x) = 0$ if and only if $x = 0$ and $\Psi(x) < x\leq\Phi(x)$ for all $x > 0$.

● $\zeta_2(x, y) = y-\eta(y)-x$ for all $x, y\in[0, \infty)$, where $\eta:[0, \infty)\rightarrow[0, \infty)$ is a lower semi continuous function and $\eta(x) = 0$ if and only if $x = 0$.

● $\zeta_3(x, y) = \alpha y-x$ for all $x, y\in[0, \infty)$, where $\alpha\in[0, 1)$.

● $\zeta_4(x, y) = y-\int_{0}^{x}\varphi(x)dx$ for all $x, y\in[0, \infty)$, where $\varphi:[0, \infty)\rightarrow[0, \infty)$ is a function such that $\int_{0}^{\epsilon}\varphi(x)dx$ exists and $\int_{0}^{\epsilon}\varphi(x)dx > \epsilon$ for all $\epsilon > 0.$

Now, we add the following example to this effect.

● $\zeta_5(x, y) = \frac{y}{\alpha y+1}-x$ for all $x, y\in[0, \infty)$ and $\alpha > 0$.

For more examples and related results on simulation functions, one can consult e.g. ^{[21,25,26,27,28,29,30,31,32,33]} and references cited therein.

Now, we recollect the definition of $\mathcal{Z}$-contraction as follows:

Definition 2.2. ^[21] Let $(M, d)$ be a metric space and $S:M\rightarrow M$. Then $S$ is said to be a $\mathcal{Z}$-contraction w.r.t. some $\zeta\in\mathcal{Z}$ if

If we take $\zeta(x, y) = \alpha y-x$ for all $x, y\in[0, \infty)$ with $\alpha\in[0, 1),$ then $\mathcal{Z}$-contraction reduces to Banach contraction.

Remark 2.1. Due to the condition $(\zeta_2)$, we have $\zeta(x, x) < 0$ for all $x > 0$. Therefore, if a mapping $S$ is a $\mathcal{Z}$-contraction then it cannot be an isometry.

Using $\mathcal{Z}$-contraction, Khojasteh et al.^[21] obtained the following theorem and deduced several known as well as unknown new results by varying simulation functions.

Theorem 2.1. ^[21] Let $(M, d)$ be a complete metric space and $S:M\rightarrow M$ be a $\mathcal{Z}$-contraction w.r.t. some $\zeta$. Then $S$ has a unique fixed point.

Recently, Kumam et al.^[24] extended the result of Khojasteh et al.^[21] by introducing the concept of Suzuki type $\mathcal{Z}$-contraction.

Definition 2.3. ^[24] Let $(M, d)$ be a metric space and $S:M\rightarrow M$. Given $\zeta\in\mathcal Z$, we say that $S$ is Suzuki type $\mathcal{Z}$-contraction w.r.t. some $\zeta$ if the following holds:

for all $r, s\in M$ with $r\not = s$.

Also, authors in ^[24] obtained the following fixed point result with an additional assumption on the involved mapping as follows:

Theorem 2.2. ^[24] Let $(M, d)$ be a complete metric space and $S:M\rightarrow M$ a Suzuki type $\mathcal{Z}$-contraction w.r.t. some $\zeta$. Then $S$ has a unique fixed point and for every $r_0\in M$, the Picard sequence $S^n(r_0)$ for all $n\in\mathbb{N}$, converges to the fixed point of $S$, provided $S$ enjoys the property $(K)$ (see Definition 2.5, ^[24]).

In order to prove our results, we require some basic relation theoretic notions, definitions and relevant results described in the following.

Any subset $\mathcal{R}$ of $M\times M$ is said to be a binary relation on a non-empty set $M$. Trivially, $\emptyset$ and $M\times M$ are known as the empty relation and the universal relation on $M,$ respectively. From now on, a non-empty binary relation will be denoted by $\mathcal{R}$. If $(r, s)\in\mathcal{R}$ and $(s, t)\in\mathcal{R}$ imply $(r, t)\in\mathcal{R},$ for any $r, s, t\in M,$ then $\mathcal{R}$ is said to be transitive relation on $M$. Furthermore, if $S$ is a self mapping on $M,$ then $\mathcal{R}$ is said to be $S$-transitive if it is transitive on $S(M)$. The inverse of $\mathcal{R}$ is denoted by $\mathcal{R}^{-1}$ and is defined as $\mathcal{R}^{-1}: = \{(r, s)\in M\times M:(s, r)\in\mathcal{R}\}$ and $\mathcal{R}^s: = \mathcal{R}\cup\mathcal{R}^{-1}$. Two elements $r$ and $s$ of $M$ are said to be $\mathcal{R}$-comparable if $(r, s)\in\mathcal{R}$ or $(s, r)\in\mathcal{R}$ and is denoted by $[r, s]\in\mathcal{R}.$

Proposition 2.1. ^[8] For a binary relation $\mathcal{R}$ defined on a non-empty set $M,$

Definition 2.4. ^[8] Let $\mathcal{R}$ be a binary relation on a non-empty set $M.$ A sequence $\{r_n\}\subset M$ is called $\mathcal{R}$-preserving if

Definition 2.5. ^[8] Let $\mathcal{R}$ be a binary relation on a non-empty set $M$ and $S:M\rightarrow M.$ Then $\mathcal{R}$ is said to be $S$-closed if for any $r, s\in M$,

Definition 2.6. ^[34] Let $(M, d)$ be a metric space and $\mathcal{R}$ be binary relation on $M$. We say $M$ is $\mathcal{R}$-complete if every $\mathcal{R}$-preserving Cauchy sequence converges to some point of $M.$

Remark 2.2. Every complete metric space is $\mathcal{R}$-complete for arbitrary binary relation $\mathcal{R}$. On the other hand, under the universal relation $\mathcal{R}$-completeness coincides with the usual completeness.

Definition 2.7. ^[8] Let $(M, d)$ be a metric space and $\mathcal{R}$ a binary relation on $M.$ We say $\mathcal{R}$ is $d$-self-closed if whenever $\mathcal{R}$-preserving sequence $\{r_n\}$ converges to $r$, then there exists a subsequence $\{r_{n(l)}\}$ of $\{r_n\}$ with $[r_{n(l)}, r]\in\mathcal{R}$ for all $l\in\mathbb {N}_0$.

Definition 2.8. ^[20] Let $(M, d)$ be a metric space, $S:M\rightarrow M$ and $\mathcal{R}$ be a binary relation on $M$. Then $S$ is said to be $\mathcal{R}$-continuous at $r\in M$ if for any $\mathcal{R}$-preserving sequence $\{r_n\}$ in $M$ with $r_n\stackrel{d}\longrightarrow r$, implies $Sr_n\stackrel{d}\longrightarrow Sr$. If $S$ is $\mathcal{R}$-continuous at each point of $M,$ then we say that $S$ is $\mathcal{R}$-continuous.

Remark 2.3. Every continuous mapping can be treated as $\mathcal{R}$-continuous mapping (irrespective of a binary relation $\mathcal{R}$). On the other hand, $\mathcal{R}$-continuity coincides with the usual continuity under the universal relation.

Definition 2.9. ^[35] For $r, s\in M$, a path (of length $n$, $n\in\mathbb{N}$) in $\mathcal{R}$ from $r$ to $s$ is a sequence (finite) $\{r_0, r_1, r_2, ..., r_n\}\subseteq M$ such that $r_0 = r, \ r_n = s$ with $(r_i, r_{i+1})\in\mathcal{R}$ for each $i\in\{0, 1, ..., n-1\}$.

Notice that a path of length $n$ involves $n+1$ elements of $M$, although they are not necessarily distinct.

Definition 2.10. ^[20] A subset $N\subseteq M$ is said to be $\mathcal{R}$-connected if for each $r, s\in N$, there exists a path from $r$ to $s$ in $\mathcal{R}$.

We use the following notations to this effect.

(●) $M(S; \mathcal{R}): = \{r\in M :(r, Sr)\in\mathcal{R}\}$, where $S:M\rightarrow M$ be any given mapping;

(●) $\varUpsilon(r, s, \mathcal{R}): =$ the family of all paths from $r$ to $s$ in $\mathcal{R}$, where $r, s\in M$.

In 2018, Sawangsup and Sintunavarat ^[22] introduced the notation of $\mathcal{Z}_\mathcal{R}$-contraction as follows:

Definition 2.11. ^[22] Let $(M, d)$ be a metric space equipped with a binary relation $\mathcal{R}$ and $\zeta\in\mathcal Z$. A mapping $S:M\rightarrow M$ is said to be a $\mathcal{Z}_\mathcal{R}$-contraction w.r.t. $\zeta$ if the following holds:

In ^[22] authors obtained the following relation theoretic fixed point result in the setting of a complete metric space equipped with a transitive binary relation.

Theorem 2.3. Let $(M, d)$ be a metric space, $\mathcal{R}$ a binary relation on M and $S:M\rightarrow M.$ If the following hold:

(i) $M(S; \mathcal{R})\not = \emptyset$;

(ii) $\mathcal{R}$ is $S$-closed;

(iii) $\mathcal{R}$ is transitive;

(iv) $S$ is a $(\mathcal Z, \mathcal{R})$-contraction w.r.t. some $\zeta\in\mathcal{Z}$;

(v) $M$ is complete;

(vi) either $S$ is continuous or $\mathcal{R}$ is $d$-self-closed,

then $S$ has a fixed point. Furthermore, if $\varUpsilon(r, s, \mathcal{R})$ is non-empty for all $r, s\in M,$ then the fixed point of $S$ is unique.

3.   Main results

In this section, motivated by the notion of Suzuki type $\mathcal{Z}$-contraction, we define the notion of Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction as follows:

Definition 3.1. Let $\mathcal{R}$ be a binary relation on metric space $(M, d)$ and $S:M\rightarrow M.$ Given $\zeta\in\mathcal Z$, we say that $S$ is Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction if the following holds:

where $(r, s)\in\mathcal{R^*}: = \{(r, s)\in\mathcal{R}: Sr\not = Ss\}.$

Due to the symmetricity of the metric $d,$ we have the following proposition.

Proposition 3.1. Let $(M, d)$ be a metric space equipped with a binary relation $\mathcal{R}$ and $S:M\rightarrow M$. For a given $\zeta\in\mathcal{Z}$, the below mentioned conditions are equivalent:

(i) for all $r, s\in M\ \mathit{\text{with}}\ (r, s)\in\mathcal{R^*}\ \mathit{\text{and}}\ \frac{1}{2}d(r, Sr) < d(r, s)\ \mathit{\text{implies}}\ \zeta(d(Sr, Ss), d(r, s))\geq0;$

(ii) for all $r, s\in M\ \mathit{\text{with}}\ [r, s]\in\mathcal{R^*}\ \mathit{\text{and}}\ \frac{1}{2}d(r, Sr) < d(r, s)\ \mathit{\text{implies}}\ \zeta(d(Sr, Ss), d(r, s))\geq0.$

The following implications involving Definitions 2.2, 2.3, 2.11 and 3.1 naturally holds.

but the reverse implications are not true in general (see $Examples 3.4.\ and\ 3.5.$ in ^[22] for $\mathcal{Z_\mathcal{R}}$-contraction and Example $3.1.$ in ^[24] for Suzuki type $\mathcal{Z}$-contraction which are not $\mathcal{Z}$-contraction). Here, we provide an example of Suzuki type $\mathcal{Z}_\mathcal{R}$-contraction which is neither Suzuki type $\mathcal{Z}$-contraction nor $\mathcal{Z_\mathcal{R}}$-contraction.

Example 3.1. Let $\big(M = (-2, 8), d\big)$ be a metric space endowed with a binary relation $\mathcal{R}: = \{(0, 2), (3, 4), (5, 2), (5, 3), (6, 1), (6, 6), (6, 7)\}$, where $d$ is usual metric on $M$. Define a mapping $S:M\rightarrow M$ by

Observe that $\mathcal{R^*} = \{(0, 2), (5, 2)\}$ but the condition $\frac{1}{2}d(r, Sr) < d(r, s)$ is mate out merely by one element $(r, s) = (5, 2)\in\mathcal{R^*}$. Now, if we take $\zeta_*(x, y) = \frac{y}{3}-x$ for all $x, y\in[0, \infty),$ then $S$ remains a Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction w.r.t. $\zeta_*$ but not $\mathcal{Z_\mathcal{R}}$-contraction, as $(0, 2)\in\mathcal{R}$ and

then in view of $(\zeta_2)$, we can not find any $\zeta\in\mathcal{Z}$ such that equation (2.3) is satisfied. Also, $2, 0\in M$ with $S2\not = S0$ such that $\frac{1}{2}d(2, S2) < d(2, 0)$ but $d(S0, S2) = 2 = d(0, 2)$, then again due to $(\zeta_2)$, there does not exist any $\zeta\in\mathcal{Z}$ such that equation (2.2) is satisfied and hence $S$ is not a Suzuki type $\mathcal{Z}$-contraction.

Our first new result is the next:

Theorem 3.1. Let $(M, d)$ be a metric space, $\mathcal{R}$ be a binary relation on $M$ and $S:M\to M$. Suppose that the following conditions hold:

(i) $M(S; \mathcal{R})$ is non-empty;

(ii) $\mathcal{R}$ is $S$-closed and $S$-transitive;

(iii) $S$ is Suzuki type $\mathcal Z_\mathcal{R}$-contraction w.r.t. some $\zeta\in\mathcal{Z}$;

(iv) $M$ is $\mathcal{R}$-complete;

(v) either $S$ is $\mathcal{R}$-continuous or $\mathcal{R}$ is $d$-self-closed.

Then $S$ has a fixed point. Moreover, for each $r_0\in M(S; \mathcal{R})$, the Picard sequence $S^n(r_0)$ for all $n\in\mathbb{N}$, converges to a fixed point of $S$.

Proof. Since $M(S; \mathcal{R})\not = \emptyset,$ let $r_0$ be an arbitrary point such that $r_0\in M(S; \mathcal{R}).$ Now define a sequence $\{r_n\}$ by $r_n = S^nr_0, \ \text{for all}\ n\in\mathbb{N}_0.$ Since $(r_0, Sr_0)\in\mathcal{R}$, then by $S$-closedness of $\mathcal{R}$, we have

Now, if there exists some $n_0\in\mathbb{N}_0$ such that $d(r_{n_0}, Sr_{n_0}) = 0$ then the result follows immediately. Otherwise, for all $n\in\mathbb{N}_0$, $d(r_{n}, Sr_{n}) > 0$ so that $Sr_n\not = Sr_{n+1}$ which implies that $(r_n, r_{n+1})\in\mathcal{R^*}$ and $\frac{1}{2}d(r_n, Sr_n) < d(r_n, Sr_n).$ Since $S$ is Suzuki type $\mathcal Z_\mathcal{R}$-contraction, we have

which implies that $d(r_{n+1}, r_{n+2}) < d(r_n, r_{n+1})$ for all $n\in\mathbb{N}_0$. Therefore, $\{d(r_n, r_{n+1})\}_{n = 0}^{\infty}$ is a monotonically decreasing sequence of positive real numbers and hence there exists $l\geq0$, such that $\lim\limits_{n\to\infty}d(r_n, r_{n+1}) = l.$ We claim that $l = 0.$ On contrary, assume that $l > 0$ then using (3.1) and $(\zeta_3)$, we obtain

which is a contradiction and hence $l = 0, i.e.,$

Next, we wish to show the Cauchy-ness of the sequence $\{r_n\}$. To accomplish this, on contrary assume that $\{r_n\}$ is not Cauchy, then there exists $\epsilon > 0$ and $l_0\in\mathbb{N}_0$ with $m(l) > n(l) > l \geq l_0,$ such that

Thus, we can have

taking $l\to \infty$ and using (3.4), we get

and hence

Then from (3.4) and (3.5), one can select a positive integer $N\in\mathbb{N}$ such that

As the sequence $\{r_n\}$ is $\mathcal{R}$-preserving and $\mathcal{R}$ is $S$-transitive, therefore $(r_{m(l)}, r_{n(l)})\in\mathcal{R^*}$ and we get

Now taking $l\to\infty$ and on using (3.5), (3.6) and $(\zeta_3)$, we deduce

which is a contradiction. Thus, the sequence $\{r_n\}$ is an $\mathcal{R}$-preserving Cauchy sequence in $M$. Owing to the $\mathcal{R}$-completeness of $M$ ensures the existence of $r^*\in M$ such that $r_n\stackrel{d}\longrightarrow r^*$.

Firstly, assume that $S$ is $\mathcal{R}$-continuous, then we have

and hence $r^*$ is a fixed point of $S$.

Alternatively, suppose that $\mathcal{R}$ is $d$-self-closed. Then, there exists a subsequence $\{r_{n(l)}\}$ of $\{r_n\}$ with $[r_{n(l)}, r^*]\in\mathcal{R}$ for all $l\in\mathbb {N}_0$. Now, we assert that

Let on contrary that there exists $k\in\mathbb{N}$ such that

so that

and

Now, from (3.3) and (3.8), we have

which is a contradiction and therefore (3.7) remains true.

Now, without loss of generality, we may assume that $r_{n(l)}\not = r^*$ for all $l\in\mathbb {N}_0.$ Since $S$ is Suzuki type $\mathcal Z_\mathcal{R}$-contraction then it follows from (3.7), either

or

hold, for all $l\in\mathbb{N}.$

We show that $r^*$ is a fixed point of $S$. On contrary, suppose that if it is not so, then $Sr^*\not = r^*, \ i.e., \ d(Sr^*, r^*) > 0.$

If the first inequality holds then using $(\zeta_2)$, we obtain

which is a contradiction. Hence, $d(Sr^*, r^*) = 0$, $i.e.,$ $r^*$ remains fixed under $S$. Similar arguments can be utilized to prove this conclusion in the event of second inequality as well. This concludes the proof.

Next, we prove corresponding uniqueness fixed point result as follows:

Theorem 3.2. In addition to the assumptions of Theorem 3.1, if $\varUpsilon(r, s; \mathcal{R}|_{S(M)})$ is non-empty for all $r, s\in S(M),$ then the fixed point of $S$ is unique.

Proof. On the lines of the proof of Theorem 3.1, one can show that $Fix(S)$ is non-empty. Now, if $Fix(S)$ is singleton then there is nothing to prove. Otherwise, there exists two distinct elements $r^*, s^*\in Fix(S)$. As $\varUpsilon(r, s; \mathcal{R}|_{S(M)})$ is non-empty for all $r, s\in S(M)$, there exists a path of some finite length $n$ from $r^*$ to $s^*$ in $\mathcal{R}|_{S(M)}$ say $\{Sr_0, Sr_1, Sr_2, ..., Sr_n\}$ such that $r^* = Sr_0, s^* = Sr_n$ with $(Sr_i, Sr_{i+1})\in\mathcal{R}|_{S(M)}$ for each $i = 0, 1, 2, ..., n-1$. As $\mathcal{R}$ is $S$-transitive, we conclude

Now, using the fact that $\frac{1}{2}d(r^*, Sr^*) < d(r^*, s^*)$ and $S$ is Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction, we have

a contradiction. Therefore, the fixed point of $S$ is unique.

Observation 3.1. Observe that Theorem 3.2 has been proved without using any additional condition on the mapping $S$ unlike Kumam et al. ^[24] wherein authors required additional condition ($i.e.,$ property $(K)$) to obtain the fixed point result for Suzuki type $\mathcal{Z}$-contraction (see Theorem 2.2) which is easily deducible from Theorem 3.2 by setting $\mathcal{R}$ to be universal relation ($i.e., \mathcal{R} = M\times M)$.

If we choose $\mathcal{R} = \{(r, s)\in M\times M\ |\ r\preceq s\}$ in Theorem 3.1, then we deduce the following corollary which appears to be a new addition to the existing literature.

Corollary 3.1. Let $(M, d, \preceq)$ be an ordered metric space and $S:M\rightarrow M.$ Suppose that the following conditions hold:

(i) there exists $r_0\in M$ such that $r_0\preceq Sr_0$;

(ii) $S$ is increasing;

(iii) $S$ is Suzuki type $\mathcal Z_\preceq$-contraction w.r.t. some $\zeta\in\mathcal{Z}$;

(iv) $M$ is $\preceq$-complete;

(v) either $S$ is $\preceq$-continuous or $\preceq$ is $d$-self-closed.

Then $S$ has a fixed point. Moreover, for each $r_0\in M$ such that $r_0\preceq Sr_0$, the Picard sequence $S^n(r_0)$ for all $n\in\mathbb{N}$ converges to a fixed point of $S$.

Next, we deduce the following corollary which remains a sharpened version of Theorem 2.3 due to Sawangsup and Sintunavarat ^[22] wherein relatively weaker notions namely $\mathcal{R}$-completeness of $M$, $\mathcal{R}$-continuity and $S$-transitivity of binary relation are utilized.

Corollary 3.2. Let $(M, d)$ be a metric space, $\mathcal{R}$ be a binary relation on $M$ and $S:M\to M$. Suppose that the following conditions hold:

(i) $M(S; \mathcal{R})$ is non-empty;

(ii) $\mathcal{R}$ is $S$-closed and $S$-transitive;

(iii) $S$ is $\mathcal Z_\mathcal{R}$-contraction w.r.t. some $\zeta\in\mathcal{Z}$;

(iv) $M$ is $\mathcal{R}$-complete;

(v) either $S$ is $\mathcal{R}$-continuous or $\mathcal{R}$ is $d$-self-closed.

Then $S$ has a fixed point. Moreover, for each $r_0\in M(S; \mathcal{R})$, the Picard sequence $S^n(r_0)$ for all $n\in\mathbb{N}$, converges to a fixed point of $S$.

Now we have the following example to demonstrate the improvements accomplished in our newly obtained results.

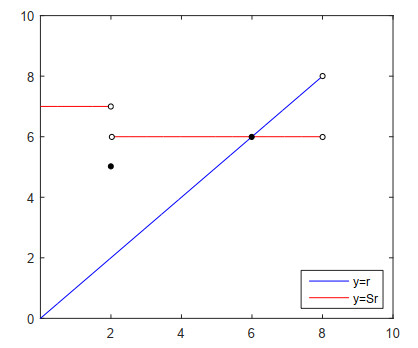
Example 3.2. Let $\big(M = [0, 8), d\big)$ be a metric space endowed with a binary relation $\mathcal{R}: = \{(0, 2), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (5, 7), (6, 5), (6, 6), (6, 7), (7, 5), (7, 6), (7, 7)\}$, where $d$ is usual metric on $M$. Define a mapping $S:M\rightarrow M$ by

then $M(S; \mathcal{R})\not = \emptyset$ as $(5, S5) = (5, 6)\in\mathcal{R}$, $S$ is $\mathcal{R}$-continuous which is not continuous in usual sense. Also, $\mathcal{R}$ is $S$-closed, $M$ is $\mathcal{R}$-complete and $\mathcal{R}$ is $S$-transitive. Observe that $\mathcal{R^*} = \{(0, 2), (5, 2)\}$ but the condition $\frac{1}{2}d(r, Sr) < d(r, s)$ is satisfied only for $(r, s) = (5, 2)\in\mathcal{R^*}$. Now, if we take $\zeta(x, y) = \alpha y-x$ for all $x, y\in[0, \infty)$ and for any $\alpha\in[\frac{1}{3}, 1)$, then we obtain

which shows that $S$ is a Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction with respect to $\zeta\in\mathcal{Z}$. Therefore, all the conditions of Theorem 3.1 are satisfied and hence in view of Theorem 3.1, $S$ has a fixed point. Furthermore, as $\mathcal{R}$ is $S$-transitive, $i.e.,$ $\mathcal{R}|_{S(M)}$ is transitive and $(r, s)\in\mathcal{R}$ for all $r, s\in S(M)$, we have $\varUpsilon(r, s; \mathcal{R}|_{S(M)})$ is non-empty for all $r, s\in S(M)$. Thus in view of Theorem 3.2, fixed point of $S$ is unique (namely $r = 6$).

We have drawn Figure 1 with the help of MATLAB wherein the intersecting point of red and blue lines represent the unique fixed point.

To establish the genuineness of our extension over corresponding results, we show that $S$ is neither a Suzuki type $\mathcal{Z}$-contraction nor a $\mathcal{Z_\mathcal{R}}$-contraction. To substantiate the claim, we take $2, 0\in M$ then $\frac{1}{2}d(2, S2) < d(2, 0)$. Assume that there is a $\zeta\in\mathcal{Z}$ such that equation (2.2) is satisfied, then

a contradiction which amounting to say that one can not find any $\zeta\in\mathcal{Z}$ such that equation (2.2) is satisfied. Hence, $S$ is not a Suzuki type $\mathcal{Z}$-contraction. Also, $(0, 2)\in\mathcal{R}$ and

then for the same reason (as in (3.9)), we can not find any $\zeta\in\mathcal{Z}$ such that equation (2.3) is satisfied which shows that $S$ is not a $\mathcal{Z_\mathcal{R}}$-contraction. Also, notice that $\mathcal{R}$ is not transitive as $\{(4, 5), (5, 2)\}\in\mathcal{R}$ but $(4, 2)\notin\mathcal{R}$ and $M$ is incomplete, therefore, Theorem 2.2 of Kumam et al.^[24] and Theorem 2.3 of Sawangsup and Sintunavarat ^[22] can not be applied to this example whereas our newly obtained Theorems 3.1 and 3.2 are applicable. This leads us to conclude that our results are genuinely different to the corresponding results due to Kumam et al.^[24] and Sawangsup and Sintunavarat ^[22] in respect of underlying space, involved binary relation and contractive condition.

4.   Applications to nonlinear matrix equations

Fixed point theory has a broad set of applications in other branches of mathematics as well as in the other sciences ^[36,37,38]. Here we describe the application of our main result in nonlinear matrix equations. In order to do so, we need the following notations and terminologies:

We write

● $M(n): =$ family of all complex matrices of order $n$;

● $H(n): =$ family of all Hermitian matrices in $M(n)$;

● $P(n): =$ family of all positive definite matrices in $M(n)$;

● $H^+(n): =$ family of all positive semi-definite matrices in $M(n)$.

If $X\in P(n)$ ($X \in H^+(n)$), we write $X\succ 0$ ($X\succeq 0$). Moreover, $X\succ Y$ ($X\succeq Y$) means $X-Y\succ 0$ ($X-Y\succeq 0$). The symbol $\|\cdot\|$ denotes the spectral norm of a matrix $R$ defined by $\|R\| = \sqrt{\lambda^+(R^*R)}$, where $\lambda^+(R^*R)$ is the largest eigenvalue of $R^*R$ and $R^*$ is the conjugate transpose of $R$. Also, $\|R\|_{tr} = \sum_{k = 1}^{n}s_k(R)$, where $s_k(R)$ $(1\leq k\leq n)$ are the singular values of $R\in M(n)$. Then, $(H(n), \|\cdot\|_{tr})$ is complete metric space ^[18,39,40].

Now, we apply our results to obtain a solution for the following nonlinear matrix equation:

where $G$ be a positive definite Hermitian matrix and $\mathcal{Q}$ is an order preserving ^* continuous mapping from $H(n)$ into $\mathcal{P}(n)$ with $\mathcal{Q}(0) = 0$, $R_k$ are arbitrary $n\times n$ matrices and $R^*_k$ their conjugates.

^*$\mathcal{Q}$ is order preserving if $R, Q \in H(n)$ with $R\preceq Q$ implies that $\mathcal{Q}(R)\preceq \mathcal{Q}(Q)$.

The following two lemmas will be needed in our forthcoming discussion.

Lemma 4.1. ^[18] If $R\succeq 0$ and $Q\succeq 0$ are $n \times n$ matrices, then $0\leq tr(RQ)\leq \|R\|tr(Q)$.

Lemma 4.2. ^[41] If $R \in H(n)$ such that $R\prec I_n$, then $\|R\| < 1$.

Theorem 4.1. Consider the matrix equation (4.1). Assume that there exist two real numbers $\tau > 0$ and $h > 0$ such that

(i) for every $X, Y \in H(n)$ with $X\preceq Y$ such that $\sum_{k = 1}^{m}R^*_k \mathcal{Q}(X)R_k\not = \sum_{k = 1}^{m}R^*_k \mathcal{Q}(Y)R_k$ and $\big|tr\big(X-G-\sum_{k = 1}^{m}R^*_k \mathcal{Q}(X)R_k\big)\big| < 2\big|tr\big(Y-X)\big|$, we have $\big|tr\big(\mathcal{Q}(Y)-\mathcal{Q}(X)\big)\big|\leq \frac{|tr(Y-X)|}{h\big(1+\tau |tr(Y-X)|\big)}$;

(ii) $\sum_{k = 1}^{m}R_kR^*_k\prec hI_n$ and there exists $G$ such that $\sum_{k = 1}^{m}R_k^*\mathcal{Q}(G)R_k\succ 0$.

Then the matrix equation (4.1) has a solution. Furthermore, the iteration $M_n = G+\sum_{k = 1}^{n}R^*_k\mathcal{Q}(X_{n-1})R_k$ converges under the trace norm $\|\cdot\|_{tr}$ to the solution of the equation (4.1), where $X_0 \in H(n)$ such that $X_0\preceq \sum_{k = 1}^{m}R_k^*\mathcal{Q}(X_0)R_k$.

Proof. We define a map $\mathcal{S}:H(n) \to H(n)$ by

and a binary relation

Then $\mathcal{S}$ is well defined, $\mathcal{R}$-continuous, $\mathcal{R}$ is $\mathcal{S}$-closed and $\mathcal{S}$-transitive. As $\sum_{k = 1}^{m}R_k^*\mathcal{Q}(G)R_k\succ 0$, for some $G\in H(n),$ we have $(G, \mathcal{S}(G))\in\mathcal{R}$ and therefore $H(n)\big(\mathcal{S}; \mathcal{R}\big)\not = \emptyset$. Now, $X$ is a solution of the matrix equation (4.1) if and only if it is a fixed point of $\mathcal{S}$. To accomplish this, it is enough to show that $\mathcal{S}$ is a Suzuki type $\mathcal{Z}_\mathcal{R}$-contraction w.r.t. a mapping $\zeta:[0, \infty)\times[0, \infty)\rightarrow\mathbb{R}$ defined by

Take any $S, T \in H(n)$ such that $(S, T)\in\mathcal{R^*}: = \{(S, T)\in\mathcal{R}:\mathcal{S}(S)\not = \mathcal{S}(T)\}$ with $\frac{1}{2}\|S-\mathcal{S}(S)\|_{tr} < \|T-S\|_{tr}$. Then,

or,

so,

This shows that $\mathcal{S}$ is a Suzuki type $\mathcal{Z}_\mathcal{R}$-contraction. Therefore, all the hypotheses of Theorem 3.1 are satisfied. Now, using Theorem 3.1, there exists Ŝ $\in H(n)$ such that $\mathcal{S}$(Ŝ) = Ŝ, $i.e.,$ the equation (4.1) has a solution.

Due to the generality of condition $(i)$ over all corresponding conditions utilized by all other authors, no other corresponding theorem in the existing literature ^{[18,22,28,39,40]}(other than Theorem 3.1) can be utilized to prove the present theorem which establishes the genuineness of our present theorem.

Theorem 4.2. In view of the assumptions of Theorem 4.1, solution of the matrix equation (4.1) is unique.

Proof. In view of Theorem 4.1, we have $Fix(\mathcal{S})$ is non-empty. Now, due to the existence a greatest lower bound and a least upper bound for every $S, T \in\mathcal{S} (H(n))$, we have $\varUpsilon(S, T; \mathcal{R}|_{\mathcal{S}(H(n))})$ is non-empty for all $S, T \in\mathcal{S} (H(n))$. Therefore, using Theorem 3.2, we deduce that $\mathcal{S}$ has a unique solution and hence the matrix equation (4.1) has a unique solution in $H(n)$. This concludes the proof.

Remark 4.1. In ^[22], authors proposed an application to matrix equations by considering the relation $\mathcal{R}: = \preceq$, which has an obvious flaw in the proof of Theorem 5.3, because, with $X = Y$, line +12 on page 15 ^[22] gives rise $0 < 0$, which is indeed a contradiction.

5.   Conclusion

In this article, we have presented an existence along with corresponding uniqueness fixed point results for newly introduced Suzuki type $\mathcal{Z_\mathcal{R}}$-contraction employing an amorphous binary relation on metric spaces without completeness which are genuine extensions over the corresponding results due to Kumam et al.^[24] and Sawangsup and Sintunavarat ^[22] in respect of underlying space, involved binary relation and contractive condition. Also, we have utilized our main results to discuss the existence and uniqueness of solutions of a family of nonlinear matrix equations. On the similar lines we can undertake the investigation of the existence of a common fixed point for two or more maps under suitable conditions.

Acknowledgments

The authors are grateful to all three reviewers and the handling editor for their critical and constructive suggestions towards the improvements of this paper. Also, the first author gratefully acknowledges the financial assistance from CSIR (Council of Scientific and Industrial Research, India) in the form of SRF (Senior Research Fellowship) during his Ph.D. studies.

Conflict of interest

The authors declare no conflicts of interest.