Stability of an adaptive immunity viral infection model with multi-stages of infected cells and two routes of infection

Abbreviations: AJCC: American joint committee on cancer; AUC: Area under the curve; BP: Biological process; CC: Cellular component; COAD: Colon adenocarcinoma; CRC: Colorectal cancer; DEirlncRNA: Different expression immune related lncRNA; DEG: Different expression gene; GO: Gene ontology; HR: Hazard ratio; IRLP: Immune-related lncrna pair; KEGG: Kyoto encyclopedia of genes and genomes; LncRNA: Long non-coding RNA; MF: Molecular function; OS: Overall survival; PPI: Protein-protein interaction; READ: Rectum adenocarcinoma; ROC: Receiver operating characteristic; TCGA: The cancer genome atlas; TME: Tumor microenvironment

1.   Introduction

According to the latest GLOBOCAN 2018 data, colorectal cancer (CRC) is the fourth most commonly diagnosed cancer worldwide (10.2%) and the fourth cause of malignancy related death in the world ^[1]. Due to a lack of notable symptoms in the early stages, most of patients usually diagnosed at an advanced stage with local progression or distant metastasis. Although there has been substantial progress in the management of CRC, the five years survival down to 50%-70.4% once metastasis occurs ^[2]. Therefore, there is an urgent need for the development of CRC early diagnosis.

At present, the clinical TNM stage classification is most commonly used to detection of cancer stage and estimate prognosis in CRC patients. But, there still exist the problem that TNM stage system inconsistent with the five years survival in clinical ^[3,4]. Therefore, more effective and sensitive biomarkers are urgently needed for screening, diagnosis, prognosis in CRC. With the development of genetic testing, gene-based biomarkers have become more and more popular and improved the standard in the diagnosis and treatment of CRC ^[5].

Long-non coding RNAs (lncRNAs) refer to a class of transcripts with over 200 nucleotides in length and have no or limited coding protein capacity ^[6]. LncRNAs are involved in diverse biological processes including cell cycle, cell differentiation and myogenesis ^[7]. Moreover, mounting evidence suggests that the tumor microenvironment (TME) serves pivotal roles in determining tumor behavior. Recently, tumor immunotherapy using the immune system to anti-tumor response and elimination of tumor cells are breakthrough treatments for several malignancies ^[8]. Therefore, the regulation of immune-related gene expression appears especially important in hosting immune responses to combat cancer cells. Although a majority of the studies thus far have focused on coding genes, researchers have begun to pay more attention to lncRNAs recently ^[9]. For example, lncRNA MIR17HG can directly bound to PD-L1 to regulate tumor-immune microenvironment and plays an oncogenic role in CRC ^[10]. And lncRNAs have also been verified as potential biomarkers for many cancers ^[11].

In this study, we analyzed the data set of lncRNA expression in the cancer genome atlas (TCGA), and a prognostic model of 10 immune-related lncRNA pair (IRLP) associated with the clinical prognosis of CRC was identified according to bioinformatic prediction. The effect of the signature model involved in the regulation of tumor immune microenvironment and checkpoints. In addition, biological function and lncRNA-protein networks of the signature model were explored as well.

2.   Materials and methods

2.1.   Research roadmap

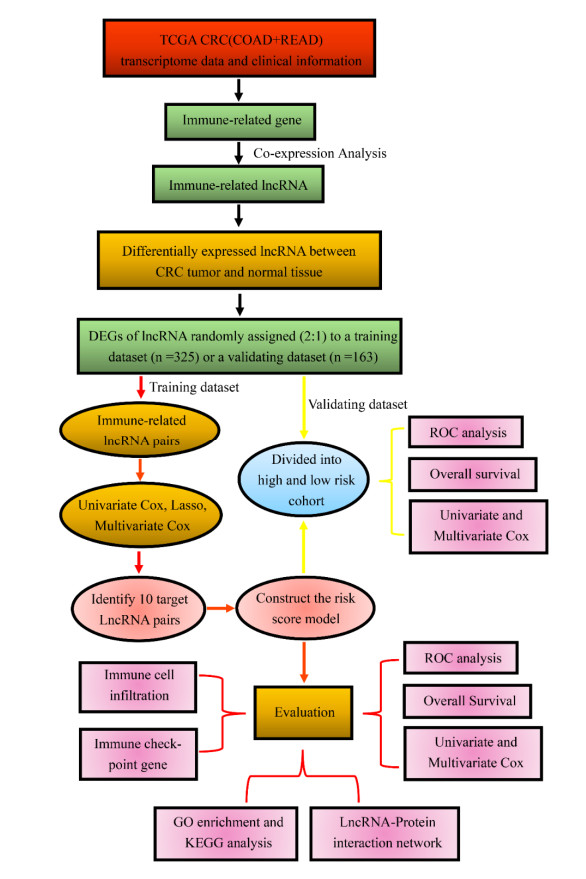
The workflow of the analyses carried out in this study is shown in Figure 1 Co-expression module and differential expression analysis were used to identify immune-related lncRNAs from TCGA-COAD and -READ data. The patients were then divided randomly into the training and validating group. Thereafter, prognostic lncRNA pairs were determined using univariate Cox, Lasso, and multivariate Cox regression analysis. From these analyses, 10 IRLPs were used to construct a signature model. The model was then evaluated using ROC analysis, overall survival (OS), univariate and multivariate Cox, immune cell infiltration, immune checkpoints, GO enrichment and KEGG analysis, as well as lncRNA-protein interaction network. Lastly, the validating group was also tested against the signature model.

2.2.   CRC patient data

The COAD-FPKM and READ-FPKM RNA-seq data and their corresponding clinical data were retrieved from TCGA database (https://portal.gdc.cancer.gov). This dataset was composed of 488 CRC tissues and 42 paired non-cancerous normal tissues. In addition, a list of immune-related genes was downloaded from the ImmPort database (https://www.immport.org/). Data containing complete OS was used to determine the correlation between immune-related lncRNAs and the corresponding prognosis of CRC.

2.3.   Construction of the IRLP signature

We identified a list of immune-related genes from the ImmPort database and used the list to calculate the correlation between immune-related genes and lncRNAs from the TCGA database. LncRNAs with a correlation coefficient > 0.7 and p < 0.001 were selected for further analysis. Differential lncRNA expression between CRC and non-cancerous normal tissues was determined using the 'limma' package, and lncRNAs with |log2FC| > 1 and P value < 0.05 were considered as statistically significant. The patients were then divided randomly into the training (n = 325) and validation group (n = 163) in the ratio of 2:1. A pairwise comparison was performed between each lncRNA expression value within each sample of TCGA to obtain a score for IRLP signature. In each lncRNA pair, when the first gene exhibited a higher expression relative to the other one, the score was set to 1, otherwise was 0. Samples with a ratio of 0 and 1 less than 20% were excluded. We further carried out univariate (p < 0.01), LASSO and multivariate Cox regression analyses to select genes that were significantly associated with survival and included them in the IRLP signature. Receiver operating characteristic (ROC) curve analysis on the training dataset was used to determine the threshold risk score to divide the patients into high-risk and low-risk groups. The formula can be expressed as follows: RiskScore = ∑Ni = 1Expi*Wi, where exp is the expression value of every DEirlncRNA pair, and W is the multivariate cox regression analysis coefficient of each DEirlncRNA pair in the signature.

2.4.   Verification of the IRLP signature

The pairwise comparison analysis was performed in validation group (n = 163), and then the 'limma' package was used to screened out the identified 10 immune-related lncRNA pairs from the validating group. Furthermore, multivariate Cox regression analysis and the riskscore formula were performed to work out the risk score of each patient in validating group. And the ROC, OS, univariate and multivariate cox regression analysis were performed as well.

2.5.   Assessment of the immune-related lncRNA risk score model

ROC curve analysis was used to evaluate the performance of the IRLPs risk model (short for risk model) in predicting 1-, 2- and 3-years OS in the training cohort and validating cohort. Univariate and multivariate Cox proportional hazards regression analysis were employed to verify if the risk model was independent of age, gender, American Joint Committee on Cancer (AJCC) stage, T stage, N stage, and M stage as a prognostic factor. Afterwards, calibration curves and a nomogram representing the clinical parameters and the risk model were established to evaluate the risk model.

2.6.   Immune cell infiltration and immune checkpoints

CIBERSORT is an algorithm that employs linear support vector regression to characterize the cell composition of tissues based on their gene expression profiles ^[12]. We used CIBERSORT (https://cibersortx.stanford.edu/) to determine the degree of infiltration of the tumor microenvironment by 22 tumor-infiltrating immune cells. The results of this analysis were used to establish the relationship between the risk model and the number of tumor-infiltrating immune cells. We further characterized the tumor microenvironment through differential gene expression analysis of immune checkpoints between the high-and low-risk groups.

2.7.   Biological function analysis and lncRNA-protein networks of the signature model

Results of co-expression analysis identified 21 immune-related genes that correlated with 10 IRLPs. Gene ontology (GO) terms and Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways enrichment analysis for the 21 immune-related genes was carried using DAVID Bioinformatics Resources (https://david.ncifcrf.gov/). Enrichment terms with count > 2 and p < 0.05 were selected for further analysis. The biological functional enrichments were visualized using the ggplot2 Package in R. Furthermore, we constructed and downloaded the protein–protein interaction (PPI) network of the 21 immune-related genes using the STRING database (https://string-db.org/) and along with the risk model were visualized using Cytoscape software (version 3.6.1). Ten hub genes in the network were chosen based on the MCC algorithm using cytoHubba app in Cytoscape.

2.8.   Statistical analysis

Statistical analysis was carried out using R software (version 3.6.3). The R packages used in this study include: 'Limma' (version 3.46.0), 'pheatmap' (1.0.12 version), 'Survival' (3.2-7 version), 'survminer' (0.4.8 version), 'glmnet' (version 4.0-2), 'survivalROC' (version 1.0.3), 'ggpubr' (0.4.0 version), 'ComplexHeatmap' (2.6.2 version) and 'ggplot2' (version 3.3.2). Pearson correlation was used to determine the linear association between two groups. P < 0.05 was considered to be significant. Statistical significance was defined as follows: *P < 0.05, **P < 0.01, ***P < 0.001.

3.   Results

3.1.   Construction of the IRLP signature

In this study, the TCGA CRC transcriptome data was used as an exploratory dataset (Figure 1). We used the immune-related gene list identified from ImmPort to select 1340 immune-related genes from the transcriptome data for further study. Co-expression analysis was used to select 302 immune-related lncRNAs with a Pearson correlation coefficient over 0.7. A total of 118 differentially expressed lncRNAs, including 102 up-regulated and 16 down-regulated lncRNAs, were identified from the normal and tumor tissues using edgeR. The heatmap and volcano plot of these differentially expressed lncRNAs are shown in Figures 2A, B.

After the data was randomly divided into two groups, a pairwise comparison analysis was performed in the training group. A total of 4073 lncRNA pairs were obtained based on these differentially expressed lncRNAs. Univariate Cox regression analysis and Lasso Cox regression were used to select 13 IRLPs with prognostic potential in the training group (Figures 3A, B). Finally, multivariate Cox proportional hazards modeling was employed to select 10 IRLPs that were used to construct the risk model (Figures 3C, D). We also calculated the risk score for each patient in the TCGA dataset based on the risk model. ROC curve analysis was performed to determine the threshold value (2.199) of the model, that could categorize the patients into a high- or low-risk groups (Figure 3E).

3.2.   Evaluation of 10-gene IRLP risk model as independent prognostic factor for CRC

The Kaplan-Meier survival curves were used to compare the OS between the high- and low-risk groups in both the training (Figure 4A) and validating cohorts (Figure 4B). The OS of the low-risk group was significantly higher than that of the high-risk group in both cohorts. As shown in Figures 4C, D, the AUC values for the training cohort (0.842, 0.869 and 0.884 for the 1-, 2- and 3-year OS, respectively) and validating cohort (0.738, 0.690 and 0.739) showed that the risk model was able to discriminate between the high- and low-risk groups. In addition, the risk curves and scatterplots illustrated that the patients with higher risk scores had a higher risk of mortality in the training (Figures 4E, G) and validating cohorts (Figures 4G, H).

Univariate and multivariate Cox analyses were used to investigate if the 10-gene IRLPs risk model was independent of age, gender, AJCC stage, T stage, N stage, and M stage as a prognostic factor. The results showed that the risk model of univariate Cox analysis was 1.023 (Hazard Ratio (HR): 1.017-1.029, p < 0.001) and the multivariate Cox was 1.028 (HR: 1.019-1.037, p < 0.001) in the training cohort (Figures 5A, C), while the risk model of univariate and multivariate Cox analysis was 1.485 (HR: 1.210-1.822, p < 0.001) and 1.815 (HR: 1.380-2.387, p < 0.001) in the validating cohort, respectively (Figure 5B, D). On the other hand, the AUC values for the training cohort (0.842) and validating cohort (0.738) showed that the model had good discriminative ability when compared with clinical features (Figures E, F). As a result, the 10-gene IRLPs risk model can serve as an independent prognosis factor in CRC.

The correlation between the risk model and various clinical parameters was then assessed. The results showed that there were positive correlations between the risk score and age, clinical stage, T stage, N stage and M stage, while there was no relation between the risk score and patient gender (Figures 6A-F). A heatmap showing various clinical parameters differentially distributed in different cohorts is depicted in Figure 6G.

3.3.   Immune cell infiltration and immune checkpoints assessment of the risk model

To further explore the ability of the risk model to predict the infiltration of immune cells in CRC, CIBERSORT was used to analyze the relationship between the risk score and 22 immune cells. Only Macrophages M0 infiltration was correlated with the risk model. High levels of Macrophages M0 were detected in the low-risk group (Figure 7A).

Immune checkpoints are molecules that modulate signaling pathways in the regulation of immune response and have an important role in the field of anti-cancer immunotherapy. According to the results shown in Figure 7, the expression levels of CD160, TNFSF15, HHLA2 and IDO2 were significantly higher in the low-risk group, while the levels of KIR3DL1 and PD-1 were higher in the high-risk group, although the latter had no significant difference (Figure 7B).

3.4.   Functional enrichment analysis and lncRNA-protein networks of the risk model

The GO annotation system includes three major branches: cellular component (CC), biological process (BP) and molecular function (MF). GO and KEGG enrichment analysis were performed to predict the function of the 21 immune-related genes that correlated with the 10 IRLPs. The first three of these enrichments were as follows (Figure 8A-C): Neuronal cell body, plasma membrane and receptor complex were enriched for CC; while for BP, they were signal transduction by protein phosphorylation, activin receptor signaling pathway and signal transduction; and for MF, they include growth factor binding, receptor signaling protein serine/threonine kinase activity and transmembrane receptor protein serine/threonine kinase activity. Further analysis of KEGG pathways included 31 pathways, containing Chronic myeloid leukemia, ErbB signaling pathway and Pathways in cancer (Figure 8D).

Using the 21 immune-related genes downloaded from the STRING database and the 10 IRLPs, we established a lncRNA-protein network, which consisted of 38 nodes and 102 edges (Figure 8E). Ten hub genes, which include three lncRNAs (AL157786.1, LINC01355, AF117829.1) and seven protein coding gene (PIK3CA, SOS1, CBLB, CBL, CREB1, ACVR2A and TGFBR1) were identified from the lncRNA-protein network using the MCC algorithm (Figure 8F).

4.   Discussion

CRC is one of the leading causes of cancer-related mortality in the world. Advances in CRC research has allowed the characterization of CRC into different molecular subtypes presenting with distinct clinical features ^[13]. On the other hand, LncRNAs have been shown to modulate cancer progression by influencing the molecular characteristics of tumors ^[14,15]. LncRNAs regulate various immune-related genes ^[16,17,18], and have recently been associated with drug resistance and immune escape in human cancers ^[19]. It is therefore important to establish an immune-related lncRNA signature for CRC that can be used to develop novel strategies for CRC prevention and treatment.

We built the signature model using a method based on the ranking and pairing comparison of relative gene expression. And we used data retrieved from TCGA to construct a 10-gene IRLPs signature for the prognosis of CRC. Using the model, we divided the patients into two groups with different immune microenvironment for evaluating clinical features, immune cell infiltration, immune check-point, GO enrichment, KEGG analysis and the interaction network between lncRNAs and immune-related protein coding genes.

We performed LASSO, univariate and multivariate Cox regression to select immune-related lncRNA pairs for establishing the IRLPs signature model. The model was composed of 10 immune-related lncRNA pairs containing 17 unique immune-related lncRNAs, which were overexpressed in cancer tissues compared to normal tissues. Each of the IRLPs was an independent prognostic factor for CRC patients. The model was able to categorize the CRC patients into low-risk and high-risk groups in the training and the validating cohorts and acted as an independent prognostic factor for CRC. Furthermore, ROC analysis revealed that the AUCs of the model (0.842 and 0.738 in training and validating cohorts, respectively) were higher than those of other clinical features. Although, there have been a series of methods for immune related lncRNA signature establishment, but the prognostic power of each study was different (Table 1) ^{[20,21,22,23]}. Firstly, the AUC value of our model was higher than that of models proposed in other studies. Secondly, we used a method based on the ranking and pairing comparison of relative gene expression, and this approach for constructing the model eliminates the need for data scaling and normalization when using different platforms ^[24,25]. Thirdly, our model contains relatively fewer lncRNAs, while maintaining a high AUC value. Therefore, considering clinical application value, the 10-gene IRLP risk signature is a reliable prognostic model with potential clinical significance.

The CIBERSORT algorithm has high specificity and sensitivity ^[12], and is able to evaluate the gene expression data of 22 different types of immune cells. A recent study showed that the infiltration of tumors by M0 macrophages was associated with favorable prognosis ^[26], a finding that is consistent with the results from our study. And macrophages are indispensable in immunotherapy of tumor. It can remove anti-PD1 antibodies from T cells to weaken their response, when the antibodies target the PD1-PDL1 axis ^[27]. Cancer immunotherapy is a novel anti-cancer approach that targets immune checkpoint receptors such as PD1/PDL1 ^[28]. Therefore, we compared the expression of immune checkpoints between the low- and high-risk groups. The analysis showed that there was higher expression of inhibitory immune checkpoints (PD1 (no statistical significance) and KIR3DL1), and low expression of stimulatory checkpoints (CD160, HHLA2, IDO2 and TNFSF15), in the high-risk patients. The upregulation of KIR3DL1 causes a reduction in CD4+ T cell count and is associated with rapid disease progression ^[29]. Reduced CD160 expression impairs the function of NK cells, causes immune escape of cancer and is associated with poor outcomes in patients with hepatocellular carcinoma ^[30]. HHLA2 can promote tumor differentiation and increase the levels of CD8+ infiltrating lymphocytes. Downregulation of HHLA2 contributes to the immunosuppressive microenvironment and progression of ovarian cancer ^[31]. IDO2 acts as a stimulatory immune checkpoint to enhance the efficacy of dendritic cell-based cancer immunotherapy ^[32]. Finally, TNFSF15 is a member of the tumor necrosis factor family, and can influence the proliferation, activation and differentiation of immune cells ^[33]. Down regulation of TNFSF15 is associated with poor prognosis in various cancers ^[34,35,36]. Thus, the risk model might be a promising reference function for cancer immunotherapy.

KEGG enrichment analysis was carried out to predict the biological pathways involved in the regulation of CRC by the 10-gene IRLP signature. The results indicated that the gene signature was enriched in pathways such as Chronic myeloid leukemia, ErbB signaling pathway, Pathways in cancer, Insulin signaling pathway and Signaling pathways regulating pluripotency of stem cells. These pathways play key roles in the progression of CRC. For example, CARF increases the expression of MAPK8 and JUN by binding directly to their promoters, which in turn activates the ErbB signaling pathway that maintains the stemness of CRC ^[37]. PIK3CA and BRAF are members of the Insulin signaling pathway, and are the most common biomarkers for the genetic testing of CRC. Mutations in PIK3CA and/or BRAF in CRC are associated with poor outcome ^[38], and PIK3CA mutation is associated with poor prognosis among patients with curatively resected CRC ^[39].

To better understand the correlation between lncRNA and immune-related genes, a lncRNA-protein network was established. From this network, 10 hub genes were identified including 7 protein coding genes: PIK3CA, SOS1, CBLB, CBL, CREB1, ACVR2A and TGFBR1. These genes have been associated with CRC ^{[39,40,41,42,43,44,45]}. For example, SOS1 is a key activator and feedback node of KRAS, which is the most frequently mutated driver of CRC ^[46]. Downregulation of SOS1 expression can lead to decreased survival of cancer cells harboring a KRAS mutation ^[47]. CBL have been reported to promote the progression of colon cancer by forming a complex with MUC1 and CIN85, and increased level of CBL in the early stage of colon cancer contributes to a poor prognosis ^[42]. ACVR2A acts a protective factor and a decrease in its expression is crucial for cancer progression and distant metastasis and may serve as a prognostic biomarker for the patients with colon cancer ^[44].

Here remain several limitations. On the one hand, our study was limited by its retrospective nature. Further prospective clinical researches are needed to validate these results. On the other hand, we only performed enrichment analysis and made assumptions regarding the function of 17 immune related lncRNAs without additional research for further understanding of the underlying mechanism.

5.   Conclusions

In conclusion, we constructed a 10-gene prognostic IRLPs signature for CRC patients based on the immune-related genes in the TCGA database. The signature was associated with immune checkpoints that play key roles in immune regulation and immunotherapy of CRC Molecular functional and lncRNA-protein network analysis were used to understand the molecular mechanisms underlying the carcinogenic effect and progression. Further prospective clinical researches and additional vitro experiments are needed to be done in the future study for making the results more convincing.

Acknowledgments

This study was supported by the Natural Guiding Plan foundation of Liaoning Province, grant number [2019-ZD-0584]; Natural Grant Program foundation of Liaoning Province, grant number [2020-ZLLH-44]; National Science Foundation of China, grant number [81902383]; Revitalizing Liaoning Talents Program, grant number [XLYC1907004]; Cultivation Program of National Science Foundation of Liaoning Cancer Hospital, grant number [2021-ZLLH-03].

Conflict of interest

All authors declare no conflicts of interest in this paper.